Десятичные приставки
| Наименование | Обозначение | Множитель |
| гига | Г | 109 |
| мега | М | 106 |
| кило | к | 103 |
| деци | д | 10–1 |
| санти | с | 10–2 |
| милли | м | 10–3 |
| микро | мк | 10–6 |
| нано | н | 10–9 |
| пико | п | 10–12 |
Физические постоянные (константы)
| число π | π = 3,14 |
| ускорение свободного падения | g = 10 м/с2 |
| гравитационная постоянная | G = 6,7·10–11 Н·м2/кг2 |
| газовая постоянная | R = 8,31 Дж/(моль·К) |
| постоянная Больцмана | k = 1,38·10–23 Дж/К |
| постоянная Авогадро | NA = 6,02·1023 1/моль |
| скорость света в вакууме | с = 3·108 м/с |
| коэффициент пропорциональности в законе Кулона | k = 1/(4πε0) = 9·109 Н·м2/Кл2 |
| модуль заряд электрона | e = 1,6·10-19 Кл |
| масса электрона | me = 9,1·10–31 кг |
| масса протона | mp = 1,67·10–27 кг |
| постоянная Планка | h = 6,62·10-34 Дж·с |
| радиус Солнца | 6,96·108 м |
| температура поверхности Солнца | T = 6000 K |
| радиус Земли | 6370 км |
Соотношение между различными единицами измерения
| температура | 0 К = –273 0С |
| атомная единица массы | 1 а.е.м. = 1,66·10–27 кг |
| 1 атомная единица массы эквивалентна | 931,5 МэВ |
| 1 электронвольт | 1 эВ = 1,6·10-19 Дж |
| 1 астрономическая единица | 1 а.е. ≈ 150 000 000 км |
| 1 световой год | 1 св. год ≈ 9,46·1015 м |
| 1 парсек | 1 пк ≈ 3,26 св. года |
Масса частиц
| электрона | 9,1·10–31кг ≈ 5,5·10–4 а.е.м. |
| протона | 1,673·10–27 кг ≈ 1,007 а.е.м. |
| нейтрона | 1,675·10–27 кг ≈ 1,008 а.е.м. |
Плотность
| воды | 1000 кг/м3 |
| древесины (сосна) | 400 кг/м3 |
| керосина | 800 кг/м3 |
| подсолнечного масла | 900 кг/м3 |
| алюминия | 2700 кг/м3 |
| железа | 7800 кг/м3 |
| ртути | 13 600 кг/м3 |
Удельная теплоёмкость
| воды | 4,2·10 3 Дж/(кг·К) |
| льда | 2,1·10 3 Дж/(кг·К) |
| железа | 460 Дж/(кг·К) |
| свинца | 130 Дж/(кг·К) |
| алюминия | 900 Дж/(кг·К) |
| меди | 380 Дж/(кг·К) |
| чугуна | 500 Дж/(кг·К) |
Удельная теплота
| парообразования воды | 2,3·10 6 Дж/кг |
| плавления свинца | 2,5·10 4 Дж/кг |
| плавления льда | 3,3·10 5 Дж/кг |
Нормальные условия:
| давление | 105 Па |
| температура | 00 C |
Молярная маcса молекул
| азота | 28·10–3 кг/моль |
| аргона | 40·10–3 кг/моль |
| водорода | 2·10–3 кг/моль |
| воздуха | 29·10–3 кг/моль |
| воды | 18·10–3 кг/моль |
| гелия | 4·10–3 кг/моль |
| кислорода | 32·10–3 кг/моль |
| лития | 6·10–3 кг/моль |
| неона | 20·10–3 кг/моль |
| углекислого газа | 44·10–3 кг/моль |
Перейти к контенту
Десятичные приставки
| Наименование | Обозначение | Множитель |
| гига | Г | 109 |
| мега | М | 106 |
| кило | к | 103 |
| деци | д | 10–1 |
| санти | с | 10–2 |
| милли | м | 10–3 |
| микро | мк | 10–6 |
| нано | н | 10–9 |
| пико | п | 10–12 |
Физические постоянные (константы)
| число π | π = 3,14 |
| ускорение свободного падения | g = 10 м/с2 |
| гравитационная постоянная | G = 6,7·10–11 Н·м2/кг2 |
| газовая постоянная | R = 8,31 Дж/(моль·К) |
| постоянная Больцмана | k = 1,38·10–23 Дж/К |
| постоянная Авогадро | NA = 6,02·1023 1/моль |
| скорость света в вакууме | с = 3·108 м/с |
| коэффициент пропорциональности в законе Кулона | k = 1/(4πε0) = 9·109 Н·м2/Кл2 |
| модуль заряд электрона | e = 1,6·10-19 Кл |
| масса электрона | me = 9,1·10–31 кг |
| масса протона | mp = 1,67·10–27 кг |
| постоянная Планка | h = 6,62·10-34 Дж·с |
| радиус Солнца | 6,96·108 м |
| температура поверхности Солнца | T = 6000 K |
| радиус Земли | 6370 км |
Соотношение между различными единицами измерения
| температура | 0 К = –273 0С |
| атомная единица массы | 1 а.е.м. = 1,66·10–27 кг |
| 1 атомная единица массы эквивалентна | 931,5 МэВ |
| 1 электронвольт | 1 эВ = 1,6·10-19 Дж |
| 1 астрономическая единица | 1 а.е. ≈ 150 000 000 км |
| 1 световой год | 1 св. год ≈ 9,46·1015 м |
| 1 парсек | 1 пк ≈ 3,26 св. года |
Масса частиц
| электрона | 9,1·10–31кг ≈ 5,5·10–4 а.е.м. |
| протона | 1,673·10–27 кг ≈ 1,007 а.е.м. |
| нейтрона | 1,675·10–27 кг ≈ 1,008 а.е.м. |
Плотность
| воды | 1000 кг/м3 |
| древесины (сосна) | 400 кг/м3 |
| керосина | 800 кг/м3 |
| подсолнечного масла | 900 кг/м3 |
| алюминия | 2700 кг/м3 |
| железа | 7800 кг/м3 |
| ртути | 13 600 кг/м3 |
Удельная теплоёмкость
| воды | 4,2·10 3 Дж/(кг·К) |
| льда | 2,1·10 3 Дж/(кг·К) |
| железа | 460 Дж/(кг·К) |
| свинца | 130 Дж/(кг·К) |
| алюминия | 900 Дж/(кг·К) |
| меди | 380 Дж/(кг·К) |
| чугуна | 500 Дж/(кг·К) |
Удельная теплота
| парообразования воды | 2,3·10 6 Дж/кг |
| плавления свинца | 2,5·10 4 Дж/кг |
| плавления льда | 3,3·10 5 Дж/кг |
Нормальные условия:
| давление | 105 Па |
| температура | 00 C |
Молярная маcса молекул
| азота | 28·10–3 кг/моль |
| аргона | 40·10–3 кг/моль |
| водорода | 2·10–3 кг/моль |
| воздуха | 29·10–3 кг/моль |
| воды | 18·10–3 кг/моль |
| гелия | 4·10–3 кг/моль |
| кислорода | 32·10–3 кг/моль |
| лития | 6·10–3 кг/моль |
| неона | 20·10–3 кг/моль |
| углекислого газа | 44·10–3 кг/моль |
Справочные данные из демоверсии, которые могут понадобиться вам при выполнении работы.
Десятичные приставки
Константы
Соотношения между различными единицами
Масса частиц
Астрономические величины
Плотность
Удельная теплоёмкость
Удельная теплота
Нормальные условия
Молярная маcса
→ sp-fizika.pdf
→ Другой справочник с формулами.
→ Основные формулы по физике.
→ 180 формул по физике на одном листе.
- Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
Справочные материалы ЕГЭ по физике 2022-2023
Десятичные приставки
Наименование — Обозначение — Множитель
- гига — Г — 109
- мега — М — 106
- кило — к — 103
- гекто — г — 102
- деци — д — 10–1
- санти — с — 10–2
- милли — м — 10–3
- микро — мк — 10–6
- нано — н — 10–9
- пико — п — 10–12
Физические постоянные (константы)
- число π: π = 3,14
- ускорение свободного падения: g = 10 м/с2
- гравитационная постоянная: G = 6,7·10–11 Н·м2/кг2
- универсальная газовая постоянная: R = 8,31 Дж/(моль·К)
- постоянная Больцмана: k = 1,38·10–23 Дж/К
- постоянная Авогадро: NA = 6·1023 1/моль
- скорость света в вакууме: с = 3·108 м/с
- коэффициент пропорциональности в законе Кулона: k = 1/(4πε0) = 9·109 Н·м2/Кл2
- модуль заряд электрона (элементарный электрический заряд): e = 1,6·10−19 Кл
- постоянная Планка: h = 6,6·10-34 Дж·с
Соотношение между различными единицами измерения
- температура: 0 К = –273 0С
- атомная единица массы: 1 а.е.м. = 1,66·10–27 кг
- 1 атомная единица массы эквивалентна: 931,5 МэВ
- 1 электронвольт: 1 эВ = 1,6·10−19 Дж
Масса частиц
- электрона — 9,1·10–31 кг ≈ 5,5·10–4 а.е.м.
- протона — 1,673·10–27 кг ≈ 1,007 а.е.м.
- нейтрона — 1,675·10–27 кг ≈ 1,008 а.е.м.
Плотность
- воды — 1000 кг/м3
- древесины (сосна) — 400 кг/м3
- керосина — 800 кг/м3
- подсолнечного масла — 900 кг/м3
- алюминия — 2700 кг/м3
- железа — 7800 кг/м3
- ртути — 13 600 кг/м3
Удельная теплоёмкость
- воды — 4,2·103 Дж/(кг·К)
- льда — 2,1·103 Дж/(кг·К)
- железа — 460 Дж/(кг·К)
- свинца — 130 Дж/(кг·К)
- алюминия — 900 Дж/(кг·К)
- меди — 380 Дж/(кг·К)
- чугуна — 500 Дж/(кг·К)
Удельная теплота
- парообразования воды — 2,3·106 Дж/кг
- плавления свинца — 2,5·104 Дж/кг
- плавления льда — 3,3·105 Дж/кг
Нормальные условия
- давление: 105 Па
- температура: 0 °С
Молярная масса молекул
- азота: 28·10–3 кг/моль
- аргона: 40·10–3 кг/моль
- водорода: 2·10–3 кг/моль
- воздуха: 29·10–3 кг/моль
- воды: 18·10–3 кг/моль
- гелия: 4·10–3 кг/моль
- кислорода: 32·10–3 кг/моль
- лития: 6·10–3 кг/моль
- неона: 20·10–3 кг/моль
- углекислого газа: 44·10–3 кг/моль
- Взрослым: Skillbox, Хекслет, Eduson, XYZ, GB, Яндекс, Otus, SkillFactory.
- 8-11 класс: Умскул, Лектариум, Годограф, Знанио.
- До 7 класса: Алгоритмика, Кодланд, Реботика.
- Английский: Инглекс, Puzzle, Novakid.
Постулаты Бора
Основу квантовой теории атома Бора составляют два постулата.
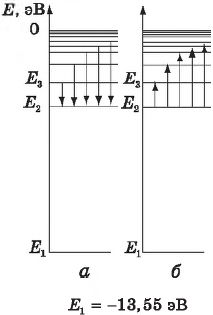
Первый постулат Бора гласит: атомная система может находиться только в особых стационарных, или квантовых, состояниях, каждому из которых соответствует определенная энергия $Е_n$; в стационарном состоянии атом не излучает энергию.
Этот постулат противоречит классической механике, согласно которой энергия движущихся электронов может быть любой. Он противоречит также и электродинамике Максвелла, так как допускает возможность ускоренного движения электронов без излучения электромагнитных волн.
Второй постулат Бора: излучение света происходит при переходе атома из стационарного состояния с большей энергией $Е_k$ в стационарное состояние с меньшей энергией $Е_n$. Энергия излученного фотона равна разности энергий стационарных состояний:
$hν_{kn}=E_k-E_n$
Отсюда можно получить частоту излучения:
$ν_{kn}={E_k-E_n}/{h}={E_k}/{h}-{E_n}/{h}$
При поглощении света атом переходит из стационарного состояния с меньшей энергией в стационарное состояние с большей энергией.
Модель атома водорода Бора
Для построения модели простейшей системы — атома водорода — Бор постулировал также правило определения стационарных значений энергии атома (уровней энергии) — так называемое правило квантования.
Правило квантования орбит Бора заключается в следующем.
Стационарным состояниям атома соответствуют разрешенные дискретные значения энергии электрона, такие, что при движении по стационарным круговым орбитам электрон должен иметь дискретные значения момента количества движения:
$m_{e}υr=n{h}/{2π}, n=1,2,3…,$
где $m_{e}$ — масса электрона, $υ$ — его скорость, $r$ — радиус орбиты, $h$ — постоянная Планка, $n$ называется главным квантовым числом (является номером орбиты в спектре атома водорода, в частности).
Используя законы механики Ньютона и правило квантования, Бор вычислил допустимые радиусы орбит и значения энергии стационарных состояний. Минимальный радиус орбиты определяет размер атома (он оказался равным $0.53·10^{-10}$м). Значения энергий стационарных состояний в электронвольтах отложены на вертикальной оси. (В атомной физике энергию выражают в электронвольтах, сокращенно — эВ. $1$ эВ — это энергия, приобретаемая электроном при прохождении разности потенциалов $1$ В. $1$ эВ$ = 1.6·10^{-19}$ Дж.)
Правило квантования орбит и постулаты Бора позволили ему самому и другим ученым объяснить наблюдавшиеся закономерности в оптическом спектре излучения атома водорода, а также в рентгеновских спектрах, и дать физическое истолкование Периодического закона элементов.
Поглощение света
Поглощение света — процесс, обратный излучению, при котором атом с нижних энергетических уровней переходит на верхние уровни. При этом он поглощает излучение тех же частот, которые излучает при переходе с верхних энергетических уровней на нижние.
Гипотеза Планка о квантах
Гипотеза Планка — предположение, что атомы испускают электромагнитную энергию (свет) не непрерывно, а отдельными порциями — квантами.
Энергия каждой порции пропорциональна частоте излучения:
$E=hν,$
где $h=6.63·10^{-34}$ $Дж·с$ — постоянная Планка, $ν$ — частота света.
Постоянная Планка (квант действия) — фундаментальная физическая константа. Введена М. Планком в 1900 г. Наиболее точное значение постоянной Планка $h = 6.626176(36) · 10^{-34}$ $Дж·с$. Чаще пользуются постоянной $h={h}/{2π}=1.0545887(57)·10^{-34}$ $Дж·с$, также называемой постоянной Планка. Формула $p↖{→}={mυ↖{→}}{√{1-{υ^2}/{c^2}}$ — это вторая из простых великих формул физики (первая — формула Эйнштейна, связывающая энергию покоя тела с его массой). После открытия Планка начала развиваться квантовая теория.
Фотоэффект
-
Темы кодификатора ЕГЭ: гипотеза М.Планка о квантах, фотоэффект, опыты А.Г.Столетова, уравнение Эйнштейна для фотоэффекта.
-
Опыты Столетова
-
Зависимость фототока от напряжения
-
Законы фотоэффекта
-
Трудности классического объяснения фотоэффекта
-
Гипотеза Планка о квантах
-
Уравнение Эйнштейна для фотоэффекта
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: гипотеза М.Планка о квантах, фотоэффект, опыты А.Г.Столетова, уравнение Эйнштейна для фотоэффекта.
Фотоэффект — это выбивание электронов из вещества падающим светом. Явление фотоэффекта было открыто Генрихом Герцем в 1887 году в ходе его знаменитых экспериментов по излучению электромагнитных волн.
Напомним, что Герц использовал специальный разрядник (вибратор Герца) — разрезанный пополам стержень с парой металлических шариков на концах разреза. На стержень подавалось высокое напряжение, и в промежутке между шариками проскакивала искра. Так вот, Герц обнаружил, что при облучении отрицательно заряженного шарика ультрафиолетовым светом проскакивание искры облегчалось.
Герц, однако, был поглощён исследованием электромагнитных волн и не принял данный факт во внимание. Год спустя фотоэффект был независимо открыт русским физиком Александром Григорьевичем Столетовым. Тщательные экспериментальные исследования, проведённые Столетовым в течение двух лет, позволили сформулировать основные законы фотоэффекта.
к оглавлению ▴
Опыты Столетова
В своих знаменитых экспериментах Столетов использовал фотоэлемент собственной конструкции (Фотоэлементом называется любое устройство, позволяющее наблюдать фотоэффект). Его схема изображена на рис. 1.
Рис. 1. Фотоэлемент Столетова
В стеклянную колбу, из которой выкачан воздух (чтобы не мешать лететь электронам), введены два электрода: цинковый катод и анод
. На катод и анод подаётся напряжение, величину
которого можно менять с помощью потенциометра и измерять вольтметром
.
Сейчас на катод подан «минус», а на анод — «плюс», но можно сделать и наоборот (и эта перемена знака — существенная часть опытов Столетова). Напряжению на электродах приписывается тот знак, который подан на анод (Поэтому поданное на электроды напряжение часто называют анодным напряжением). В данном случае, например, напряжение
положительно.
Катод освещается ультрафиолетовыми лучами УФ через специальное кварцевое окошко, сделанное в колбе (стекло поглощает ультрафиолет, а кварц пропускает). Ультрафиолетовое излучение выбивает с катода электроны , которые разгоняются напряжением
и летят на анод. Включённый в цепь миллиамперметр
регистрирует электрический ток. Этот ток называется фототоком, а выбитые электроны, его создающие, называются фотоэлектронами.
В опытах Столетова можно независимо варьировать три величины: анодное напряжение, интенсивность света и его частоту.
к оглавлению ▴
Зависимость фототока от напряжения
Меняя величину и знак анодного напряжения, можно проследить, как меняется фототок. График этой зависимости, называемый характеристикой фотоэлемента, представлен на рис. 2.
Рис. 2. Характеристика фотоэлемента
Давайте обсудим ход полученной кривой. Прежде всего заметим, что электроны вылетают из катода с различными скоростями и в разных направлениях; максимальную скорость, которую имеют фотоэлектроны в условиях опыта, обозначим .
Если напряжение отрицательно и велико по модулю, то фототок отсутствует. Это легко понять: электрическое поле, действующее на электроны со стороны катода и анода, является тормозящим (на катоде «плюс», на аноде «минус») и обладает столь большой величиной, что электроны не в состоянии долететь до анода. Начального запаса кинетической энергии не хватает — электроны теряют свою скорость на подступах к аноду и разворачиваются обратно на катод. Максимальная кинетическая энергия вылетевших электронов оказывается меньше, чем модуль работы поля при перемещении электрона с катода на анод:
Здесь кг — масса электрона,
Кл — его заряд.
Будем постепенно увеличивать напряжение, т.е. двигаться слева направо вдоль оси из далёких отрицательных значений.
Поначалу тока по-прежнему нет, но точка разворота электронов становится всё ближе к аноду. Наконец, при достижении напряжения , которое называется задерживающим напряжением, электроны разворачиваются назад в момент достижения анода (иначе говоря, электроны прибывают на анод с нулевой скоростью). Имеем:
(1)
Таким образом, величина задерживающего напряжения позволяет определить максимальную кинетическую энергию фотоэлектронов.
При небольшом превышении задерживающего напряжения появляется слабый фототок. Его формируют электроны, вылетевшие с максимальной кинетической энергией почти точно вдоль оси колбы (т.е. почти перпендикулярно катоду): теперь электронам хватает этой энергии, чтобы добраться до анода с ненулевой скоростью и замкнуть цепь. Остальные электроны, которые имеют меньшие скорости или полетели в сторону от анода, на анод не попадают.
При повышении напряжения фототок увеличивается. Анода достигает большее количество электронов, вылетающих из катода под всё большими углами к оси колбы. Обратите внимание, что фототок присутствует при нулевом напряжении!
Когда напряжение выходит в область положительных значений, фототок продолжает возрастать. Оно и понятно: электрическое поле теперь разгоняет электроны, поэтому всё большее их число получают шанс оказаться на аноде. Однако достигают анода пока ещё не все фотоэлектроны. Например, электрон, вылетевший с максимальной скоростью перпендикулярно оси колбы (т.е. вдоль катода), хоть и развернётся полем в нужном направлении, но не настолько сильно, чтобы попасть на анод.
Наконец, при достаточно больших положительных значениях напряжения ток достигает своей предельной величины , называемой током насыщения, и дальше возрастать перестаёт.
Почему? Дело в том, что напряжение, ускоряющее электроны, становится настолько велико, что анод захватывает вообще все электроны, выбитые из катода — в каком бы направлении и с какими бы скоростями они не начинали движение. Стало быть, дальнейших возможностей увеличиваться у фототока попросту нет — ресурс, так сказать, исчерпан.
к оглавлению ▴
Законы фотоэффекта
Величина тока насыщения — это, по существу, количество электронов, выбиваемых из катода за одну секунду. Будем менять интенсивность света, не трогая частоту. Опыт показывает, что ток насыщения меняется пропорционально интенсивности света.
Первый закон фотоэффекта. Число электронов, выбиваемых из катода за секунду, пропорционально интенсивности падающего на катод излучения (при его неизменной частоте).
Ничего неожиданного в этом нет: чем больше энергии несёт излучение, тем ощутимее наблюдаемый результат. Загадки начинаются дальше.
А именно, будем изучать зависимость максимальной кинетической энергии фотоэлектронов от частоты и интенсивности падающего света. Сделать это несложно: ведь в силу формулы (1) нахождение максимальной кинетической энергии выбитых электронов фактически сводится к измерению задерживающего напряжения.
Сначала меняем частоту излучения при фиксированной интенсивности. Получается такой график (рис. 3):
Рис. 3. Зависимость энергии фотоэлектронов от частоты света
Как видим, существует некоторая частота , называемая красной границей фотоэффекта, разделяющая две принципиально разные области графика. Если
, то фотоэффекта нет.
Если же , то максимальная кинетическая энергия фотоэлектронов линейно растёт с частотой.
Теперь, наоборот, фиксируем частоту и меняем интенсивность света. Если при этом , то фотоэффект не возникает, какова бы ни была интенсивность! Не менее удивительный факт обнаруживается и при
: максимальная кинетическая энергия фотоэлектронов от интенсивности света не зависит.
Все эти факты нашли отражение во втором и третьем законах фотоэффекта.
Второй закон фотоэффекта. Максимальная кинетическая энергия фотоэлектронов линейно возрастает с частотой света и не зависит от его интенсивности.
Третий закон фотоэффекта. Для каждого вещества существует красная граница фотоэффекта — наименьшая частота света , при которой фотоэффект ещё возможен. При
фотоэффект не наблюдается ни при какой интенсивности света.
к оглавлению ▴
Трудности классического объяснения фотоэффекта
Как можно было бы объяснить фотоэффект с точки зрения классической электродинамики и волновых представлений о свете?
Известно, что для вырывания электрона из вещества требуется сообщить ему некоторую энергию , называемую работой выхода электрона. В случае свободного электрона в металле это работа по преодолению поля положительных ионов кристаллической решётки, удерживающего электрон на границе металла. В случае электрона, находящегося в атоме, работа выхода есть работа по разрыву связи электрона с ядром.
В переменном электрическом поле световой волны электрон начинает совершать колебания.
И если энергия колебаний превысит работу выхода, то электрон будет вырван из вещества.
Однако в рамках таких представлений невозможно понять второй и третий законы фотоэффекта. Действительно, почему кинетическая энергия выбитых электронов не зависит от интенсивности излучения? Ведь чем больше интенсивность, тем больше напряжённость электрического поля в электромагнитной волне, тем больше сила, действующая на электрон, тем больше энергия его колебаний и с тем большей кинетической энергией электрон вылетит из катода. Логично? Логично. Но эксперимент показывает иное.
Далее, откуда берётся красная граница фотоэффекта? Чем «провинились» низкие частоты? Казалось бы, с ростом интенсивности света растёт и сила, действующая на электроны; поэтому даже при низкой частоте света электрон рано или поздно будет вырван из вещества — когда интенсивность достигнет достаточно большого значения. Однако красная граница ставит жёсткий запрет на вылет электронов при низких частотах падающего излучения.
Кроме того, неясна безынерционность фотоэффекта. Именно, при освещении катода излучением сколь угодно слабой интенсивности (с частотой выше красной границы) фотоэффект начинается мгновенно — в момент включения освещения. Между тем, казалось бы, электронам требуется некоторое время для «расшатывания» связей, удерживающих их в веществе, и это время «раскачки» должно быть тем больше, чем слабее падающий свет. Аналогия такая: чем слабее вы толкаете качели, тем дольше придётся их раскачивать до заданной амплитуды.
Выглядит опять-таки логично, но опыт — единственный критерий истины в физике! — этим доводам противоречит.
Так на рубеже XIX и XX столетий в физике возникла тупиковая ситуация: электродинамика, предсказавшая существование электромагнитных волн и великолепно работающая в диапазоне радиоволн, отказалась объяснять явление фотоэффекта.
Выход из этого тупика был найден Альбертом Эйнштейном в 1905 году. Он нашёл простое уравнение, описывающее фотоэффект. Все три закона фотоэффекта оказались следствиями уравнения Эйнштейна.
Главная заслуга Эйнштейна состояла в отказе от попыток истолковать фотоэффект с позиций классической электродинамики. Эйнштейн привлёк к делу смелую гипотезу о квантах, высказанную Максом Планком пятью годами ранее.
к оглавлению ▴
Гипотеза Планка о квантах
Классическая электродинамика отказалась работать не только в области фотоэффекта. Она также дала серьёзный сбой, когда её попытались использовать для описания излучения нагретого тела (так называемого теплового излучения).
Суть проблемы состояла в том, что простая и естественная электродинамическая модель теплового излучения приводила к бессмысленному выводу: любое нагретое тело, непрерывно излучая, должно постепенно потерять всю свою энергию и остыть до абсолютного нуля. Как мы прекрасно знаем, ничего подобного не наблюдается.
В ходе решения этой проблемы Макс Планк высказал свою знаменитую гипотезу.
Гипотеза о квантах. Электромагнитная энергия излучается и поглощается не непрерывно, а отдельными неделимыми порциями — квантами. Энергия кванта пропорциональна частоте излучения:
(2)
Cоотношение (2) называется формулой Планка, а коэффициент пропорциональности — постоянной Планка.
Принятие этой гипотезы позволило Планку построить теорию теплового излучения, прекрасно согласующуюся с экспериментом. Располагая известными из опыта спектрами теплового излучения, Планк вычислил значение своей постоянной:
Дж·с. (3)
Успешность гипотезы Планка наводила на мысль, что законы классической физики неприменимы к малым частицам вроде атомов или электронов, а также к явлениям взаимодействия света и вещества. Подтверждением данной мысли как раз и послужило явление фотоэффекта.
к оглавлению ▴
Уравнение Эйнштейна для фотоэффекта
Гипотеза Планка говорила о дискретности излучения и поглощения электромагнитных волн, то есть о прерывистом характере взаимодействия света с веществом. При этом Планк считал, что распространение света — это непрерывный процесс, происходящий в полном соответствии с законами классической электродинамики.
Эйнштейн пошёл ещё дальше: он предположил, что свет в принципе обладает прерывистой структурой: не только излучение и поглощение, но также и распространение света происходит отдельными порциями — квантами, обладающими энергией .
Планк рассматривал свою гипотезу лишь как математический трюк и не решился опровергнуть электродинамику применительно к микромиру. Физической реальностью кванты стали благодаря Эйнштейну.
Кванты электромагнитного излучения (в частности, кванты света) стали впоследствии называться фотонами. Таким образом, свет состоит из особых частиц — фотонов, движущихся в вакууме со скоростью .
Каждый фотон монохроматического света, имеющего частоту , несёт энергию
.
Фотоны могут обмениваться энергией и импульсом с частицами вещества (об импульсе фотона речь пойдёт в следующем листке); в таком случае мы говорим о столкновении фотона и частицы. В частности, происходит столкновение фотонов с электронами металла катода.
Поглощение света — это поглощение фотонов, то есть неупругое столкновение фотонов с частицами (атомами, электронами). Поглощаясь при столкновении с электроном, фотон передаёт ему свою энергию. В результате электрон получает кинетическую энергию мгновенно, а не постепенно, и именно этим объясняется безынерционность фотоэффекта.
Уравнение Эйнштейна для фотоэффекта есть не что иное, как закон сохранения энергии. На что идёт энергия фотона ? при его неупругом столкновении с электроном? Она расходуется на совершение работы выхода
по извлечению электрона из вещества и на придание электрону кинетической энергии
:
(4)
Слагаемое оказывается максимальной кинетической энергией фотоэлектронов. Почему максимальной? Этот вопрос требует небольшого пояснения.
Электроны в металле могут быть свободными и связанными. Свободные электроны «гуляют» по всему металлу, связанные электроны «сидят» внутри своих атомов. Кроме того, электрон может находиться как вблизи поверхности металла, так и в его глубине.
Ясно, что максимальная кинетическая энергия фотоэлектрона получится в том случае, когда фотон попадёт на свободный электрон в поверхностном слое металла — тогда для выбивания электрона достаточно одной лишь работы выхода.
Во всех других случаях придётся затрачивать дополнительную энергию — на вырывание связанного электрона из атома или на «протаскивание» глубинного электрона к поверхности.
Эти лишние затраты приведут к тому, что кинетическая энергия вылетевшего электрона окажется меньше.
Замечательное по простоте и физической ясности уравнение (4) содержит в себе всю теорию фотоэффекта. Давайте посмотрим, какое объяснение получают законы фотоэффекта с точки зрения уравнения Эйнштейна.
1. Число выбиваемых электронов пропорционально числу поглощённых фотонов. С увеличением интенсивности света количество фотонов, падающих на катод за секунду, возрастает.
Стало быть, пропорционально возрастает число поглощённых фотонов и, соответственно, число выбитых за секунду электронов.
2. Выразим из формулы (4) кинетическую энергию:
Действительно, кинетическая энергия выбитых электронов линейно растёт с частотой и не зависит от интенсивности света.
Зависимость кинетической энергии от частоты имеет вид уравнения прямой, проходящей через точку . Этим полностью объясняется ход графика на рис. 3.
3. Для того, чтобы начался фотоэффект, энергии фотона должно хватить как минимум на совершение работы выхода: . Наименьшая частота
, определяемая равенством
как раз и будет красной границей фотоэффекта. Как видим, красная граница фотоэффекта определяется только работой выхода, т.е. зависит лишь от вещества облучаемой поверхности катода.
Если , то фотоэффекта не будет — сколько бы фотонов за секунду не падало на катод. Следовательно, интенсивность света роли не играет; главное — хватает ли отдельному фотону энергии, чтобы выбить электрон.
Уравнение Эйнштейна (4) даёт возможность экспериментального нахождения постоянной Планка. Для этого надо предварительно определить частоту излучения и работу выхода материала катода, а также измерить кинетическую энергию фотоэлектронов.
В ходе таких опытов было получено значение , в точности совпадающее с (3). Такое совпадение результатов двух независимых экспериментов — на основе спектров теплового излучения и уравнения Эйнштейна для фотоэффекта — означало, что обнаружены совершенно новые «правила игры», по которым происходит взаимодействие света и вещества. В этой области классическая физика в лице механики Ньютона и электродинамики Максвелла уступает место квантовой физике — теории микромира, построение которой продолжается и сегодня.
Это была необходимая теория. Разберем задачи ЕГЭ по теме «Фотоэффект».
Задача 1. Поток фотонов с энергией 10 эВ выбивает из металла электроны. Какова максимальная кинетическая энергия электронов, если работа выхода электронов с поверхности данного металла равна 6 эВ?
Решение:
Eф = Авых + Ек.
Eк = Eф — Авых = 10 – 6 = 4 эВ.
Ответ: 4.
Задача 2. Когда на металлическую пластину падает электромагнитное излучение с длиной волны , максимальная кинетическая энергия фотоэлектронов равна 4,5 эВ. Если длина волны падающего излучения равна
,то максимальная кинетическая энергия фотоэлектронов равна 1 эВ. Чему равна работа выхода электронов из металла?
Решение:
Запишем уравнение фотоэффекта для двух случаев:
Домножим второе уравнение на 2 и вычтем из первого уравнения второе:
_________________________________
Ответ: 2,5.
Задача 3. Красная граница фотоэффекта исследуемого металла соответствует длине волны нм. Какова длина волны света, выбивающего из него фотоэлектроны, максимальная кинетическая энергия которых в 2 раза меньше работы выхода?
Решение:
По условию задачи,
Подставим это в уравнение фотоэффекта:
Ответ: 400.
Задача 4. Фотоны с энергией 2,1 эВ вызывают фотоэффект с поверхности цезия, для которого работа выхода равна 1,9 эВ. На сколько нужно уменьшить энергию фотона, чтобы максимальная кинетическая энергия фотоэлектронов уменьшилась в 2 раза?
Решение:
Запишем два уравнения фотоэффекта для двух случаев и учтём, что по условию задачи
Тогда получаем:
Из первого уравнения получаем, что
Тогда из второго уравнения получаем, что
Значит энергию падающих фотонов нужно уменьшить на
Ответ: 0,1.
Задача 5. Работа выхода электронов из металла равна Дж. Задерживающая разность потенциалов для фотоэлектронов, вылетевших с поверхности этого металла под действием излучения с некоторой длиной волны
, равна 3 В. Чему будет равна задерживающая разность потенциалов для фотоэлектронов в случае длины волны излучения
?
Решение:
Переведём работу выхода в электронвольты:
Теперь из уравнения фотоэффекта найдём энергию фотонов в первом случае:
Если длину волны увеличить в 2 раза, то энергия фотона уменьшится тоже в 2 раза, так как энергия фотона обратно пропорциональна длине волны. Тогда во втором случае энергия фотона будет равна:
Тогда:
Ответ: 1.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Фотоэффект» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023
Десятичные приставки
|
Наименование |
Обозначение |
Множитель |
Наименование |
Обозначение |
Множитель |
|
мега- |
М |
106 |
санти- |
с |
10-2 |
|
кило- |
к |
103 |
милли- |
м |
10—3 |
|
гекто- |
г |
102 |
микро- |
мк |
10-6 |
Основные физические константы
|
Число π |
π = 3,14 |
|
Ускорение свободного падения на Земле |
g = 10 м/с2 |
|
Гравитационная постоянная |
G = 6,7 ∙ 10-11 Н ∙ м2/кг2 |
|
Универсальная газовая постоянная |
R = 8,31 Дж/(моль ∙ К) |
|
Постоянная Больцмана |
k = 1,38 ∙ 10—23 Дж/К |
|
Постоянная Авогадро |
NА = 6 ∙ 1023 1/моль |
|
Скорость света в вакууме |
с = 3 ∙ 108 м/с |
|
Коэффициент пропорциональности в законе Кулона |
k = 9 ∙ 109 Н ∙ м2/Кл2 |
|
Модуль заряда электрона (элементарный электрический заряд) |
е = 1,6 ∙ 10—19 Кл |
|
Постоянная Планка |
h = 6,6 ∙ 10-34 Дж ∙ с |
Соотношение между различными единицами
|
Температура |
0 К = -273,15° С |
|
Атомная единица массы |
1 а.е.м. = 1,66 ∙ 10—27 кг |
|
1 атомная единица массы эквивалентна |
931,5 МэВ |
|
1 электронвольт |
1 эВ = 1,6 ∙ 10—19 Дж |
Масса частиц
|
Электрона |
9,1 ∙ 10—31 кг ≈ 5,5 ∙ 10—4 а.е.м. |
|
Протона |
1,637 ∙ 10—27 кг ≈ 1,007 а.е.м. |
|
Нейтрона |
1,675 ∙ 10—27 кг ≈ 1,008 а.е.м. |
Нормальные условия
|
Давление |
105 Па |
Температура |
0° С |
Плотность тел
|
Бензин |
710 кг/м3 |
Древесина |
600 кг/м3 |
|
Спирт |
800 кг/ м3 |
Алюминий |
2700 кг/м3 |
|
Масло машинное |
900 кг/м3 |
Сталь |
7800 кг/м3 |
|
Вода морская |
1030 кг/м3 |
Медь |
8900 кг/м3 |
|
Вода |
1000 кг/м3 |
Мрамор |
2700 кг/м3 |
|
Ртуть |
13600 кг/м3 |
Лёд |
900 кг/м3 |
Удельное электрическое сопротивление (Ом ∙ мм2/м)
|
Алюминий 0,028 |
Ртуть 0,96 |
|
Железо 0,10 |
Медь 0,017 |
|
Удельная теплоёмкость |
|
|
Воды 4200 Дж/(кг ∙ град) Льда 2100 Дж/(кг ∙ град) Железа 444 Дж/(кг ∙ град) Меди 380 Дж/(кг ∙ град) |
Олова 230 Дж/(кг ∙ град) Свинца 130 Дж/(кг ∙ град) Стали 460 Дж/(кг ∙ град) |
|
Удельная теплота плавления |
|
|
Свинца 2,5 ∙ 104 Дж/кг Льда 3,3 ∙ 105 Дж/кг |
Стали 82 ∙ 103 Дж/ кг |
|
Удельная теплота парообразования |
|
|
Воды 2,3 ∙ 106 Дж/кг |