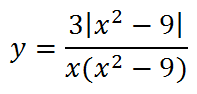Слайд 2
График функции у = |х| а) Если х≥0, то |х| = х функция у = х, т.е. график совпадает с биссектрисой первого координатного угла. б) Если х<0, то |х| = -х и у = — х. При отрицательных значениях аргумента х график данной функции – прямая у = -х, т.е. биссектриса второго координатного угла. Построить Далее
Слайд 3
y =
Слайд 4
у = | х ² — х -6 | Проверь 1.Построим график функции у =х ² — х -6 2 . Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ.
Слайд 6
Для построения графика функции у = |f(х) | достаточно : 1.Построить график функции у = f(х) ; 2. На участках, где график расположен в нижней полуплоскости, т.е., где f(х) <0, симметрично отражаем относительно оси абсцисс.
Слайд 7
График функции у = f |(х)|
Слайд 8
Для построения графика функции у = f |(х)| достаточно: 1. построить график функции у = f(х) для х>0; 2. Для х<0, симметрично отразить построенную часть относительно оси ОУ.
Слайд 10
Построить график функции у=0,25 х ² — | х | -3. 1) Поскольку | х | = х при х≥0, требуемый график совпадает с параболой у=0,25 х² — х — 3. Если х < 0, то поскольку х ² = | х |² , | х | =-х и требуемый график совпадает с параболой у=0,25 х² + х — 3. 2) Если рассмотрим график у=0,25 х² — х — 3 при х≥0 и отобразить его относительно оси ОУ мы получим тот же самый график. Построить
Слайд 11
Построить график функции у = | 2|х | — 3| 1. Построить у = 2|х | — 3 , для 2 |х| — 3 > 0 , |х | >1,5 т.е. х < -1,5 и х > 1,5 а) у = 2х — 3 , для х > 0 б) д ля х<0, симметрично отра жаем построенную часть относительно оси ОУ. 2. Построить у = -2 |х| + 3 , для 2|х | — 3 < 0. т.е. -1,5 < х < 1,5 а) у = -2х + 3 , для х > 0 б) д ля х<0, симметрично отражаем построенную часть относительно оси ОУ.
Слайд 12
1. у = | 2|х | — 3| 1) Построить у = 2х-3, для х>0. 2) Построить прямую, симметричную построенной относительно оси ОУ. 3) Участки графика, расположенные в нижней полуплоскости, отображаем симметрично относительно оси ОХ. Сравнивая оба графика, видим что они одинаковые.
Слайд 13
у = | х ² – 5|х| | 1. Построим у = х ² – 5 |х|, для х ² – 5 |х| > 0 т.е. х > 5 и х < -5 а) у = х ² – 5 х , для х > 0 б) д ля х<0, симметрично отражаем построенную часть относительно оси ОУ. 2. Построим у = — х ² + 5 |х| , для х ² – 5 |х| < 0. т.е. -5≤ х≤5 а) у = — х ² + 5 х , для х > 0 б) д ля х<0, симметрично отражаем построенную часть относительно оси ОУ.
Слайд 14
2. у = | х ² – 5|х| | а ) Построим график функции у = х ² – 5 х для х>0. б) Построим часть графика, симметричную построенной относительно оси ОУ в) Часть графика, расположенные в нижней полуплоскости, преобразовываем на верхнюю полуплоскость симметрично оси ОХ. Сравнивая оба графика, видим что они одинаковые.
Слайд 15
о х 1 2 3 4 5 6 7 -7 -6 -5 -4 -3 -2 -1 у 9 8 7 6 5 4 3 2 1 -1 -2 -3 -4 -5 -6 Найдите все положительные значения к , при которых прямая у=кх пересекает в одной точке ломанную, заданную условиями: Х >3 Х < — 3 -3 < x < 3 Построить у=1, -3 < x < 3 2. у=-2х-5, x < — 3 3. у=-2х-5, x < 3
Слайд 16
-1 -2 -3 -4 -5 -6 1 2 3 4 5 6 7 1. у = I х I 2. у = I х +1 I Ответ: (- 1 ; 4 ) , (-4;-1), (4;1). Построить о -7 -6 -5 -4 -3 -2 -1 9 8 7 6 5 4 3 2 1 у х 2. у = I х +1 I – 4 Решить систему уравнений
Цель урока:
- повторить построение графиков функций
содержащих знак модуля; - познакомиться с новым методом построения
графика линейно-кусочной функции; - закрепить новый метод при решении задач.
Оборудование:
- мультимедиа проектор,
- плакаты.
Ход урока
Актуализация знаний
На экране слайд 1 из презентации.
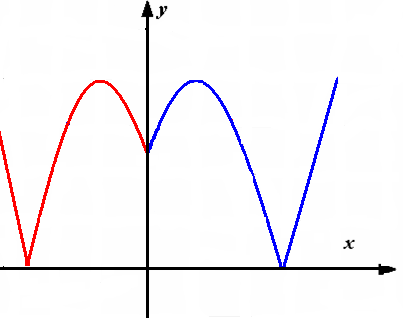
Что является графиком функции y=|x| ? (слайд 2).
(совокупность биссектрис 1 и 2 координатных
углов)
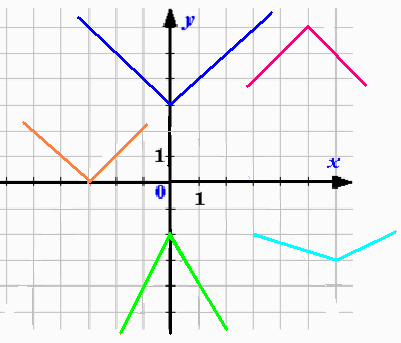
Найдите соответствие между функциями и
графиками, объясните ваш выбор (слайд 3).
Рисунок 1
y=| x+3|
y=| x| +3
y=-2| x| -2
y=6-| x-5|
y=1/3| x-6| -3
Расскажите алгоритм построения графиков
функций вида y=|f(x)| на примере функции y=|x2-2x-3|
(слайд 4)
Ученик: чтобы построить график данной функции
нужно
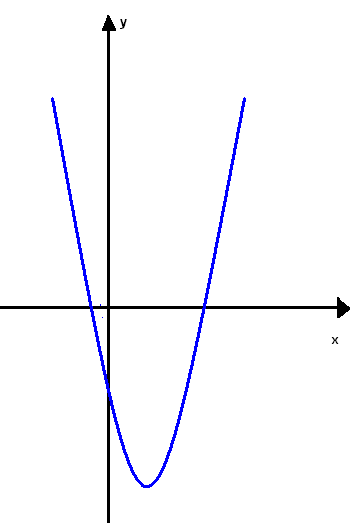
— построить параболу y=x2-2x-3
— часть графика над ОХ сохранить, а часть
графика расположенную ниже ОХ отобразить
симметрично относительно оси ОХ (слайд 5)
Рисунок 2
Рисунок 3
Расскажите алгоритм построения графиков
функций вида y=f(|x|) на примере функции y=x2-2|x|-3
(слайд 6).
Ученик: Чтобы построить график данной функции
нужно:
— построить параболу.
— часть графика при х 0
сохраняется и отображается симметрии
относительно оси ОУ (слайд 7)
Рисунок 4
Расскажите алгоритм построения графиков
функций вида y=|f(|x|)| на примере функции y=|x2-2|x|-3|
(слайд 8).
Ученик: Чтобы построить график данной функции
нужно:
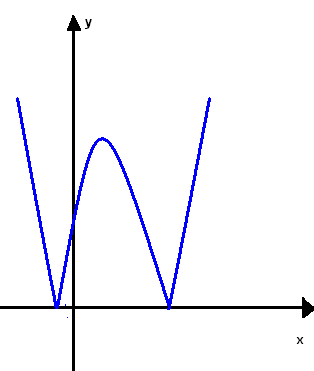
— нужно построить параболу у=x2-2x-3
— строим у= x2-2|x|-3, часть графика сохраняем
и симметрично отображаем относительно ОУ
— часть над ОХ сохраняем, а нижнюю часть
симметрично отображаем относительно ОХ (слайд 9)
Рисунок 5
Следующее задание выполняем письменно в
тетрадях.
1. Построить график линейно-кусочной
функции у=|х+2|+|х-1|-|х-3|
Ученик на доске с комментарием:
— находим нули подмодульных выражений х1=-2,
х2=1, х3=3
— разбиваем ось на промежутки
— для каждого промежутка запишем функцию
при х < -2, у=-х-4
при -2
х<1, у=х
при 1
х<3, у = 3х-2
при х
3, у = х+4
— строим график линейно-кусочной функции.
Мы с вами построили график функции используя
определение модуля (слайд 10).
Рисунок 6
Предлагаю вашему вниманию “метод вершин”,
который позволяет строить график
линейно-кусочной функции (слайд 11). Алгоритм
построения дети записывают в тетрадь.
Метод вершин
Алгоритм:
- Найдем нули каждого подмодульного выражения
- Составим таблицу, в которой кроме нулей запишем
по одному значению аргумента слева и справа - Нанесем точки на координатную плоскость и
соединим последовательно
2. Разберем этот метод на той же функции
у=|х+2|+|х-1|-|х-3|
Учитель на доске, дети в тетрадях.
Метод вершин:
— найдем нули каждого подмодульного выражения;
— составим таблицу, в которой кроме нулей
запишем по одному значению аргумента слева и
справа
х -3 -2 1 3 4
у -1 -2 1 7 8
— нанесем точки на координатную плоскость и
соединим последовательно.
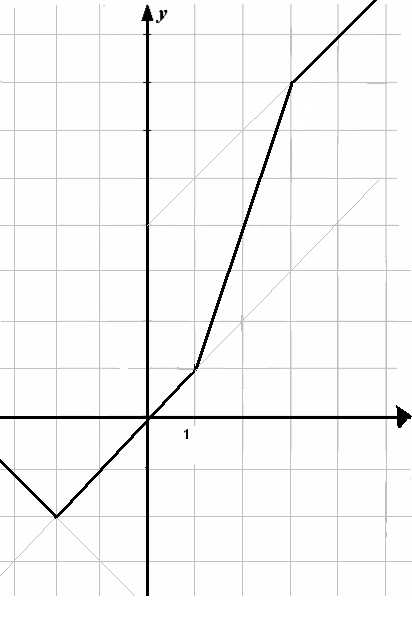
Графиком линейно-кусочной функции является
ломанная с бесконечными крайними звеньями (слайд
12) .
Рисунок 7
Каким же методом график получается быстрее и
легче?
3. Чтобы закрепить данный метод предлагаю
выполнить следующее задание:
При каких значения х функция у=|х-2|-|х+1|
принимает наибольшее значение.
Следуем алгоритму; ученик на доске.
у=|х-2|-|х+1|
х1=2, х2=-1
у(-2)=4-1=3
у(-1)=3
у(2)=-3
у(3)=1-4=3, соединяем последовательно точки.
унаиб = 3
4. Дополнительное задание
При каких значениях а уравнение ||4+x|-|x-2||=a имеет
два корня.
5. Домашняя работа
а) При каких значениях Х функция у =|2x+3|+3|x-1|-|x+2|
принимает наименьшее значение.
б) Построить график функции y=||x-1|-2|-3| .
Автор: Ольга Александровна
●
07.02.2018
●
Пора изучить задание 23! Графики функции да ещё и с модулем. Ммм, вкуснятина. Видео довольно объёмное, но и тема не простая. Смотрите, вспоминайте, практикуйтесь. Дадим жару в ОГЭ!
Забрать свой бесплатный урок с любым из репетиторов можно здесь
© devblog.tutoronline.ru,
при полном или частичном копировании материала ссылка на первоисточник обязательна.
Поделиться статьей с помощью:
Остались вопросы?
Задайте свой вопрос и получите ответ от профессионального преподавателя.
Наши курсы
23. Исследование функций и их графиков
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Функции с модулем x, y
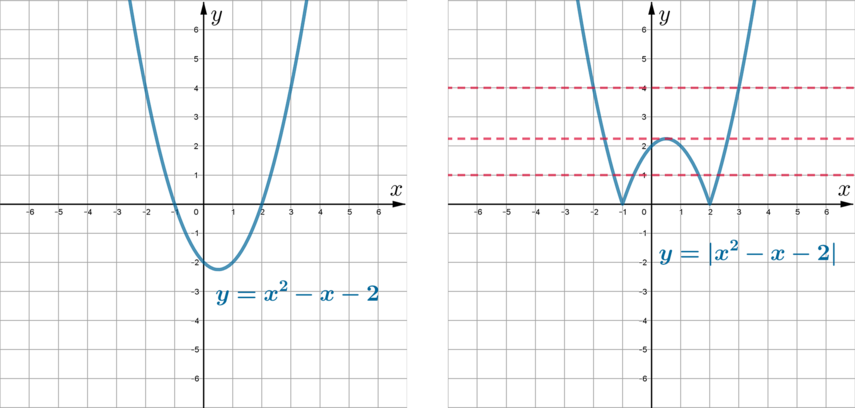
Постройте график функции [y=|x^2-x-2|, .]
Какое наибольшее число общих точек может иметь график данной функции с прямой, параллельной оси абсцисс?
Данная функция имеет вид (|f(x)|). Для того, чтобы построить график такой функции, нужно построить график функции (f(x)) и затем ту часть графика, что находится ниже оси (Ox), симметрично оси абсцисс отобразить наверх.
Построим график (y=x^2-x-2). Это парабола, ветви которой направлены вверх, вершина находится в точке (x_0=frac12), (y_0=-2,frac14). Точки пересечения с осью (Ox) ищутся из уравнения (x^2-x-2=0). Следовательно, парабола проходит через точки ((-1;0)) и ((2;0)).
(Чтобы найти координаты вершины параболы (y=ax^2+bx+c), нужно воспользоваться формулами (x_0=-frac b{2a}), (y_0=y(x_0)).)
Из рисунка видно, что график (y=|x^2-x-2|) может иметь с прямой (y=k) две, три или четыре общие точки, или же не иметь общих точек. Следовательно, ответ 4.
Ответ: 4
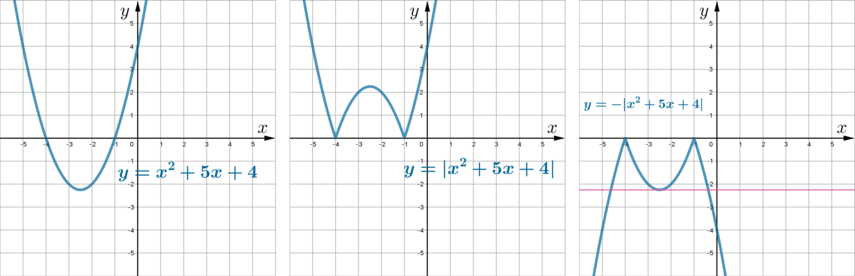
Постройте график функции [y=-|x^2+5x+4|, .]
Определите, при каких значениях (k) график данной функции имеет ровно 3 общие точки с прямой (y=k).
Данная функция имеет вид (-|f(x)|). Для того, чтобы построить график такой функции, нужно построить график функции (f(x)), затем ту часть графика, что находится ниже оси (Ox), симметрично отобразить наверх (тогда мы получим график (|f(x)|)) и затем весь график симметрично оси абсцисс отобразить относительно (Ox) (тогда мы получим (-|f(x)|)).
Построим график (y=x^2+5x+4). Это парабола, ветви которой направлены вверх, вершина находится в точке (x_0=-frac52), (y_0=-2,frac14). Точки пересечения с осью (Ox) ищутся из уравнения (x^2+5x+4=0). Следовательно, парабола проходит через точки ((-1;0)) и ((-4;0)).
(Чтобы найти координаты вершины параболы (y=ax^2+bx+c), нужно воспользоваться формулами (x_0=-frac b{2a}), (y_0=y(x_0)).)
Из рисунка видно, что график (y=-|x^2+5x+4|) может иметь с прямой (y=k) две, три или четыре общие точки, или же не иметь общих точек, причем три точки будет тогда, когда (y=k) проходит через вершину параболы, то есть через точку (left(-frac52; -2frac14right)). Следовательно, (k=-2frac14=-2,25).
Ответ: -2,25
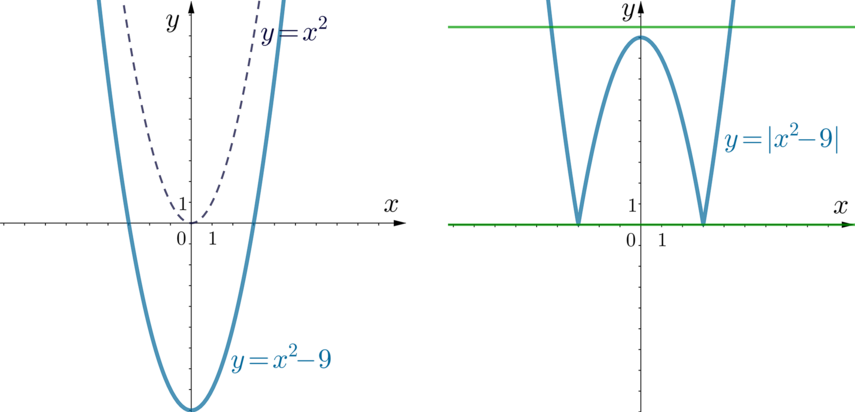
Постройте график функции [y=|x^2-9|, .]
Определите, при каких значениях (k) график данной функции имеет ровно 2 общие точки с прямой (y=k).
Данная функция имеет вид (|f(x)|). Для того, чтобы построить график такой функции, нужно построить график функции (f(x)), затем ту часть графика, что находится ниже оси (Ox), симметрично оси абсцисс отобразить наверх (тогда мы получим график (|f(x)|)).
Построим график (y=x^2-9). Это парабола, ветви которой направлены вверх. Чтобы построить график данной параболы, можно построить график (y=x^2) и опустить его на 9 единиц вниз по оси (Oy).
Из рисунка видно, что график (y=|x^2-9|) будет иметь две общие точки с прямой (y=k), если она будет находиться либо выше прямой (y=9) (прямой, проходящей через вершину параболы), либо совпадать с осью абсцисс. Следовательно, либо (k>9), либо (k=0).
Ответ: k = 0, k > 9
Постройте график функции [y=dfrac{3|x|-1}{|x|-3x^2}, .]
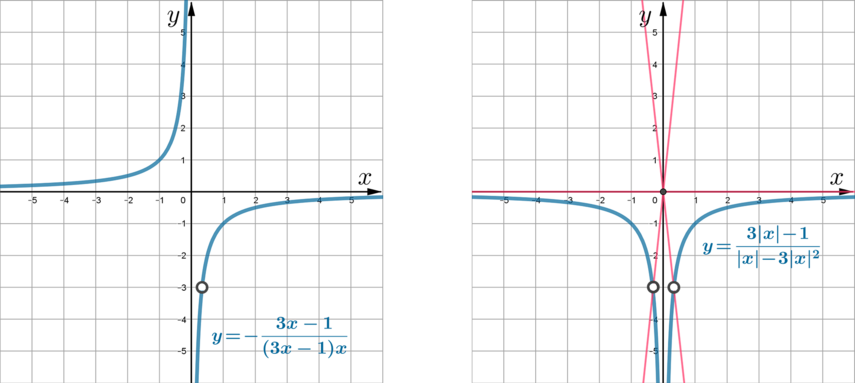
Определите, при каких значениях (k) прямая (y=kx) не имеет с графиком общих точек.
Заметим, что (x^2=|x|^2). Следовательно, функцию можно переписать как [y=dfrac{3|x|-1}{|x|-3|x|^2}] Таким образом, данная функция имеет вид (y=y(|x|)). Чтобы изобразить график такой функции, нужно изобразить график функции (y(x)), затем стереть ту часть графика, что находится левее оси (Oy), а часть графика, находящуюся правее (Oy), симметрично оси абсцисс отобразить влево.
Значит, рассмотрим [y=dfrac{3x-1}{x-3x^2}=-dfrac{3x-1}{(3x-1)x}] График данной функции – это график функции (y=-frac1x) с выколотой точкой (x=frac13) (так как (3x-1ne0)).
Графиком (y=-frac1x) является стандартная гипербола, находящаяся во 2 и 4 четвертях.
Прямая (y=kx), проходящая через начало координат, не имеет с искомым графиком (который изображен на правом рисунке) общих точек, если
1) проходит через одну из точек (left(frac13; -3right)) или (left(-frac13; -3right));
2) совпадает с осью абсцисс.
Если (y=kx) проходит через (left(frac13; -3right)), то (-3=kcdot
frac13), откуда (k=-9).
Аналогично находим остальные (k=9) и (k=0).
Ответ: -9;0;9

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Построение функций, содержащих модуль.
1.Построение графика функции Y = |f(х)|.
1.Построить график функции у = f(х).
2.Часть графика, лежащую не ниже оси ОХ, оставить без изменения.
Часть графика, лежащую ниже оси ОХ, симметрично отобразить относительно оси ОХ.
2.Построение графика функции Y = f ( |X| ).
1. Построить график функции у = f(х).
2.Удалить часть графика функции у = f(х), находящуюся слева от оси ОY.
Часть графика, лежащую на оси ОY и справа от неё симметрично отобразить относительно оси ОY.
3.Построение графика уравнения |Y |= f(X).
1. Построить график функции у = f(х).
2.Часть графика, лежащую не ниже оси ОХ, оставить без изменения.
3.Удалить часть графика функции у = f(х). , лежащую ниже оси ОХ.
4.Оставшуюся часть графика симметрично отразить
относительно оси ОХ.
4.Построение графика уравнения |Y | = | f(X) |
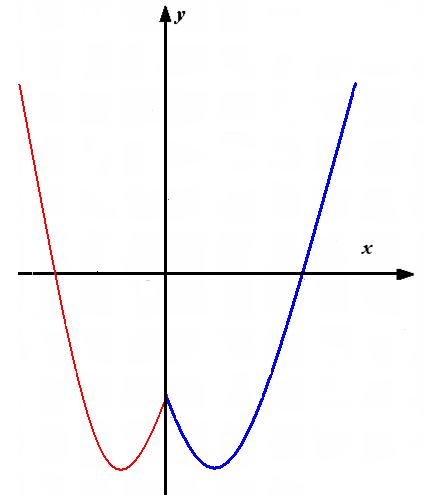
1.Построить график функциии y = f(х).
2.Построить график функции y = — f(х).
3.Объединение графиков – искомый график.
| y | = x;
2) | y | = x — 3;
3) | y | = — x + 2;
4) | y | = 2x + 3;
5) | y | = — x + 1;
6) | y – 2 | = x;
7) | y + 1 | = x + 3;

9.
Задания из ГИА.(С3)
Задача 1. Построить график функции и определить, при каких значениях
график функции
имеет с графиком 1 общую точку. Построить все такие прямые.
Задача 2. Построить график функции и определить, при каких значениях
график функции
имеет с графиком три или более общие точки.
Задача 3. Построить график функции и определить, при каких значениях
график функции
имеет с ним три и более общие точки.
Задача 4. Построить график функции 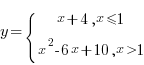
график функции
имеет с ним 2 общие точки.
Задача 5. Построить график функции и определить, при каких значениях
график функции
не имеет с графиком общих точек.
Задача 6. Построить график функции и определить, при каких значениях
он не имеет общих точек с графиком функции
.
Задача 7. Построить график функции и определить, при каких значениях
график функции
имеет с графиком 1 общую точку.
Задача 8. Построить график функции и определить, при каких значениях
график функции
имеет с ним 2 общие точки. Задача 9. Построить график функции и определить, при каких значениях
график функции
не имеет с ним общих точек. Задача 10. Построить график функции
и определить, при каких значениях
график функции
имеет с ним одну общую точку. Задача 11. При каких
вершины парабол
и
расположены по одну сторону от оси х?