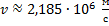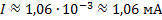Всего: 46 1–20 | 21–40 | 41–46
Добавить в вариант
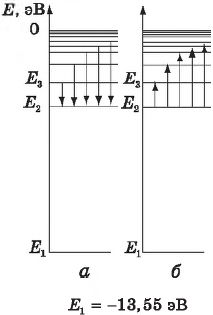
На рисунке изображена упрощённая диаграмма нижних энергетических уровней атома водорода (Е0 = 13,6 эВ). Стрелками отмечены некоторые возможные переходы атома между этими уровнями.
Установите соответствие между показанными на рисунке процессами поглощения фотона наибольшей частоты и излучения фотона наименьшей длины волны и энергией соответствующего фотона. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ПРОЦЕСС
А) поглощение фотона наименьшей длины волны
Б) излучение фотона наибольшей частоты
Установите соответствие между названиями постулатов и их формулировками. К каждой позиции первого столбца подберите нужную позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ИХ ФОРМУЛИРОВКИ
1) переходя из одного состояния в другое, атом излучает (поглощает) половину раз-ности энергий в начальном и конечном состояниях
2) переходя из одного состояния в другое, атом излучает (поглощает) квант энергии, равный разности энергий в начальном и конечном состояниях
3) атом может находиться только в одном из двух возможных состояний
4) атом может находиться только в одном из состояний с определенным значением энергии
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
В атоме водорода уровни энергии описываются формулой Наибольшая длина волны излучаемого фотона при переходе на второй уровень энергии равна 650 нм. Чему будет равна наибольшая длина волны излучаемого фотона при переходе на уровень энергии 4.
Источник: ЕГЭ по физике 01.04.2019. Досрочная волна. (Часть С)
На рисунке изображена упрощённая диаграмма нижних энергетических уровней атома. Нумерованными стрелками отмечены некоторые возможные переходы атома между этими уровнями. Какие из этих переходов связаны с поглощением кванта света наибольшей длины волны и излучением кванта света с наименьшей энергией? Установите соответствие между процессами поглощения и испускания света и стрелками, обозначающими энергетические переходы атома. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ПРОЦЕССЫ
А) поглощение кванта света наибольшей длины волны
Б) излучение кванта света с наименьшей энергией
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Источник: Демонстрационная версия ЕГЭ—2021 по физике
В атоме водорода уровни энергии описываются формулой Наибольшая длина волны излучаемого фотона при переходе на второй уровень энергии равна 655 нм. Найдите E0.
Источник: ЕГЭ по физике 01.04.2019. Досрочная волна. Вариант 1
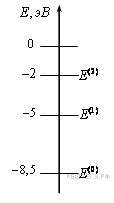
На рисунке изображена схема низших энергетических уровней атома. В начальный момент времени атом находится в состоянии с энергией
Согласно постулатам Бора с какой энергией данный атом может излучать фотоны? (Ответ дать в 10−19 Дж.)
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Дальний Восток. Вариант 1.
В первом эксперименте атомы водорода облучают потоком фотонов такой частоты, что электроны в атомах переходят с энергетического уровня с номером n > 1 на энергетический уровень с номером n + 1. При постановке второго эксперимента частоту фотонов подбирают такой, что электроны в атомах переходят с энергетического уровня с номером n − 1 на энергетический уровень с номером n. Определите, как изменяются во втором эксперименте по сравнению с первым длина волны падающего на атом фотона и приращение энергии атома в результате поглощения фотона.
Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Длина волны падающего
на атом фотона |
Приращение энергии атома в результате поглощения фотона |
В первом эксперименте атомы водорода облучают потоком фотонов такой частоты, что электроны в атомах переходят с энергетического уровня с номером n > 1 на энергетический уровень с номером n + 1. При постановке второго эксперимента частоту фотонов подбирают такой, что электроны в атомах переходят с энергетического уровня с номером n + 2 на энергетический уровень с номером n + 1. Определите, как изменяются во втором эксперименте по сравнению с первым длина волны падающего на атом фотона и приращение энергии атома в результате поглощения фотона.
Для каждой величины определите соответствующий характер изменения:
1) увеличивается
2) уменьшается
3) не изменяется
Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.
| Длина волны падающего
на атом фотона |
Приращение энергии атома в результате поглощения фотона |
На рисунке изображена упрощённая диаграмма нижних энергетических уровней атома. Нумерованными стрелками отмечены некоторые возможные переходы атома между этими уровнями. Какие из этих четырёх переходов связаны с излучением света с наибольшей длиной волны и поглощением света с наименьшей энергией?
Установите соответствие между процессами поглощения и излучения света и энергетическими переходами атома, указанными стрелками.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ПРОЦЕССЫ
А) излучение света с наибольшей длиной волны
Б) поглощение света с наименьшей энергией
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Источник: Демонстрационная версия ЕГЭ—2023 по физике
Источник: Демонстрационная версия ЕГЭ—2014 по физике.
На рисунке изображена упрощённая диаграмма энергетических уровней атома. Нумерованными стрелками отмечены некоторые возможные переходы атома между этими уровнями. Какие из этих переходов связаны с поглощением света наименьшей длины волны и излучением кванта света с наибольшей энергией?
Установите соответствие между процессами поглощения и испускания света и стрелками, указывающими энергетические переходы атома.
К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ПРОЦЕСС
А) поглощение света наименьшей длины волны
Б) излучение кванта света с наибольшей энергией
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Атом водорода переходит из возбужденного состояния в основное. При этом испускается фотон, который уносит энергию. Установите соответствие между уносимой фотоном энергией и номером энергетического уровня, с которого осуществляется переход электрона. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ЭНЕРГИЯ, УНОСИМАЯ ФОТОНОМ
НОМЕР N УРОВНЯ, С КОТОРОГО
ОСУЩЕСТВЛЯЕТСЯ ПЕРЕХОД ЭЛЕКТРОНА
1) n = 2
2) n = 3
3) n = 4
4) n = 5
Атом водорода переходит из возбужденного состояния в основное. При этом испускается фотон, который уносит энергию. Установите соответствие между уносимой фотоном энергией и номером энергетического уровня, с которого осуществляется переход электрона. К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ЭНЕРГИЯ, УНОСИМАЯ ФОТОНОМ
НОМЕР N УРОВНЯ, С КОТОРОГО
ОСУЩЕСТВЛЯЕТСЯ ПЕРЕХОД ЭЛЕКТРОНА
1) n = 2
2) n = 3
3) n = 4
4) n = 5
Задания Д32 C3 № 3059
На рисунке изображены несколько энергетических уровней атома и указаны длины волн фотонов, излучаемых и поглощаемых при переходах с одного уровня на другой.
Экспериментально установлено, что минимальная длина волны для фотонов, излучаемых при переходах между этими уровнями, равна Какова величина
если
?
На рисунке изображена упрощённая диаграмма энергетических уровней атома. Нумерованными стрелками отмечены некоторые возможные переходы атома между этими уровнями. Установите соответствие между процессами поглощения света наибольшей длины волны и испускания света наибольшей длины волны и стрелками, указывающими энергетические переходы атома. К каждой позиции первого столбца подберите соответствующую позицию второго и запишите в таблицу выбранные цифры под соответствующими буквами.
ПРОЦЕСС
А) поглощение света наибольшей длины волны
Б) излучение света наибольшей длины волны
Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:
Источник: Демонстрационная версия ЕГЭ—2013 по физике.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 1.
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 3.
Задания Д32 C3 № 4898
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 5., ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 6.
Всего: 46 1–20 | 21–40 | 41–46
В сегодняшней статье нашей традиционной рубрики «Физика» займемся решением задач. Тема: постулаты Бора.
Ищите полезную информацию для учебы? Подпишитесь на наш телеграм-канал! А если хотите заказ со скидкой, загляните на второй канал для клиентов – там много всяческих бонусов.
Нужна помощь?
Доверь свою работу кандидату наук!
Задачи на тему постулаты Бора с решениями
Постулаты Бора – сложная тема. Но решение задач по ней довольно простое, достаточно знать и уметь применять лишь несколько формул. Кстати, для удобства мы собрали полезные формулы в одном месте. А если вообще не знаете, как подступиться к задачам по физике, прочтите общую памятку по решению.
Задача на постулаты Бора №1
Условие
Вычислить энергию ε фотона, испускаемого при переходе электрона в атоме водорода с третьего энергетического уровня на первый.
Решение
Энергия фотона, испускаемого атомом водорода при переходе с одного энергетического уровня на другой, равна:
ε=Ei1n21-1n22Ei=13,6 эВ
Здесь Ei — энергия ионизации атома водорода.
Рассчитаем:
ε=13,6112-132=12,09 эВ
Ответ: 12,09 эВ.
Задача на постулаты Бора №2
Условие
Найдите максимальную длину волны, излучаемой в серии Бальмера.
Решение
Запишем формулу Бальмера-Ридберга:
1λ=R122-1n2
Максимальная длина волны соответствует минимальному значению разности:
122-1n2
То есть:
122-132=536
Отсюда найдем:
λmax=36R·5R=1,0973732 м-1λmax=361,0973732·5=656 нм
Ответ: 656 нм.
Задача на постулаты Бора №3
Условие
При переходе электрона в атоме из стационарного состояния с энергией – 4,8 эВ излучается фотон, энергия которого равна 3,1 эВ. Определите энергию конечного состояния электрона.
Решение
Атом испускает фотон, а значит, электрон переходит в стационарное состояние с меньшей энергией, которая будет равна разности энергии первоначального состояния и энергии испущенного фотона:
Е=-4,8-3,1=-7,9 эВ
Ответ: -7,9 эВ.
Задача на постулаты Бора №4
Условие
Определить изменение энергии ∆E электрона в атоме водорода при излучении атомом фотона с частотой ϑ=6,28·1014 Гц. Ответ дать в электрон-вольтах.
Решение
Изменение энергии электрона равно энергии испущенного фотона:
∆E=εф
Энергия фотона равна:
εф=hϑ
Рассчитаем:
εф=6,62·10-34·6,28·1014=4,16·10-19 Дж=4,16·10-191,6·10-19=2,6 эВ
Ответ: 2,6 эВ.
Задача на постулаты Бора №5
Условие
На сколько изменилась кинетическая энергия электрона в атоме водорода при излучении атомом фотона с длиной волны λ=486 нм?
Решение
Согласно второму постулату Бора:
∆E=Ek-En=hϑhϑ=hcλ∆E=6,62·10-34·3·108486·10-9=4,086·10-19Дж=2,554 эВ
Ответ: 2,554 эВ.
Вопросы на тему постулаты Бора
Вопрос 1. Сформулируйте постулаты Бора.
Ответ. Квантовые постулаты Бора – это два основных допущения, введённые Н.Бором для объяснения устойчивости атома и спектральных закономерностей (в рамках модели атома Резерфорда).
- Первый постулат: атом может находиться только в особых стационарных или квантовых состояниях, каждому из которых соответствует своя энергия; в стационарном состоянии атом не излучает. Стационарным состояниям атома соответствуют стационарные орбиты, по которым движутся электроны. Следовательно, электрон может находиться на нескольких вполне определенных орбитах. Каждой орбите электрона соответствует вполне определенная энергия.
- Второй постулат: при переходе из одного стационарного состояния в другое испускается или поглощается квант электромагнитного излучения.
Вопрос 2. В каком случае энергия поглощается атомом, а в каком испускается?
Ответ. При переходе электрона с ближней орбиты на более удаленную орбиту, атомная система поглощает квант энергии. При переходе с более удаленной орбиты электрона на ближнюю орбиту по отношению к ядру атомная система излучает квант энергии.
Вопрос 3. Какие противоречия есть в теории Бора?
Ответ. Теория Бора была крупным шагом в развитии атомной физики и явилась важным этапом в создании квантовой механики. Однако эта теория обладает внутренними противоречиями. С одной стороны она применяет законы классической физики, а с другой – основывается на квантовых постулатах. Теория Бора рассматривает спектры атома водорода и водородоподобных систем и позволяет вычислить частоты спектральных линий, однако не может объяснить их интенсивности и ответить на вопрос: почему совершаются те или иные переходы? Серьезным недостатком теории Бора также является невозможность описания с ее помощью спектра атома гелия – одного из простейших атомов, непосредственно следующего за атомом водорода.
Вопрос 4. Чему равна энергия фотона, испускаемого атомом при переходе в другое энергетическое состояние?
Ответ. Энергия фотона равна разности энергий атома в двух состояниях.
Вопрос 5. Может ли атом излучать и поглощать фотоны с любой частотой?
Ответ. Нет! Согласно постулатам Бора, атом может поглощать и излучать фотоны только с некоторыми определенными значениями частоты.
Посмотри примеры работ и убедись, что мы поможем на совесть!
Нужна помощь в решении задач? Профессиональный сервис для учащихся готов ее предоставить!
Постулаты Бора
Основу квантовой теории атома Бора составляют два постулата.
Первый постулат Бора гласит: атомная система может находиться только в особых стационарных, или квантовых, состояниях, каждому из которых соответствует определенная энергия $Е_n$; в стационарном состоянии атом не излучает энергию.
Этот постулат противоречит классической механике, согласно которой энергия движущихся электронов может быть любой. Он противоречит также и электродинамике Максвелла, так как допускает возможность ускоренного движения электронов без излучения электромагнитных волн.
Второй постулат Бора: излучение света происходит при переходе атома из стационарного состояния с большей энергией $Е_k$ в стационарное состояние с меньшей энергией $Е_n$. Энергия излученного фотона равна разности энергий стационарных состояний:
$hν_{kn}=E_k-E_n$
Отсюда можно получить частоту излучения:
$ν_{kn}={E_k-E_n}/{h}={E_k}/{h}-{E_n}/{h}$
При поглощении света атом переходит из стационарного состояния с меньшей энергией в стационарное состояние с большей энергией.
Модель атома водорода Бора
Для построения модели простейшей системы — атома водорода — Бор постулировал также правило определения стационарных значений энергии атома (уровней энергии) — так называемое правило квантования.
Правило квантования орбит Бора заключается в следующем.
Стационарным состояниям атома соответствуют разрешенные дискретные значения энергии электрона, такие, что при движении по стационарным круговым орбитам электрон должен иметь дискретные значения момента количества движения:
$m_{e}υr=n{h}/{2π}, n=1,2,3…,$
где $m_{e}$ — масса электрона, $υ$ — его скорость, $r$ — радиус орбиты, $h$ — постоянная Планка, $n$ называется главным квантовым числом (является номером орбиты в спектре атома водорода, в частности).
Используя законы механики Ньютона и правило квантования, Бор вычислил допустимые радиусы орбит и значения энергии стационарных состояний. Минимальный радиус орбиты определяет размер атома (он оказался равным $0.53·10^{-10}$м). Значения энергий стационарных состояний в электронвольтах отложены на вертикальной оси. (В атомной физике энергию выражают в электронвольтах, сокращенно — эВ. $1$ эВ — это энергия, приобретаемая электроном при прохождении разности потенциалов $1$ В. $1$ эВ$ = 1.6·10^{-19}$ Дж.)
Правило квантования орбит и постулаты Бора позволили ему самому и другим ученым объяснить наблюдавшиеся закономерности в оптическом спектре излучения атома водорода, а также в рентгеновских спектрах, и дать физическое истолкование Периодического закона элементов.
Поглощение света
Поглощение света — процесс, обратный излучению, при котором атом с нижних энергетических уровней переходит на верхние уровни. При этом он поглощает излучение тех же частот, которые излучает при переходе с верхних энергетических уровней на нижние.
Гипотеза Планка о квантах
Гипотеза Планка — предположение, что атомы испускают электромагнитную энергию (свет) не непрерывно, а отдельными порциями — квантами.
Энергия каждой порции пропорциональна частоте излучения:
$E=hν,$
где $h=6.63·10^{-34}$ $Дж·с$ — постоянная Планка, $ν$ — частота света.
Постоянная Планка (квант действия) — фундаментальная физическая константа. Введена М. Планком в 1900 г. Наиболее точное значение постоянной Планка $h = 6.626176(36) · 10^{-34}$ $Дж·с$. Чаще пользуются постоянной $h={h}/{2π}=1.0545887(57)·10^{-34}$ $Дж·с$, также называемой постоянной Планка. Формула $p↖{→}={mυ↖{→}}{√{1-{υ^2}/{c^2}}$ — это вторая из простых великих формул физики (первая — формула Эйнштейна, связывающая энергию покоя тела с его массой). После открытия Планка начала развиваться квантовая теория.
Атом Бора.
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев.
Темы кодификатора ЕГЭ: постулаты Бора.
Планетарная модель атома, успешно истолковав результаты опытов по рассеянию -частиц, в свою очередь столкнулась с очень серьёзными трудностями.
Как мы знаем, любой заряд, движущийся с ускорением, излучает электромагнитные волны. Это — неоспоримый факт классической электродинамики Максвелла, подтверждаемый многочисленными наблюдениями.
Нам также хорошо известно, что электромагнитные волны несут энергию. Стало быть, ускоренно движущийся заряд, излучая, теряет энергию, которая этим излучением уносится.
А теперь давайте возьмём произвольный электрон в планетарной модели. Он двигается вокруг ядра по замкнутой орбите, так что направление его скорости постоянно меняется. Следовательно, электрон всё время имеет некоторое ускорение (например, при равномерном движении по окружности это будет центростремительное ускорение), и поэтому должен непрерывно излучать электромагнитные волны. Расходуя свою энергию на излучение, электрон будет постепенно приближаться к ядру; в конце концов, исчерпав запас своей энергии полностью, электрон упадёт на ядро.
Если исходить из того, что механика Ньютона и электродинамика Максвелла работают внутри атома, и провести соответствующие вычисления, то получается весьма озадачивающий результат: расход энергии электрона на излучение (с последующим падением электрона на ядро) потребует совсем малого времени — порядка секунды. За это время атом должен полностью «коллапсировать» и прекратить своё существование.
Таким образом, классическая физика предрекает неустойчивость атомов, устроенных согласно планетарной модели. Этот вывод находится в глубоком противоречии с опытом: ведь на самом деле ничего такого не наблюдается. Предметы нашего мира вполне устойчивы и не коллапсируют на глазах! Атом может сколь угодно долго пребывать в невозбуждённом состоянии, не излучая при этом электромагнитные волны.
Постулаты Бора.
Оставалось признать, что внутри атомов перестают действовать известные законы классической физики. Микромир подчиняется совсем другим законам.
Первый прорыв в познании законов микромира принадлежит великому датскому физику Нильсу Бору. Он предложил три постулата, резко расходящиеся с механикой и электродинамикой, но тем не менее позволяющих правильно описать простейший из атомов — атом водорода.
Классическая физика хорошо описывает непрерывные процессы — движение материальной точки, изменение состояния идеального газа, распространение электромагнитных волн… Энергия объекта, подчиняющегося механике или электродинамике, в принципе может принимать любые значения. Однако линейчатые спектры указывают на дискретность процессов, происходящих внутри атомов. Эта дискретность должна фигурировать в законах новой теории.
Первый постулат Бора. Всякий атом (и вообще, всякая атомная система) может находиться не во всех состояниях с любым, наперёд заданным значением энергии. Возможен лишь дискретный набор избранных состояний, называемых стационарными, в которых энергия атома принимает значения Находясь в стационарном состоянии, атом не излучает электромагнитные волны.
Как видим, первый постулат Бора вопиющим образом противоречит классической физике: налагается запрет на любые значения энергии, кроме избранного прерывистого набора, и признаётся, что электроны, вроде бы движущиеся ускоренно, на самом деле не излучают.
Выглядит фантастически, не правда ли? Однако в том же 1913 году, когда Бор предложил свои постулаты, существование стационарных состояний было подтверждено экспериментально — в специально поставленном опыте немецких физиков Франка и Герца. Таким образом, стационарные состояния — это не выдумка, а объективная реальность.
Значения разрешённого набора называются уровнями энергии атома. Что происходит при переходе с одного уровня энергии на другой?
Второй постулат Бора. Если атом переходит из стационарного состояния с большей энергией в стационарное состояние с меньшей энергией
, то разность этих энергий может высвободиться в виде излучения. В таком случае излучается фотон с энергией
. (1)
Эта же формула работает и при поглощении света: в результате столкновения с фотоном атом переходит из состояния в состояние с большей энергией
, а фотон при этом исчезает.
Для примера на рис. 1 показано излучение фотона при переходе атома с энергетического уровня на уровень
. Переход заключается в том, что электрон «соскакивает» с одной орбиты на другую, расположенную ближе к ядру.
Рис. 1. Излучение фотона атомом
Формула (1) даёт качественное представление о том, почему атомные спектры испускания и поглощения являются линейчатыми.
В самом деле, атом может излучать волны лишь тех частот, которые соответствуют разностям значений энергии разрешённого дискретного набора ; соответственно, набор этих частот также получается дискретным. Вот почему спектр излучения атомов состоит из отдельно расположенных резких ярких линий.
Вместе с тем, атом может поглотить не любой фотон, а только тот, энергия которого в точности равна разности
каких-то двух разрешённых значений энергии
и
. Переходя в состояние с более высокой энергией
, атомы поглощают ровно те самые фотоны, которые способны излучить при обратном переходе в исходное состояние
. Попросту говоря, атомы забирают из непрерывного спектра те линии, которые сами же и излучают; вот почему тёмные линии спектра поглощения холодного атомарного газа находятся как раз в тех местах, где расположены яркие линии спектра испускания этого же газа в нагретом состоянии.
Качественного объяснения характера атомных спектров, однако, недостаточно. Хотелось бы иметь теорию, позволяющую вычислить частоты наблюдаемых спектров. Бору удалось это сделать в самом простом случае — для атома водорода.
Атом водорода.
Атом водорода состоит из ядра с зарядом , которое называется протоном, и одного электрона с зарядом
(через
обозначена абсолютная величина заряда электрона). При построении своей теории атома водорода Бор сделал три дополнительных предположения.
1. Прежде всего, мы ограничиваемся рассмотрением только круговых орбит электрона. Таким образом, электрон движется вокруг протона по окружности радиуса с постоянной по модулю скоростью
(рис. 2).
Рис. 2. Модель атома водорода
2. Величина , равная произведению импульса электрона
на радиус орбиты
, называется моментом импульса электрона. В каких единицах измеряется момент импульса?
Смотрим:
=кг*м/с*м=(кг*м/
)*м*с=Н*м*с=Дж*с.
Это в точности размерность постоянной Планка! Именно здесь Бор увидел появление дискретности, необходимой для квантового описания атома водорода.
Правило квантования (третий постулат Бора). Момент импульса электрона может принимать лишь дискретный набор значений, кратных «перечёркнутой» постоянной Планка:
, (2)
3. Выше мы говорили, что классическая физика перестаёт работать внутри атома. Так оно в действительности и есть, но вопреки этому мы предполагаем, что электрон притягивается к протону с силой, вычисляемой по закону Кулона, а движение электрона подчиняется второму закону Ньютона:
. (3)
Эти три предположения позволяют довольно просто получить формулы для уровней энергии атома водорода. Переписываем соотношение (3) в виде:
. (4)
Из правила квантования (2) выражаем :
,
и подставляем это в (4):
.
Отсюда получаем формулу для допустимых радиусов орбит электрона:
. (5)
Теперь перейдём к нахождению энергии электрона. Потенциальная энергия кулоновского взаимодействия электрона с ядром равна:
(Она отрицательна, так как отсчитывается от бесконечно удалённой точки, в которой достигает максимального значения.)
Полная энергия электрона равна сумме его кинетической и потенциальной энергий:
.
Вместо подставим правую часть выражения (4):
. (6)
Полная энергия, как видим, отрицательна. Если на радиус орбиты никаких ограничений не накладывается, как это имеет место в классической физике, то энергия может принимать любые по модулю значения. Но согласно (5) существует лишь дискретный набор возможных значений радиуса; подставляя их в (6), получаем соответствующий набор допустимых значений энергии атома водорода:
. (7)
Основное состояние атома водорода — это состояние с наименьшей энергией . В основном состоянии атом может находиться неограниченно долго. Вычисление даёт:
Дж
эВ:
Мы видим, что если атом находится в основном состоянии, то для выбивания электрона нужно сообщить атому энергию, равную как минимум 13,6 эВ. Эта величина носит название энергии ионизации атома водорода.
По формуле (5) легко вычислить радиус орбиты основного состояния:
см.
То есть, диаметр атома оказывается равным как раз см — величине, известной из опыта. Таким образом, теория Бора впервые смогла объяснить размер атома!
Кроме того, в рамках теории Бора удаётся получить формулы для вычисления частот (или длин волн) спектра атома водорода. Так, согласно второму постулату Бора и формуле (7) имеем:
. (8)
На практике чаще имеют дело с длинами волн. Учитывая, что , формулу (8) можно переписать так:
. (9)
Константа м
называется постоянной Ридберга. Теория Бора даёт значение этой постоянной, очень хорошо согласующееся с экспериментом.
Длины волн спектра атома водорода образуют серии, характеризующиеся фиксированным значением в формуле (9). Все длины волн данной серии излучаются при переходах на уровень
с вышележащих энергетических уровней
.
Переходы в основное состояние:
образуют серию Лаймана. Длины волн этой серии описываются формулой (9) при :
.
Линии серии Лаймана лежат в ультрафиолетовом диапазоне.
Переходы на второй уровень:
образуют серию Бальмера. Длины волн этой серии подчиняются формуле (9) при :
.
Первые четыре линии серии Бальмера лежат в видимом диапазоне (рис. 3), остальные — в ультрафиолетовом.
Рис. 3. Видимый спектр атома водорода (серия Бальмера)
Переходы на третий уровень:
образуют серию Пашена. Длины волн этой серии описываются формулой (9) при :
.
Все линии серии Пашена лежат в инфракрасном диапазоне.
Имеются ещё три «именованных» серии: это серия Брэккета (переходы на уровень), серия Пфунда (переходы на уровень
) и серия Хэмпфри (переходы на уровень
). Все линии этих серий лежат в далёкой инфракрасной области.
Достоинства и недостатки теории Бора.
О достоинствах модели атома водорода, предложенной Бором, мы так или иначе уже сказали. Резюмируем их.
— Теория Бора продемонстрировала, что для описания атомных объектов принципиально недостаточно представлений классической физики. В микромире работают другие, совершенно новые законы.
Для микромира характерно квантование — дискретность изменения величин, описывающих состояние объекта. В качестве меры квантования, как показала теория Бора, может выступать постоянная Планка , которая является универсальной константой и играет фундаментальную роль во всей физике микромира (а не только в явлениях излучения и поглощения света).
— Теория Бора впервые и совершенно точно указала на факт наличия стационарных энергетических состояний атома, образующих дискретный набор. Этот факт оказался общим свойством объектов микромира.
— В рамках модели Бора удалось получить формулы для вычисления частот спектра атома водорода и объяснить размер атома. Классическая физика была не в состоянии решить эти проблемы.
Однако теория Бора, разумеется, не могла претендовать на роль общей теории, описывающей микромир. Модель Бора обладала рядом существенных недостатков.
— Теория Бора непоследовательна. С одной стороны, она отвергает описание атома на основе классической физики, так как постулирует наличие стационарных состояний и правила квантования, непонятных с точки зрения механики и электродинамики. С другой стороны, классические законы — второй закон Ньютона и закон Кулона — используются для записи уравнения движения электрона по круговой орбите.
— Теория Бора не смогла дать адекватное описание самого простого после водорода атома гелия. Подавно не могло быть и речи о распространении теории Бора на более сложные атомы.
— Даже в самом атоме водорода теория Бора смогла описать не всё. Например, дав выражения для частот спектральных линий, модель Бора не объясняла различие в их интенсивностях. Кроме того, неясен оставался механизм образования молекулы водорода из двух атомов.
Несмотря на свои недостатки, теория Бора стала важнейшим этапом развития физики микромира. Полуклассическая-полуквантовая модель Бора послужила промежуточным звеном между классической физикой и последовательной квантовой механикой , построенной десятилетием позже — в 1920-х годах.
Разберем задачи ЕГЭ на темы: «Строение атома», «Модель Резерфорда-Бора», «Энергетические уровни», «Излучение фотона».
Задача 1.
На рисунке изображена схема низших энергетических уровней атома. В начальный момент времени атом находится в состоянии с энергией Е(2). Согласно постулатам Бора, с какой энергией данный атом может излучать фотоны? (Ответ дать в 10−19 Дж.)
Решение:
Согласно постулатам Бора, атом, находящийся в стационарных состояниях, не излучает энергии. Излучение энергии возможно при переходе атома с уровня с большим значением энергии на уровень с меньшим значением энергии. Поглощение энергии, наоборот, возможно при переходе атома с меньшим уровнем энергии на больший.
С учетом представленной диаграммы, излучение атома возможно при переходе с уровня Е(2) на уровень Е(1), так как Е(2)> Е(1). Поэтому, энергия излучаемых фотонов (hv) может быть определена, как разность энергий
Подставив численные значения, рассчитаем энергию излучаемых фотонов.
(Дж).
Ответ: 3.
Задача 2.
Электрон в атоме водорода находится в основном (самом низком, с номером n = 1) энергетическом состоянии. Атом поглощает фотон с импульсом 6,8 · 10–27 кг·м/с. Найдите номер энергетического уровня, на который в результате этого перейдёт электрон.
Дано:
n1=1;
p = 6,8·10–27 кг·м/с.
Найти:
n-?
Решение:
Уровни энергии в атоме водорода определяются формулой:
(эВ), где n=1, 2, 3… и т. д. (1)
Следовательно, атом на уровне n1=1 обладает энергией, которую можно рассчитать по формуле (1).
(эВ).
Найдем связь между импульсом фотона и его энергией:
(2)
Таким образом, энергия фотона может быть определена по формуле (2).
(Дж).
С учетом, что 1 эВ, получим
(эВ).
Атом, получив энергию от фотона, переходит в стационарное состояние с большим уровнем энергии.
(эВ).
Из формулы (1) необходимо вывести номер энергетического уровня.
Ответ: 4.
Задача 3.
На рисунке изображена упрощенная диаграмма нижних энергетических уровней атома. Нумерованными стрелками отмечены некоторые возможные переходы атома между этими уровнями. Какой из этих четырех переходов связан с поглощением света наибольшей энергии, а какой — с излучением света с наибольшей длиной волны?
Установите соответствие между процессами поглощения и испускания света и стрелками, указывающими энергетические переходы атома.
К каждой позиции первого столбца подберите соответствующую позицию из второго столбца и запишите в таблицу выбранные цифры под соответствующими буквами.
ПРОЦЕССЫ
А) поглощение света наибольшей энергии;
Б) излучение света с наибольшей длиной волны.
ЭНЕРГЕТИЧЕСКИЕ ПЕРЕХОДЫ
1) 1
2) 2
3) 3
4) 4
Ответ:
Решение:
По указанной диаграмме необходимо определить переходы, соответствующие поглощению и излучению света.
Переходы, указанные стрелками 1 и 2, соответствуют излучению энергии, так как атом переходит с большего уровня энергии на меньший.
Здесь надо учесть, что
и
Так как , то, согласно формуле Планка
, меньшая длина волны соответствует большему значению энергии излучения. Поэтому при переходе
будет излучаться большее количество энергии. Вторая стрелка будет соответствовать излучению света с наименьшей длиной волны.
Стрелки 3 и 4 соответствуют поглощению энергии, так как в этих случаях атом переходит на уровни, соответствующие большему значению энергии. Рассуждения, аналогичные первому случаю, приводят к следующему выводу:
и
Так как , то четвертая стрелка будет соответствовать поглощению света наибольшей энергии.
Ответ:
Задача 4.
Значения энергии электрона в атоме водорода задаются формулой: (эВ), где n=1, 2, 3… и т. д.
При переходах с верхних уровней энергии на нижние атом излучает фотон. Переходы с верхних уровней на уровень c n = 1 образуют серию Лаймана, на уровень c n = 2 – серию Бальмера и т. д. Найдите отношение γ максимальной длины волны фотона в серии Бальмера к максимальной длине волны фотона в серии Лаймана.
Решение:
Согласно формуле Планка , максимальная длина волны соответствует излучению света с наименьшим значением энергии. Поэтому для серии Лаймана это переход с уровня 2 на уровень 1 (см. рис. 1). Рассчитаем значение энергии, которая излучается в этом случае.
(эВ).
(эВ).
Длина волны, соответствующая этому переходу, может быть определена из формулы:
(1)
Аналогично для серии Бальмера, излучение с наибольшей длиной волны (наименьшей энергии излучения), соответствует переходу с уровня 3 на уровень 2 (см. рис. 2).
(эВ).
(эВ).
Длина волны, соответствующая этому переходу, может быть определена из формулы:
(2)
Тогда, для нахождения соотношения для длин волн
Разделим уравнение (2) на уравнение (1):
В расчетах значения энергий можно оставить в эВ, так как перевод в систему «СИ» ответа не изменит.
С учетом системы «СИ»:
(1 эВ Дж).
Ответ: 5,4.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Атом Бора.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать необходимые и поступить в ВУЗ или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.03.2023
1. Фотон с длиной волны, соответствующей красной границе фотоэффекта, выбивает электрон из металлической пластинки (катода), помещенной в сосуд, из которого откачан воздух. Электрон разгоняется однородным электрическим полем напряженностью Е. Пролетев путь 5*10-4м, он приобретает скорость 3*106. Какова напряженность электрического поля? Релятивистские эффекты не учитывать.
Ответ: 50000 в/м
2 Предположим, что схема нижних энергетических уровней атомов некоего элемента имеет вид, показанный на рисунке, и атомы находятся в состоянии с энергией Е1. Электрон, столкнувшись с одним из таких покоящихся атомов, в результате столкновения получил некоторую дополнительную энергию. Импульс электрона после столкновения с атомом оказался равным 1,2*10-24. Определите кинетическую энергию электрона до столкновения. Возможностью испускания света атомом при столкновении с электроном пренебречь. Эффектом отдачи пренебречь.
Ответ:2,3*10-19дж
3. Уровни энергии электрона в атоме водорода задаются формулой Е=-13,6/n2 эВ, . При переходе атома из состояния Е1 в состояние Е2 атом испускает фотон. Попав на поверхность фотокатода, фотон выбивает фотоэлектрон. Длина волны света, соответствующая красной границе фотоэффекта для материала поверхности фотокатода, 300нм. Чему равна максимально возможная кинетическая энергия фотоэлектрона? Чему равен максимально возможный модуль импульса фотоэлектрона?
Ответ:Е=6,1эВ; Р=13*10-25
4 Электрон, имеющий импульс 2*10-24, сталкивается с покоящимся протоном, образуя атом водорода в состоянии с энергией Еп (п=2). В процессе образования атома излучается фотон. Найдите частоту этого фотона, пренебрегая кинетической энергией атома. Уровни энергии электрона в атоме водорода задаются формулой , Е=-13,6/n2 эВ
Ответ:4,1*1015
5 Покоящийся атом водорода массой 1,679*10-27 кг излучает фотон с энергией 16,32*10-19 Дж в результате перехода электрона из возбуждённого состояния в основное. В результате отдачи атом начинает двигаться поступательно в сторону, противоположную фотону. Найдите кинетическую энергию атома, если его скорость мала по сравнению со скоростью света.
Ответ:8,81*10-27
6. Мальчик, занимавшийся весной на улице выжиганием по дереву при помощи фокусировки солнечного света лупой, случайно забрызгал деревянную поверхность, и на ней появились капли воды объёмом V = 1 мм3. Сколько времени займёт испарение одной такой капли, если солнечная постоянная равна С = 1,4 кВт/м2, диаметр лупы D = 5 см, начальная температура капель близка к 0 °С и весь сфокусированный лупой свет поглощается каплей?
Справка: Солнечная постоянная – это энергия излучения Солнца, попадающая в единицу времени на единицу площади при нормальном падении солнечного света.
Ответ 1сек
7 Два покрытых кальцием электрода, один из которых заземлён, находятся в вакууме. Один из электродов заземлён. К ним подключён конденсатор ёмкостью C1 = 20 000пФ. Появившийся в начале фототок при длительном освещении прекращается, при этом на конденсаторе возникает заряд q = 2 · 10−8 Кл. Работа выхода электронов из кальция A = 4,42 · 10−19 Дж. Определите длину волны света, освещающего катод.
Ответ:330 нм
8. Фотокатод, покрытый кальцием, освещается светом с длиной волны λ = 300 нм. Работа выхода электронов из кальция равна Авых = 4,42·10–19 Дж. Вылетевшие из катода электроны попадают в однородное магнитное поле перпендикулярно линиям индукции этого поля и движутся по окружности с максимальным радиусом R = 4 мм. Каков модуль индукции магнитного поля В?
Ответ 10-3 тл
9 Ныряльщик, находящийся в бассейне, смотрит вверх с глубины h на спокойную поверхность воды и видит через неё, что его тренер стоит на кромке бассейна, причём ступни ног находятся на уровне воды, а голова видна ныряльщику под углом φ = 45º к вертикали. Показатель преломления воды n = 4/3, расстояние по горизонтали от глаз ныряльщика до ног тренера равно l = 7 м, рост тренера H = 1,77 м. Чему равна глубина h, с которой смотрит ныряльщик?
Ответ 2 м
10. Значения энергии электрона в атоме водорода задаются формулой: Е=-13,6/n2 эВ При переходах с верхних уровней энергии на нижние атом излучает фотон. Переходы с верхних уровней на уровень c n = 1 образуют серию Лаймана, на уровень c n = 2 – серию Бальмера т. д. Найдите отношение γ максимальной длины волны фотона в серии Бальмера к максимальной длине волны фотона в серии Лаймана.
Ответ 5,4
11. У самой поверхности воды в реке летит комар, стая рыб находится на расстоянии 2 м от поверхности воды. Каково максимальное расстояние до комара, на котором он еще виден рыбам на этой глубине? Относительный показатель преломления света на границе воздух-вода равен 1,33
Ответ 3м
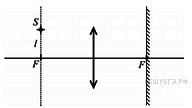
12. Точечный источник света S находится в передней фокальной плоскости собирающей линзы на расстоянии 2см от ее главной оптической оси. За линзой в ее задней фокальной плоскости находится плоское зеркало (см. рис.). Построить действительное изображение S» источника в данной оптической системе и найти расстояние между точками S и S» .
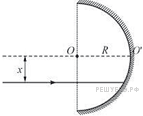
13. Школьник на уроке физики получил вогнутое полусферическое зеркало радиусом R и лазерную указку, дающую узкий параллельный пучок света с длиной волны 660нм. Он пустил луч света от указки параллельно главной оптической оси зеркала на расстоянии х от неё (см. рисунок). Затем школьник так подобрал расстояние х, что луч, отразившись от зеркала один раз, отклонился от оси на максимальный угол фи и вышел за пределы зеркала. Чему при таком отражении равен модуль изменения импульса каждого фотона лазерного луча?
Ответ 1,7*10-27
14. Точечный источник мощностью Р= 1 мВт излучает монохроматический свет с длиной волны = 600 нм равномерно во всех направлениях (такой источник называется изотропным). На каком расстоянии r от него концентрация фотонов (то есть число фотонов в единице объема) равна 2*10-5? Объем сферического слоя радиусом r и толщиной ∆r равен 4π∆rr2.
Ответ 2м
15. На экране, перпендикулярном главной оптической оси некоторой тонкой линзы, получили действительное изображение небольшого предмета, находящегося на расстоянии a = 50 см от этой линзы, с линейным увеличением Г = 1. После замены этой линзы на другую, находящуюся в том же месте и на том же расстоянии до предмета, увеличение изображения предмета при новом положении экрана, соответствующем резкому изображению, стало меньше в n = 0,5 раза. Чему равна оптическая сила D2 второй линзы?
Ответ 3 дптр
16. Равнобедренный прямоугольный треугольник ABC расположен перед тонкой собирающей линзой оптической силой 2,5 дптр так, что его катет АС лежит на главной оптической оси линзы (см. рисунок). Вершина прямого угла С лежит дальше от центра линзы, чем вершина острого угла А. Расстояние от центра линзы до точки А равно удвоенному фокусному расстоянию линзы, АС = 4 см. Постройте изображение треугольника и найдите площадь получившейся фигуры.
Ответ 6,5см*см
17 Определите фокусное расстояние тонкой линзы, если линейные размеры изображения тонкого карандаша, помещённого на расстоянии = 48 см от линзы и расположенного перпендикулярно главной оптической оси, меньше размеров карандаша в = 2 раза.
Ответ 16 см или -48 см
18 Свет с длиной волны 5461 ангстрем падает нормально на дифракционную решётку. Одному из главных дифракционных максимумов соответствует угол дифракции 30°, а наибольший порядок наблюдаемого спектра равен 5. Найдите период данной решётки.
Справка: 1 ангстрем = 10-10 м.
ответ 3,3 мкм
19. Небольшой груз, подвешенный на длинной нити, совершает гармонические колебания, при которых его максимальная скорость достигает 0,1 м/с. При помощи собирающей линзы с фокусным расстоянием 0,2 м изображение колеблющегося груза проецируется на экран, расположенный на расстоянии 0,5 м от линзы. Главная оптическая ось линзы перпендикулярна плоскости колебаний маятника и плоскости экрана. Максимальное смещение изображения груза на экране от положения равновесия равно 0,1м. Чему равна длина нити l?
Ответ 4,4 м
20 Бассейн глубиной 3 м заполнен водой, относительный показатель преломления на границе воздух-вода 1,33. Каков радиус светового круга на поверхности воды от электрической лампы на дне бассейна?
Ответ 3,4 м
Решение задач по теме «Модель атома Н. Бора»
Задача 1
Определите скорость v и ускорение a электрона на первой боровской орбите, радиус которой определяется формулой 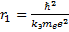
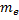
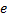
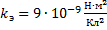
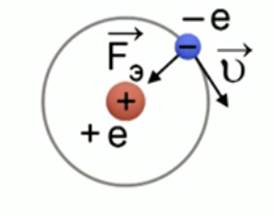
Дано: 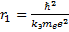
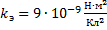
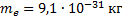
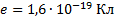
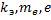
Найти: 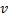
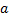
Решение
В формуле радиуса первой боровской орбиты:
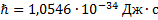
Радиус окружности, по которому происходит движение, равен:
Рис. 1. Иллюстрация к задаче №1
Согласно модели Бора, вокруг ядра атома водорода, заряд которого 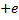
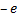
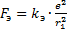
Также эта сила является центростремительной, то есть:
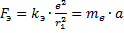
Следовательно, ускорение равно:
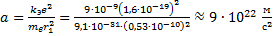
Центростремительное ускорение равно:
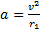
Отсюда скорость равна:
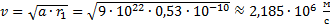
Ответ: 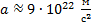
Задача 2
Найти силу электрического тока, который вызывает электрон, двигаясь по первой боровской орбите.
Дано: 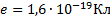
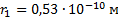
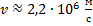
Найти: 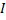
Решение
Известно, что сила тока равна:
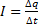
Для данной задачи:
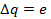
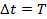
Период обращения электрона равен:
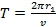
Следовательно, сила тока, возникающего при движении электрона по орбите радиусом 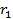
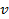
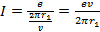
Подставим в данное выражение известные данные:
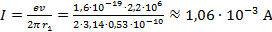
Ответ:
Задача 3
Найти максимальную частоту, максимальную длину волны и максимальный импульс фотона в видимой части спектра, излучённого при переходе электрона на второй энергетический уровень в атоме водорода.
Дано: 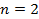
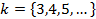
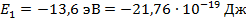
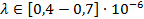
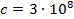
Найти: 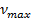
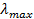
Решение
Согласно второму постулату Бора:
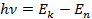
где 
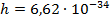
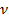
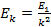
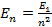
Следовательно, частота излучения фотона равна:

Частота и длина волны связаны следующим соотношением:
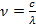
Зная световой диапазон в длинах волн (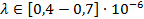
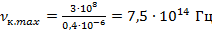
Более высокие частоты относятся к ультрафиолетовой части спектра и человеческим глазом не фиксируются.
Минимальное значение частоты при излучении будет при 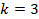
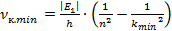
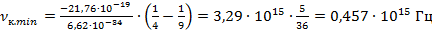
Подставим данное значение в формулу связи между длиной волны и частотой. Если частота минимальная, то значение длины волны будет максимальное:
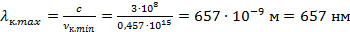
Данное значение входит в световой диапазон – это красная линия в излучении атома водорода.
Для того чтобы вычислить максимальное значение частоты фотона в видимой части спектра, необходимо подставлять значения k от 4-х и выше.
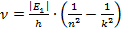
Если подставить значение 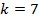
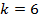
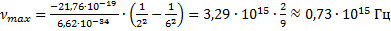
Мы попали в световой диапазон, так как он ограничивается значением 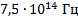
Полученная максимальная частота соответствует минимальной длине волны, равной:
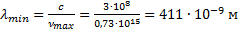
Минимальная длина волны была найдена для определения максимального импульса фотона.
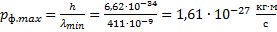
Ответ: ;
;
.
Атомная физика
Теория Бора
1. Первый постулат Бора (условие стационарности орбит):
(mvr=n{cdot}frac{h}{2pi}),
где (m) — масса электрона, (n) — номер орбиты (главное квантовое число (n=1,2,3,…)), (v) — скорость электрона на орбите радиуса (r), (h) — постоянная Планка.
2. Второй постулат Бора:
(nu=frac{W_i-W_j}{h}),
где (nu) — частота излучения при переходе с (i)-й на (j)-ю орбиту , (W_i) и (W_j) — энергии электрона на этих орбитах.
(3). Частота излучения для водородоподобных ионов:
(nu=RcZ^2(frac{1}{j^2}-frac{1}{i^2})),
где (Z) — порядковый номер элемента, (c) — скорость света, (R ) — постоянная Ридберга, (e) — заряд электрона, (varepsilon_0) — диэлектрическая постоянная вакуума.
4. Постоянная Ридберга
(R=frac{e^4m}{8varepsilon_0^2h^3c}).
5. Уровень энергии электрона, соответствующий различным квантовым состояниям:
(E_n=-frac{e^4mZ^2}{8n^2h^2varepsilon_0^2}) дж = (-frac{e^3mZ^2}{8n^2h^2varepsilon_0^2}) эв = (-frac{13.60Z^2}{n^2}) эв.
Примеры решения задач.
Задача 1.
Определить радиус (a_0) первой боровской орбиты и скорость (v) электрона на ней. Какова напряженность поля ядра на первой орбите?
Решение задачи.
Найти: (a_0), (v_0), (E_0)
Дано: (n=1)
Свяжем ИСО с ядром атома (ядро в нашей ИСО будет неподвижным).
Между ядром и электроном действует Кулоновская сила, которая и является центростремительной силой:
(frac{Ze^2}{4pi{varepsilon_0}r^2}=frac{mv^2}{r}) откуда
(frac{Ze^2}{4pi{varepsilon_0}r}=mv^2) (1).
Согласно первому постулату Бора (mvr=n{cdot}frac{h}{2pi}), откуда получим (mv^2=n^2{cdot}frac{h^2}{4pi^2r^^2m}).
Подставляя это значение в (1) получим:
(frac{Ze^2}{4pi{varepsilon_0}r}=frac{n^2h^2}{4pi^2r^^2m}), откуда легко выражается
(r=frac{{varepsilon_0}n^2h^2}{pi{Z}e^2m}). (2)
Полагая в (2) (n=1) получим
(a_0=frac{{varepsilon_0}1^2h^2}{pi{Z}e^2m}=0,53{cdot}10^{-10}) м.
Выражение для скорости электрона на орбите можем получить из первого постулата Бора
(v=frac{nh}{2pi{rm}}).
Подставляя сюда значение радиуса из (2), получим
(v=frac{Ze^2}{2{varepsilon_0}nh}) (3).
Полагая здесь (n=1), получим (v_0=2,183{cdot}10^6) м/с.
Напряженность электростатического поля ядра (точечного заряда) задается формулой
(E=frac{e}{4pi{varepsilon_0}r^2}) (4).
Полагая здесь (r=a_0), получим напряженность поля на первой боровской орбите
(E_0=frac{e}{4pi{varepsilon_0}a_0^2}=5,13{cdot}10^{11}) в/м.
Задача 2.
Определить, во сколько раз увеличится радиус орбиты электрона у атома водорода, находящегося в основном состоянии, при возбуждении его квантом с энергией 12,09 эв.
Решение.
Найти: (n)
Дано:
(n_1=1),
(Delta{E}=12.09) эв.
Примем за ИСО — ядро атома.
В задаче 1 мы получили выражение для радиуса орбиты электрона в зависимости от главного квантового числа
(r=frac{{varepsilon_0}h^2}{pi{Z}e^2m}{cdot}n^2).
Отсюда мы видим, что при переходе из основного состояния (n_1=1) в возбужденное (n=n_2) радиус орбиты электрона возрастает в (n_2^2) раз.
Определим теперь главное квантовое число, соответствующее переходу атома в возбужденное состояние.
(Delta{E}=E_2-E_1=13.6(1-frac{1}{n_2^2})).
Отсюда получаем (n_2^2=9). Радиус орбиты электрона возрастет в 9 раз.
Задача 3.
Атомарный водород находится при давлении 10-2 мм.рт.ст. и температуре 300 К. Определить значение полной энергии электрона в атоме, при которой радиус его орбиты равен половине среднего расстояния между центрами атомов в данных условиях.
Решение задачи.
Найти: (E_n)
Дано:
(p=133.3{cdot}10^{-2}) н/м2,
(T=300) K.
Свяжем ИСО с сосудом в котором находится водород.
Из формул для энергии электрона и его радиуса
(E_n=-frac{e^4mZ^2}{8n^2h^2varepsilon_0^2})
и
(r=frac{{varepsilon_0}n^2h^2}{pi{Z}e^2m})
получим формулу, выражающую энергию через радиус орбиты
(E_n=-frac{e^2Z}{8{pi}{varepsilon_0}r}).
Пусть расстояние между атомами (D), тогда (r=frac{D}{2}) и
(E_n=-frac{e^2Z}{4{pi}{varepsilon_0}D}).
Расстояние между атомами определим из уравнения Клапейрона-Менделеева (pV=RT) или (pV=NkT),
но (V=ND^3), откуда
(D=sqrt[3]{frac{kT}{p}}).
Тогда
(E_n=-frac{e^2Z}{4{pi}{varepsilon_0}}{cdot}sqrt[3]{frac{p}{kT}}).
(E_n=-1.58{cdot}10^{-21}) дж =(-9.58{cdot}10^{-3}) эв.