Потенциальная энергия физика егэ

в условии
в решении
в тексте к заданию
в атрибутах

Категория:

Атрибут:

Всего: 44    1–20 | 21–40 | 41–44

Добавить в вариант

Небольшое тело массой 0,2 кг бросили вертикально вверх. На рисунке показан график зависимости потенциальной энергии E_п тела от времени t в течение полета. На какую максимальную высоту поднялось тело? Ответ выразите в метрах.

Массивный груз, подвешенный к потолку на невесомой пружине, совершает вертикальные свободные колебания. Пружина всё время остаётся растянутой. Как ведут себя потенциальная энергия пружины и потенциальная энергия груза в поле тяжести, когда груз движется вверх от положения равновесия?

Для каждой величины определите соответствующий характер изменения:

1)  увеличивается;

2)  уменьшается;

3)  не изменяется.

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Потенциальная

энергия пружины

 Потенциальная

энергия груза

в поле тяжести
   

Источник: ЕГЭ по физике 2017. Досрочная волна. Вариант 101

Растянутая на 2 см стальная пружина обладает потенциальной энергией упругой деформации 4 Дж. На сколько увеличится потенциальная энергия упругой деформации при растяжении этой пружины еще на 2 см? (Ответ дайте в джоулях.)

В результате торможения в верхних слоях атмосферы высота полёта искусственного спутника над Землёй уменьшилась с 400 до 300 км. Как изменились в результате этого скорость спутника, его потенциальная энергия и период обращения?

Для каждой величины определите соответствующий характер изменения:

1)  увеличилась

2)  уменьшилась

3)  не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Скорость Период

обращения

Потенциальная

энергия

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 3., ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 5.

В результате торможения в верхних слоях атмосферы высота полёта искусственного спутника над Землёй уменьшилась с 400 до 300 км. Как изменились в результате этого скорость спутника, его потенциальная энергия и центростремительное ускорение?

Для каждой величины определите соответствующий характер изменения:

1)  увеличилась

2)  уменьшилась

3)  не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Скорость Потенциальная энергия Ускорение
     

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Сибирь. Вариант 6.

Искусственный спутник Земли перешёл с одной круговой орбиты на другую, на новой орбите скорость его движения меньше, чем на прежней. Как изменились при этом потенциальная энергия спутника в поле тяжести Земли и

его период обращения вокруг Земли?

Для каждой величины определите соответствующий характер изменения:

1)  увеличилась

2)  уменьшилась

3)  не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Потенциальная энергия Период обращения спутника вокруг Земли
   

Источник: Демонстрационная версия ЕГЭ−2019 по физике

Механическая энергия системы изменилась от величины –5 Дж до величины 3 Дж. Это означает, что на данную механическую систему действовали внешние силы. Какова работа этих сил? (Ответ дайте в джоулях.)

Однородный столб массой m и высотой H стоит вертикально. После того, как основание столба подпиливают у самой земли, он начинает падать. При этом нижний конец столба не отрывается от земли. Через некоторое время столб составляет с вертикалью угол α. Установите соответствие между физическими величинами и формулами, по которым их можно определить. К каждой позиции первого столбца подберите соответствующую позицию второго столбца.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А)  потенциальная энергия столба относительно поверхности земли в момент начала падения

Б)  потенциальная энергия столба относительно поверхности земли в момент, когда столб составляет с вертикалью угол α

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Однородный столб массой m и высотой H стоит вертикально. После того, как основание столба подпиливают у самой земли, он начинает падать. При этом нижний конец столба не отрывается от земли. Через некоторое время столб составляет с горизонтом угол α. Установите соответствие между физическими величинами и формулами, по которым их можно определить. К каждой позиции первого столбца подберите соответствующую позицию второго столбца.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А)  потенциальная энергия столба относительно поверхности земли в момент начала падения

Б)  потенциальная энергия столба относительно поверхности земли в момент, когда столб составляет с горизонтом угол α

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Тело массой 2 кг, брошенное с уровня земли вертикально вверх со скоростью 10 м/с, упало обратно на землю. Какой потенциальной энергией обладало тело относительно поверхности земли в верхней точке траектории? Сопротивлением воздуха пренебречь. (Ответ дайте в джоулях.)

Какова энергия упругой деформации сжатой на 10 см пружины, если её жёсткость равна 5000 Н/м? Ответ дайте в джоулях.

Человек взялся за конец лежащего на земле однородного стержня длиной 2 м и массой 100 кг и поднял этот конец на высоту 1 м. Какую работу он совершил? (Ответ дайте в джоулях.) Ускорение свободного падения принять равным 10 м/с2.

Комета движется по эллиптической орбите вокруг Солнца. Изменяются ли перечисленные в первом столбце физические величины во время ее удаления от Солнца и если изменяются, то как? Считаем, что на комету действует только сила тяготения Солнца. Установите соответствие между физическими величинами, перечисленными в первом столбце, и возможными видами их изменений, перечисленными во втором столбце. Запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А)  Скорость

Б)  Ускорение

В)  Кинетическая энергия

Г)  Потенциальная энергия

Д)  Полная механическая энергия

ИХ ИЗМЕНЕНИЯ

1)  Не изменяется

2)  Только увеличивается по величине

3)  Только уменьшается по величине

4)  Увеличивается по величине и изменяется по направлению

5)  Уменьшается по величине и изменяется по направлению

6)  Увеличивается по величине, не изменяется по направлению

7)  уменьшается по величине, не изменяется по направлению

A Б В Г Д
     

Маленькой шайбе, покоящейся у основания гладкой наклонной плоскости, сообщают начальную скорость V0, направленную вдоль наклонной плоскости вверх (см. рис.). Наклонная плоскость достаточно длинная. Установите соответствие между зависимостями физических величин от времени и графиками.

ФИЗИЧЕСКАЯ ВЕЛИЧИНА

А)  модуль ускорения a

Б)  потенциальная энергия U (относительно начального положения шайбы)

ГРАФИК

Запишите в ответ цифры, расположив их в порядке, соответствующем буквам:

Упругая лёгкая пружина жёсткостью 80 Н/м одним концом прикреплена к лапке штатива. К свободному концу пружины подвешен груз массой 200 г. Определите потенциальную энергию растянутой пружины. Ответ запишите в миллиджоулях.

Потенциальная энергия упругой пружины при её растяжении на 2 см равна 2 Дж. Найдите модуль изменения потенциальной энергии этой пружины при уменьшении её растяжения на 0,5 см. Ответ дайте в джоулях.

Источник: Демонстрационная версия ЕГЭ—2023 по физике

Искусственный спутник движется по эллиптической орбите вокруг Земли. Изменяются ли перечисленные в первом столбце физические величины во время его приближения к Земле и если изменяются, то как? Установите соответствие между физическими величинами, перечисленными в первом столбце, и возможными видами их изменений, перечисленными во втором столбце. Запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А)  Скорость

Б)  Ускорение

В)  Кинетическая энергия

Г)  Потенциальная энергия

Д)  Полная механическая энергия

ИХ ИЗМЕНЕНИЯ

1)  Не изменяется

2)  Только увеличивается по величине

3)  Только уменьшается по величине

4)  Увеличивается по величине и изменяется по направлению

5)  Уменьшается по величине и изменяется по направлению

6)  Увеличивается по величине, не изменяется по направлению

7)  уменьшается по величине, не изменяется по направлению

A Б В Г Д
     

Комета движется по эллиптической орбите вокруг Солнца. Как изменяются перечисленные в первом столбце физические величины во время её приближения к Солнцу, если считать, что на нее действует только тяготение Солнца? Установите соответствие между физическими величинами, перечисленными в первом столбце, и изменениями, перечисленными во втором столбце. Запишите в таблицу выбранные цифры под соответствующими буквами.

ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ

А)  Скорость

Б)  Ускорение

В)  Кинетическая энергия

Г)  Потенциальная энергия

Д)  Полная механическая энергия

ИХ ИЗМЕНЕНИЯ

1)  Не изменяется

2)  Только увеличивается по величине

3)  Только уменьшается по величине

4)  Увеличивается по величине и изменяется по направлению

5)  Уменьшается по величине и изменяется по направлению

6)  Увеличивается по величине, не изменяется по направлению

7)  уменьшается по величине, не изменяется по направлению

A Б В Г Д
     

В результате перехода с одной круговой орбиты на другую скорость движения спутника Земли увеличивается. Как изменяются в результате этого перехода потенциальная энергия спутника и центростремительное ускорение?

Для каждой величины определите соответствующий характер изменения:

1.  увеличилась

2.  уменьшилась

3.  не изменилась

Запишите в таблицу выбранные цифры для каждой физической величины. Цифры в ответе могут повторяться.

Потенциальная энергия Центростремительное ускорение

Источник: ЕГЭ по физике 01.04.2019. Досрочная волна. Вариант 1

Всего: 44    1–20 | 21–40 | 41–44

Источник

Энергия.

  • Работа.

  • Мощность.

  • Механическая энергия.

  • Кинетическая энергия.

  • Потенциальная энергия тела вблизи поверхности Земли.

  • Потенциальна яэнергия деформированной пружины.

  • Закон сохранения механической энергии.

  • Закон изменения механической энергии.

Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев

Темы кодификатора ЕГЭ: работа силы, мощность, кинетическая энергия, потенциальная энергия, закон сохранения механической энергии.

Мы приступаем к изучению энергии — фундаментального физического понятия. Но предварительно нужно разобраться с другой физической величиной — работой силы.

к оглавлению ▴

Работа.

Пусть на тело действует постоянная сила vec F и тело, двигаясь прямолинейно по горизонтальной поерхности, совершило перемещение vec s. Сила vec F не обязательно является непосредственной причиной перемещения (так, сила тяжести не является непосредственной причиной перемещения шкафа, который передвигают по комнате).

Предположим сначала, что векторы силы и перемещения сонаправлены (рис. 1; остальные силы, действующие на тело, не указаны)

Рис. 1.A=Fs

В этом простейшем случае работа A определяется как произведение модуля силы на модуль перемещения:

A=Fs. (1)

Единицей измерения работы служит джоуль (Дж): Дж=Н cdot м. Таким образом, если под действием силы 1 Н тело перемещается на 1 м, то сила совершает работу 1 Дж.

Работа силы, перпендикулярной перемещению, по определению считается равной нулю. Так, в данном случае сила тяжести и сила реакции опоры не совершают работы.

Пусть теперь вектор силы образует с вектором перемещения острый угол alpha (рис. 2).

Разложим силу vec F на две составляющие: vec F _{parallel } (параллельную перемещению) и vec F _{perp } (перпендикулярную перемещению). Работу совершает только vec F _{parallel }. Поэтому для работы силы vec F получаем:

A=vec F _{parallel }s=Fcosalpha cdot s. Итак,

A=Fs cosalpha . (2)

Если вектор силы образует с вектором перемещения тупой угол alpha, то работа по-прежнему определяется формулой (2). В этом случае работа оказывается отрицательной.

Например, работа силы трения скольжения, действующей на тело в рассмотренных ситуациях, будет отрицательной, так как сила трения направлена противоположно перемещению. В этом случае имеем:

alpha=180^{circ}, cos alpha=-1, и для работы силы трения получаем:

A_{TP}=-F_{TP}s=-mu mgs,

где m — масса тела,mu — коэффициент трения между телом и опорой.

Соотношение (2) означает, что работа является скалярным произведением векторов силы и перемещения:

A=vec F vec s.

Это позволяет вычислять работу через координаты данных векторов:

A=F_{displaystyle x}s_{displaystyle x}+F_{displaystyle y}s_{displaystyle y}+F_{displaystyle z}s_{displaystyle z}.

Пусть на тело действуют несколько сил vec F_{1},vec F_{2},..,vec F_{n} и vec F — равнодействующая этих сил. Для работы силы vec F имеем:

A=vec F vec s=(vec F_{1}+vec F_{2}+...+vec F_{n})vec s=vec F_{1}vec s+vec F_{2}vec s+...+vec F_{n}vec s,

или

A=A_{1}+A_{2}+...+A_{n},

где A_{1}, A_{2},...,A_{n} — работы сил F_{1}, F_{2},...,F_{n}. Итак, работа равнодействующей приложенных к телу сил равна сумме работ каждой силы в отдельности.

к оглавлению ▴

Мощность.

Часто имеет значение быстрота, с которой совершается работа. Скажем, на практике важно знать, какую работу сможет выполнить данное устройство за фиксированное время.

Мощность — это величина, характеризующая скорость совершения работы. Мощность N есть отношение работы A ко времени t, за которое эта работа совершена:

N=frac{displaystyle A}{displaystyle t}.

Мощность измеряется в ваттах (Вт). 1 Вт = 1 Дж/с, то есть 1 Вт — это такая мощность, при которой работа в 1 Дж совершается за 1 с.

Предположим, что силы, действующие на тело, уравновешены, и тело движется равномерно и прямолинейно со скоростью vec v. В этом случае существует полезная формула для мощности, развиваемой одной из действующих сил vec F.

За время t тело совершит перемещение vec s= vec v t. Работа силы vec F будет равна:

A=vec F vec s=vec F vec v t.

Отсюда получаем мощность:

N=vec F vec v ,

или

N=Fv cos alpha ,

где alpha -угол между векторами силы и скорости.

Наиболее часто эта формула используется в ситуации, когда vec F — сила «тяги» двигателя автомобиля (которая на самом деле есть сила трения ведущих колёс о дорогу). В этом случае alpha = 0, и мы получаем просто:

N=Fv .

к оглавлению ▴

Механическая энергия.

Энергия является мерой движения и взаимодействия любых объектов в природе. Имеются различные формы энергии: механическая, тепловая, электромагнитная, ядерная. . .

Опыт показывает, что энергия не появляется ниоткуда и не исчезает бесследно, она лишь переходит из одной формы в другую. Это самая общая формулировка закона сохранения энергии.

Каждый вид энергии представляет собой некоторое математическое выражение. Закон сохранения энергии означает, что в каждом явлении природы определённая сумма таких выражений остаётся постоянной с течением времени.

Измеряется энергия в джоулях, как и работа.

Механическая энергия является мерой движения и взаимодействия механических объектов (материальных точек, твёрдых тел).

Мерой движения тела является кинетическая энергия. Она зависит от скорости тела. Мерой взаимодействия тел является потенциальная энергия. Она зависит от взаимного расположения тел.

Механическая энергия системы тел равна сумме кинетической энергии тел и потенциальной энергии их взаимодействия друг с другом.

к оглавлению ▴

Кинетическая энергия.

Кинетической энергией тела (принимаемого за материальную точку) называется величина

K=frac{displaystyle mv^{displaystyle 2}}{displaystyle 2},

где m — масса тела, v — его скорость.

Кинетической энергией системы из N тел называется сумма кинетических энергий каждого тела:

K=frac{displaystyle m_{displaystyle 1}v_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}+frac{displaystyle m_{displaystyle 2}v_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}+...+frac{displaystyle m_{displaystyle N}v_{displaystyle N}^{displaystyle 2}}{displaystyle 2}.

Если тело движется под действием силы vec F, то кинетическая энергия тела, вообще говоря, меняется со временем. Оказывается, именение кинетической энергии тела за некоторый промежуток времени равно работе силы vec F. Покажем это для случая прямолинейного равноускоренного движения.

Пусть vec{v_{1}} — начальная скорость, vec{v_{2}} — конечная скорость тела. Выберем ось X вдоль траектории тела (и, соответственно, вдоль вектора силы vec F). Для работы силы vec F получаем:

A=vec{F}vec{s}=F_{x}s_{displaystyle s}=ma_{displaystyle x}s_{displaystyle x}= ma_{displaystyle x}frac{{v_{displaystyle 2x}}^{displaystyle 2}-{v_{displaystyle 1x}}^{displaystyle 2}}{displaystyle 2a_{displaystyle x}}=frac{{displaystyle mv_{displaystyle 2x}}^{displaystyle 2}-{displaystyle mv_{displaystyle 1x}}^{displaystyle 2}}{displaystyle 2}.

(мы воспользовались формулой для s_{x} , выведенной в статье «Равноускоренное движение»). Заметим теперь, что в данном случае проекция скорости отличается от модуля скорости разве что знаком; поэтому {v_{displaystyle 1x}}^{displaystyle 2}={v_{displaystyle 1}}^{displaystyle 2} и {v_{displaystyle 2x}}^{displaystyle 2}={v_{displaystyle 2}}^{displaystyle 2} . В результате имеем:

A=frac{displaystyle mv_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}-frac{displaystyle mv_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}=K_{displaystyle 2}-K_{displaystyle 1}=Delta K,

что и требовалось.

На самом деле соотношение Delta K=A справедливо и в самом общем случае криволинейного движения под действием переменной силы.

Теорема о кинетической энергии. Изменение кинетической энергии тела равно работе, совершённой приложенными к телу внешними силами за рассматриваемый промежуток времени.

Если работа внешних сил положительна, то кинетическая энергия увеличивается (Delta K>0, тело разгоняется).

Если работа внешних сил отрицательна, то кинетическая энергия уменьшается (Delta K<0, тело замедляет движение). Пример — торможение под действием силы трения, работа которой отрицательна.

Если же работа внешних сил равна нулю, то кинетическая энергия тела за это время не меняется. Нетривиальный пример — равномерное движение по окружности, совершаемое грузом на нити в горизонтальной плоскости. Сила тяжести, сила реакции опоры и сила натяжения нити всегда перпендикулярны скорости, и работа каждой из этих сил равна нулю в течение любого промежутка времени. Соответственно, кинетическая энергия груза (а значит, и его скорость) остаётся постоянной в процессе движения.

Задача. Автомобиль едет по горизонтальной дороге со скоростью v и начинает резко тормозить. Найти путь s, пройденный автомобилем до полной остановки, если коэффициент трения шин о дорогу равен mu.

Решение. Начальная кинетическая энергия автомобиля K_{displaystyle 1}=frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}, конечная кинетическая энергия K_{displaystyle 2}=0. Изменение кинетической энергии Delta K=K_{displaystyle 2}-K_{displaystyle 1}=-frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}.

На автомобиль действуют сила тяжести m vec g, реакция опоры vec N и сила трения vec f. Сила тяжести и реакция опоры, будучи перпендикулярны перемещению автомобиля, работы не совершают. Работа силы трения:

A=-fs=- mu Ns=- mu mgs.

Из теоремы о кинетической энергии теперь получаем:

Delta K=A Rightarrow - frac{displaystyle mv^{displaystyle 2}}{displaystyle 2}=- mu mgs Rightarrow s=frac{displaystyle v^{displaystyle 2}}{displaystyle 2 mu g}.

к оглавлению ▴

Потенциальная энергия тела вблизи поверхности Земли.

Рассмотрим тело массы m, находящееся на некоторой высоте над поверхностью Земли. Высоту считаем много меньше земного радиуса. Изменением силы тяжести в процессе перемещения тела пренебрегаем.

Если тело находится на высоте h, то потенциальная энергия тела по определению равна:

W=mgh

где g — ускорение свободного падения вблизи поверхности Земли.

Высоту не обязательно отсчитывать от поверхности Земли. Как мы увидим ниже (формулы (3), (4)), физическим смыслом обладает не сама по себе потенциальная энергия, но её изменение. А изменение потенциальной энергии не зависит от уровня отсчёта. Выбор нулевого уровня потенциальной энергии в конкретной задаче диктуется исключительно соображениями удобства.

Найдём работу, совершаемую силой тяжести при перемещении тела. Предположим, что тело перемещается по прямой из точки P, находящейся на высоте h_{1}, в точку Q, находящуюся на высоте h_{2} (рис. 3).

Рис. 3.A=mg(h1-h2)[/math]

Угол между силой тяжести m vec g и перемещением тела vec s обозначим alpha . Для работы силы тяжести получим:

A=m vec g vec s=mgs cos alpha.

Но, как видно из рис. 3, s cos alpha=h_{1}-h_{2}. Поэтому

A=mg(h_{1}-h_{2})=mgh_{1}-mgh_{2},

или

A=W_{1}-W_{2}. (3)

Учитывая, что W_{1}-W_{2}=-(W_{2}-W_{1})=- Delta W, имеем также:

A=- Delta W. (4)

Можно доказать, что формулы (3) и (4) справедливы для любой траектории, по которой тело перемещается из точки P в точку Q, а не только для прямолинейного отрезка.

Работа силы тяжести не зависит от формы траектории, по которой перемещается тело, и равна разности значений потенциальной энергии в начальной и конечной точках траектории. Иными словами, работа силы тяжести всегда равна изменению потенциальной энергии с противоположным знаком. В частности, работа силы тяжести по любому замкнутому пути равна нулю.

Сила называется консервативной, если при перемещении тела работа этой силы не зависит от формы траектории, а определяется только начальным и конечным положением тела. Сила тяжести, таким образом, является консервативной. Работа консервативной силы по любому замкнутому пути равна нулю. Только в случае консервативной силы возможно ввести такую величину, как потенциальная энергия.

к оглавлению ▴

Потенциальна яэнергия деформированной пружины.

Рассмотрим пружину жёсткости k. Начальная деформация пружины равна x_{1}. Предположим,
что пружина деформируется до некоторой конечной величины деформации x_{2}. Чему равна при этом работа силы упругости пружины?

В данном случае силу на перемещение не умножишь, так как сила упругости меняется в процессе деформации пружины. Для нахождения работы переменной силы требуется интегрирование. Мы не будем приводить здесь вывод, а сразу выпишем конечный результат.

Оказывается, сила упругости пружины также является консервативной. Её работа зависит лишь от величин x_{1} и x_{2} и определяется формулой:

A=frac{kx_{displaystyle 1}^{displaystyle 2}}{displaystyle 2}-frac{displaystyle kx_{displaystyle 2}^{displaystyle 2}}{displaystyle 2}.

Величина

W=frac{displaystyle kx^{displaystyle 2}}{displaystyle 2}

называется потенциальной энергией деформированной пружины (x — величина деформации).

Следовательно,

A=W_{1}-W_{2}=- Delta W,

что полностью аналогично формулам (3) и (4).

к оглавлению ▴

Закон сохранения механической энергии.

Консервативные силы называются так потому, что сохраняют механическую энергию замкнутой системы тел.

Механическая энергия E тела равна сумме его кинетической и потенциальной энергий:

E=K+W.

Механическая энергия системы тел равна сумме их кинетических энергий и потенциальной энергии их взаимодействия друг с другом.

Предположим, что тело совершает движение под действием силы тяжести и/или силы упругости пружины. Будем считать, что трения нет. Пусть в начальном положении кинетическая и потенциальная энергии тела равны K_{1} и W_{1} , в конечном положении — K_{2} и W_{2}. Работу внешних сил при перемещении тела из начального положения в конечное обозначим A.

По теореме о кинетической энергии

K_{2}-K_{1}=A.

Но работа консервативных сил равна разности потенциальных энергий:

A=W_{1}-W_{2}.

Отсюда получаем:

K_{2}-K_{1}=W_{1}-W_{2},

или

K_{1}+W_{1}=K_{2}+W_{2}.

Левая и правая части данного равенства представляют собой механическую энергию тела в начальном и конечном положении:

E_{1}=E_{2}.

Следовательно, при движении тела в поле силы тяжести и/или на пружине механическая энергия тела остаётся неизменной при отсутствии трения. Справедливо и более общее утверждение.

Закон сохранения механической энергии. Если в замкнутой системе действуют только консервативные силы, то механическая энергия системы сохраняется.

При этих условиях могут происходить лишь превращения энергии: из кинетической в потенциальную и наоборот. Общий запас механической энергии системы остаётся постоянным.

к оглавлению ▴

Закон изменения механической энергии.

Если между телами замкнутой системы имеются силы сопротивления (сухое или вязкое трение), то механическая энергия системы будет уменьшаться. Так, автомобиль останавливается в результате торможения, колебания маятника постепенно затухают и т. д. Силы трения неконсервативны: работа силы трения очевидным образом зависит от пути, по которому перемещается тело между данными точками. В частности, работа силы трения по замкнутому пути не равна нулю.

Снова рассмотрим движение тела в поле силы тяжести и/или на пружине. Вдобавок на тело действует сила трения, которая за рассматриваемый промежуток времени совершает отрицательную работу A_{TP}. Работу консервативных сил (тяжести и упругости) по-прежнему обозначаем A.

Изменение кинетической энергии тела равно работе всех внешних сил:

K_{2}-K_{1}=A+A_{TP}.

Но A=W_{1}-W_{2}, следовательно

K_{2}-K_{1}=W_{1}-W_{2}+A_{TP}.

Отсюда

K_{2}+W_{2}-(K_{1}+W_{1})=A_{TP},

или

E_{2}-E_{1}=A_{TP}.

В левой части стоит величина Delta E=E_{2}-E_{1} — изменение механической энергии тела:

Delta E=A_{TP}.

Итак,при движении тела в поле силы тяжести и/или на пружине изменение механической энергии тела равно работе силы трения. Так как работа силы трения отрицательна,изменение механической энергии также отрицательно: механическая энергия убывает.
Справедливо и более общее утверждение.

Закон изменения механической энергии. Изменение механической энергии замкнутой системы равно работе сил трения, действующих внутри системы.

Ясно, что закон сохранения механической энергии является частным случаем данного утверждения.

Конечно, убыль механической энергии не противоречит общефизическому закону сохранения энергии. В данном случае механическая энергия превращается в энергию теплового движения частиц вещества и их потенциальную энергию взаимодействия друг с другом, т. е. переходит во внутреннюю энергию тел системы.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Энергия.» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Данная тема посвящена решению задач, связанных с расчетом
потенциальной энергии тела.

Задача 1. В кубическом аквариуме плавает в воде
массивная тонкостенная прямоугольная коробка. В дне коробки аккуратно проделали
маленькое отверстие, после чего она набрала воды и утонула. Как изменилась
потенциальная энергия механической системы, включающей в себя воду и коробку?

РЕШЕНИЕ

Потенциальная энергия тела в гравитационном поле Земли
определяется произведением массы тела, ускорения свободного падения и высоты,
на которой находится тело относительно нулевого уровня, в качестве которого
выберем дно аквариума.

Так как по условию задачи коробка тонкостенная, то объем
самих стенок пренебрежимо мал. Следовательно, уровень воды в аквариуме с
утонувшей коробкой будет совпадать с уровнем воды, когда коробки в аквариуме вообще
нет.

И так, когда коробка плавала, сила тяжести уравновешивалась архимедовой
силой. А как известно, сила Архимеда равна весу вытесненной жидкости. Таким
образом, уровень воды в аквариуме с плавающей коробкой
выше, чем в аквариуме без коробки. Поэтому, когда коробка тонет, уровень воды
уменьшается. Следовательно, уменьшается и потенциальная энергия воды, так как
ее центр масс опускается. Сама коробка также опускается на дно, следовательно,
ее потенциальная энергия тоже уменьшается.

ОТВЕТ: для системы «коробка-вода» потенциальная
энергия уменьшится.

Задача 2. Определите массу однородного куба,
находящегося на горизонтальной плоскости, если для его переворота с одной грани
на соседнюю требуется совершить минимальную работу в 200 Дж. Длина ребра куба 1
м.

Задача 3. На рисунке изображена зависимость силы
упругости от абсолютного удлинения пружины. Чему равно отношение работы,
совершенной для увеличения абсолютного удлинения от 0 до 4 см, к работе,
совершенной для абсолютного удлинения от 4 см до 8 см?

РЕШЕНИЕ

Работа силы упругости равна изменению потенциальной энергии
упруго деформированного тела, взятому с обратным знаком.

Потенциальная энергия пружины определяется по формуле:

Так как в первоначальный момент времени пружина не
деформирована, то ее потенциальная энергия равна нулю.

Энергия пружины в состоянии А будет равна

где х1 — это величина абсолютного удлинения
пружины при ее первом растяжении.

Аналогично будет определяться потенциальная энергия пружины в
состоянии B

На основании записанных формул, составим уравнения для работы
сил упругости для двух состояний

Так как нам требуется определить отношение работ, то выполним
почленное деление первого уравнения на второе

ОТВЕТ: А1/А2 =
1/3.

Эту же задачу можно было решить и другим способом —
графическим.

Известно, что работа силы численно равна площади фигуры под
графиком силы. В случае, когда пружину растягивают первый раз, данной фигурой
будет являться прямоугольный треугольник, площадь которого равна половине
произведения его катетов.

Задача 4. Санки съезжают с горы высотой 10 м и углом
наклона 30о и движутся дальше по горизонтальному участку.
Коэффициент трения на всем пути одинаков и равен 0,3. Определите расстояние,
которое пройдут санки по горизонтальному участку до полной остановки.

«Очень важно не перестать задавать вопросы.

Любопытство не случайно дано человеку».

Альберт Эйнштейн

Источник

«Кинетическая и потенциальная  энергия»

Код ОГЭ 1.17. Кинетическая и потенциальная  энергия. Формула для вычисления кинетической энергии. Формула для вычисления потенциальной энергии тела, поднятого над Землей.

Энергия – физическая величина, характеризующая состояние тела или системы тел. Причиной изменения состояния системы тел (изменения энергии) является работа внешних по отношению к рассматриваемой системе сил. В механике энергия тела или системы тел определяется взаимным положением тел (потенциальная энергия) и их скоростями (кинетическая энергия).

Единица измерения энергии в СИ – джоуль.

 Кинетическая энергия – часть механической энергии, энергия движущегося тела. Скалярная величина, численно равная половине произведения массы тела на квадрат скорости: 

Теорема о кинетической энергии: Работа, совершаемая силой при изменении скорости тела, равна изменению кинетической энергии тела: A = Wk2 – Wk1 = ΔWk.

Причём если А > 0, то Wk увеличивается, и если А < 0, то Wk уменьшается.
Эта теорема справедлива для любого движения и для сил любой природы.

Кинетическая энергия – величина относительная, зависящая от выбора СО, так как скорость тела зависит от выбора СО. Если тело разгоняется из состояния покоя, то Wk1 = 0, А = Wk2. Следовательно, физический смысл кинетической энергии: кинетическая энергия численно равна работе, которую необходимо совершить, чтобы разогнать тело из состояния покоя до данной скорости.

 Внимание! Кинетическая энергия механической системы тел равна сумме кинетических энергий всех частей системы.

 Потенциальная энергия – часть механической энергии тела (системы тел), энергия взаимодействия тел или частей тела. Потенциальная энергия определяется взаимным расположением тел или частей тела, то есть расстояниями между ними.

Потенциальная энергия относительна, зависит от выбора системы отсчёта, в частности от выбора тела отсчёта, которому соответствует нулевой уровень потенциальной энергии.

Потенциальная энергия тела в поле силы тяжести численно равна произведению массы тела на ускорение свободного падения и на высоту относительно выбранного нулевого уровня: Wп = mgh.

Связь работы силы тяжести и изменения потенциальной энергии:
A = mg (h1 – h2) = – (mgh2 – mgh2) = – (Wп2 – Wп1) = – ΔWп

 Внимание! Работа сила тяжести равна изменению потенциальной энергии тела в поле силы тяжести, взятому с противоположным знаком.

Кинетическая и потенциальная  энергия

Конспект урока «Кинетическая и потенциальная  энергия».

Следующая тема: «Механическая энергия».

Источник

Как относиться к тому, что в демонстрационный вариант ЕГЭ включается вопрос на знание того, чего нет в кодификаторе ЕГЭ по физике и в школьной программе? Честно говоря — не знаю. Давайте, на всякий случай, разберем этот и похожие вопросы.

Итак, вопрос (он пока в старом формате, что неудивительно — он из года 2014).

За­да­ние 3 № 5603. Ис­кус­ствен­ный спут­ник об­ра­ща­ет­ся во­круг Земли по вы­тя­ну­той эл­лип­ти­че­ской ор­би­те. Вы­бе­ри­те вер­ное утвер­жде­ние о по­тен­ци­аль­ной энер­гии и пол­ной ме­ха­ни­че­ской энер­гии спут­ни­ка.

1) По­тен­ци­аль­ная и пол­ная ме­ха­ни­че­ская энер­гия спут­ни­ка до­сти­га­ют мак­си­маль­ных зна­че­ний в точке мак­си­маль­но­го уда­ле­ния от Земли.

2) По­тен­ци­аль­ная и пол­ная ме­ха­ни­че­ская энер­гия спут­ни­ка до­сти­га­ют мак­си­маль­ных зна­че­ний в точке ми­ни­маль­но­го уда­ле­ния от Земли.

3) По­тен­ци­аль­ная энер­гия до­сти­га­ет мак­си­маль­но­го зна­че­ния в точке мак­си­маль­но­го уда­ле­ния от Земли, пол­ная ме­ха­ни­че­ская энер­гия спут­ни­ка не­из­мен­на.

4) По­тен­ци­аль­ная энер­гия до­сти­га­ет мак­си­маль­но­го зна­че­ния в точке ми­ни­маль­но­го уда­ле­ния от Земли, пол­ная ме­ха­ни­че­ская энер­гия спут­ни­ка не­из­мен­на.

Источник: Демонстрационная версия ЕГЭ—2014 по физике.

Аналогичная задача: За­да­ние 3 № 5498.

Источник: ЕГЭ по физике 06.06.2013. Основная волна. Центр. Вариант 6.

А вот еще один.

За­да­ние 3 № 4081. Ис­кус­ствен­ный спут­ник ле­та­ет во­круг Земли по кру­го­вой ор­би­те. Если на очень боль­шом рас­сто­я­нии от Земли по­тен­ци­аль­ная энер­гия спут­ни­ка равна нулю, то пол­ная ме­ха­ни­че­ская энер­гия этого спут­ни­ка на дан­ной ор­би­те

1) по­ло­жи­тель­на

2) от­ри­ца­тель­на

3) равна нулю

4) может быть любой — в за­ви­си­мо­сти от ско­ро­сти спут­ни­ка

Источник: МИОО: Ди­а­гно­стич­ская работа по фи­зи­ке 17.12.2012 ва­ри­ант 1.

2 Потенциальная энергия взаимодействия тела с Землей

Запомним следующую формулу, выражающую потенцияльную энергию взаимодействия массы $m$ с Землей. Массу Земли обозначим $M_{з}$.

  $$E_{пот} = — G frac {m M_{з}} {R} (1) $$

Здесь $G$ — гравитационная постоянная, $R$ — расстояние от центра Земли до центра масс тела массы $m$. Обратим внимание на знак минус перед потенциальной энергией, он очень важен. Потенциальная энергия в поле тяжести всегда отрицательна*.

3 Соотношение между потенциальной и кинетической энергией

  Получим теперь соотношение между кинетической и потенциальной энергией спутника, движущегося по круговой орбите радиуса $R$  вокруг Земли.

 Центростремительное ускорение спутника вызывается силой тяжести, что позволяет нам записать второй закон Ньютона в следующем виде:

$$ {v^2} {R} = G frac {m M_{з}} {R^2} (2) $$

Здесь  $v$ — скорость движения спутника по орбите.

Разделив обе части предыдущего равентства на $m$  и умножив на $R$, получим выражение квадрата скорости через массу Земли и радиус траектории:

$$  v^2= G frac {M_{з}} {R} (3) $$

Из этого выражения лекго получить кинетическую энергию спутника, умножив его на  $m$ и разделив на 2:

$$ E_{кин} = m frac {v^2} {2} = G frac {m M_{з}} {2R} (4) $$

 Сравнивая это выражение с выражением для потенциальной энергии спутника, получаем:

$$ E_{кин} = — frac {1} {2} E_{пот} $$

4 Полная энергия

 Полная энергия есть сумма потенциальной и инетической энергий. Используя полученные выше выражения, с учетом соотношения между ними получаем:

$$ E_{полная} = E_{кин} + E_{пот}= — frac {1} {2} E_{пот} + E_{пот} = frac {1} {2} E_{пот} = — G frac {m M_{з}} {2R} (5) $$

Или, выражая полную энергию через кинетическую:

$$ E_{полная} = — E_{кин} = — G frac {m M_{з}} {2R} (6) $$

 Из этих формул мы видим, что полная энергия, как и потенциальная*, всегда отрицательна.

5 Решения задач из 1

5.1 Ответ на вопрос 5603.

Поскольку, как мы видим из (1), потенциальная энергия всегда отрицательна, на больших расстояниях она достигает максимального значения — минимального по модулю, но максимального с учетом ее отрицательности. При этом полная энергия сохраняется, значит, кинетическая энергия минимальна в точке максимального удаления от Земли. То есть, ответ 3

5.2 В аналогичной задаче 5498 условие сформулировано так же, а вопросы звучат следующим образом:

1) Ки­не­ти­че­ская энер­гия до­сти­га­ет ми­ни­маль­но­го зна­че­ния в точке ми­ни­маль­но­го уда­ле­ния от Земли, пол­ная ме­ха­ни­че­ская энер­гия спут­ни­ка не­из­мен­на.

2) Ки­не­ти­че­ская энер­гия до­сти­га­ет ми­ни­маль­но­го зна­че­ния в точке мак­си­маль­но­го уда­ле­ния от Земли, пол­ная ме­ха­ни­че­ская энер­гия спут­ни­ка не­из­мен­на.

3) Ки­не­ти­че­ская и пол­ная ме­ха­ни­че­ская энер­гия спут­ни­ка до­сти­га­ют ми­ни­маль­ных зна­че­ний в точке ми­ни­маль­но­го уда­ле­ния от Земли.

4) Ки­не­ти­че­ская и пол­ная ме­ха­ни­че­ская энер­гия спут­ни­ка до­сти­га­ют ми­ни­маль­ных зна­че­ний в точке мак­си­маль­но­го уда­ле­ния от Земли.

 Рассуждения те же, правильный ответ 2

5.3 Ответ на вопрос 4081

Выражение (5) показывает, что полная энергия спутника всегда отрицательна, то есть правильный ответ — 2

*Формула (1) получается в случае выбора начала отсчета потенциальной энергии на бесконечности. Действительно, именно на бесконечности потенциальная энергия равна нулю.

Источник

За это задание ты можешь получить 2 балла. Уровень сложности: повышенный.
Средний процент выполнения: 67.9%
Ответом к заданию 4 по физике может быть последовательность цифр, чисел или слов. Порядок записи имеет значение.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

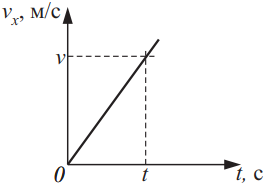
На рисунке изображён график зависимости проекции скорости тела массой m от времени (t). На основании графика выберите два верных утверждения из приведённого ниже списка для момента времени t. Укажите их номера.

  1. Движущаяся сила вычисляется по формуле F = m · v · t.
  2. Работу силы можно найти по формуле $A = {m· v}/{2t}$.
  3. Движущаяся сила вычисляется по формуле $F = {mv}/{t}$.
  4. Работу силы можно найти по формуле $A = {m·v^2}/{2}$.
  5. Работу силы можно найти по формуле $A = {m·v^2}/{2t^2}$.
Решение

3) Движущаяся сила $F=ma$, где $a={υ-υ_0}/{y}={υ}/{t}$, поскольку $υ_0=0$, что видно графика. Тогда $F=ma={mυ}/{t}$.

4) Работа силы равна изменению кинетической энергии, т.е. $A=∆E_к={mυ^2}/{2}-{mυ_0^2}/{2}$, поскольку $υ_0=0$, то $A={mυ^2}/{2}-0={mυ^2}/{2}$.

Ответ: 34

Задача 2

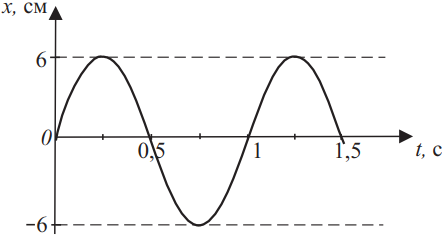
По экспериментальным данным построен график зависимости координаты колебания от времени на рисунке. Из приведённого ниже списка на основании анализа представленного графика выберите все верные утверждения и укажите их номера.

  1. В момент времени, равный 10 периодам колебаний, тело находится в точке с координатой x = 6 см.
  2. Координату тела в момент времени t можно найти по формуле x = 6 sin(π · t).
  3. В момент времени, равный 10 периодам колебаний, тело находится в точке с координатой x = 0 см.
  4. Координату тела в момент времени t можно найти по формуле x = 6 cos(2π · t).
  5. Координату тела в момент времени t можно найти по формуле x = 6 sin(2π · t).
Решение

1) Из графика видно, что период колебаний тела $T=1с$, амплитудное значение координаты $x_m=6$см. Значит, угловая частота тела $ω={2π}/{T}={2π}/{1}=2π$. Запишем уравнение колебаний в общем виде: $x=x_m·sin({2π}/{T}·t)$. Подставим наши данные, имеем: $x=6·sin({2πt}/{1})=6·sin(2π·t)$. Координата колебания подчиняется закону синуса, следовательно, в момент времени, равный 10 периодам колебаний, тело находится в точке с координатой $х=0$ см.

Ответ: 35

Задача 3

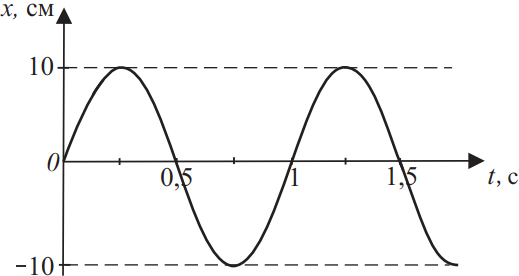
Координата колеблющегося тела меняется так, как показано на графике рисунке. Из приведённого ниже списка на основании анализа представленного графика выберите все верные утверждения и укажите их номера.

  1. Период колебаний тела равен 1 с.
  2. Координату тела в момент времени t можно найти по формуле x = 0,1 sin(π · t + π/4).
  3. Тело совершает колебания с периодом 0,1 с.
  4. Координату тела в момент времени t можно найти по формуле x = 10 sin(2π · t).
  5. Координату тела в момент времени t можно найти по формуле x = 10 cos(2π · t + π/4).
Решение

1) Из графика видно, что период колебаний тела равен 1с.

4) Поскольку координата колеблющегося тела изменяется по закону синуса, $x_m=10$см — амплитудное значение координаты и начальная фаза $ϕ_0=0$, то координату тела в момент времени $t$ можно найти по формуле $x=10·sin(2π·t)$.

Ответ: 14

Задача 4

Ученик исследовал зависимость модуля силы упругости F пружины от её растяжения x. Результаты эксперимента приведены в таблице. Из приведённого ниже списка выберите два правильных утверждения и укажите их номера.

F, H 0 0,5 1 1,5 2 2,5
x, м 0 0,02 0,04 0,06 0,08 0,10
  1. Коэффициент упругости пружины равен 2,5 Н/м.
  2. При увеличении массы груза растяжение пружины уменьшается.
  3. Потенциальная энергия пружины пропорциональна растяжению пружины.
  4. Потенциальная энергия пружины при её растяжении на 0,08 м равна 0,08 Дж.
  5. При подвешенном к пружине грузе массой 100 г её удлинение составит 4 см.
Решение

Исходя из теории упругости и результатов опыта, определим $E_n={kx^2}/{2}={25·0.08^2}/{2}=0.08$Дж. $k={E}/{x}={2}/{0.08}=25$н/м, а при $F_т=1H; x=0.04$м.

Ответ: 45

Задача 5

Грузик, подвешенный на нити, совершает гармонические колебания. В таблице представлены значения координаты грузика через одинаковые промежутки времени. Из приведённого ниже списка выберите все правильные утверждения и укажите их номера.

t, c 0 0,1 0,2 0,3 0,4 0,5 0,6 0,7
x, см 6 3 0 3 6 3 0 3
  1. Максимальная скорость грузика равна 0,15 м/с.
  2. Период колебаний шарика равен 0,4 с.
  3. В момент времени 0,1 с кинетическая энергия шарика максимальна.
  4. Полная механическая энергия шарика остаётся неизменной.
  5. Амплитуда колебаний шарика равна 6 мм.
Решение

Исходя из теории о гармонических колебаниях и данной таблицы, полная механическая энергия шарика остается неизменной. (4 — верно).
Период колебании — время за которое происходит одно полное колебание — 0,4 с (2 — верно)
Максимальная скорость шарика связана с амплитудой ( $υ_{max}=А ω ={А2π}/{T}= {0,03* 2*3.14}/{0,4}=0,471$м/с. (1 — неверно)
Максимальная кинетическая энергия будет в момент прохождения шариком положения равновесия x=3 см, это соответствует времени t=0,1 с (3 — верно)
Амплитуда колебания — это максимальное отклонение от положения равновесия, так как координата колеблется между значениями 6 см и 0, положению равновесия будет соответствовать координата х=3 см, значит амплитуда: А=6-3=3 см (5 — неверно)

Ответ: 234

Задача 6

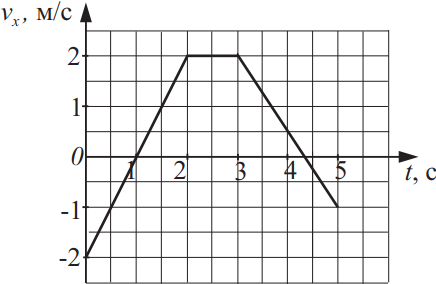
Тело массой 15 кг движется вдоль оси Ox в инерциальной системе отсчёта. График зависимости проекции скорости vx этого тела на ось Ox от времени представлен на рисунке. Из приведённого ниже списка выберите два верных утверждения на основании анализа представленного графика и укажите их номера.

  1. В течение первых двух секунд перемещение тела равно 2 м.
  2. Модуль ускорения тела в промежутке времени от 1 с до 2 с на 25% больше модуля ускорения тела в промежутке времени от 3 с до 4 с.
  3. В течение первой секунды кинетическая энергия тела увеличилась на 30 Дж.
  4. В промежутке времени от 1 с до 2 с импульс тела увеличился в 2 раза.
  5. В момент времени 4 с модуль равнодействующей сил, действующих на тело, равен 22,5 Н.
Решение

Из теории кинематики и данного графика можно сказать, что модуль ускорения тела с 1 до 2 на 25% больше 3-4, т.е. $a_{1-2}=2м/с^2; a_{3-4}=1.5м/с^2$. В момент времени 4с модуль равнодействующих сил, $F=22.5H$, т.к. $a_4=1.5м/с^2$, $F_p=ma_4=15·1.5=22.5H$

Ответ: 25

Задача 7

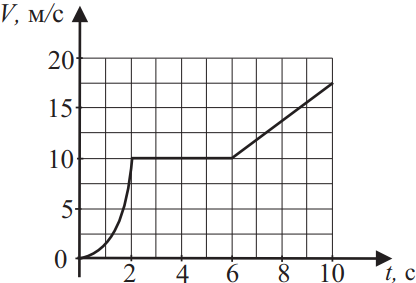
На рисунке представлен график зависимости скорости V от времени t для тела, движущегося прямолинейно. Используя данные графика, выберите из приведённого ниже списка все верные утверждения и укажите их номера.

  1. Первые две секунды тело двигалось равноускоренно.
  2. Со 2-й по 6-ю секунду тело переместилось на 40 м.
  3. Со 2-й по 6-ю секунду тело переместилось на меньшее расстояние, чем за первые две секунды.
  4. Средняя скорость тела во время движения со 2-й по 10-ю секунду равна 12,5 м/с.
  5. С 6-й по 10-ю секунду тело двигалось равноускоренно.
Решение

1) Неверно, так как равноускоренному движению соответствует линейный график: $v(t)=v_0+at$.

2)Верно. Из данного рисунка видно, что с 2 по 6 сек, тело прошло 40 м (площадь под графиком)

3) Неверно. Площадь под графиком со 2 по 6-ю секунды гораздо больше, чем площадь под графиком за первые две секунды.

4)Чтобы найти среднюю скорость, нужно разделить весь путь со 2-й по 10-ю секунду на всё соответствующее время, т.е. на 8 с. При этом путь определяем как площадь под графиком, так как у нас есть график в координатах v(t):
$S=S_1+S_2=8·10+{4·7,5}/2=110$ м.
Тогда $v_{ср}={110}/8=13,75$. Утверждение 4 — неверно.

5) Верно. С 6 по 10 сек, тело двигалось равноускоренно, т.к. за равные промежутки времени скорость увеличивается на одну ту же величину (линейная зависимость v(t)).

Ответ: 25

Задача 8

Математический маятник совершает незатухающие колебания между точками А и Б. Точка О соответствует положению равновесия маятника. Используя текст и рисунок, выберите из предложенного ниже списка все верные утверждения. Укажите их номера.

  1. За время, равное периоду колебаний, маятник проходит путь, равный длине дуги АБ.
  2. При перемещении маятника из положения О в положение В потенциальная энергия уменьшается, а кинетическая энергия увеличивается.
  3. В точке О кинетическая энергия маятника максимальна.
  4. Расстояние АБ соответствует амплитуде колебаний координаты.
  5. В точках А и Б потенциальная энергия маятника принимает максимальное значение.
Решение
  1. За время, равное периоду колебаний, маятник проходит путь, равный ДВУМ длинам дуги АБ — «туда и обратно». 1 — неверно.
  2. При перемещении маятника из положения О в положение В потенциальная энергия УВЕЛИЧИВАЕТСЯ (т.к. высота растёт), а кинетическая энергия УМЕНЬШАЕТСЯ (т.к. маятник замедляется). 2 — неверно
  3. В точке О кинетическая энергия маятника максимальна, так как положение равновесия груз маятника проходит с наибольшей скоростью — верно
  4. Амплитуда колебаний координаты — это половина расстояния АБ — отклонение от положения равновесия. 4 — неверно.
  5. В точках А и Б потенциальная энергия маятника принимает максимальное значение, так как груз находится на наибольшей высоте. 5 — верно.

В точке О кинетическая энергия максимальна. Потенциальная энергия принимает максимальное значение в точках А и Б.

Ответ: 35

Задача 9

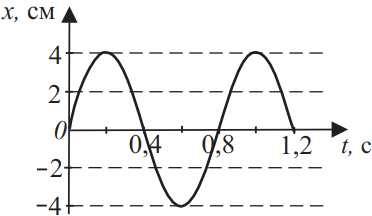
Координата колеблющегося тела меняется так, как показано на графике рисунка. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика и укажите их номера.

  1. Период колебаний тела равен 1 с.
  2. Амплитуда колебаний равна 8 см.
  3. Частота колебаний равна 1,25 Гц.
  4. Амплитуда колебаний равна 4 см.
  5. Период колебаний тела равен 0,4 с.
Решение

Из данного графика очевидно, что $A=4$см (2 — неверно, 4 — верно), период колебаний T=0.8 c (1, 5 — неверно), а частота $v={1}/{T}={1}/{0.8}=1.25$Гц.(3 — верно)

Ответ: 34

Задача 10

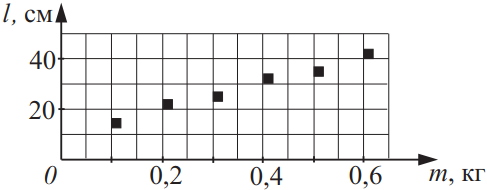
На рисунке приведён график зависимости длины пружины от величины нагрузки. Из приведённого ниже списка выберите два утверждения, соответствующих результатам этого эксперимента, и укажите их номера.

  1. Коэффициент упругости пружины примерно равен 20 Н/м.
  2. Коэффициент упругости пружины примерно равен 30 Н/м.
  3. Коэффициент упругости пружины примерно равен 50 Н/м.
  4. Коэффициент упругости пружины примерно равен 10 Н/м.
  5. Для данного эксперимента выполняется закон Гука.
Решение

$k=F/(l-l_0)$
Если продолжить прямую, видно, что длина недеформированной пружины 10 см
$k=2/(0.2-0.1)=20$ Н/м

Ответ: 15

Задача 11

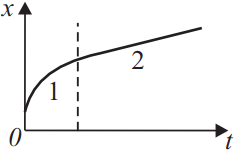
Бусинка скользит по неподвижной горизонтальной спице. На графике изображена зависимость координаты бусинки от времени. Ось Ox параллельна спице. Из приведённого ниже списка на основании графика выберите два верных утверждения о движении бусинки и укажите их номера.

  1. На участке 1 проекция ускорения ax бусинки отрицательна.
  2. На участке 1 модуль скорости остаётся неизменным, а на участке 2 — уменьшается.
  3. На участке 1 модуль скорости увеличивается, а на участке 2 — уменьшается.
  4. На участке 1 модуль скорости уменьшается, а на участке 2 — остаётся неизменным.
  5. В процессе движения вектор скорости бусинки менял направление на противоположное.
Решение

Скорость — это производная координаты по времени. Графически это $tgα$ наклонной графика зависимости координаты от времени. Заметим, что координата все время растет, но на участке 1 — скорость уменьшается, следовательно, проекция ускорения отрицательна. На участке 2, скорость неизменна, а координата растет, тело не меняет направление движения.

Ответ: 14

Задача 12

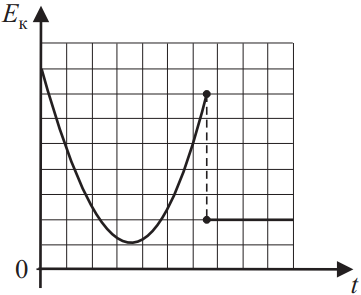
На рисунке представлен схематичный вид графика изменения кинетической энергии тела с течением времени. Выберите два верных утверждения, описывающих движение в соответствии с данным графиком.

  1. В конце наблюдения кинетическая энергия тела равна нулю.
  2. Кинетическая энергия тела в течение всего времени наблюдения увеличивается.
  3. Кинетическая энергия тела в начальный момент времени максимальна.
  4. Тело брошено вертикально вверх с балкона и упало на Землю.
  5. В конце наблюдения скорость тела не равна нулю.
Решение

1) В конце наблюдения $E_к=0$, неверно, т.к. при $t=t_к⇒E_к≠0$, если $E_к=0$, то график должен проходить через ось ординат.

2) $E_к$, в течении всего времени увеличивается, неверно, т.к. при $t={t_к}/{2}$ $E_к=min$, в середине пути кинетическая энергия минимальна.

3) Исходя из графика $E_к$ максимальная в момент (верно) $t=0$.

4) Неверно, т.к. график вертикально брошенного тела, выглядит иначе.

5) При $t_к=t; E_к≠0$ (верно), т.к. $υ≠0⇔E_к≠0$.

Ответ: 35

Задача 13

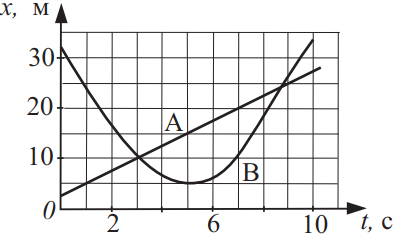
На рисунке приведены графики зависимости координаты от времени для двух тел A и B, движущихся по прямой, вдоль которой и направлена ось Ox. Из приведённого ниже списка выберите два верных утверждения о характере движения тел и укажите их номера.

  1. Тело A движется равномерно.
  2. Тело A движется с постоянным ускорением, равным 5 м/с2.
  3. Первый раз тела A и B встретились в момент времени, равный 3 с.
  4. Вторично тела A и B встретились в момент времени, равный 7 с.
  5. В момент времени t = 5 с тело B достигло максимальной скорости движения.
Решение

1) Тело А движется равномерно, т.к. равномерное движение — это движение, при котором тело за равные промежутки времени проходит одинаковые расстояния (подходит).

2) Ускорение тела А равно нулю, т.к. оно движется с постоянной скоростью $υ={20-10}/{7-3}=2.5м/с$ (не подходит).

3) Графики зависимости координаты от времени для двух тел А и В пересекаются в момент времени $t=3c$, значит, первый раз тела А и В встретились в момент времени, равный 3с (подходит).

Ответ: 13

Задача 14

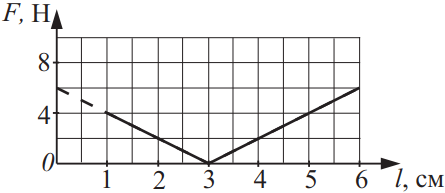
При проведении эксперимента ученик исследовал зависимость модуля силы упругости пружины, которая выражается формулой F (l) = k|l − l0|, где l0 — длина пружины в недеформированном состоянии, от её длины. График полученной зависимости приведён на рисунке. Из приведённого ниже списка выберите все верные утверждения на основании анализа графика и укажите их номера.

  1. Длина пружины в недеформированном состоянии равна 6 см.
  2. Длина пружины в недеформированном состоянии равна 3 см.
  3. При действии силы 2 Н деформация пружины равна 2 см.
  4. При действии силы 4 Н деформация пружины равна 2 см.
  5. Коэффициент жёсткости пружины равен 50 Н/м.
Решение

1) Из графика видно, что длина пружины в не деформированном состоянии равна 3 см, т.к. при l=3см сила упругости $F=OH$(не подходит).

2) Длина пружины в не деформированном состоянии равна 3 см (подходит).

3) При действии сила 2Н деформация пружины равна |2см-3см|=|-1см|=1см или |4см-3см|=1см (не подходит).

4) При действии сила 4Н пружина сжимается или растягивается на 2см, поскольку |1см-3см|=|-2см|=1см или |5см-3см|=2см (подходит).

Ответ: 24

Задача 15

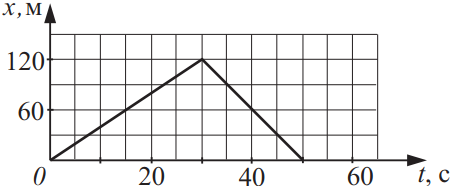
На рисунке приведена зависимость координаты движущегося тела от времени. Из приведённого ниже списка выберите два верных утверждения

  1. Скорость движения тела в интервале времени от 30 до 50 с на 2 м/с больше, чем скорость в интервале времени от 0 до 30 с.
  2. Скорость тела возрастала в интервале времени от 0 до 30 с и убывала в интервале от 30 до 50 с.
  3. Максимальная скорость движения на всём пути равна 2,4 м/с.
  4. За всё время движения тело прошло путь 120 м.
  5. За всё время движения тело прошло путь 240 м.
Решение

1) $υ_1[30-50c]={x_к-x_н}/{t_к-t_н}={0-120}/{50-30}=-{120}/{20}=-6м/с$. Знак «минус» говорит о том, что тело движется в обратном направлении, поэтому возьмем по модулю $υ[30-50c]=6м/с; υ_2[0-30c]={x_к-x_н}/{t_к-t_н}={120-0}/{30-0}={120}/{30}=4м/с; ∆υ=υ_1[30-50c]-υ_2[0-30c]=6-4=2м/с$(подходит).

2) Скорость тела возрастала в интервале времени от 0 до 30с и в интервале от 30 до 50с (не подходит).

3) Максимальная скорость на всем пути равна 6м/с (не подходит).

4) За все время движения тело прошло путь: $S=S_1+S_2=υ_1·∆t_1+υ_1·∆t_2=6·(50-30)+4·(30-0)=6·20+4·30=120+120=240$м (не подходит).

5) За все время движения тело прошло путь 240м (подходит).

Ответ: 15

Задача 16

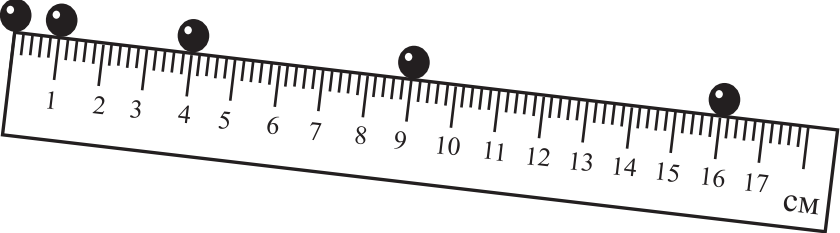
На рисунке приведена стробоскопическая фотография движущегося шарика по жёлобу, образующему некоторый угол с горизонтом. Положения шарика на фотографии показаны через равные промежутки времени. Из приведённого ниже списка выберите два верных утверждения на основании анализа стробоскопической фотографии и укажите их номера.

  1. Движение шарика равномерное.
  2. Скорость шарика увеличивается.
  3. Шарик движется под действием переменной силы.
  4. Если промежуток времени между двумя последовательными положениями шарика равен 2 с, то его ускорение равно 0,5 см/с2.
  5. Импульс шарика в процессе движения остаётся постоянным.
Решение

1) Шарик за одинаковые промежутки времени проходит разные расстояния, значит, его движение неравномерное (не подходит).

2) Движение шарика равноускоренное, значит, скорость шарика увеличивается (подходит).

3) Шарик движется под действием постоянной силы $F↖{→}=ma↖{→}$ (не подходит).

4) $S=0.16м; t=4·2=8c; υ_0=0м/с; a=0.005м/с^2$. При равноускоренном движении перемещение равно: $S=υ_0е+{at^2}/{2}=0·8+{0.005·(8)^2}/{2}={0.005·64}/{2}=32·0.005=0.16=16$см (подходит).

Ответ: 24

Задача 17

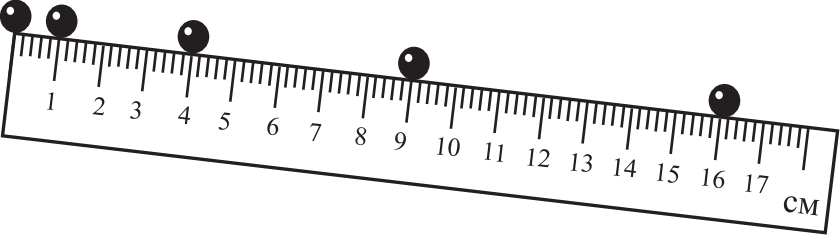
На рисунке приведена стробоскопическая фотография движущегося шарика по жёлобу, образующему некоторый угол с горизонтом. Положения шарика на фотографии показаны через равные промежутки времени. Из приведённого ниже списка выберите два верных утверждения на основании анализа стробоскопической фотографии и укажите их номера.

  1. Шарик движется с переменным ускорением.
  2. Скорость шарика уменьшается.
  3. Шарик движется под действием постоянной силы.
  4. Если промежуток времени между двумя последовательными положениями шарика равен 2 с и он начинал движение из состояния покоя, то его скорость в точке с координатой 9 см равна 3 см/с.
  5. Импульс шарика в процессе движения уменьшается.
Решение

1) Шарик движется с постоянным ускорением (не подходит).

2) Скорость шарика увеличивается, т.к. за равные промежутки времени он проходит все больше расстояния (не подходит).

3) Шарик движется под действием постоянной силы $F=m·a$ (подходит).

4) $υ_k=υ_0+at$(1), т.к. $υ_0=0$м/с, поскольку начинает движение из состояния покоя, то $υ_k=at$(2). Перемещение $S={at^2}/{2}⇒a={2·S}/{t^2}$(3), где $S=0.09$м, $t=6c$ (т.к. 3 вспышки стробослота), тогда $a={2·0.09}/{36}=0.005$, тогда $υ=at=0.005·6=0.03=3$см/с (подходит).

Ответ: 34

Задача 18

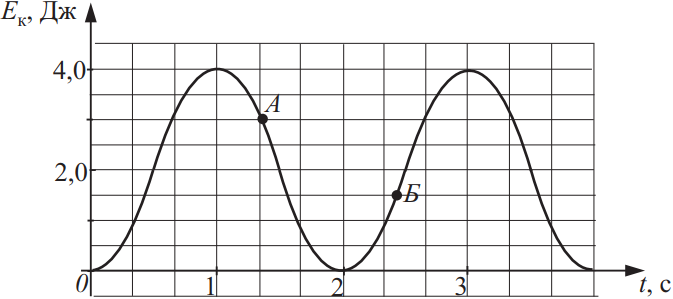
На рисунке приведён график зависимости кинетической энергии тела от времени t. Выберите все верные утверждения на основании анализа представленного графика.

  1. Тело движется под действием постоянной силы.
  2. Потенциальная энергия тела в точке Б равна 1,5 Дж.
  3. Период колебаний тела равен 4 с.
  4. Максимальное значение потенциальной энергии равно значению потенциальной энергии в точке А.
  5. Полная механическая энергия тела равна 4 Дж.
Решение

1. Из графика видно, что время одного полного колебания равно 4с, т.к. в течение одного полного колебания тело проходит три максимальных значения (или три минимальных значения) кинетической энергии, т.е. период колебаний тела равен 4с (верно).

2. Поскольку полная механическая энергия тела равна: $E=E_{к,max}=E_{к,max}=E_к+Е_п$(1), а максимальная кинетическая энергия тела равна 4 Дж, то полная механическая энергия тела равна 4 Дж (верно).

Ответ: 35

Задача 19

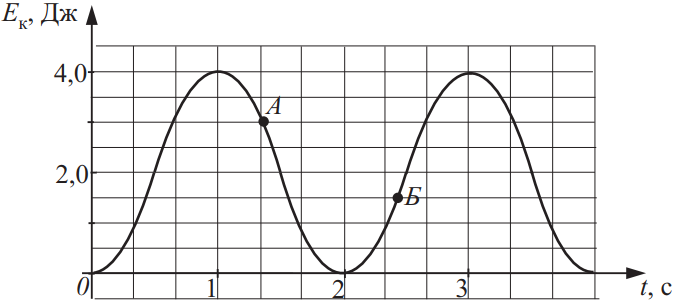
На рисунке приведён график зависимости кинетической энергии тела от времени t. Из приведённого ниже списка выберите все верные утверждения на основании анализа представленного графика и укажите их номера.

  1. Тело совершает гармонические колебания.
  2. Потенциальная энергия тела в точке A равна 1 Дж.
  3. Период колебаний тела равен 2 с.
  4. Максимальное значение потенциальной энергии равно потенциальной энергии в точке Б.
  5. Частота колебаний тела равна 4 Гц.
Решение

1. Тело совершает гармонические колебания, т.к. гармонические колебания — это колебания, подчиняющиеся закону синуса или косинуса, а на графике мы видим синусоиду (1 — верно).

2. Поскольку полная механическая энергия тела равна: $E=E_{п,max}=E_{п,max}=E_к+Е_п$(1), где $E_к$ — кинетическая энергия тела, $E_{к,max}=4$Дж, $E_п$ — потенциальная энергия тела. В точке А $E_к=3$Дж, значит, $E_п=E-E_к=E_{к,max}-E_к=4-3=1$Дж (2 — верно)

3. За один период колебаний тела, успевает произойти два колебания кинетической энергии, поэтому период колебаний тела равен 4с, а не 2. (3 — неверно)

4. Максимальное значение потенциальной энергии будет в той точке, в которой кинетическая энергия минимальна. Точка Б под это условие не подходит (4 — неверно)

5. Частота колебания тела равна: $v=1/T=1/4=0,25$ Гц (5 — неверно)

Ответ: 12

Задача 20

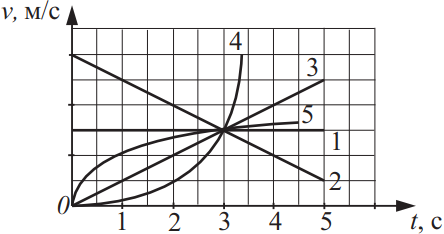
На рисунке представлены графики зависимости проекции скорости v на некоторую ось от времени t для пяти тел. Из приведённого ниже списка выберите два верных утверждения на основании анализа представленных графиков и укажите их номера.

  1. Наибольшей начальной скоростью обладало второе тело.
  2. Первое тело покоится.
  3. Наименьший путь за первые три секунды прошло второе тело.
  4. Третье тело движется равноускоренно.
  5. Пятое тело совершает равнопеременное движение.
Решение

Из графика видно, что в момент времени t=0с наибольшей начальной скоростью обладает тело 2.

Третье тело движется равноускоренно, т.к. график скорости напрвлен вверх.

Ответ: 14

Рекомендуемые курсы подготовки

Источник

Понравилась статья? Поделить с друзьями:
  • Потемнело низко с тревожными криками пронеслись в глубь леса испуганные птицы егэ вариант
  • Пофиг на экзамены
  • Поучительный рассказ для 5 класса сочинение
  • Потапова егэ по русскому
  • Поучение младшей сестре по литературе 7 класс сочинение