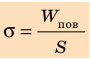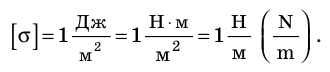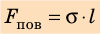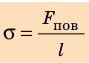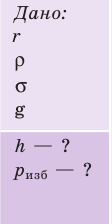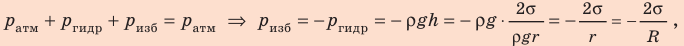Сегодня поверхностно рассматриваем тему поверхностного натяжения и решаем соответствующие задачи по физике.
Даже если вы не большой любитель жидкости, подписывайтесь на наш телеграм-канал, это интересно и полезно для всех.
Поверхностное натяжение, задачи
Задача №1. Поверхностное натяжение
Условие
Для определения коэффициента поверхностного натяжения воды была использована пипетка с диаметром выходного отверстия d=2 мм. Оказалось, что n=40 капель имеют массу m=1,9 г. Каким по этим данным получится коэффициент поверхностного натяжения «сигма»?
Решение
На каплю действует сила тяжести и сила поверхностного натяжения. Эти силы уравновешивают друг друга. Из условия задачи можно найти массу одной капли m0 и длину ее окружности l:
Далее запишем условие равновесия капли:
Отсюда находим коэффициент поверхностного натяжения:
Ответ: 75,63*10^-3 Н/м.
Задача №2. Капиллярные явления
Условие
В капиллярной трубке радиусом 0,5 мм жидкость поднялась на высоту 11 мм. Оценить плотность данной жидкости, если ее коэффициент поверхностного натяжения равен 22 мН/м.
Решение
Для капилляра существует формула:
Альфа в этой формуле – угол смачивания стенки капилляра жидкостью. Пример его равным 90 градусов.
Ответ: 800 килограмм на кубический метр.
Задача №3. Поверхностное натяжение
Условие
В дне сосуда со ртутью имеется круглое отверстие диаметром 70 мкм. При какой максимальной высоте слоя ртути H она не будет вытекать через отверстие?
Решение
Ртуть не будет вытекать до тех пор, пока сила ее давления не превысит силу поверхностного натяжения:
Значения коэффициента поверхностного натяжения разных жидкостей берутся в справочнике.
Ответ: 0,2 м.
Задача №4. Поверхностное натяжение
Условие
Швейная игла имеет длину 3,5 см и массу 0,3 г. Будет ли игла лежать на поверхности воды, если ее положить аккуратно?
Решение
Найдем силу тяжести, которая действует на иглу и сравним ее с силой поверхностного натяжения.
Ответ: Так как сила тяжести больше, игла утонет.
Задача №5. Поверхностное натяжение
Условие
Тонкое алюминиевое кольцо радиусом 7,8 см соприкасается с мыльным раствором. Каким усилием можно оторвать кольцо от раствора? Температуру раствора считать комнатной. Масса кольца 7 г.
Решение
На кольцо действуют силы поверхностного натяжения, сила тяжести и внешняя сила, стремящаяся оторвать кольцо от поверхности. Найдем силу поверхностного натяжения:
Множитель «2» используется в формуле, так как кольцо взаимодействует с жидкостью двумя своими сторонами.
Теперь запишем условие отрыва кольца:
Значение поверхностного натяжения мыльного раствора при комнатной температуре возьмем из таблицы, подставим числа, и получим:
Ответ: 0,11 Н.
Вопросы на тему «Поверхностное натяжение и свойства жидкостей»
Вопрос 1. Что такое жидкость?
Ответ. Жидкость – физическое тело, которое не может самостоятельно сохранять свою форму. Агрегатное состояние вещества между твердым телом и газом.
Вопрос 2. Какие свойства жидкости вы знаете?
Ответ. Среди основных свойств жидкости можно выделить:
- текучесть;
- вязкость;
- сохранение объема;
- поверхностное натяжение.
Вопрос 3. Что такое поверхностное натяжение?
Ответ. Поверхностное натяжение – это явление, при котором жидкость стремиться приобрести форму с наименьшей возможной площадью поверхности.
Примеры поверхностного натяжения в природе:
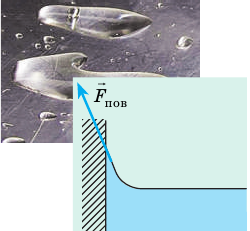
- Именно благодаря поверхностному натяжению в поле силы тяжести Земли жидкость приобретает форму капли.
- В отсутствие силы тяжести жидкости капля примет шарообразную форму.
- Водомерка удерживается на поверхности воды благодаря силе поверхностного натяжения.
Коэффициент поверхностного натяжения – коэффициент, равный работе, которую необходимо совершить для образования поверхности жидкости площадью S при постоянной температуре.
Вопрос 4. Что такое капиллярные явления?
Ответ. Капиллярные явления – подъем или опускание жидкости в капиллярах (трубках малого диаметра).
Вопрос 5. Что называется смачиванием?
Ответ. Смачивание – это искривление поверхности жидкости вблизи твердого тела. Возникает из-за взаимодействия молекул жидкости с молекулами твердого тела.
Количественная характеристика этого явления – угол смачивания.
Нужна помощь в решении заданий по учебе? Профессиональный студенческий сервис всегда готов ее оказать! Оформляйте заявку в любое время суток и забудьте о наболевших вопросах.
Поверхностное натяжение: задачи среднего уровня
В этой статье рассмотрены чуть более сложные задачи на поверхностное натяжение. Задачи попроще ищите в похожих статьях. Также понадобится знание уравнения Менделеева-Клапейрона.
Задача 1.
В закрытом сосуде с воздухом при давлении находится мыльный пузырек диаметром
Поверхностное натяжение: простые задачи
В этой статье рассмотрим простые задачи на поверхностное натяжение: будем определять коэффициент поверхностного натяжения, силу поверхностного натяжения — при этом надо помнить, что если имеем дело с пленкой, то у нее две стороны, поэтому силу нужно удваивать в этом случае.
Задача 1. С какой силой действует мыльная пленка…
23.05.2017 10:20:17 | Автор: Анна
|
|
Поверхностное натяжение. Капиллярные явления.

Для начала вспомним все, что мы знаем о поверхностном натяжении. Это явление наблюдается на поверхностях жидкостей и связано с тем, что молекулы на поверхности слабо взаимодействуют с паром жидкости, в то время как молекулы внутри объема испытывают равные силы притяжения со стороны всех…
09.08.2014 12:43:16 | Автор: Анна
|
|
в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 238 … 41–60 | 61–80 | 81–100 | 101–120 | 121–140 | 141–160 | 161–180 | 181–200 …
Добавить в вариант
Задания Д29 C2 № 9292
На вертикальной оси укреплена горизонтальная штанга, по которой могут без трения перемещаться два груза массами m1 = 100 г и m2 = 300 г, связанные тонкой нерастяжимой нитью длиной l = 18 см. Определите, с какой частотой штанга вращается вокруг вертикальной оси, если натяжение нити составляет 100 Н.
Источник: ЕГЭ по физике 07.06.2017. Основная волна
Задания Д28 C1 № 3558
Какую силу давления оказывает нить на ось блока? Массы грузов одинаковы и равны
Трение не учитывать. Нить невесома и нерастяжима.
1) mg
2)
3)
4)
Однородный брусок AB массой M постоянного прямоугольного сечения лежит на гладкой горизонтальной поверхности стола, свешиваясь с него менее чем наполовину (см. рисунок). К правому концу бруска прикреплена лёгкая нерастяжимая нить. Другой конец нити закреплён на меньшем из двух дисков идеального составного блока. На большем диске этого блока закреплена другая лёгкая нерастяжимая нить, на которой висит груз массой m = 1 кг. Диски скреплены друг с другом, образуя единое целое, где R = 10 см, r = 5 см.
Сделайте рисунок с указанием сил, действующих на брусок M, блок и груз m. Найдите минимальное значение M, при котором система тел остаётся неподвижной. Обоснуйте применимость используемых законов к решению задачи.
Источник: Демонстрационная версия ЕГЭ—2023 по физике
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Центр. Вариант 4.
Пластилиновый шарик массой подвешенный на нити длиной
отводят в сторону и отпускают. В нижней точке качения шарик налетает на покоящийся брусок. В результате абсолютно неупругого соударения брусок приобретает скорость
Определите массу бруска M, если в момент столкновения натяжение нити было
Какие законы Вы используете для описания взаимодействия тел? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ 20.06.2016 по физике. Основная волна волна. Вариант 68 (Часть С)
Математический маятник, грузик которого имеет массу m = 8 г, совершает малые колебания в поле силы тяжести с периодом T1 = 0,7 с. Грузик зарядили и включили направленное вниз однородное вертикальное электрическое поле, модуль напряжённости которого равен E = 3 кВ/м. В результате этого период колебаний маятника стал равным T2 = 0,5 с. Найдите заряд q грузика.
Математический маятник, грузик которого имеет массу m = 10 г, совершает малые колебания в поле силы тяжести с периодом T1 = 0,6 с. Грузик зарядили и включили направленное вниз однородное вертикальное электрическое поле, модуль напряжённости которого равен E = 2 кВ/м. В результате этого период колебаний маятника стал равным T2 = 0,4 с. Найдите заряд q грузика.
Задания Д29 C2 № 3813
Система из грузов m и M и связывающей их лёгкой нерастяжимой нити в начальный момент покоится в вертикальной плоскости, проходящей через центр закреплённой сферы. Груз m находится в точке А на вершине сферы (см. рис.). В ходе возникшего движения груз m отрывается от поверхности сферы, пройдя по ней дугу 30°. Найдите массу m, если М = 100 г. Размеры груза m ничтожно малы по сравнению с радиусом сферы. Трением пренебречь. Сделайте схематический рисунок с указанием сил, действующих на грузы.
Источник: Демонстрационная версия ЕГЭ—2013 по физике.
Задания Д29 C2 № 7934
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рис.). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 45°. Найдите модуль силы
действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
Источник: ЕГЭ 20.06.2016 по физике. Основная волна. Вариант 428. (Часть С)
Задания Д29 C2 № 7955
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рис.). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 30°. Найдите модуль силы
действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
Источник: ЕГЭ 20.06.2016 по физике. Основная волна волна. Вариант 3 (Часть С)
Система грузов M, m1 и m2, показанная на рисунке, движется из состояния покоя. Поверхность стола — горизонтальная гладкая. Коэффициент трения между грузами M и m1 равен μ = 0,3. Грузы M и m2 связаны легкой нерастяжимой нитью, которая скользит по блоку без трения. Пусть M = 2,4 кг, m1 = m2 = m. При каких значениях m грузы M и m1 движутся как одно целое? Сделайте рисунок с указанием сил, действующих на грузы.
Какие законы Вы использовали для описания движения системы грузов? Обоснуйте их применимость к данному случаю.
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рис.). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 45°. Найдите модуль силы
действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
Какие законы Вы используете для описания равновесия стержня? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ 20.06.2016 по физике. Основная волна. Вариант 428. (Часть С)
Тонкий однородный стержень АВ шарнирно закреплён в точке А и удерживается горизонтальной нитью ВС (см. рис.). Трение в шарнире пренебрежимо мало. Масса стержня m = 1 кг, угол его наклона к горизонту α = 30°. Найдите модуль силы
действующей на стержень со стороны шарнира. Сделайте рисунок, на котором укажите все силы, действующие на стержень.
Какие законы Вы используете для описания равновесия стержня? Обоснуйте их применение к данному случаю.
Источник: ЕГЭ 20.06.2016 по физике. Основная волна волна. Вариант 3 (Часть С)
Система из грузов m и M и связывающей их лёгкой нерастяжимой нити в начальный момент покоится в вертикальной плоскости, проходящей через центр закреплённой сферы. Груз m находится в точке А на вершине сферы (см. рис.). В ходе возникшего движения груз m отрывается от поверхности сферы, пройдя по ней дугу 30°. Найдите массу m, если М = 100 г. Размеры груза m ничтожно малы по сравнению с радиусом сферы. Трением пренебречь. Сделайте схематический рисунок с указанием сил, действующих на грузы.
Какие законы Вы использовали для описания движения тел? Обоснуйте их применимость к данному случаю.
Источник: Демонстрационная версия ЕГЭ—2013 по физике.
Однородный тонкий стержень массой m = 1 кг одним концом шарнирно прикреплён к потолку, а другим концом опирается на массивную горизонтальную доску, образуя с ней угол α = 30°. Под действием горизонтальной силы
доска движется поступательно влево с постоянной скоростью (см. рис.). Стержень при этом неподвижен. Найдите F, если коэффициент трения стержня по доске μ = 0,2. Трением доски по опоре и трением в шарнире пренебречь.
Какие законы Вы используете для описания равновесия системы тел? Обоснуйте их применение к данному случаю.
Источник: Демонстрационная версия ЕГЭ—2016 по физике.
Задания Д29 C2 № 3657
Два одинаковых груза массой каждый подвешены на концах невесомой и нерастяжимой нити, перекинутой через невесомый блок с неподвижной осью. На один из них кладут перегрузок массой
после чего система приходит в движение. Найдите модуль силы F, действующей на ось блока во время движения грузов. Трением пренебречь.
Задания Д12 B23 № 5374
Массивный груз, покоящийся на горизонтальной опоре, привязан к лёгкой нерастяжимой верёвке, перекинутой через идеальный блок. К верёвке прикладывают постоянную силу направленную под углом
к горизонту (см. рисунок). Зависимость модуля ускорения груза от модуля силы
представлена на графике. Чему равна масса груза?
1) 0,85 кг
2) 0,42 кг
3) 0,60 кг
4) 6,0 кг
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Центр. Вариант 1.
Задания Д12 B23 № 5409
Массивный груз, покоящийся на горизонтальной опоре, привязан к лёгкой нерастяжимой верёвке, перекинутой через идеальный блок. К верёвке прикладывают постоянную силу направленную под углом
к горизонту (см. рисунок). Зависимость модуля ускорения груза от модуля силы
представлена на графике. Чему равна масса груза?
1) 3 кг
2) 0,3 кг
3) 0,6 кг
4) 6 кг
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Центр. Вариант 2.
Задания Д12 B23 № 5444
Массивный груз, покоящийся на горизонтальной опоре, привязан к лёгкой нерастяжимой верёвке, перекинутой через идеальный блок. К верёвке прикладывают постоянную силу направленную под углом
к горизонту (см. рисунок). Зависимость модуля ускорения груза от модуля силы
представлена на графике. Чему равна масса груза?
1) 1,2 кг
2) 0,3 кг
3) 0,6 кг
4) 6 кг
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Центр. Вариант 3.
Задания Д12 B23 № 5514
Массивный груз, покоящийся на горизонтальной опоре, привязан к лёгкой нерастяжимой верёвке, перекинутой через идеальный блок. К верёвке прикладывают постоянную силу направленную под углом
к горизонту (см. рисунок). Зависимость модуля ускорения груза от модуля силы
представлена на графике. Чему равна масса груза?
1) 3,0 кг
2) 0,42 кг
3) 0,21 кг
4) 0,30 кг
Источник: ЕГЭ по физике 06.06.2013. Основная волна. Центр. Вариант 6.
Всего: 238 … 41–60 | 61–80 | 81–100 | 101–120 | 121–140 | 141–160 | 161–180 | 181–200 …
Канал видеоролика: ЕГЭ Физика
Смотреть видео:
Свежая информация для ЕГЭ и ОГЭ по Физике (листай):
С этим видео ученики смотрят следующие ролики:

ЕГЭ. Олимпиады. ВУЗ — Задача 2.4.2. (поверхностное натяжение)
ЕГЭ Физика

ЕГЭ. Олимпиады. ВУЗ — Задача 1.1.1. (кинематика)
ЕГЭ Физика

ЕГЭ. Олимпиады. ВУЗ — Задача 1.2.1. (динамика)
ЕГЭ Физика

ЕГЭ. Олимпиады. ВУЗ — Задача 1.3.1. (законы сохранения в механике)
ЕГЭ Физика
Облегчи жизнь другим ученикам — поделись! (плюс тебе в карму):
05.08.2019
- Комментарии
RSS
Написать комментарий
Нет комментариев. Ваш будет первым!
Ваше имя:
Загрузка…
Содержание:
Поверхностное натяжение жидкости:
В отличие от газов жидкости имеют свободную поверхность. Молекулы, расположенные на поверхности жидкости, и молекулы внутри жидкости находятся в разных условиях:
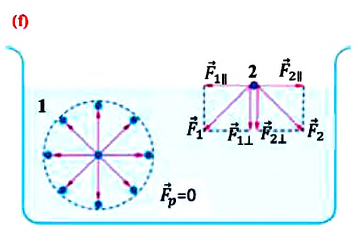
a) молекулы внутри жидкости окружены другими молекулами жидкости со всех сторон. Молекула 1 внутри жидкости испытывает действие соседних молекул со всех сторон, поэтому равнодействующая сил притяжения, действующих на нее, равна нулю (f; молекула 1);
b) молекулы на поверхности жидкости испытывают действие со стороны соседних молекул жидкости только сбоку и снизу. Притяжение со стороны молекул газа (пара жидкости или воздуха) над жидкостью во много раз слабее, чем со стороны молекул жидкости, поэтому не принимаются во внимание (f; молекула 2). В результате каждая из равнодействующих сил
Сила поверхностного натяжения
Сила поверхностного натяжения — это сила, направленная по касательной к поверхности жидкости, перпендикулярно к линии, ограничивающей поверхность жидкости, и стремящаяся сократить площадь поверхности жидкости. Сила поверхностного натяжения прямо пропорциональна длине границы соприкосновения свободной поверхности жидкости с твердым телом:
Здесь 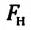
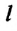
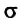
Коэффициент поверхностного натяжения
Коэффициент поверхностного натяжения — численно равен силе поверхностного натяжения, приходящейся на единицу длины линии, ограничивающей поверхность жидкости:
Значение коэффициента поверхностного натяжения зависит от вида жидкости и ее температуры, то есть с увеличением температуры жидкости коэффициент его поверхностного натяжения уменьшается и при критической температуре равен нулю. Единица коэффициента поверхностного натяжения в СИ:
Смачивающая и несмачивающая жидкость. При внимательном рассмотрении можно увидеть искривление поверхности жидкости на границе между жидкостью и твердым телом.
Мениск — это искривление свободной поверхности жидкости в месте ее соприкосновении с поверхностью твердого тела (или другой жидкости). Угол между поверхностью мениска и поверхностью твердого тела называется краевым углом.
Значение краевого угла 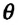
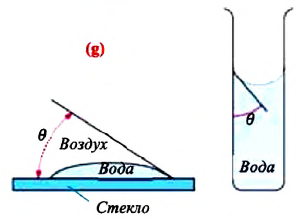
Смачивающая жидкость —это жидкость, у которой краевой угол острый. Сила взаимного притяжения между молекулами смачивающей жидкости и твердого тела больше, чем силы взаимного притяжения между молекулами самой жидкости. В результате свободная поверхность жидкости в сосуде становится вогнутой, например, вода в стеклянном сосуде — смачивающая жидкость (g).
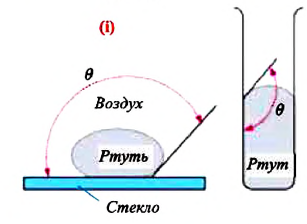
Несмачивающая жидкость — это жидкость, у которой краевой угол тупой. Сила взаимного притяжения между молекулами несмачивающей жидкости и твердого тела меньше, чем сила взаимного притяжения между молекулами самой жидкости. В результате свободная поверхность жидкости в сосуде бывает выпуклой, например, ртуть в стеклянном сосуде — несмачивающая жидкость (i).
Капиллярные явления
В повседневной жизни встречаются и используются тела, с легкостью впитывающие в себя воду, например, полотенце, промокательная бумага, сахар, кирпич, растения и др. Это свойство в телах объясняется существованием в них большого количества очень узких трубочек — капилляров.
Капилляр — это узкая трубка (канал) диаметром меньше 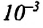
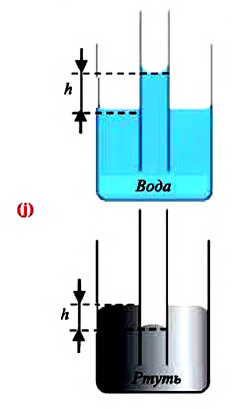
Капиллярными явлениями называют явления подъема смачивающей и опускания несмачивающей жидкости по капилляру относительно общего уровня жидкости под действием сил поверхностного натяжения (j).
В таблице 6.4 дана зависимость между величинами, характеризующими жидкость, поднимающуюся в капилляре.
Таблица 6.4
|
Характеристики жидкости, поднимающейся в капилляре |
Формула |
| Вес жидкости, поднимающейся в капилляре |
Где |
| Масса жидкости, поднимающейся в капилляре | 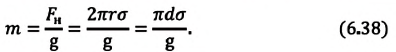 |
| Высота жидкости, поднимающейся в капилляре |
Если жидкость полностью смачиваемая, то получаем в Где |
| Давление жидкости, поднимающейся в капилляре | 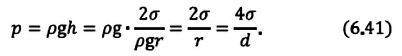 |
Поверхностное натяжение жидкости
Некоторые виды пауков могут передвигаться по поверхности воды не проваливаясь, как будто эта поверхность покрыта невидимой тонкой пленкой. такое же впечатление создается, если наблюдать за вытеканием воды из маленького отверстия — вода течет не тоненькой струйкой, а образует капли. Бумажная салфетка впитывает воду, едва коснувшись ее поверхности. какая сила является причиной всех этих явлений?
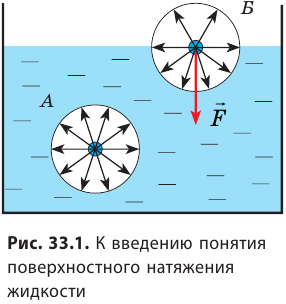
Каковы особенности поверхностного слоя жидкости
На свободной поверхности жидкости молекулы находятся в особых условиях, отличающихся от условий, в которых находятся молекулы внутри жидкости. Рассмотрим две молекулы — А и Б (рис. 33.1): молекула А находится внутри жидкости, а молекула Б — на ее поверхности. Молекула А окружена другими молекулами жидкости равномерно, поэтому силы, действующие на молекулу А со стороны молекул, попадающих в сферу межмолекулярного взаимодействия, скомпенсированы, то есть их равнодействующая равна нулю.
Молекула Б с одной стороны окружена молекулами жидкости, а с другой — молекулами газа. Со стороны жидкости на нее действует гораздо больше молекул, чем со стороны газа, поэтому равнодействующая F межмолекулярных сил направлена в глубь жидкости. Чтобы молекула из глубины попала в поверхностный слой, нужно совершить работу против межмолекулярных сил. Это означает, что молекулы поверхностного слоя жидкости (по сравнению с молекулами внутри жидкости) обладают избыточной потенциальной энергией. Эта избыточная энергия является частью внутренней энергии жидкости и называется поверхностной энергией (Wпов). Очевидно, что чем больше площадь S поверхности жидкости, тем больше поверхностная энергия: W S пов = σ , где σ (сигма) — коэффициент пропорциональности, который называют поверхностным натяжением жидкости.
Поверхностное натяжение жидкости — физическая величина, которая характеризует данную жидкость и равна отношению поверхностной энергии к площади поверхности жидкости:
Единица поверхностного натяжения в СИ — ньютон на метр:
Поверхностное натяжение жидкости определяется силами межмолекулярного взаимодействия, поэтому оно зависит:
- от природы жидкости: у летучих жидкостей (эфир, спирт, бензин) поверхностное натяжение меньше, чем у нелетучих (ртуть, жидкие металлы);
- температуры жидкости: чем выше температура жидкости, тем меньше поверхностное натяжение;
- присутствия в составе жидкости поверхностно активных веществ — их наличие уменьшает поверхностное натяжение;
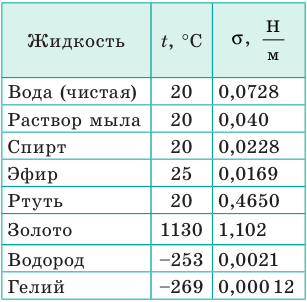
- свойств газа, с которым жидкость граничит. В таблицах обычно приводят значение поверхностного натяжения на границе жидкости и воздуха при определенной температуре (табл. 1).
Таблица 1
Поверхностное натяжение σ некоторых жидкостей
Что такое сила поверхностного натяжения
Поскольку поверхностный слой жидкости обладает избыточной потенциальной энергией (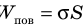
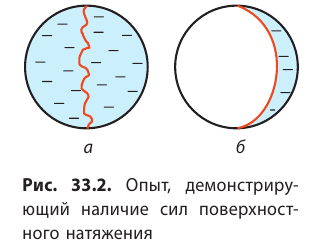
Наличие сил поверхностного натяжения делает поверхность жидкости похожей на натянутую резиновую пленку, однако упругие силы в резиновой пленке зависят от площади ее поверхности (от того, насколько пленка деформирована), а поверхность жидкости всегда «натянута» одинаково, то есть силы поверхностного натяжения не зависят от площади поверхности жидкости. Наличие сил поверхностного натяжения можно доказать с помощью такого опыта. Если проволочный каркас с закрепленной на нем нитью опустить в мыльный раствор, каркас затянется мыльной пленкой, а нить приобретет произвольную форму (рис. 33.2, а).
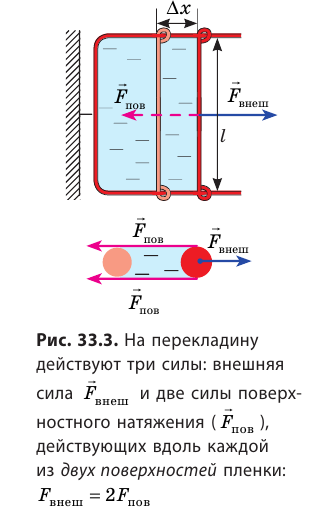
Если осторожно проткнуть иглой мыльную пленку по одну сторону от нити, сила поверхностного натяжения мыльного раствора, действующая с другой стороны, натянет нить (рис. 33.2, б). Опустим в мыльный раствор проволочную рамку, одна из сторон которой подвижна. На рамке образуется мыльная пленка (рис. 33.3). Будем растягивать эту пленку, действуя на перекладину (подвижную сторону рамки) с некоторой силой 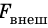
Если под действием этой силы перекладина переместится на ∆x , то внешние силы совершат работу: 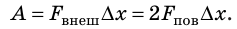
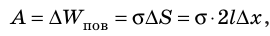
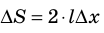
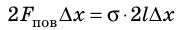
Таким образом, поверхностное натяжение σ численно равно силе поверхностного натяжения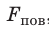
С одним из методов определения поверхностного натяжения жидкости вы ознакомитесь, выполняя лабораторную работу № 7.
- Заказать решение задач по физике
Где проявляется поверхностное натяжение
В жизни вы постоянно сталкиваетесь с проявлениями сил поверхностного натяжения. Так, благодаря ему на поверхности воды удерживаются легкие предметы (рис. 33.4) и некоторые насекомые.
Рис. 33.4. Монетка удерживается на поверхности воды благодаря силе поверхностного натяжения. (Чтобы провести такой опыт, монетку нужно потереть между пальцев и осторожно опустить на поверхность воды.)
Когда вы ныряете, ваши волосы расходятся во все стороны, но как только вы окажетесь над водой, волосы слипнутся, так как в этом случае площадь свободной поверхности воды намного меньше, чем при раздельном расположении прядей в воде. По этой же причине можно лепить фигуры из влажного песка: вода, обволакивая песчинки, прижимает их друг к другу.
Рис. 33.5. Капля удерживается около небольшого отверстия до тех пор, пока сила поверхностного натяжения уравновешивает силу тяжести
Стремлением жидкости уменьшить площадь поверхности объясняется и тот факт, что в условиях невесомости вода принимает форму шара, — при заданном объеме шарообразной форме соответствует наименьшая площадь поверхности. Форму шара приобретают тонкие мыльные пленки (мыльные пузыри). Поверхностным натяжением объясняется образование пены: пузырек газа, достигнув поверхности жидкости, имеет над собой тонкий слой жидкости; если пузырек мал, то архимедовой силы недостаточно, чтобы разорвать двойной поверхностный слой, и пузырек «застревает» вблизи поверхности. Благодаря поверхностному натяжению жидкость не выливается из маленького отверстия тоненькой струйкой, а капает (рис. 33.5), дождь не проливается через ткань зонта или палатки и т. д.
Почему одни жидкости собираются в капли, а другие растекаются
Наличие сил поверхностного натяжения проявляется в сферической форме мелких капелек росы, в каплях воды, разбегающихся по раскаленной плите, в капельках ртути на поверхности стекла. Однако при соприкосновении с твердым телом сферическая форма капли, как правило, не сохраняется. Форма свободной поверхности жидкости зависит также от сил взаимодействия молекул жидкости с молекулами твердого тела.
Если силы взаимодействия между молекулами жидкости больше, чем силы взаимодействия между молекулами жидкости и твердого тела, жидкость не смачивает поверхность твердого тела (рис. 33.6). Например, ртуть не смачивает стекло, а вода не смачивает покрытую сажей поверхность.
Рис. 33.6. Капля несмачивающей жидкости принимает форму, близкую к сферической, а поверхность жидкости вблизи стенки сосуда является выпуклой
Если же капельку ртути поместить на цинковую пластину, то капелька будет стремиться растечься по поверхности пластины; так же ведет себя и капелька воды на стекле (рис. 33.7). Если силы взаимодействия между молекулами жидкости меньше сил взаимодействия между молекулами жидкости и твердого тела, жидкость смачивает поверхность твердого тела.
Рис. 33.7. Капля смачивающей жидкости стремится растечься по поверхности твердого тела, а вблизи стенки сосуда поверхность жидкости принимает вогнутую форму
Почему жидкость поднимается в капиллярах
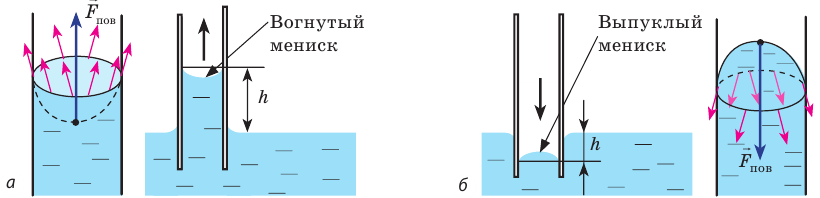
В природе часто встречаются тела, пронизанные многочисленными мелкими капиллярами (от лат. capillaris — волосяной) — узкими каналами произвольной формы. Такую структуру имеют бумага, дерево, почва, многие ткани и строительные материалы. В цилиндрических капиллярах искривленная поверхность жидкости представляет собой часть сферы, которую называют мениском. У смачивающей жидкости образуется вогнутый мениск (рис. 33.8, а), а у несмачивающей — выпуклый (рис. 33.8, б).
Рис. 33.8. капиллярные явления: а — смачивающая жидкость поднимается по капилляру; б — несмачивающая жидкость опускается в капилляре
Поверхность жидкости стремится к минимуму потенциальной энергии, а искривленная поверхность обладает большей площадью по сравнению с площадью сечения капилляра, поэтому поверхность жидкости стремится выровняться и под ней возникает избыточное (отрицательное или положительное) давление — лапласово давление (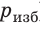
Под вогнутой поверхностью (жидкость смачивает капилляр) лапласово давление отрицательное и жидкость втягивается в капилляр. Так поднимаются влага и питательные вещества в стеблях растений, керосин по фитилю, влага в почве. Вследствие лапласового давления салфетки или ткань впитывают воду, брюки в дождливую погоду сильно намокают снизу и т. д. Под выпуклой поверхностью (жидкость не смачивает капилляр) лапласово давление положительное и жидкость в капилляре опускается. Чем меньше радиус капилляра, тем больше высота подъема (или опускания) жидкости (см. задачу ниже).
Пример решения задачи
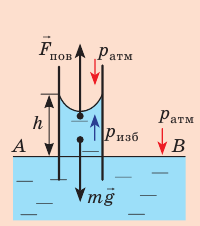
Капиллярную трубку радиусом r одним концом опустили в жидкость, смачивающую внутреннюю поверхность капилляра. На какую высоту поднимется жидкость в капилляре, если плотность жидкости ρ, а ее поверхностное натяжение σ ? Чему равно лапласово давление под вогнутой поверхностью капилляра? Смачивание считайте полным.
Решение:
На жидкость в капилляре действуют сила тяжести и сила поверхностного натяжения (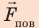
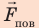
Поиск математической модели, решение
Поскольку m V = ρ , а объем воды в цилиндрическом капилляре 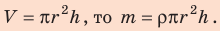
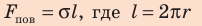
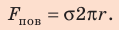
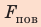

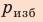
где R — радиус кривизны мениска (при полном смачивании r=R).
Ответ: (Данные выводы следует запомнить!)
Выводы:
- Свойства паров в физике
- Кипение жидкостей в физике
- Электромагнитные явления в физике
- Электромагнитные волны и их свойства
- Расчет количества теплоты при нагревании и охлаждении
- Удельная теплота сгорания топлива
- Плавление и кристаллизация в физике
- Испарение жидкостей в физике

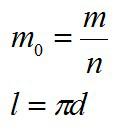
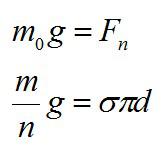
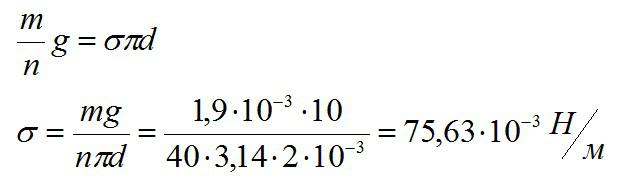
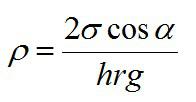
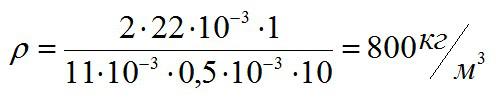
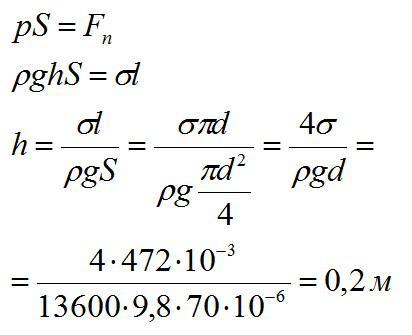
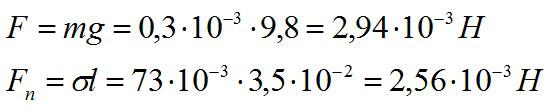
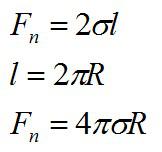
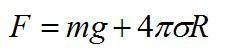
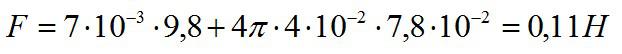


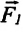


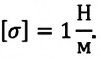
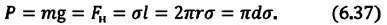
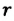 — радиус капилляра,
— радиус капилляра, 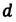 — диаметр капилляра.
— диаметр капилляра.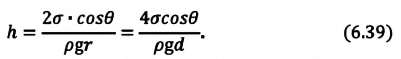
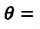
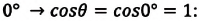

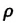 — плотность жидкости, поднимающейся в капилляре. Высота подъема жидкости в капилляре зависит от рода жидкости и обратно пропорциональна радиусу капилляра.
— плотность жидкости, поднимающейся в капилляре. Высота подъема жидкости в капилляре зависит от рода жидкости и обратно пропорциональна радиусу капилляра.