Повторение математики перед экзаменом

Положительно: это отличная возможность стать ближе к учителю и узнать что-то новое

Отрицательно: темы, о которых рассказывают на уроках, мне не интересны

Нейтрально: я хожу на них только потому что урок стоит в расписании

Учитель спрашивает, о чем мы хотим поговорить и прислушивается к нам

На те, которые прописаны в плане от Министерства образования (Россия – страна возможностей, День защитника отечества, год педагога и наставника и т.д.)

На темы об истории страны, в том числе и СВО

Другое (писать в комментариях)

Да

Нет

Самим предлагать темы

Самостоятельно проводить такие уроки

Выезжать на такие уроки за пределы школы (в театры, музеи, кинотеатры)

Добавить к урокам больше интерактива (не просто слушать учителя, а выполнять интересные задания, делать проекты)

Ничего, мне и так все нравится

Мы разговариваем с учителем на равных, можем делиться своим мнением и задавать волнующие вопросы

Как обычный урок: учитель объясняет тему перед классом

Мы создаем проекты, готовим презентации, делаем поделки, играем игры и т.д.

Учитель находит для нас интересных людей, которые делятся с нами своим опытом

Другое

До 5

5-7

8-9

10-11

Обычно базовую математику выбирают ребята, у которых есть план: надо как можно скорее разделаться с бесполезным для поступления предметом и сосредоточиться на своем наборе вступительных. Из этой статьи вы узнаете, как сдать базовую математику максимально быстро и просто.

В этом материале мы сделаем акцент на простых номерах, которые принесут вам балл почти задаром! Они обозначены пометкой «Обязательно делать» — таких заданий 10. Как раз с запасом на ошибки, ведь минимум для сдачи базовой математики — 7 баллов.

Для тех, кто хочет получить выше тройки — это 12 баллов и выше, — мы дали рекомендации по еще 3 задачам. В сумме получается 13 номеров. Решите их все, и твердая четверка у вас в кармане.

Какие задания решать, чтобы сдать базовую математику

Задание 1: обязательно делать

Проверяется ваше умение разделить случаи, когда требуется округлить величину в большую сторону, а когда — в меньшую.

Если вы ходите в магазин с наличными, то сталкиваетесь с подобными задачами каждый день. Разделим 100 рублей на стоимость одной упаковки йогурта. Не забывайте приводить все величины к одной размерности:

100 : 14,6 = 6, 849…

Так сколько баночек йогурта вам продадут? На 7 штук денег не хватает, значит, округлить полученную величину надо до целого в меньшую сторону. Математическое правило округление в этой задаче не поможет.

Ответ: 6.

Если одна пачка рассчитана на 6 рулонов, то на 63 рулона:

63 : 6 = 10,5. 

Но полпачки вам не продаст. Включаем логику: возьмем меньше — не хватит еще половины пачки на три последних рулона. Значит, округлить надо в большую сторону, взять клей с небольшим запасом. Математическое правило округления снова игнорируем.

Ответ: 11.

Задание 2: обязательно делать

Это задача на здравый смысл. Нужно соотнести величины с их возможными значениями.

Вряд ли грузовой автомобиль может весить как 3 шоколадки (300 г), а взрослый человек — 8 т.

Давайте вместе подберем значения.

• Взрослый человек обычно весит от 50 до 100 кг — что из этого подходит? Конечно, 65 кг.
• Грузовой автомобиль достаточно большой и тяжелый, скорее всего, он весит несколько тонн. Нам подходит 8 т.
• Книга обычно не такая большая и весит до 1 кг. Из оставшегося подойдет 300 г.
• А пуговка совсем маленькая. Значит, берем самый легкий вес — 5 г.

Ответ:

Главное — внимательно перенести ответы в бланк: 3142.

Задание 3: обязательно делать

Задание на работу с графиком, диаграммой или таблицей. Вооружайтесь карандашом, читайте условие с предельной внимательностью и безжалостно отмечайте нужные по условию значения на изображении в КИМ. Вы и представить не можете, сколько выпускников теряет тут баллы по невнимательности.

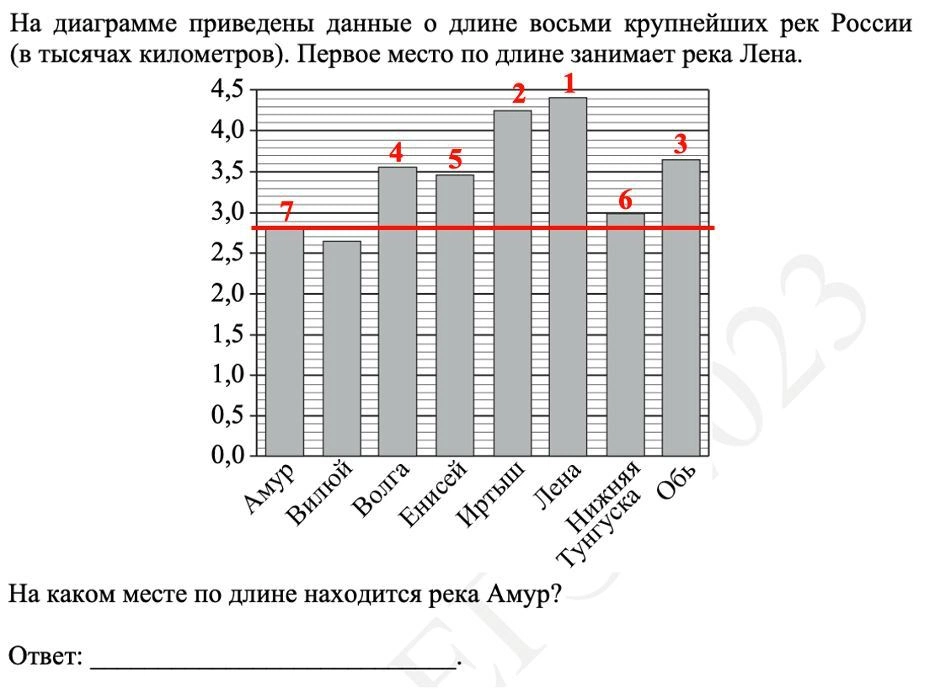
Мы ярко отметили уровень, соответствующий Амуру, в итоге посчитать все более длинные реки стало проще простого. У вас на экзамене будет так же наглядно!

Ответ: 7.

Задание 4: обязательно делать

Задание проверяет навык работы с формулами. Алгоритм решения напоминает решение задачек на уроке по физике:

• Выписываем формулу из условия.
• Определяем, что нужно найти: единственную букву, значение которой не дано.
• Выражаем искомую величину.
• Подставляем значения из условия в формулу.
• Ищем неизвестное.

Самое трудное тут — правильно выразить искомую величину. Для этого повторяем порядок выполнения арифметических операций, свойства умножения, тренируемся перекидывать через равно множители и слагаемые.

И да, в базе эта задача проста настолько, что даже перекидывать ничего не придется. Нужная величина уже будет слева от равно.

Задание 5: обязательно делать

Простая задача на определение вероятности, которая поможет вам точно сдать базовую математику.

Решаем с помощью формулы:

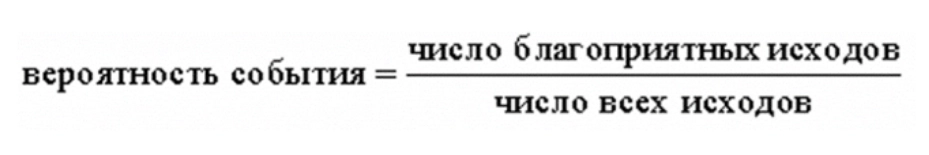
Внимательно читайте вопрос: спрашивают вероятность купить исправную лампочку. Если из ста 3 неисправны, значит, остальные в порядке и подойдет любая из оставшихся 97. Это и есть наши благоприятные исходы из формулы.

97 : 100 = 0,97.

Ответ: 0,97.

Будьте внимательны: иногда в задаче есть указание к округлению. Значит, ответ у вас выйдет некрасивый, в виде бесконечной десятичной дроби, которую вы округлите до нужного разряда.

Еще один подвох: формулировка с предлогом «на». К примеру, «На 100 лампочек 3 неисправны. Найдите вероятность купить неисправную». Подходящие исходы тут даны явно: 3 неисправные лампочки. А вот число всех исходов спрятано, и найти его будет нужно сложением исправных и неисправных лампочек: 100 + 3 = 103.

Задание 6: обязательно делать

Задание проверяет навык чтения информации из таблицы и подбора подходящего по условию варианта.

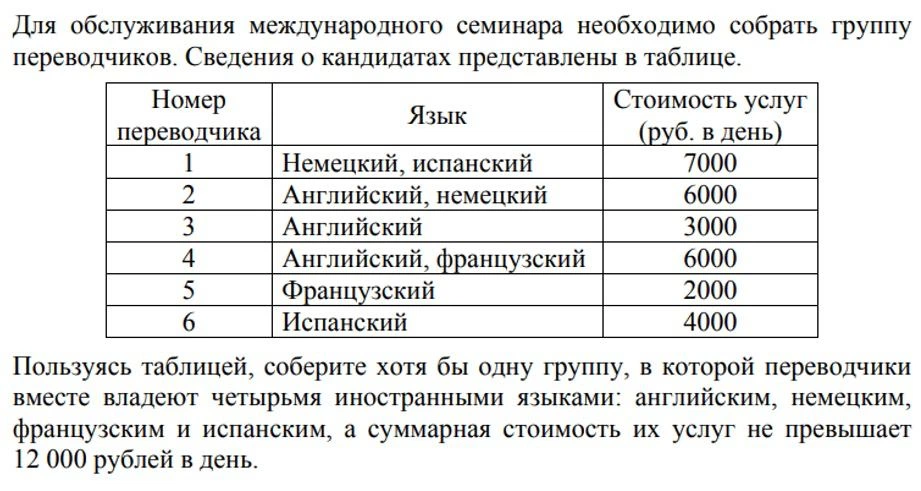
Например, вы нашли вариант позвать первого, третьего и пятого переводчиков. Получите весь набор языков как раз за 12 тысяч. Но обратите внимание, что это решение далеко не единственное.

Ответ: 135.

Задание 7

Мы не выделяем это задание в обязательные, так как для его выполнения понадобится навык анализа поведения функции по графику. Но, как его решать, сейчас коротко расскажем.

Запомним: точка максимума будет на «горке», точка минимума — в «ямке». Функция убывает, если идет вниз слева направо. Возрастает, если идет вверх слева направо.

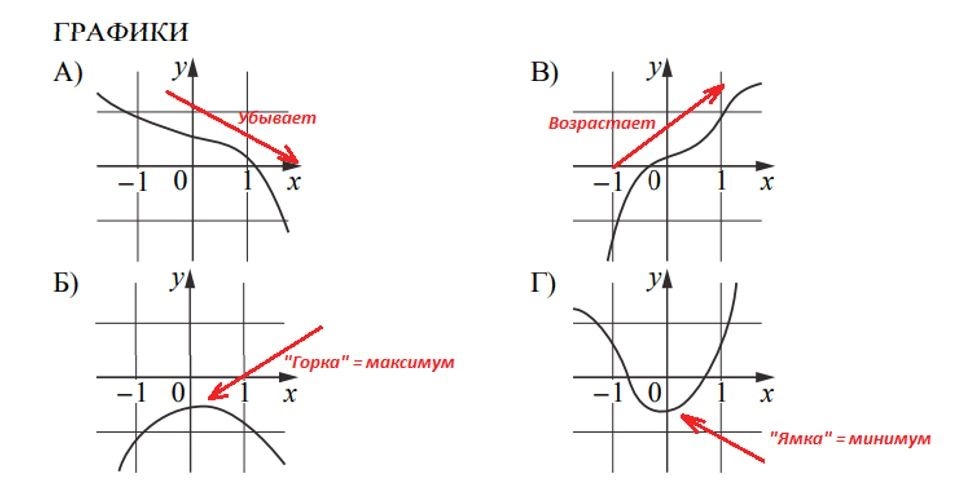
Если не повезет, то придется вспомнить азы теории по производной.

Здесь все дело в касательных. Нужно внимательно к ним присмотреться. Если касательная к графику возрастает, то значение производной будет положительное, если убывает — отрицательное. Производная будет тем больше по величине (модулю), чем быстрее возрастает или убывает касательная.

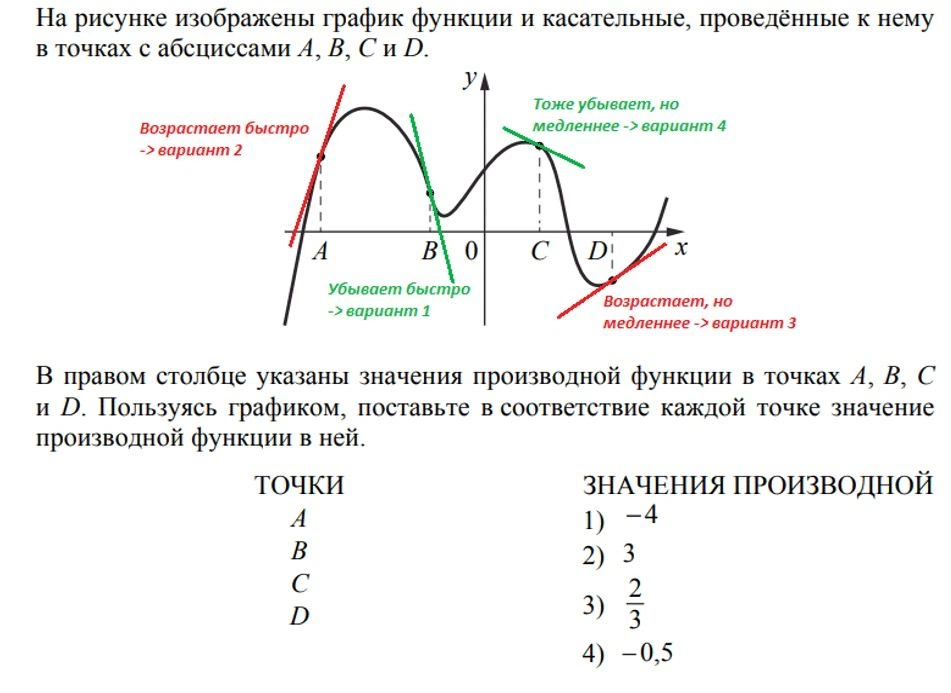
Ответ: 2143.

Задание 8: обязательно делать

Задача проверяет умение делать логичные выводы из утверждения. Иногда попадаются совсем простые задания, к таким даже дополнительно готовиться не надо.

Все, что от вас требуется, — схематично изобразить на черновике ясень, рябину и осину, указать известную разницу в высоте и внимательно сопоставить картинку с утверждениями.

Важно: не додумывайте дополнительные условия, не указанные в тексте задачи. Учитесь читать строго то, что написано.

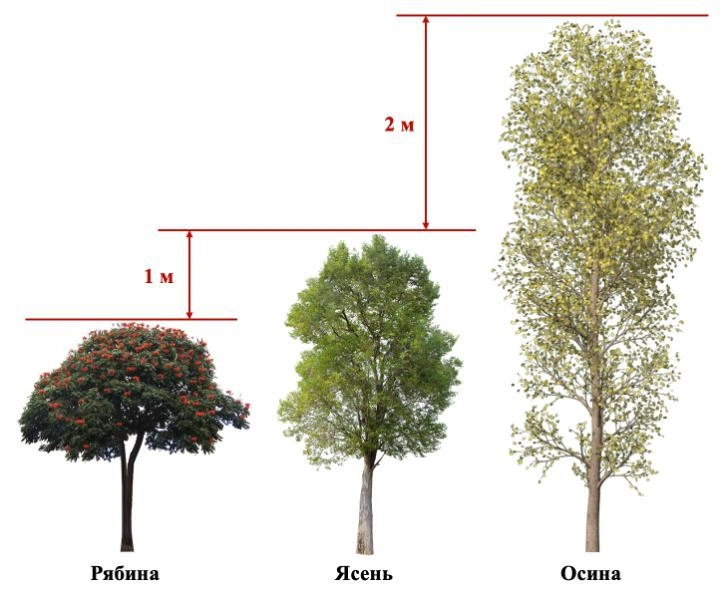
Исходя из рисунка выше получаем, что верны только утверждения 1 и 4.

Ответ: 14.

А бывают случаи, когда с визуализацией задачки придется постараться.

Тут иллюстрация не так очевидна, но нам помогут круги Эйлера. Этот инструмент позволяет наглядно изобразить множество объектов. В данном случае — школьников. Давайте прикинем, как ребята могут распределиться по кружкам.

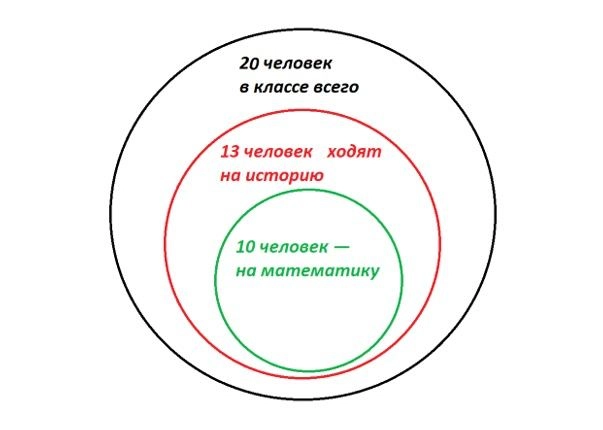
Например, так. Тут из 20 человек на кружки в итоге ходят 13. Причем 10 из них очень активны и выбрали сразу два предмета. Трое ограничились только историей.

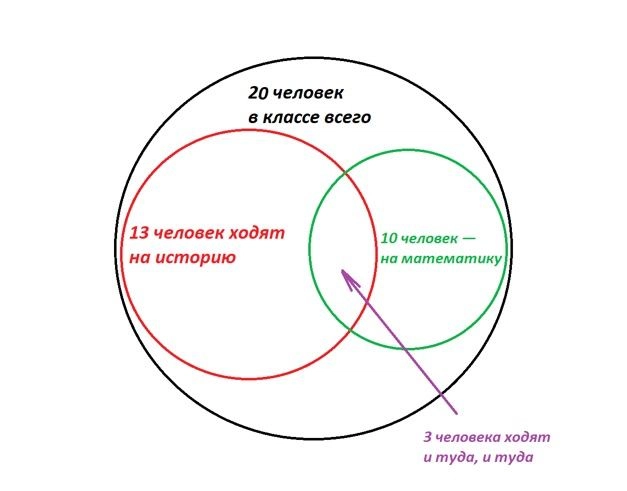
Или вот так. Если ребята задались целью по максимуму не пересекаться на дополнительных занятиях, то… У них не получится, и как минимум трое запишутся сразу на оба факультатива.

Конечно, возможны еще промежуточные варианты, но мы нарисовали два крайних. Теперь попробуем ответить на вопросы.

1. Смотрим на первую картинку. Даже если все ребята будут очень стараться посетить оба кружка, они ограничены условиями задачи и максимум на оба попадут 10 человек из 20. Нет.
2. Тут надо рассмотреть другую крайность, которую мы изобразили на второй картинке. Как бы ребята ни старались не встречаться на кружках, хотя бы трое попадут на оба сразу. Да.
3. Уж точно неверно. На обеих наших картинках есть ребята, которые ходят на историю, но не ходят на математику. Нет.
4. Смотрим на первую картинку. Оба кружка могут посещать максимум 10 человек. 

Ответ: 24.

Так что для решения иногда мало логики — понадобится еще немного воображения. Потренируйтесь, и ваши шансы получить балл увеличатся.

Задание 14: обязательно делать

Задание проверяет базовые навыки счета, которым учат в 5–6-м классах. Чтобы получить балл и сдать базовую математику, надо:

• уметь выполнять арифметические действия с обыкновенными и десятичными дробями;
• правильно расставлять порядок действий;
• быть предельно внимательными.

Уделите пару вечеров отработке алгоритмов сложения, вычитания, умножения и деления обыкновенных и десятичных дробей, и это задание у вас в кармане.

Задание 15

Составители экзамена проверяют ваш навык работы с процентами и единицами отношения. Такие задачи бывают четырех типов.

Тип 1. Найти часть от числа

Часть может быть выражена в процентах или сразу в виде дроби. Например, придется искать треть от чего-то.

Рассмотрим на примере реальной задачи из экзамена:

Прочувствуйте специфику задачи: нам известно целое — вся зарплата до вычета налога. А работать мы будем с кусочком — 13 процентами. Сколько это в рублях, нам еще предстоит узнать.

Чтобы ответить на вопрос задачи, нужно сделать три шага:

1. Перевести процент в десятичную дробь.

Для этого всегда надо количество процентов поделить на 100.

13 : 100 = 0,13.

2. Найти, сколько это от зарплаты в рублях.

Запоминаем главное правило для этого типа задач: чтобы найти дробь от числа, надо число умножить на эту дробь.

12 500 ∙ 0,13 = 1 625 (руб.) — налог, который удержат с зарплаты Ивана Кузьмича.

3. Ответить на вопрос задачи.

У нас просили зарплату после вычета налога, а не сам налог.

12 500 – 1625 = 10 875 (руб.).

Ответ: 10 875.

Будьте внимательны: многие совершают ошибку именно на последнем шаге!

Тип 2. Найти число по его части

Прочувствуйте разницу с прошлой задачей: тут 124 — и есть 25%, то есть одна и та же величина выражена в процентах и в абсолютных величинах, в данном случае — в учениках. Просят узнать целое — 100%.

1. Переводим процент в десятичную дробь:

25 : 100 = 0,25.

2. Находим, сколько учеников всего.

Правило для этого типа задач: чтобы найти целое, надо часть разделить на дробь.

124 : 0,25 = 496 (уч.) — всего.

Ответ: 496.

Тип 3. Найти, сколько процентов часть составляет от целого

Особенность подобных заданий: не дано процентов, есть только абсолютные величины. В данном случае — стоимость футболки в рублях.

1. Находим, какую долю новая цена составляет от первоначальной.

Запоминаем правило: чтобы найти, какую долю часть составляет от целого, надо часть разделить на целое.

680 : 800 = 0,85.

2. Переводим долю в процент.

В прошлых задачах мы уже дважды выполнили обратное действие. В этот раз сделаем наоборот: умножим полученную дробь на 100.

0,85 ∙ 100 = 85% — столько процентов новая цена составляет от старой.

3. Отвечаем на вопрос задачи.

Нас спросили, на сколько процентов цена снизилась, что стала 85% от первоначальной. Конечно, изначально она была 100%. Итого:

100 – 85 = 15%.

Ответ: 15%.

Тип 4. Задачи на соотношение

Если перефразировать условие, то за первого кандидата проголосовали 3 части избирателей, а за второго — 2 части. Особенность этих частей в том, что они одинаковые по величине.

Если одна будет состоять из 10 человек, то за первого кандидата будет 30, а за второго — 20.

1. Считаем общее количество частей:

3 + 2 = 5.

2. Узнаем, сколько голосов составляет одна такая часть.

Тут речь о процентах проголосовавших. Сколько всего проголосовало? Конечно, 100%! Значит, каждая из пяти частей «весит»

100 : 5 = 20%.

3. Отвечаем на вопрос задачи.

За проигравшего проголосовало меньше частей избирателей. В нашем случае 2.

20 ∙ 2 = 40%.

Ответ: 40%.

Решение этих задач удобнее всего оформить табличкой:

1 часть = 100% : 5 = 20%.

Если рассчитываете решать текстовую задачу, включите здравый смысл. Ответ всегда можно проверить на адекватность благодаря обычной логике. 

Задание 16: обязательно делать

Задание на решение выражения. На самом деле оно проверяет знание теории, так как в этом задании вам могут встретиться:

• выражения со степенями,
• иррациональные выражения,
• логарифмические выражения,
• тригонометрические выражения.

Ваша задача, соответственно, — знать:

• свойства степеней

• свойства корней

• свойства логарифмов

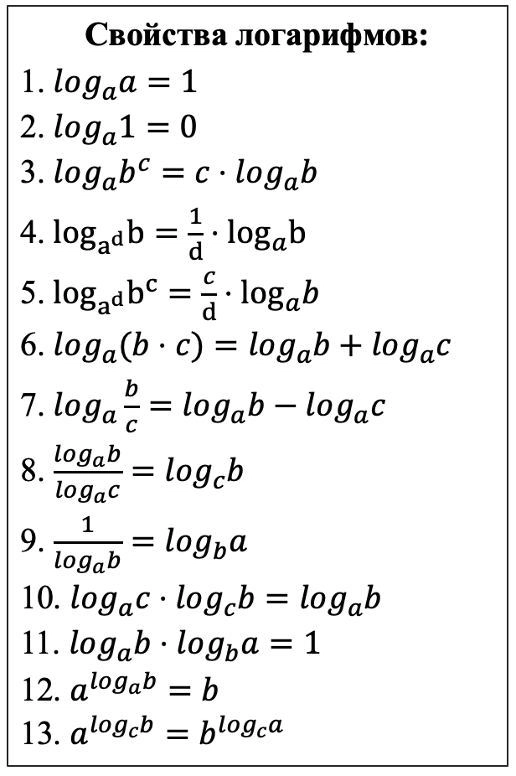
• формулы тригонометрии

Вы можете подробно ознакомиться с ними и научиться выводить в этой статье.

Обратите внимание: нужная теория будет в справочных материалах на экзамене, но это не поможет, если вы не научитесь применять ее для решения заданий. Практика обязательна!

Задание 17: обязательно делать

В номере с уравнениями вам не встретятся тригонометрические. Зато вы точно увидите там:

• линейные уравнения

Раскрываем скобки, если они есть, слагаемые с х переносим в одну сторону от равно, без х — в другую. Приводим подобные и решаем простейшее уравнение.

• квадратные уравнения

Бывают полные и неполные, всего надо повторить три алгоритма решения! А формула дискриминанта еще и в справочных материалах есть.

• иррациональные уравнения

Это те, что с корнем. Чтобы избавиться от корня, возводим обе части уравнения в квадрат и решаем получившееся уравнение. Есть нюансы с областью допустимых значений: подставьте полученные корни в исходное уравнение и проверьте, выполняется ли равенство. Если нет, то подставленное значение решением не будет.

• показательные уравнения

Ваша задача — с помощью формул свойств степеней привести уравнение к виду, когда слева и справа от равно в основании степени будет одно и то же число. После приравниваем показатели и решаем. Вот так:

Ответ: 7.

• логарифмические уравнения

С помощью формул свойств логарифмов приводим уравнение к виду, когда слева и справа от равно будет логарифм с одинаковым основанием. После приравниваем выражения под логарифмом и решаем.

Ответ: 67.

Прелесть уравнений в том, что ответ всегда можно проверить подстановкой вместо x в уравнение. Не забывайте проверять, ведь это возможность убедиться на 100%, что вы не упустите заветный балл.

Задание 19

Если хотите сдать базовую математику и решить номер 19, надо ознакомиться со свойствами целых чисел и признаками делимости. Иногда решение можно найти даже подбором! Попробуйте — времени на базовом ЕГЭ вам точно хватит.

Для начала нужно запомнить все признаки делимости.

А теперь посмотрим на типичное задание 19.

Тут помогут признаки делимости. Отдельного признака для 12 нет, потому нам надо разложить его на множители, признаки делимости для которых есть. 

• На 3: сумма всех цифр делится на 3.
• На 4: число, образованное последними двумя цифрами, делится на 4.

Начнем с признака для 4. Пока что наше число заканчивается на 13 и на 4 не делится. Попробуем вычеркнуть последнюю цифру, и число будет заканчиваться на 61. Тоже не подходит. Вычеркнем еще одну: теперь на конце 76… Вот оно! От изначального числа осталось 751576, две цифры уже вычеркнули, осталось убрать одну.

Теперь проверим признак для 3: 7 + 5 + 1 + 5 + 7 + 6 = 31. Какое ближайшее число разделится на 3? Конечно, 30. Если мы вычеркнем единичку, все сойдется.

Ответ: 75576.

Другой вариант задания:

А задание такого типа можно попытаться подобрать, расположений не слишком много. Мы все же постараемся порассуждать, чтобы уменьшить количество возможных вариантов.

Чтобы число делилось на 10, оно должно заканчиваться на 0. Например, это получится, если сложить 7 + □7 + □□6. Уже немного легче. Остальное просто подберем. Под условие задачи подойдет 7 + 27 + 356 = 390.

Ответ: 390.

Какие задания мы не разобрали и почему

Теперь вы знаете, как сдать базовую математику, решив всего семь заданий. Но некоторые номера базового ЕГЭ включают слишком большое разнообразие прототипов, и методы их решения не ограничиваются парой простых алгоритмов.

Например, в эту группу относятся все задания по геометрии: с 9 по 13. Чтобы решать геометрию, мало знать основные фигуры и формулы. Необходим навык, который вырабатывается только практикой. Однако у нас есть статья про окружность — в ней вы найдете много полезной информации.

Задание 18 обычно, хотя и не всегда, содержит неравенство.

Это объемный блок теории, которую тоже необходимо подкреплять практикой. Но, может, вам повезет и попадется задачка на расположение значений на числовой прямой.

Тут достаточно примерно прикинуть значения и аккуратно внести ответы в бланк. Ясно, что 7/3  больше 2, но меньше 3. Корень из 26 равен 5 с копейками, а степень –1 из 3/5 сделает 5/3, или чуть больше 1,5. Подобные задания надо пытаться делать обязательно!

Задание 20. С этим заданием ученики знакомы еще с 9-го класса, так как оно было под номером 21 на ОГЭ. Это текстовая задача:

• на производительность,
• движение (по прямой, воде, окружности),
• сплавы и смеси,
• проценты (пиджаки, рубашки, брюки; бюджет семьи; акции, которые растут и падают),
• прогрессии.

В задании 21 на ОГЭ не было прогрессий, но они были в первой части на ОГЭ, так что ничего нового.

Задание 21. Здесь попадаются разные типы неочевидных задач на логику — чем-то они даже похожи на олимпиадные. Решение каждой нужно рассматривать отдельно и подробно. Если хотите прочитать о том, какие задачи бывают в 21-м номере, пишите в комментариях, и Maximum поделится своими методами решения!

Не знаете, какой вуз выбрать? Воспользуйтесь бесплатной консультацией в нашем центре. Что это такое? Все просто: вы расскажете о себе и о своих интересах. А специалист посоветует, на какие специальности обратить внимание, в какой вуз поступать, какие ЕГЭ сдавать. Так вы сэкономите время на подготовку и сможете выбрать образование, которое точно окажется для вас интересным и полезным!

Система
подготовки к ЕГЭ по математике

Учитель
математики МОУ СОШ 15 г.Борзя 

Тюкавкина
Елена Анатольевна

      Существует множество вариантов
подготовки учеников к итоговой аттестации. Но, идеального варианта подготовки
не существует. Хочу поделиться опытом своей работы по подготовке обучающихся 11
класса к сдаче итоговой аттестации.

При подготовке обучающихся к ЕГЭ выделяю
следующие направления деятельности:

1) Методическая подготовка учителя к ЕГЭ. 
                                                                     2)
Создание банка заданий.                                                                                                       3)
Организация вводного, текущего и итогового повторения.                                           4)
Диагностика и анализ качества знаний обучающихся при подготовке к
ЕГЭ:                                                                                                                                           5)
Организация самостоятельной работы обучающихся при подготовке к
ЕГЭ.                                                                                           
                                6) Психологическая подготовка обучающихся к
ЕГЭ.   

     Подробнее остановлюсь на методической
подготовке.         

Основные цели и задачи, стоящие перед
учителем:

1.  Повторить отдельные темы или весь курс
математики 5-9 класса и пройти, с учениками  курс математики 10-11 класса.

Задача учителя – не «натаскать» учеников перед
экзаменом, а передать ученику полное и целостное понимание всего курса школьной
математики. Не показать разрозненные приемы решения отдельных задач, а научить
решать творчески и при этом математически грамотно любую экзаменационную
задачу.

2. При работе с учеником учителю
необходимо выявить пробелы, возникшие при изучении тех или иных тем, и
проработать эти темы наиболее тщательно.

К сожалению, старшеклассники практически
всегда имеют такие пробелы.

3. Одна из задач учителя — дать навыки
решения простых задач ЕГЭ быстро и без калькулятора.

Как показывает статистика, большая часть
ошибок на экзамене связана с арифметическими вычислениями. Именно из-за ошибок
в вычислениях выпускник часто теряет баллы и получает результат ниже, чем
рассчитывал. Связано это с тем, что на уроках в школе и тем более при
выполнении домашних заданий многие ученики привыкают пользоваться
калькулятором.

4. Следующая задача учителя — научить
выпускника рассчитывать время на экзамене.

Профильный ЕГЭ по математике – это и
относительно простые задачи части 1, которые можно считать выпускным экзаменом
за курс средней школы, и задачи части 2, более сложные, требующие подробного
ответа и выполняющие роль вступительного экзамена в вуз. На все эти задачи
дается 3 часа 55 минут. Это значит, что у ученика нет времени искать методом
проб и ошибок решение задачи на экзамене. Ему необходимо заранее знать все
алгоритмы и нюансы решения каждой задачи, уметь доводить решение до результата,
не бросая на полпути, уметь оценивать и проверять результат, а также следить за
временем, зная, сколько минут можно потратить на решение тех или иных задач.

5.  Одна из важнейших задач учителя — дать
будущему студенту базу для дальнейшего освоения высшей математики и других
связанных с математикой дисциплин при учебе в вузе.

Чем более качественной была подготовка
выпускника школы к ЕГЭ, тем проще студенту, будут даваться математические
дисциплины в вузе.

Основные принципы работы по подготовке к
ЕГЭ.

— Любую тему школьной математики нужно
объяснить просто и понятно, сохраняя при этом необходимую математическую
строгость изложения.

— Изучение каждой темы начинается с
основных понятий, определений, связи этих понятий с уже пройденными темами.
Любой новый термин, который вводится в курсе, объясняется через уже известные
ученику.

— Курс математики изучается как целостная
система. При этом учитель знает, какое место займет данная тема в общей
математической картине учащегося, когда она понадобится в будущем и как связана
с темами, которые еще предстоит пройти.

— Каждая тема занимает свое определенное
место. Такой порядок тем обусловлен необходимостью построить систему знаний,
прежде всего понятную для ученика, где каждый новый «уровень знаний» логически
опирается на предыдущие.

— Основа мотивации учащихся – небольшие
ежедневные успехи в освоении математики. Необходимо чтобы независимо от
предыдущего уровня подготовки, ученик видел результаты занятий с первых же
пройденных тем. Тогда его мотивация становится выше, самооценка растет, и за
счет этого он выходит на более высокий уровень.

— Один из основных принципов– понимание
вместо зубрежки. Математические понятия вводятся на понятном уровне, причем не
изолированно, а как элементы системы, связанные и с пройденным ранее
материалом, и с тем, который будет в дальнейшем.

— Освоение каждой темы предполагает
решение довольно большого количества практических задач по данной теме. Часть
из этих задач разбирается на уроках и дополнительных занятиях, часть задается
на дом или изучается самостоятельно, с помощью ЦОР.

                  Подготовка к ЕГЭ 
разделена на несколько блоков.

Первый блок

курса подготовки к ЕГЭ – арифметика  и
алгебра. Курс начинается с тем «Текстовые задачи» и «Задачи на проценты». Это
материал 5-8 класса, который чаще всего к 11 классу оказывается многими
учениками уже забытым.

Текстовые задачи.

1.Задачи на проценты на ЕГЭ по математике.

2. Текстовые задачи на работу.

3. Задачи на смеси, сплавы, растворы.

4. Задачи на движение.

5. Задачи с физическим содержанием.

6. Теория вероятностей на ЕГЭ по
математике.

7. Задачи с экономическим содержанием
(подготовительные занятия)

Цели такого подхода следующие:

—  Повторить основные темы алгебры:
арифметические действия, порядок действий, десятичные и обыкновенные дроби и
действия с ними, решение квадратных и дробно-рациональных уравнений.

— Повторить и улучшить основные
математические навыки учащихся.

— Вспомнить навыки составления и решение
уравнений. Построение математических моделей.

— Освоить навыки быстрого счета и проверки
ответа. На ЕГЭ пользоваться калькулятором не разрешается, поэтому выпускнику
надо уметь считать быстро без калькулятора.

Второй блок

Геометрия и стереометрия на ЕГЭ по
математике, часть 1.

1. Планиметрия, основные формулы.
Вычисление площадей фигур, формулы площади прямоугольника, параллелограмма,
треугольника, трапеции.

2. Тригонометрия на ЕГЭ по математике.
Определения синуса, косинуса, тангенса угла в прямоугольном треугольнике.

3. Внешний угол треугольника – как найти
его синус, косинус и тангенс. Понятие смежных углов. Высота в прямоугольном
треугольнике.

4. Определения медианы, биссектрисы,
высоты. Простые геометрические построения. Сумма углов треугольника.

5. Векторы на плоскости.

6.  Стереометрия. Формулы объема и площади
поверхности многогранников и тел вращения.

Планиметрия и тем более стереометрия –
темы, по которым даже школьные хорошисты в начале курса подготовки к ЕГЭ
показывают плохие результаты.

Геометрии и стереометрии в школьной
программе по математике уделяется значительно меньше внимания, чем алгебре.

Изучение планиметрии в школьной математике
в 7 классе начинается с аксиом и доказательства очевидных для ученика
утверждений. Как правило, ученик уже на этом этапе перестает что-либо понимать.
В 10 классе, опять с непонятных аксиом, начинается стереометрия.

В курсе подготовки к ЕГЭ изучение
геометрии начинаю с темы Площади фигур. Формулы для площадей прямоугольника,
треугольника, параллелограмма, трапеции иллюстрируются простыми и наглядными
примерами.

Рекомендую ученикам на начальном этапе
пользоваться справочным материалом, содержащим изображения, определения,
формулы, основные свойства геометрических фигур.

На этом этапе вводятся также понятия
синуса, косинуса, тангенса и котангенса острого угла в прямоугольном
треугольнике, основные формулы тригонометрии в прямоугольном треугольнике,
формулы для тригонометрических функций смежных углов.

Подбор задач осуществляется по уровню
сложности, для того чтобы результатом каждого занятия становился рост понимания
и уверенности учащегося.

Аналогичным образом происходит изучение
стереометрии.

Изучение стереометрии начинается со
знакомства с основными типами многогранников и тел вращения, понятия объема и
площади поверхности, формулы для вычисления объемов и площадей поверхности.

На этом этапе используются для наглядности
объемные модели многогранников и тел вращения. То, что можно подержать в руках,
повернуть и рассмотреть с разных сторон, оказывается для начинающего более
понятным и применимым, чем оперирующие отвлеченными понятиями аксиомы.   Обучающиеся
выполняют практическую работу по изготовлению моделей многогранников, что
невозможно без развертки многогранника. А это в свою очередь помогает
сформировать понятие площади поверхности многогранника.

Третий блок

Алгебра

1. Корни и степени.

2. Понятие функции. Исследование графика
функции. Понятия возрастания и убывания функции, нулей функции, промежутков
знакопостоянства, точек максимума и минимума функции, четности и нечетности
функции.

3. Квадратичная функция и квадратичные
неравенства.

4. Дробно-рациональная функция и метод
интервалов. Решение дробно-рациональных неравенств.

5. Модуль числа. Уравнения и неравенства с
модулем.

6. Показательная функция. Показательные
уравнения (часть 1 + задачи из классических сборников).

7. Логарифмы. Преобразования
логарифмических выражений. Логарифмические уравнения (часть 1 + задачи из
классических сборников).

8. Логарифмическая функция. Понятие
обратной функции.

9. Задачи с физическим содержанием по
пройденным темам.

Этот блок посвящен понятию функции в
математике – ключевому в курсе алгебры 10-11 класса.

В школьной программе тема «Функции»
начинает изучаться  в 7 классе, причем семиклассники чаще всего воспринимают
эту тему поверхностно, не понимая, зачем она нужна. Далее, при изучении других
типов функций, в школе самому определению функции уже не уделяется достаточного
внимания, поскольку формально его «прошли» в 7 классе. В итоге абитуриент,
закончив общеобразовательную школу и став студентом, обычно не готов к изучению
математического анализа и тоже заучивает его формально, чтобы только сдать
сессию.

Темы этого блока содержат максимальное, по
сравнению с другими, количество строгих определений и математических
формулировок, без знания которых ученик не может понять последующий материал.
Это, например, определения модуля, арифметического квадратного корня,
логарифма, точек максимума и минимума функции.

И закреплением темы являются задачи с
физическим содержанием, теперь уже включающие в себя показательные,
логарифмические и степенные зависимости одной величины от другой.

Четвертый блок

Тригонометрия на ЕГЭ по математике.

1. Определения синуса, косинуса, тангенса
для произвольного угла.

2. Тригонометрический круг.
Тригонометрические функции.

3. Формулы тригонометрии.

4. Тригонометрические преобразования.
Простейшие тригонометрические уравнения.

5. Обратные тригонометрические функции и
их графики.

6. Тригонометрические уравнения (часть 2).

Тема «Тригонометрия» базируется на
знаниях, полученных  во втором блоке и начинается с повторения понятий
тригонометрических функций острого угла в прямоугольном треугольнике. Для
введения определений тригонометрических функций произвольного угла используется
тригонометрическая окружность.

С помощью тригонометрической окружности
объясняются понятия и правила, которые в школьной программе ученику часто
приходится бессмысленно зубрить . Эта удобная иллюстрация заменяет десяток
таблиц.

Особая тема – решение простейших
тригонометрических уравнений и обратные тригонометрические функции. Решения
простейших тригонометрических уравнений также идут с опорой на окружность.
Формулы не заучиваются, а выводятся из простых соображений и определений. Тема
«Обратные тригонометрические функции» является логическим продолжением темы
«Обратная функция», пройденной в блоке 3 (Алгебра).

 Пятый блок

Производная функции. Геометрический смысл
производной.

1. Производная функции. Исследование
функции с помощью производной.

2. Первообразная функции.

Тема «Производная функции» закономерно
изучается после того, как учащемуся уже знакомы тригонометрические функции.
Точнее, к этому моменту учащийся уже знаком со всеми типами элементарных
функций: степенными, показательными, логарифмическими, тригонометрическими и
обратными тригонометрическими, знает особенности их графиков, а также знаком с
основными характеристиками поведения функции, такими, как возрастание и
убывание функции, точка минимума и точка максимума, наибольшее и наименьшее
значение функции на отрезке. Также к этому моменту ученик владеет методом
интервалов и знает, как находить промежутки закон постоянства
дробно-рациональной функции.

Понятие производной функции даю на основе
геометрического смысла производной – как тангенс угла наклона касательной или
угловой коэффициент касательной. Понятие предела функции при этом не вводится,
поскольку эта непростая тема требует более высокого, чем у среднего
старшеклассника, уровня математической подготовки. Особое внимание уделяется
связи поведения функции с поведением производной.

Шестой блок

Стереометрия на ЕГЭ по математике.

1.Классический метод решения задач по
стереометрии.

2.Векторы в пространстве.
Векторно-координатный метод.

Работа начинается с подготовительной темы
– методы построения сечений объемных тел и развитие пространственного мышления
учащихся. При этом важно не просто нарисовать сечение, а описать его построение
и положение вершин сечения относительно исходного объемного тела.

Особое внимание уделяется грамотному и
математически корректному оформлению решения, строгому доказательству каждого
утверждения, построению дополнительных чертежей вычленению из стереометрической
задачи планиметрических.

Векторно-координатный способ дается в
объеме школьной программы, причем особое значение также имеет грамотное и математически
корректное оформлению решения.

Учащиеся получают рекомендации по
применению каждого из методов в тех или иных задачах.

 Седьмой блок

Неравенства на ЕГЭ по математике.

1. Неравенства на ЕГЭ по математике.

2. Показательные и логарифмические неравенства.
(часть 2).

3. Метод рационализации (замены
множителя). Метод оценки.

Тема «Неравенства отличается обманчивой
легкостью и рекордным количеством ошибок.

В этом блоке рассматриваются приемы
решения неравенств различных типов: иррациональных неравенств, неравенств с
модулем, логарифмических и показательных неравенств. Особое внимание уделяется
разбору типичных ошибок и отработке навыков правильного решения и оформления.

Восьмой блок

Задачи с экономическим содержанием на ЕГЭ
по математике.

1. Задачи с экономическим содержанием на
ЕГЭ по математике.

2. Арифметическая и геометрическая
прогрессии.

3. Формулы для решения задач с
экономическим содержанием.

В этом блоке рассматриваются способы
решения таких задач, а также готовые формулы и приемы. Методические материалы
по этой теме, как и по другим, постоянно дорабатываются, чтобы находиться в
соответствии с последними тенденциями ЕГЭ по математике.

Девятый блок

Задачи с параметрами на ЕГЭ по математике.

1. Элементарные функции и их графики.

2. Преобразования графиков функций.

3. Множества точек на плоскости.
Окружность, круг, полуокружность, ромбик, сумма модулей, полуплоскость, полоса,
отрезок.

4. Тренировочные задачи с параметрами.

5. Квадратичные уравнения и неравенства с
параметрами.

6. Графический метод решения задач с
параметрами.

7. Метод симметрии, параметр как
переменная и другие методы.

Эта задача – из тех, о которых не пишут в
школьных учебниках.

Необходимая подготовительная работа в
изучении данной темы – это типы элементарных функций и их графики (5 типов),
преобразования графиков функций (сдвиги, растяжения-сжатия, инверсии по
горизонтали и вертикали), построение графиков сложных функций.

От привычных функций одной переменной и их
графиков происходит плавный переход к неявным функциям, задающих множества
точек на плоскости. Учащийся знакомится с такими базовыми схемами решения задач
с параметрами, как окружность, круг, полуокружность, ромбик, сумма модулей,
полуплоскость, полоса, отрезок, и с уравнениями, задающими эти объекты на
плоскости.

Десятый блок

Нестандартные задачи на ЕГЭ по математике.

1. Делимость. Признаки делимости. Деление
с остатком.

2. Метод «Оценка плюс пример».

3. Реальные нестандартные задачи на ЕГЭ по
математике.

Задача 19, последняя в вариантах ЕГЭ по
математике, считается самой необычной. В учебниках для 10-11 класса нет даже
намеков на существование таких задач.

Теоретической основной решения задачи
являются признаки делимости, приемы записи для деления с остатком, знание об
арифметической и геометрической прогрессиях, в том числе целочисленных,
основная теорема алгебры (о каноническом разложении натурального числа на
множители). 

Среди методов одним из основных является
«Оценка плюс пример». Сложность задачи еще и в том, что эта задача
подразумевает умение выражать свои мысли точным математическим языком, требует
определенной математической культуры.

 Повторение всех тем и решение
вариантов ЕГЭ.

Пробные ЕГЭ для учащихся проводятся 1 раз
в месяц, причем задачи, не пройденные к данному моменту, не обязательны для
решения. На заключительном этапе подготовки обязательны все задачи.

Заключительная часть подготовки к ЕГЭ
нацелена на тренировку решения варианта ЕГЭ без ошибок и в точно отведенное
время.

Мы используем файлы cookie, чтобы персонализировать контент, адаптировать и оценивать результативность рекламы, а также обеспечить безопасность. Перейдя на сайт, вы соглашаетесь с использованием файлов cookie.

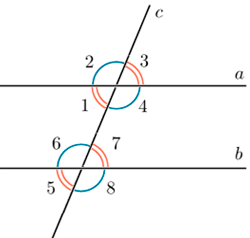
1. Углы

Вертикальные углы равны (на рис. 1 и 3; 6 и 8 и др.).

Внутренние накрест лежащие углы при параллельных прямых и секущей равны. (на рис. 4 и 6; 1 и 7).

Сумма внутренних односторонних углов при параллельных прямых и секущей равна 180˚ (на рис. 4 и 7; 1 и 6).

Соответственные углы при параллельных прямых и секущей равны. (на рис. 3 и 7; 1 и 5 и др.).

Если одна из двух параллельных прямых перпендикулярна третьей прямой, то и другая перпендикулярна третьей прямой.

2. Медиана, биссектриса, высота

Биссектриса треугольника — отрезок, соединяющий вершину треугольника с точкой на противоположной стороне и делящий угол треугольника пополам.

Высота треугольника – перпендикуляр опущенный из вершины угла на противоположную сторону.

Медиана треугольника — это отрезок, соединяющий вершину треугольника с серединой противолежащей стороны.

В любом треугольники все биссектрисы пересекаются в одной точке, все медианы пересекаются в одной точке, все медианы пересекаются в одной точке.

3. Треугольник

Сумма углов в любом треугольнике 180˚.

Средняя линия треугольника – прямая проходящая через середины двух сторон. Средняя линия параллельна одной из сторон и равна половине этой стороны.

Виды треугольников: тупоугольный (один угол тупой), прямоугольный (один угол прямой 90˚), остроугольный (все углы острые, меньше 90˚).

Равнобедренный треугольник — треугольник, у которого равны две стороны.

Свойства равнобедренного треугольника:

• в равнобедренном треугольнике углы при основании равны;
• в равнобедренном треугольнике медиана, проведенная к основанию, является биссектрисой и высотой;

Равносторонний треугольник — треугольник,
у которого все стороны равны. (все углы по 60 градусов)

Всякий равносторонний треугольник является равнобедренным,
но не всякий равнобедренный — равносторонним.

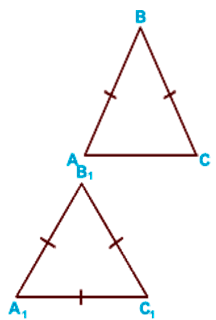
Три признака равенства треугольников

I признак по двум сторонам и углу между ними

II признак (по стороне и прилежащим углам)

III признак (по трем сторонам)

Признаки подобия треугольников

I признак по двум равным углам

II признак по двум пропорциональным сторонам и углу между ними

III признак по трем пропорциональным сторонам

Площади подобных фигур относятся как коэффициент подобия в квадрате.

Объемы подобных фигур относятся как коэффициент подобия в кубе.

Треугольник называется прямоугольным, если один из его углов прямой.

Стороны, прилежащие к прямому углу называются катетами, а сторона, лежащая против прямого угла, – гипотенузой. (самая большая сторона это гипотенуза, две др катеты).

Свойства прямоугольного треугольника

Сумма острых углов прямоугольного треугольника равна 90 градусов.

Катет, лежащий против угла в 30˚, равен половине гипотенузы.

Центр описанной окружности прямоугольного треугольника лежит на середине гипотенузы.

Медиана прямоугольного треугольника, проведенная из вершины прямого угла на гипотенузу, является радиусом описанной около этого треугольника окружности.

Теорема Пифагора:

В прямоугольном треугольнике квадрат гипотенузы равен сумме квадратов катетов: a² + b² = c².

Пифагоровы тройки:

• 3, 4, 5
• 6, 8, 10
• 5, 12, 13
• 9, 12, 15

Признаки равенства прямоугольных треугольников

• По двум катетам.
• По гипотенузе и катету.
• По катету и прилежащему острому углу.
• По катету и противолежащему острому углу.
• По гипотенузе и острому углу.

Признаки подобия прямоугольных треугольников:

• По острому углу.
• По пропорциональности двух катетов.
• По пропорциональности катета и гипотенузы.

Синусом острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.

Косинусом острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.

Тангенсом острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.

Котангенсом острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.

Высота, проведенная из вершины прямого угла, разбивает прямоугольный треугольник на два подобных треугольника. Каждый из этих треугольников подобен исходному.

Высота прямоугольного треугольника: h=ab/c или h = (где АВ гипотенуза, СЕ высота опущенная на гипотенузу).

В прямоугольном треугольнике медиана, проведённая из вершины прямого угла, равна половине гипотенузы: m=c/2 (R=​с/2=m​c).

3. Четырехугольники

Сумма углов в любом четырехугольнике 360˚.

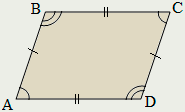
Параллелограмм

Параллелограммом называется четырёхугольник, противолежащие стороны которого попарно параллельны.

У параллелограмма противолежащие стороны равны и противолежащие углы равны.

Сумма любых двух соседних углов параллелограмма равна 180°.

Диагонали параллелограмма пересекаются и точкой пересечения делятся пополам.

Каждая диагональ делит параллелограмм на два равных треугольника.

Две диагонали параллелограмма делят его на четыре равновеликих треугольника.

Сумма квадратов диагоналей параллелограмма равна сумме квадратов всех его сторон.

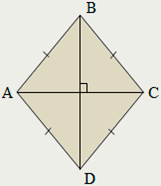
Ромб

Ромбом называется параллелограмм, у которого все стороны равны.

Диагонали ромба пересекаются под прямым углом и являются биссектрисами его углов.

Прямоугольник

Прямоугольником называется параллелограмм, у которого все углы прямые.

Диагонали прямоугольника равны и точкой пересечения делятся на четыре равных отрезка.

Квадрат.

Квадрат – это прямоугольник, у которого все стороны равны.

Диагонали квадрата равны и перпендикулярны.

Сторона и диагональ квадрата связаны соотношениями: .

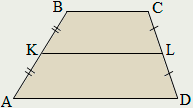
Трапеция

Трапецией называется четырёхугольник у которого только две противолежащие стороны параллельны.

Параллельные стороны называются основаниями трапеции, непараллельные – боковыми сторонами.

Средняя линия трапеции параллельна её основаниям и равна их полусумме.

Равнобокой называется трапеция, у которой боковые стороны равны.

У равнобокой трапеции: диагонали равны; углы при основании равны; сумма противолежащих углов равна 180.

Стороны и диагональ равнобокой трапеции связаны соотношением: d² = ab+c².

Трапеция называется прямоугольной, если одна из её боковых сторон перпендикулярна основаниям.

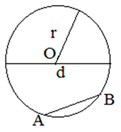
4. Окружность

Отрезок, соединяющий центр окружности с любой точкой окружности называется радиусом (r) окружности.

Отрезок, соединяющий две точки окружности, называется хордой. Хорда, проходящая через центр окружности, называется диаметром окружности.

Прямая, имеющая с окружностью одну общую точку, называется касательной. Касательная и радиус проведенный в точку касания пересекаются под прямым углом.

Прямая, имеющая с окружностью две общие точки, называется секущей.

Центральный угол окружности – это угол, вершина которого лежит в центре окружности. Центральный угол равен дуге на которую он опирается.

Вписанный угол – это угол, вершина которого лежит на окружности, а стороны пересекают ее. Вписанный угол равен половине дуги на которую опирается.

Через три точки, не лежащие на одной прямой, можно провести окружность, и притом только одну.

Вписанный угол, опирающийся на диаметр равен 90˚.

Все вписанные углы, опирающиеся на одну и туже дугу равны.

Теорема косинусов:

a² = b² + c² – 2bccosa

Теорема синусов:

5. Формулы площадей

См. продолжение статьи

Профильный ЕГЭ по математике сдают не все. Это вариант для тех, кто намерен поступить в технический Вуз или освоить профессию, связанную с экономикой или математикой. Чтобы сдать данный экзамен, вам нужно будет показать глубокие знания предмета.

Основные требования

Во время сдачи базового госэкзамена вам понадобятся познания, которые были получены из школьного курса алгебры и геометрии. Вы должны уметь решать разнообразные неравенства и уравнения, а также знать терминологию и алгоритмы решения разных задач. А вот чтобы выполнить тесты высокой сложности, вы должны знать:

• планиметрию;
• стереометрию;
• прогрессию.

Помимо этого от учащегося потребуется знание финансовой математики и умение работать с параметрическими системами, уравнениями, неравенствами, процентами.

Во время подготовки вам придется повторить теорию. При этом вы должны совмещать ее с практикой, чтобы уметь применять все выученные правила, теоремы, аксиомы.

Принципы подготовительного процесса

С самого начала года необходимо готовиться к ЕГЭ. Благодаря этому можно качественно усвоить весь необходимый материал.

Желательно повторять вслух все прочитанное, чтобы запомнить правила.

Некоторые аксиомы и теоремы нужно будет просто выучить. А после этого применять их при работе с тренировочными упражнениями.

Если вы готовитесь вместе с одноклассниками, контролируйте друг друга. Так материал быстрее усвоится.

Анализируйте ошибки во время решения задач. Благодаря этому вы значительно продвинетесь в подготовке.

Не забывайте про решение практических заданий. Во время сдачи тестирования этот навык вам очень пригодится.

Хочешь быть в курсе новостей ЦТ?
Подписывайся на Адукар в соцсетях!

Начни подготовку к ЦТ и ЦЭ прямо сейчас!

Адукар обещает крутых преподавателей и много полезной практики.