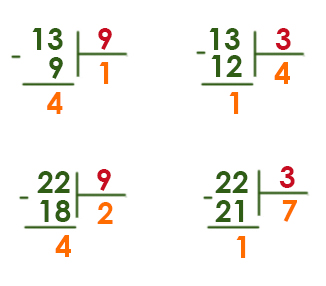
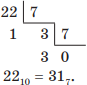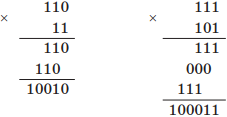На уроке рассматривается 14 задание, решение и объяснение ЕГЭ по информатике
Содержание:
- Объяснение заданий 14 ЕГЭ по информатике
- Перевод числа из любой системы счисления в десятичную
- Особенности при переводах в разные системы счисления
- Решение заданий 14 ЕГЭ по информатике
- Определите наибольшее/наименьшее значение x, y
- Сколько цифр или сумма цифр
- Найти основание системы счисления и уравнения
14-е задание: «Операции в системах счисления»
Уровень сложности
— повышенный,
Требуется использование специализированного программного обеспечения
— нет,
Максимальный балл
— 1,
Примерное время выполнения
— 5 минут.
Проверяемые элементы содержания: Знание позиционных систем счисления
До ЕГЭ 2021 года — это было задание № 16 ЕГЭ
Типичные ошибки и рекомендации по их предотвращению:
«Основные ошибки связаны с невнимательностью при выполнении арифметических действий
в недесятичных системах счисления. Например, вычитания единицы в ситуации типа: 10100002 – 1»
ФГБНУ «Федеральный институт педагогических измерений»
С основами темы можно ознакомиться в теории к заданию 1.
Перевод числа из любой системы счисления в десятичную
Чтобы перевести, например, 10045N, из системы счисления с основанием N в десятичную систему, нужно умножить значение каждой цифры на N в степени, равной разряду этой цифры:
Особенности при переводах в разные системы счисления
Некоторые правила, которые нужно знать, при работе с системами счисления:
- последняя цифра (крайняя справа) в записи числа в системе счисления с основанием
N– представляет собой остаток от деления этого числа наN:
710 = 1112 7/2 = остаток 1
N – это остаток от деления этого числа на N², и так далее:710 = 1112 112=310 7/22 = остаток 310 (112)
10N записывается как единица и N нулей:
2N в двоичной системе записывается как единица и N нулей:3N записывается в троичной системе в виде единицы и N нулей:a; общее правило:10N-1 записывается как N девяток:2N-1 в двоичной системе записывается как N единиц:3N-1 записывается в троичной системе как N двоек:aN-1 в системе счисления с основанием a записывается как N старших цифр этой системы, то есть, цифр (a-1)10N-10M = 10M * (10N-M – 1) записывается как N-M девяток, за которыми стоят M нулей:2N – 2K при K < N в двоичной системе записывается как N – K единиц и K нулей:
Решение заданий 14 ЕГЭ по информатике
Плейлист видеоразборов задания на YouTube:
Задание демонстрационного варианта 2022 года ФИПИ
Определите наибольшее/наименьшее значение x, y
14_14:
Операнды арифметического выражения записаны в системе счисления с основанием 15.
82x19₁₅ – 6x073₁₅
В записи чисел переменной x обозначена неизвестная цифра из алфавита 15-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратно 11. Для найденного значения x вычислите частное от деления значения арифметического выражения на 11 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
✍ Решение:
-
✎ Решение с использованием программирования:
PascalABC.net:
|
||
|
Python:
|
||
| С++: |
Ответ: 7806
Сколько цифр или сумма цифр
14_12:
Значение арифметического выражения
43∙7103 – 21∙757 + 98
записали в системе счисления с основанием 7.
Найдите сумму цифр получившегося числа и запишите её в ответе в десятичной системе счисления.
✍Решение:
✎ Решение с использованием программирования:
PascalABC.net, Решение 1:
|
||
PascalABC.net, Решение 2:
|
||
Python:
|
||
| С++: |
Результат: 276
14_1:
Значение арифметического выражения:
21024 + 464 — 64
записали в системе счисления с основанием 2.
Сколько цифр «1» содержится в этой записи?
Типовые задания для тренировки
✍Решение:
✎ Решение с использованием программирования:
PascalABC.net, Решение 1:
|
||
PascalABC.net, Решение 2:
|
||
Python:
|
||
| С++: |
✎ Решение теоретическое:
- Существует правило:
- Чтобы воспользоваться этим правилом, преобразуем общее выражение к степеням двойки:
2N = 10..02(1 единица и N нулей)
21024 + (22)64 - 26 = 21024 + 2128 - 26
10...0 (1024 нуля) + 10...0 (128 нулей) - 10...0 (6 нулей)
10....00000 - 1024 нуля + 10..0 - 128 нулей _________________________ 10....10..0
10....00000 - 1024 нуля + 10..0 - 128 нулей _________________________ 10....10..0 - запомним единицу
2N — 2K = 1…1 (N - K единиц)0…0(K нулей)
10..0000000 - 128 нулей - 1000000 _________________________ 11..1000000 - 122 единицы и 6 нулей
122 + 1 = 123 единицы
Результат: 123
Также можно посмотреть видео решения 14 задания ЕГЭ по информатике (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_3: 14 задание. Демоверсия ЕГЭ 2018 информатика:
Значение арифметического выражения:
4910 + 730 – 49
записали в системе счисления с основанием 7.
Сколько цифр «6» содержится в этой записи?
Типовые задания для тренировки
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net, решение 1:
|
||
PascalABC.net, решение 2:
|
||
Python:
|
||
| С++: |
✎ Решение теоретическое:
- Приведем все числа к степеням 7:
720 + 730 - 72
730 + 720 - 72
1. an = 10..0a n 2. an - am = (a-1)..(a-1)0..0a n-m m
730 = 10..0
30
0 + (20 - 2) = 18
Результат: 18
Подробное решение 14 задания демоверсии ЕГЭ смотрите на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_2:
Значение арифметического выражения:
4500 + 3*42500 + 16500 — 1024
записали в системе счисления с основанием 4.
Сколько цифр «3» содержится в этой записи?
Типовые задания для тренировки
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net:
|
||
Python:
|
||
| С++: |
Результат: 496
Подробное решение данного 14 задания ЕГЭ по информатике можно посмотреть на видео (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_5:
Значение арифметического выражения: 81024 + 832 – 65 – записали в системе счисления с основанием 8. Сколько цифр «7» содержится в этой записи?
Типовые задания для тренировки
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net:
|
||
Python:
|
||
| С++: |
✎ Решение теоретическое:
- Приведем все числа к степеням восьмерки:
65 = 64 + 1 = 82 + 80;
81024 + 832 - (82 + 80); 81024 + 832 - 82 - 80
1. an = 10..0a n 2. an - am = (a-1)..(a-1)0..0a n-m m
81024 = 10..0
1024
3.-2n = -2n+1 + 2n
! Формула предназначена для чисел в двоичной системе счисления, но для подсчета цифр "7" в 8-й (или "6" в 7-й и т.п.) ее можно использовать (для поиска единиц или нулей она не подходит!!!)
-82 = -83 + 82
! обратите внимание, что тождество неверно, но
при поиске количества "7" этой формулой можно воспользоваться
(для поиска единиц или нулей она не подходит!)
Получаем:
81024 + 832 - 83 + 82- 80
0 + (32 - 3) + (2 - 0) = 31
Результат: 31
14_13:
Сколько значащих нулей в двоичной записи числа 4350 + 8340 – 2320 – 12?
✍ Решение:
✎ Решение с использованием программирования:
PascalABC.net, решение 1:
|
||
PascalABC.net, решение 2:
|
||
Python:
|
||
| С++: |
✎ Решение теоретическое:
- По возможности приведем каждое слагаемое к степеням 2. Получим:
4350 + 8340 – 2320 – 12
(22)350 + (23)340 - 2320 - 3*22 = (22)350 + (23)340 - 2320 - 12 = 2700 + 21020 - 2320 - (23 + 22)
21020 + 2700 - 2320 - 23 - 22
-2n = -2n+1+2n и преобразуем выражение:21020 + 2700 - 2321+ 2320- 24 + 23 - 22
21020 -> один не ноль 2700 - 2321 -> 379 не нулей 2320- 24 -> 316 не нулей 23 - 22 -> один не ноль Итого: 1+ 379+316 +1 = 697
1021 - 697 = 324
Результат: 324
Найти основание системы счисления и уравнения
14_7:
Укажите, сколько всего раз встречается цифра 2 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 3.
Типовые задания для тренировки
✍ Решение:
- Для начала достаточно перевести первое и последнее число предложенного интервала в троичную систему счисления. Сделаем это:
1.
13 | 3
12 4 | 3
1 3 1
1
1310 = 1113
2.
23 | 3
21 7 | 3
2 6 2
1
2310 = 2123
111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212
111, 112, 120, 121, 122, 200, 201, 202, 210, 211, 212
Ответ: 13
✍ Решение:
- Разделим уравнение на три части и вычислим каждую часть отдельно (выделим части разным цветом):
204N+1 = 204N + 2616 1 2 3
1.
210
204N+1
По формуле получаем:
2*(N+1)2 + 0*(N+1)1 + 4*(N+1)0 =
= 2*(N2 + 2N + 1) + 0 + 4 = 2N2 + 4N + 6
2.
210
204N
По формуле получаем:
2*N2 + 0*N1 + 4*N0 =
= 2N2 + 4
3. 2616 = 3810
2N2 + 4N + 6 = 2N2 + 4 + 38; 4N = 36; N = 9
Результат: 9
✍ Решение:
- Вместо обозначения искомой системы счисления введем неизвестное x:
144x + 24x = 201x
144 + 24 = 201 1*x2 + 4*x1 + 4*x0 + 2*x1 + 4*x0 = 2*x2 + 0*x1 + 1*x0
x2 - 6x - 7 = 0
D = b2 - 4ac = 36 - 4*1*(-7) = 64
x = (-b ± √D)/2a
x1 = (6 + 8)/2 = 7
x2 = (6 - 8)/2 - не подходит
x = 7
Ответ: 7
14_9:
В некоторой системе счисления записи десятичных чисел 68 и 94 заканчиваются на 3. Определите основание системы счисления.
Типовые задания для тренировки
✍ Решение:
- Вспомним правило:
- Примем искомую систему счисления за x. Тогда, исходя из приведенного правила имеем:
Последняя цифра записи числа в системе счисления с основанием X — это остаток от деления этого числа на X
94 / x = некоторое число и остаток 3 и 68 / x = некоторое число и остаток 3
91/x 65/x
91 - 65 = 26 65 - 26 = 39 39 - 26 = 13 26 - 13 = 13
Ответ: 13
14_10:
Некоторое число X из десятичной системы счисления перевели в системы счисления с основаниями 16, 8. Часть символов при записи утеряна. Позиции утерянных символов обозначены *:
X = *516 = *0*8
Сколько чисел соответствуют условию задачи?
Типовые задания для тренировки
✍ Решение:
- Данные числа с утерянными символами переведем из 16-й и из 8-й системы счисления в двоичную. Перевод будем делать триадами и тетрадами, неизвестные позиции оставим пустыми:
1. *516
* | 5 16
* * * * | 0 1 0 1 2
2. *0*8
* | 0 | * 8
* * *|0 0 0|* * * 2
* * 0 0 0 1 0 1
1. 01000101 2. 10000101 3. 11000101
Ответ: 3
Предлагаем посмотреть видео решения данного 14 задания ЕГЭ (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_4:
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 75 оканчивается на 13.
Типовые задания для тренировки
✍ Решение:
- Так как 75 должно оканчиваться на 13, то имеем два общих случая:
1. 7510 = 13N 2. 7510 = ...13N (число оканчивается на 13)
1 случай:
75|N N|1 отсюда имеем => 75 - N = 3; т.е. N = 72 3
2 случай:
75|N 72|y отсюда имеем => 75 = Ny + 3, где N - целое, неотриц. 3
75|N 72| y |N => y = Nz + 1, где z - целое, неотриц. 3 y-1|z 1
75 = Ny + 3 y = Nz + 1
75 = N (Nz + 1) + 3; 75 = N2z + N + 3; 75 = N2z + N
z = (72 - N)/N2
72 - 5 / 52 = 67 / 25 не делится, - не подходит!
75 | 4
72 | 18| 4
3 16| 2
2 => не подходит! должна быть единица
75 | 6
72 | 12| 6
3 12| 1
0 => не подходит! должна быть единица
75 | 7
70
5 => не подходит! должна быть 3
75 | 8
72 | 9| 8
3 8| 1
1 => подходит!
Результат: 8,72
Видеоразбор решения (аналитический способ):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
14_11:
Выражение 25*325 записано в троичной системе счисления. Определите, сколько в этой записи цифр 0, 1 и 2.
✍ Решение:
-
Рассмотрим каждый сомножитель отдельно.
- Первый сомножитель:
25 = 32 Переведем в троичную систему счисления (делением на 3, переписываем остатки). Результат: 3210 = 10123
325 = 10..0{25 нулей}3
1000 x 1012 = ---- 2000 1000 0000 1000 ------- 1012000
Ответ: «0»=26, «1»=2, «2»=1
Смотрите видео разбора на нашем канале (аналитическое решение):
📹 YouTube здесь
📹 Видеорешение на RuTube здесь
Всего: 185 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Запись числа N в системе счисления с основанием 7 содержит две цифры, запись этого числа в системе счисления с основанием 6 содержит три цифры, а запись в системе счисления с основанием 11 заканчивается на 2.
Чему равно N?
К записи натурального числа в восьмеричной системе счисления справа приписали два нуля. Во сколько раз увеличилось число? Ответ запишите в десятичной системе счисления.
Чему равно наименьшее основание позиционной системы счисления x, при котором 225x = 405y?
Ответ записать в виде целого числа.
Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
Сколько значащих цифр в записи десятичного числа 357 в системе счисления с основанием 7?
В системе счисления с некоторым основанием десятичное число 144 записывается в виде 264. Укажите это основание.
Запись десятичного числа в системах счисления с основаниями 3 и 5 в обоих случаях имеет последней цифрой 0. Какое минимальное натуральное десятичное число удовлетворяет этому требованию?
Источник: Демонстрационная версия ЕГЭ—2013 по информатике.
Десятичное число 81 в некоторой системе счисления записывается как 144. Определите основание системы счисления.
Укажите, сколько всего раз встречается цифра 2 в записи чисел 10, 11, 12, …, 17 в системе счисления с основанием 5.
Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 30, запись которых в системе счисления с основанием 5 начинается на 3?
Укажите, сколько всего раз встречается цифра 3 в записи чисел 19, 20, 21, …, 33 в системе счисления с основанием 6.
Укажите, сколько всего раз встречается цифра 2 в записи чисел 13, 14, 15, …, 23 в системе счисления с основанием 3.
Запись числа 6810 в системе счисления с основанием N оканчивается на 2 и содержит 4 цифры. Чему равно основание этой системы счисления N?
Решите уравнение:
1005 + x = 2004.
Ответ запишите в семеричной системе (основание системы счисления в ответе писать не нужно).
Решите уравнение:
608 + x = 2005.
Ответ запишите в шестеричной системе (основание системы счисления в ответе писать не нужно).
В системе счисления с некоторым основанием десятичное число 15 записывается в виде 30. Укажите это основание.
Источник: ЕГЭ по информатике 08.07.2013. Вторая волна. Вариант 602.
Решите уравнение:
608 + x = 609
Ответ запишите в шестеричной системе (основание системы счисления в ответе писать не нужно).
Восьмеричное число 77 в некоторой системе счисления записывается как 53. Определите основание системы счисления.
Источник: Тренировочная работа по ИНФОРМАТИКЕ 11 класс 30 сентября 2016 года Вариант ИН10104
Запишите натуральное число, десятичная запись которого состоит из двух цифр, шестнадцатеричная запись заканчивается цифрой B, а пятеричная — цифрой 3.
Запишите натуральное число, десятичная запись которого состоит из двух цифр, шестнадцатеричная запись заканчивается цифрой A, а пятеричная — цифрой 3.
Всего: 185 1–20 | 21–40 | 41–60 | 61–80 …
Представление числовой информации. Сложение и умножение в разных системах счисления
Представление числовой информации с помощью систем счисления
Для представления информации в компьютере используется двоичный код, алфавит которого состоит из двух цифр — 0 и 1. Каждая цифра машинного двоичного кода несет количество информации, равное одному биту.
Система счисления — это система записи чисел с помощью определенного набора цифр.
Система счисления называется позиционной, если одна и та же цифра имеет различное значение, которое определяется ее местом в числе.
Позиционной является десятичная система счисления. Например, в числе 999 цифра «9» в зависимости от позиции означает 9, 90, 900.
Римская система счисления является непозиционной. Например, значение цифры Х в числе ХХІ остается неизменным при вариации ее положения в числе.
Позиция цифры в числе называется разрядом. Разряд числа возрастает справа налево, от младших разрядов к старшим.
Количество различных цифр, употребляемых в позиционной системе счисления, называется ее основанием.
Развернутая форма числа — это запись, которая представляет собой сумму произведений цифр числа на значение позиций.
Например: 8527 = 8 ⋅ 103 + 5 ⋅ 102 + 2 ⋅ 101 + 7 ⋅ 100.
Развернутая форма записи чисел произвольной системы счисления имеет вид
$∑↙{i=n-1}↖{-m}a_iq^i$,
где $X$ — число;
$a$ — цифры численной записи, соответствующие разрядам;
$i$ — индекс;
$m$ — количество разрядов числа дробной части;
$n$ — количество разрядов числа целой части;
$q$ — основание системы счисления.
Например, запишем развернутую форму десятичного числа $327.46$:
$n=3, m=2, q=10.$
$X=∑↙{i=2}↖{-2}a_iq^i=a_2·10^2+a_1·10^1+a_0·10^0+a_{-1}·10^{-1}+a_{-2}·10^{-2}=3·10^2+2·10^1+7·10^0+4·10^{-1}+6·10^{-2}$
Если основание используемой системы счисления больше десяти, то для цифр вводят условное обозначение со скобкой вверху или буквенное обозначение: В — двоичная система, О — восмеричная, Н — шестнадцатиричная.
Например, если в двенадцатеричной системе счисления 10 = А, а 11 = В, то число 7А,5В12 можно расписать так:
7А,5В12 = В ⋅ 12-2 + 5 ⋅ 2-1 + А ⋅ 120 + 7 ⋅ 121.
В шестнадцатеричной системе счисления 16 цифр, обозначаемых 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, A, B, C, D, E, F, что соответствует следующим числам десятеричной системы счисления: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15. Примеры чисел: 17D,ECH; F12AH.
Перевод чисел в позиционных системах счисления
Перевод чисел из произвольной системы счисления в десятичную
Для перевода числа из любой позиционной системы счисления в десятичную необходимо использовать развернутую форму числа, заменяя, если это необходимо, буквенные обозначения соответствующими цифрами. Например:
11012 = 1 ⋅ 23 + 1 ⋅ 22 + 0 ⋅ 21 + 1 ⋅ 20 = 1310;
17D,ECH = 12 ⋅ 16–2 + 14 ⋅ 16–1 + 13 ⋅ 160 + 7 ⋅ 161 + 1 ⋅ 162 = 381,921875.
Перевод чисел из десятичной системы счисления в заданную
Для преобразования целого числа десятичной системы счисления в число любой другой системы счисления последовательно выполняют деление нацело на основание системы счисления, пока не получат нуль. Числа, которые возникают как остаток от деления на основание системы, представляют собой последовательную запись разрядов числа в выбранной системе счисления от младшего разряда к старшему. Поэтому для записи самого числа остатки от деления записывают в обратном порядке.
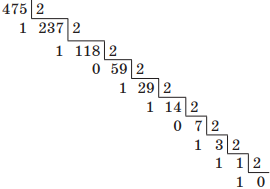
Например, переведем десятичное число 475 в двоичную систему счисления. Для этого будем последовательно выполнять деление нацело на основание новой системы счисления, т. е. на 2:
Читая остатки от деления снизу вверх, получим 111011011.
Проверка:
1 ⋅ 28 + 1 ⋅ 27 + 1 ⋅ 26 + 0 ⋅ 25 + 1 ⋅ 24 + 1 ⋅ 23 + 0 ⋅ 22 + 1 ⋅ 21 + 1 ⋅ 20 = 1 + 2 + 8 + 16 + 64 + 128 + 256 = 47510.
Для преобразования десятичных дробей в число любой системы счисления последовательно выполняют умножение на основание системы счисления, пока дробная часть произведения не будет равна нулю. Полученные целые части являются разрядами числа в новой системе, и их необходимо представлять цифрами этой новой системы счисления. Целые части в дальнейшем отбрасываются.
Например, переведем десятичную дробь 0,37510 в двоичную систему счисления:
Полученный результат — 0,0112.
Не каждое число может быть точно выражено в новой системе счисления, поэтому иногда вычисляют только требуемое количество разрядов дробной части.
Перевод чисел из двоичной системы счисления в восьмеричную и шестнадцатеричную и обратно
Для записи восьмеричных чисел используются восемь цифр, т. е. в каждом разряде числа возможны 8 вариантов записи. Каждый разряд восьмеричного числа содержит 3 бита информации (8 = 2І; І = 3).
Таким образом, чтобы из восьмеричной системы счисления перевести число в двоичный код, необходимо каждую цифру этого числа представить триадой двоичных символов. Лишние нули в старших разрядах отбрасываются.
Например:
1234,7778 = 001 010 011 100,111 111 1112 = 1 010 011 100,111 111 1112;
12345678 = 001 010 011 100 101 110 1112 = 1 010 011 100 101 110 1112.
При переводе двоичного числа в восьмеричную систему счисления нужно каждую триаду двоичных цифр заменить восьмеричной цифрой. При этом, если необходимо, число выравнивается путем дописывания нулей перед целой частью или после дробной.
Например:
11001112 = 001 100 1112 = 1478;
11,10012 = 011,100 1002 = 3,448;
110,01112 = 110,011 1002 = 6,348.
Для записи шестнадцатеричных чисел используются шестнадцать цифр, т. е. для каждого разряда числа возможны 16 вариантов записи. Каждый разряд шестнадцатеричного числа содержит 4 бита информации (16 = 2І; І = 4).
Таким образом, для перевода двоичного числа в шестнадцатеричное его нужно разбить на группы по четыре цифры и преобразовать каждую группу в шестнадцатеричную цифру.
Например:
11001112 = 0110 01112 = 6716;
11,10012 = 0011,10012 = 3,916;
110,01110012 = 0110,0111 00102 = 65,7216.
Для перевода шестнадцатеричного числа в двоичный код необходимо каждую цифру этого числа представить четверкой двоичных цифр.
Например:
1234,AB7716 = 0001 0010 0011 0100,1010 1011 0111 01112 = 1 0010 0011 0100,1010 1011 0111 01112;
CE456716 = 1100 1110 0100 0101 0110 01112.
При переводе числа из одной произвольной системы счисления в другую нужно выполнить промежуточное преобразование в десятичное число. При переходе из восьмеричного счисления в шестнадцатеричное и обратно используется вспомогательный двоичный код числа.
Например, переведем троичное число 2113 в семеричную систему счисления. Для этого сначала преобразуем число 2113 в десятичное, записав его развернутую форму:
2113 = 2 ⋅ 32 + 1 ⋅ 31 + 1 ⋅ 30 = 18 + 3 + 1 = 2210.
Затем переведем десятичное число 2210 в семеричную систему счисления делением нацело на основание новой системы счисления, т. е. на 7:
Итак, 2113 = 317.
Примеры решения задач
Пример 1. В системе счисления с некоторым основанием число 12 записывается в виде 110. Указать это основание.
Решение. Обозначим искомое основание п. По правилу записи чисел в позиционных системах счисления 1210 = 110n = 0 ·n0 + 1 · n1 + 1 · n2. Составим уравнение: n2 + n = 12 . Найдем натуральный корень уравнения (отрицательный корень не подходит, т. к. основание системы счисления, по определению, натуральное число большее единицы): n = 3 . Проверим полученный ответ: 1103 = 0· 30 + 1 · 31 + 1 · 32 = 0 + 3 + 9 = 12 .
Ответ: 3.
Пример 2. Указать через запятую в порядке возрастания все основания систем счисления, в которых запись числа 22 оканчивается на 4.
Решение. Последняя цифра в записи числа представляет собой остаток от деления числа на основание системы счисления. 22 — 4 = 18. Найдем делители числа 18. Это числа 2, 3, 6, 9, 18. Числа 2 и 3 не подходят, т. к. в системах счисления с основаниями 2 и 3 нет цифры 4. Значит, искомыми основаниями являются числа 6, 9 и 18. Проверим полученный результат, записав число 22 в указанных системах счисления: 2210 = 346 = 249 = 1418.
Ответ: 6, 9, 18.
Пример 3. Указать через запятую в порядке возрастания все числа, не превосходящие 25, запись которых в двоичной системе счисления оканчивается на 101. Ответ записать в десятичной системе счисления.
Решение. Для удобства воспользуемся восьмеричной системой счисления. 1012 = 58. Тогда число х можно представить как x = 5 · 80 + a1 · 81 + a2 · 82 + a3 · 83 + … , где a1, a2, a3, … — цифры восьмеричной системы. Искомые числа не должны превосходить 25, поэтому разложение нужно ограничить двумя первыми слагаемыми ( 82 > 25), т. е. такие числа должны иметь представление x = 5 + a1 · 8. Поскольку x ≤ 25 , допустимыми значениями a1 будут 0, 1, 2. Подставив эти значения в выражение для х, получим искомые числа:
a1 = 0; x = 5 + 0 · 8 = 5;.
a1=1; x = 5 + 1 · 8 = 13;.
a1 = 2; x = 5 + 2 · 8 = 21;.
Выполним проверку:
510 = 1012;
1310 = 11012;
2110 = 101012.
Ответ: 5, 13, 21.
Арифметические операции в позиционных системах счисления
Правила выполнения арифметических действий над двоичными числами задаются таблицами сложения, вычитания и умножения.
| Сложение | Вычитание | Умножение |
| 0 + 0 = 0 | 0 – 0 = 0 | 0 ⋅ 0 = 0 |
| 0 + 1 = 1 | 1 – 0 = 1 | 0 ⋅ 1 = 0 |
| 1 + 0 = 1 | 1 – 1 = 0 | 1 ⋅ 0 = 0 |
| 1 + 1 = 10 | 10 – 1 = 1 | 1 ⋅ 1 = 1 |
Правило выполнения операции сложения одинаково для всех систем счисления: если сумма складываемых цифр больше или равна основанию системы счисления, то единица переносится в следующий слева разряд. При вычитании, если необходимо, делают заем.
Пример выполнения сложения: сложим двоичные числа 111 и 101, 10101 и 1111:
Пример выполнения вычитания: вычтем двоичные числа 10001 – 101 и 11011 – 1101:
Пример выполнения умножения: умножим двоичные числа 110 и 11, 111 и 101:
Аналогично выполняются арифметические действия в восьмеричной, шестнадцатеричной и других системах счисления. При этом необходимо учитывать, что величина переноса в следующий разряд при сложении и заем из старшего разряда при вычитании определяется величиной основания системы счисления.
Например, выполним сложение восьмеричных чисел 368 и 158, а также вычитание шестнадцатеричных чисел 9С16 и 6716:
При выполнении арифметических операций над числами, представленными в разных системах счисления, нужно предварительно перевести их в одну и ту же систему.
Представление чисел в компьютере
Формат с фиксированной запятой
В памяти компьютера целые числа хранятся в формате с фиксированной запятой: каждому разряду ячейки памяти соответствует один и тот же разряд числа, «запятая» находится вне разрядной сетки.
Для хранения целых неотрицательных чисел отводится 8 битов памяти. Минимальное число соответствует восьми нулям, хранящимся в восьми битах ячейки памяти, и равно 0. Максимальное число соответствует восьми единицам и равно
1 ⋅ 27 + 1 ⋅ 26 + 1 ⋅ 25 + 1 ⋅ 24 + 1 ⋅ 23 + 1 ⋅ 22 + 1 ⋅ 21 + 1 ⋅ 20 = 25510.
Таким образом, диапазон изменения целых неотрицательных чисел — от 0 до 255.
Для п-разрядного представления диапазон будет составлять от 0 до 2n – 1.
Для хранения целых чисел со знаком отводится 2 байта памяти (16 битов). Старший разряд отводится под знак числа: если число положительное, то в знаковый разряд записывается 0, если число отрицательное — 1. Такое представление чисел в компьютере называется прямым кодом.
Для представления отрицательных чисел используется дополнительный код. Он позволяет заменить арифметическую операцию вычитания операцией сложения, что существенно упрощает работу процессора и увеличивает его быстродействие. Дополнительный код отрицательного числа А, хранящегося в п ячейках, равен 2n − |А|.
Алгоритм получения дополнительного кода отрицательного числа:
1. Записать прямой код числа в п двоичных разрядах.
2. Получить обратный код числа. (Обратный код образуется из прямого кода заменой нулей единицами, а единиц — нулями, кроме цифр знакового разряда. Для положительных чисел обратный код совпадает с прямым. Используется как промежуточное звено для получения дополнительного кода.)
3. Прибавить единицу к полученному обратному коду.
Например, получим дополнительный код числа –201410 для шестнадцатиразрядного представления:
| Прямой код | Двоичный код числа 201410 со знаковым разрядом | 1000011111011110 |
| Обратный код | Инвертирование (исключая знаковый разряд) | 1111100000100001 |
| Прибавление единицы | 1111100000100001 + 0000000000000001 | |
| Дополнительный код | 1111100000100010 |
При алгебраическом сложении двоичных чисел с использованием дополнительного кода положительные слагаемые представляют в прямом коде, а отрицательные — в дополнительном коде. Затем суммируют эти коды, включая знаковые разряды, которые при этом рассматриваются как старшие разряды. При переносе из знакового разряда единицу переноса отбрасывают. В результате получают алгебраическую сумму в прямом коде, если эта сумма положительная, и в дополнительном — если сумма отрицательная.
Например:
1) Найдем разность 1310 – 1210 для восьмибитного представления. Представим заданные числа в двоичной системе счисления:
1310 = 11012 и 1210 = 11002.
Запишем прямой, обратный и дополнительный коды для числа –1210 и прямой код для числа 1310 в восьми битах:
| 1310 | –1210 | |
| Прямой код | 00001101 | 10001100 |
| Обратный код | — | 11110011 |
| Дополнительный код | — | 11110100 |
Вычитание заменим сложением (для удобства контроля за знаковым разрядом условно отделим его знаком «_»):
Так как произошел перенос из знакового разряда, первую единицу отбрасываем, и в результате получаем 00000001.
2) Найдем разность 810 – 1310 для восьмибитного представления.
Запишем прямой, обратный и дополнительный коды для числа –1310 и прямой код для числа 810 в восьми битах:
| 810 | –1310 | |
| Прямой код | 00001000 | 10001101 |
| Обратный код | — | 11110010 |
| Дополнительный код | — | 11110011 |
Вычитание заменим сложением:
В знаковом разряде стоит единица, а значит, результат получен в дополнительном коде. Перейдем от дополнительного кода к обратному, вычтя единицу:
11111011 – 00000001 = 11111010.
Перейдем от обратного кода к прямому, инвертируя все цифры, за исключением знакового (старшего) разряда: 10000101. Это десятичное число –510.
Так как при п-разрядном представлении отрицательного числа А в дополнительном коде старший разряд выделяется для хранения знака числа, минимальное отрицательное число равно: А = –2n–1, а максимальное: |А| = 2n–1 или А = –2n–1 – 1.
Определим диапазон чисел, которые могут храниться в оперативной памяти в формате длинных целых чисел со знаком (для хранения таких чисел отводится 32 бита памяти). Минимальное отрицательное число равно
А = –231 = –214748364810.
Максимальное положительное число равно
А = 231 – 1 = 214748364710.
Достоинствами формата с фиксированной запятой являются простота и наглядность представления чисел, простота алгоритмов реализации арифметических операций. Недостатком является небольшой диапазон представимых чисел, недостаточный для решения большинства прикладных задач.
Программный комплекс NetTest
|
1. Решите уравнение 608 + x = 1207 Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно. |
| Ответ: |
|
2. Решите уравнение 547 + x = 3205 Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно. |
| Ответ: |
|
3. Запись числа 325 в системе счисления с основанием N содержит 3 цифры и оканчивается на 1. Чему равно минимально возможное основание системы счисления? |
| Ответ: |
|
4. Запись числа 281 в системе счисления с основанием N содержит 3 цифры и оканчивается на 1. Чему равно максимально возможное основание системы счисления? |
| Ответ: |
|
5. Сколько единиц в двоичной записи числа 82014 - 2614 + 45 ? |
| Ответ: |
|
6. Сколько единиц в двоичной записи числа 22014 - 4650 - 38 ? |
| Ответ: |
|
7. Сколько единиц в двоичной записи числа 8148 - 4123 + 2654 - 17 ? |
| Ответ: |
|
8. Сколько значащих нулей в двоичной записи числа 41024 + 81025 - 21026 - 140 |
| Ответ: |
|
9. Значение арифметического выражения: 274 - 95 + 38 - 25 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи? |
| Ответ: |
|
10. Значение арифметического выражения: 5⋅367 + 610 - 36 записали в системе счисления с основанием 6. Сколько цифр «5» содержится в этой записи? |
| Ответ: |
| © К. Поляков, 2021 | kpolyakov.spb.ru |
Подготовка к ЕГЭ – 2021, Занятие 1.
Позиционные системы счисления, задание 14
Презентацию по теме можно посмотреть здесь.
На уроках информатики мы никогда ничего не зубрим! Ученики должны понимать все, о чем говорится на уроках, и запоминать новое путем повторений пройденного, сравнений и ассоциаций с уже знакомыми темами и понятной информацией.
Для максимально быстрого и однозначно верного решения задач мы придерживаемся принципа: чем меньше вычислений и другой работы мы делаем, тем меньше времени тратиться на решение задачи и тем меньшую вероятность появления ошибок получаем в результате. При этом, соглашаясь с Аристотелем, что «Ум заключается не только в знании, но и в умении прилагать знания на деле», я настаиваю на способах решений, соответствующих этому принципу, хотя существуют и другие варианты. На своих уроках я придерживаюсь изложения темы именно в этом ключе. Сначала это бывает сложно, особенно тем, кто приходит ко мне на уроки уже знакомым с иначе излагаемым материалом и не желающим переучиваться. Но хочу научить Вас решать быстро и без ошибок, экономя время и силы для новых задач. Поверьте, этому несложно научиться, нужно только поверить в свои силы — и все получится! При этом проверочные работы и тесты проводятся мной на время с расчетом решения задач именно по такому принципу.
При изучении этой темы обращаю особое внимание на таблицу степеней двойки и на ряд закономерностей. При этом знание таблицы является необходимым и достаточным условием для максимально быстрого и однозначно точного решения, а дополнительное знание закономерностей позволит выполнить все еще быстрее и точнее.
Ниже приведена таблица степеней двойки, где n – это степень, а 2n – результат возведения числа 2 в степень n:
|
n |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
2n |
1 |
2 |
4 |
8 |
16 |
32 |
64 |
128 |
256 |
512 |
1024 |
2048 |
4096 |
Таблицу не обязательно заранее учить наизусть. Нужно при решении задач пользоваться ею, но при этом заглядывать в нее все реже и реже, пытаясь сначала вспомнить значение степени. Тогда эта таблица сама «уляжется» в голове и очень поможет на экзамене в этой и в других темах!
Теперь перейдем к теории рассматриваемой темы.
Система счисления или нумерация – это способ записи (обозначения) чисел.
Возьмем это за основу работы с разными системами счисления, поскольку только способ записи у них будет разный, а все закономерности одинаковые. Поэтому в случае возникновения трудностей в понимании темы обращаемся к десятичной системе счисления и переносим аналог на остальные.
Символы, при помощи которых записываются числа, называются цифрами, а их совокупность – алфавитом системы счисления. Количество цифр, составляющих алфавит, называется основанием (размерностью) системы счисления. Число в любой системе счисления состоит из цифр, входящих в алфавит этой системы.
В системе счисления, которой мы пользуемся в повседневной жизни – 10 цифр (от 0 до 9), и поэтому такая система счисления называется десятичной.
Аналогично, если в системе счисления будет две цифры (0 и 1), то она называется двоичной, восемь цифр (от 0 до 7) – восьмеричной и т.д.
Основание алфавита указывается в виде индекса числа, записанного в десятичной системе счисления, например: 10112, 1528, 1А716.
При этом основание десятичной системы счисления можно не указывать (будем использовать то, что всем нам привычно — «по умолчанию»).
Обратим внимание, что
-
наименьшей цифрой в алфавите любой системе счисления является ноль, а наибольшая цифра всегда на единицу меньше основания
Системы счисления бывают двух видов — позиционные и непозиционные.
Система счисления называется позиционной, если количественный эквивалент цифры зависит от ее положения (позиции) в записи числа.
Например, запишем одинаковыми цифрами несколько разных чисел:
1234 = 1 тысяча + 2 сотни + 3 десятка + 1 единица
3124 = 3 тысячи + 1 сотня + 2 десятка + 4 единицы
4321 = 4 тысячи + 3 сотни + 2 десятка +1 единица.
Таким образом, числа, составленные из одних и тех же цифр, но стоящих в числах на разных позициях, имеют различные значения (математический вес).
Как и в привычной нам десятичной, так и в любой другой позиционной системе счисления значение числа образуется суммой результатов умножения цифр на «веса» (степени основания) соответствующих разрядов.
Например,
3948 = 3*1000+9*100+4*10+8*1 = 3*103+9*102+4*101+8*100
10112 = 1*23+0*22+1*21+1*20 или 10112 = 1*20+1*21+0*22+1*23
(далее будем пользоваться последней приведенной в примере формой записи, чтобы не делать лишних действий и не нумеровать степени двойки слева направо для их правильного использования).
При этом форма записи числа в виде 3948 называется свернутой, а в виде 3*103+9*102+4*101+8*100 – развернутой формой записи числа.
Примером непозиционных систем могут служить древнеегипетская, древнеславянская или римская система счисления.
Самым ярким примером непозиционной системы счисления является известная всем римская система счисления, в которой каждый символ обозначает всегда одно и тоже число независимо от его позиции в числе. Так в римской системе счисления из двух цифр X — десять и I — один можно составить числа: XI (одиннадцать), IX (девять), XIX (девятнадцать) или другие, но во всех них значения цифр в зависимости от занимаемых позиций не меняются, а значение числа получается разным при смене порядка следования цифр друг за другом.
Будем называть позиционные системы счисления дружественными (родственными), если в основании у них лежит одно и то же число, но в разных степенях. При этом «дружат» они через систему счисления с основанием в первой степени.
Например, двоичная, четверичная, восьмеричная и шестнадцатеричная системы счисления «дружат» через двоичную, т.к. в основании у них лежит число 2, но в разных степенях:
2=21, 4=22, 8=23, 16=24
Будем считать, что десятичная система счисления не дружит ни с какой другой, так как ближайшая к ней система счисления с основанием 100 в практических вычислениях нам не встречается.
Правила перевода между различными системами счисления делятся на две группы – перевод между дружественными и недружественными системами.
Перевод между недружественными системами счисления всегда выполняется через десятичную систему следующим образом:
-
из десятичной системы счисления в любую – делением исходного числа на основание системы счисления, в которую переводим; при этом остатки от деления и последнее частное должны быть меньше этого основания. Частное и остатки от деления собираются справа налево.
-
из любой системы счисления в десятичную — умножением цифр на «веса» (степени основания) соответствующих разрядов и все полученные значения складываются.
Например, переведем десятичное число 25 в двоичную систему счисления (рис.1):
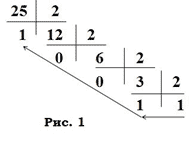
Тогда 2510 = 110012
и обратно 110012 = 1*20+0*21+0*22+1*23+1*24
2510 = 2213
и обратно 2213 = 1*30+2*31+2*32
2510 = 416 и обратно 416 = 1*60+4*61
Для быстрого и точного перевода между дружественными (причем только между ними!) двоичной, восьмеричной и шестнадцатеричной системами счисления построим таблицу соответствия десятичных, восьмеричных и шестнадцатеричных чисел двоичным, и назовем эту таблицу таблицей «дружбы» (рис.2). Левая часть этой таблицы включает цифры восьмеричной системы счисления, а правая дополняет ее для всех цифр шестнадцатеричной системы счисления.
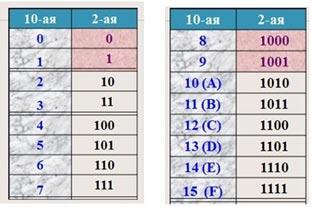
Рис. 2
Заметим, что так как каждая цифра в любой системе счисления занимает только одну позицию (один разряд числа), то в шестнадцатеричной системе счисления для записи цифр со значением больше 9 (10, 11 и т.д. здесь – это цифры!) используют латинские заглавные буквы от A до F .
Данная таблица разделена двойными линиями в местах условного ее разделения на дружественные системы счисления (двоичную, четверичную, восьмеричную и шестнадцатеричную).
Обратите внимание, что длина чисел в двоичной системе счисления зависит от степени двойки в основании дружественной системы счисления:
-
т.к. 8=23, то при переводе из восьмеричной системы счисления в двоичную мы записываем каждое двоичное число тремя разрядами (триадами);
-
т.к. 16=24, то при переводе из восьмеричной системы счисления в двоичную мы записываем каждое двоичное число четырьмя разрядами (тетрадами);
Именно это позволяет легко осуществлять перевод между дружественными системами счисления, записывая каждую цифру исходного числа соответствующей ему в таблице двоичной цифрой с учетом того, чтобы длина двоичной цифры при этом строго соответствовала степени двойки основания исходной системы счисления:
-
8=23, то меняем одну восьмеричную цифру на три двоичные — триады,
-
16 = 24, тогда меняем каждую шестнадцатеричную цифру на четыре двоичные — тетрады,
дополняя их при необходимости до нужной длины незначащими нулями слева (добавление нулей справа от исходного числа является результатом умножения числа на 10, 100 и т.д., т.е. изменяет исходное число).
Например,
1528 = 001 101 0102 = 1 101 0102
(при этом первые два нуля не указываются, т.к. они незначащие), а
15216 = 0001 0101 00102 = 1 0101 00102
(при этом первые три нуля также не указываются).
Выполним перевод из восьмеричной системы счисления в шестнадцатеричную и обратно через двоичную систему счисления.
Перегруппировка двоичных разрядов по четыре и по три во второй части выражений выполняется справа налево по количеству разрядов в степени результирующей системы счисления, а дальнейшая запись числа – как обычно, слева направо.
Например,
1528 = 1 101 0102 = 110 10102 = 6А16
15216 = 1 0101 00102 = 101 010 0102 = 5228
Теперь обратим внимание еще на несколько закономерностей, которые можно заметить в вышеприведенной таблице «дружбы» и аналогичных ей таблицах других систем счисления, в том числе и десятичной.
Закономерность № 1
-
Любое основание в своей системе счисления выглядит как 10, т.е.
N10 = 10n
(210=102 – посмотрите в таблице, 810=108, 1610=1016 и т.д.).
Закономерность № 2.
-
Степень любого основания в своей системе счисления выглядит как единица и количество нулей, равных степени, т.е.
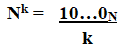
(посмотрите в таблице: 4=22=1002, 8=23 =10002, тогда 16=24=100002).
Закономерность № 3.
-
Число, стоящее перед k-й степенью основания, в своей системе счисления выглядит как последовательность из k самых больших цифр этой системы счисления, т.е.
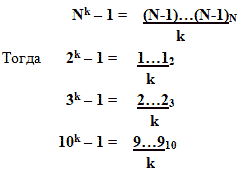
(посмотрите в таблице: 3=22 – 1=112, 7=23 — 1=1112, тогда 15=24-1=11112).
Закономерность № 4.
-
Длина числа при переводе десятичного числа в любую систему счисления легко определяется по формуле:
где Ch – исходное число,
L — длина после перевода в систему счисления с основанием N.
(например: 22 ≤ 5 23, тогда при переводе в двоичную систему счисления длина числа будет равна 3, посмотрите в таблице: 5=1012;
23 ≤ 13 24, тогда при переводе в двоичную систему счисления длина числа будет равна 3, посмотрите в таблице: 13=10112).
Если закономерности 1, 2 и 3 применяются для быстрого и точного перевода чисел между системами счисления, то закономерность 4 удобно использовать для первичной проверки правильности перевода чисел из десятичной системы счисления в любую другую, что позволит сэкономить время на проверке результата перевода и даст возможность избежать ошибок).
Но использование закономерностей дает нам еще ряд преимуществ!
Так, помня о нашем принципе быстрых и точных вычислений и в соответствии с закономерностями 1 и 3, рекомендуется выполнять перевод из десятичной системы счисления в двоичную разложением числа на степени двойки следующим образом. Вычитаем из числа степень двойки, которая меньше числа, но максимально приближенную к нему, Затем с остатком проделываем те же действия до тех пор, пока не разложим все число на степени двойки.
Например:
25 = 16 + 8 + 1 = 24 + 23 + 20
(25 – 16 = 9 ; 9 = 8 + 1)
После этого, заменяем присутствующие степени двойки единицами (в соответствии с закономерностью 2), а пропущенные – нулями в порядке следования степеней, получая двоичную запись числа:
25 = 16 + 8 + 1 = 24 + 23 + 20 = 110012
(отсутствующие вторую и первую степени двойки заменяем нулями).
На чем еще можно сэкономить время и избежать ошибок?
Например, для перевода большого двоичного числа в десятичную систему счисления можно использовать в качестве промежуточной восьмеричную или шестнадцатеричную системы счисления:
1100111012 = 110 011 1012 = 6358 = 5*80+3*81+6*82 = 5 + 24 + 384 = 413
1100111012 = 1 1001 11012 = 19D16= 13*160+9*161+1*162 = 13 + 144 + 256 = 413
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Решим несколько задач по этой теме с использованием изложенных выше закономерностей.
Примечание. Так как любое число в нулевой степени равно единице, а любое число в первой степени равно самому числу, то при решении задач можно не писать степень в разряде единиц и десятков.
1. Переведите двоичное число 1110101 в десятичную систему счисления.
Решение:
11101012= 1 110 1012 = 1658 = 5+6*81+1*82 =5+48+64=117
Или:
11101012= 111 01012 = 7516 = 5+7*161=5+112=117
Ответ: 117
2. Переведите двоичное число 1100011 в десятичную систему счисления.
Решение:
11000112 = 110 00112 = 7316 = 3+6*161=3+96=99
Ответ: 99
3. Переведите число 135 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число — количество единиц.
Решение:
135 = 128+4+2+1= 27 + 22 + 21 + 20
Ответ: 4
Заметим, что этот ответ получен без окончательного перевода числа в двоичную систему счисления, достаточно посчитать количество двоек в степенях. Это позволило сэкономить время решения задачи и избежать возможных ошибок при дальнейшей записи.
4. Переведите число 125 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число — количество единиц.
Решение:
125 = 127 – 2 = 11111112 -102 = 11111012
Ответ: 6
5. Переведите число FE из шестнадцатеричной системы счисления в двоичную систему счисления.
Решение:
FE16 = 1111 11102 (используем запись тетрадами из таблицы «дружбы»).
Ответ: 11111110
6. Переведите число 143 из десятичной системы счисления в двоичную систему счисления. Сколько значащих нулей содержит полученное число? В ответе укажите одно число — количество нулей.
Решение:
143 = 128+8+4+2+1 = 27 + 23 + 22 + 21 + 20,
то пропущены всего три (6, 5 и 4 степени двойки, которые при записи двоичного числа заполняются нулями.
Ответ: 3
7. Переведите число 305 из десятичной системы счисления в двоичную систему счисления. Сколько единиц содержит полученное число? В ответе укажите одно число — количество единиц.
Решение:
305 = 256 + 32 + 16 + 1
(305-256=49, 49 — 32=17=16+1)
(т.к. в сложении участвуют всего 4 степени двойки, то результат будет содержать всего 4 единицы. Степени можно даже не писать)
Ответ: 4
8. Вычислите: 101010102 – 2528 + 716. Ответ запишите в десятичной системе счисления.
Решение: Для решения задач такого типа нужно сначала перевести все числа в одну систему счисления, а уже потом выполнять действия между ними.
Переведем первое число в восьмеричную систему счисления:
101010102 = 2528
Тогда получаем выражение: 2528 – 2528 + 716 = 716 = 710
Ответ: 7
9. Вычислите значение выражения B916 − 2718. В ответе запишите вычисленное значение в десятичной системе счисления.
Решение: Переведем первое число в восьмеричную систему счисления:
В916 = 1011 10012 = 10 111 0012 = 2718. Тогда 2718 — 2718 = 0.
Ответ: 0
10. Вычислите значение выражения EB16 − 3528. Ответ запишите в десятичной системе счисления.
Решение: Переведем первое число в восьмеричную систему счисления:
EB16= 111010112= 3528
Тогда разница между двумя исходными числами равна 1.
Ответ: 1
11. Укажите наименьшее четырёхзначное восьмеричное число, двоичная запись которого содержит 5 единиц. В ответе запишите только само восьмеричное число, основание системы счисления указывать не нужно.
Решение: Наименьшее двоичное число, содержащее 5 единиц, равно 111112.
Но чтобы восьмеричное число было четырехзначным нужно, чтобы оно состояло из 4 триад (из 12 цифр). При этом первой цифрой двоичного числа обязательно должна быть 1 (два незначащих нуля в начале можно не писать), а остальные единицы будут занимать последние разряды числа. Тогда получаем:
001 000 001 1112 = 10178
Ответ: 1017
12. Найдите значение выражения 1116 + 118 : 112. Ответ запишите в двоичной системе счисления.
Решение: В таких задачах, где нужно выполнять быстро и без ошибок вычисления в различных системах счисления, а результат требуется получить в десятичной, то и решение быстрее и проще выполнить в десятичной системе счисления. Поэтому переводим туда все исходные числа и считаем:
1116 = 16+1 = 17
118 = 8+1 = 9
112 = 2+1 = 3
Тогда 17 + 9 : 3 = 20
20 = 16 + 4 = 24 + 22 = 101002
Ответ: 10100
13. Даны 4 целых числа, записанные в двоичной системе:
10001011, 10111000, 10011011, 10110100.
Сколько среди них чисел, больших, чем A416+208?
Решение: Для выполнения действий над числами, представленными в разных системах счисления, нужно сначала перевести их в наиболее удобную для вас систему счисления, и только потом решать задачу. Для меня наиболее удобной является восьмеричная система счисления:
100010112 = 2138, 101110002 = 5608, 100110112 = 2338, 101101002 = 2468
A416 = 101001002 = 2448, и 2448+208=2648.
Тогда из предложенных чисел подходит только второе число.
Ответ: 1
14. Запись числа 6910 в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Чему равно основание этой системы счисления N?
Решение: Для решения этой задачи используем две закономерности.
Во-первых, последней цифрой числа при переводе из одной системы счисления в другую всегда является первый остаток от деления числа на основание системы счисления, куда переводим. Тогда искомое основание N должно быть кратно 68 (69=х*N+1, то х*N=68): 2, 4, 7 и т.д. Во-вторых, по закономерности 4, получаем N3 ≤ 69 4.
Тогда при выполнении этих условий искомое число N будет равно 4.
Ответ: 4
15. В системе счисления с основанием N запись числа 4110 оканчивается на 2, а запись числа 13110 — на 1. Чему равно число N?
Решение: Т.к. в остатках чисел у нас есть цифры 2 и 1, то N ≤3. При этом N нужно найти число, кратное числам 39 и 130. Следовательно, N = 13.
Ответ: 13
16. В какой системе счисления выполняется равенство 12 · 13 = 211? В ответе укажите число – основание системы счисления.
Решение: При переводе числа 211N в десятичную систему счисления получаем уравнение:
211N = 2*N3 + 1*N +1
Для перевода множителей 12 и 13 в десятичную систему счисления вспомним закономерность 1. Тогда 12N = N+2, 13N = N+3.
Следовательно, получаем уравнение:
(N+2)(N+3) = 2*N2 + N +1
Корнями данного уравнения являются 5 и -1. Но т.к. основание системы счисления является натуральным числом, то N = 5.
Ответ: 5
17. Укажите наименьшее основание системы счисления, в которой запись числа 50 трехзначна.
Решение: По закономерности 4 получаем N2 ≤ 50 3.
Следовательно, нам нужно найти наименьшее число, куб которого больше 50.
Ответ: 4
Мы подошли к 14 заданию из ЕГЭ по информатике 2022. Оно связано с различными системами счисления. Что такое различные системы счисления, мы рассматривали в этой статье. Так же будет полезно посмотреть эту статью.
Переходим к первому тренировочному 14-ому заданию из ЕГЭ по информатике. Раньше это задание было под номером 16.
Задача (ЕГЭ по информатике, 2019, Москва)
Значение выражения 536 + 524 — 25 записали в системе счисления с основанием 5. Сколько цифр «4» содержится в этой записи?
Решение:
Первый способ. (С помощью Питона)
f = 5**36 + 5**24 - 25 s='' while f>0: s = s + str(f%5) f = f // 5 print(s.count('4'))
В переменную f записываем функцию. Две звёздочки подряд обозначают возведение в степень. Заводим строчку s, где и будет сформировано число в пятеричной системе.
Сам перевод числа f в пятеричную систему происходит в цикле WHILE.
Записываем остатки от деления на 5 в строку s. Делаем так же, как если бы переводили в ручную. И так же производим само целочисленное деление. Это мы тоже делаем, когда переводим на листке бумаги.
В строке s получается число в пятеричной системе, но в цифры в этой записи стоят в обратном порядке. Ведь, когда мы переводим в ручную, остатки должны записать задом наперёд.
Здесь и не важен порядок цифр, важно количество четвёрок!
С помощью функции count находим количество четвёрок в строке s.
В ответе напишем 22.
Второй способ. (Классический)
Сформулируем главное правило, на которое будем опираться при решении подобного типа задач.
Примеры:
54 (в десятичной системе) — это 100005 (в пятеричной системе)
72 (в десятичной системе) — это 1007 (в семеричной системе)
29 (в десятичной системе) — это 10000000002 (в двоичной системе)
Перепишем наше выражение, чтобы все числа были в виде степени представлены.
536 + 524 — 52
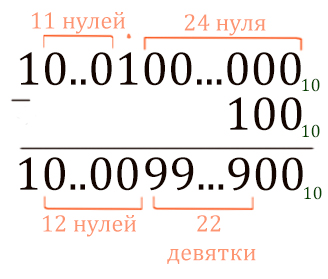
Посчитаем 536 + 524 в пятеричной системе столбиком, используя основное правило.
Здесь всё просто: ноль прибавить ноль, будет ноль. Единица плюс ноль, будет один.
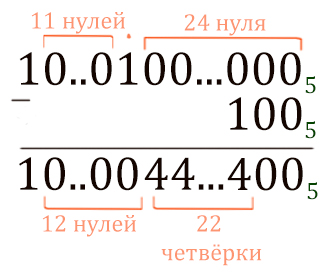
Теперь от получившегося числа нужно отнять 52 (1005).
Первые два разряда посчитать легко. Ноль минус ноль, будет ноль.
Третий разряд: из нуля отнять единицу мы не можем, поэтому занимаем у более старших разрядов.
В более старших разрядах тоже нули, поэтому идём до единицы, у которой можно занять. Получается 22 четвёрки.
Вот как было бы, если бы считали в нашей родной десятичной системе счисления в аналогичной ситуации.
Здесь мы считаем в десятичной системе, поэтому получаются девятки. В нашей задаче считали в пятеричной системе, поэтому получаются четвёрки.
В ответе напишем 22 четвёрки.
Ответ: 22
Задача (ЕГЭ по информатике, 2020, Москва)
Значение выражения 168 × 420 — 45 — 64 записали в системе счисления с основанием 4. Сколько цифр «3» содержится в этой записи?
Решение:
Первый способ. (С помощью Питона)
f = 16**8 * 4**20 - 4**5 - 64 s='' while f>0: s = s + str(f%4) f = f // 4 print(s.count('3'))
Второй способ. (Классический)
Преобразуем наше выражение. Приведём всё к 4-ам.
168 × 420 — 45 — 64 =
= (42)8 × 420 — 45 — 43 =
= 416 × 420 — 45 — 43 =
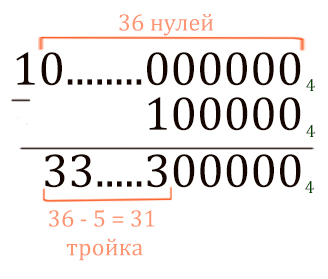
= 436 — 45 — 43
Здесь не можем применить технику устного счёта, потому что стоят два минуса. Значит, будем решать с помощью столбиков.
Сначала посчитаем 436 — 45.
Теперь от этого числа нужно отнять 43 (10004)
Получается 32 тройки.
В последнем вычислении нет ничего сложно. В десятичной системе вы бы легко вычислили в аналогичной ситуации.
Ответ: 32
Задача (Тренировочная)
Укажите через запятую в порядке возрастания все десятичные натуральные числа, не превосходящие 17, запись которых в троичной системе счисления оканчивается на две одинаковые цифры.
Решение:
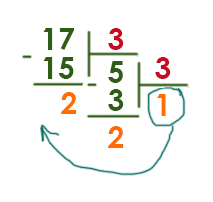
1) Переведём число 17 в троичную систему.
Получилось 1223.
2) Теперь выпишем все числа, которые не превосходят 1223 (Т.е. 1223 тоже подходит!), запись которых в троичной системе счисления оканчивается на две одинаковые цифры. В троичной системе могут применяться цифры 0, 1, 2.
1223
1223
1113
1003
223
113
Теперь переведём эти числа в десятичную систему.
1223 = 2 × 30 + 2 × 31 + 1 × 32 = 1710
1113 = 1 × 30 + 1 × 31 + 1 × 32 = 1310
1003 = 0 × 30 + 0 × 31 + 1 × 32 = 910
223 = 2 × 30 + 2 × 31 = 810
113 = 1 × 30 + 1 × 31 = 410
Ответ: 4, 8, 9, 13, 17
Ещё один интересный тип задания номер 14, который вполне может быть на реальном ЕГЭ по информатике 2022.
Задача (Уравнение)
Чему равно наименьшее основание позиционной системы счисления x, при котором 225x = 405y?
Ответ записать в виде целого числа.
Решение:
Переведём каждое из чисел 225x и 405y в десятичную систему счисления и приравняем, т.к. эти числа равны.
5 × x0 + 2 × x1 + 2 × x2 = 5 × y0 + 0 × y1 + 4 × y2
Любое число в нулевой степени — это 1. Значит, 5 × x0 = 5 × y0 = 5. Эти два выражения равны одному и тому же значению, следовательно, их можно убрать и слева, и справа.
2x + 2x2 = 4y2
x + x2 = 2y2
x(1 + x) = 2y2
Получили уравнение в целых числах. Слева умножение двух последовательных чисел. Нужно начать подбирать целые числа.
При y = 6 :
x (1 + x) = 2 × 62 = 72 ; Произведение двух последовательных чисел 8 * 9 = 72. Значит, x = 8.
Мы начали проверку с числа 6, потому что у нас в уравнении присутствуют цифра 5. Значит, система счисления может быть минимум с основанием 6.
Получается, что наименьшее значение x равно 8.
В подобных задач нужно знать, что числа обязательно найдутся, нужно их просто хорошо поискать.
Для качественной проработки 14 задания из ЕГЭ по информатике 2022 разберём ещё некоторые задачи.
Задача (Основание системы)
Запись числа 338 в системе счисления с основанием N содержит 3 цифры и оканчивается на 2. Чему равно максимально возможное основание системы счисления?
Решение:
В этой задаче применим формулу:
Примером для данной формулы можно взять два разряда в двоичной системе. Максимальное число в двоичной системе равно 112. А в десятичной системе это число равно 310. Т.е. 22 — 1.
338 число будет точно больше, чем двухзначное число с основанием N.
Получается неравенство:
338 > N2 — 1
N2 < 339
N — положительное целое число. Тогда:
N < √339 ≈ 18
N ≤ 18
Сказано, что число в системе с основанием N оканчивается на 2. Поэтому первый остаток должен быть равен 2!
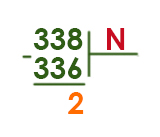
Будем идти вниз от числа 18 и проверять, на что делится 336.
Число 336 должно делится на N.
Подошло число 16 (16 * 21 = 336!)
Ответ: 16
Продолжаем подготовку к 14 заданию из ЕГЭ по информатике 2022
Задача (На понимание)
Запись числа в девятеричной системе счисления заканчивается цифрой 4. Какой будет последняя цифра в записи этого числа в троичной системе счисления?
Решение:
Подберём такие числа в десятичной системе, которые в остатке при первом делении на 9 дадут 4!
Посмотрим, какой остаток будет при делении этого же числа на 3 при первом делении. Получается 1. Это и будет ответ.
Ответ: 1
Задача (Закрепление материала)
Укажите через запятую в порядке возрастания все основания систем счисления, в которых запись числа 23 оканчивается на 2.
Решение:
Нужно перебрать все числа от 3 до 23 и определить, какие из них при делении числа 23 дадут остаток 2.
23 : 3 = 7 (ост. 2) +
23 : 4 = 5 (ост. 3) —
23 : 5 = 4 (ост. 3) —
23 : 6 = 3 (ост. 5) —
23 : 7 = 3 (ост. 2) +
23 : 8 = 2 (ост. 7) —
23 : 9 = 2 (ост. 5) —
23 : 10 = 2 (ост. 3) —
23 : 11 = 2 (ост. 1) —
23 : 12 = 1 (ост. 11) —
23 : 13 = 1 (ост. 10) —
23 : 14 = 1 (ост. 9) —
23 : 15 = 1 (ост. 
23 : 16 = 1 (ост. 7) —
23 : 17 = 1 (ост. 6) —
23 : 18 = 1 (ост. 5) —
23 : 19 = 1 (ост. 4) —
23 : 20 = 1 (ост. 3) —
23 : 21 = 1 (ост. 2) +
23 : 22 = 1 (ост. 1) —
23 : 23 = 1 (ост. 0) —
Подходят числа 3, 7, 21.
Здесь можно и написать программу:
for i in range(3, 24): if 23%i==2: print(i)
Ответ: 3, 7, 21
Задача (Добьём 14 задание из ЕГЭ по информатике 2022)
В некоторой системе счисления записи десятичных чисел 66 и 40 заканчиваются на 1. Определите основание системы счисления.
Решение:
Нужно найти такое число, чтобы числа 66 и 40 при делении на это число давали остаток 1.
Т.е. искомое число должно быть делителем чисел 65 (66-1) и 39 (40-1). У числа 39 не так много делителей: 1, 3, 13, 39
Видим, что число 65 делится на 13 (65 : 13 = 5). Поэтому искомое число равно 13.
Ответ: 13
Задача (Для чемпионов!)
В какой системе счисления выполняется равенство 12 · 13 = 222?
В ответе укажите число – основание системы счисления.
Решение:
Если бы мы находились в десятичной системе, то последней цифрой была бы 6 (2 * 3). Но у нас 2! Т.е. Система счисления меньше или равна 6, т.к. если бы система счисления была больше 6, то у нас была бы 6 последняя цифра.
Шестёрка не «поместилась» в младший разряд, от неё осталось только 2. Остальные 4 единицы ушли в более старший разряд. Если 4 единицы составляют единицу более старшего разряда, то значит, мы находимся в четверичной системе.
Ответ: 4
Задача (Новый тип, Статград окт 2022)
В выражении 1xBAD16 + 2CxFE16 x обозначает некоторую цифру из алфавита шестнадцатеричной системы счисления. Определите наименьшее значение x, при котором значение данного выражения кратно 15. Для найденного x вычислите частное от деления данного выражения на 15 и запишите его в ответе в десятичной системе счисления.
Решение:
Здесь дана сумма чисел, которые написаны в шестнадцатеричной системе счисления.
Мы будем перебирать каждую цифру из шестнадцатеричной системы (0-15) с помощью цикла. Нас будут интересовать те значения x, при котором сумма этих чисел будет делится на 15.
for x in range(0, 16): a=13*16**0 + 10*16**1 + 11*16**2 + x*16**3 + 1*16**4 b=14*16**0 + 15*16**1 + x*16**2 + 12*16**3 + 2*16**4 if (a+b)%15==0: print(x, (a+b)//15)
Чтобы проверить, делится ли данное выражение на 15, переводим оба слагаемых в нашу родную десятичную систему. Переводим стандартным образом, об этом можно прочитать здесь.
В задаче нужно написать для наименьшего найденного значения x результат от деления данной суммы на 15.
Получается 18341
Ответ: 18341
Задача(Новый тип, закрепление)
(Богданов) Операнды арифметического выражения записаны в системе счисления с основанием 17:
9759x17 + 3×10817
В записи чисел переменной x обозначена неизвестная цифра из алфавита 17-ричной системы счисления. Определите наименьшее значение x, при котором значение данного арифметического выражения кратного 11. Для найденного значения x вычислите частное от деления значения арифметического выражения на 11 и укажите его в ответе в десятичной системе счисления. Основание системы счисления в ответе указывать не нужно.
Решение:
Решим задание с помощью предыдущего шаблона на языке Python.
for x in range(0, 17): a=x*17**0 + 9*17**1 + 5*17**2 + 7*17**3 + 9*17**4 b=8*17**0 + 0*17**1 + 1*17**2 + x*17**3 + 3*17**4 if (a+b)%11==0: print(x, (a+b)//11)
Ответ: 95306
Задача (Новый тип, две переменные)
(В. Шубинкин) Числа M и N записаны в системах счисления с основаниями 15 и 13 соответственно.
M = 2y23x515, N = 67x9y13
В записи чисел переменными x и y обозначены допустимые в данных системах счисления неизвестные цифры. Определите наименьшее значение натурального числа A, при котором существуют такие x, y, что M + A кратно N.
Решение:
Принцип решения данной задачи похож на решение 15 задания из ЕГЭ по информатике.
for A in range(1, 5000): for x in range(0, 13): for y in range(0, 13): M=5*15**0 + x*15**1 + 3*15**2 + 2*15**3 + y*15**4 + 2*15**5 N=y*13**0 + 9*13**1 + x*13**2 + 7*13**3 + 6*13**4 if (M+A)%N==0: print(A)
Нужно найти A, значит, начинаем перебирать A. Идём от 1, т.к. речь идёт о натуральных числах. Перебираем x и y. Они могут принимать значения из алфавита в 13-ой системе. Берём меньшую, т.к. эти переменные и в первом числе, и во втором одинаковые.
Если выполняется условие задачи, то нам интересно такое A при котором это произошло.
В этой задаче A получается достаточно большим, поэтому перебираем эту переменную до 5000.
Ответ: 1535
На этом всё! Вы прошли чемпионскую тренировку по подготовке 14 задания из ЕГЭ по информатике 2022. Успехов на экзамене!
«В переменную f записываем функцию». В переменную f мы записываем не функцию, а выражение
Господа, вот это я понимаю, по-настоящему чемпионская подготовка. Тут же и язык свой придумали, и решение на нём сделали. Скажите, зачем над змеёй то издеваться? Очень уж режет слух неправильное произношение. «Пайтон» — вот как должно быть. Я бы промолчал, увидев это раз, но видя подобное насилие над словом постоянно — молчать более не могу
Для ласт задачи модно сделать код куда проще и короче
for a in range(1, 10000):
for x in ‘0123456789ABC’:
for y in ‘0123456789ABC’:
M = int(f’2{y}23{x}5′, 15)
N = int(f’67{x}9{y}’, 13)
if (M + a) % N == 0:
print(a)
break
Первое задание, первое решение, очепятка: «В ответе напишем 4»,
вместо: «В ответе напишем 22».
И спасибо Вам за этот сайт!)
Позиционные системы счисления, примеры решения задач к ЕГЭ — 2023, задание 14, часть 2 (по ДЕМО-версии-2021)
(базовый уровень, примерное время решения – 2 минуты).
Есть вопросы и замечания — пишите!
Обозначим через N основание системы счисления.
Тогда наибольшая цифра в системе счисления с основанием N равна N-1.
Следует помнить, что:
- Любое основание N в своей системе счисления выглядит как 10, т.е.
N10 = 10N
(например: 210=102, 310=103, 810=108, 1610=1016 и так далее).
- Степень любого основания N в своей системе счисления выглядит как единица и количество нулей, равных степени, т.е.
Nk = 1 0…0N
k
(например: 4=22=1002, 8=23 =10002, 16=24=100002 и так далее).
- Число, стоящее перед k-той степенью основания, в своей системе счисления выглядит как последовательность из k самых больших цифр этой системы счисления, т.е.
Nk — 1 = (N-1)…(N-1)N
k
Тогда 2k – 1 = 1…12
k
(например: 3=22-1=112, 7=23 -1=1112, 15=24-1=11112 и так далее).
- Число Nk– Nm = Nk · (Nk-m – 1) записывается в системе счисления с основанием N как k-m старших цифр этой системы счисления, за которыми следует k нулей:
Nm – Nk = (N-1)…(N-1) 0…0N
m – k k
Тогда
2m – 2k = 1…1 0…02
m – k k
(например: 103 — 102 = 900, 103 — 101 = 990, 105 — 103 = 99000, 25 – 22 = 111002, 35 – 32 = 222003 и так далее).
Примеры и способы решения задач.
Задача 1.
Сколько единиц в двоичной записи числа 81025 + 21024 – 3 ?
Решение.
Приведем все числа в заданном примере к одному виду с основанием 2 и упорядочим их в порядке убывания степеней, с учетом того, что 3 = 4 — 1:
81025 + 21024 – 3 = 23075 + 21024 – 22 + 20
Количество единиц в разности 21024 – 22 будет 1024-2 = 1022 единицы + 1 единица (число 24032) + 1 единица от числа 20, то всего получаем 1022+1+1 = 1024 единицы.
Ответ: 1024
Задача 2.
Сколько единиц в двоичной записи числа 82014 – 2614 + 45?
Решение.
Приведем все числа в заданном примере к одному виду с основанием 2 и упорядочим их в порядке убывания степеней, с учетом того, что 45 = 32 + 8 + 4 + 1:
82014 – 2614 + 45 = 26042 — 2614 + 25 + 23+ 22 + 20
Количество единиц в разности 26042 — 2614 будет 6042 – 614 = 5428 единиц + 4 единицы от чисел 25, 23, 22 и 20 , то всего получаем 5428+4 = 5432 единицы.
Ответ: 5432
Задача 3.
Значение арифметического выражения 410 + 290 — 16 записали в системе счисления с основанием 2. Сколько цифр «1» содержится в этой записи?
Решение.
Приведем все числа в заданном примере к одному виду с основанием 2 и упорядочим их в порядке убывания степеней:
220 + 290 – 24 = 290 + 220 – 24
Тогда после перевода в двоичную систему счисления в числе 290будет 1 единица, в разности 220 – 24 будет
20 — 4 = 16 единиц и 4 нуля. Следовательно, в полученном результате получаем всего 16 + 1 = 17 единиц.
Ответ: 17
Задача 4.
Значение арифметического выражения 6410 + 260 — 16 записали в системе счисления с основанием 8. Сколько цифр «7» содержится в этой записи?
Решение.
Приведем все числа в заданном примере к одному виду с основанием 8 и упорядочим их в порядке убывания степеней, учитывая, что 16 = 8 + 8:
412 + 260 — 16 = 820 + 830 – 16 = 830 + 820– 81 – 81
Ищем в разности крайнюю левую степень восьмерки и крайнюю правую 820 – 81, при этом среднюю 81 на время «теряем».
Определяем количество семерок в разности 820 – 81, получаем 20 — 1 = 19 семерок.
Так как «внутри» этой разности есть еще 81, то просто вычитаем одну семерку: 19 – 1 = 18.
Ответ: 18.
Задача 5.
Сколько единиц в двоичной записи числа 42018 + 8305 – 2130 – 120 ?
Решение.
Приведем все числа в заданном примере к одному виду с основанием 2 и упорядочим их в порядке убывания степеней, с учетом того, что 45 = 32 + 8 + 4 + 1:
42018 + 8305 – 2130 – 120 = 24036 + 2915 – 2130 — 27 + 23
Ищем в разности (2915 – 2130 — 27) крайнюю левую степень двойки и крайнюю правую 2915– 27, при этом среднюю 2130 на время «теряем».
Определяем количество семерок в разности 2915– 27, получаем 915-7 = 908 единиц.
Так как «внутри» этой разности есть еще 2130, то просто вычитаем одну единицу: 908 – 1 = 907.
Прибавляем 2 единицы от чисел 24036 и 23, то всего получаем 907 + 2 = 909 единиц.
Ответ: 909
Задача 6.
Значение арифметического выражения 99 – 39 + 919 – 19 записали в системе счисления с основанием 3. Сколько цифр «2» содержится в этой записи?
Решение.
Приведем все числа в заданном примере к одному виду с основанием 3 и упорядочим их в порядке убывания степеней, учитывая, что 19 = 27 – 8 + 1+1:
99 – 39 + 919 – 27 + 9 — 1 -1 = 318 + 338 – 33 + 32 – 30 = 338 + 318 – 33 + 32 – 30 – 30
Разбиваем нашу запись на две разности 318 – 33 и 32 – 30 и вычисляем их отдельно.
Количество двоек в разности 318 – 33 будет 18-3 = 15, в разности 32 – 30 будет равно 2, всего 15 + 2 = 17 двоек. Вычитаем из них еще одну единицу, так как 30 = 12. При этом последняя цифра меняется как 2-1=1, в результате получаем 17-1 = 16 двоек.
Ответ: 16
Задача 7.
Сколько значащих нулей в двоичной записи числа 4512 + 8512 – 2128 – 250 ?
Решение.
Приведем все числа в заданном примере к одному виду с основанием 2 и упорядочим их в порядке убывания степеней, учитывая, что 250 = 256 – 4 – 2 = 28 – 22 — 21:
4512 + 8512 – 2128 – 256+ 4 + 2 = 21024 + 21536 – 2128 – 28 + 22 + 21 = = 21536 + 21024 – 2128 – 28 + 22 + 21
Ищем в разности 21024 – 2128 – 28 крайнюю левую степень двойки и крайнюю правую 21024 –28, при этом среднюю 2128 на время «теряем».
В разности 21024 –28 будет 1024 — 8 = 1016 единиц и 8 нулей.
Так как «внутри» этой разности есть еще 2128, то просто заменяем одну единицу (на 128 месте) на ноль и получаем 1015 единиц и 9 нулей.
С этого момента можно решать задачу двумя способами:
1) Между 21536 и 21024 (до конца числа) есть еще 1536-1024=512 нулей, два из которых заняты единицами (22+21), тогда получаем еще 512-2 = 510 нулей.
Итого в результате вычислений получаем 510+9 = 519 нулей.
Можно показать это вычисление на схеме, где вычисляемая выше разность выделена черным цветом:
Всего 1 ед. + 1534 нуля + 2 ед.в конце _
1 ед.+1022 нуля + 2 ед.в конце
21536 _ + _ 21024 – 2128 – 28 + 22+ 21
1 ед.+510 нулей + 1015 ед. + 9 нулей + 2 ед.
2) Посчитать общее число единиц после выполнения вычислений и вычесть их общей длины исходного двоичного числа.
21536 + 21024 – 2128 – 28 + 22 + 21
1 ед. + 1015 ед. + 2 ед . = 1018 ед.
Так как 21536 = 10…0 2 равна 1537 знаков, то в нем будет 1537-1018 = 519 нулей.
1536
Ответ: 519
Задача 8.
Сколько единиц в двоичной записи числа 42016 + 22018 – 8600 + 6 ?
Решение.
Приведем все числа в заданном примере к одному виду с основанием 2 и упорядочим их в порядке убывания степеней, учитывая, что 6 = 4 + 2:
42016 + 22018 – 8600 + 6 = 24032 + 22018 – 21800 + 22 + 21
После перевода числа 24032 в двоичную систему оно будет состоять из 1 единицы и 4032 нулей.
Количество единиц в разности 22018 – 21800 будет 2018-1800 = 218 единиц + 1 единица (число 24032) + 2 единицы от чисел 22 и 21, то всего получаем 218+3 = 221 единицу.
Ответ: 221
Задача 9.
Сколько единиц в двоичной записи числа 42016 – 22018 + 8800 – 80?
Решение.
Приведем все числа в заданном примере к одному виду с основанием 2 и упорядочим их в порядке убывания степеней, учитывая, что 80 = 64 + 16:
42016 – 22018 + 8800 – 80= 24032— 22018 + 22400 – 26 — 24 = 24032 + 22400 — 22018 – 26 — 24
Далее рассмотрим два способа решения задачи.
1). После перевода числа 24032 в двоичную систему оно будет состоять из 1 единицы и 4032 нулей.
Из записи 22400 — 22018– 26 — 24 возьмем разность первого и последнего чисел 22400 — 24 и получаем 2396 единиц. Вычитаем из них 2 единицы, которые дают числа 26 и 24, остается 2394 единицы.
Тогда всего получаем 1 + 2394 = 2395 единиц.
2). Будем решать данную задачу путем последовательных вычитаний.
После перевода числа 24032 в двоичную систему оно будет состоять из 1 единицы и 4032 нулей.
Количество единиц в разности 24000 – 22018 будет 4000-2018 = 382 и 2018 нулей.
Оставляем 381 единицу, используя далее 1 единицу и 2018 нулей, что равно числу 22018.
Далее, в разности 22018 — 26 будет 2012 единиц и 6 нулей.
Оставляем 2011 единиц, остается число 26. Тогда разность 26 – 24 получаем 2 единицы.
Складываем все единицы и получаем 1 + 381 + 2011 + 2 = 2395 единиц.
Ответ: 2395