По теме: методические разработки, презентации и конспекты
Реализация принципа практической направленности подготовки обучающихся на уроках математики в 5 – 9 классах
Тема исследования: «Реализация принципа практической направленности подготовки обучающихся на уроках математики в 5 – 9 классах».Объектом исследования является процесс обучения математике обучаю…
Решение задач практической направленности на уроках математики в старших классах коррекционной школы.
Решение задач практической направленности на уроках математики в старших классах коррекционной школы….
Обобщение педагогического опыта учителя математики I квалификационной категории Куликовой Татьяны Николаевны по теме:«Усиление практической направленности математики через организацию систематического проведения практических и лабораторных работ».
Существенную роль в повышении эффективности обучения школьников играет сформированность у них практических умений и навыков, которые необходимы как для изучения математики, так и для повседневно…
Тетрадь по математике для учащихся 4 классов коррекционных школ VIII вида «Задачи практической направленности».
В данном материале представлена тетрадь по математике для учащихся 4 классов коррекционных школ VIII вида «Задачи практической направленности».Вышеназванная тетрадь создана по сборнику «Дополнит…
Презентация к уроку математики «Решение задач практической направленности на нахождение площади»
Презентация к уроку математики в 8 классе по учебнику В.В. Эк…
Задачи для марафона по решению математических задач практической направленности
Подобраны задания для решения прикладных задач…
Использование задач практической направленности при обучении математике детей с интеллектуальной недостаточностью.
Требования современного общества к выпускникам школ определили необходимость пересмотра стандартов как общего, так и специального образования. Система специального образования имеет определённую …
Задачи с практическим содержанием
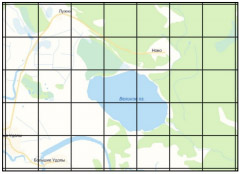
На рисунке изображен план местности (шаг сетки плана соответствует расстоянию 1 км на местности). Оцените, скольким квадратным километрам равна площадь озера Великое, изображенного на плане. Ответ округлите до целого числа.
#901
Марина Павловна внимательно изучает цены в каталогах, прежде чем пойти за покупками. На сей раз она составила таблицу с ценами на продукты для выпечки из разных магазинов. Мука продаётся килограммами, а дрожжи и ванилин — пакетиками по 10 г.
| Магазин | Мука, 1 кг | Дрожжи, 10 г | Ванилин, 10 г |
| «Пекарь» | 62 руб. | 18 руб. | 18 руб. |
| «Повар» | 49 руб. | 12 руб. | 14 руб. |
| «Булка» | 52 руб. | 13 руб. | 12 руб. |
Для булочек к чаю ей нужно купить 1 кг муки, 1 пакетик дрожжей, 2 пакетика ванилина. При этом она знает, что в «Пекаре» скидка 15% на все три продукта, а в «Булке» — 5% на муку. Вычисли, в каком магазине Марина Павловна сможет сделать наименее выгодные покупки. В ответ внеси суммарную стоимость покупки.
#872
На плане изображено плодоовощное хозяйство, расположенное на территории прямоугольной формы (сторона каждой клетки на плане равна 20 м). Въезд и выезд осуществляются через единственные ворота.
При входе на территорию хозяйства слева от ворот находится кукурузное поле. Рядом с ним расположен яблоневый сад. Также имеется цех по переработке овощей и фруктов, расположенный рядом с полем, засеянным капустой. При входе справа от ворот находится стоянка для грузовиков и сельхозтехники. На территории стоянки расположен склад готовой продукции. Участок с теплицами, в которых выращивают клубнику, граничит с яблоневым садом и капустным полем. К хозяйству подведено электричество.
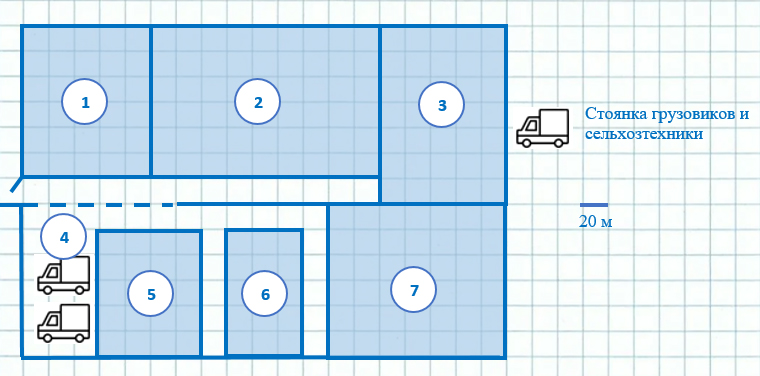
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на схеме. Заполните таблицу, в ответ запишите последовательность четырёх цифр.
| Объекты | Яблоневый сад | Капустное поле | Цех по переработке овощей и фруктов | Теплицы с клубникой |
| Цифры |
2. Урожайность кукурузы в этом хозяйстве в среднем составила 4 тонны с одного гектара земли. Цех по переработке выпускает банки консервированной кукурузы массой нетто основного продукта 280 грамм каждая. Какое максимальное количество банок кукурузы выпустил цех?
3. Найдите суммарную площадь участков земли, занятых под сельскохозяйственные культуры. Ответ дайте в гектарах.
4. По периметру кукурузного поля планируется поставить забор. Найдите его длину (в метрах).
5. Собственник хозяйства рассматривает два варианта водоснабжения: централизованное и автономное из артезианской скважины. Цены на оборудование и стоимость его установки, данные о расходе воды и ее стоимости даны в таблице.
| Водоснабжение | Стоимость оборудования, руб. | Стоимость монтажа, руб. | Средний расход воды, м3/ч | Тариф, руб./м3 |
| Централизованное | 180 960 | 210 700 | 20 | 20,2 |
| Автономное | 205 710 | 480 350 | 20 | 11 |
Обдумав оба варианта, собственник решил оборудовать автономное водоснабжение. Через сколько часов непрерывной работы водоснабжения экономия от использования автономного водоснабжения вместо централизованного компенсирует разность в стоимости установки оборудования и монтажа?
#853
Два друга Петя и Вася задумались о том, как рассчитать площадь поверхности зонта.
На первый взгляд зонт кажется круглым, а его купол напоминает часть сферы (сферический сегмент). Но если присмотреться, то видно, что купол зонта состоит из восьми отдельных клиньев, натянутых на каркас из восьми спиц (рис. 1). Сферическая форма в раскрытом состоянии достигается за счет гибкости спиц и эластичности ткани, из которой изготовлен зонт.
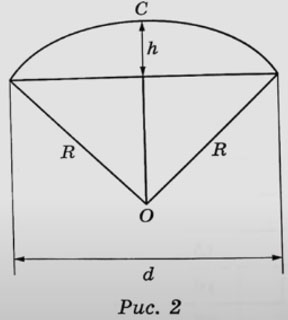
Петя и Вася сумели измерить расстояние между концами соседних спиц а. Оно оказалось равно 38 см. Высота купола зонта h (рис. 2) оказалась равна 25 см, а расстояние d между концами, образующих дугу окружности, проходящей через вершину зонта, — равно 100 см.
1. Длина зонта в сложенном состоянии равна 25 см и складывается из длины ручки (рис. 3) и трети длины спицы (зонт в три сложения). Найдите длину спицы, если длина ручки зонта равна 6,2 см.
2. Поскольку зонт сшит из треугольников, рассуждал Петя, площадь его поверхности можно найти как сумму площадей треугольников. Вычислите площадь поверхности зонта методом Пети, если высота каждого равнобедренного треугольника, проведенная к основанию, равна 53,1 см. Ответ дайте в квадратных сантиметрах с округлением до десятков.
3. Вася предположил, что купол зонта имеет форму сферического сегмента. Вычислите радиус R сферы купола, зная, что ОС=R (рис. 2). Ответ дайте в сантиметрах.
4. Вася нашел площадь купола зонта как площадь поверхности сферического сегмента по формуле S=2πRh, где R – радиус сферы, а h – высота сегмента. Рассчитайте площадь поверхности купола способом Васи. Число π округлите до 3,14. Ответ дайте в квадратных сантиметрах с округлением до целого.
5. Рулон ткани имеет длину 35 м и ширину 80 см. На фабрике из этого рулона были вырезаны треугольные клинья для 29 зонтов, таких же, как зонт, который был у Пети и Васи. Каждый треугольник с учетом припуска на швы имеет площадь 1050 кв. см. Оставшаяся ткань пошла в обрезки. Сколько процентов ткани рулона пошла в обрезки?
#847
Брюки дороже рубашки на 20%, а пиджак дороже рубашки на 44%. На сколько процентов пиджак дороже брюк?
#841
В соревновании по стрельбе за каждый промах в серии из 20 выстрелов стрелок получал штрафные очки: за первый промах — два штрафных очка, за каждый последующий промах — на 0,5 очка больше, чем за предыдущий. Сколько раз попал в цель стрелок, получивший 11 штрафных очков?
#836
Прототипы задания 1 из ЕГЭ по математике (профильный уровень).
#789
На плане изображен многофункциональный культурно-образовательный комплекс, который состоит из нескольких корпусов и обнесен забором прямоугольной формы (сторона каждой клетки на плане 3 м). Вход на территорию комплекса и выход осуществляется через единственные ворота. От входа через весь комплекс проходит главная аллея, вдоль которой стоят восемь фонарей. При входе на территорию комплекса разбит яблоневый сад (цифра 3 на плане). В начале сада находится подсобное помещение, а в глубине — детская площадка площадью 144 кв. м. За яблоневым садом расположено административное здание. Справа от входа — здание магазина (цифра 6 на плане) и образовательная оранжерея. Главная аллея площадью 153 кв. м. вымощена тротуарной плиткой 1,5 м х 1,5 м. Дорожка от главной аллеи к административному зданию имеет ширину 1,5 м и вымощена такой же плиткой. В ночное время территория комплекса освещается фонарями.
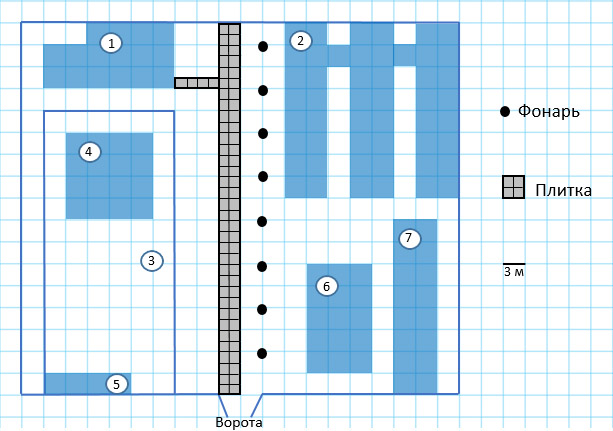
1. Для объектов, указанных в таблице, определите, какими цифрами они обозначены на плане. Заполните таблицу, в бланк ответов перенесите последовательность цифр.
| Объекты | Подсобное помещение | Образовательная оранжерея | Административный комплекс | Детская площадка | Прогулочная оранжерея |
| Цифры |
2. Во время строительства комплекса была использована тротуарная плитка, которую доставляли на стройку в виде упаковок по 5 штук в каждой. Сколько упаковок плитки понадобилось, чтобы уложить аллею и дорожку?
3. Какую часть яблоневого сада занимает подсобное помещение? Ответ дать в процентах, при необходимости округлить с точностью до 0,01.
4. Какое максимальное количество детей может одновременно находится на детской площадке, если по нормам на каждого ребенка положено не менее 7 квадратных метров?
5. В образовательной оранжерее решили посадить редкие виды цветов. Какое максимальное количество растений можно посадить, если количество посадок не должно превосходить числа, которое вычисляется по формуле n = sa, где s — площадь оранжереи, а = 75%.
6. Руководство комплекса планирует заменить уличные фонари. Они есть двух видов: с классическими светильниками или светодиодными. В таблице указаны стоимость опоры, стоимость лампы, монтаж для одного фонаря, средняя потребляемая мощность и стоимость электроэнергии.
| Стоимость опоры | Стоимость лампы | Монтаж | Средняя потребляемая мощность | Стоимость электроэнергии | |
| Фонарь с классическим светильником | 5 400 руб | 200 руб | 16 300 руб | 440 кВт | 3,7 руб/кВт · ч |
| Фонарь со светодиодным светильником | 6 830 руб | 440 руб | 18 330 руб | 40 кВт | 3,7 руб/кВт · ч |
Изучив предлагаемые варианты, руководство решило устанавливать фонари со светодиодными светильниками. Через сколько часов непрерывной работы таких фонарей экономия от их использования компенсирует разность в стоимости установки по сравнению с фонарями с классическими светильниками.
7. Найдите площадь, которую занимает административный комплекс. Ответ дайте в квадратных метрах.
8. Найдите расстояние от административного здания до магазина (расстояние между двумя ближайшими точками по прямой) в метрах.
9. В прогулочной оранжерее решили повесить праздничные флажки. Для этого натянули два троса, каждый через две максимально удаленные точки (по диагонали). Под каким углом пересекаются эти тросы?
10. В яблоневом саду решили вырыть пруд круглой формы, радиус которого 6 м. Какая площадь останется для яблонь после появления пруда? Ответ дайте в квадратных метрах. Площадь круга вычисляется по формуле S = πR2, где π = 3, R — радиус.
#769
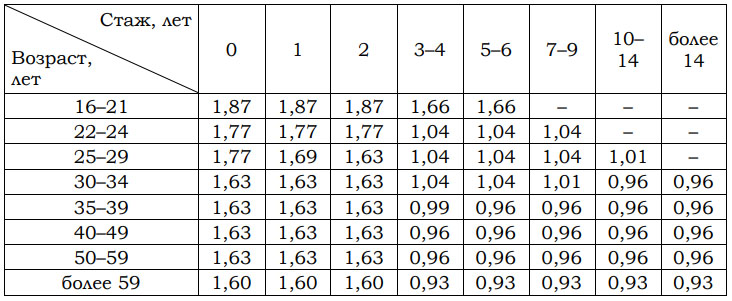
Каждый водитель в Российской Федерации должен быть застрахован по программе обязательного страхования гражданской ответственности (ОСАГО). Стоимость полиса получается умножением базового тарифа на несколько коэффициентов. Коэффициенты зависят от водительского стажа, мощности автомобиля, количества предыдущих страховых выплат и других факторов. Коэффициент бонус-малус (КБМ) зависит от класса водителя. Это коэффициент, понижающий или повышающий стоимость полиса в зависимости от количества ДТП в предыдущий год. Сначала водителю присваивается класс 3. Срок действия полиса, как правило, один год. Каждый последующий год класс водителя рассчитывается в зависимости от числа страховых выплат в течение истекшего года, в соответствии со следующей таблицей.
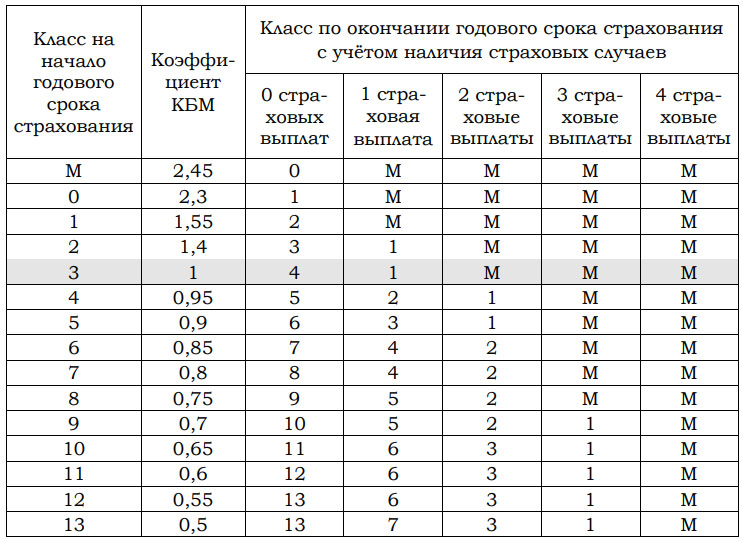
1. Борис страховал свою гражданскую ответственность два года. В течение первого года была сделана одна страховая выплата, после этого выплат не было. Какой класс будет присвоен Борису на начало третьего года страхования?
2. Чему равен КБМ на начало третьего года страхования?
3. Коэффициент возраста и водительского стажа (КВС) также влияет на стоимость полиса (см. таблицу).
Когда Борис получил водительские права и впервые оформил полис, ему было 20 лет. Чему равен КВС на начало 3-го года страхования?
4. В начале второго года страхования Борис заплатил за полис 28 985 руб. Во сколько рублей обойдётся Борису полис на третий год, если значения других коэффициентов (кроме КБМ и КВС) не изменятся?
5. Борис въехал на участок дороги протяжённостью 3,8 км с камерами, отслеживающими среднюю скорость движения. Ограничение скорости на дороге – 80 км/ч. В начале и в конце участка установлены камеры, фиксирующие номер автомобиля и время проезда. По этим данным компьютер вычисляет среднюю скорость на участке. Борис въехал на участок в 14:28:23, а покинул его в 14:30:47. Нарушил ли Борис скоростной режим? Если да, на сколько км/ч средняя скорость на данном участке была выше разрешённой?
#760
Для маркировки автомобильных шин применяется единая система обозначений. Первое число означает ширину В шины (ширину протектора) в миллиметрах (см. рисунок). Второе число — отношение высоты боковины Н к ширине шины В в процентах. Последующая буква указывает конструкцию шины. Например, буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции. За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса в дюймах (в одном дюйме 25,4 мм). По сути, это диаметр d внутреннего отверстия в шине. Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Последний символ в маркировке — индекс скорости. Возможны дополнительные маркировки, означающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие. Завод производит легковые автомобили определённой модели и устанавливает на них шины с маркировкой 185/70 R14. Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.
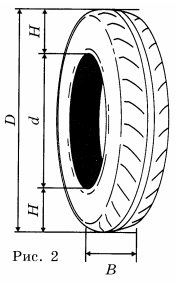
1. Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен 16 дюймам?
2. Найдите диаметр колеса автомобиля, выходящего с завода. Ответ дайте в миллиметрах.
3. На сколько миллиметров увеличится диаметр колеса, если заменить шины, установленные на заводе, на шины 195/70 R14?
4. На сколько метров увеличится путь, пройденный автомобилем, когда колесо сделает 1000 оборотов, если заменить шины установленные на заводе шинами с маркировкой 195/70 R14? Округлите результат до целых.
5. Спидометр автомобиля, собранного на заводе, показывает скорость точно. На сколько процентов показания спидометра будут отличаться от реальной скорости, если заменить шины, установленные на заводе шинами с маркировкой 195/70 R14? Округлите результат до десятых.
#759
Общепринятые форматы листов бумаги обозначают буквой A и цифрой: A0, A1, A2 и так далее. Если лист формата A0 разрезать пополам, получаются два листа формата A1. Если лист A1 разрезать пополам, получаются два листа формата A2 и так далее. При этом отношение длины листа к его ширине у всех форматов, обозначенных буквой A, одно и то же (то есть листы всех форматов подобны друг другу). Это сделано специально — чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменяется). В таблице 1 даны размеры листов бумаги четырёх форматов: от AЗ до A6.
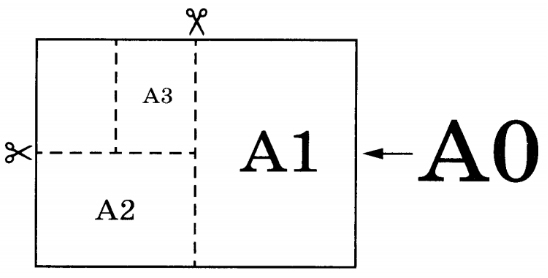
| Порядковые номера | Ширина (мм) | Длина (мм) |
| 1 | 210 | 297 |
| 2 | 297 | 420 |
| 3 | 105 | 148 |
| 4 | 148 | 210 |
1. Для листов бумаги форматов А6, А5, А4 и А3 определите, какими порядковыми номерами обозначены их размеры в таблице. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
| Форматы бумаги | А6 | А5 | А4 | А3 |
2. Сколько листов бумаги формата А6 получится при разрезании одного листа бумаги формата А0?
3. Найдите длину меньшей стороны листа бумаги формата А2. Ответ дайте в миллиметрах.
4. Найдите площадь листа бумаги формата А5. Ответ дайте в квадратных сантиметрах.
5. Размер (высота) типографского шрифта измеряется в пунктах. Один пункт равен 1/72 дюйма, т.е. 0,3528 мм. Какой высоты нужен шрифт (в пунктах), чтобы текст был расположен на листе формата А3 так же, как этот текст, напечатанный шрифтом высотой 10 пунктов на листе формата А4? Размер шрифта округляется до целого.
#720
Для маркировки автомобильных шин применяется единая система обозначений (см. таблицу). Первое число означает ширину В шины (ширину протектора) в миллиметрах (см. рисунок). Второе число — отношение высоты боковины Н к ширине шины В в процентах. Последующая буква указывает конструкцию шины. Например, буква R означает, что шина радиальная, то есть нити каркаса в боковине шины расположены вдоль радиусов колеса. На всех легковых автомобилях применяются шины радиальной конструкции. За обозначением типа конструкции шины идёт число, указывающее диаметр диска колеса в дюймах (в одном дюйме 25,4 мм). По сути, это диаметр d внутреннего отверстия в шине. Таким образом, общий диаметр колеса D легко найти, зная диаметр диска и высоту боковины. Возможны дополнительные маркировки, означающие допустимую нагрузку на шину, сезонность использования, тип дорожного покрытия и другие. Завод производит легковые автомобили определённой модели и устанавливает на них шины с маркировкой 175/60 R15. Завод допускает установку шин с другими маркировками. В таблице показаны разрешённые размеры шин.

1. Какой наименьшей ширины шины можно устанавливать на автомобиль, если диаметр диска равен 16 дюймам? Ответ дайте в миллиметрах.
2. На сколько миллиметров радиус колеса с маркировкой 195/60 R14 больше, чем радиус колеса с маркировкой 165/70 R14?
3. Найдите диаметр D колеса автомобиля, выходящего с завода. Ответ дайте в сантиметрах.
4. На сколько миллиметров уменьшится диаметр D колеса, если заменить шины, установленные на заводе, шинами с маркировкой 195/45 R16?
5. На сколько процентов увеличится пробег автомобиля при одном обороте колеса, если заменить шины, установленные на заводе, шинами с маркировкой 195/55 R15? Округлите результат до десятых.
#718
Миша летом отдыхает у дедушки и бабушки в деревне Николаевке. Миша с дедушкой собираются съездить на велосипедах в село Игнатьево на железнодорожную станцию. Из Николаевки в Игнатьево можно проехать по прямой лесной дорожке. Есть более длинный путь по шоссе — через деревню Свистуху до деревни Берёзовки, где нужно повернуть под прямым углом налево на другое шоссе, ведущее в Игнатьево. Есть и третий маршрут: в Свистухе можно свернуть на прямую тропинку, которая идёт мимо пруда прямо в Игнатьево. По шоссе Миша с дедушкой едут со скоростью 20 км/ч, а по лесной дорожке и тропинке 15 км/ч. Расстояние по шоссе от Николаевки до Свистухи равно 16 км, от Николаевки до Берёзовки — 36 км, а от Берёзовки до Игнатьево 15 км.
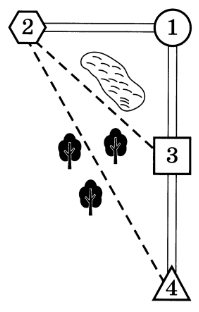
1. Пользуясь описанием, определите, какими цифрами на плане обозначены населённые пункты. В ответ запишите полученную последовательность четырёх цифр.
| Населенные пункты | д. Березовка | с. Игнатьево | д. Николаевка | д. Свистуха |
| Цифры |
2. Сколько километров проедут Миша с дедушкой, если они поедут по шоссе через Берёзовку?
3. Найдите расстояние от д. Николаевка до с. Игнатьево по прямой. Ответ дайте в километрах.
4. Сколько минут затратят на дорогу Миша с дедушкой, если поедут на станцию через Берёзовку?
5. Определите, на какой маршрут до станции потребуется меньше всего времени. В ответ укажите сколько минут потратят на дорогу Миша с дедушкой, если проедут этим маршрутом.
#717
Сергей Петрович решил построить на дачном участке теплицу длиной 4 м. Для этого он сделал прямоугольный фундамент. Для каркаса теплицы Сергей Петрович заказал металлические дуги в форме полуокружностей длиной 5 м каждая и покрытие для обтяжки.
Отдельно требуется купить плёнку для передней и задней стенок теплицы. В передней стенке планируется вход, показанный на рисунке прямоугольником BCC1B1, где точки B, O и C делят отрезок AD на четыре равные части. Внутри теплицы Сергей Петрович планирует сделать три грядки по длине теплицы — одну центральную широкую грядку и две узкие грядки по краям. Между грядками будут дорожки шириной 40 см, для которых необходимо купить тротуарную плитку размером 20 см х 20 см.
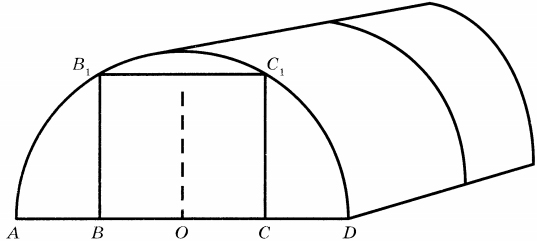
1. Какое наименьшее количество дуг нужно заказать, чтобы расстояние между соседними дугами было не более 60 см?
2. Сколько упаковок плитки необходимо купить для дорожек между грядками, если она продаётся в упаковках по 6 штук?
3. Найдите ширину теплицы. Ответ дайте в метрах с точностью до десятых.
4. Найдите ширину центральной грядки, если она в два раза больше ширины узкой грядки. Ответ дайте в сантиметрах с точностью до десятков.
5. Найдите высоту входа в теплицу. Ответ дайте в сантиметрах.
#716
Общепринятые форматы листов бумаги обозначают буквой A и цифрой: A0, A1, A2 и так далее. Если лист формата A0 разрезать пополам, получаются два листа формата A1. Если лист A1 разрезать пополам, получаются два листа формата A2 и так далее. При этом отношение длины листа к его ширине у всех форматов, обозначенных буквой A, одно и то же (то есть листы всех форматов подобны друг другу). Это сделано специально — чтобы можно было сохранить пропорции текста на листе при изменении формата бумаги (размер шрифта при этом тоже соответственно изменяется). В таблице 1 даны размеры листов бумаги четырёх форматов: от AЗ до A6.

| Порядковые номера | Ширина (мм) | Длина (мм) |
| 1 | 105 | 148 |
| 2 | 210 | 297 |
| 3 | 297 | 420 |
| 4 | 148 | 210 |
1. Для листов бумаги форматов АЗ, А4, А5 и А6 определите, какими порядковыми номерами обозначены их размеры в таблице. Заполните таблицу ниже, в бланк ответов перенесите последовательность четырёх цифр.
| Форматы бумаги | А3 | А4 | А5 | А6 |
2. Сколько листов бумаги формата А5 получится при разрезании одного листа бумаги формата А0?
3. Найдите длину большей стороны листа бумаги формата А2. Ответ дайте в миллиметрах.
4. Найдите площадь листа бумаги формата АЗ. Ответ дайте в квадратных сантиметрах.
5. Найдите отношение длины большей стороны листа к меньшей у бумаги формата А1. Ответ дайте с точностью до десятых.
#715
Задачи в этой статье специально подобраны они так, чтобы представить все возможные типы заданий с таким номером. Часть из них взяты из Банка заданий ФИПИ, другие – авторские.
Вычисления, простейшие уравнения и пропорции
1. Стоимость 1 килограмма тыквы составляет 75 рублей. Антон купил тыкву весом 4 кг 400 г. Сколько рублей сдачи он должен получить с 350 рублей?
Купленная тыква стоит рублей. Сдача с 350 рублей составит
рублей.
2. Бегун пробежал 50 м за 5 секунд. Найдите среднюю скорость бегуна на дистанции. Ответ дайте в километрах в час.
За 1 секунду бегун пробежит 10 метров. За 60 секунд (1 минуту) 600 метров. За 1 час он пробежал бы с той же скоростью в 60 раз больше, т.е. метров. Скорость бегуна 36 км/ч.
3. Самолет вылетает из Магадана в 15.15 и прилетает в Москву в 15.00 того же дня. Найдите среднюю скорость авиаперелета (в км/ч), если разница во времени между Москвой и Магаданом 8 часов, а длина воздушной трассы 6200 км.
Вылет и прилет всегда указываются по местному времени. Если бы самолет вылетел из Магадана ровно в 15.00 по местному времени, он бы находился в пути 8 часов. Поскольку время вылета 15.15, самолет был в полете 7 часов 45 минут, то есть часа.
Задачи на округление (с недостатком, с избытком)
Вспомним правила округления чисел.
Мы применяем их для десятичных дробей, заменяя число на его приближённое значение, записанное с меньшим количеством значащих цифр. Однако в задачах ЕГЭ мы руководствуемся не только правилами округления, но здравым смыслом.
4. Теплоход рассчитан на 750 пассажиров и 25 членов команды. Каждая спасательная шлюпка может вместить 70 человек. Какое наименьшее число шлюпок должно быть на теплоходе, чтобы в случае необходимости в них можно было разместить всех пассажиров и всех членов команды?
Правильный ответ: 12 шлюпок. Делим 775 на 70, получаем 11 и 5 в остатке. Значит, одиннадцать шлюпок будут полностью загружены пассажирами, а в двенадцатой будет сидеть пять человек. И даже если бы там было два человека или один, все равно ответ — 12 шлюпок. Ответ «одиннадцать, а остальные как-нибудь доплывут» — не принимается, это не фильм «Титаник».
В этой задаче мы округлили с избытком. Так же, как и в следующей.
5. Для покраски 1 кв. м потолка требуется 240 г краски. Краска продаётся в банках по 2,5 кг. Какое наименьшее количество банок краски нужно купить для покраски потолка площадью 50 кв. м?
Чтобы покрасить 50 кв. метров. потолка, нужно г = 12 кг краски. Разделив 12 на 2,5, получим 4,8. Округляем в сторону большего! Неполную банку краски вам не продадут.
Ответ: 5.
6. Больному прописано лекарство, которое нужно пить по 0,5 г 3 раза в день в течение 21 дня. В одной упаковке 10 таблеток лекарства по 0,5 г. Какого наименьшего количества упаковок хватит на весь курс лечения?
Больному нужно принять г лекарства. В одной упаковке содержится
г лекарства. Разделив 31,5 на 5, получим 6,3. Округляем до большего.
Ответ: 7.
А в следующих двух задачах мы округляем до меньшего (с недостатком).
7. Павел Иванович купил американский автомобиль, на спидометре которого скорость измеряется в милях в час. Американская миля равна 1609 м. Какова скорость автомобиля в километрах в час, если спидометр показывает 50 миль в час? Ответ округлите до целого числа.
По условию, 1 миля равна 1609 м, 50 миль/ч составляют м/ч = 80450 м/ч = 80,45 км/ч. Округляя найденную величину, получаем 80.
8. На день рождения полагается дарить букет из нечетного числа цветов. Тюльпаны стоят 30 рублей за штуку. У Никиты есть 500 рублей. Из какого наибольшего числа тюльпанов он может купить букет Наташе на день рождения?
Разделив 500 на 30, получим Округлив до меньшего, получим 16. Принято, что букет должен состоять из нечетного числа тюльпанов. Значит, ответ: 15.
Задачи на проценты
Во многих задачах используется понятие — процент.
Вспомним, что — это одна сотая часть от чего-либо.
Что такое дробь (то есть часть) от числа? Когда мы говорим «одна четверть от » — это значит, что дробь
умножается на величину
. «
от
минут» означают, что
надо умножить на
.
Чтобы найти дробь (или часть) от числа, надо дробь умножить на это число.
Итак, от какой-либо величины;
;
;
.
В задачах (да и в жизни) часто говорится об изменении какой-либо величины на определенный процент. Что это значит?
Повышение цены на означает, что к прежней цене
прибавили
. Наоборот, скидка на
означает, что прежняя цена уменьшилась на
. Если первоначальная цена равна
, то новая цена составит
.
9. Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10 ?
Очевидно, что 10 от 40 — это
.
Новая цена ручки составит 44 рубля. На 900 рублей можно купить 20 ручек.
Легко? Да, очень легко. Однако не будем слишком расслабляться. Даже среди детских задач под номером 1 встречаются интересные экземпляры.
Вот, например, задача №1, с которой справляются далеко не все выпускники:
10. Цена на электрический чайник была повышена на 16 и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?
Запомним важное правило: за принимается та величина, с которой мы сравниваем. Цена была повышена на
по сравнению с чем? — с прежней ценой. Значит, прежняя цена — это
, новая цена —
. Составляем пропорцию:
Решаем пропорцию. Получаем, что рублей.
Напомним, что пропорция — это равенство вида . Основное правило пропорции: произведение крайних членов равно произведению средних, то есть
.
Если какая-либо величина в пропорции неизвестна, ее можно найти именно по этому правилу.
Например, из пропорции находим
:
Еще одна задача на проценты. Обратите на нее внимание — она не так проста, как может показаться на первый взгляд.
11. Налог на доходы составляет от заработной платы. После удержания налога на доходы Марья Константиновна получила 9570 рублей. Сколько рублей составляет заработная плата Марьи Константиновны?
Марья Константиновна получила 9570 рублей после удержания налога. Следовательно, у нее уже удержали, а выдали ей ее заработной платы. Составляем пропорцию:
Решаем пропорцию:
Получаем, что зарплата Марьи Константиновны составляет одиннадцать тысяч рублей. Возможно, эта печальная история бедной женщины поможет вам выбрать себе правильное будущее 
Следующая задача — самая сложная из тех, которые могут вам встретиться под номером 1.
12. В городе N живет 200000 жителей. Среди них детей и подростков. Среди взрослых
не работает (пенсионеры, студенты, домохозяйки и т.п.). Сколько взрослых жителей работает?
В чем сложность этой задачи и почему ее редко решают правильно? Дело в том, что « процентов» или «
процентов» — величины относительные. Каждый раз за сто процентов могут приниматься разные величины. Помните правило: за сто процентов принимается в каждом случае то, с чем мы сравниваем.
Получим, что дети и подростки составляют от жителей. Значит, их число — это от
, то есть
надо умножить на
. Получим, что городе
детей и подростков.
Следовательно, взрослых 170000.
Среди взрослых не работает. Теперь за
мы принимаем число взрослых. Получается, что число работающих взрослых жителей равно 55
от 170000, то есть 93500.
Ответ: 93500.
Спасибо за то, что пользуйтесь нашими материалами.
Информация на странице «Задание №2 и №6 Базовый ЕГЭ по математике.. Простейшие текстовые задачи» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.
Публикация обновлена:
09.03.2023