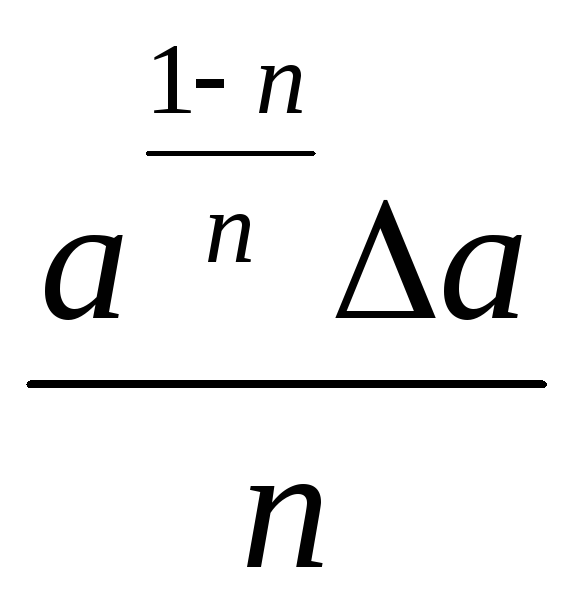Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
Объём жидкости измерили при помощи мензурки (см. рис.). Погрешность измерения объёма при помощи данной мензурки равна её цене деления. Укажите объём воды (в мл) с учётом погрешности измерения. В ответе запишите значение и погрешность слитно без пробела.
Источник: Демонстрационная версия ЕГЭ—2015 по физике.
2
Чему равно напряжение на лампочке (см. рис.), если погрешность прямого измерения напряжения составляет половину цены деления вольтметра? В ответе запишите значение и погрешность слитно без пробела.
Источник: Демонстрационная версия ЕГЭ−2017 по физике
3
При помощи миллиамперметра измеряется ток в некоторой электрической цепи. Миллиамперметр изображён на рисунке. Чему равен ток в цепи, если погрешность прямого измерения тока составляет половину цены деления миллиамперметра? Ответ приведите в миллиамперах. В ответе запишите значение и погрешность слитно без пробела.
Источник: РЕШУ ЕГЭ
4
При помощи вольтметра измеряется напряжение в некоторой электрической цепи. Вольтметр изображён на рисунке. Чему равно напряжение в цепи, если погрешность прямого измерения напряжения составляет половину цены деления вольтметра? Ответ приведите в вольтах. В ответе запишите значение и погрешность слитно без пробела.
Источник: РЕШУ ЕГЭ
5
Длину бруска измеряют с помощью сантиметровой линейки. Запишите результат измерения, учитывая, что погрешность измерения равна половине цены деления. Ответ приведите в сантиметрах. В ответе запишите значение и погрешность слитно без пробела.
Источник: РЕШУ ЕГЭ
Пройти тестирование по этим заданиям
Измерения
называются прямыми, если значения
величин определяются приборами
непосредственно (например, измерение
длины линейкой, определение времени
секундомером и т. д.). Измерения называютсякосвенными, если значение измеряемой
величины определяется посредством
прямых измерений других величин, которые
связаны с измеряемой определенной
зависимостью.
Случайные погрешности при прямых измерениях
Абсолютная
и относительная погрешность. Пусть
проведеноNизмерений
одной и той же величиныxв отсутствии систематической погрешности.
Отдельные результаты измерений имеют
вид:x1,x2,
…,xN.
В качестве наилучшего выбирается среднее
значение измеренной величины:
.
(1)
Абсолютной
погрешностьюединичного измерения
называется разность вида:
.
Среднее
значение абсолютной погрешности Nединичных измерений:
(2)
называется
средней абсолютной погрешностью.
Относительной
погрешностью называется отношение
средней абсолютной погрешности к
среднему значению измеряемой величины:
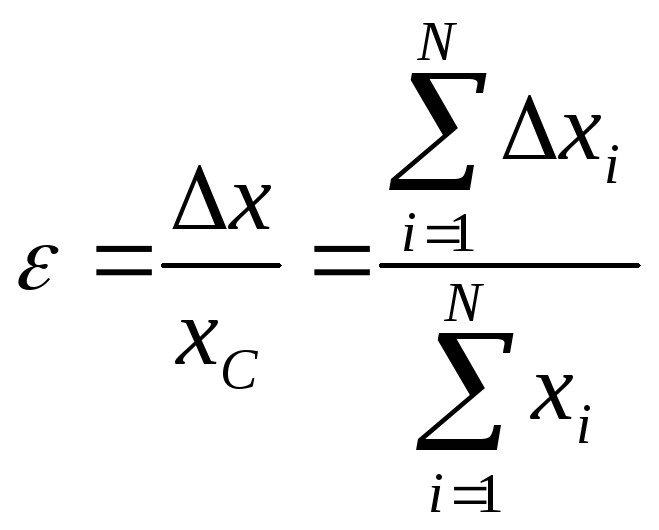
(3)
Приборные погрешности при прямых измерениях
-
Если
нет особых указаний, погрешность прибора
равна половине его цены деления (линейка,
мензурка). -
Погрешность
приборов, снабженных нониусом, равна
цене деления нониуса (микрометр – 0,01
мм, штангенциркуль – 0,1 мм). -
Погрешность
табличных величин равна половине
единицы последнего разряда (пять единиц
следующего порядка за последней значащей
цифрой). -
Погрешность
электроизмерительных приборов
вычисляется согласно классу точности
С,
указанному на шкале прибора:
Например:
и
,
где Umax
и Imax
– предел измерения прибора.
-
Погрешность
приборов с цифровой индикацией равна
единице последнего разряда индикации.
После оценки
случайной и приборной погрешностей в
расчет принимается та, значение которой
больше.
Вычисление погрешностей при косвенных измерениях
Большинство
измерений являются косвенными. В этом
случае искомая величина Х является
функцией нескольких переменных а,
b,
c…,
значения которых можно найти прямыми
измерениями: Х = f(a,b,c…).
Среднее арифметическое
результата косвенных измерений будет
равно:
X
= f(a,b,c…).
Одним из способов
вычисления погрешности является способ
дифференцирования натурального логарифма
функции Х = f(a,b,c…).
Если, например, искомая величина Х
определяется соотношением Х =
,
то после логарифмирования получаем:lnX
= lna
+ lnb
+ ln(c+d).
Дифференциал этого
выражения имеет вид:
.
Применительно к
вычислению приближенных значений его
можно записать для относительной
погрешности в виде:
=
.
(4)
Абсолютная
погрешность при этом рассчитывается
по формуле:
Х = Х(5)
Таким
образом, расчет погрешностей и вычисление
результата при косвенных измерениях
производят в следующем порядке:
1)
Проводят измерения всех величин, входящих
в исходную формулу для вычисления
конечного результата.
2)
Вычисляют средние арифметические
значения каждой измеряемой величины и
их абсолютные погрешности.
3)
Подставляют в исходную формулу средние
значения всех измеренных величин и
вычисляют среднее значение искомой
величины:
X
= f(a,b,c…).
4)
Логарифмируют исходную формулу Х =
f(a,b,c…)
и записывают выражение для относительной
погрешности в виде формулы (4).
5)
Рассчитывают относительную погрешность
=
.
6) Рассчитывают
абсолютную погрешность результата по
формуле (5).
7) Окончательный
результат записывают в виде:
Абсолютные
и относительные погрешности простейших
функций приведены в таблице:
|
Функция |
Абсолютная погрешность |
Относительная погрешность |
|
a+b |
a+b |
|
|
a-b |
a+b |
|
|
ab |
ab+ba |
|
|
|
|
|
|
|
|
|
|
sin a |
|
|
|
cos a |
|
|
Теория по физике на тему «Погрешность»
- 14.12.2016
Теория по физике на тему «Погрешность»
- определение понятия «погрешность»
- правило определения погрешности
- правила округления
- погрешность при измерении большого количества элементов
- погрешность измерительных приборов
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Сохранить ссылку:
Комментарии (0)
Добавить комментарий
Добавить комментарий
Комментарии без регистрации. Несодержательные сообщения удаляются.
Имя (обязательное)
E-Mail
Подписаться на уведомления о новых комментариях
Отправить
Механика — квантовая физика, методы научного познания
В. З. Шапиро
В задании 22 ЕГЭ по физике проверяется, как вы применяете знание физики в практической деятельности и повседневной жизни. В задании дается изображение какого-либо школьного физического прибора, по которому надо определить показания с учетом погрешности измерения.
Что необходимо знать и уметь?
- Вычислять цену деления измерительного прибора. Для этого надо найти два ближайших штриха, обозначенных числами, из большего вычесть меньшее и поделить на число делений.
- Определить границы измерения для приборов, имеющих две шкалы измерения, например, вольтметра, амперметра, барометра. Соответственно, надо выбрать необходимую шкалу для определения показаний прибора.
- Определить погрешность измерения в соответствии с ее описанием в условии. Погрешность измерения может быть равна цене деления или половине цены деления измерительного прибора. Расчет в соответствии с условием задачи.
- В некоторых задачах погрешности измерений могут быть приведены в условии для разных шкал. При выборе определенной шкалы измерений выбирается соответствующая ей погрешность.
- Запись ответа в бланк с учетом требований: каждая цифра и запятая в отдельной клеточке. Если погрешность указана до десятых (или сотых), то показания прибора точно также должны быть указаны до десятых (или сотых).
- Чему равна сила тока в лампочке (см. рисунок), если погрешность прямого измерения силы тока амперметром на пределе измерения 3 А равна 0,15 А, а на пределе измерения 0,6 А равна 0,03 А?
Ответ: ( ± ) А.
Согласно рисунку, амперметр подключен к зажимам 0 и 0,6 А. Поэтому определять показания необходимо по нижней шкале. Цена деления этой шкалы равна (0,4 — 0,2):5 = 0,02 (А). Показания амперметра равны 0,28 А. Для выбранной шкалы погрешность измерений указана в условии задачи. Она равна 0,03 А.
Ответ: (0,28 ± 0,03) А.
В бланк надо записать ответ в следующем виде:
| 0 | , | 2 | 8 | 0 | , | 0 | 3 |
Секрет решения. Задание является достаточно простым, но требует внимательного чтения условия. Если в задаче приводится в качестве измерительного прибора термометр со шкалой, проградуированной в градусах Цельсия, а ответ требуется дать по шкале Кельвина, то надо учесть, что погрешности по этим двум шкалам одинаковые. Добавление к погрешности +273 является грубой ошибкой.
+273 требуется только для перевода температуры из шкалы Цельсия в шкалу Кельвина.
2. Погрешность прямого измерения силы динамометром, на котором висит груз, равна цене деления. Каков вес груза?
Ответ: ( ± ) Н.
Цена деления динамометра определяется следующим расчетом:
(1,5 – 1) : 5 = 0,1 (Н).
Показания динамометра равны 1,1 Н.
Погрешность измерения, согласно условию задачи, равна цене деления, т.е. 0,1 Н.
Ответ: (1,1 ± 0,1) Н.
В бланк надо записать ответ в следующем виде:
| 1 | , | 1 | 0 | , | 1 |
Секрет решения. Задание достаточно простое, но требует внимательного проведения простых расчетов. Главное – правильная запись в бланк ответов №1 показаний динамометра с учетом погрешности измерений.
- Определите показания вольтметра (см. рисунок), если погрешность прямого измерения напряжения составляет половину цены деления вольтметра.
Ответ: ( ___________ ± ___________) В.
Цена деления вольтметра определяется следующим расчетом:
(2 – 1) : 5 = 0,2 (Н).
Показания вольтметра равны 2 В.
Погрешность измерения, согласно условию задачи, составляет половину цены деления, т.е. 0,1 В.
Ответ: (2,0 ± 0,1) В.
| 2 | , | 0 | 0 | , | 1 |
Секрет решения. В этой задаче надо обратить внимание на то, что погрешность измерений равна половине цены деления. При заполнении бланка ответов №1 показания вольтметра необходимо указать с учетом десятичной записи числа (2,0).
Спасибо за то, что пользуйтесь нашими статьями.
Информация на странице «Задание 22 ЕГЭ по физике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из разделов нашего сайта.
Публикация обновлена:
08.03.2023
Как записывать погрешность измерений егэ физика
Как записывать погрешность измерений егэ физика
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 22 № 11945
Пакет, в котором находится 200 шайб, положили на весы. Весы показали 60 г. Чему равна масса одной шайбы по результатам этих измерений, если погрешность весов равна ±10 г? Массу самого пакета не учитывать. В ответе массу шайбы (в граммах) и погрешность запишите слитно, без пробелов.
Найдём массу одной шайбы: 60 г/200 = 0,3 г. Погрешность равномерно распределяется между погрешностями измерения массы шайб, то есть погрешность равна 10 г/200 = 0,05 г. Измеренную величину нужно записывать с тем количеством знаков, которое ещё позволяет погрешность, то есть 0,3 г нужно представить как 0,30 г.
—>
Задание 22 № 11945
Задание 22 11945.
Phys-ege. sdamgia. ru
17.02.2018 15:31:27
2018-02-17 15:31:27
Источники:
Https://phys-ege. sdamgia. ru/problem? id=11945
Как определять погрешность измерений (учебник Физика 10) » /> » /> .keyword { color: red; } Как записывать погрешность измерений егэ физика
Физика. Информатика. Портфолио
Физика. Информатика. Портфолио.
Как определять погрешность измерений (учебник Физика 10)
Информация о материале Автор: Laborant Категория: Погрешности Опубликовано: 07 декабря 2016 Обновлено: 12 декабря 2016 Просмотров: 33050
1. Как определять погрешности измерений.
Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.
Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.
Прямое измерение — определение значения физической величины непосредственно средствами измерения.
Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.
Введем следующие обозначения:
А, В, С, . — физические величины.
Апр — приближенное значение физической величины, т. е. значение, полученное путем прямых или косвенных измерений.
ΔА — абсолютная погрешность измерения физической величины.
Ε — относительная погрешность измерения физической величины, равная:
ΔИА — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; см. табл. 1).
Δ0А — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения); она равна в большинстве случаев половине цены деления, при измерении времени — цене деления секундомера или часов.
Абсолютные инструментальные погрешности средств измерений
| № | Средства измерения | Предел измерения | Цена деления | Абсолютная инструментальная погрешность |
| 1 | Линейка | |||
| Ученическая | До 50 см | 1 мм | ± 1 мм | |
| Чертежная | До 50 см | 1 мм | ± 0,2 мм | |
| Инструментальная (стальная) | 20 см | 1 мм | ± 0,1 мм | |
| Демонстрационная | 100 см | 1 см | ± 0,5 см | |
| 2 | Лента измерительная | 150 см | 0,5 см | ± 0,5 см |
| 3 | Измерительный цилиндр | До 250 мл | 1 мл | ± 1 мл |
| 4 | Штангенциркуль | 150 мм | 0,1 мм | ± 0,05 мм |
| 5 | Микрометр | 25 мм | 0,01 мм | ± 0,005 мм |
| 6 | Динамометр учебный | 4 Н | 0,1 Н | ± 0,05 Н |
| 7 | Весы учебные | 200 г | — | ± 0,01 г |
| 8 | Секундомер | 0-30 мин | 0,2 с | ± 1 с за 30 мин |
| 9 | Барометр-анероид | 720-780 мм рт. ст. | 1 мм рт. ст. | ± 3 мм рт. ст. |
| 10 | Термометр лабораторный | 0-100 0 С | 1 0 С | ± 1 0 С |
| 11 | Амперметр школьный | 2 А | 0,1 А | ± 0,05 А |
| 12 | Вольтметр школьный | 6 В | 0,2 В | ± 0,15 В |
Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:
Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔА = 0,17 ≈ 0,2); числовое значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А = 10,332 ≈ 10,3).
Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, обычно отличаются друг от друга. В этом случае Апр находят как среднее арифметическое значение всех измерений, а погрешность ΔА (ее называют случайной погрешностью) определяют методами математической статистики.
В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. Для получения результата достаточно одного измерения.
Относительная погрешность косвенных измерений определяется так, как показано в таблице 2.
Формулы для вычисления относительной погрешности косвенных измерений
| № | Формула для физической величины | Формула для относительной погрешности |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Абсолютная погрешность косвенных измерений определяется по формуле ΔА = Апрε (ε выражается десятичной дробью).
2. О классе точности электроизмерительных приборов.
Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γпр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность ΔиА от всей шкалы прибора (Amax):
Класс точности указывают на шкале прибора или в его паспорте (знак % при этом не пишут). Существуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γпр) и всю его шкалу (Аmах), определяют абсолютную погрешность ΔиА измерения физической величины А этим прибором:
3. Как сравнивать результаты измерений.
1. Записать результаты измерений в виде двойных неравенств:
2. Сравнить полученные интервалы значений: если интервалы не перекрываются, то результаты неодинаковы; если перекрываются — одинаковы при данной относительной погрешности измерений.
Физика. Информатика. Портфолио.
Информация о материале Автор: Laborant Категория: Погрешности Опубликовано: 07 декабря 2016 Обновлено: 12 декабря 2016 Просмотров: 33050
1. Как определять погрешности измерений.
Выполнение лабораторных работ связано с измерением различных физических величин и последующей обработкой их результатов.
Измерение — нахождение значения физической величины опытным путем с помощью средств измерений.
Прямое измерение — определение значения физической величины непосредственно средствами измерения.
Косвенное измерение — определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемыми прямыми измерениями.
Введем следующие обозначения:
А, В, С, . — физические величины.
Апр — приближенное значение физической величины, т. е. значение, полученное путем прямых или косвенных измерений.
ΔА — абсолютная погрешность измерения физической величины.
Ε — относительная погрешность измерения физической величины, равная:
ΔИА — абсолютная инструментальная погрешность, определяемая конструкцией прибора (погрешность средств измерения; см. табл. 1).
Δ0А — абсолютная погрешность отсчета (получающаяся от недостаточно точного отсчета показаний средств измерения); она равна в большинстве случаев половине цены деления, при измерении времени — цене деления секундомера или часов.
Абсолютные инструментальные погрешности средств измерений
| № | Средства измерения | Предел измерения | Цена деления | Абсолютная инструментальная погрешность |
| 1 | Линейка | |||
| Ученическая | До 50 см | 1 мм | ± 1 мм | |
| Чертежная | До 50 см | 1 мм | ± 0,2 мм | |
| Инструментальная (стальная) | 20 см | 1 мм | ± 0,1 мм | |
| Демонстрационная | 100 см | 1 см | ± 0,5 см | |
| 2 | Лента измерительная | 150 см | 0,5 см | ± 0,5 см |
| 3 | Измерительный цилиндр | До 250 мл | 1 мл | ± 1 мл |
| 4 | Штангенциркуль | 150 мм | 0,1 мм | ± 0,05 мм |
| 5 | Микрометр | 25 мм | 0,01 мм | ± 0,005 мм |
| 6 | Динамометр учебный | 4 Н | 0,1 Н | ± 0,05 Н |
| 7 | Весы учебные | 200 г | — | ± 0,01 г |
| 8 | Секундомер | 0-30 мин | 0,2 с | ± 1 с за 30 мин |
| 9 | Барометр-анероид | 720-780 мм рт. ст. | 1 мм рт. ст. | ± 3 мм рт. ст. |
| 10 | Термометр лабораторный | 0-100 0 С | 1 0 С | ± 1 0 С |
| 11 | Амперметр школьный | 2 А | 0,1 А | ± 0,05 А |
| 12 | Вольтметр школьный | 6 В | 0,2 В | ± 0,15 В |
Максимальная абсолютная погрешность прямых измерений складывается из абсолютной инструментальной погрешности и абсолютной погрешности отсчета при отсутствии других погрешностей:
Абсолютную погрешность измерения обычно округляют до одной значащей цифры (ΔА = 0,17 ≈ 0,2); числовое значение результата измерений округляют так, чтобы его последняя цифра оказалась в том же разряде, что и цифра погрешности (А = 10,332 ≈ 10,3).
Результаты повторных измерений физической величины А, проведенных при одних и тех же контролируемых условиях и при использовании достаточно чувствительных и точных (с малыми погрешностями) средств измерения, обычно отличаются друг от друга. В этом случае Апр находят как среднее арифметическое значение всех измерений, а погрешность ΔА (ее называют случайной погрешностью) определяют методами математической статистики.
В школьной лабораторной практике такие средства измерения практически не используются. Поэтому при выполнении лабораторных работ необходимо определять максимальные погрешности измерения физических величин. Для получения результата достаточно одного измерения.
Относительная погрешность косвенных измерений определяется так, как показано в таблице 2.
Формулы для вычисления относительной погрешности косвенных измерений
| № | Формула для физической величины | Формула для относительной погрешности |
| 1 | ||
| 2 | ||
| 3 | ||
| 4 |
Абсолютная погрешность косвенных измерений определяется по формуле ΔА = Апрε (ε выражается десятичной дробью).
2. О классе точности электроизмерительных приборов.
Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности γпр измерительного прибора показывает, сколько процентов составляет абсолютная инструментальная погрешность ΔиА от всей шкалы прибора (Amax):
Класс точности указывают на шкале прибора или в его паспорте (знак % при этом не пишут). Существуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора (γпр) и всю его шкалу (Аmах), определяют абсолютную погрешность ΔиА измерения физической величины А этим прибором:
3. Как сравнивать результаты измерений.
1. Записать результаты измерений в виде двойных неравенств:
2. Сравнить полученные интервалы значений: если интервалы не перекрываются, то результаты неодинаковы; если перекрываются — одинаковы при данной относительной погрешности измерений.
Δ 0 А абсолютная погрешность отсчета получающаяся от недостаточно точного отсчета показаний средств измерения ; она равна в большинстве случаев половине цены деления, при измерении времени цене деления секундомера или часов.
Fizika. degtjarka8.ru
20.02.2017 22:57:20
2017-02-20 22:57:20
Источники:
Http://fizika. degtjarka8.ru/index. php/fizika/vsjo-o-pogreshnostyakh/147-kak-opredelyat-pogreshnost-izmerenij
ЕГЭ 11кл. типовые задания на погрешность: Физика » /> » /> .keyword { color: red; } Как записывать погрешность измерений егэ физика
Научный форум dxdy
Научный форум dxdy
Помогите, как решать типовые задания с учетом погрешности. Просматривал несколько вариантов ЕГЭ, и нашел подобные задания, хотя раньше их нигде не встречал. Как правильно рассчивать такие вещи?
Исследовалась зависимость напряжения на обкладках воздушного конденсатора от заряда этого конденсатора. Результаты измерений представлены в таблице.
Q, мкКл 0 0,1 0,2 0,3 0,4 0,5
U, кВ 0 0,5 1,5 3,0 3,5 3,5
Погрешности измерений величин q и U равнялись соответственно 0,05 мкКл и 0,25 кВ. Емкость конденсатора примерно равна
1) 250 пФ 2) 10 нФ 3) 100 пФ 4) 750 мкФ
Формула, как я понимаю, здесь только одна:
А как находить — не знаю..
Варианты ответа отличаются на порядки, поэтому я бы себе не морочил голову, а посчитал ёмкость для каждого измерения (кроме первого — при нулевом напряжении заряд при любой ёмкости будет нулевым), и посчитал среднее значение ёмкости для всех измерений, а потом просто взял ближайший результат.
Вариант, конечно, хороший, но кто знает, какие варианты ответов будут в следующем году, да и просто для общего развития хотелось бы знать практический подход к заданиям такого вида.
А это и есть правильный подход.
Вопрос только в том, что значит «примерно равна». Если это подразумевает равенство с точностью до погрешности, то надо еще и погрешность косвенного измерения считать, но, если память мне не врет, в школьной программе этого не было.
Последний раз редактировалось int13 20.01.2009, 15:55, всего редактировалось 1 раз.
Ученик предположил, что электрическое сопротивление отрезка металлического провода прямо пропорционально его длине. Для проверки этой гипотезы он взял отрезки проводов из алюминия и меди. Результаты измерения длины отрезков и их сопротивления ученик отметил точками на графике зависимости сопротивления от длины проводника (см. рисунок). Погрешности измерения длины и сопротивления равны соответственно 5 см и 0,1 Ом. Какой вывод следует из результатов эксперимента?
1) С учетом погрешности измерений эксперимент подтвердил правильность гипотезы.
2) Порядок постановки эксперимента не соответствовал выдвинутой гипотезе.
3) Погрешности измерений настолько велики, что не позволили проверить гипотезу.
4) Большинство результатов измерений подтверждает гипотезу, но при измерении сопротивления отрезка провода длиной 5 м допущена грубая ошибка.
Как в данном случае учесть данную погрешность? Что бы четко можно было обьяснить тем же самым ученикам, сдающим ЕГЭ, как все это выполняется?
Можно вычислять, но наверное проще всего так:
Из условия, по предположению ученика, из дополнительного соображения, что при, получаем, что. То есть наша зависимость должна идти из точки. Далее, наносим доверительные интервалы (то есть вместо точек сделать прямоугольнички, размеры которых определяются погрешностями) и смотри, можно ли провести из нуля луч так, чтобы он попал во все нанесённые нами интервалы. Если не попадает много точек, то мы говорим, что предположение ошибочно, либо оценка погрешности измерений проведена некорректно, если все точки попадают, то радуемся, если выпадает одна-две точки, то говорим, что измерения этих точек проведены с грубой погрешностью.
Так, наверное, конечно проще.. А если вычислять — это вызовет большие затруднения? Просто хотелось бы составить полную картину.. Было бы просто замечательно, если бы вы могли представить хотя бы сам ход вычислений..
Добавлено спустя 10 минут 42 секунды:
И вообще, можно ли по этому графику утверждать, что те точки что выше, например, для одного вида металла, а те что ниже, для другого? Может просто погрешность «прыгает» настолько, что получается ответ 4. В самом задании ведь ничего об этом не сказано. Да и площади проводников должны быть одинаковые.
Допустим, такой вопрос попался на экзамене. Ответ выбран, а как обьяснить на чем основывался при выборе ответа? С прямоугольничками помоему, как то не очень доходчиво..
Могу предположить, но не уверен, что в задаче предусматривается построить зависимость по средним значениям. То есть вычислить среднее значение, а потом посмотреть, попадают ли точки на $» />
Добавлено спустя 5 минут 15 секунд:
И вообще, можно ли по этому графику утверждать, что те точки что выше, например, для одного вида металла, а те что ниже, для другого? Может просто погрешность «прыгает» настолько, что получается ответ 4.
Спасибо.. И все же, помоему, не самая простая задача для рядового ученика 11 класса.. Или в условии все-таки чего-то не хватает..
Формула, как я понимаю, здесь только одна:
А как находить — не знаю..
2009, 15 55, всего редактировалось 1 раз.
Dxdy. ru
04.05.2018 2:51:53
2018-05-04 02:51:53
Источники:
Https://dxdy. ru/post179628.html
В задании 22 ЕГЭ по физике (2017) нужно уметь определять погрешности вычислений различных величин. Теория вычисления различных погрешностей — сложная самостоятельная наука, которую преподают обычно в вузах. Для школы и для успешной сдачи экзамена нам потребуются базовые знания, которые я и собрала в этой статье.
В практической деятельности человеку приходится измерять различные величины, производить различные вычисления. Результатами измерений, подсчетов и вычислений являются числа. Однако точные измерения невозможны ввиду несовершенства наших органов зрения, неточности измерительных приборов и некоторых свойств самих измеряемых объектов.
При различных измерениях одной и той же величины получают различные приближенные значения. Каждое из этих приближений отличается от истинного значения на некоторую величину, называемую погрешностью.
Абсолютной погрешностью называется модуль разности истинного и приближенного значения некоторой величины, обозначается она буквой и измеряется в тех же единицах, что и вычисляемая величина:
Где — истинное значение,
— приближенное.
Из этого определения следует, что истинное значение величины равно приближенному значению плюс-минус абсолютная погрешность :
Абсолютная погрешность приближения не характеризует качества измерений, т.к., например, точность 1 см для определения ширины стадиона является высокой, а для определения длины листа бумаги — низкой. Поэтому для характеристики точности измерения вводится понятие относительной погрешности.
Относительной погрешностью приближения называется отношение абсолютной погрешности приближения к модулю числа приближенного значения. Обозначается относительная погрешность буквой (эпсилон) и выражается в процентах:
Далее я приведу таблицу правил определения погрешностей сумм, разностей, произведений и т.п.
Погрешности
Ну и теперь порешаем задачи, чтобы окончательно разобраться.
Задача 1.
Чтобы оценить, каков будет период малых колебаний математического маятника, используем для вычислений на калькуляторе формулу . По оценке «на глазок» длина нити равна
м. Калькулятор показывает на экране число 2,4322335. Чему равен, с учётом погрешности оценки длины нити, период колебаний маятника? (Ответ дайте в секундах, значение и погрешность запишите через точку с запятой без пробелов.)
Относительная погрешность определения периода равна
С другой стороны, по таблице находим, что
Тогда
Тогда
Так как по правилам вычисления погрешностей мы должны оставить одну значащую цифру, то получим c, так как погрешность определена с точностью до сотых, то период тоже округляем до сотых:
. Имеем:
Ответ: 2,43;0,08
Задача 2.
При определении массы масла плотностью 0,9 г/см ученик измерил объём масла с использованием мерного цилиндра:
см
. Запишите в ответ массу масла в граммах с учётом погрешности измерений через точку с запятой без пробелов.
Определяем массу масла:
Определим погрешность вычисления:
Оставляя одну значащую цифру, имеем: г — тогда с такой же точностью и саму величину запишем:
Ответ: 16,2;0,5
Описание презентации по отдельным слайдам:
-
1 слайд
Погрешность от чего и как вычислить
Работу выполнила:
Жеманова Екатерина Сергеевна
учитель физики
Для 10 класса «Готовимся к ЕГЭ» урок 1 «Основы теории погрешностей. Погрешности прямых измерений. Представление результатов в форме таблиц и графиков» -
2 слайд
Почему возникают погрешности
Прибор
Глазомер
Потери в окружающую среду -
3 слайд
1. Измерение- нахождение значения физической величины опытным путем с помощью средств измерения.
-
4 слайд
Прямое измерение
2. Прямое измерение- определение значения физической величины непосредственно средствами измерения. -
5 слайд
Косвенное измерение
3. Косвенное измерение- определение значения физической величины по формуле, связывающей ее с другими физическими величинами, определяемые прямым измерением. -
6 слайд
Относительная погрешность
Чтобы найти относительную погрешность измерения нужно абсолютную погрешность разделить на приближенное значение. -
7 слайд
Максимальная абсолютная погрешность
Максимальная абсолютная погрешность складывается из абсолютной инструментальной и абсолютной погрешности отсчета при отсутствии других погрешностей.
Абсолютную погрешность обычно округляют до одной значащей цифры. -
8 слайд
результаты
Результаты повторных измерений физической величины отличаются друг от друга. В этом случае приближенное значение находят как среднее арифметическое значение всех измерений, а абсолютную погрешность определяют методом математической статистики. -
9 слайд
Абсолютная погрешность
Абсолютная погрешность равна произведению приближенного значения на относительную погрешность. -
10 слайд
О классе точности электроизмерительных приборов
Для определения абсолютной инструментальной погрешности прибора надо знать его класс точности. Класс точности измерительного прибора показывает сколько процентов составляет абсолютная инструментальная погрешность от всей шкалы прибора. -
11 слайд
Существуют следующие классы точности электроизмерительных приборов: 0,1; 0,2; 0,5; 1; 1,5; 2,5; 4. Зная класс точности прибора и всю его шкалу определяют абсолютную погрешность измерения физической величины этим прибором.
-
12 слайд
Как сравнить результаты измерений
Записать результаты измерений в виде двойных неравенств.
Сравнить полученные интервалы значений: если интервалы не перекрываются, то результаты неодинаковы, если перекрываются одинаковы при данной относительной погрешности измерений. -
13 слайд
Как оформлять отчет о проделанной работе.
лабораторная работа
наименование работы
цель работы
чертеж
формулы искомых величин и их погрешностей
таблица с результатами измерений и вычислений
окончательный результат, вывод -
14 слайд
Список литературы
Учебник «Физика 10» Г. Я. Мякишев