в условии
в решении
в тексте к заданию
в атрибутах
Категория:
Атрибут:
Всего: 451 1–20 | 21–40 | 41–60 | 61–80 …
Добавить в вариант
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 108°. Найдите число вершин многоугольника.
Угол между двумя соседними сторонами правильного многоугольника, равен 160°. Найдите число вершин многоугольника.
Угол между двумя соседними сторонами правильного многоугольника, равен 156°. Найдите число вершин многоугольника.
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 168°. Найдите число вершин многоугольника.
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 160°. Найдите число вершин многоугольника.
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 90°. Найдите число вершин многоугольника.
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 140°. Найдите число вершин многоугольника.
Угол между двумя соседними сторонами правильного многоугольника, вписанного в окружность, равен 156°. Найдите число вершин многоугольника.
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 20. Найдите его площадь.
Диагонали четырехугольника равны 4 и 5. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 6?
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной
Диагонали четырехугольника равны 6 и 2. Найдите периметр четырехугольника, вершинами которого являются середины сторон данного четырехугольника.
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 39?
Чему равна сторона правильного шестиугольника, вписанного в окружность, радиус которой равен 28?
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной
Около окружности, радиус которой равен 1, описан многоугольник, периметр которого равен 8. Найдите его площадь.
В треугольнике ABC угол A равен 43 градусам, углы B и C — острые, высоты BD и CE пересекаются в точке Найдите угол
Ответ дайте в градусах.
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 50. Найдите его площадь.
Всего: 451 1–20 | 21–40 | 41–60 | 61–80 …
Сумма углов многоугольника. Доказательство.
А теперь давай все-таки разберемся, откуда же взялась формула суммы углом многоугольника ( displaystyle 180^circ(n-2)).
Зачем?
Понимаешь, приемчик, который мы сейчас применим, часто оказывается полезным при решении разных задач.
Несмотря на то, что теорема о сумме углов многоугольника верна для всякого многоугольника, доказательство красивое и простое только для выпуклых многоугольников.
Итак, давай разделим многоугольник на треугольники.
Вот так: из одной точки проведем все диагонали, что можно. Сколько их будет? Считаем:
Всего вершин: ( displaystyle n)
Из вершины ( displaystyle B) можем провести диагонали во все вершины, кроме:
- Самой вершины B
- Вершины A
- Вершины C
Значит всего диагоналей ( displaystyle (n-3)). А на сколько треугольников распался наш многоугольник?
Представь себе: на ( displaystyle n-2). Порисуй, посчитай – удостоверься, что треугольников оказывается ровно на один больше.
Итак, у нас ровно ( displaystyle n-2) треугольника. И сумма углов многоугольника просто равна сумме углов треугольников, на которые мы разбили многоугольник.
Чему равна сумма углов треугольника? Помнишь? Конечно ( displaystyle 180{}^circ ).
Ну вот, ( displaystyle n-2) треугольника, в каждом по ( displaystyle 180{}^circ ), значит:
Сумма углов многоугольника равна ( displaystyle 180{}^circ )( displaystyle (n-2))
Вот и доказали.
Что же из этого может оказаться полезным? Два момента:
Правильные многоугольники
Многоугольник называется правильным, если все его углы и все его стороны равны.
Так, например: квадрат – правильный четырехугольник, а вот прямоугольник – нет, хоть и все углы у него равные, и ромб – нет, хоть и все стороны равны. Нужно непременно, чтобы все углы и все стороны были равны.
Первый вопрос:
А можно ли найти величину одного (а значит и всех) угла правильного многоугольника?
И ответ: можно!
Давай посмотрим на примере.
Пусть есть, скажем, правильный восьмиугольник:
Сумма всех его углов равна ( displaystyle 180{}^circ left( 8-2 right)=1080{}^circ ).
А сколько всего углов? Восемь конечно, и они все одинаковые.
Значит любой угол, скажем ( displaystyle angle A) можно найти:
( displaystyle angle A=frac{1080{}^circ }{8}=135{}^circ ).
Что мы еще должны знать?
Любой правильный многоугольник можно вписать в окружность и вокруг любого правильного многоугольника можно описать окружность.
При этом центры этих окружностей совпадают.
Смотри, как это выглядит!
И более того, всегда можно посчитать соотношение между радиусом вписанной и описанной окружностей.
Давай опять на примере восьмиугольника.
Посмотри на ( displaystyle Delta OKG). В нем ( displaystyle OK=r,OG=R.)
Значит, ( displaystyle frac{r}{R}=sin angle x) – и это не только в восьмиугольнике!
Чему же равен в нашем случае ( displaystyle angle x)?
Ровно половине ( displaystyle angle G), представь себе!
Значит ( displaystyle angle x=frac{135{}^circ }{2}=67,5{}^circ ).
Смешно? Но так и есть! Поэтому для восьмиугольника ( displaystyle frac{r}{R}=sin 67,5{}^circ ).
Может возникнуть еще один вопрос: а можно ли посчитать углы «около» точки ( displaystyle O)?
И тот же ответ: конечно можно!
Опять рассмотрим наш восьмиугольник. Вот мы хотим найти ( displaystyle angle alpha) (то есть ( displaystyle angle HOG)).
7 октября 2022
В закладки
Обсудить
Жалоба
Правильные многоугольники
Методическая разработка к уроку.
Правильным многоугольником называется выпуклый многоугольник, у которого все углы равны и все стороны равны.
prav-m.ppt
prav-m.pdf
Автор: Валиева Р.М.
Видеоурок: Правильные многоугольники
Лекция: Правильные многоугольники. Вписанная окружность и описанная окружность правильного многоугольника
Правильные многоугольники – это те, которые имеют равные длины сторон и одинаковую градусную меру углов.
Любой правильный многоугольник можно вписать и описать окружностью.
Вписанной в многоугольник называется та окружность, которая касается всех сторон фигуры, при этом делит все стороны на равные отрезки.
Если же вершины многоугольника лежат на окружности, то такой многоугольник называется вписанным в окружность. Более того, многоугольник своими вершинами делит окружность на равные дуги.
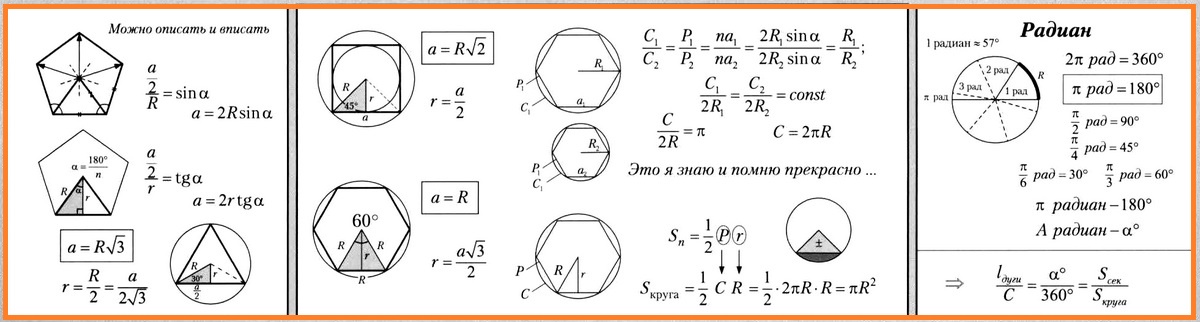
В таблице расписаны все формулы для нахождения сторон, радиусов и площадей описанных или вписанных окружностей.
Обратите внимание, r – радиус вписанной окружности, а R – радиус описанной окружности. N – количество вершин многоугольника.
ЕГЭ Профиль №16. Многоугольники
Правильные многоугольники
Наглядная геометрия 9 класс. Опорный конспект 4. Правильные многоугольники
Правильный многоугольник — это такой многоугольник, у которого все стороны и все углы равны. Равносторонний треугольник и квадрат — правильные многоугольники. Если разделить окружность на п равных частей и соединить соседние точки отрезками, то получим правильный многоугольник. Вокруг всякого правильного многоугольника можно описать окружность, в него также можно вписать окружность, и центры этих окружностей совпадают.
Мы научимся строить правильный треугольник, правильный четырехугольник (квадрат) и правильный шестиугольник при помощи циркуля и линейки и выведем формулы, связывающие радиусы вписанной и описанной окружностей с длиной стороны правильного многоугольника.
Если число сторон вписанного правильного многоугольника увеличивать, то его периметр будет стремиться к длине окружности, а площадь — к площади круга. Отсюда можно получить формулы длины окружности и площади круга: С = 2πR и S = πR2.
Вы знаете, что углы измеряются в градусах. Градус, как известно, равен 1/180 части развернутого угла. Мы познакомимся еще с одной очень важной единицей измерения углов, которая связана с окружностью, — 1 радианом. 1 рад = 57°.
ТАБЛИЦА «Правильные многоугольники»
1. Правильный многоугольник. Теорема об описанной и вписанной окружностях.
Правильным называется многоугольник, у которого все стороны и углы равны.
Теорема. Вокруг всякого правильного многоугольника можно описать окружность. Во всякий правильный многоугольник можно вписать окружность. Центры этих окружностей совпадают.
Доказательство. Проведем биссектрисы двух углов правильного многоугольника. Получим равнобедренный треугольник (углы при основании равны как половины равных углов). Соединив точку пересечения биссектрис с третьей вершиной многоугольника, получим треугольник, равный 1-му (по двум сторонам и углу между ними). Продолжая соединять эту точку с остальными вершинами, получим множество равных равнобедренных треугольников. Тогда полученная точка равноудалена от всех вершин правильного многоугольника. Значит, она — центр описанной окружности. Так как высоты этих треугольников, опущенные на их основания, равны, то данная точка равноудалена и от сторон правильного многоугольника. Значит, она — центр вписанной окружности.
2. Выражение стороны а через R и r для правильного n-угольника.
Соединим центр правильного многоугольника с двумя соседними вершинами. Получим равнобедренный треугольник с углом при вершине, равным 360°/n. Половина его равна 180°/n, где n — число сторон. Из прямоугольного треугольника находим:
3. Выражение R и r через сторону а для правильного 3-угольника.
4. Выражение R и r через сторону а для правильного 4-угольника.
5. Выражение R и r через сторону а для правильного 6-угольника.
6. Формула длины окружности. Вывод.
Теорема. Длина окружности С = 2πR.
Доказательство. Рассмотрим ДВА правильных вписанных многоугольника с одинаковым числом сторон n. При увеличении числа сторон их периметры Р1 и Р2 будут стремиться к длинам окружностей, т. е. к С1 и С2. Поэтому
Мы получили, что отношение длины окружности С к ее диаметру 2R есть величина постоянная для всех окружностей. Это отношение обозначается буквой π («пи» — первая буква древнегреческого слова «периметрон» — окружность). Так как для любой окружности C/2R = π, то длина окружности С = 2 πR.
По числу букв в словах фразы «Это я знаю и помню прекрасно, но многие цифры мне лишни, напрасны» можно воспроизвести 12 первых знаков числа π: π = 3,14159265358….
7. Формула площади круга. Вывод.
Теорема. Площадь круга S = πR2.
8. Длина дуги и площадь сектора.
Длина дуги и площадь сектора пропорциональны градусной мере дуги или центрального угла сектора:
Формулы длины дуги и площади сектора не нужно запоминать — они находятся из логически понятной пропорции:
- а) длина дуги составляет от длины окружности такую же часть, какую составляет ее градусная мера от 360°;
- б) площадь сектора составляет от площади круга такую же часть, какую составляет его центральный угол (его дуга) от 360°.
9. Площадь сегмента.
Площадь сегмента равна площади сектора минус или плюс площадь равнобедренного треугольника, образованного радиусами этого сектора. Минус — если центральный угол сектора меньше 180°, и плюс — если больше 180°. Если центральный угол равен 180°, то этот сегмент — полукруг, и его площадь равна πR2/2.
10. Радианная мера угла.
Радианом называется центральный угол, опирающийся на дугу окружности, равную 1 радиусу.
Так как длина окружности С = 2πR, то в окружности укладывается 2π радиусов (≈ 6,28 радиуса), а в полуокружности — π радиусов (≈3,14 радиуса).
2π радиан = 360°. ⇒ π радиан = 180°. ⇒ 1 радиан = 180°/π ≈ 57°
При расчетах слово «радиан» не пишут: π/2 =90°, π/3 = 60°, π/4 =45°, π/6 = 30°.
11. Перевод градусной меры угла в радианную и наоборот.
ЭТО НУЖНО ЗНАТЬ !
Это опорный конспект № 4 по геометрии для 9 класса «Правильные многоугольники». Выберите дальнейшие действия:
- Вернуться к Списку конспектов по геометрии
- Смотреть Опорный конспект 1. Окружности
- Смотреть Опорный конспект 2. Описанные и вписанные окружности
- Смотреть Опорный конспект 3. Теорема синусов. Теорема косинусов