Правильный тетраэдр егэ

Всего: 20    1–20

Добавить в вариант

Внутри правильного тетраэдра с ребром a‍ расположены четыре равных шара. Каждый шар касается трёх других и трёх граней тетраэдра. Найдите радиусы шаров.

Длина диагонали куба ABCDA1B1C1D1 равна 3. На луче A1C отмечена точка P так, что A1P  =  4.

а)  Докажите, что PBDC1 — правильный тетраэдр.

б)  Найдите длину отрезка AP.

Источник: ЕГЭ по математике 2017. Досрочная волна, резервная волна. Вариант А. Ларина (часть С)

В правильном тетраэдре ABCD точки K и M  — середины рёбер AB и CD соответственно. Плоскость α содержит прямую KM и параллельна прямой AD.

а)  Докажите, что сечение тетраэдра плоскостью α — квадрат.

б)  Найдите площадь сечения тетраэдра ABCD плоскостью α, если AB=2 корень из 3.

Источник: Основная волна ЕГЭ по математике 29.05.2019. Вариант 991, Задания 14 (С2) ЕГЭ 2019

Точка M середина ребра AB правильного тетраэдра DABC.

а)  Докажите, что ортогональная проекция точки M на плоскость ACD лежит на медиане AP грани ACD.

б)  Найдите угол между прямой DM и плоскостью ACD.

Источник: А. Ларин. Тренировочный вариант № 331. (часть C).

В правильном тетраэдре MNPQ через биссектрисы NA и QB граней MNP и QNP проведены параллельные плоскости.

а)  Найдите отношение суммы объемов отсекаемых от MNPQ тетраэдров к объему MNPQ

б)  Найдите расстояние между NA и QB, если ребро тетраэдра равно 1.

Источник: А. Ларин. Тренировочный вариант № 297.

В правильном тетраэдре ABCD точка К  — середина ребра АВ, точка Е лежит на ребре CD и EC : ED  =  1 : 2.

а)  Найдите угол между прямыми ВС и КЕ.

б)  Найдите расстояние между прямыми ВС и КЕ, если ребро тетраэдра равно корень из 6.

Источник: А. Ларин. Тренировочный вариант № 298.

В правильном тетраэдре ABCD точка K  — центр грани ABD, точка M  — центр грани ACD.

а)  Докажите, что прямые BC и KM параллельны.

б)  Найдите угол между прямой KM и плоскостью ABD.

Источник: А. Ларин. Тренировочный вариант № 291.

В правильный тетраэдр ABCD вписан шар. Из точки D на грань ABC тетраэдра опущена высота DE. Точка P является серединой отрезка DE. Через точку P проведена плоскость, перпендикулярно к DE. Из всех точек, которые принадлежат одновременно шару и проведенной плоскости, взята точка O, являющаяся ближайшей к точке A. Найти расстояние от точки O до грани ABD, если объем шара равен 1.

Источник: А. Ларин: Тренировочный вариант № 47.

В правильном тетраэдре ABCD точка K  — центр грани ABD, точка M  — центр грани ACD.

а)  Докажите, что прямые BC и KM параллельны.

б)  Найдите угол между прямой KM и плоскостью ABD.

Источник: А. Ларин. Тренировочный вариант № 276.

В правильном тетраэдре ABCD проведена высота DH. K  — середина отрезка CH. BM  — медиана боковой грани BCD.

а)  Докажите, что угол между DH и BM равен углу BMK.

б)  Найдите угол между DH и BM.

В правильном тетраэдре ABCD М  — середина ребра AD.

а)  Докажите, что проекция точки M на плоскость BCD делит высоту DN треугольника BCD в отношении 1 : 2, считая от вершины D.

б)  Найдите угол между медианой BM грани ABD и плоскостью BCD.

В правильном тетраэдре ABCD точки K и N середины рёбер AB и AD соответственно. Прямая DO перпендикулярна плоскости ABC. Расстояние между прямыми KN и DO равно 3. Найти площадь сечения тетраэдра проходящего через середины трёх смежных рёбер.

Источник: А. Ларин: Тренировочный вариант № 73.

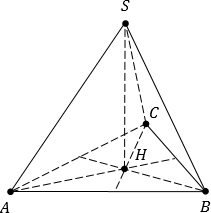
В правильном тетраэдре АВСD точка Н  — центр грани АВС, а точка М  — середина ребра СD.

а)  Докажите, что прямые АВ и СD перпендикулярны.

б)  Найдите угол между прямыми DН и ВМ.

Источник: ЕГЭ по математике 25.06.2018. Основная волна, резервный день. Вариант 992 (C часть), Задания 14 (С2) ЕГЭ 2018

Длина ребра правильного тетраэдра ABCD равна 1. M  — середина ребра BC, L  — середина ребра AB.

а)  Докажите, что плоскость, параллельная прямой CL и содержащая прямую DM, делит ребро AB в отношении 3 : 1, считая от вершины A.

б)  Найдите угол между прямыми DM и CL.

Дан правильный тетраэдр MABC с ребром 1.

а)  Докажите, что CMperp AB.

б)  Найдите расстояние между прямыми AL и MO, где L  — середина ребра MC, O  — центр грани ABC.

Длина ребра правильного тетраэдра ABCD равна x. M  — середина ребра BC, L  — середина ребра AB.

а)  Докажите, что плоскость, содержащая прямую DM и параллельная прямой CL, делит ребро AB в отношении 3:1, считая от вершины A.

б)  Найдите угол между прямыми DM и CL.

В правильном тетраэдре SABC точка M  — середина ребра AB, а точка N расположена на ребре SC так, что SN : NC  =  3 : 1.

а)  Докажите, что плоскости SMC и ANB перпендикулярны.

б)  Найдите длину отрезка MN, если длина ребра AB равна 8.

Источник: А. Ларин. Тренировочный вариант № 354.

SMNK  — правильный тетраэдр. На ребре SK отмечена точка Р такая, что КР : PS  =  1 : 3, точка L  — середина ребра MN.

а)  Докажите, что плоскости SLK и MPN перпендикулярны.

б)  Найдите длину отрезка PL, если длина ребра MN равна 4.

Источник: А. Ларин. Тренировочный вариант № 398.

В тетраэдре ABCD, все рёбра которого равны 1, отметили середину ребра CD  — точку E.

а)  Докажите, что плоскость ABE перпендикулярна ребру CD.

б)  Найдите расстояние от точки A до прямой BE.

Каждое из ребер треугольной пирамиды ABCD имеет длину 1. Точка P на ребре AB, точка Q на ребре BC, точка R на ребре CD взяты так, что AP= дробь: числитель: 1, знаменатель: 2 конец дроби ;BQ=CR= дробь: числитель: 1, знаменатель: 3 конец дроби . Плоскость PQR пересекает прямую AD в точке S. Найти величину угла между прямыми SP и SQ.

Источник: А. Ларин: Тренировочный вариант № 42.

Всего: 20    1–20

Источник
2618 Точка M середина ребра AB правильного тетраэдра DABC.
а) Докажите, что ортогональная проекция точки M на плоскость ACD лежит на медиане AP грани ACD.
б) Найдите угол между прямой DM и плоскостью ACD
Решение		 Точка M середина ребра AB правильного тетраэдра DABC ! Тренировочный вариант 331 от Ларина Задание 14 ...X
2175 В правильном тетраэдре ABCD с ребром, равным 6, точки M и N – середины ребер AB и CD.
а) Докажите, что угол между прямыми MN и BC равен 45^@
б) Найдите расстояние между прямыми MN и AD
Решение		 В правильном тетраэдре ABCD с ребром, равным 6, точки M и N – середины ребер AB и CD ! ларин егэ 2020 профильный уровень Вариант 304 Задание 14 ...X
1644 В правильном тетраэдре ABCD точка К – центр грани ABD, точка M – центр грани ACD. а) Докажите, что прямые BC и КМ параллельны. б) Найдите угол между прямой КМ и плоскостью ABD
Решение		 ларин егэ по математике 2020 Вариант 291 Задание 14 ! ларин егэ по математике 2019 профильный уровень Вариант 276 Задание 14 ...X
1119 В правильном тетраэдре ABC точка H — центр грани ABC, а точка M — середина ребра CD. а) Докажите, что прямые AB и CD перпендикулярны. б) Найдите угол между прямыми DH и BM.
Решение		 Резервный день егэ 2018 математика профиль 25 июня Задание 14 вариант 992! Ответы 25-06-2018 Задача 14 Вариант 992 ...X
500 В правильном тетраэдре с ребром a точки M, N, K — середины AB, BC, DC соответственно. Найти угол между прямой (MK) и плоскостью (ADN)
Решение		   ...X
445 Дан правильный тетраэдр DABC. Точка M — середина AD. Найти угол между прямой (BM) и плоскостью (BCD)
Решение		   ...X
423 Дан правильный тетраэдр DABC. Точки M и N — середины рёбер AD и BD соответственно. Найти угол между плоскостями (BCM) и (ACN)
Решение		   ...X
378 Внутри правильного тетраэдра ABCD c ребром 12 расположен конус так, что его вершина является серединой ребра CD, а окружность основания конуса вписана в сечение тетраэдра, проходящее через середину ребра BC, параллельно CD и AB. Найти объём конуса
Решение		 #Задача-Аналог   331   ...X
352 В правильный тэтраэдр SABC с ребром 24 вписан шар. В трёхгранный угол с вершиной S вписан второй шар, который касается первого шара. Найти объём второго шара
Решение		   ...X
351 Для правильного тэтраэдра с ребром a найти: его объём; радиус шара, вписанного в тэтраэдр; радиус шара, описанного около тэтраэдра. Доказать, что центры описанного и вписанного в него шаров совпадают.
Решение		   ...X

К следующей страницеПоказать ещё…

Показана страница 1 из 2

Show filter builder dialog   Clear

||||Hide

Источник

Правильный тетраэдр

Правильный тетраэдр — тетраэдр, все грани которого являются правильными треугольниками.

Обозначения

  • $a$ — длина стороны тетраэдра

Находим $DE$

Пусть E — середина грани BC. Так как треугольник BCD правильный, угол BEC равен 90 градусам. Из прямоугольного треугольника BEC $$ DE=sqrt{CD^2-EC^2}=sqrt{a^2-frac{a^2}{4}}=frac{sqrt{3}cdot a}{2} $$

Категория: 

  • ЕГЭ по математике


Источник

Видео по теме

Задача 1. В правильной четырехугольной пирамиде SABCD  точка  O – центр основания, S  – вершина,  SB=13,;BD=24. Найдите длину отрезка SO.

fgk

Решение: + показать

Задача 2.  В правильной четырехугольной пирамиде SABCD  точка O – центр основания, S – вершина, SO=8, BD=30.  Найдите боковое ребро SC.

Решение: + показать

Задача 3. Стороны основания правильной четырехугольной пирамиды равны 60, боковые ребра равны 78. Найдите площадь поверхности этой пирамиды.

Решение: + показать

Задача 4.  В правильной четырёхугольной пирамиде SABCD  точка O  —  центр основания, S — вершина, SO=48, SD=60.  Найдите длину отрезка AC.

Решение: + показать

Задача 5. Основанием пирамиды является прямоугольник со сторонами 5 и 6. Ее объем равен 40. Найдите высоту этой пирамиды.

Решение: + показать

Задача 6. В правильной четырёхугольной пирамиде SABCD  с основанием ABCD боковое ребро SA равно 39, сторона основания равна 15sqrt2. Найдите объём пирамиды.

Решение: + показать

Задача 7. В правильной четырёхугольной пирамиде все рёбра равны 7. Найдите площадь сечения пирамиды плоскостью, проходящей через середины боковых рёбер.

Решение: + показать

Задача 8.  Даны две правильные четырёхугольные пирамиды. Объём первой пирамиды равен 9. У второй пирамиды высота в 1,5 раза больше, а сторона основания в 2 раза больше, чем у первой. Найдите объём второй пирамиды.

Решение: + показать

Задача 9.  В правильной четырёхугольной пирамиде боковое ребро равно 22, а тангенс угла между боковой гранью и плоскостью основания равен sqrt{14}. Найти сторону основания пирамиды.

Решение: + показать

Задача 10. Основанием пирамиды является прямоугольник со сторонами 4 и 6. Ее объем равен 48. Найдите высоту этой пирамиды.

18f3561bdbae5ca26a77784787b7d0bc

Решение: + показать

Задача 11. Стороны основания правильной четырехугольной пирамиды равны 42, боковые ребра равны 75. Найдите площадь поверхности этой пирамиды.

8913063b078b7196c5a3071ca02c523b

Решение: + показать

Задача 12. В правильной треугольной пирамиде SABC  медианы основания ABC пересекаются в точке O. Площадь треугольника ABC  равна 9, объем пирамиды равен 6. Найдите длину отрезка OS.

u

Решение: + показать

Задача 13.  В правильной треугольной пирамиде SABC точка L — середина ребра AC, S — вершина. Известно, что BC = 6, а SL = 5. Найдите площадь боковой поверхности пирамиды.

ts

Решение: + показать

Задача 14. Найдите объем правильной треугольной пирамиды, стороны основания которой равны 11, а высота равна 4sqrt3. 

u

Решение: + показать

Задача 15.  Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 5, а объем равен 6sqrt3.

u

Решение: + показать

Задача 16. Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.

н

Решение: + показать

Задача 17. Объем правильной шестиугольной пирамиды 324. Сторона основания равна 6. Найдите боковое ребро.

н

Решение: + показать

Задача 18. Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в два раза?

1694cdf5de68632ee14aa0c5c5fefad1

Решение: + показать

Задача 19. Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в 5 раз?

d5e28b2cf1aaba18d4a7a6a87f80215a

Решение: + показать

Задача 20.  Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в пять раз?

п

Решение: + показать

Задача 21. Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60°. Высота пирамиды равна 12. Найдите объем пирамиды.

8fb4942644d6aea0ba85825e7c81c610

Решение: + показать

Задача 22. Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 12. Найдите объем пирамиды.

a8a2781d4cd5ed8f62d05cbf4f061676

Решение: + показать

Задача 23. От треугольной призмы, объем которой равен 129, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.

g

Решение: + показать

Задача 24. Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 8. Найдите объем шестиугольной пирамиды. Видео по теме 1 2 

efc4238b7e0c4ff80662906a06e27364

Решение: + показать

Задача 25.  Сторона основания правильной шестиугольной пирамиды равна 8, боковое ребро равно 16. Найдите объём пирамиды.

1694cdf5de68632ee14aa0c5c5fefad1

Решение: + показать

Задача 26. Сторона основания правильной шестиугольной пирамиды равна 11, а угол между боковой гранью и основанием равен 45^{circ}. Найдите объем пирамиды.

Решение: + показать

Задача 27. Найдите объём правильной шестиугольной пирамиды SABCDEF, если объём треугольной пирамиды SABD равен 34.

Решение: + показать

Задача 28.  Объем параллелепипеда ABCDA_1B_1C_1D_1 равен 9. Найдите объем треугольной пирамиды ABCA_1. 

Решение: + показать

Задача 29. Объем куба равен 123. Найдите объем четырехугольной пирамиды, основанием которой является грань куба, а вершиной — центр куба.

Решение: + показать

Задача 30. Найдите объем пирамиды, изображенной на рисунке. Ее основанием является многоугольник, соседние стороны которого перпендикулярны, а одно из боковых ребер перпендикулярно плоскости основания и равно 3.

Решение: + показать

Задача 31. Объем правильной четырехугольной пирамиды SABCD равен 120. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.

рб

Решение: + показать

Задача 32. От треугольной пирамиды, объем которой равен 34, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

ор

Решение: + показать

Задача 33.  Ребра тетраэдра равны 16. Найдите площадь сечения, проходящего через середины четырех его ребер.

ь

Решение: + показать

  Вы можете пройти тест

Источник

Координаты вершин правильного тетраэдра

20 июня 2013

Пирамиды традиционно считаются сложными фигурами в задаче C2. А уж если в основании пирамиды лежит треугольник (т.е. пирамида становится тетраэдром), то все становится совсем грустно. В общем, если в ЕГЭ по математике вам попадется правильный тетраэдр, примите мои поздравления: это самая мерзкая и сложная фигура, которая встречается на настоящем экзамене.

Тем не менее, после небольшой тренировки все становится вполне решаемо. И в этом уроке мы пошагово разберем каждую вершину тетраэдра и найдем каждую координату. Вы убедитесь: все, что нам действительно надо знать — это две теоремы:

  1. Теорема Пифагора — без нее не решается вообще ни одна задача C2, потому что на этой теореме построена сама идея декартовой системы координат;
  2. Теорема о медианах. А именно: медианы треугольника пересекаются в одно точке и делятся ею в отношении 2 : 1, считая от вершины.

Вот и весь список! Вы знаете эти теоремы? Тогда поехали!

Задача. В правильном тетраэдре SABC, все ребра которого равны 1, введите систему координат и найдите координаты вершин.

Правильный тетраэдр SABC и высота SH

[Подпись к рисунку]

Смотрите также:

  1. Четырехугольная пирамида: как найти координаты вершин
  2. Уравнение плоскости в задаче C2. Часть 1: матрицы и определители
  3. Решение ЕГЭ-2011: вариант 1, часть B
  4. Не пишите единицы измерения в задаче B12
  5. Быстрое возведение чисел в квадрат без калькулятора
  6. Задача B4: тарифы на сотовую связь
Источник

Понравилась статья? Поделить с друзьями:
  • Правильные ударения в словах список для егэ 2020
  • Право на авторство пример егэ
  • Правильные ударения в словах русского языка список популярных егэ
  • Право как социальный регулятор егэ текст
  • Правильные ответы на экзамене в автошколе black russia