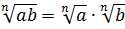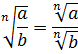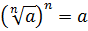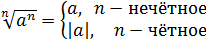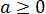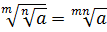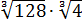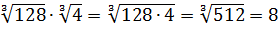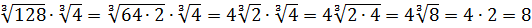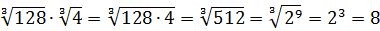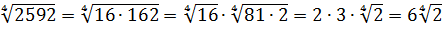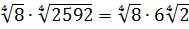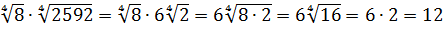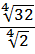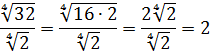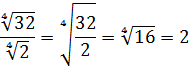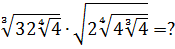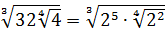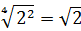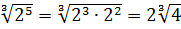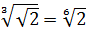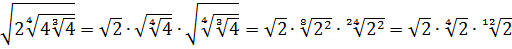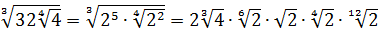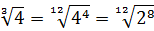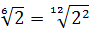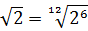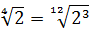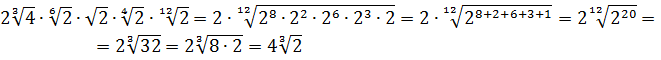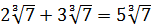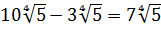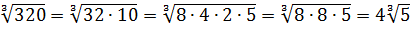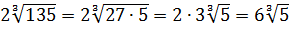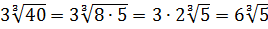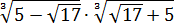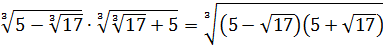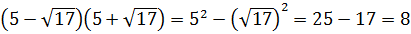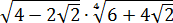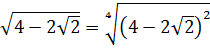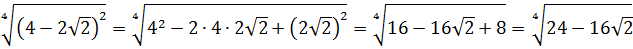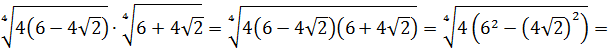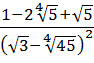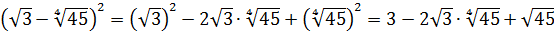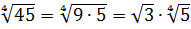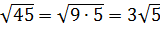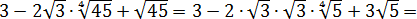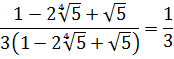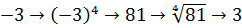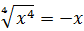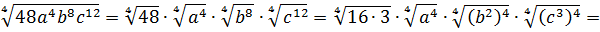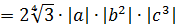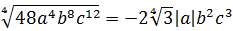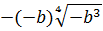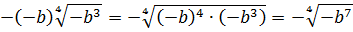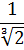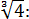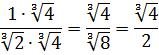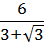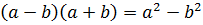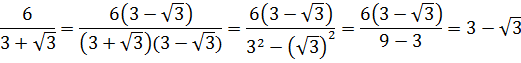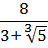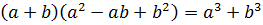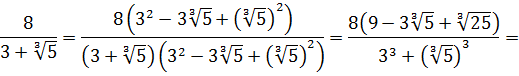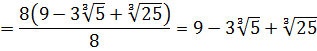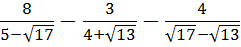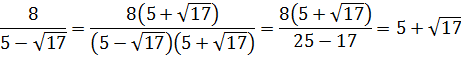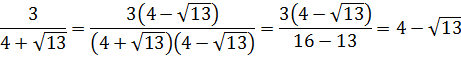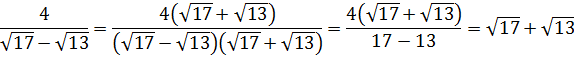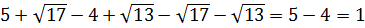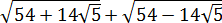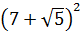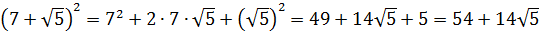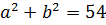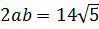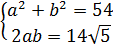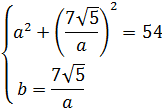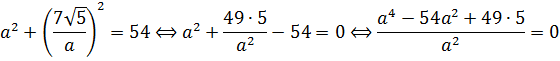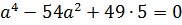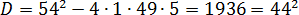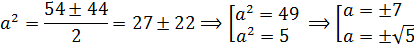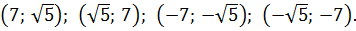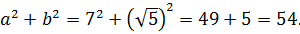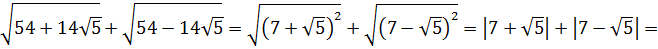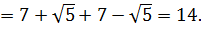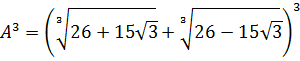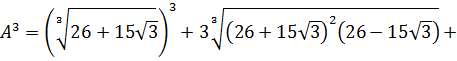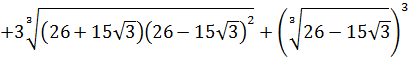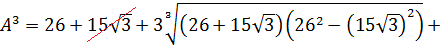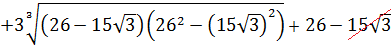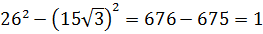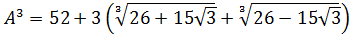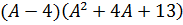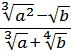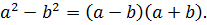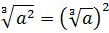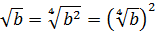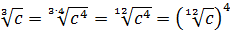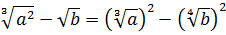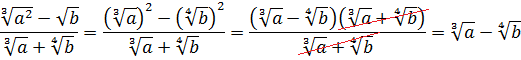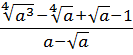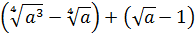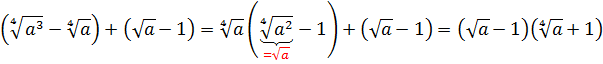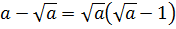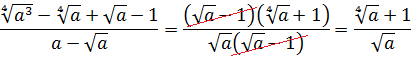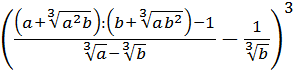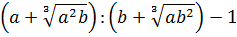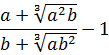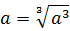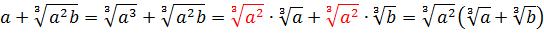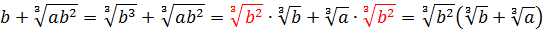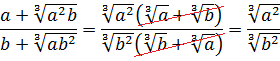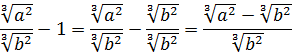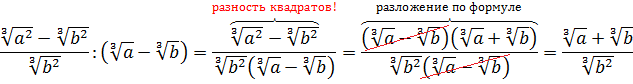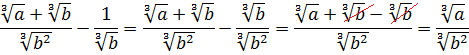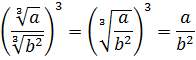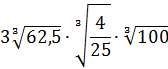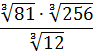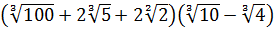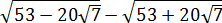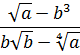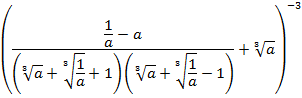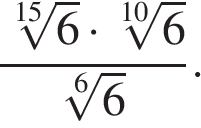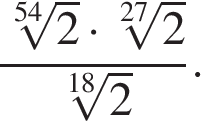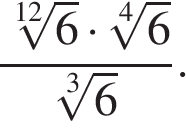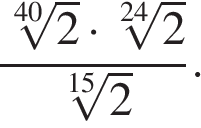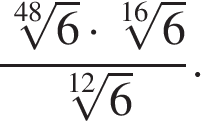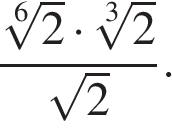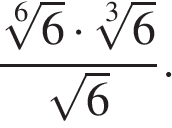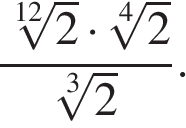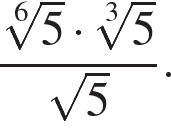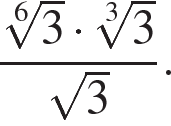Преобразование числовых иррациональных выражений решу егэ

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

03
Авг 2013

Категория: 06 ВычисленияИррациональные выражения, уравнения и неравенства

06. Иррациональные выражения

2013-08-03
2022-09-11

Автор: egeMax |

комментариев 20

Иррациональные выражения и их преобразования

        В прошлый раз мы вспомнили (или узнали — кому как), что же такое корень n-й степени, научились извлекать такие корни, разобрали по винтикам основные свойства корней и решали несложные примеры с корнями.

        Этот урок будет продолжением предыдущего и будет посвящён преобразованиям самых разных выражений, содержащих всевозможные корни. Такие выражения называются иррациональными. Здесь появятся и выражения с буквами, и дополнительные условия, и избавление от иррациональности в дробях, и некоторые продвинутые приёмы в работе с корнями. Те приёмы, которые будут рассматриваться в данном уроке, станут хорошей базой для решения задач ЕГЭ (и не только) практически любого уровня сложности. Итак, давайте приступим.

        Прежде всего я продублирую здесь основные формулы и свойства корней. Чтобы не скакать из темы в тему. Вот они:

 при 

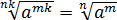
        Формулы эти надо обязательно знать и уметь применять. Причём в обе стороны — как слева направо, так и справа налево. Именно на них и основывается решение большинства заданий с корнями любой степени сложности. Начнём пока с самого простого — с прямого применения формул или их комбинаций.

Простое применение формул

        В этой части будут рассматриваться простые и безобидные примеры — без букв, дополнительных условий и прочих хитростей. Однако даже в них, как правило, имеются варианты. И чем навороченнее пример, тем больше таких вариантов. И у неопытного ученика возникает главная проблема — с чего начинать? Ответ здесь простой — не знаешь, что нужно — делай что можно. Лишь бы ваши действия шли в мире и согласии с правилами математики и не противоречили им.) Например, такое задание:

        Вычислить: 

        Даже в таком простеньком примере возможны несколько путей к ответу.

        Первый — просто перемножить корни по первому свойству и извлечь корень из результата:

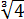
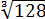
        Второй вариант такой:  не трогаем, работаем с . Выносим множитель из-под знака корня, а дальше — по первому свойству. Вот так:

        Решать можно как больше нравится. В любом из вариантов ответ получается один — восьмёрка. Мне, например, проще перемножить 4 и 128 и получить 512, а из этого числа отлично извлекается кубический корень. Если кто-то не помнит, что 512 — это 8 в кубе, то не беда: можно записать 512 как 2⁹ (первые 10 степеней двойки, я надеюсь, помните?) и по формуле корня из степени:

        Другой пример.

        Вычислить: .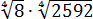

        Если работать по первому свойству (всё загнать под один корень), то получится здоровенное число, из которого корень потом извлекать — тоже не сахар. Да и не факт, что он извлечётся ровно.) Поэтому здесь полезно в числе 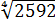 вынести множители из-под корня. Причём вынести по максимуму:

        И теперь всё наладилось:

        Осталось восьмёрку и двойку записать под одним корнем (по первому свойству) и — готово дело.

        Добавим теперь немного дробей.

        Вычислить:

        

        Пример совсем примитивный, однако и в нём имеются варианты. Можно с помощью вынесения множителя преобразовать числитель и сократить со знаменателем:

        А можно сразу воспользоваться формулой деления корней:

        Как видим, и так, и сяк — всяко правильно.) Если не споткнуться на полпути и не ошибиться. Хотя где тут ошибаться-то…

        Разберём теперь самый последний пример из домашнего задания прошлого урока:

        Упростить:

            

        Совершенно немыслимый набор корней, да ещё и вложенных. Как быть? Главное — не бояться! Здесь мы первым делом замечаем под корнями числа 2, 4 и 32 — степени двойки. Первое что нужно сделать — привести все числа к двойкам: всё-таки чем больше одинаковых чисел в примере и меньше разных, тем проще.) Начнём отдельно с первого множителя:

        Число 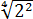 можно упростить, сократив двойку под корнем с четвёркой в показателе корня:

        Теперь, согласно корню из произведения:

.

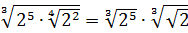
        В числе 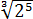 выносим двойку за знак корня: 

        А с выражением 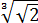 расправляемся по формуле корня из корня:

        Значит, первый множитель запишется вот так:

.

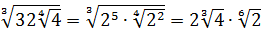
        Вложенные корни исчезли, числа стали поменьше, что уже радует. Вот только корни разные, но пока так и оставим. Надо будет — преобразуем к одинаковым. Берёмся за второй множитель.)

        Второй множитель преобразовываем аналогично, по формуле корня из произведения и корня из корня. Где надо — сокращаем показатели по пятой формуле:

        Вставляем всё в исходный пример и получаем:

        Получили произведение целой кучи совершенно разных корней. Неплохо было бы привести их все к одному показателю, а там — видно будет. Что ж, это вполне возможно. Наибольший из показателей корней равен 12, а все остальные — 2, 3, 4, 6 — делители числа 12. Поэтому будем приводить все корни по пятому свойству к одному показателю — к 12:

        Считаем и получаем:

        Красивого числа не получили, ну и ладно. Нас просили упростить выражение, а не посчитать. Упростили? Конечно! А вид ответа (целое число или нет) здесь уже не играет никакой роли.

Немного сложения / вычитания и формул сокращённого умножения

        К сожалению, общих формул для сложения и вычитания корней в математике нету. Однако, в заданиях сплошь и рядом встречаются эти действия с корнями. Здесь необходимо понимать, что любые корни — это точно такие же математические значки, как и буквы в алгебре.) И к корням применимы те же самые приёмы и правила, что и к буквам — раскрытие скобок, приведение подобных, формулы сокращённого умножения и т.п.

        Например, каждому ясно, что 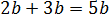. Точно так же одинаковые корни можно совершенно спокойно между собой складывать/вычитать:

        Если корни разные, то ищем способ сделать их одинаковыми — внесением/вынесением множителя или же по пятому свойству. Если ну никак не упрощается, то, возможно, преобразования более хитрые.

        Смотрим первый пример.

        Найти значение выражения: .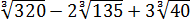

        Все три корня хоть и кубические, но из разных чисел. Чисто не извлекаются и между собой складываются/вычитаются. Стало быть, применение общих формул здесь не катит. Как быть? А вынесем-ка множители в каждом корне. Хуже в любом случае не будет.) Тем более что других вариантов, собственно, и нету:

        Стало быть, .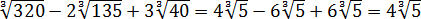

        Вот и всё решение. Здесь мы от разных корней перешли к одинаковым с помощью вынесения множителя из-под корня. А затем просто привели подобные.) Решаем дальше.

        Найти значение выражения: 

        С корнем из семнадцати точно ничего не поделаешь. Работаем по первому свойству — делаем из произведения двух корней один корень:

        А теперь присмотримся повнимательнее. Что у нас под большим кубическим корнем? Разность ква.. Ну, конечно! Разность квадратов:

        Теперь осталось только извлечь корень: .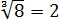

        Дальше очень похожий пример, но посложнее.

        Вычислить: 

        Здесь придётся проявить математическую смекалку.) Мыслим примерно следующим образом: «Так, в примере произведение корней. Под одним корнем разность, а под другим — сумма. Очень похоже на формулу разности квадратов. Но… Корни — разные! Первый квадратный, а второй — четвёртой степени… Хорошо бы сделать их одинаковыми. По пятому свойству можно легко из квадратного корня сделать корень четвёртой степени. Для этого достаточно подкоренное выражение возвести в квадрат.»

        Если вы мыслили примерно так же, то вы — на полпути к успеху. Совершенно верно! Превратим первый множитель в корень четвёртой степени. Вот так:

       Теперь, ничего не поделать, но придётся вспомнить формулу квадрата разности. Только в применении к корням. Ну и что? Чем корни хуже других чисел или выражений?! Возводим:

       «Хм, ну возвели и что? Хрен редьки не слаще. Стоп! А если вынести четвёрку под корнем? Тогда выплывет то же самое выражение, что и под вторым корнем, только с минусом, а ведь именно этого мы и добиваемся!»

        Верно! Выносим четвёрку:

.

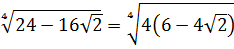
        А теперь — дело техники:

.

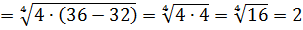
        Вот так распутываются сложные примеры. ) Теперь пора потренироваться с дробями.

        Вычислить:

        

        Ясно, что надо преобразовывать числитель. Как? По формуле квадрата суммы, разумеется. У нас есть ещё варианты разве? Возводим в квадрат, выносим множители, сокращаем показатели (где надо):

        Во как! Получили в точности знаменатель нашей дроби. ) Значит, вся дробь, очевидно, равна единице:

        Ещё пример. Только теперь на другую формулу сокращённого умножения.)

        Вычислить:

            

        Понятно, что квадрат разности надо в дело применять. Выписываем знаменатель отдельно и — поехали!

        Выносим множители из-под корней:

        Следовательно, 

.

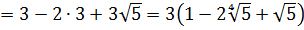
        Теперь всё нехорошее великолепно сокращается и получается:

        Что ж, поднимаемся на следующий уровень.

Буквы и дополнительные условия

        Буквенные выражения с корнями — штука более хитрая, чем числовые выражения, и является неиссякаемым источником досадных и очень грубых ошибок. Перекроем этот источник.) Ошибки всплывают из-за того, что частенько таких заданиях фигурируют отрицательные числа и выражения. Они либо даны нам прямо в задании, либо спрятаны в буквах и дополнительных условиях. А нам в процессе работы с корнями постоянно надо помнить, что в корнях чётной степени как под самим корнем, так и в результате извлечения корня должно быть неотрицательное выражение. Ключевой формулой в задачах этого пункта будет четвёртая формула:

        С корнями нечётной степени вопросов никаких — там всегда всё извлекается что с плюсом, что с минусом. И минус, если что, выносится вперёд. Будем сразу разбираться с корнями чётных степеней.) Например, такое коротенькое задание.

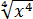
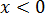
        Упростить: , если .

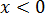
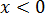
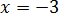
        Казалось бы, всё просто. Получится просто икс. ) Но зачем же тогда дополнительное условие  ? В таких случаях полезно прикинуть на числах. Чисто для себя.) Если , то икс — заведомо отрицательное число. Минус три, например. Или минус сорок. Пусть . Можно минус три возвести в четвёртую степень? Конечно! Получится 81. Можно из 81 извлечь корень четвёртой степени? А почему нет? Можно! Получится тройка. Теперь проанализируем всю нашу цепочку:

        Что мы видим? На входе было отрицательное число, а на выходе — уже положительное. Было минус три, стало плюс три.) Возвращаемся к буквам. Вне всяких сомнений, по модулю это будет точно икс, но только сам икс у нас с минусом (по условию!), а результат извлечения (в силу арифметического корня!) должен быть с плюсом. Как получить плюс? Очень просто! Для этого достаточно перед заведомо отрицательным числом поставить минус.) И правильное решение выглядит так:

        Кстати сказать, если бы мы воспользовались формулой 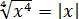, то, вспомнив определение модуля, сразу получили бы верный ответ. Поскольку

|x| = -x при x<0.

        Дальше тренируемся.)

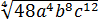
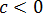
        Вынести множитель за знак корня: , где .

        Первый взгляд — на подкоренное выражение. Тут всё ОК. При любом раскладе оно будет неотрицательным. Начинаем извлекать. По формуле корня из произведения, извлекаем корень из каждого множителя:

        Откуда взялись модули, объяснять, думаю, уже не надо.) А теперь анализируем каждый из модулей.

        Множитель |a| так и оставляем без изменений: у нас нету никакого условия на букву a. Мы не знаем, положительное она или отрицательная. Следующий модуль |b²| можно смело опустить: в любом случае выражение b² неотрицательно. А вот насчёт |c³| — тут уже задачка.) Если 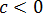, то и c³<0. Стало быть, модуль надо раскрыть с минусом: |c³| = —c³. Итого верное решение будет такое:

        А теперь — обратная задача. Не самая простая, сразу предупреждаю!

        Внести множитель под знак корня: .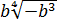

        Если вы сразу запишете решение вот так

,

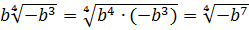
то вы попали в ловушку. Это неверное решение! В чём же дело?

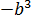
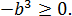
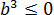
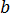
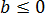
        Давайте вглядимся в выражение под корнем . Под корнем четвёртой степени, как мы знаем, должно находиться неотрицательное выражение. Иначе корень смысла не имеет.) Поэтому  А это, в свою очередь, значит, что  и, следовательно, само  также неположительно: .

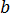
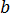
        И ошибка здесь состоит в том, что мы вносим под корень неположительное число : четвёртая степень превращает его в неотрицательное и получается неверный результат — слева заведомый минус, а справа уже плюс. А вносить под корень чётной степени мы имеем право только неотрицательные числа или выражения. А минус, если есть, оставлять перед корнем.) Как же нам выделить неотрицательный множитель в числе , зная, что оно само стопудово отрицательное? Да точно так же! Поставить минус.) А чтобы ничего не поменялось, скомпенсировать его ещё одним минусом. Вот так:

        И теперь уже неотрицательное число (-b) спокойно вносим под корень по всем правилам:

        Этот пример наглядно показывает, что, в отличие от других разделов математики, в корнях правильный ответ далеко не всегда вытекает автоматически из формул. Необходимо подумать и лично принять верное решение.) Особенно следует быть внимательнее со знаками в иррациональных уравнениях и неравенствах.

        Разбираемся со следующим важным приёмом в работе с корнями — избавлением  от иррациональности.

Избавление от иррациональности в дробях

        Если в выражении присутствуют корни, то, напомню, такое выражение называется выражением с иррациональностью. В некоторых случаях бывает полезно от этой самой иррациональности (т.е. корней) избавиться. Как можно ликвидировать корень? Корень у нас пропадает при… возведении в степень. С показателем либо равным показателю корня, либо кратным ему. Но, если мы возведём корень в степень (т.е. помножим корень сам на себя нужное число раз), то выражение от этого поменяется. Нехорошо.) Однако в математике бывают темы, где умножение вполне себе безболезненно. В дробях, к примеру. Согласно основному свойству дроби, если числитель и знаменатель умножить (разделить) на одно и то же число, то значение дроби не изменится.

        Допустим, нам дана вот такая дробь:

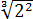
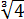
        Можно ли избавиться от корня в знаменателе? Можно! Для этого корень надо возвести в куб. Чего нам не хватает в знаменателе для полного куба? Нам не хватает множителя , т.е. . Вот и домножаем числитель и знаменатель дроби на 

        Корень в знаменателе исчез. Но… он появился в числителе. Ничего не поделать, такова судьба.) Нам это уже не важно: нас просили знаменатель от корней освободить. Освободили? Безусловно.)

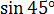
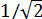
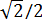
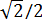
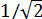
        Кстати, те, кто уже в ладах с тригонометрией, возможно, обращали внимание на то, что в некоторых учебниках и таблицах, к примеру,  обозначают по-разному: где-то , а где-то . Вопрос — что правильно? Ответ: всё правильно! ) Если догадаться, что  – это просто результат освобождения от иррациональности в знаменателе дроби .

        Зачем нам освобождаться от иррациональности в дробях? Какая разница — в числителе корень сидит или в знаменателе? Калькулятор всё равно всё посчитает.) Ну, для тех, кто не расстаётся с калькулятором, разницы действительно практически никакой… Но, даже считая на калькуляторе, можно обратить внимание на то, что делить на целое число всегда удобнее и быстрее, чем на иррациональное. А уж про деление в столбик вообще умолчу.)

        Следующий пример только подтвердит мои слова.

        Освободиться от иррациональности в знаменателе дроби:

        Как здесь ликвидировать квадратный корень в знаменателе? Если числитель и знаменатель помножить на выражение 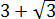, то в знаменателе получится квадрат суммы. Сумма квадратов первого и второго чисел дадут нам просто числа безо всяких корней, что очень радует. Однако… всплывёт удвоенное произведение первого числа на второе, где корень из трёх всё равно останется. Не канает. Как быть? Вспомнить другую замечательную формулу сокращённого умножения! Где никаких удвоенных произведений, а только квадраты:

        Такое выражение, которое при домножении какой-то суммы (или разности) выводит на разность квадратов, ещё называют сопряжённым выражением. В нашем примере сопряжённым выражением будет служить разность 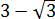. Вот и домножаем на эту разность числитель и знаменатель:

        Что тут можно сказать? В результате наших манипуляций не то что корень из знаменателя исчез — вообще дробь исчезла! Даже с калькулятором отнять корень из трёх от тройки проще, чем считать дробь с корнем в знаменателе. Ещё пример.

        Освободиться от иррациональности в знаменателе дроби:

        Как здесь выкручиваться? Формулы сокращённого умножения с квадратами сразу не катят — не получится полной ликвидации корней из-за того, что корень у нас в этот раз не квадратный, а кубический. Надо, чтобы корень как-то возвёлся в куб. Стало быть, применять надо какую-то из формул с кубами. Какую? Давайте подумаем. В знаменателе — сумма 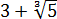. Как нам добиться возведения корня в куб? Домножить на неполный квадрат разности! Значит, применять будем формулу суммы кубов. Вот эту:

        В качестве a у нас тройка, а в качестве b — корень кубический из пяти:

        И снова дробь исчезла.) Такие ситуации, когда при освобождении от иррациональности в знаменателе дроби у нас вместе с корнями полностью исчезает сама дробь, встречаются очень часто. Как вам вот такой примерчик!

        Вычислить:

        

        Попробуйте просто сложить эти три дроби! Без ошибок! Один общий знаменатель чего стоит. А что, если попробовать освободиться от иррациональности в знаменателе каждой дроби? Что ж, пробуем:

        Ух ты, как интересно! Все дроби пропали! Напрочь. И теперь пример решается в два счёта:

           

        Просто и элегантно. И без долгих и утомительных вычислений.

        Именно поэтому операцию освобождения от иррациональности в дробях надо уметь делать. В подобных навороченных примерах только она и спасает, да.) Разумеется, внимательность никто не отменял. Бывают задания, где просят избавиться от иррациональности в числителе. Эти задания ничем от рассмотренных не отличаются, только от корней очищается числитель.)

Более сложные примеры

        Осталось рассмотреть некоторые специальные приёмы в работе с корнями и потренироваться распутывать не самые простые примеры. И тогда полученной информации уже будет достаточно для решения заданий с корнями любого уровня сложности. Итак — вперёд.) Для начала разберёмся, что делать со вложенными корнями, когда формула корня из корня не работает. Например, вот такой примерчик.

        Вычислить: 

        Корень под корнем… К тому же под корнями сумма или разность. Стало быть, формула корня из корня (с перемножением показателей) здесь не действует. Значит, надо что-то делать с подкоренными выражениями: у нас просто нету других вариантов. В таких примерах чаще всего под большим корнем зашифрован полный квадрат какой-нибудь суммы. Или разности. А корень из квадрата уже отлично извлекается! И теперь наша задача — его расшифровать.) Такая расшифровка красиво делается через систему уравнений. Сейчас всё сами увидите.)

        Итак, под первым корнем у нас вот такое выражение:

        А вдруг, не угадали? Проверим! Возводим в квадрат по формуле квадрата суммы:

        Всё верно.) Но… Откуда я взял это выражение 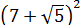? С неба?

        Нет.) Мы его чуть ниже получим честно. Просто по данному выражению я показываю, как именно составители заданий шифруют такие квадраты. Что такое 54? Это сумма квадратов первого и второго чисел. Причём, обратите внимание, уже без корней! А корень остаётся в удвоенном произведении, которое в нашем случае равно . Поэтому распутывание подобных примеров начинается с поиска удвоенного произведения. Если распутывать обычным подбором. И, кстати, о знаках. Тут всё просто. Если перед удвоенным плюс, то квадрат суммы. Если минус, то разности.) У нас плюс — значит, квадрат суммы.) А теперь — обещанный аналитический способ расшифровки. Через систему.)

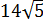
        Итак, у нас под корнем явно тусуется выражение (a+b)², и наша задача — найти a и b. В нашем случае сумма квадратов даёт 54. Вот и пишем:

        Теперь удвоенное произведение. Оно у нас 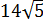. Так и записываем:

        Получили вот такую системку:

        Решаем обычным методом подстановки. Выражаем из второго уравнения, например,  и подставляем в первое:

        Решим первое уравнение:

           

           

       Получили биквадратное уравнение относительно a. Считаем дискриминант: 

       Значит,

       Получили аж четыре возможных значения a. Не пугаемся. Сейчас мы всё лишнее отсеем.) Если мы сейчас для каждого из четырёх найденных значений  посчитаем соответствующие значения , то получим четыре решения нашей системы. Вот они:

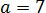
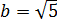
        И тут вопрос — а какое из решений нам подходит? Давайте подумаем. Отрицательные решения можно сразу отбросить: при возведении в квадрат минусы «сгорят», и всё подкоренное выражение в целом не изменится.) Остаются первые два варианта. Выбрать их можно совершенно произвольно: от перестановки слагаемых сумма всё равно не меняется.) Пусть, например, , а .

        Итого получили под корнем квадрат вот такой суммы:

        Всё чётко.)

        Я не зря так детально описываю ход решения. Чтобы было понятно, как происходит расшифровка.) Но есть одна проблемка. Аналитический способ расшифровки хоть и надёжный, но весьма длинный и громоздкий: приходится решать биквадратное уравнение, получать четыре решения системы и потом ещё думать, какие из них выбрать… Хлопотно? Согласен, хлопотно. Этот способ безотказно работает в большинстве подобных примеров. Однако очень часто можно здорово сократить себе работу и найти оба числа творчески. Подбором.) Да-да! Сейчас, на примере второго слагаемого (второго корня), я покажу более лёгкий и быстрый способ выделения полного квадрата под корнем.

        Итак, теперь у нас вот такой корень: .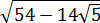

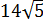
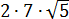
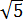
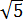
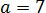
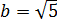
        Размышляем так: «Под корнем — скорее всего, зашифрованный полный квадрат. Раз перед удвоенным минус — значит, квадрат разности. Сумма квадратов первого и второго чисел даёт нам число 54. Но какие это квадраты? 1 и 53? 49 и 5? Слишком много вариантов… Нет, лучше начать распутывать с удвоенного произведения. Наши  можно расписать как  . Раз произведение удвоенное, то двойку сразу отметаем. Тогда кандидатами на роль a и b остаются 7 и . А вдруг, это 14 и /2? Не исключено. Но начинаем-то всегда с простого!» Итак, пусть , а . Проверим их на сумму квадратов:

        Получилось! Значит, наше подкоренное выражение — это на самом деле квадрат разности:

 

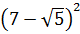
        Вот такой вот способ-лайт, чтобы не связываться с системой. Не всегда работает, но во многих таких примерах его вполне достаточно. Итак, под корнями — полные квадраты. Осталось только правильно извлечь корни, да досчитать пример:

        А теперь разберём ещё более нестандартное задание на корни.)

        Докажите, что число A – целое, если .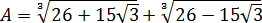

        Впрямую ничего не извлекается, корни вложенные, да ещё и разных степеней… Кошмар! Однако, задание имеет смысл.) Стало быть, ключ к его решению имеется.) А ключ здесь такой. Рассмотрим наше равенство

как уравнение относительно A. Да-да! Хорошо бы избавиться от корней. Корни у нас кубические, поэтому возведём-ка обе части равенства в куб. По формуле куба суммы:

       Кубы и корни кубические друг друга компенсируют, а под каждым большим корнем забираем одну скобку у квадрата и сворачиваем произведение разности и суммы в разность квадратов:

        Отдельно сосчитаем разность квадратов под корнями:

        Отлично! Значит, всё наше равенство ещё сильнее упростится:

   

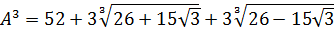
        А теперь делаем финт ушами — заменяем сумму корней в скобках на A (согласно условию примера!).

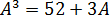
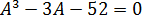
        Получаем кубическое уравнение  или .

        Здесь как раз тот случай, когда один из корней легко угадывается — это 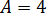. Значит, наш многочлен  можно разложить как

        Как разложить? Либо по схеме Горнера, либо делением «уголком» на скобку (A-4), либо даже группировкой (если представить -3A как -16A+13A). Объяснять подробно деление уголком или схему Горнера в теме про корни — уже совсем отклоняться от курса.) Кто в теме — и так поймёт.

        А теперь легко заметить, что квадратный трёхчлен во вторых скобках имеет отрицательный дискриминант, а значит, наше уравнение имеет единственный действительный корень 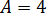. И поэтому наша страшная сумма корней  в действительности равна просто 4. То есть, явно целому числу. Что и требовалось доказать.)

        А теперь — поупрощаем некоторые дробные выражения с корнями. От простого — к сложному. Здесь всё точно так же, как и с многочленами. Только в применении к корням.) Я же говорил, что действия с корнями ничем не отличаются от таковых с буквами. И к корням с таким же успехом применима вся алгебра седьмого класса — формулы сокращённого умножения, разложение на множители, приведение подобных и т.п.

        Например, такое задание.

        Сократить дробь:

        

        Пример явно намекает на применение формулы разности квадратов:

        Спрашивается, а где же здесь квадраты? Сплошные корни… Сейчас покажу.

        Берём числитель нашей дробушки: .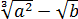

        Что такое 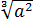? По свойству корня из степени, мы можем вынести квадрат наружу. Вот так:

        Хорошо, а из 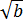 как квадрат сделать? Не вопрос! По пятому свойству, домножаем на двойку показатели корня и подкоренного выражения:

        По такой технологии, между прочим, можно совершенно любой корень превратить в совершенно любую степень. Какую хотим.   Как, например,  представить в виде 4-й степени? Нет проблем: 

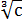
        Хотим из степеней корни делаем, хотим — наоборот, степени из корней. Что хотим, то и творим. Математика, однако!

        Итак, весь наш числитель можно представить как разность квадратов:

        А дальше никаких проблем — раскладываем числитель на множители и сокращаем:

        Следующий пример.

        Упростить:

        

        Действуем аналогично. Раскладываем на множители и сокращаем. В числителе применяем группировку. Например, вот такую:

        А в знаменателе просто выносим общий множитель :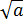

        Подставляем всё в нашу дробь и сокращаем:

        Как видим, разложение на множители очень популярно в теме с корнями. Очень! И особенно — формула разности квадратов. Именно поэтому формулы сокращённого умножения так важно знать и уметь применять.

        Ну и на десерт распутаем что-нибудь навороченное. )

        Упростить:

        

        Чтобы не запутаться и не наляпать ошибок, будем действовать по порядку. При взгляде на любой пример всегда задаём сами себе вопрос: «Что в примере мне больше всего не нравится?» В данном примере большинство скажет: «Числитель первой дроби!» Верно! Вот и упростим его отдельно: остальная часть примера от этого никак не пострадает.) Итак,

        Вместо знака деления удобно использовать черту дроби. Вот так:

        Сначала упростим дробь. Как? Попробуем сократить.) Для этого, ясное дело, надо разложить на множители числитель и знаменатель, да… Берём отдельно числитель 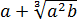. Можно его разложить на множители? Можно! Для этого из a надо сделать корень. Вот так:

        Если теперь подставить вместо a выражение 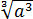, то всплывёт общий множитель.

        Со знаменателем полная аналогия:

        Таким образом,

        Теперь от упрощённой дроби отнимаем единичку. Как? Делаем из единички дробь и — вперёд!

        Следующим пунктом идёт деление полученной дроби на выражение 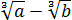. Это означает, что оно пойдёт у нас в знаменатель:

        Уфф… Дальше… Отнимаем от полученного выражения дробь :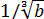

        И, наконец, последнее усилие. Возводим результат в куб:

        Ну как, всё понятно? Тогда — вперёд, набиваем руку и делаем примеры!

        Вычислить:

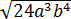
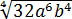
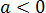
        Вынести множители за знак корня: ,  , где .

        Внести множители под знак корня: ,  .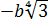

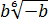
        Освободиться от иррациональности в знаменателе дробей:

        , .

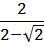
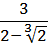
        Вычислить: 

        Доказать, что A – целое число, если .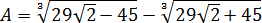

        Упростить:

        Ответы (пока) давать не буду — иначе неинтересно. До встречи и успехов!

Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых нужно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11. Или почти всю.

Например, задание №6 Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических. Задачи на определение модуля и понятие функции. В общем, типов задач здесь множество, по всему курсу алгебры.

И помните, что в ответе в заданиях первой части Профильного ЕГЭ по математике у вас должны получаться целые числа или конечные десятичные дроби.

Дробно-рациональные выражения. Формулы сокращенного умножения

Темы для повторения: Формулы сокращенного умножения, Приемы быстрого счета

Если вам встретится такое задание на ЕГЭ – значит, повезло!

1. Найдите значение выражения 

Не спешите перемножать десятичные дроби. Посмотрите на задачу внимательно.

Первый множитель в знаменателе умножили на 10, а второй поделили на 10, просто передвинув запятую.

Ответ: 100.

2. Найдите значение выражения

Ответ: 20.

Корни и степени. Иррациональные выражения

Темы для повторения: Арифметический квадратный корень.

Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .

.

3. Вычислите .

Применили одну из формул сокращенного умножения.

Ответ: 8.

4. Вычислите:

Упростим множители:

Ответ: 8.

Действия со степенями

Темы для повторения:
Вспомним правила действий со степенями.

5. Найдите значение выражения:  при

Применили формулу частного степеней

Ответ: 256.

6. Вычислите 

Ответ: 2.

7. Вычислите , если .

Спокойно, не пугаемся. И конечно, не спешим подставлять значение Сначала упростим выражение.

Ответ: 4,5.

8. Вычислите

Применили формулу для произведения степеней:

Ответ: 12.

9. Вычислите

Записали корни в виде степеней (это удобно!) и применили формулу произведения степеней.

Ответ: 3.

Логарифмические выражения

Темы для повторения:
Логарифмы

Логарифм положительного числа по основанию — это показатель степени, в которую надо возвести , чтобы получить .

.

При этом > 0, > 0,

Основные логарифмические формулы:

Основное логарифмическое тождество:

Логарифм произведения равен сумме логарифмов:

Логарифм частного равен разности логарифмов:

Формула для логарифма степени:

Формула перехода к новому основанию:

10. Вычислите: .

Снова формула перехода к другому основанию.

, поэтому

11. Найдите , если .

12. Найдите значение выражения .

13. Найдите значение выражения .

.

14. Найдите значение выражения .

Тригонометрия. Формулы тригонометрии и формулы приведения

Темы для повторения:
Тригонометрический круг.
Формулы тригонометрии.
Формулы приведения.

15. Вычислите:

16. Найдите , если и .

Т.к. , то

17. Найдите , если и

Т.к. , то

18. Найдите значение выражения:

Применили формулу приведения.

19. Упростите выражение:

Применили формулу приведения.

20. Найдите , если .

21. Вычислите , если

Алгебраические выражения, корни, степени и логарифмы. И еще тригонометрия. Это всё, что может встретиться в задании 6 Профильного ЕГЭ по математике?

Оказывается, и это не всё! Еще нужно знать, что такое модуль. И как найти .

Другие типы заданий

Темы для повторения:
Модуль числа.
Что такое функция.

22. Найдите значение выражения
при .

Запомним:

.

Если , то и .

При этом и .

При получаем: .

Ответ: 2.

23. Найдите значение выражения

при .

При получим:

Ответ: 12.

24. Найдите , если , при .

Что такое ? Это функция, каждому числу ставящая в соответствие число . Например, ;

Тогда:

Заметим, что .

Значит, при
.

25. Найдите , если , при .

— функция, каждому числу b ставящая в соответствии число
.

Тогда при

, и значение выражения равно 1.