Преобразование логарифмических выражений егэ профиль - Помощь в подготовке к экзаменам и поступлению

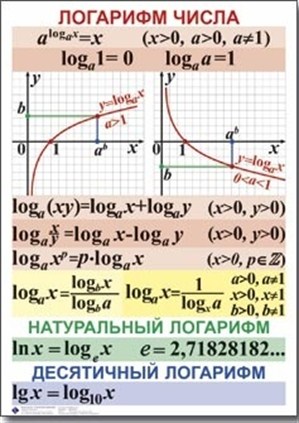
Логарифмом положительного числа $b$ по основанию а, где $a>0$, $a≠1$, называется показатель степени, в которую надо возвести число $а$, чтобы получить $b$.

Пример:

$log_{2}8=3$, т.к. $2^{3}=8;$

$log_{3}{1}/{27}=-3$, т.к $3^{-3}={1}/{27}$

Особенно можно выделить три формулы:

$log_{a}a=1;$

$log_{a}1=0;$

$log_{a}a^b=b.$

Основное логарифмическое тождество:

$a^{log_{a}b}=b$

Это равенство справедливо при $b>0, a>0, a≠1$

Пример:

$4^{log_{4}5}=5;$

$3^{-2log_{3}5}={3^{log_{3}5^{-2}}}=5^{-2}={1}/{25}$

Десятичным логарифмом числа называют логарифм этого числа по основанию $10$ и пишут $lg⁡b$ вместо $log_{10}b$.

Пример:

$lg100000=lg10^5=5$

Ответ: $5$

Натуральным логарифмом числа называют логарифм этого числа по основанию $е$, где $е$ – иррациональное число, приближенно равное $2.7$. При этом пишут $lnb$, вместо $log_{e}b$

Свойства логарифмов.

Все свойства логарифмов мы будем рассматривать для $a>0, a≠1, b>0, c>0, m$ – любое действительное число.

1. Для любых действительных чисел $m$ и $n$ справедливы равенства:

$log{_а}b^m=mlog_{a}b;$

$log_{a^m}b={1}/{m}log_{a}b.$

$log_{a^n}b^m={m}/{n}log_{a}b$

Пример:

$log_{3}3^{10}=10log_{3}3=10;$

$log_{5^3}7={1}/{3}log_{5}7;$

$log_{3^7}4^5={5}/{7}log_{3}4;$

2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.

$log_{a}(bc)=log_{a}b+log_{a}c$

Пример:

Вычислить $log_{12}2+log_{12}72$

Применим второе свойство наоборот: сумма логарифмов по одинаковому основанию равна логарифму произведения подлогарифмических выражений

$log_{12}2+log_{12}72=log_{12}2·72=log_{12}144=2$

Ответ: $2$

3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию

$log_{a}{b}/{c}=log_{a}b-log_{a}c$

Пример:

Вычислить $log_{5}75-log_{5}3$

Решение:

Разность логарифмов с одинаковыми основаниями равна логарифму частного подлогарифмических выражений

$log_{5}75-log_{5}3=log_{5}{75}/{3}=log_{5}25=2$

Ответ: $2$

4. При умножении двух логарифмов можно поменять местами их основания

$log_{a}b·log_{c}d=log_{c}b·log_{a}d$, если $a$, $b$, $c$, $d>0$, $a≠1$, $b≠1.$

5. $c^{log_{a}b}=b^{log_{a}c}$, где $а, b, c>0, a≠1$

6. Формула перехода к новому основанию

$log_{a}b={log_{c}b}/{log_{c}a}$

7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение

$log_{a}b={1}/{log_{b}a}$

Пример:

Найдите значение выражения: ${log_{2}∜{13}}/{log_{2}13}$

Решение:

В выражении видим, что был произведен переход к новому основанию $2$. Нам необходимо вернуться к старому основанию $13$.

${log_{2}∜{13}}/{log_{2}13}=log_{13}∜{13}$

Далее вычислим получившийся логарифм, для этого подлогарифмическое выражение необходимо представить в виде степени. Любой корень можно выразить в виде степени с дробным показателем, в знаменателе показателя будет находиться показатель корня

$∜{13}=13^{{1}/{4}}$

$log_{13}∜{13}=log_{13}13^{{1}/{4}}={1}/{4}=0.25$

Ответ: $0.25$

Источник

Главная
Новости
ЕГЭ
- ЕГЭ Профиль 2023
- ЕГЭ Профиль 2022
- ЕГЭ Профиль 2016-2021
- Варианты профильного ЕГЭ
- ЕГЭ База 2023
- ЕГЭ База 2022
- ЕГЭ База 2016-2021
ОГЭ
- ОГЭ 2019
- ОГЭ 2023
ГВЭ
- ГВЭ 11 класс
ВПР
- ВПР 4 класс
- ВПР 5 класс
- ВПР 6 класс
- ВПР 7 класс
- ВПР 8 класс
Алгебра
- Алгебра 7-9
- Алгебра 10-11
Геометрия
- Геометрия 7-9
- Геометрия 10-11
YouTube
Прочее
- Class100
- Разработки
- Обо мне
- Репетитор

ЕГЭ Профиль №9. Вычисление значений логарифмических выражений

ЕГЭ Профиль №9. Вычисление значений логарифмических выраженийadmin2018-08-14T13:34:02+03:00

Источник

ЗАДАНИЕ В11. ЛОГАРИФМИЧЕСКИЕ ВЫРАЖЕНИЯ.

1.1. Найдите значение выражения $({{log }_{7}4}16)cdot ({{log }_{7}3}36)$ .

2. Найдите значение выражения $({{log }_{7}2}4)cdot ({{log }_{7}1}81)$ .

3. Найдите значение выражения $({{log }_{7}0}125)cdot ({{log }_{5}9}16)$ .

4. Найдите значение выражения $({{log }_{5}8}216)cdot ({{log }_{5}7}729)$ .

5. Найдите значение выражения $({{log }_{5}6}343)cdot ({{log }_{5}5}8)$ .

6. Найдите значение выражения $({{log }_{5}4}81)cdot ({{log }_{5}3}64)$

7. Найдите значение выражения $({{log }_{5}2}512)cdot ({{log }_{5}1}32)$ .

8. Найдите значение выражения $({{log }_{5}0}27)cdot ({{log }_{2}9}343)$ .

9. Найдите значение выражения $({{log }_{2}8}125)cdot ({{log }_{2}7}64)$ .

10. Найдите значение выражения $({{log }_{2}6}9)cdot ({{log }_{2}5}49)$ .

11. Найдите значение выражения $({{log }_{2}4}36)cdot ({{log }_{2}3}81)$ .

12. Найдите значение выражения $({{log }_{2}2}8)cdot ({{log }_{2}1}9)$ .

13. Найдите значение выражения $({{log }_{2}0}36)cdot ({{log }_{7}9}256)$ .

14. Найдите значение выражения $({{log }_{7}8}128)cdot ({{log }_{7}7}36)$ .

15. Найдите значение выражения $({{log }_{7}6}243)cdot ({{log }_{7}5}512)$ .

2.1. Найдите значение выражения $7cdot {{7}4^{{{log }_{7}3}4}}$ .

2. Найдите значение выражения $6cdot {{7}2^{{{log }_{7}1}2}}$ .

3. Найдите значение выражения $9cdot {{7}0^{{{log }_{5}9}3}}$ .

4. Найдите значение выражения $9cdot {{5}8^{{{log }_{5}7}2}}$ .

5. Найдите значение выражения $13cdot {{5}6^{{{log }_{5}5}2}}$ .

6. Найдите значение выражения $8cdot {{5}4^{{{log }_{5}3}6}}$ .

7. Найдите значение выражения $9cdot {{5}2^{{{log }_{5}1}6}}$ .

8. Найдите значение выражения $5cdot {{5}0^{{{log }_{7}9}6}}$ .

9. Найдите значение выражения $5cdot {{7}8^{{{log }_{7}7}2}}$ .

10. Найдите значение выражения $10cdot {{7}6^{{{log }_{7}5}7}}$ .

11. Найдите значение выражения $9cdot {{7}4^{{{log }_{7}3}3}}$ .

12. Найдите значение выражения: $13cdot8^{mathop{mathrm{7}2}_{7}13}.$

13. Найдите значение выражения: $11cdot6^{mathop{mathrm{7}0}_{5}99}.$

14. Найдите значение выражения: $2cdot10^{mathop{mathrm{5}8}_{5}74}.$

15. Найдите значение выражения: $2cdot4^{mathop{mathrm{5}6}_{5}54}.$

3.1. Найдите значение выражения ${{5}4^{{{log }_{5}3}5}}$ .

2. Найдите значение выражения ${{5}2^{{{log }_{5}1}7}}$ .

3. Найдите значение выражения ${{5}0^{{{log }_{7}9}12}}$ .

4. Найдите значение выражения ${{7}8^{{{log }_{7}7}3}}$ .

5. Найдите значение выражения ${{7}6^{{{log }_{7}5}11}}$ .

6. Найдите значение выражения ${{7}4^{{{log }_{7}3}8}}$ .

7. Найдите значение выражения ${{7}2^{{{log }_{7}1}8}}$ .

8. Найдите значение выражения ${{7}0^{{{log }_{3}9}5}}$ .

9. Найдите значение выражения ${{3}8^{{{log }_{3}7}11}}$ .

10. Найдите значение выражения ${{3}6^{{{log }_{3}5}6}}$ .

11. Найдите значение выражения ${{3}4^{{{log }_{3}3}7}}$ .

12. Найдите значение выражения ${{3}2^{{{log }_{3}1}4}}$ .

13. Найдите значение выражения ${{3}0^{{{log }_{2}9}6}}$ .

14. Найдите значение выражения ${{2}8^{{{log }_{2}7}11}}$ .

15. Найдите значение выражения ${{2}6^{{{log }_{2}5}2}}$ .

4.1. Найдите значение выражения ${{log }_{2}4}2$ .

2. Найдите значение выражения ${{log }_{2}3}8$ .

3. Найдите значение выражения ${{log }_{2}2}5$ .

4. Найдите значение выражения ${{log }_{2}1}125$ .

5. Найдите значение выражения ${{log }_{2}0}0,01$ .

6. Найдите значение выражения ${{log }_{5}9}125$ .

7. Найдите значение выражения ${{log }_{5}8}25$ .

8. Найдите значение выражения ${{log }_{5}7}8$ .

9. Найдите значение выражения ${{log }_{5}6}400$ .

10. Найдите значение выражения ${{log }_{5}5}0,008$ .

11. Найдите значение выражения ${{log }_{5}4}8$ .

12. Найдите значение выражения ${{log }_{5}3}8000$ .

13. Найдите значение выражения ${{log }_{5}2}16$ .

14. Найдите значение выражения ${{log }_{5}1}64$ .

15. Найдите значение выражения ${{log }_{5}0}0,5$ .

5.1. Найдите значение выражения ${{log }_{3}9}8$ .

2. Найдите значение выражения ${{log }_{3}8}512$ .

3. Найдите значение выражения ${{log }_{3}7}0,2$ .

4. Найдите значение выражения ${{log }_{3}6}16$ .

5. Найдите значение выражения ${{log }_{3}5}0,05$ .

6. Найдите значение выражения ${{log }_{3}4}64$ .

7. Найдите значение выражения ${{log }_{3}3}0,1$ .

8. Найдите значение выражения ${{log }_{3}2}3125$ .

9. Найдите значение выражения ${{log }_{3}1}5$ .

10. Найдите значение выражения ${{log }_{3}0}0,008$ .

11. Найдите значение выражения ${{log }_{5}9}125$ .

12. Найдите значение выражения ${{log }_{5}8}0,5$ .

13. Найдите значение выражения ${{log }_{5}7}400$ .

14. Найдите значение выражения ${{log }_{5}6}625$ .

15. Найдите значение выражения ${{log }_{5}5}10000$ .

6.1.Найдите значение выражения ${{log }_{5}4}60-{{log }_{5}3}12$ .

2. Найдите значение выражения ${{log }_{5}2}270-{{log }_{5}1}7,5$

3. Найдите значение выражения

4. Найдите значение выражения ${{log }_{5}0}234-{{log }_{2}9}6,5$

5. Найдите значение выражения ${{log }_{2}8}90-{{log }_{2}7}2,5$

6. Найдите значение выражения ${{log }_{2}6}54-{{log }_{2}5}1,5$

7. Найдите значение выражения ${{log }_{2}4}252-{{log }_{2}3}1,75$ .

8. Найдите значение выражения ${{log }_{2}2}208-{{log }_{2}1}3,25$ .

9. Найдите значение выражения ${{log }_{2}0}160-{{log }_{7}9}2,5$ .

10. Найдите значение выражения ${{log }_{7}8}300-{{log }_{7}7}0,75$ .

11. Найдите значение выражения ${{log }_{7}6}80-{{log }_{7}5}1,25$ .

12. Найдите значение выражения $log_8 {7}4 - log_8 {7}3$ .

13. Найдите значение выражения $log_6 {7}2 - log_6 {7}1$ .

14. Найдите значение выражения $log_8 {7}0 - log_8 {2}9$ .

15. Найдите значение выражения $log_2 {2}8 - log_2 {2}7$ .

7.1. Найдите значение выражения ${{log }_{2}6}0,2+{{log }_{2}5}4$ .

2. Найдите значение выражения ${{log }_{2}4}3125+{{log }_{2}3}0,008$ .

3. Найдите значение выражения ${{log }_{2}2}25+{{log }_{2}1}625$ .

4. Найдите значение выражения ${{log }_{2}0}625+{{log }_{7}9}8000$ .

5. Найдите значение выражения ${{log }_{7}8}0,01+{{log }_{7}7}4$ .

6. Найдите значение выражения ${{log }_{7}6}0,5+{{log }_{7}5}2$ .

7. Найдите значение выражения ${{log }_{7}4}0,125+{{log }_{7}3}32$ .

8. Найдите значение выражения ${{log }_{7}2}32+{{log }_{7}1}10$ .

9. Найдите значение выражения ${{log }_{7}0}400+{{log }_{2}9}20$ .

10. Найдите значение выражения ${{log }_{2}8}5+{{log }_{2}7}64$ .

11. Найдите значение выражения ${{log }_{2}6}10+{{log }_{2}5}64$ .

12. Найдите значение выражения ${{log }_{2}4}125+{{log }_{2}3}100000$ .

13. Найдите значение выражения ${{log }_{2}2}8+{{log }_{2}1}0,5$ .

14. Найдите значение выражения ${{log }_{2}0}512+{{log }_@import url('https://themes.googleusercontent.com/fonts/css?kit=wAPX1HepqA24RkYW1AuHYA');ol{margin:0;padding:0}.c11{border-bottom-width:1pt;border-top-style:solid;width:45.9pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c16{border-bottom-width:1pt;border-top-style:solid;width:369.6pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c19{border-bottom-width:1pt;border-top-style:solid;width:46.2pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c15{border-bottom-width:1pt;border-top-style:solid;width:45.8pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c13{border-bottom-width:1pt;border-top-style:solid;width:50pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c9{border-bottom-width:1pt;border-top-style:solid;width:46pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c5{vertical-align:baseline;color:#000000;font-size:12pt;font-style:normal;background-color:#ffffff;font-family:$ .

15. Найдите значение выражения ${{log }_@import url('https://themes.googleusercontent.com/fonts/css?kit=wAPX1HepqA24RkYW1AuHYA');ol{margin:0;padding:0}.c11{border-bottom-width:1pt;border-top-style:solid;width:45.9pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c16{border-bottom-width:1pt;border-top-style:solid;width:369.6pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c19{border-bottom-width:1pt;border-top-style:solid;width:46.2pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c15{border-bottom-width:1pt;border-top-style:solid;width:45.8pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c13{border-bottom-width:1pt;border-top-style:solid;width:50pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c9{border-bottom-width:1pt;border-top-style:solid;width:46pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c5{vertical-align:baseline;color:#000000;font-size:12pt;font-style:normal;background-color:#ffffff;font-family:$ .

8.1. Найдите значение выражения ${{log }_@import url('https://themes.googleusercontent.com/fonts/css?kit=wAPX1HepqA24RkYW1AuHYA');ol{margin:0;padding:0}.c11{border-bottom-width:1pt;border-top-style:solid;width:45.9pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c16{border-bottom-width:1pt;border-top-style:solid;width:369.6pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c19{border-bottom-width:1pt;border-top-style:solid;width:46.2pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c15{border-bottom-width:1pt;border-top-style:solid;width:45.8pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c13{border-bottom-width:1pt;border-top-style:solid;width:50pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c9{border-bottom-width:1pt;border-top-style:solid;width:46pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c5{vertical-align:baseline;color:#000000;font-size:12pt;font-style:normal;background-color:#ffffff;font-family:$ .

2. Найдите значение выражения ${{log }_@import url('https://themes.googleusercontent.com/fonts/css?kit=wAPX1HepqA24RkYW1AuHYA');ol{margin:0;padding:0}.c11{border-bottom-width:1pt;border-top-style:solid;width:45.9pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c16{border-bottom-width:1pt;border-top-style:solid;width:369.6pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c19{border-bottom-width:1pt;border-top-style:solid;width:46.2pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c15{border-bottom-width:1pt;border-top-style:solid;width:45.8pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c13{border-bottom-width:1pt;border-top-style:solid;width:50pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c9{border-bottom-width:1pt;border-top-style:solid;width:46pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c5{vertical-align:baseline;color:#000000;font-size:12pt;font-style:normal;background-color:#ffffff;font-family:$ .

3. Найдите значение выражения ${{log }_@import url('https://themes.googleusercontent.com/fonts/css?kit=wAPX1HepqA24RkYW1AuHYA');ol{margin:0;padding:0}.c11{border-bottom-width:1pt;border-top-style:solid;width:45.9pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c16{border-bottom-width:1pt;border-top-style:solid;width:369.6pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c19{border-bottom-width:1pt;border-top-style:solid;width:46.2pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c15{border-bottom-width:1pt;border-top-style:solid;width:45.8pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c13{border-bottom-width:1pt;border-top-style:solid;width:50pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c9{border-bottom-width:1pt;border-top-style:solid;width:46pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c5{vertical-align:baseline;color:#000000;font-size:12pt;font-style:normal;background-color:#ffffff;font-family:$ .

4. Найдите значение выражения ${{log }_@import url('https://themes.googleusercontent.com/fonts/css?kit=wAPX1HepqA24RkYW1AuHYA');ol{margin:0;padding:0}.c11{border-bottom-width:1pt;border-top-style:solid;width:45.9pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c16{border-bottom-width:1pt;border-top-style:solid;width:369.6pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c19{border-bottom-width:1pt;border-top-style:solid;width:46.2pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c15{border-bottom-width:1pt;border-top-style:solid;width:45.8pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c13{border-bottom-width:1pt;border-top-style:solid;width:50pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c9{border-bottom-width:1pt;border-top-style:solid;width:46pt;border-right-style:solid;padding:0pt 5.8pt 0pt 5.8pt;border-bottom-color:#000000;border-top-width:1pt;border-bottom-style:solid;vertical-align:top;border-top-color:#000000;border-left-color:#000000;border-right-color:#000000;border-left-style:solid;border-right-width:1pt;border-left-width:1pt}.c5{vertical-align:baseline;color:#000000;font-size:12pt;font-style:normal;background-color:#ffffff;font-family:$ .

5. Найдите значение выражения ${{log }_{1,8}}5-{{log }_{1,8}}9$ .

6. Найдите значение выражения ${{log }_{1,25}}4-{{log }_{1,25}}5$ .

7. Найдите значение выражения ${{log }_{0,8}}20-{{log }_{0,8}}16$ .

8. Найдите значение выражения ${{log }_{0,35}}20-{{log }_{0,35}}7$ .

9. Найдите значение выражения ${{log }_{1,5}}4-{{log }_{1,5}}6$ .

10. Найдите значение выражения ${{log }_{0,6}}25-{{log }_{0,6}}15$ .

11. Найдите значение выражения ${{log }_{2,2}}5-{{log }_{2,2}}11$ .

12. Найдите значение выражения ${{log }_{3,25}}4-{{log }_{3,25}}13$ .

13. Найдите значение выражения ${{log }_{6,5}}2-{{log }_{6,5}}13$ .

14. Найдите значение выражения ${{log }_{0,3}}20-{{log }_{0,3}}6$ .

15. Найдите значение выражения ${{log }_{0,2}}10-{{log }_{0,2}}2$ .

9.1. Найдите значение выражения $frac{{{log }_{3}}25}{{{log }_{3}}5}$ .

2. Найдите значение выражения $frac{{{log }_{6}}512}{{{log }_{6}}8}$ .

3. Найдите значение выражения $frac{{{log }_{6}}4}{{{log }_{6}}2}$ .

4. Найдите значение выражения $frac{{{log }_{3}}121}{{{log }_{3}}11}$ .

5. Найдите значение выражения $frac{{{log }_{2}}1331}{{{log }_{2}}11}$ .

6. Найдите значение выражения $frac{{{log }_{4}}27}{{{log }_{4}}3}$ .

7. Найдите значение выражения $frac{{{log }_{3}}8}{{{log }_{3}}2}$ .

8. Найдите значение выражения $frac{{{log }_{2}}225}{{{log }_{2}}15}$ .

9. Найдите значение выражения $frac{{{log }_{3}}64}{{{log }_{3}}8}$ .

10. Найдите значение выражения $frac{{{log }_{5}}121}{{{log }_{5}}11}$ .

11. Найдите значение выражения $frac{{{log }_{5}}9}{{{log }_{5}}3}$ .

12. Найдите значение выражения $frac{{{log }_{4}}36}{{{log }_{4}}6}$ .

13. Найдите значение выражения $frac{{{log }_{6}}125}{{{log }_{6}}5}$ .

14. Найдите значение выражения $frac{{{log }_{2}}121}{{{log }_{2}}11}$ .

15. Найдите значение выражения $frac{{{log }_{2}}144}{{{log }_{2}}12}$ .

10.1. Найдите значение выражения $frac{{{log }_{7}}13}{{{log }_{49}}13}$ .

2. Найдите значение выражения $frac{{{log }_{9}}8}{{{log }_{81}}8}$ .

3. Найдите значение выражения $frac{{{log }_{2}}7}{{{log }_{4}}7}$ .

4. Найдите значение выражения $frac{{{log }_{5}}8}{{{log }_{25}}8}$ .

5. Найдите значение выражения $frac{{{log }_{3}}14}{{{log }_{9}}14}$ .

6. Найдите значение выражения $frac{{{log }_{3}}4}{{{log }_{81}}4}$ .

7. Найдите значение выражения $frac{{{log }_{3}}13}{{{log }_{9}}13}$ .

8. Найдите значение выражения $frac{{{log }_{3}}7}{{{log }_{9}}7}$ .

9. Найдите значение выражения $frac{{{log }_{3}}17}{{{log }_{81}}17}$ .

10. Найдите значение выражения $frac{{{log }_{2}}14}{{{log }_{4}}14}$ .

11. Найдите значение выражения $frac{{{log }_{6}}4}{{{log }_{36}}4}$ .

12. Найдите значение выражения $frac{{{log }_{6}}5}{{{log }_{36}}5}$ .

13. Найдите значение выражения $frac{{{log }_{3}}2}{{{log }_{27}}2}$ .

14. Найдите значение выражения $frac{{{log }_{2}}3}{{{log }_{4}}3}$ .

15. Найдите значение выражения $frac{{{log }_{9}}13}{{{log }_{81}}13}$ .

11.1. Найдите значение выражения ${{log }_{5}}9cdot {{log }_{3}}25$ .

2. Найдите значение выражения ${{log }_{5}}7cdot {{log }_{7}}25$ .

3. Найдите значение выражения ${{log }_{3}}13cdot {{log }_{13}}9$ .

4. Найдите значение выражения ${{log }_{7}}8cdot {{log }_{8}}49$ .

5. Найдите значение выражения ${{log }_{3}}11cdot {{log }_{11}}27$ .

6. Найдите значение выражения ${{log }_{2}}5cdot {{log }_{5}}8$ .

7. Найдите значение выражения ${{log }_{7}}5cdot {{log }_{5}}49$ .

8. Найдите значение выражения ${{log }_{7}}4cdot {{log }_{4}}49$ .

9. Найдите значение выражения ${{log }_{7}}9cdot {{log }_{9}}49$ .

10. Найдите значение выражения ${{log }_{5}}7cdot{{log }_{7}25}$ .

11. Найдите значение выражения ${{log }_{5}}9cdot {{log }_{3}}25$ .

12.1. Найдите значение выражения $frac{{{9}^{{{log }_{5}}50}}}{{{9}^{{{log }_{5}}2}}}$ .

2. Найдите значение выражения $frac{{{6}^{{{log }_{12}}432}}}{{{6}^{{{log }_{12}}3}}}$ .

3. Найдите значение выражения $frac{{{5}^{{{log }_{7}}98}}}{{{5}^{{{log }_{7}}2}}}$ .

4. Найдите значение выражения $frac{{{2}^{{{log }_{13}}507}}}{{{2}^{{{log }_{13}}3}}}$ .

5. Найдите значение выражения $frac{{{5}^{{{log }_{6}}108}}}{{{5}^{{{log }_{6}}3}}}$ .

6. Найдите значение выражения $frac{{{2}^{{{log }_{10}}200}}}{{{2}^{{{log }_{10}}2}}}$ .

7. Найдите значение выражения $frac{{{5}^{{{log }_{13}}507}}}{{{5}^{{{log }_{13}}3}}}$ .

8. Найдите значение выражения $frac{{{8}^{{{log }_{11}}242}}}{{{8}^{{{log }_{11}}2}}}$ .

9. Найдите значение выражения $frac{{{7}^{{{log }_{9}}162}}}{{{7}^{{{log }_{9}}2}}}$ .

10. Найдите значение выражения $frac{{{3}^{{{log }_{13}}507}}}{{{3}^{{{log }_{13}}3}}}$ .

11. Найдите значение выражения $frac{{{2}^{{{log }_{12}}288}}}{{{2}^{{{log }_{12}}2}}}$ .

12. Найдите значение выражения $frac{{{9}^{{{log }_{12}}288}}}{{{9}^{{{log }_{12}}2}}}$ .

13. Найдите значение выражения $frac{{{6}^{{{log }_{8}}192}}}{{{6}^{{{log }_{8}}3}}}$ .

14. Найдите значение выражения $frac{{{6}^{{{log }_{10}}300}}}{{{6}^{{{log }_{10}}3}}}$ .

15. Найдите значение выражения $frac{{{4}^{{{log }_{11}}242}}}{{{4}^{{{log }_{11}}2}}}$ .

13.1. Найдите значение выражения $(1-{{log }_{2}}12)(1-{{log }_{6}}12)$ .

2. Найдите значение выражения $(1-{{log }_{6}}24)(1-{{log }_{4}}24)$ .

3. Найдите значение выражения $(1-{{log }_{8}}48)(1-{{log }_{6}}48)$ .

4. Найдите значение выражения $(1-{{log }_{8}}24)(1-{{log }_{3}}24)$ .

5. Найдите значение выражения $(1-{{log }_{3}}24)(1-{{log }_{9}}24)$ .

6. Найдите значение выражения $(1-{{log }_{7}}28)(1-{{log }_{4}}28)$ .

7. Найдите значение выражения $(1-{{log }_{7}}63)(1-{{log }_{9}}63)$ .

8. Найдите значение выражения $(1-{{log }_{2}}18)(1-{{log }_{9}}18)$ .

9. Найдите значение выражения $(1-{{log }_{5}}45)(1-{{log }_{9}}45)$ .

10. Найдите значение выражения $(1-{{log }_{9}}18)(1-{{log }_{2}}18)$ .

11. Найдите значение выражения $(1-{{log }_{2}}6)(1-{{log }_{3}}6)$ .

12. Найдите значение выражения $(1-{{log }_{7}}14)(1-{{log }_{2}}14)$ .

13. Найдите значение выражения $(1-{{log }_{5}}95)(1-{{log }_{19}}95)$ .

14. Найдите значение выражения $(1-{{log }_{4}}24)(1-{{log }_{6}}24)$

15. Найдите значение выражения $(1-{{log }_{7}}56)(1-{{log }_{8}}56)$ .

14.1. Найдите значение выражения $6{{log }_{7}}sqrt[3]{7}$ .

2. Найдите значение выражения $104{{log }_{3}}sqrt[8]{3}$

3. Найдите значение выражения $75{{log }_{11}}sqrt[5]{11}$

4. Найдите значение выражения $50{{log }_{10}}sqrt[5]{10}$

5. Найдите значение выражения $42{{log }_{2}}sqrt[6]{2}$

6. Найдите значение выражения $64{{log }_{4}}sqrt[4]{4}$

7. Найдите значение выражения $64{{log }_{5}}sqrt[4]{5}$ .

8. Найдите значение выражения $10{{log }_{6}}sqrt[4]{6}$ .

9. Найдите значение выражения $18{{log }_{5}}sqrt[9]{5}$ .

10. Найдите значение выражения $6{{log }_{3}}sqrt[6]{3}$ .

11. Найдите значение выражения $21{{log }_{8}}sqrt[7]{8}$ .

12. Найдите значение выражения $12{{log }_{7}}sqrt[8]{7}$ .

13. Найдите значение выражения $14{{log }_{6}}sqrt[7]{6}$ .

14. Найдите значение выражения $2{{log }_{2}}sqrt[5]{2}$ .

15. Найдите значение выражения $12{{log }_{5}}sqrt[3]{5}$ .

15.1. Найдите значение выражения ${{log }_{sqrt[6]{13}}}13$ .

2. Найдите значение выражения ${{log }_{sqrt[4]{10}}}10$ .

3. Найдите значение выражения ${{log }_{sqrt[5]{10}}}10$ .

4. Найдите значение выражения ${{log }_{sqrt[9]{4}}}4$ .

5. Найдите значение выражения ${{log }_{sqrt[3]{10}}}10$ .

6. Найдите значение выражения ${{log }_{sqrt[5]{12}}}12$ .

7. Найдите значение выражения ${{log }_{sqrt[4]{6}}}6$ .

8. Найдите значение выражения ${{log }_{sqrt[9]{13}}}13$ .

9. Найдите значение выражения ${{log }_{sqrt[3]{7}}}7$ .

10. Найдите значение выражения ${{log }_{sqrt[8]{6}}}6$ .

11. Найдите значение выражения ${{log }_{sqrt[9]{10}}}10$ .

12. Найдите значение выражения ${{log }_{sqrt[7]{10}}}10$ .

13. Найдите значение выражения ${{log }_{sqrt[5]{13}}}13$ .

14. Найдите значение выражения ${{log }_{sqrt[7]{6}}}6$ .

15. Найдите значение выражения ${{log }_{sqrt[3]{4}}}4$ .

16.1. Найдите значение выражения $frac{{{log }_{3}}18}{2+{{log }_{3}}2}$ .

2. Найдите значение выражения $frac{{{log }_{6}}180}{2+{{log }_{6}}5}$ .

3. Найдите значение выражения $frac{{{log }_{3}}63}{2+{{log }_{3}}7}$ .

4. Найдите значение выражения $frac{{{log }_{2}}52}{2+{{log }_{2}}13}$ .

5. Найдите значение выражения $frac{{{log }_{8}}320}{2+{{log }_{8}}5}$ .

6. Найдите значение выражения $frac{{{log }_{2}}48}{3+{{log }_{2}}6}$ .

7. Найдите значение выражения $frac{{{log }_{9}}324}{2+{{log }_{9}}4}$ .

8. Найдите значение выражения $frac{{{log }_{6}}144}{2+{{log }_{6}}4}$ .

9. Найдите значение выражения $frac{{{log }_{5}}150}{2+{{log }_{5}}6}$ .

10. Найдите значение выражения $frac{{{log }_{8}}384}{2+{{log }_{8}}6}$ .

11. Найдите значение выражения $frac{{{log }_{3}}108}{3+{{log }_{3}}4}$ .

12. Найдите значение выражения $frac{{{log }_{4}}96}{2+{{log }_{4}}6}$ .

13. Найдите значение выражения $frac{{{log }_{3}}54}{2+{{log }_{3}}6}$ .

14. Найдите значение выражения $frac{{{log }_{11}}242}{2+{{log }_{11}}2}$ .

15. Найдите значение выражения $frac{{{log }_{2}}56}{3+{{log }_{2}}7}$ .

17.1. Найдите значение выражения $frac{{{log }_{3}}5}{{{log }_{3}}7}+{{log }_{7}}0,2$ .

2. Найдите значение выражения $frac{{{log }_{8}}20}{{{log }_{8}}5}+{{log }_{5}}0,05$ .

3. Найдите значение выражения $frac{{{log }_{2}}20}{{{log }_{2}}12}+{{log }_{12}}0,05$ .

4. Найдите значение выражения $frac{{{log }_{10}}10}{{{log }_{10}}7}+{{log }_{7}}0,1$ .

5. Найдите значение выражения $frac{{{log }_{4}}10}{{{log }_{4}}9}+{{log }_{9}}0,1$ .

6. Найдите значение выражения $frac{{{log }_{6}}2}{{{log }_{6}}3}+{{log }_{3}}0,5$ .

7. Найдите значение выражения $frac{{{log }_{4}}2}{{{log }_{4}}5}+{{log }_{5}}0,5$ .

8. Найдите значение выражения $frac{{{log }_{2}}2}{{{log }_{2}}3}+{{log }_{3}}0,5$ .

9. Найдите значение выражения $frac{{{log }_{2}}5}{{{log }_{2}}6}+{{log }_{6}}0,2$ .

10. Найдите значение выражения $frac{{{log }_{2}}10}{{{log }_{2}}9}+{{log }_{9}}0,1$ .

11. Найдите значение выражения $frac{{{log }_{9}}5}{{{log }_{9}}14}+{{log }_{14}}0,2$ .

12. Найдите значение выражения $frac{{{log }_{4}}5}{{{log }_{4}}7}+{{log }_{7}}0,2$ .

13. Найдите значение выражения $frac{{{log }_{6}}5}{{{log }_{6}}5}+{{log }_{5}}0,2$ .

14. Найдите значение выражения $frac{{{log }_{7}}20}{{{log }_{7}}3}+{{log }_{3}}0,05$ .

15. Найдите значение выражения $frac{{{log }_{7}}4}{{{log }_{7}}6}+{{log }_{6}}0,25$ .

18.1. Найдите значение выражения ${{log }_{0,8}}3cdot {{log }_{3}}1,25$ .

2. Найдите значение выражения ${{log }_{1,25}}7cdot {{log }_{7}}0,8$ .

3. Найдите значение выражения ${{log }_{0,5}}5cdot {{log }_{5}}2$ .

4. Найдите значение выражения ${{log }_{0,4}}8cdot {{log }_{8}}2,5$ .

5. Найдите значение выражения ${{log }_{0,4}}6cdot {{log }_{6}}2,5$ .

6. Найдите значение выражения ${{log }_{0,8}}3cdot {{log }_{3}}1,25$ .

7. Найдите значение выражения ${{log }_{0,5}}9cdot {{log }_{9}}2$ .

8. Найдите значение выражения ${{log }_{0,5}}3cdot {{log }_{3}}2$ .

9. Найдите значение выражения ${{log }_{0,8}}4cdot {{log }_{4}}1,25$ .

10. Найдите значение выражения ${{log }_{0,4}}2cdot {{log }_{2}}2,5$ .

11. Найдите значение выражения ${{log }_{0,8}}5cdot {{log }_{5}}1,25$ .

12. Найдите значение выражения ${{log }_{0,2}}3cdot {{log }_{3}}5$ .

13. Найдите значение выражения ${{log }_{2,5}}4cdot {{log }_{4}}0,4$ .

14. Найдите значение выражения ${{log }_{0,4}}3cdot {{log }_{3}}2,5$ .

15. Найдите значение выражения ${{log }_{2,5}}8cdot {{log }_{8}}0,4$ .

19.1. Найдите значение выражения ${{5}^{{{log }_{25}}49}}$ .

2. Найдите значение выражения ${{3}^{{{log }_{9}}16}}$ .

3. Найдите значение выражения ${{2}^{{{log }_{4}}16}}$ .

4. Найдите значение выражения ${{4}^{{{log }_{16}}81}}$ .

5. Найдите значение выражения ${{4}^{{{log }_{16}}25}}$ .

6. Найдите значение выражения ${{3}^{{{log }_{81}}16}}$ .

7. Найдите значение выражения ${{7}^{{{log }_{49}}9}}$ .

8. Найдите значение выражения ${{8}^{{{log }_{64}}4}}$ .

9. Найдите значение выражения ${{5}^{{{log }_{25}}36}}$ .

10. Найдите значение выражения ${{7}^{{{log }_{49}}25}}$ .

11. Найдите значение выражения ${3}^{{log }_{9}16}$ .

12. Найдите значение выражения ${{8}^{{{log }_{64}}4}}$ .

13. Найдите значение выражения ${{5}^{{{log }_{25}}36}}$ .

14. Найдите значение выражения ${{7}^{{{log }_{49}}25}}$ .

15. Найдите значение выражения ${3}^{{log }_{9}16}$ .

20.1.Найдите значение выражения $log _{sqrt{7}}^{2}49$ .

2. Найдите значение выражения $log _{sqrt{11}}^{2}121$ .

3. Найдите значение выражения $log _{sqrt{2}}^{2}4$ .

4. Найдите значение выражения $log _{sqrt{8}}^{2}512$ .

5. Найдите значение выражения $log _{sqrt{8}}^{2}8$ .

6. Найдите значение выражения $log _{sqrt{8}}^{2}64$ .

7. Найдите значение выражения $log _{sqrt{7}}^{3}7$ .

8. Найдите значение выражения $log _{sqrt{13}}^{2}169$ .

9. Найдите значение выражения $log _{sqrt{7}}^{2}49$ .

10. Найдите значение выражения $log _{sqrt{15}}^{3}3375$ .

11. Найдите значение выражения $log _{sqrt{5}}^{2}125$ .

12. Найдите значение выражения $log _{sqrt{14}}^{2}14$ .

13. Найдите значение выражения $log _{sqrt{7}}^{3}343$ .

14. Найдите значение выражения $log _{sqrt{15}}^{3}15$ .

15. Найдите значение выражения $log _{sqrt{3}}^{2}9$ .

21.1. Найдите значение выражения ${{5}^{3+{{log }_{5}}2}}$ .

2. Найдите значение выражения ${{3}^{2+{{log }_{3}}7}}$ .

3. Найдите значение выражения ${{8}^{2+{{log }_{8}}13}}$ .

4. Найдите значение выражения ${{8}^{2+{{log }_{8}}12}}$ .

5. Найдите значение выражения ${{4}^{3+{{log }_{4}}15}}$ .

6. Найдите значение выражения ${{2}^{3+{{log }_{2}}15}}$ .

7. Найдите значение выражения ${{6}^{2+{{log }_{6}}11}}$ .

8. Найдите значение выражения ${{3}^{2+{{log }_{3}}2}}$ .

9. Найдите значение выражения ${{5}^{3+{{log }_{5}}7}}$ .

10. Найдите значение выражения ${{9}^{2+{{log }_{9}}7}}$ .

11. Найдите значение выражения ${{3}^{3+{{log }_{3}}14}}$ .

12. Найдите значение выражения ${{4}^{2+{{log }_{4}}12}}$ .

13. Найдите значение выражения ${{2}^{3+{{log }_{2}}9}}$ .

14. Найдите значение выражения ${{4}^{3+{{log }_{4}}3}}$ .

15. Найдите значение выражения ${{3}^{2+{{log }_{3}}15}}$ .

22.1. Найдите значение выражения ${{8}^{2{{log }_{8}}3}}$ .

2. Найдите значение выражения ${{6}^{2{{log }_{6}}14}}$ .

3. Найдите значение выражения ${{9}^{2{{log }_{9}}8}}$ .

4. Найдите значение выражения ${{2}^{2{{log }_{2}}10}}$ .

5. Найдите значение выражения ${{7}^{3{{log }_{7}}5}}$ .

6. Найдите значение выражения ${{8}^{2{{log }_{8}}15}}$ .

7. Найдите значение выражения ${{3}^{2{{log }_{3}}8}}$ .

8. Найдите значение выражения ${{7}^{2{{log }_{7}}6}}$ .

9. Найдите значение выражения ${{6}^{2{{log }_{6}}9}}$ .

10. Найдите значение выражения ${{5}^{3{{log }_{5}}12}}$ .

11. Найдите значение выражения ${{9}^{5{{log }_{9}}10}}$ .

12. Найдите значение выражения ${{6}^{2{{log }_{6}}10}}$ .

13. Найдите значение выражения ${{8}^{3{{log }_{8}}7}}$ .

14. Найдите значение выражения ${{6}^{2{{log }_{6}}7}}$ .

15. Найдите значение выражения ${{5}^{3{{log }_{5}}4}}$ .

23.1. Найдите значение выражения ${{64}^{{{log }_{8}}sqrt{3}}}$ .

2. Найдите значение выражения ${{16}^{{{log }_{4}}sqrt{13}}}$ .

3. Найдите значение выражения ${{25}^{{{log }_{5}}sqrt{6}}}$ .

4. Найдите значение выражения ${{49}^{{{log }_{7}}sqrt{5}}}$ .

5. Найдите значение выражения ${{81}^{{{log }_{9}}sqrt{8}}}$ .

6. Найдите значение выражения ${{4}^{{{log }_{2}}sqrt{3}}}$ .

7. Найдите значение выражения ${{36}^{{{log }_{6}}sqrt{9}}}$ .

8. Найдите значение выражения ${{9}^{{{log }_{3}}sqrt{5}}}$ .

9. Найдите значение выражения ${{9}^{{{log }_{3}}sqrt{7}}}$ .

10. Найдите значение выражения ${{9}^{{{log }_{3}}sqrt{15}}}$ .

11. Найдите значение выражения ${{4}^{{{log }_{2}}sqrt{12}}}$ .

12. Найдите значение выражения ${{25}^{{{log }_{5}}sqrt{7}}}$ .

13. Найдите значение выражения ${{25}^{{{log }_{5}}sqrt{6}}}$ .

14. Найдите значение выражения ${{16}^{{{log }_{4}}sqrt{7}}}$ .

15. Найдите значение выражения ${{16}^{{{log }_{4}}sqrt{14}}}$ .

24.1.Найдите значение выражения ${log }_{4}{{log }_{5}25}$ .

2. Найдите значение выражения ${{log }_{16}}{{log }_{6}}36$

3. Найдите значение выражения ${{log }_{16}}{{log }_{3}}9$

4. Найдите значение выражения ${{log }_{16}}{{log }_{4}}16$

5. Найдите значение выражения ${{log }_{4}}{{log }_{9}}81$

6. Найдите значение выражения ${{log }_{16}}{{log }_{2}}4$

7. Найдите значение выражения ${{log }_{4}}{{log }_{4}}16$

8. Найдите значение выражения ${{log }_{4}}{{log }_{7}}49$

9. Найдите значение выражения ${{log }_{9}}{{log }_{3}}27$

10. Найдите значение выражения ${{log }_{9}}{{log }_{4}}64$

11. Найдите значение выражения ${log }_{4}{{log }_{6}36}$ .

12. Найдите значение выражения ${log }_{64}{{log }_{2}256}$ .

13. Найдите значение выражения ${log }_{2}{{log }_{4}16}$ .

14. Найдите значение выражения ${log }_{3}{{log }_{9}729}$ .

15. Найдите значение выражения ${log }_{2}{{log }_{2}4}$ .

25.1. Найдите значение выражения $frac{24}{3^{{log }_{3}2}}$ .

2. Найдите значение выражения $frac{65}{{{9}^{{{log }_{9}}5}}}$ .

3. Найдите значение выражения $frac{30}{{{3}^{{{log }_{3}}2}}}$ .

4. Найдите значение выражения $frac{56}{{{6}^{{{log }_{6}}7}}}$ .

5. Найдите значение выражения $frac{36}{{{7}^{{{log }_{7}}4}}}$ .

6. Найдите значение выражения $frac{78}{{{5}^{{{log }_{5}}6}}}$ .

7. Найдите значение выражения $frac{70}{{{8}^{{{log }_{8}}5}}}$ .

8. Найдите значение выражения $frac{40}{{{3}^{{{log }_{3}}4}}}$ .

9. Найдите значение выражения $frac{98}{{{5}^{{{log }_{5}}7}}}$ .

10. Найдите значение выражения $frac{5}{8^{{log }_{8}10}}$ .

11. Найдите значение выражения $frac{14}{2^{{log }_{2}7}}$ .

12. Найдите значение выражения $frac{16}{3^{{log }_{3}5}}$ .

13. Найдите значение выражения $frac{45}{5^{{log }_{5}10}}$ .

14. Найдите значение выражения $frac{33}{5^{{log }_{5}11}}$ .

15. Найдите значение выражения $frac{2}{6^{{log }_{6}4}}$ .

26.1. Найдите значение выражения ${log }_{frac{1}{13}}sqrt{13}$ .

2. Найдите значение выражения ${{log }_{frac{1}{18}}}sqrt{18}$ .

3. Найдите значение выражения ${{log }_{frac{1}{5}}}sqrt{5}$ .

4. Найдите значение выражения ${{log }_{frac{1}{19}}}sqrt{19}$ .

5. Найдите значение выражения ${{log }_{frac{1}{8}}}sqrt{8}$ .

6. Найдите значение выражения ${{log }_{frac{1}{11}}}sqrt{11}$ .

7. Найдите значение выражения ${{log }_{frac{1}{6}}}sqrt{6}$ .

8. Найдите значение выражения ${{log }_{frac{1}{21}}}sqrt{21}$ .

9. Найдите значение выражения ${log }_{frac{1}{22}}sqrt{22}$ .

10. Найдите значение выражения ${log }_{frac{1}{15}}sqrt{15}$ .

11. Найдите значение выражения ${log }_{frac{1}{2}}sqrt{2}$ .

12. Найдите значение выражения ${log }_{frac{2}{21}}sqrt{10,5}$ .

13. Найдите значение выражения ${log }_{frac{2}{3}}sqrt{1,5}$ .

14. Найдите значение выражения ${log }_{frac{1}{14}}sqrt{14}$ .

15. Найдите значение выражения ${log }_{frac{1}{23}}sqrt{23}$ .

27.1.Найдите значение выражения ${log }_{3}8.1+{log }_{3}10$ .

2. Найдите значение выражения ${{log }_{3}}6,75+{{log }_{3}}4$ .

3. Найдите значение выражения ${{log }_{3}}1,8+{{log }_{3}}5$ .

4. Найдите значение выражения ${{log }_{11}}24,2+{{log }_{11}}5$ .

5. Найдите значение выражения ${{log }_{3}}2,25+{{log }_{3}}4$ .

6. Найдите значение выражения ${{log }_{3}}16,2+{{log }_{3}}5$ .

7. Найдите значение выражения ${{log }_{9}}16,2+{{log }_{9}}5$ .

8. Найдите значение выражения ${{log }_{9}}8,1+{{log }_{9}}10$ .

9. Найдите значение выражения ${{log }_{13}}16,9+{{log }_{13}}10$ .

10. Найдите значение выражения ${{log }_{3}}20,25+{{log }_{3}}4$ .

11. Найдите значение выражения ${log }_{2}0,2+{log }_{2}20$ .

12. Найдите значение выражения ${log }_{2}1+{log }_{2}4$ .

13. Найдите значение выражения ${log }_{8}6,4+{log }_{8}10$ .

14. Найдите значение выражения ${log }_{3}4,5+{log }_{3}2$ .

15. Найдите значение выражения ${log }_{3}1,8+{log }_{3}5$ .

28.1.Найдите значение выражения $frac{{log }_{6}sqrt{13}}{{log }_{6}{13}}$ .

2. Найдите значение выражения $frac{{{log }_{2}}sqrt[5]{27}}{{{log }_{2}}27}$ .

3. Найдите значение выражения $frac{{{log }_{9}}sqrt[5]{17}}{{{log }_{9}}17}$ .

4. Найдите значение выражения $frac{{{log }_{6}}sqrt{11}}{{{log }_{6}}11}$ .

5. Найдите значение выражения $frac{{{log }_{3}}sqrt[4]{17}}{{{log }_{3}}17}$ .

6. Найдите значение выражения $frac{{{log }_{3}}sqrt{5}}{{{log }_{3}}5}$ .

7. Найдите значение выражения $frac{{{log }_{8}}sqrt[5]{17}}{{{log }_{8}}17}$ .

8. Найдите значение выражения $frac{{{log }_{5}}sqrt[5]{11}}{{{log }_{5}}11}$ .

9. Найдите значение выражения $frac{log_{5}{sqrt[4]{17}}}{log_{5}17}$ .

10. Найдите значение выражения $frac{log_{0,3}{sqrt[25]{47}}}{log_{0,3}47}$ .

11. Найдите значение выражения $frac{{log }_{7}sqrt{13}}{{log }_{7}{13}}$ .

12. Найдите значение выражения $frac{{log }_{2}sqrt{3}}{{log }_{2}{9}}$ .

13. Найдите значение выражения $frac{{log }_{4}sqrt{15}}{{log }_{4}{225}}$ .

14. Найдите значение выражения $frac{{log }_{3}sqrt{2}}{{log }_{3}{2}}$ .

15. Найдите значение выражения $frac{{log }_{8}sqrt{14}}{{log }_{8}{196}}$ .

29.1. Найдите значение выражения , если $log_b a=frac{1}{7}$ .

2. Найдите значение выражения $log_a (ab^{2})$ , если $log_b a=frac{2}{11}$ .

3. Найдите значение выражения $log_a (a^{3}b^{8})$ , если $log_b a=frac{1}{3}$ .

4. Найдите значение выражения $log_a (a^{2}b^{6})$ , если $log_b a=frac{2}{11}$ .

5. Найдите значение выражения $log_a (a^{5}b^{8})$ , если $log_b a=frac{1}{2}$ .

6. Найдите значение выражения $log_a (a^{3}b^{6})$ , если $log_b a=frac{2}{13}$ .

7. Найдите значение выражения $log_a (a^{5}b^{9})$ , если $log_b a=frac{3}{4}$ .

8. Найдите значение выражения $log_a (a^{3}b^{5})$ , если $log_b a=frac{5}{14}$ .

9. Найдите значение выражения $log_a (a^{4}b^{6})$ , если $log_b a=frac{2}{15}$ .

10. Найдите значение выражения $log_a (a^{7}b^{6})$ , если $log_b a=frac{1}{5}$ .

11. Найдите значение выражения $log_a (a^{6}b^{3})$ , если $log_b a=frac{1}{11}$ .

12. Найдите значение выражения $log_a (a^{4}b)$ , если $log_b a=frac{1}{19}$ .

13. Найдите значение выражения $log_a (a^{2}b^{8})$ , если $log_b a=frac{4}{7}$ .

14. Найдите значение выражения $log_a (a^{3}b^{10})$ , если $log_b a=frac{2}{5}$ .

15. Найдите значение выражения $log_a (a^{6}b^{2})$ , если $log_b a=frac{1}{6}$ .

30.1. Найдите $log_a frac{a}{b^3}$ , если .

2. Найдите $log_a frac{a^{6}}{b^{4}}$ , если .

3. Найдите $log_a frac{a}{b^{5}}$ , если .

4. Найдите $log_a frac{a^{4}}{b^{5}}$ , если .

5. Найдите $log_a frac{a^{6}}{b^{2}}$ , если .

6. Найдите $log_a frac{a}{b^{9}}$ , если .

7. Найдите $log_a frac{a^{5}}{b^{6}}$ , если .

8. Найдите $log_a frac{a^{3}}{b^{5}}$ , если .

9. Найдите $log_a frac{a^{10}}{b^{4}}$ , если .

10. Найдите $log_a frac{a^{3}}{b^{4}}$ , если .

11. Найдите $log_a frac{a^{5}}{b^{4}}$ , если .

12. Найдите $log_a frac{a^{2}}{b^{8}}$ , если .

13. Найдите $log_a frac{a^{10}}{b}$ , если .

14. Найдите $log_a frac{a}{b^{8}}$ , если .

15. Найдите $log_a frac{a^{8}}{b^{9}}$ , если .

31.1. Найдите , если .

2. Найдите $log_a (a^{6}b^{10})$ , если .

3. Найдите $log_a (a^{3}b^{4})$ , если .

4. Найдите $log_a (a^{8}b^{3})$ , если .

5. Найдите $log_a (a^{2}b^{6})$ , если .

6. Найдите $log_a (a^{9}b^{3})$ , если .

7. Найдите $log_a (a^{3}b^{5})$ , если .

8. Найдите $log_a (a^{5}b^{4})$ , если .

9. Найдите $log_a (a^{7}b^{4})$ , если .

10. Найдите $log_a (a^{8}b^{9})$ , если .

11. Найдите $log_a (a^{9}b^{3})$ , если .

12. Найдите $log_a (a^{7}b^{5})$ , если .

13. Найдите $log_a (a^{5}b^{9})$ , если .

14. Найдите $log_a (a^{10}b^{6})$ , если .

15. Найдите $log_a (a^{8}b)$ , если .

32.1. Вычислите значение выражения: $(3^{log_{2}3})^{log_{3}2}$ .

2. Вычислите значение выражения: $(5^{log_{3}7})^{log_{5}3}$ .

3. Вычислите значение выражения: $(3^{log_{2}5})^{log_{5}2}$ .

4 Вычислите значение выражения: $(5^{log_{7}2})^{log_{2}7}$ .

5. Вычислите значение выражения: $(5^{log_{5}7})^{log_{7}3}$ .

6. Вычислите значение выражения: $(7^{log_{3}2})^{log_{2}3}$ .

7. Вычислите значение выражения: $(7^{log_{7}5})^{log_{5}2}$ .

8. Вычислите значение выражения: $(2^{log_{2}7})^{log_{7}3}$ .

9. Вычислите значение выражения: $(5^{log_{5}7})^{log_{7}2}$ .

10. Вычислите значение выражения: $(7^{log_{5}3})^{log_{7}5}$ .

11. Вычислите значение выражения: $(3^{log_{3}2})^{log_{2}3}$ .

12. Вычислите значение выражения: $(5^{log_{5}3})^{log_{3}5}$ .

13. Вычислите значение выражения: $(5^{log_{5}2})^{log_{2}3}$ .

14. Вычислите значение выражения: $(3^{log_{7}2})^{log_{2}7}$ .

15. Вычислите значение выражения: $(7^{log_{7}2})^{log_{2}5}$ .

В11. ЛОГАРИФМИЧЕСКИЕ ВЫРАЖЕНИЯ. ОТВЕТЫ.

Источник

Задание 903

Найдите значение выражения $$log^{3}_{sqrt{3}}{{frac{1}{3}}^3}$$

Ответ: -216

Скрыть

Рассмотрим сам логарифм: $$ log_{sqrt{3}}{{frac{1}{3}}^3}=log_{3^{1/2}}{3^{-3}}=frac{1}{frac{1}{2}}*left(-3right)log_33=-6 $$ Так как он был в третьей степени, то возведем -6 в нее и получим -216

Задание 939

Известно, что $$log_a b *log_b c = -5$$ . Найдите значение выражения $$log_c a$$

Ответ: -0.2

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$log_a b *log_b c = frac{1}{log_b a}*log_b c=frac{log_b c}{log_b a}=log_a c=-5$$ $$log_c a=frac{1}{log_a c}=frac{1}{-5}=-0.2$$

Задание 2494

Найдите значение выражения: $$6^{2+log_{6}8}$$

Ответ: 288

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$6^{2+log_{6}8}=$$ $$=36cdot 6^{log_{6}8}=36cdot 8=288$$

Задание 2825

Найдите значение выражения: $$frac{log_{9}10}{log_{9}11}+log_{11}0,1$$

Ответ: 0

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$frac{log_{9}10}{log_{9}11}+log_{11}0,1=$$ $$=log_{11}10+log_{11}0,1=log_{11}(10cdot 0,1)=log_{11}1=0$$

Задание 3030

Найдите значение выражения $$64^{log_{8}sqrt{3}}$$

Ответ: 3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$64^{log_{8}sqrt{3}}=8^{2log_{8}sqrt{3}}=8^{log_{8}3}=3$$

Задание 3114

Найдите значение выражения $$lg(lgsqrt[10]{10})$$

Ответ: -1

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$lg(lgsqrt[10]{10})=lgfrac{1}{10}cdotlg 10=lgfrac{1}{10}=-1$$

Задание 3285

Найдите значение выражения $$log_5 312,5 — log_5 2,5$$

Ответ: 3

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$log_5 312,5 — log_5 2,5 = log_5 frac{312,5}{2,5}= log_5 125 = 3$$

Задание 3372

Найдите значение выражения: $$(log_{0,5}sqrt{8sqrt[3]{2}})^{-1}$$

Ответ: -0,6

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!

Скрыть

$$(log_{0,5}sqrt{8sqrt[3]{2}})^{-1}=$$ $$=(log_{0,5}(2^{3}cdot2^{frac{1}{3}})^{frac{1}{2}})^{-1}=$$ $$=(-1cdotlog_{2}2^{frac{5}{3}})^{-1}=(-frac{5}{3})^{-1}=-frac{3}{5}=-0,6$$

Задание 4236

Найдите значение выражения $$(log_{2}16)cdot(log_{6}36)$$

Ответ: 8

Задание 4237

Найдите значение выражения $$7cdot5^{log_{5}4}$$

Ответ: 28

Задание 4238

Найдите значение выражения $$36^{log_{6}5}$$

Ответ: 25

Задание 4239

Найдите значение выражения $$log_{0,25}2$$

Ответ: -0,5

Задание 4240

Найдите значение выражения $$log_{4}8$$

Ответ: 1,5

Задание 4241

Найдите значение выражения $$log_{5}60-log_{5}12$$

Ответ: 1

Задание 4242

Найдите значение выражения $$log_{5}0,2+log_{0,5}4$$

Ответ: -3

Нумерация страниц

Текущая страница
1
Page
2
Page
3
Page
4
Page
5
Page
6
Page
7
Page
8
Следующая страница
Последняя страница

Источник

9. Преобразование числовых и буквенных выражений

1. Вспоминай формулы по каждой теме

2. Решай новые задачи каждый день

3. Вдумчиво разбирай решения

Числовые логарифмические выражения

Логарифм по основанию (a) от (b) – это число (t), которое показывает, в какую степень нужно возвести (a), чтобы получить (b).
Ограничения: числа (a) и (b) такие, что (a>0, ane 1, b>0).
Таким образом, верно основное логарифмическое тождество [Large{{color{royalblue}{a^t=b quadLeftrightarrowquad
log_a{b}=t}}}]
Т.к. мы имеем право возводить в любую степень, то (tin
mathbb{R}).

(blacktriangleright) Если (a,b,c) – числа, удовлетворяющие ограничениям: (a,b,c>0, ane 1), то справедливы следующие формулы:

[begin{array}{|ccc|}
hline textbf{(1)} log_a1=0&&textbf{(2)} log_aa=1\
&&\
textbf{(3)} log_{a^n}{b^m}=frac mnlog_ab&&textbf{(4)}
a^{log_bc}=c^{log_ba}\
&&\
textbf{(5)} log_a{bc}=log_ab+log_ac&&textbf{(6)}
log_a{dfrac bc}=log_ab-log_ac\
&&\
textbf{(7)} log_abcdot log_bc=log_ac & text{или}
&textbf{(7′}) log_bc=dfrac{log_ac}{log_ab}\
&&\
hline
end{array}]

Заметим, что при выполнении ограничений данные формулы верны в обе стороны!

Некоторые частные случаи, которыми удобно пользоваться:

(blacktriangleright) Частные случаи формул (3) и (4): [m=log_a{a^m} text{и} b=a^{log_ab}]
С помощью первой формулы нагляднее видно, как заменить число на логарифм по нужному основанию:
(4=log_2{2^4}=log_2{16});

а с помощью второй – как заменить число на степень с нужным основанием:
(4=3^{log_34}).

(blacktriangleright) Частные случаи формул (7) и (7’): [log_abcdot log_ba=1 text{и}

log_ab=dfrac1{log_ba}]
Пример:
(log_3{25}+dfrac2{log_{frac15}3}={small{text{(применили}}}
{small{text{ формулу}}}
(2))=log_3{25}+2log_3{dfrac15}=log_3{25}+log_3{dfrac1{25}}=log_3{left(25cdotdfrac1{25}right)}=0)

Задание
1

#553

Уровень задания: Равен ЕГЭ

Найдите значение выражения ((log_{17}289) cdot left(log_{500}dfrac{1}{500}right)).

По определению логарифма (log_{17}289) – это степень, в которую надо возвести 17, чтобы получить 289. Таким образом, (log_{17}289 = 2). Аналогично можно сделать вывод, что [log_{500}dfrac{1}{500} = -1.] Итого: ((log_{17}289) cdot left(log_{500}dfrac{1}{500}right) = -2).

Ответ: -2

Задание
2

#554

Уровень задания: Равен ЕГЭ

Найдите значение выражения (16^{log_{2}5}).

Так как (a^{log_{b}c} = c^{log_{b}a}), то (16^{log_{2}5} = 2^{4 cdot log_{2}5} = 2^{log_{2}5^4} = 2^{log_{2}625} = 625^{log_{2}2} = 625^1 = 625).

Ответ: 625

Задание
3

#555

Уровень задания: Равен ЕГЭ

Найдите значение выражения (log_{81}243).

По свойствам логарифма (log_{81}243 = log_{3^4}3^5 = dfrac{5}{4}log_{3}3 = dfrac{5}{4} = 1,25).

Ответ: 1,25

Задание
4

#556

Уровень задания: Равен ЕГЭ

Найдите значение выражения (log_{11}242 — log_{121}4).

По свойствам логарифма [log_{121}4 = log_{11^2}4 = 0,5log_{11}4 = log_{11}(4^{0,5}) = log_{11}2.] Тогда (log_{11}242 — log_{121}4 = log_{11}242 — log_{11}2 = log_{11}dfrac{242}{2} = log_{11}121 = log_{11}11^2 = 2log_{11}11 = 2).

Ответ: 2

Задание
5

#557

Уровень задания: Равен ЕГЭ

Найдите значение выражения (log_{0,7}20 — log_{0,7}14).

По свойствам логарифма [log_{0,7}20 — log_{0,7}14 = log_{0,7}dfrac{20}{14} = log_{frac{7}{10}}dfrac{10}{7} = -1,] ведь по определению логарифма (log_{frac{7}{10}}dfrac{10}{7}) – это степень, в которую надо возвести (dfrac{7}{10}), чтобы получить (dfrac{10}{7}).

Ответ: -1

Задание
6

#558

Уровень задания: Равен ЕГЭ

Найдите значение выражения (dfrac{log_{15}1000}{log_{225}{10^4}}).

По свойствам логарифма [dfrac{log_{15}1000}{log_{225}{10^4}} = dfrac{log_{15}1000}{0,5log_{15}{10^4}} = dfrac{log_{15}1000}{log_{15}{(10^4})^{0,5}} = dfrac{log_{15}1000}{log_{15}{10^2}} = log_{100}1000 = log_{10^2}10^3 = dfrac{3}{2}log_{10}10 = dfrac{3}{2} = 1,5.]

Ответ: 1,5

Задание
7

#559

Уровень задания: Равен ЕГЭ

Найдите значение выражения (log_{7}144 cdot log_{12}343).

По свойствам логарифма [log_{7}144 cdot log_{12}343 = log_{7}(12^2) cdot log_{12}(7^3) = 2cdot 3 cdot log_{7}12 cdot log_{12}7 = 6 cdot log_{7}12 cdot log_{12}7 = 6cdotlog_{7}7 = 6,] потому что (log_{a}bcdotlog_{b}c = log_{a}c).

Ответ: 6

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ

Источник

14 января 2018

В закладки

Обсудить

Жалоба

Логарифмы в заданиях ЕГЭ

Большая часть заданий, включенных в ЕГЭ, представляет собой задания на вычисление значений числовых логарифмических выражений.

При подготовке следует обратить внимание на формулу перехода к новому основанию логарифма и следствия из нее. Задачи на использование этих формул в школьных учебниках практически не встречаются.

Материал для проведения самостоятельных работ. 15 вариантов по 28 заданий. Ответы прилагаются.

log-sm.docx

Источник

Пример:

$log_{2}8=3$, т.к. $2^{3}=8;$

$log_{3}{1}/{27}=-3$, т.к $3^{-3}={1}/{27}$

Особенно можно выделить три формулы:

$log_{a}a=1;$

$log_{a}1=0;$

$log_{a}a^b=b.$

Основное логарифмическое тождество:

$a^{log_{a}b}=b$

Это равенство справедливо при $b>0, a>0, a≠1$

Пример:

$4^{log_{4}5}=5;$

$3^{-2log_{3}5}={3^{log_{3}5^{-2}}}=5^{-2}={1}/{25}$

Десятичным логарифмом числа называют логарифм этого числа по основанию $10$ и пишут $lg⁡b$ вместо $log_{10}b$.

Пример:

$lg100000=lg10^5=5$

Ответ: $5$

Свойства логарифмов.

Все свойства логарифмов мы будем рассматривать для $a>0, a≠1, b>0, c>0, m$ – любое действительное число.

1. Для любых действительных чисел $m$ и $n$ справедливы равенства:

$log{_а}b^m=mlog_{a}b;$

$log_{a^m}b={1}/{m}log_{a}b.$

$log_{a^n}b^m={m}/{n}log_{a}b$

Пример:

$log_{3}3^{10}=10log_{3}3=10;$

$log_{5^3}7={1}/{3}log_{5}7;$

$log_{3^7}4^5={5}/{7}log_{3}4;$

2. Логарифм произведения равен сумме логарифмов по тому же основанию от каждого множителя.

$log_{a}(bc)=log_{a}b+log_{a}c$

Пример:

Вычислить $log_{12}2+log_{12}72$

$log_{12}2+log_{12}72=log_{12}2·72=log_{12}144=2$

Ответ: $2$

3. Логарифм частного равен разности логарифмов от числителя и знаменателя по тему же основанию

$log_{a}{b}/{c}=log_{a}b-log_{a}c$

Пример:

Вычислить $log_{5}75-log_{5}3$

Решение:

Разность логарифмов с одинаковыми основаниями равна логарифму частного подлогарифмических выражений

$log_{5}75-log_{5}3=log_{5}{75}/{3}=log_{5}25=2$

Ответ: $2$

4. При умножении двух логарифмов можно поменять местами их основания

$log_{a}b·log_{c}d=log_{c}b·log_{a}d$, если $a$, $b$, $c$, $d>0$, $a≠1$, $b≠1.$

5. $c^{log_{a}b}=b^{log_{a}c}$, где $а, b, c>0, a≠1$

6. Формула перехода к новому основанию

$log_{a}b={log_{c}b}/{log_{c}a}$

7. В частности, если необходимо поменять местами основание и подлогарифмическое выражение

$log_{a}b={1}/{log_{b}a}$

Пример:

Найдите значение выражения: ${log_{2}∜{13}}/{log_{2}13}$

Решение:

${log_{2}∜{13}}/{log_{2}13}=log_{13}∜{13}$

$∜{13}=13^{{1}/{4}}$

$log_{13}∜{13}=log_{13}13^{{1}/{4}}={1}/{4}=0.25$

Ответ: $0.25$

Задания, решение которых заключается в преобразовании логарифмических выражений, довольно часто встречаются на ЕГЭ.

Чтобы успешно справиться с ними при минимальной затрате времени кроме основных логарифмических тождеств, необходимо знать и правильно использовать ещё некоторые формулы.

Это: a^log_а^b= b, где а, b > 0, а ≠ 1 (Она вытекает непосредственно из определения логарифма).

log_a b = log_с b / log_с а или log_аb = 1/log_b а
где а, b, с > 0; а, с ≠ 1.

log_а^m bⁿ = (m/n) log_|а| |b|
где а, b > 0, а ≠ 1, m, n Є R, n ≠ 0.

а^log_с^b= b^log_с^агде а, b, с > 0 и а, b, с ≠ 1

Чтобы показать справедливость четвертого равенства прологарифмируем левую и правую часть по основанию а. Получим log_а(а^log_с^b) = log_а(b^log_с^а) или log_сb = log_са · log_а b; log_сb = log_с а · (log_сb / log_са); log_с b = log_сb.

Мы доказали равенство логарифмов, значит, равны и выражения, стоящие под логарифмами. Формула 4 доказана.

Пример 1.

Вычислите 81^log₂₇⁵^log₅⁴.

Решение.

81 = 3⁴, 27 = 3³.

log₂₇5 = 1/3 log₃ 5, log₅4 = log₃ 4 / log₃ 5. Следовательно,

log₂₇ 5 · log₅ 4 = 1/3 log₃ 5 · (log₃ 4 / log₃5) = 1/3 log₃4.

Тогда 81^log₂₇^{5 log}₅⁴= (3⁴)^{1/3 log}₃⁴= (3^log₃⁴)^4/3= (4)^4/3 = 4³√4.

Самостоятельно можно выполнить следующее задание.

Вычислить (8^log₂³+ 3^1/^log₂³) — log_0,25.

В качестве подсказки 0,2 = 1/5 = 5^-1;log_0,2 5 = -1.

Ответ: 5.

Пример 2.

Вычислите (√11)^log√3^9-^log₁₂₁⁸¹.

Решение.

Выполним замену выражений: 9 = 3², √3 = 3^1/2, log_√3 9 = 4,

121 = 11², 81 = 3⁴, log₁₂₁ 81 = 2 log₁₁ 3 (использовалась формула 3).

Тогда (√11)^log√3^9-^log₁₂₁⁸¹ = (11^1/2)^4-2^log₁₁³ = (11)^2-^log₁₁³= 11² / (11)^log₁₁³= 11² / (11^log₁₁³) = 121/3.

Пример 3.

Вычислите log₂ 24/ log₉₆ 2- log₂ 192 / log ₁₂ 2.

Решение.

Логарифмы, содержащиеся в примере, заменим логарифмами с основанием 2.

log₉₆ 2 = 1/log₂ 96 = 1/log₂(2⁵ · 3) = 1/(log₂ 2⁵ + log₂ 3) = 1/(5 + log₂ 3);

log₂ 192 = log₂ (2⁶· 3) = (log₂ 2⁶+ log₂3) = (6 + log₂3);

log₂ 24 = log₂(2³ · 3) = (log₂ 2³ + log₂3) = (3 + log₂ 3);

log₁₂2 = 1/log₂ 12 = 1/log₂ (2²· 3) = 1/(log₂ 2² + log₂ 3) = 1/(2 + log₂ 3).

Тогда log₂24 / log₉₆ 2 – log₂ 192 / log₁₂ 2 = (3 + log₂ 3) / (1/(5 + log₂ 3)) – ((6 + log₂3) / (1/(2 + log₂ 3)) =

= (3 + log₂3) · (5 + log₂ 3) – (6 + log₂ 3)(2 + log₂ 3).

После раскрытия скобок и приведения подобных слагаемых получим число 3. (При упрощении выражения можно log₂ 3 обозначить через n и упрощать выражение

(3 + n) · (5 + n) – (6 + n)(2 + n)).

Ответ: 3.

Самостоятельно можно выполнить следующее задание:

Вычислить (log₃ 4 + log₄ 3 + 2) · log₃ 16 · log²₁₄₄ 3.

Здесь необходимо сделать переход к логарифмам по основанию 3 и разложение на простые множители больших чисел.

Ответ:1/2

Пример 4.

Даны три числа А = 1/(log₃0,5), В = 1/(log_0,5 3), С = log_0,5 12 – log_0,5 3. Расположите их в порядке возрастания.

Решение.

Преобразуем числа А = 1/(log₃ 0,5) = log_0,5 3; С = log_0,5 12 – log_0,53 = log_0,5 12/3 = log_0,5 4 = -2.

Сравним их

log_0,53 > log_0,5 4 = -2 и log_0,5 3 < -1 = log_0,5 2, так как функция у = log_0,5 х – убывающая.

Или -2 < log_0,53 < -1. Тогда -1 < 1/(log_0,53) < -1/2.

Ответ. Следовательно, порядок размещения чисел: С; А; В.

Пример 5.

Сколько целых чисел расположено на интервале (log₃¹/₁₆; log²₆ 48).

Решение.

Определим между какими степенями числа 3 находится число¹/₁₆. Получим ¹/₂₇ <¹/₁₆ <¹/₉.

Так как функция у = log₃ х – возрастающая, то log₃(¹/₂₇) < log₃ (¹/₁₆) < log₃(¹/₉); -3 < log₃ (¹/₁₆) < -2.

log₆48 = log₆(36 ·⁴/₃) = log₆36 + log₆(⁴/₃) = 2 + log₆(⁴/₃). Сравним log₆(⁴/₃) и ¹/₅. А для этого сравним числа ⁴/₃ и 6^1/5. Возведём оба числа в 5 степень. Получим (⁴/₃)⁵ =¹⁰²⁴/₂₄₃ = 4⁵²/₂₄₃ < 6. Следовательно,

log₆ (⁴/₃) < ¹/₅. 2 < log₆ 48 < 2¹/₅. Числа, входящие в двойное неравенство, положительные. Их можно возводить в квадрат. Знаки неравенства при этом не изменятся. Тогда 4 < log_6² 48 < 4²¹/_25.

Следовательно, интервал (log₃¹/₁₆; log₆48) включает в себя промежуток [-2; 4] и на нём размещаются целые числа -2; -1; 0; 1; 2; 3; 4.

Ответ: 7 целых чисел.

Пример 6.

Вычислите 3^lglg^2/^lg³— lg20.

Решение.

3^lg^lg^2/^lg³ = (3^1/^lg3)^lg^lg² = (3^lо^g₃¹⁰)^lg^lg²= 10^lg^lg²= lg2.

Тогда 3^lglg2/lg3 — lg 20 = lg 2 – lg 20 = lg 0,1 = -1.

Ответ: -1.

Пример 7.

Известно, что log₂(_√3+ 1) + log₂ (√6 – 2) = А. Найдите log₂(_√3–1) + log₂(√6 + 2).

Решение.

Числа (√3 + 1) и (√3 – 1); (√6 – 2) и (√6 + 2) – сопряжённые.

Проведем следующее преобразование выражений

√3 – 1 = (√3 – 1) · (√3 + 1)) / (√3 + 1) = 2/(√3 + 1);

√6 + 2 = (√6 + 2) · (√6 – 2)) / (√6 – 2) = 2/(√6 – 2).

Тогда log₂ (_√3– 1) + log₂(√6 + 2) = log₂(2/(_√3 + 1)) + log₂ (2/(√6 – 2)) =

= log₂2 – log₂(_√3+ 1) + log₂ 2 – log₂ (√6 – 2) = 1 – log₂(_√3+ 1) + 1 – log₂ (√6 – 2) =

= 2 – log₂(_√3+ 1) – log₂ (√6 – 2) = 2 – А.

Ответ: 2 – А.

Пример 8.

Упростите и найдите приближенное значение выражения (log₃ 2 · log₄ 3 · log₅ 4 · log₆ 5 · … · log₁₀ 9.

Решение.

Все логарифмы приведём к общему основанию 10.

(log₃ 2 · log₄ 3 · log₅ 4 · log₆ 5 · … · log₁₀ 9 = (lg 2 / lg 3) · (lg 3 / lg 4)· (lg 4 / lg 5) · (lg 5 / lg 6) · … · (lg 8 / lg 9) · lg 9 = lg 2 ≈ 0,3010. (Приближенное значение lg 2 можно найти с использованием таблицы, логарифмической линейки либо калькулятора).

Ответ: 0,3010.

Пример 9.

Вычислить log_а²_b³√(a¹¹ b^-3), если log _√_аb³= 1. (В этом примере, _а² b³ – основание логарифма).

Решение.

Если log_√_аb³= 1, то 3/(0,5 log_а b = 1. И log_аb = 1/6.

Тогда log_а²_b3√(a¹¹b^-3) = 1/2 log_а^₂_b³ (a¹¹b^-3) = log_а (a¹¹b^-3) / (2log_а(a²b³)) = (log_а a¹¹+ log_а b^-3) / (2(log_{а a²} + log_а b³)) = (11 – 3log_а b) / (2(2 + 3log_а b)) Учитывая то, что log_аb = 1/6 получим (11 – 3 ·¹/₆) / (2(2 + 3 ·¹/₆)) = 10,5/5 = 2,1.

Ответ: 2,1.

Самостоятельно можно выполнить следующее задание:

Вычислить log_√3⁶ √2,1, если log_0,727 = а.

Ответ: (3 + а) / (3а).

Пример 10.

Вычислить 6,5^4/^log₃¹⁶⁹· 3^1/^log₄¹³+ log125.

Решение.

6,5^4/^log₃¹⁶⁹· 3^1/^log₄¹³+ log125 = (13/2)^4/2^log₃¹³· 3^2/^log₂¹³+ 2log₅ 5 ³= (13/2)²^log₁₃³· 3² ^log₁₃²+ 6 = (13^log₁₃³/ 2^log₁₃³)²· (3 ^log₁₃²)² + 6 = (3/2^log₁₃³)²· (3^log₁₃²)² + 6 = (3²/(2^log₁₃³)² ) · (2^log₁₃³)²+ 6.

(2^log₁₃³= 3^log₁₃²(формула 4))

Получим 9 + 6 = 15.

Ответ: 15.

Остались вопросы? Не знаете, как найти значение логарифмического выражения?
Чтобы получить помощь репетитора – зарегистрируйтесь.
Первый урок – бесплатно!

Источник