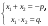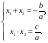Выражения, содержащие знак радикала (корень), называются иррациональными.
Арифметическим корнем натуральной степени $n$ из неотрицательного числа а называется некоторое неотрицательное число, при возведении которого в степень $n$ получается число $а$.
$(√^n{a})^n=a$
В записи $√^n{a}$, «а» называется подкоренным числом, $n$ — показателем корня или радикала.
Свойства корней $n$-ой степени при $а≥0$ и $b≥0$:
1. Корень произведения равен произведению корней
$√^n{a∙b}=√^n{a}∙√^n{b}$
Пример:
Вычислить $√^5{5}∙√^5{625}$
Решение:
Корень произведения равен произведению корней и наоборот: произведение корней с одинаковым показателем корня равно корню из произведения подкоренных выражений
$√^n{a}∙√^n{b}=√^n{a∙b}$
$√^5{5}∙√^5{625}=√^5{5∙625}=√^5{5∙5^4}=√^5{5^5}=5$
Ответ: $5$
2. Корень из дроби – это отдельно корень из числителя, отдельно из знаменателя
$√^n{{a}/{b}}={√^n{a}}/{√^n{b}}$, при $b≠0$
3. При возведении корня в степень, в эту степень возводится подкоренное выражение
$(√^n{a})^k=√^n{a^k}$
4. Если $а≥0$ и $n,k$ — натуральные числа, больше $1$, то справедливо равенство.
$√^n{√^k{a}}=√^{n∙k}a$
5. Если показатели корня и подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится.
$√^{n∙m}a^{k∙m}=√^n{a^k}$
6. Корень нечетной степени можно извлекать из положительных и отрицательных чисел, а корень четной степени – только из положительных.
7. Любой корень можно представить в виде степени с дробным (рациональным) показателем.
$√^n{a^k}=a^{{k}/{n}}$
Пример:
Найдите значение выражения ${√{9∙√^11{с}}}/{√^11{2048∙√с}}$ при $с>0$
Решение:
Корень произведения равен произведению корней
${√{9∙√^11{с}}}/{√^11{2048∙√с}}={√9∙√{√^11{с}}}/{√^11{2048}∙√^11{√с}}$
Корни из чисел мы можем извлечь сразу
${√9∙√{√^11{с}}}/{√^11{2048}∙√^11{√с}}={3∙√{√^11{с}}}/{2∙√^11{√с}}$
Далее применим формулу
$√^n{√^k{a}}=√^{n∙k}a$
${3∙√{√^11{с}}}/{2∙√^11{√с}}={3∙√^22{с}}/{2∙√^22{с}}$
Корни $22$ степени из $с$ мы сокращаем и получаем ${3}/{2}=1,5$
Ответ: $1,5$
Если у радикала с четным показателем степени мы не знаем знак подкоренного выражения, то при извлечении корня выходит модуль подкоренного выражения.
Пример:
Найдите значение выражения $√{(с-7)^2}+√{(с-9)^2}$ при $7 < c < 9$
Решение:
Если над корнем не стоит показатель, то это означает, что мы работаем с квадратным корнем. Его показатель равен двум, т.е. четный. Если у радикала с четным показателем степени мы не знаем знак подкоренного выражения, то при извлечении корня выходит модуль подкоренного выражения.
$√{(с-7)^2}+√{(с-9)^2}=|c-7|+|c-9|$
Определим знак выражения, стоящего под знаком модуля, исходя из условия $7 < c < 9$
Для проверки возьмем любое число из заданного промежутка, например, $8$
Проверим знак каждого модуля
$8-7>0$
$8-9<0$, при раскрытии модуля пользуемся правилом: модуль положительного числа равен самому себе, отрицательного числа — равен противоположному значению. Так как у второго модуля знак отрицательный, при раскрытии меняем знак перед модулем на противоположный.
$|c-7|+|c-9|=(с-7)-(с-9)=с-7-с+9=2$
Ответ: $2$
Свойства степеней с рациональным показателем:
1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.
$a^n∙a^m=a^{n+m}$
2. При возведении степени в степень основание остается прежним, а показатели перемножаются
$(a^n)^m=a^{n∙m}$
3. При возведении в степень произведения в эту степень возводится каждый множитель
$(a∙b)^n=a^n∙b^n$
4. При возведении в степень дроби в эту степень возводиться числитель и знаменатель
$({a}/{b})^n={a^n}/{b^n}$
Дроби
Практика: решай 6 задание и тренировочные варианты ЕГЭ по математике (профиль)
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Преобразования выражений»
Открытый банк заданий по теме преобразования выражений. Задания B9 из ЕГЭ по математике (профильный уровень)
Геометрические фигуры в пространстве: нахождение длины, площади, объема
Задание №927
Условие
Найдите значение выражения (1-log_315)(1-log_515).
Показать решение
Решение
Выполним преобразования:
(1-log_315)(1-log_515)= (1-log_3(3cdot5))(1-log_5(3cdot5)))= (1-(log_33+log_35))(1-(log_53+log_55))= (1-(1+log_35))(1-(log_53+1))= -log_35cdot(-log_53)= log_35cdotfrac{1}{log_35}= 1.
Ответ
1
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №926
Условие
Найдите -4cos2alpha, если cosalpha=-0,6.
Показать решение
Решение
Выполним преобразования:
-4cos2alpha= -4cdot(2cos^2alpha-1)= -4cdot(2cdot(-0,6)^2-1)= -4cdot(-0,28)= 1,12.
Ответ
1,12
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №925
Условие
Найдите значение выражения (16a^2-25)cdotleft ( frac{1}{4a-5}-frac{1}{4a+5} right )+a-13 при a=143.
Показать решение
Решение
Выполним преобразования:
(16a^2-25)cdotfrac{4a+5-(4a-5)}{(4a-5)(4a+5)}+a-13= (16a^2-25)cdotfrac{4a+5-4a+5}{(4a-5)(4a+5)}+a-13= frac{(4a)^2-5^2}{1}cdotfrac{10}{(4a-5)(4a+5)}+a-13= frac{(4a-5)(4a+5)cdot10}{(4a-5)(4a+5)}+a-13= 10+a-13= a-3= 143-3= 140.
Ответ
140
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №924
Условие
Найдите 2cosleft ( frac{7pi}{2}+alpha right ), если cosalpha=0,6 и alphainleft ( frac{7pi}{2}; 4pi right ).
Показать решение
Решение
Если alphainleft ( frac{7pi}{2}; 4pi right ), то sinalpha<0.
sinalpha= -sqrt{1-cos^2alpha}= -sqrt{1-(0.6)^2}= -sqrt{0,64}= -0,8.
2cosleft (frac{7pi}{2}+alpha right)= 2sinalpha= 2cdot(-0,8)= -1,6.
Ответ
-1,6
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №923
Условие
Найдите значение выражения ((4x+5y)^2-16x^2-25y^2):5xy.
Показать решение
Решение
Выполним преобразования:
((4x+5y)^2-16x^2-25y^2):5xy= (16x^2+40xy+25y^2-16x^2-25y^2):5xy= 40xy:5xy= 8.
Ответ
8
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №922
Условие
Найдите значение выражения 4log_3(log_5 125).
Показать решение
Решение
Выполним преобразования:
4log_3(log_5 5^3)=4log_3 3=4cdot1=4.
Ответ
4
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №921
Условие
Найдите значение выражения 19a^{10}a^{14}:(5a^{12})^2.
Показать решение
Решение
Выполним преобразования:
19a^{10}a^{14}:(5a^{12})^2= 19a^{10+14}:(5^2a^{12cdot2})= frac{19a^{24}}{25a^{24}}= 0,76.
Ответ
0,76
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №920
Условие
Найдите значение выражения frac{sqrt[3]{3}cdotsqrt[6]{3}}{sqrt3}.
Показать решение
Решение
По свойству корней выполняются равенства: sqrt[3]{3}=sqrt[6]{3^2}; sqrt[6]{3^2}=sqrt3.
Поэтому frac{sqrt[3]{3}cdotsqrt[6]{3}}{sqrt3}= frac{sqrt[6]{3^2}cdotsqrt[6]{3}}{sqrt3}= frac{sqrt[6]{3^3}}{sqrt3}= frac{sqrt3}{sqrt3}= 1.
Ответ
1
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №919
Условие
Найдите значение выражения 3^{0,74}cdot9^{0,13}.
Показать решение
Решение
Выполним преобразования:
3^{0,74}cdot(3^2)^{0,13}= 3^{0,74}cdot3^{0,26}= 3^{0,74+0,26}= 3^1= 3
Ответ
3
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №918
Условие
Найдите значение выражения sqrt{65^2-16^2}.
Показать решение
Решение
Используем формулу сокращенного умножения.
a^2-b^2=(a+b)(a-b)
Получим:
sqrt{65^2-16^2}=sqrt{(65+16)(65-16)}=sqrt{49cdot81}=7cdot9=63.
Ответ
63
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
Задание
8
#470
Уровень задания: Равен ЕГЭ
Найдите значение выражения (left(dfrac{2 — frac{1}{2}}{sqrt{2} + frac{1}{sqrt{2}}}right)^2).
[left(dfrac{2 — frac{1}{2}}{sqrt{2} + frac{1}{sqrt{2}}}right)^2 = left(dfrac{1,5}{sqrt{2}(1 + frac{1}{2})}right)^2 = left(dfrac{1,5}{sqrt{2}cdot 1,5}right)^2 = left(dfrac{1}{sqrt{2}}right)^2 = 0,5.]
Ответ: 0,5
Задание
9
#468
Уровень задания: Равен ЕГЭ
Найдите значение выражения ((3002^2 — 3000^2)cdotdfrac{1}{3001}).
[(3002^2 — 3000^2)cdotdfrac{1}{3001} = (3002 — 3000)(3002 + 3000)cdotdfrac{1}{3001} = 2cdot 6002cdotdfrac{1}{3001} = 2cdot 2 = 4.]
Ответ: 4
Задание
10
#466
Уровень задания: Равен ЕГЭ
Найдите значение выражения ((2017^2 — 2015^2)cdotdfrac{2}{2cdot 4032}).
[(2017^2 — 2015^2)cdotdfrac{2}{2cdot 4032} = (2017 — 2015)(2017 + 2015)cdotdfrac{2}{2cdot 4032} = 2cdot 4032cdotdfrac{2}{2cdot 4032} = 2.]
Ответ: 2
Задание
11
#467
Уровень задания: Равен ЕГЭ
Найдите значение выражения (0,001cdot(1234^2 — 234^2)).
[0,001cdot(1234^2 — 234^2) = dfrac{1}{1000}cdot(1234 — 234)(1234 + 234) = dfrac{1}{1000}cdot 1000cdot 1468 = 1468.]
Ответ: 1468
Задание
12
#1943
Уровень задания: Равен ЕГЭ
Найдите значение выражения (displaystyle frac{87^3 + 43^3}{87^2 — 87cdot43 + 43^2}).
[frac{87^3 + 43^3}{87^2 — 87cdot43 + 43^2} = frac{(87 + 43)cdot(87^2 — 87cdot43 + 43^2)}{87^2 — 87cdot43 + 43^2} = 87 + 43 = 130]
Ответ: 130
Задание
13
#2942
Уровень задания: Равен ЕГЭ
Найдите значение выражения (displaystyle frac{59^3 — 41^3}{18} +
59cdot41).
[begin{gathered}
frac{(59 — 41)(59^2 + 59cdot41 + 41^2)}{18} + 59cdot41 =
frac{18cdot(59^2 + 59cdot41 + 41^2)}{18} + 59cdot41 =\= 59^2 +
59cdot41 + 41^2 + 59cdot41 = 59^2 + 2cdot59cdot41 + 41^2 =\=
(59 + 41)^2 = 100^2 = 10,000end{gathered}]
Ответ: 10000
Задание
14
#2623
Уровень задания: Равен ЕГЭ
Найдите значение выражения
[dfrac{(sqrt7+sqrt{17})^2}{12+sqrt{119}}]
(Задача от подписчиков.)
Возведем в квадрат числитель по формуле ((a+b)^2=a^2+2ab+b^2):
[(sqrt7+sqrt{17})^2=(sqrt7)^2+2cdot sqrt7cdot sqrt{17}+(sqrt{17})^2=
7+2sqrt{7cdot 17}+17=24+2sqrt{119}=2(12+sqrt{119})]
Таким образом, все выражение примет вид:
[dfrac{2(12+sqrt{119})}{12+sqrt{119}}=2.]
Ответ: 2
Преобразование выражений
Теоретический материал
Рациональные выражения
Формулы сокращенного умножения многочленов
|
4. (a + b)(a2 – ab + b2) = a3 + b3. |
7. (a – b)3 = a3 – 3a2b + 3ab2 – b3. |
|
5. (a – b)(a2 + ab + b2) = a3 – b3. |
|
|
6. (a + b)3 = a3 + 3a2b + 3ab2 + b3. |
Формулы корней квадратного уравнения
Алгебраическое уравнение 2-й степени называют квадратным. Общий вид квадратного уравнения с одним неизвестным ax2 + bx + c = 0, где a 0.
-
Дискриминант: D = b2 – 4ac.
Если D
Если D ≥ 0, то 
2. Если b – четное число, то удобнее представить общую формулу в виде
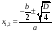

Формула разложения квадратного трехчлена на множители
ax2 + bx + c = a(x – x1)(x – x2), где x1 , x2 – корни квадратного трехчлена, a ≠ 0.
Теорема Виета
-
Если приведенное квадратное уравнение x2 + px + q = 0 имеет действительные корни, то
-
Если квадратное уравнение ax2 + bx + c = 0 (где a ≠ 0) имеет действительные корни, то
Верны и обратные утверждения.
Основные свойства степени ( x R, y R, a R, a 0, b R, b 0).
а) 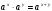
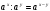
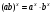
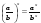


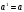

Иррациональные выражения
Определение 1. Корнем n—й степени из неотрицательного числа a (n = 2, 3, 4, 5, …) называют такое неотрицательное число, которое при возведении в степень n дает в результате число a.
Определение 2. Корнем нечетной степени n из отрицательного числа a (n = 3, 5,7, …) называют такое отрицательное число, которое при возведении в степень n дает в результате число a.
Определение 3. Если 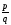
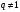


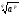

Свойства функции 
1) 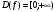
2) функция не является ни четной, ни нечетной;
3) функция возрастает на 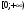
4) функция не ограничена сверху, ограничена снизу;
5) функция не имеет наибольшего значения; yнаим= 0;
6) функция непрерывна;
7) 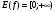
Свойства функции 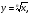
1) 
2) функция нечетна;
3) функция возрастает;
4) функция не ограничена ни сверху, ни снизу;
5) функция не имеет наибольшего и наименьшего значений;
6) функция непрерывна;
7) .
Свойства корня n—й степени (n = 2, 3, 4, 5, …) из неотрицательного числа ()
1) ; 2)
(
); 3)
;
4) ; 5)
; 6)
.
Замечания. , где
(в частности
).
, где
,
.
Теорема. При натуральном n уравнение равносильно системе
Логарифмы
Определение. Логарифм числа х по основанию а есть показатель степени, в которую надо возвести число а, чтобы получить х.
Тождество (где x 0, a 0 и a 1) называют основным логарифмическим тождеством.
Определение. Логарифмической функцией называется функция вида у = logx, где a 0, a 1.
Основные свойства логарифмической функции у = logx (a 0, a 1).
1. D(loga ) = R+ .
2. E(loga ) =R.
3. Логарифмическая функция на всей области определения возрастает при а 1 и убывает при 0 a
4. Основные свойства логарифмов.
4.1. При любых a 0 (a 1), b 0 (b 1), x 0, y 0, p R, k R верны равенства:
|
а) б) в) г) |
д) e) ж) |
|
4.2. При любых a 0 (a 1), b 0 (b 1), x ≠ 0, y ≠ 0, p N верны равенства: а) в) |
При решении логарифмических уравнений и неравенств используются теоремы, вытекающие из свойств монотонности логарифмической функции.
Теорема 1. Если , то
log f(x) = log
g(x)
Теорема 2. log (f(x)) = b f(x)= a
(a 0, a 1).
Теорема 3. Если a 1, то
log f(x) log
g(x)
Теорема 4. Если 0 a
log f(x) log
g(x)
1. ОГЭ, 1_31412. Найдите значение выражения . Ответ: −2.
2. ОГЭ, 1_337273. Найдите значение выражения . Ответ: 0,8.
3. ОГЭ, 1_287946. Найдите значение выражения . Ответ: 12,5.
4. ОГЭ, 21_311255. Упростите выражение . Ответ: 0,5.
5. ОГЭ, 21_311552. Один из корней уравнения 5x2 – 2x + 3p = 0 равен 1. Найдите второй корень. Ответ: − 0,6.
6. Найдите , если
, при
.
7. Найдите , если
.
8. Найдите , если
при
.
9. Найдите , если
.
10. Найдите при
.
11. Найдите , если
.
12. Найдите значение выражения .
13. Найдите значение выражения .
14. Найдите значение выражения при b = 6.
15. Найдите значение выражения при x = 3.
16. Найдите значение выражения .
17. Найдите корень уравнения: . Если уравнение имеет более одного корня, укажите меньший из них.
18. Найдите значение выражения .
19. Найдите значение выражения .
20. Найдите значение выражения .
21. Вычислите значение выражения: .
22. Решите уравнение .
23. Решите уравнение .
24. Решите уравнение .
25. Решите уравнение . Если уравнение имеет более одного корня, в ответе укажите меньший из них.
26. Найдите ошибку
|
|
|
|
x = – 1 c учетом О.Д.З. корней нет. Ответ: корней нет. |
Ответ: |
27. Решите уравнение . Ответ: 625.
Критерии оценивания задания 21 ОГЭ