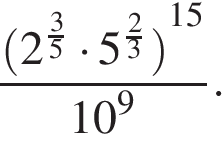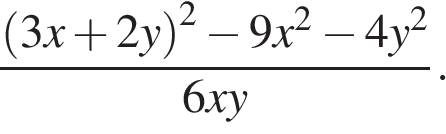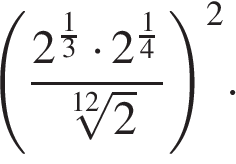Преобразование выражений егэ профиль проверочная работа - Помощь в подготовке к экзаменам и поступлению

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Преобразования выражений»

Открытый банк заданий по теме преобразования выражений. Задания B9 из ЕГЭ по математике (профильный уровень)

Геометрические фигуры в пространстве: нахождение длины, площади, объема

Задание №927

Условие

Найдите значение выражения (1-log_315)(1-log_515).

Показать решение

Решение

Выполним преобразования:

(1-log_315)(1-log_515)= (1-log_3(3cdot5))(1-log_5(3cdot5)))= (1-(log_33+log_35))(1-(log_53+log_55))= (1-(1+log_35))(1-(log_53+1))= -log_35cdot(-log_53)= log_35cdotfrac{1}{log_35}= 1.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №926

Условие

Найдите -4cos2alpha, если cosalpha=-0,6.

Показать решение

Решение

Выполним преобразования:

-4cos2alpha= -4cdot(2cos^2alpha-1)= -4cdot(2cdot(-0,6)^2-1)= -4cdot(-0,28)= 1,12.

Ответ

1,12

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №925

Условие

Найдите значение выражения (16a^2-25)cdotleft ( frac{1}{4a-5}-frac{1}{4a+5} right )+a-13 при a=143.

Показать решение

Решение

Выполним преобразования:

(16a^2-25)cdotfrac{4a+5-(4a-5)}{(4a-5)(4a+5)}+a-13= (16a^2-25)cdotfrac{4a+5-4a+5}{(4a-5)(4a+5)}+a-13= frac{(4a)^2-5^2}{1}cdotfrac{10}{(4a-5)(4a+5)}+a-13= frac{(4a-5)(4a+5)cdot10}{(4a-5)(4a+5)}+a-13= 10+a-13= a-3= 143-3= 140.

Ответ

140

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №924

Условие

Найдите 2cosleft ( frac{7pi}{2}+alpha right ), если cosalpha=0,6 и alphainleft ( frac{7pi}{2}; 4pi right ).

Показать решение

Решение

Если alphainleft ( frac{7pi}{2}; 4pi right ), то sinalpha<0.

sinalpha= -sqrt{1-cos^2alpha}= -sqrt{1-(0.6)^2}= -sqrt{0,64}= -0,8.

2cosleft (frac{7pi}{2}+alpha right)= 2sinalpha= 2cdot(-0,8)= -1,6.

Ответ

-1,6

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №923

Условие

Найдите значение выражения ((4x+5y)^2-16x^2-25y^2):5xy.

Показать решение

Решение

Выполним преобразования:

((4x+5y)^2-16x^2-25y^2):5xy= (16x^2+40xy+25y^2-16x^2-25y^2):5xy= 40xy:5xy= 8.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №922

Условие

Найдите значение выражения 4log_3(log_5 125).

Показать решение

Решение

Выполним преобразования:

4log_3(log_5 5^3)=4log_3 3=4cdot1=4.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №921

Условие

Найдите значение выражения 19a^{10}a^{14}:(5a^{12})^2.

Показать решение

Решение

Выполним преобразования:

19a^{10}a^{14}:(5a^{12})^2= 19a^{10+14}:(5^2a^{12cdot2})= frac{19a^{24}}{25a^{24}}= 0,76.

Ответ

0,76

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №920

Условие

Найдите значение выражения frac{sqrt[3]{3}cdotsqrt[6]{3}}{sqrt3}.

Показать решение

Решение

По свойству корней выполняются равенства: sqrt[3]{3}=sqrt[6]{3^2}; sqrt[6]{3^2}=sqrt3.

Поэтому frac{sqrt[3]{3}cdotsqrt[6]{3}}{sqrt3}= frac{sqrt[6]{3^2}cdotsqrt[6]{3}}{sqrt3}= frac{sqrt[6]{3^3}}{sqrt3}= frac{sqrt3}{sqrt3}= 1.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №919

Условие

Найдите значение выражения 3^{0,74}cdot9^{0,13}.

Показать решение

Решение

Выполним преобразования:

3^{0,74}cdot(3^2)^{0,13}= 3^{0,74}cdot3^{0,26}= 3^{0,74+0,26}= 3^1= 3

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №918

Условие

Найдите значение выражения sqrt{65^2-16^2}.

Показать решение

Решение

Используем формулу сокращенного умножения.

a^2-b^2=(a+b)(a-b)

Получим:

sqrt{65^2-16^2}=sqrt{(65+16)(65-16)}=sqrt{49cdot81}=7cdot9=63.

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Вариант 1 9. Вычисления и преобразования

1. Найдите значение выражения

2. Найдите значение выражения

3. Найдите , если

4. Найдите , если

5. Найдите значение выражения при

6. Найдите , если при

7. Найдите значение выражения

8. Найдите значение выражения

9. Найдите значение выражения

10. Найдите значение выражения

Вариант 2 9. Вычисления и преобразования

1. Найдите , если

2. Найдите значение выражения

3. Найдите значение выражения

4. Найдите значение выражения

5. Найдите значение выражения

6. Найдите значение выражения

7. Найдите значение выражения

8. Найдите значение выражения

9. Найдите значение выражения

10. Найдите значение выражения

Вариант 3 9. Вычисления и преобразования

1. Найдите значения выражения

2. Найдите , если и

3. Найдите значение выражения при

4. Найдите значение выражения

5. Найдите значение выражения при

6. Найдите значение выражения

7. Найдите значение выражения

8. Найдите значение выражения

9. Найдите , если При

10. Найдите значение выражения

Вариант 4 9. Вычисления и преобразования

1. Найдите значение выражения при

2. Найдите значение выражения

3. Найдите значение выражения

4. Найдите , если

5. Найдите если

6. Найдите значение выражения

7. Найдите значение выражения

8. Найдите значение выражения

9. Найдите значение выражения , если

10. Найдите значение выражения

Вариант 5 9. Вычисления и преобразования

1. Найдите значение выражения при

2. Найдите значение выражения при

3. Найдите значение выражения

4. Найдите значение выражения , если

5. Найдите , если и

6. Найдите , если и

7. Найдите , если

8. Найдите , если

9. Найдите , если

10. Найдите , если

Вариант 6 9. Вычисления и преобразования

1. Найдите значение выражения

2. Найдите значение выражения

3. Найдите значение выражения

4. Найдите значение выражения

5. Найдите значение выражения , если

6. Найдите значение выражения

7. Найдите значение выражения

8. Найдите значение выражения

9. Найдите значение выражения

10. Найдите значение выражения

Вариант 7 9. Вычисления и преобразования

1. Найдите значение выражения

2. Найдите значение выражения

3. Найдите значение выражения

4. Найдите значение выражения

5. Найдите значение выражения

6. Найдите значение выражения

7. Найдите значение выражения ( − )

8. Найдите значение выражения

9. Найдите значение выражения

10. Найдите значение выражения если и

Вариант 8 9. Вычисления и преобразования

1. Найдите значение выражения

2. Найдите значение выражения:

3. Найдите значение выражения

4. Найдите значение выражения

5. Найдите значение выражения

6. Найдите значение выражения

7. Найдите значение выражения

8. Найдите значение выражения

9. Найдите значение выражения

10. Найдите значение выражения

Вариант 9 9. Вычисления и преобразования

1. Найдите , если

2. Найдите значение выражения

3. Найдите значение выражения

4. Найдите значение выражения

5. Найдите значение выражения при

6. Найдите значение выражения

7. Найдите значение выражения

8. Найдите значение выражения при

9. Найдите значение выражения при

10. Найдите значение выражения при

Вариант 10 9. Вычисления и преобразования

1. Найдите значение выражения: при

2. Найдите значение выражения при

3. Найдите значение выражения

4. Найдите значение выражения

5. Найдите значение выражения

6. Найдите значение выражения

7. Найдите значение выражения

8. Найдите значение выражения

9. Найдите значение выражения

10. Найдите значение выражения

9. Вычисления и преобразования

Вариант 1

1
5
2
14
-0,5
0
6
2
23
1

Вариант 2

71
2
-1,5
-1,25
7
3
243
4
28
-56

Вариант 3

11,5
1,12
0,5
0,5
1
-40,5
24
14
1
-47

Вариант 4

0,75
3
2
0
0,04
-2
-5
5
-28
25

Вариант 5

4
2187
1
-28
0,6
-10
-2,5
7
-9
5

Вариант 6

25
12
49
2
12,8
7
12
1
59
-19

Вариант 7

-47
-1,5
59
-19
9,5
14,75
7
42
46
-3

Вариант 8

7
425
9
3
0,5
12
-0,5
4
0,5
121

Вариант 9

-8
4
0,5
121
333
243
80,625
16
-367
150

Вариант 10

7776
4
8
28
25
-0,5
1,5
1
-3
-1

Источник

проверить уровень математической подготовки учащихся 10 класса с позиций Единого Государственного экзамена.

Итоговая (годовая) контрольная работа по алгебре в 10 классе рассчитана на два астрономических часа. Контрольная работа содержит 12 заданий базового уровня, требующих краткого ответа, и два задания повышенного уровня, для которых следует привести полное решение. Задания соответствуют структуре заданий демонстрационной версии ЕГЭ 2015 базового уровня. К каждому заданию требуется дать краткий ответ, представленный в виде целого числа, промежутка и конечной десятичной дроби.

Каждое задание первой части оценивается одним баллом. Во второй части первое задание – два балла, второе – три балла. Вся работа оценивается семнадцатью баллами.

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ В ФОРМЕ ЕГЭ В 10 КЛАССЕ

ВАРИАНТ I

Найдите значение выражения:

Поступивший в продажу в январе мобильный телефон стоил 2400 рублей. В ноябре он стал стоить 1200 рублей. На сколько процентов снизилась цена на мобильный телефон в период с января по ноябрь?

Вычислите:

Решить уравнение:

Найдите сosα, если sinα= — 0,6 и .

Установите соответствие между величинами и их возможными значениями: к каждому элементу первого столбца подберите соответствующий элемент из второго столбца.

ВЕЛИЧИНЫ ВОЗМОЖНЫЕ ЗНАЧЕНИЯ

А) площадь почтовой марки 1) 362 кв. м

Б) площадь письменного стола 2) 1,2 кв. м

В) площадь Санкт-Петербурга 3) 1439 кв. км

Г) площадь волейбольной площадки 4) 5,2 кв. см

В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.

Ответ:

Найдите корень уравнения:

В чемпионате по гимнастике участвуют 75 спортсменок: 15 из Чехии, 30 из Словакии, остальные – из Австрии. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Австрии.

Выпускники 11 «А» класса покупают букеты цветов для последнего звонка: из 3 роз каждому учителю и из 11 роз классному руководителю и директору. Они собираются подарить букеты 20 учителям (включая директора и классного руководителя), розы покупаются по оптовой цене 35 рублей за штуку. Сколько рублей стоят все розы?

От пристани А к пристани В отправился с постоянной скоростью первый теплоход, а через 1 час после этого следом за ним со скоростью на 1 км/ч большей отправился второй. Расстояние между пристанями равно 420 км. Найдите скорость первого теплохода, если в пункт В оба теплохода прибыли одновременно. Ответ дайте в км/ч.

В прямоугольном параллелепипедеABCDA1B1C1D1 известно, что BB1=19, CD=16, BC=. Найдите длину отрезка MK, где M– середина ребра DC, K – середина ребра A1D1.

С1

Решить систему уравнений:

С2

Решить неравенство:

ИТОГОВАЯ КОНТРОЛЬНАЯ РАБОТА ПО МАТЕМАТИКЕ В ФОРМЕ ЕГЭ В 10 КЛАССЕ

ВАРИАНТ II

Найдите значение выражения : 1,4 + 3,6 ∙ .

Найдите значение выражения :

Налог на доходы составляет 13% от заработной платы. Заработная плата Ивана Кузьмича равна 13000 рублей. Какую сумму он получит после вычета налога на доходы? Ответ дайте в рублях.

Вычислите:

Решить уравнение:

Найдите сtgα, еслиcosα= — 0,6 и.

ВЕЛИЧИНЫ ВОЗМОЖНЫЕ ЗНАЧЕНИЯ

А) объём комнаты 1) 78 200

Б) объём воды в Каспийском море 2) 75

В) объём ящика для овощей 3) 50 л

Г) объём банки сметаны 4) 0,5 л

В таблице под каждой буквой, соответствующей величине, укажите номер её возможного значения.

Ответ:

Найдите корень уравнения:

В соревнованиях по толканию ядра участвуют 6 спортсменов из Великобрита-нии, 3 спортсмена из Франции, 6 спортсменов из Германии и 10 – из Италии. Порядок, в котором выступают спортсмены, определяется жребием. Найдите вероятность того, что спортсмен, выступающий последним, окажется из Франции.

Таксист за месяц проехал 10 000 км. Цена бензина 35 рублей за литр. Средний расход бензина на 100 км составляет 8 литров. Сколько рублей потратил таксист на бензин за этот месяц?

На изготовление 99 деталей первый рабочий затрачивает на 2 часа меньше, чем второй рабочий на изготовление 110 таких же деталей. Известно, что первый рабочий за час делает на 1 деталь больше, чем второй. Сколько деталей в час делает первый рабочий?

Длины сторон прямоугольника равны 8 и 6 см. Через точку O пересечения его диагоналей проведена прямая ОK, перпендикулярная его плоскости. Найдите расстояние от точки K до вершин прямоугольника, если ОK=12 см.

С1

Решить систему уравнений:

С2

Решитьнеравенство:

Проверочная работа по теме «Преобразование показательных и логарифмических выражений». 11 класс. Четыре варианта.

Автор: Алтунина Нина Сергеевна

Вариант
I

1.Представить
в виде многочлена:

а) (b –
5)(b – 4) – 3b(2b – 3);

б) 3x(x
– 2) – (x – 3)²;

в) 5(a +
1)² – 10a.

2.
Разложить на множители:

а)
3c³ – 75c;

б)
3x² + 6xy + 3y²;

в)
x³ + 8.

3.
Упростить выражение:

(y² + 6y)²
– y²(6 + 5y)(6 – 5y) – y²(12y – y²).

4.
Разложить на множители:

а) (a – b)²
– a²;

б) x³
+ y³ + 2xy(x + y).

5.
Доказать, что если из квадрата нечетного числа вычесть 1, то результат будет
делиться на 8.

6^*.
При любом натуральном n найдите остаток от деления выражения
(n + 1)(n + 5) –
(n – 2)(n + 2) на
6.

7^*.
Решите уравнение:

(2x – 1)(4x² + 2x + 1) –
8x(x² + 1) =
3x + 4.

Вариант
II

1.Представить
в виде многочлена:

а)
3c(4c – 5) –
(c – 8)(c – 7);

б)
(y – 5)²
– (5 – y)(5 + y);

в)
6(x – 2)²
+ 24x.

2.
Разложить на множители:

а)
49x – x³;

б)
7a² + 28ac + 28c²;

в)
m³ + 27.

3.
Упростить выражение:

(a²
+ 3a)² – (1 – a²)(a + 1)(1 – a)
– 5a(4a² + a).

4.
Разложить на множители:

а)
(x – y)²
– y²;

б)
c³ + d³ – 3cd(c + d).

5.
Доказать, что разность квадратов двух последовательных нечетных чисел делится
на 8.

6^*.
Докажите, что число
14⁴ – 165² + 138² – 107² кратно
31.

7^*.
Решите уравнение:

(2x + 1)(4x² – 2x + 1) – 4x(2x²
– 1) = 5x – 2.

Вариант
III

1.Представить
в виде многочлена:

а) 2a(5a
– 3) – (a – 2)(a – 4);

б) (x + 7)²
– (7 – x)(7 + x);

в) 3(n – 4)²
+ 15n.

2.
Разложить на множители:

а)
16y – y³;

б)
5m² – 40mn + 80n²;

в)
125 – d³.

3.
Упростить выражение:

(x² + 3x)²
– (x + 2)(2
– x)(4 + x²) – x²(8x – x²).

4.
Разложить на множители:

а)
с² – (с – d)²;

б)
a³ – b³ + 4ab(a² + ab + b²).

5.
Доказать, что разность квадратов двух нечетных чисел, одно из которых на
4больше другого, делится на 8.

6^*.
При любом натуральном n найдите остаток от деления выражения

(n + 2)(n + 4) –
(n – 1)(n + 1) на
6.

7^*.
Решите уравнение:

(x +
2)³ – x²(x + 5) –
(x + 1)(x – 1) = 0.

Вариант
IV

1.Представить
в виде многочлена:

а) (c – 9)(c
– 3) – 6c(3c – 2);

б) 4a(a
– 5) – (a – 10)²;

в) (b + 2)²
– 12b.

2.
Разложить на множители:

а)
7x³ – 28x;

б)
5a² – 10ab + 5b²;

в)
x³ – 8.

3.
Упростить выражение:

(x² – 2x)²
– (x – 2)(x + 2)(x² – 4) – 4x(7x – x²).

4.
Разложить на множители:

а)
m² – (m + n)²;

б)
x³ – y³ – 5x(x² + xy + y²).

5.
Доказать, что произведение двух последовательных четных чисел делится на 8.

6^*.
Докажите, что число

15⁴
– 186² + 173² – 134² кратно 39.

7^*.
Решите уравнение:

(x – 1)³
– x²(x – 4) – (x + 2)(x – 2) = 0.

Выражения, содержащие знак радикала (корень), называются иррациональными.

Арифметическим корнем натуральной степени $n$ из неотрицательного числа а называется некоторое неотрицательное число, при возведении которого в степень $n$ получается число $а$.

$(√^n{a})^n=a$

В записи $√^n{a}$, «а» называется подкоренным числом, $n$ — показателем корня или радикала.

Свойства корней $n$-ой степени при $а≥0$ и $b≥0$:

1. Корень произведения равен произведению корней

$√^n{a∙b}=√^n{a}∙√^n{b}$

Пример:

Вычислить $√^5{5}∙√^5{625}$

Решение:

Корень произведения равен произведению корней и наоборот: произведение корней с одинаковым показателем корня равно корню из произведения подкоренных выражений

$√^n{a}∙√^n{b}=√^n{a∙b}$

$√^5{5}∙√^5{625}=√^5{5∙625}=√^5{5∙5^4}=√^5{5^5}=5$

Ответ: $5$

2. Корень из дроби – это отдельно корень из числителя, отдельно из знаменателя

$√^n{{a}/{b}}={√^n{a}}/{√^n{b}}$, при $b≠0$

3. При возведении корня в степень, в эту степень возводится подкоренное выражение

$(√^n{a})^k=√^n{a^k}$

4. Если $а≥0$ и $n,k$ — натуральные числа, больше $1$, то справедливо равенство.

$√^n{√^k{a}}=√^{n∙k}a$

5. Если показатели корня и подкоренного выражения умножить или разделить на одно и то же натуральное число, то значение корня не изменится.

$√^{n∙m}a^{k∙m}=√^n{a^k}$

6. Корень нечетной степени можно извлекать из положительных и отрицательных чисел, а корень четной степени – только из положительных.

7. Любой корень можно представить в виде степени с дробным (рациональным) показателем.

$√^n{a^k}=a^{{k}/{n}}$

Пример:

Найдите значение выражения ${√{9∙√^11{с}}}/{√^11{2048∙√с}}$ при $с>0$

Решение:

Корень произведения равен произведению корней

${√{9∙√^11{с}}}/{√^11{2048∙√с}}={√9∙√{√^11{с}}}/{√^11{2048}∙√^11{√с}}$

Корни из чисел мы можем извлечь сразу

${√9∙√{√^11{с}}}/{√^11{2048}∙√^11{√с}}={3∙√{√^11{с}}}/{2∙√^11{√с}}$

Далее применим формулу

$√^n{√^k{a}}=√^{n∙k}a$

${3∙√{√^11{с}}}/{2∙√^11{√с}}={3∙√^22{с}}/{2∙√^22{с}}$

Корни $22$ степени из $с$ мы сокращаем и получаем ${3}/{2}=1,5$

Ответ: $1,5$

Если у радикала с четным показателем степени мы не знаем знак подкоренного выражения, то при извлечении корня выходит модуль подкоренного выражения.

Пример:

Найдите значение выражения $√{(с-7)^2}+√{(с-9)^2}$ при $7 < c < 9$

Решение:

Если над корнем не стоит показатель, то это означает, что мы работаем с квадратным корнем. Его показатель равен двум, т.е. четный. Если у радикала с четным показателем степени мы не знаем знак подкоренного выражения, то при извлечении корня выходит модуль подкоренного выражения.

$√{(с-7)^2}+√{(с-9)^2}=|c-7|+|c-9|$

Определим знак выражения, стоящего под знаком модуля, исходя из условия $7 < c < 9$

Для проверки возьмем любое число из заданного промежутка, например, $8$

Проверим знак каждого модуля

$8-7>0$

$8-9<0$, при раскрытии модуля пользуемся правилом: модуль положительного числа равен самому себе, отрицательного числа — равен противоположному значению. Так как у второго модуля знак отрицательный, при раскрытии меняем знак перед модулем на противоположный.

$|c-7|+|c-9|=(с-7)-(с-9)=с-7-с+9=2$

Ответ: $2$

Свойства степеней с рациональным показателем:

1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.

$a^n∙a^m=a^{n+m}$

2. При возведении степени в степень основание остается прежним, а показатели перемножаются

$(a^n)^m=a^{n∙m}$

3. При возведении в степень произведения в эту степень возводится каждый множитель

$(a∙b)^n=a^n∙b^n$

4. При возведении в степень дроби в эту степень возводиться числитель и знаменатель

$({a}/{b})^n={a^n}/{b^n}$

Лучшие репетиторы для сдачи ЕГЭ

Открытый банк заданий по теме выражения со степенями. Задания B9 из ЕГЭ по математике (профильный уровень)

Геометрические фигуры в пространстве: нахождение длины, площади, объема

Задание №921

Тип задания: 9
Тема:
Выражения со степенями

Условие

Найдите значение выражения 19a^{10}a^{14}:(5a^{12})^2.

Показать решение

Решение

Выполним преобразования:

19a^{10}a^{14}:(5a^{12})^2= 19a^{10+14}:(5^2a^{12cdot2})= frac{19a^{24}}{25a^{24}}= 0,76.

Ответ

0,76

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №919

Тип задания: 9
Тема:
Выражения со степенями

Условие

Найдите значение выражения 3^{0,74}cdot9^{0,13}.

Показать решение

Решение

Выполним преобразования:

3^{0,74}cdot(3^2)^{0,13}= 3^{0,74}cdot3^{0,26}= 3^{0,74+0,26}= 3^1= 3

Ответ

Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.

Задание №157

Тип задания: 9
Тема:
Выражения со степенями

Условие

Найдите значение выражения frac{g(x+5)}{g(x+3)}, если g(x)=3^x.

Показать решение

Решение

Чтобы решить эту задачу, необходимо представить числитель и знаменатель дроби в явном виде. Для этого возведем 3 в степень равную аргументу функции. Получим:

frac{g(x+5)}{g(x+3)}=frac{3^{x+5}}{3^{x+3}}= 3^{x+5-x-3}=3^2=9

Ответ

Задание №156

Тип задания: 9
Тема:
Выражения со степенями

Условие

Найдите значение выражения xcdot2^{-6x+3}cdot8^{2x} при x = 5.

Показать решение

Решение

Выполним преобразования:

xcdot2^{-6x+3}cdot8^{2x}= xcdot2^{-6x+3}cdotleft (2^3 right )^{2x}= xcdot2^{-6x+3}cdot2^{6x}= xcdot2^{-6x+3+6x}= xcdot2^3=8x

Подставим значение x = 5 из условия:

8x = 8cdot5=40

Ответ

Задание №132

Тип задания: 9
Тема:
Выражения со степенями

Условие

Найдите значение выражения 0,6^{tfrac{3}{11}}cdot5^{tfrac{10}{11}}cdot45^{tfrac{4}{11}}.

Показать решение

Решение

Выполним преобразования:

0,6^{tfrac{3}{11}}cdot5^{tfrac{10}{11}}cdot45^{tfrac{4}{11}}= left (frac35 right )^{tfrac{3}{11}}cdot5^{tfrac{10}{11}}cdot(5cdot9)^{tfrac{4}{11}}= 3^{tfrac{3}{11}}cdot5^{-tfrac{3}{11}}cdot5^{tfrac{10}{11}}cdot5^{tfrac{4}{11}}cdotleft (3^2 right )^{tfrac{4}{11}}= 3^{tfrac{3}{11}+tfrac{8}{11}}cdot5^{-tfrac{3}{11}+tfrac{10}{11}+tfrac{4}{11}}= 3cdot5=15.

Ответ

Лучшие репетиторы для сдачи ЕГЭ

Источник

Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых нужно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11. Или почти всю.

Например, задание №6 Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических. Задачи на определение модуля и понятие функции. В общем, типов задач здесь множество, по всему курсу алгебры.

И помните, что в ответе в заданиях первой части Профильного ЕГЭ по математике у вас должны получаться целые числа или конечные десятичные дроби.

Дробно-рациональные выражения. Формулы сокращенного умножения

Темы для повторения: Формулы сокращенного умножения, Приемы быстрого счета

Если вам встретится такое задание на ЕГЭ – значит, повезло!

1. Найдите значение выражения $frac{2,88cdot 44,5}{0,288cdot 4,45}.$

Не спешите перемножать десятичные дроби. Посмотрите на задачу внимательно.

$frac{2,88cdot 44,5}{0,288cdot 4,45}=frac{2,88cdot 44,5}{2,88cdot 0,445}=frac{44,5}{0,445}=100.$

Первый множитель в знаменателе умножили на 10, а второй поделили на 10, просто передвинув запятую.

Ответ: 100.

2. Найдите значение выражения $7frac{9}{13}:frac{5}{13}.$

$7frac{9}{13}:frac{5}{13}=frac{100}{13}cdot frac{13}{5}=20.$

Ответ: 20.

Корни и степени. Иррациональные выражения

Темы для повторения: Арифметический квадратный корень.

Арифметический квадратный корень из числа — это такое неотрицательное число, квадрат которого равен .

$left ( sqrt{a} right )^{2}=a;;sqrt{a}geq 0;;ageq 0$ .

3. Вычислите .

Применили одну из формул сокращенного умножения.

Ответ: 8.

4. Вычислите:

Упростим множители:

$=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7} right )^{2}+2sqrt{3}cdot sqrt{7}+left ( sqrt{3} right )^{2}}=$

$=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7}+sqrt{3}right )^{2}}=2left ( sqrt{7}-sqrt{3} right )left ( sqrt{7}+sqrt{3} right )=$

Ответ: 8.

Действия со степенями

Темы для повторения:
Вспомним правила действий со степенями.

$a^{m}cdot a^{n}=a^{m+n}.$

$frac{a^{m}}{a^{n}}=a^{m-n}.$

$left ( a^{m} right )^{n}=left ( a^{n} right )^{m}=a^{mn}.$

$a^{n}b^{n}=left ( ab right )^{n}.$

$frac{a^{n}}{b^{n}}=left ( frac{a}{b} right )^{n}.$

5. Найдите значение выражения: $frac{a^{8,9}}{a^{4,9}}$ при a=4.

$frac{a^{8,9}}{a^{4,9}}=a^{8,9-4,9}=a^{4}=4^{4}=256.$

Применили формулу частного степеней $frac{a^{m}}{a^{n}}=a^{m-n}.$

Ответ: 256.

6. Вычислите $left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}.$

$left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}=left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{2^{frac{1}{12}}} right )^{2}=left ( 2^{frac{1}{3}+frac{1}{4}-frac{1}{12}} right )^{2}=left ( 2^{frac{4}{12}+frac{3}{12}-frac{1}{12}} right )^{2}=$

$=left (2^{frac{1}{2}} right )^{2}=2.$

Ответ: 2.

7. Вычислите $frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}$ , если .

Спокойно, не пугаемся. И конечно, не спешим подставлять значение m=3,7. Сначала упростим выражение.

$frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}=frac{5m^{30}+13m^{30}}{4m^{30}}=frac{18m^{30}}{4m^{30}}=4,5.$

Ответ: 4,5.

8. Вычислите $0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}.$

$0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}=left ( frac{3}{4} right )^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot left ( 3cdot 4 right )^{frac{7}{8}}=frac{3^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 3^{frac{7}{8}}cdot 4^{frac{7}{8}}}{4^{frac{1}{8}}}=3cdot 4=12.$

Применили формулу для произведения степеней: $a^{m}cdot a^{n}=a^{m+n}.$

Ответ: 12.

9. Вычислите $frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}.$

$frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}=frac{3^{frac{1}{28}}cdot 3cdot 3^{frac{1}{21}}}{3^{frac{1}{12}}}=3^{frac{1}{28}+1+frac{1}{21}-frac{1}{12}}=3^{frac{3}{84}+1+frac{4}{84}-frac{7}{84}}=3.$

Записали корни в виде степеней (это удобно!) и применили формулу произведения степеней.

Ответ: 3.

Логарифмические выражения

Темы для повторения:
Логарифмы

Логарифм положительного числа по основанию — это показатель степени, в которую надо возвести , чтобы получить .

$log _{a}b=cLeftrightarrow a^{c}=b$ .

При этом > 0, > 0, aneq 1.

Основные логарифмические формулы:

Основное логарифмическое тождество: $boldsymbol{log _{a}a^{c}=c, ; a^{log _{a}b}=b}.$

Логарифм произведения равен сумме логарифмов: $boldsymbol{log _{a}left ( bc right )=log _{a}b+log _{a}c}.$

Логарифм частного равен разности логарифмов: $boldsymbol{log _{a}left ( frac{b}{c} right )=log _{a}b-log _{a}c}.$

Формула для логарифма степени: $boldsymbol{log _{a}b^{m}=mlog_{a}b}.$

Формула перехода к новому основанию: $boldsymbol{log _{a}b=frac{1}{log _{b}a},; log _{a}b=frac{log _{c}b}{log _{c}a}}.$

10. Вычислите: $log _{5}7cdot log _{7}25$ .

$log _{5}7cdot log _{7}25=log _{5}7cdot log _{7}5^{2}=2log _{5}7cdot log _{7}5=2.$

Снова формула перехода к другому основанию.

$log _{a}b=frac{1}{log _{b}a}$ , поэтому
$log _{a}bcdot log _{b};a=1.$

11. Найдите $log _{a}frac{a^{6}}{b^{4}}$ , если $log _{a}b=-2$ .

$log _{a}frac{a^{6}}{b^{4}}=log _{a}a^{6}-log _{a}b^{6}=6-4log _{a}b=6-4cdot left ( -2 right )=6+8=14.$

12. Найдите значение выражения $frac{log _{2}80}{3+log _{2}10}$ .

$frac{log _{2}80}{3+log _{2}10}=frac{log _{2}left (8cdot 10 right )}{3+log _{2}10}=frac{log _{2}8+log _{2}10}{3+log _{2}10}=frac{3+log _{2}10}{3+log _{2}10}=1.$

13. Найдите значение выражения $frac{log _{9}sqrt[10]{8}}{log _{9}8}$ .

$frac{log _{9}sqrt[10]{8}}{log _{9}8}=frac{log _{9}8^{frac{1}{10}}}{log _{9}8}=frac{1}{10}=0,1$ .

14. Найдите значение выражения $left ( 1-log _{3}18 right )left ( log _{6}54 -1right )$ .

$left ( 1-log _{3}18 right )left ( log _{6}54 -1right )=-left ( log _{3}18-log _{3}3 right )cdot left ( log _{6}54-log _{6}6 right )=-log _{3}6cdot log _{6}9=-2log _{3}6cdot log _{6}3=-2.$

Тригонометрия. Формулы тригонометрии и формулы приведения

Темы для повторения:
Тригонометрический круг.
Формулы тригонометрии.
Формулы приведения.

15. Вычислите: $44sqrt{3}tgleft ( -480^{circ} right ).$

$44sqrt{3}tgleft ( -480^{circ} right )=44sqrt{3}cdot frac{sin left ( -480^{circ} right )}{cos left ( -480^{circ} right )}=-44sqrt{3}cdot frac{sin 480^{circ}}{cos 480^{circ}}=-44sqrt{3}cdot frac{sin 120^{circ}}{cos 120^{circ}}=-44sqrt{3}cdot frac{sqrt{3}}{2}:left ( -frac{1}{2} right )=132.$

16. Найдите , если $sin alpha =-frac{2sqrt{2}}{3}$ и $alpha in left ( frac{3pi }{2};;2pi right )$ .

$cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{2sqrt{2}}{3} right )^{2}=1-frac{8}{9}=frac{1}{9}.$

Т.к. $alpha in left ( frac{3pi }{2};;2pi right )$ , то $cos alpha =frac{1}{3}.$
$3cos alpha =3cdot frac{1}{3}=1.$

17. Найдите , если $sin alpha =-frac{1}{sqrt{5}}$ и

$cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{1}{sqrt{5}} right )^{2}=1-frac{1}{5}=frac{4}{5}.$

Т.к. , то
$cos alpha =frac{2}{sqrt{5}}.$

$tgalpha =frac{sin alpha }{cos alpha }=-frac{1}{sqrt{5}}:frac{2}{sqrt{5}}=-2.$

18. Найдите значение выражения: $frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}.$

$frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{13cdot 2sin 76^{circ}cdot cos 76^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{26sin 76^{circ}}{cos 14^{circ}}=frac{26sin left ( 90^{circ}-14^{circ} right )}{cos 14^{circ}}=$

$=frac{26cos 14^{circ}}{cos 14^{circ}}=26.$

Применили формулу приведения.

19. Упростите выражение: $frac{3cos(pi - beta)+sin(frac{pi}{2}+beta)}{cos(beta+3pi)}.$

$frac{3cos left ( pi -beta right )+sin left ( frac{pi }{2}+beta right )}{cos left ( beta +3pi right )}=frac{-3cos beta +cos beta }{-cos beta }=frac{-2cos beta }{-cos beta }=2.$

Применили формулу приведения.

20. Найдите , если .

$2cos 2alpha =2left ( 1-2sin ^{2}alpha right )=2-4sin ^{2}alpha =2-4cdot left ( -0,7 right )^{2}=0,04.$

21. Вычислите $frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }$ , если

$frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }=frac{1-cos ^{2}alpha +sin ^{2}alpha +2sin alpha cos alpha }{1+cos ^{2}alpha -sin ^{2}alpha +2sin alpha cos alpha }=$

$=frac{2sin ^{2}alpha +2sin alpha cos alpha }{2cos ^{2}alpha +2sin alpha cos alpha }=frac{sin alpha left ( sin alpha +cos alpha right )}{cos alpha left ( cos alpha +sin alpha right )}=frac{sin alpha }{cos alpha }=tgalpha =0,3.$

Алгебраические выражения, корни, степени и логарифмы. И еще тригонометрия. Это всё, что может встретиться в задании 6 Профильного ЕГЭ по математике?

Оказывается, и это не всё! Еще нужно знать, что такое модуль. И как найти $sqrt{a^{2}}$ .

Другие типы заданий

Темы для повторения:
Модуль числа.
Что такое функция.

22. Найдите значение выражения
$sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}}$ при .

Запомним: $sqrt{a^{2}}=left | a right |.$

$sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}}=left | a-2 right |+left | a-4 right |$ .

Если , то и .

При этом и .

При получаем: .

Ответ: 2.

23. Найдите значение выражения

$x+sqrt{x^{2}-24x+144}$ при xleq 12 .

При xleq 12 получим:

$x+sqrt{x^{2}-24x+144}=x+sqrt{left ( x-12 right )^{2}}=x+left | x-12 right |=x+12-x=12.$

Ответ: 12.

24. Найдите $frac{gleft ( 5-x right )}{gleft ( 5+x right )}$ , если , при .

Что такое ? Это функция, каждому числу ставящая в соответствие число . Например, ;

Тогда:

Заметим, что .

Значит, при
$frac{gleft ( 5-x right )}{gleft ( 5+x right )}=1$ .

25. Найдите $frac{pleft ( b right )}{pleft ( frac{1}{b} right )}$ , если $pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ , при .

$pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ — функция, каждому числу b ставящая в соответствии число
$left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right )$ .

Тогда при bneq 0.

$pleft ( frac{1}{b} right )=left ( frac{1}{b}-9b right )left ( -frac{9}{b} +bright )=left ( b-frac{9}{b} right )left (-9b +frac{1}{b} right )=pleft ( b right )$ , и значение выражения $frac{pleft ( b right )}{pleft ( frac{1}{b} right )}$ равно 1.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 6 ЕГЭ по математике. Вычисления и преобразования» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

09
Июл 2013

Категория: Тесты по темам

Елена Репина
2013-07-09
2021-06-18

Разбор заданий, аналогичных заданиям теста, смотрите здесь.

Автор: egeMax |

Нет комментариев

Чтобы не потерять страничку, вы можете сохранить ее у себя:

Печать страницы

Похожие статьи на сайте…

Тест по задачам №6 «Равнобедренный треугольник. Вычисление углов и длин»
Тест. Преобразование тригонометрических выражений
Тест по Задачам №3. Прямоугольник
Тест по задачам №8. Конус. Цилиндр
Тест по задачам №6. Параллелограмм
Тест по задачам №9 «Преобразование иррациональных выражений»

Добавить комментарий

Материалы для подготовки к ЕГЭ
Рубрики
- 01 Геометрия (13)
- 02 Стереометрия (9)
- 03 Теория вероятностей ч.1 (1)
- 04 Теория вероятностей ч.2 (1)
- 05 Простейшие уравнения (5)
- 06 Вычисления (5)
- 07 Производная, ПО (4)
- 08 «Прикладные» задачи (5)
- 09 Текстовые задачи (7)
- 10 Графики функций (7)
- 11 Исследование функции (2)
- 12 (С1) Уравнения (78)
- 13 (С2) Стереометр. задачи (94)
- 14 (С3) Неравенства (89)
- 15 (С4) Практич. задачи (71)
- 16 (С5) Планиметр. задачи (86)
- 17 (С6) Параметры* (79)
- 18 (С7) Числа, их свойства (38)
- A1 Простейшие текст/задачи (нет в ЕГЭ-22) (3)
- A2 Читаем графики (нет в ЕГЭ-22) (1)
- Видеоуроки (44)
- ГИА (11)
  - II часть (11)
- ЕГЭ (диагностич. работы) (70)
- Иррациональные выражения, уравнения и неравенства (15)
- Логарифмы (39)
- МГУ (12)
- Метод интервалов (4)
- Метод рационализации (18)
- Модуль (9)
- Параметр (40)
- Переменка (5)
- Планиметрия (60)
- Показательные выражения, уравнения и неравенства (8)
- Разложение на множители (1)
- Рациональные выражения, уравнения и неравенства (10)
- Справочные материалы (92)
- Стереометрия (52)
- Т/P A. Ларина (443)
- Текстовые задачи (12)
- Теория чисел (2)
- Тесты по темам (80)
- Тригонометрические выражения, уравнения и неравенства (43)
- Функции и графики (10)
Дружественные сайты
Сайт А. Ларина
ЕгэТренер – О. Себедаш
Математика?Легко!
Егэ? Ок! – И. Фельдман
Свежие записи
- Тест «Гиперболы»
- Тест. Графики функций. Комбинированные задачи
- 10. Графики функций. Комбинированные задачи
- Тест. Тригонометрические функции
- 10. Тригонометрическая функция
- Тест. Кусочно-линейная функция
- 10. Кусочно-линейная функция
Архивы Архивы

Источник