Презентации по подготовке к егэ по математике профильный уровень

Слайд 1

17 .02 Подготовка к ЕГЭ

Слайд 2

Задание 1. 1. Система навигации самолёта информирует пассажира о том, что полёт проходит на высоте 37 000 футов. Выразите высоту полёта в метрах. Считайте, что 1 фут равен 30,5 см.

Слайд 3

Решение. Переведем высоту из футов в сантиметры: 37 000 · 30,5 = 1 128 500 см. Переведем высоту из сантиметров в метры: 1 128 500 : 100 = 11 285 м. Следовательно, полет проходит на высоте 11 285 метров. Ответ: 11 285

Слайд 4

Задание 2. На рисунке жирными точками показана среднесуточная температура воздуха в Бресте каждый день с 6 по 19 июля 1981 года. По горизонтали указываются числа месяца, по вертикали — температура в градусах Цельсия. Для наглядности жирные точки соединены линией. Определите по рисунку разность между наибольшей и наименьшей среднесуточными температурами за указанный период. Ответ дайте в градусах Цельсия.

Слайд 5

Решение. Из графика видно, что наибольшая и наименьшая температура за указанный период составляла 26 °C и 16 °C соответственно (см. рисунок). Их разность равняется 10 °C. Ответ: 10.

Слайд 6

Задание 3

Слайд 7

Задание 3

Слайд 8

Задание 4 Какова вероятность того, что случайно выбранный телефонный номер оканчивается двумя чётными цифрами? Решение. Вероятность того, что на одном из требуемых мест окажется чётное число равна 0,5. Следовательно, вероятность того, что на двух местах одновременно окажутся два чётных числа равна 0,5 · 0,5 = 0,25. Ответ: 0,25

Слайд 9

Задание 5

Слайд 10

Задание 6

Слайд 11

Задание 7

Слайд 12

Задание 8

Слайд 14

Задание 9

Слайд 15

Задание 10

Слайд 16

Задание 11.

Слайд 17

Задание 12

Слайд 18

Задание 13

Слайд 20

Задание 15

1.

ПРАКТИКУМ. ПРОФИЛЬНАЯ МАТЕМАТИКА. ЕГЭ 2022.
ЗАДАЧА 9. ГРАФИКИ ФУНКЦИЙ
Лектор: Тыкынаева Оксана Павловна
учитель математики
МОБУ Якутский городской лицей

2.

3.

Ответ : -10

4.

5.

Ответ : -7

6.

7.

Ответ: 31

8.

9.

Ответ: 26

10.

11.

Ответ: 48

12.

13.

Ответ: 0,75

14.

15.

Ответ: -15

16.

17.

Ответ: 0,15

18.

19.

Ответ: 14

20.

21.

Ответ: 1

22.

23.

Ответ: 9

24.

25.

Ответ: 1,5

26.

27.

Ответ: -1

28.

29.

Ответ: 2,5

30.

31.

Ответ: -1,5

32.

33.

Ответ: -0,1

34.

35.

Ответ: -20

36.

37.

Ответ: 2

38.

39.

Ответ: 1,5

40.

41.

Ответ: 5

42.

43.

Ответ: -7

44.

45.

46.

47.

Ответ:15

48.

49.

Ответ:1

50.

51.

Ответ: х=2

52.

53.

Ответ: 5

Презентация к уроку — практикуму по теме «Планиметрия», ЕГЭ, профильный уровень, задание №6. Презентацию можно использовать на уроках повторения, систематизации знаний при подготовке к ЕГЭ по математике. В презентации рассмотрены задачи с параллелограммом, прямоугольником, ромбом и трапецией из открытого банка заданий ЕГЭ по математике (сайт ФИПИ). В конце представлен тест для проверки знаний по теме.

Опубликовано 25.04.17 в 20:42 в группе «Математика — это интересно!»

В
данной
работе
предлагаются
решения
сложных
заданий
(№13
—
№19)
ЕГЭ-2021
по
математике.
Представленный
здесь
материал
предназначен
для
подготовки
к
ЕГЭ
учащихся,
имеющих
навыки
в
решении
заданий
подобного
уровня
сложности.

Задания
№13,
№15,
№17
могут
быть
предложены
сильным
учащимся
обычных
классов,
а
вот
задания
№14,
№16,
№18,
№19
целесообразно
решать
с
учащимися
физико-
математических
классов,
причем
задание
№19
под
буквой
«в»
под
силу
только
тем,
кто
имеет
определенную
подготовку
в
решении
олимпиадных
задач.

Для
оформления
всех
решений
использована
мультимедиа
презентация,
где
материал
представлен
наглядно
в
ярком,
интересном
и
доступном
виде,
что
для
учителя
и
учащихся
будет
ценно
и
полезно.
Эту
презентацию
можно
применять
как
на
уроке,
так
и
для
индивидуальной
работы.

Условия
заданий
и
методические
рекомендации
по
их
решению.

№13.

а)
Решите
уравнение
Решите
уравнение

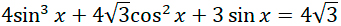
б)
Укажите
корни
этого
уравнения,
принадлежащие
отрезку

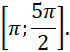
Это
задание
считается
одним
из
самых
решаемых
среди
заданий
второй
части
ЕГЭ.
Применяя
основное
тригонометрическое
тождество,
получаем
в
левой
части
данного
уравнения
тригонометрическое
выражение
относительно,
которое
можно
способом
группировки
разложить
на
множители.

Решить
получившиеся
простейшие
тригонометрические
уравнения
предлагается
с
помощью
числовой
окружности.
Важно,
чтобы
учащиеся
имели
хорошие
навыки
в
работе
с
этой
математической
моделью.
Тогда
и
отбор
корней
лучше
всего
сделать
на
числовой
окружности.

№14.

В
правильной
четырёхугольной
пирамиде
SABCD
сторона
основания
AD
равна
14,
высота
SН
равна
6.
Точка
К
—
середина
бокового
ребра
SD.
Плоскость
AKB
пересекает
боковое
ребро
SC
в
точке
P.

а)
Докажите,
что
площадь
четырёхугольника
CDKP
составляет
¾
площади
треугольника
SCD.

б)
Найдите
объем
пирамиды
ACDKP.

Стереометрическая
задача
является
для
учащихся
одной
из
сложных.
В
лучшем
случае
учащимися
выполняется
только
первая
часть
на
доказательство,
тогда,
как
вторая
часть
задачи
под
силу
лишь
не
многим.

Решение
второй
части
задачи
предлагается
тремя
способами:

• применением
  классического
  определения
  расстояния
  от
  точки
  до
  плоскости;
• методом
  координат;
• методом
  объёмов.

№15.

Решите
неравенство

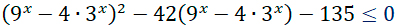
Данное
неравенство
достаточно
хорошего
уровня
сложности.
Его
решение
возможно:

• методом
  замены
  переменной,
  причем
  эту
  замену
  приходится
  выполнять
  дважды,
  что
  в
  целом
  усложняет
  решение;
• методом
  замены
  множителей,
  которому
  желательно
  обучать
  учащихся,
  так
  как
  в
  некоторых
  случаях,
  а
  именно
  в
  этом
  неравенстве
  он
  приводит
  к
  более
  простому
  решению.

№16.

Точки
A,
B,
C,
D
и
Е
лежат
на
окружности
в
указанном
порядке,
причем
AE
=
ED
=
CD,
а
прямые
AC
и
BE
перпендикулярны.
Отрезки
AC
и
BD
пересекаются
в
точке
T.

а)
Докажите,
что
прямая
EC
пересекает
отрезок
TD
в
его
середине.

б)
Найдите
площадь
треугольника
ABT,
если
BD
=
6,
AE
=

.

Данная
планиметрическая
задача
решается
здесь
двумя
разными
способами.
Здесь
важно
увидеть
свойства
различных
геометрических
фигур,
которые
позволяют
выбрать
то
или
иное
решение
задачи.

№17.

В
июле
2025
года
планируется
взять
кредит
в
банке
на
сумму
600
тысяч
рублей
на
6
лет.
Условия
его
возврата
таковы:

—
в
январе
2026,
2027,
2028
годов
долг
возрастает
на
20%
по
сравнению
с
концом
предыдущего
года;

—
в
январе
2029,
2030,
2031
годов
долг
возрастает
на
r%
по
сравнению
с
концом
предыдущего
года;

—
с
февраля
по
июнь
каждого
года
необходимо
выплатить
часть
долга;

—
в
июле
каждого
года
долг
должен
быть
на
одну
и
ту
же
величину
меньше
долга
на
июль
предыдущего
года;

Известно,
что
общая
сумма
выплат
после
полного
погашения
кредита
составит
984
тысячи
рублей.
Найдите
r.

Эта
задача
на
дифференцированный
платеж.
В
работе
предлагается
табличный
способ
решения
задачи.
Все
величины
и
данные,
и
искомые
обозначаются
переменными,
устанавливается
между
ними
связь,
а
числовые
значения
подставляются
в
самом
конце,
чтобы
получить
уравнение
с
одной
переменной
и
решить
его.

№18

Найдите
все
значения

а,
при
каждом
из
которых
имеет
ровно
два
различных
корня
уравнение

.

Это
самое
сложное
задание
данной
работы.
Его
решение
предлагается
двумя
способами:

• аналитическим,
  где
  находятся
  корни
  данного
  уравнения,
  содержащие
  параметр,
  и
  проверяются
  условия
  их
  принадлежности
  ОДЗ
  и
  совпадения;
• координатно-параметрическим
  в
  системе
  
  xOa.

№19.

Отношение
трёхзначного
натурального
числа
к
сумме
его
цифр
—
целое
число.

а)
Может
ли
это
отношение
быть
равным
55?

б)
Может
ли
это
отношение
быть
равным
87?

в)
Какое
наименьшее
значение
может
принимать
это
отношение,
если
первая
цифра
трёхзначного
числа
равна
7?

В
этой
задаче
вполне
можно
решить
первые
два
пункта.

В
пункте
а)
достаточно
привести
пример,
то
есть
можно
просто
подобрать
числа,
удовлетворяющие
условию
задачи.

В
пункте
б)
необходимо
обоснованное
доказательство
того,
что
такого
отношения
не
может
быть.

Решение
в
пункте
в)
сложное,
здесь
применяется
метод:
оценка
плюс
пример.