Презентации можно использовать учителям и учащимся при подготовке к защите индивидуальных итоговых проектов в 9 классах
Просмотр содержимого презентации
«¥«¨ª¨¥ ¬ ⥬ ⨪¨ ¤à¥¢®áâ¨.»
Великие математики древности
Проект ученицы 9 класса Г
Кочетковой Ольги
Руководитель проекта:
Мамасуева Татьяна Парфирьевна
Цель, задачи, актуальность
Цель: изучение биографии великих математиков и знакомство с самыми интересными фактами их жизни.
Задачи:
1.Узнать какие существовали математики в древности. 2.Узнать какие у них были самые интересные или самые известные труды.
Актуальность: мой проект полезен в первую очередь для учеников, потому что это интересно. Кроме того каждый человек должен знать великих людей в лицо, и знать почему их называют великими.
Содержание
1.Введение.
2.Аполлоний Пергский.
3.Аристотель.
4.Архимед.
5.Гиппарх.
6.Демокрит.
7.Пифагор.
8.Платон.
9.Фалес.
10.Эратосфен
11. Птолемей
12.Вывод
Аполлоний Пергский (262-190 гг. до н. э.)
Труды:
1.Труд о конических сечениях.
2.Отсечение отношения в двух книгах, содержащих 180 теорем.
3.Отсечение площади в двух книгах, содержащих 124 теоремы.
4.Определенное сечение в двух книгах, содержащих 83 теоремы.
5.Вставки в двух книгах, содержащих 125 теорем.
6.Касания в двух книгах, содержащих 60 теорем.
Аристотель ( 384-322 гг. до н.э.)
Философские учения:
1.Учение о четырёх причинах.
2.Акт и потенция.
3.Категории философии.
4.Бог как перводвигатель, как абсолютное начало всех начал.
5.Идея души.
6.Космология Аристотеля.
7.Учение о государстве.
Архимед Сиракузский ( 287-212 гг. до н. э.)
1.Ввел в механику такое понятие, как центр тяжести .
2.Построил планетарий, где можно наблюдать движение пяти планет.
3.Архимед открыл полуправильные многогранники, которые теперь носят его имя.
Лучшим своим открытием он считал определение поверхности и объёма шара, поэтому на своей могиле он просил выбить шар, вписанный в цилиндр. Так, даже думая о смерти, он не может забыть о математике .
Гиппарх Никейский ( 190-120 гг. до н. э.)
Вклад в науку:
1.Гиппарх составил первый в Европе звёздный каталог.
2. Открытие предварения равноденствий, или астрономической прецессии.
3.Гиппарх внёс существенный вклад в усовершенствование календаря.
4.Вычисление расстояний до Луны и Солнца и их размеров
Демокрит Абдерский ( 460-370 гг. до н. э.)
1.Демокрит развивает общеэллинское понятие меры, отмечая, что мера — это соответствие поведения человека его природным возможностям и способностям.
2.Демокрит — сторонник концепции множественности миров.
Пифагор Самосский ( 570-490 гг. до н. э. )
Античные авторы нашей эры отдают Пифагору авторство известной теоремы: квадрат гипотенузы прямоугольного треугольника равняется сумме квадратов катетов.
В современном мире Пифагор считается великим математиком и космологом древности, однако ранние свидетельства до III в. до н. э. не упоминают о таких его заслугах. Как пишет Ямвлих про пифагорейцев: «У них также был замечательный обычай приписывать всё Пифагору и нисколько не присваивать себе славы первооткрывателей, кроме, может быть, нескольких случаев».
Платон (между 429 и 427- 347 гг. до н. э.)
Учения Платона:
1.Диалектика Платона.
2.Политико-правовое учение Платона.
3.Учение о познании.
4.Учение о душе.
![Фалес (640/624 — 548/ 545 до н. э. ) Считается, что Фалес «открыл» для греков созвездие Малой Медведицы как путеводный инструмент; ранее этим созвездием пользовались финикийцы. Фалесу приписываются следующие положения: 1.Земля плавает в воде, а Солнце и другие небесные тела питаются испарениями этой воды. 2.Звезды состоят из земли, но при этом раскалены; Солнце — землистого состава [состоит из земли]; Луна — землистого состава [состоит из земли]. 3.Земля находится в центре Вселенной; при уничтожении Земли рухнет весь мир.](https://fsd.multiurok.ru/html/2020/06/16/s_5ee89c53d7499/img_s1480547_0_11.jpg)
Фалес (640/624 — 548/ 545 до н. э. )
Считается, что Фалес «открыл» для греков созвездие Малой Медведицы как путеводный инструмент; ранее этим созвездием пользовались финикийцы.
Фалесу приписываются следующие положения:
1.Земля плавает в воде, а Солнце и другие небесные тела питаются испарениями этой воды.
2.Звезды состоят из земли, но при этом раскалены; Солнце — землистого состава [состоит из земли]; Луна — землистого состава [состоит из земли].
3.Земля находится в центре Вселенной; при уничтожении Земли рухнет весь мир.
Эратосфен Киренский ( 276-194 гг. до н. э.)
Достижения:
1.Эратосфен является основателем научной хронологии.
2.Эратосфену принадлежит термин «география» (землеописание).
3.Считается, что именно Эратосфен создал первую карту мира, которая давала примерное представление о взаимной удаленности городов и стран.
Клавдий Птолемей
Достижения:
1.Птолемей — автор трактата «Гармоника» в трёх книгах (окончание третьей книги не сохранилось), в котором развернул теорию звуковысотной системы
2.Другой важный труд Птолемея середины II века нашей эры — Руководство по географии в восьми книгах представляет собой собрание знаний о географии всего известного античным народам мира
3.Теоремы о произведении диагоналей вписанного в круг четырёхугольника теорема Птолемея ,
Вывод
1.Мы узнали какие существовали великие математики.
2.Узнали их самые интересные (или самые знаменитые) открытия .
Источники информации
Аполлоний Пергский // Энциклопедический словарь Брокгауза и Ефрона : в 86 т. (82 т. и 4 доп.). — СПб., 1890—1907.
Джон Дж. О’Коннор и Эдмунд Ф. Робертсон . Аполлоний Пергский (англ.) — биография в архиве MacTutor .
© 2019 Русская историческая библиотека
Мария Солопова. Демокрит // Энциклопедия « Кругосвет ».
Демокрит / M. A. Солопова // Новая философская энциклопедия : в 4 т. / пред. науч.-ред. совета В. С. Стёпин . — 2-е изд., испр. и доп. — М. : Мысль , 2010. — 2816 с.
Храмов Ю. А. Демокрит // Физики: Биографический справочник / Под ред. А. И. Ахиезера . — Изд. 2-е, испр. и дополн. — М.: Наука , 1983. — С. 100. — 400 с. — 200 000 экз. (в пер.)
Пифагор в Викицитатнике
Пифагор на Викискладе
Ямвлих, О пифагоровой жизни
Диоген Лаэртский, Пифагор
Порфирий, Жизнь Пифагора
Бертран Рассел, История западной философии
Pythagoras of Samos (The MacTutor History of Mathematics archive)
Stanford Encyclopedia of Philosophy: Pythagoras
«Золотые стихи» пифагорейцев в Библиотеке Александра Кобринского
Бесонид, Пифагорово Слово
А.Охоцимский. Пифагор и пифагорейцы, число и огонь
Просмотр содержимого презентации
«®«®â®¥ á¥ç¥¨¥»
Золотое сечение
Выполнила обучающаяся
9 г класса
Иволгина Полина Вячеславовна
Руководитель:
Мамасуева Татьяна Парфирьевна
Содержание
- 1) Актуальность проекта
- 2) История вопроса
- 3) Золотая спираль
- 4) Золотое сечение в живописи, фотографии, дизайне
- 5) Золотое сечение в искусстве. Архитектура
- 6) Золотое сечение и тело человека
- 7) Пропорция золотого сечения в природе
-
Вывод
Актуальность проекта
- Благодаря «Золотому сечению» было сделано множество открытий в науке, архитектуре, литературе, живописи, природе, анатомии и астрономии.
- В перечисленных областях знаний оно используется и в настоящее время.
- Вы узнаете какую роль играет эта пропорция в окружающем мире, как она связана с понятием гармонии и как и почему она используется в искусстве (живописи, архитектуре, фотографии…), дизайне и в остальных жизненных аспектах.
История
- Под золотым сечением понимается такое пропорциональное деление отрезка на неравные части, при котором длина всего отрезка так относится к его большей части, как длина большей части относится к длине меньшей. Это отношение равно иррациональному числу Ф=1.618…
,
Золотая спираль
- Что общего в расположении полипептидных цепей нуклеиновых кислот, лепестков розы, раковин моллюсков, рогов млекопитающих, подсолнуха, далеких космических галактик ?
Золотое сечение в живописи, фотографии, дизайне
- Основы композиции В живописи, фотографии, дизайне золотое сечение очень часто используется в виде классических приемов композиции (о чем вы можете прочитать, заглянув на любой сайт, посвященный этим видам искусства).
Золотое сечение в искусстве. Архитектура
- Золотое сечение пронизывает
всю историю искусства.
Пропорции тела человека и золотое сечение
- Идеальным, совершенным считается тело, пропорции которого составляет золотое сечение. Основные пропорции были определены Леонардо да Винчи, и художники стали сознательно их использовать.
Пропорции золотого сечения в природе
- Форма птичьих яиц описывается золотым сечением.
- Совершенная форма тела стрекозы создана по законам золотого сечения: отношение длины хвоста и корпуса равно отношению общей длины к длине хвоста.
Вывод
- Золотое сечение – это один из основных принципов природы.
- Человеческое представление о красивом сформировалось под влиянием того – какую гармонию и порядок видит он сам в природе.
Литература
- https://ru.wikipedia.org/wiki/ Золотое_сечение
- Савин А. Число Фидия — золотое сечение (рус.) // «Квант» : Научно-популярный физико-математический журнал (издается с января 1970 года). — 1997. — № 6.
- Прохоров А. Золотая спираль, Квант, 1984, №9
- http://bapachi.by/zolotoe-sechenie-v-prirode-cheloveke-iskusstve/
Просмотр содержимого презентации
«áâ®à¨ï ¢®§¨ª®¢¥¨ï ç¨á¥« 2.0»
Муниципальное бюджетное общеобразовательное учреждение «Средняя общеобразовательная школа №59» Проект по математике «История возникновения чисел»
Выполнил обучающейся 9 Г класса Шульгин Илья Дмитриевич Руководитель: Мамасуева Татьяна Парфирьевна
Цель работы
- Выяснить как появились числа
- Как они развивались в разных народах и культурах
- Разобраться как числа стали такими какими мы видим их сейчас
- Узнать значение чисел и их мифический смысл
- Сделать вывод по работе
История возникновения чисел
У древних людей, кроме каменного топора и шкуры вместо одежды, ничего не было, поэтому считать им было нечего. Постепенно они стали приручать скот, возделывать поля; появилась торговля, и тут уж без счёта никак не обойтись. Сначала считали на пальцах. Когда пальцы на одной руке кончались, переходили на другую, а если на двух руках не хватало, переходили на ноги.
Системы счисления
От пальцевого счёта пошли пятеричная система счисления (одна рука), десятеричная (две руки), двадцатеричная (пальцы рук и ног). В древние времена не существовало единой для всех стран системы счёта. Некоторые системы исчисления брали за основу 12, другие – 60, третьи – 20, 2, 5, 8 .
Числа по-шумерски
Первыми придумали запись чисел древние шумеры. Они пользовались всего двумя цифрами. Вертикальная чёрточка обозначала одну единицу, а угол из лежачих чёрточек – десять. Эти чёрточки у них получались в виде клиньев, потому что они писали острой палочкой на сырых глиняных дощечках, которые потом обжигали. Вот так выглядели эти дощечки.
Шумерская система счисления
Шестидесятери́чная систе́ма счисле́ния — позиционная система счисления по целочисленному основанию 60. Изобретена шумерами в III тысячелетии до н. э., использовалась в древние времена на Ближнем Востоке.
Вавилонские числа
Вавилонская система счисления применялась за две тысячи лет до н. э. Для записи чисел использовались всего два знака: стоячий клин для обозначения единиц и лежачий клин для обозначения десятков внутри шестидесятеричного разряда.
Числа египтян
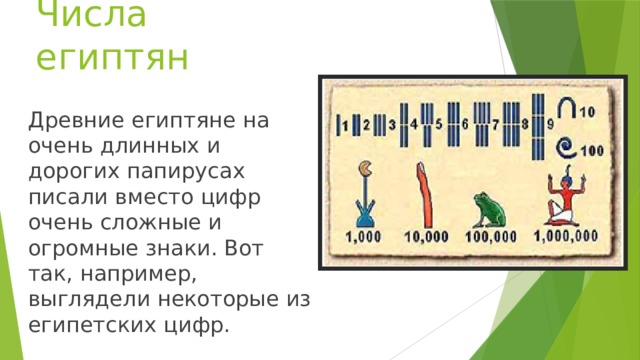
Древние египтяне на очень длинных и дорогих папирусах писали вместо цифр очень сложные и огромные знаки. Вот так, например, выглядели некоторые из египетских цифр.
Числа египтян
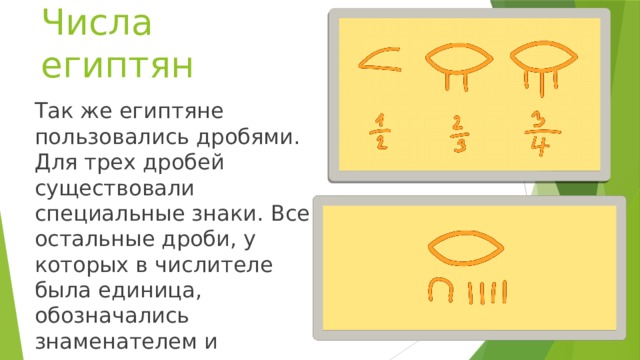
Так же египтяне пользовались дробями. Для трех дробей существовали специальные знаки. Все остальные дроби, у которых в числителе была единица, обозначались знаменателем и похожим на глаз значком сверху.
Числа египтян
Все правильные дроби записывались как сумма таких дробей.
Числа индейцев майя
Цифры майя основаны на двадцатеричной позиционной системе счисления, использовавшиеся цивилизацией Майя в доколумбовой Месоамерике. Эта система использовалась для календарных расчётов. В быту майя использовали аддитивную непозиционную систему, сходную с древнеегипетской. Об этой системе дают представление сами цифры майя, которые являются записью первых 19 натуральных чисел в пятеричной непозиционной системе счисления. Аналогичный принцип составных цифр использован в древнейшей известной шестидесятеричной позиционной системе счисления и древнекитайской десятичной позиционной системе для расчётов на счётной доске.
Числа индейцев майя
Цифры майя состояли из нуля, который обозначался пустой ракушкой, и 19 составных цифр. Эти цифры конструировались из знака единицы (точка) и знака пятёрки (горизонтальная черта). Например, цифра, обозначающая число 19, писалась как четыре точки в горизонтальном ряду над тремя горизонтальными линиями. Сходство конструкции цифр Майя с древнеегипетскими, римскими и древнекитайскими цифрами обусловлено тем, что первоначально расчёты не велись на бумаге. Цифры выкладывались на ровной поверхности специальными палочками. Майя использовали также пустую ракушку и, вероятно, камешки или косточки плодов.
Числа индейцев майя
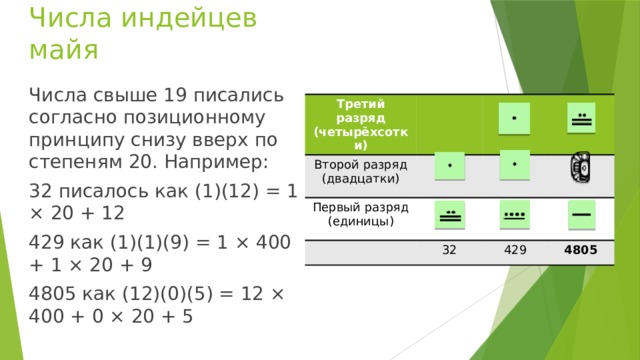
Числа свыше 19 писались согласно позиционному принципу снизу вверх по степеням 20. Например:
32 писалось как (1)(12) = 1 × 20 + 12
429 как (1)(1)(9) = 1 × 400 + 1 × 20 + 9
4805 как (12)(0)(5) = 12 × 400 + 0 × 20 + 5
Третий разряд (четырёхсотки)
Второй разряд (двадцатки)
Первый разряд (единицы)
32
429
4805
Числа индейцев майя
Для записи цифр от 1 до 19 иногда также использовались изображения божеств. Такие цифры использовались крайне редко, сохранившись лишь на нескольких монументальных стелах.
Римская система счисления и их числа
Десятичную систему счисления ввели римляне. Римские цифры до сих пор используют в часах и для оглавления книг, а также и во многих школах, но уже не для счёта. В некоторых случаях с очень большими числами над римскими числами ставили черту. Черта сверху могла обозначать увеличение значения цифры в 1000 раз: V с чертой сверху = 5000 .
Римская система счисления и их числа
Но такая система цифр тоже была слишком сложной для счёта. Так как занимала очень много места.
Числа народов Азии
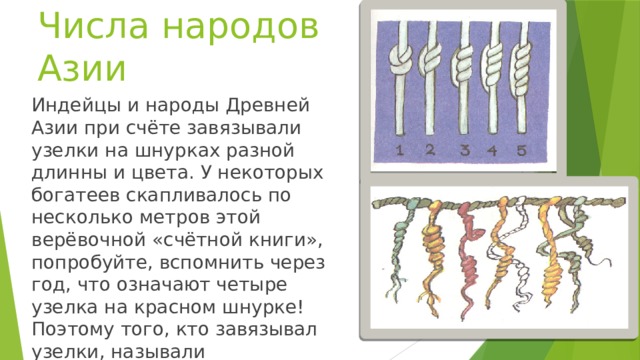
Индейцы и народы Древней Азии при счёте завязывали узелки на шнурках разной длинны и цвета. У некоторых богатеев скапливалось по несколько метров этой верёвочной «счётной книги», попробуйте, вспомнить через год, что означают четыре узелка на красном шнурке! Поэтому того, кто завязывал узелки, называли вспоминателем.
Греческая система счисления
1 α 10 ι 100 ρ
2 β 20 κ 200 σ
3 γ 30 λ 300 τ
4 δ 40 μ 400 υ
5 ε 50 ν 500 φ
6 ϝ 60 ξ 600 χ
(или ϛ)
7 ζ 70 ο 700 ψ
8 η 80 π 800 ω
9 θ 90 ϟ 900 ϡ
Греческая система счисления, также известная как ионийская или новогреческая — непозиционная система счисления. Алфавитная запись чисел, в которой в качестве символов для счёта, употребляют буквы классического греческого алфавита, а также некоторые буквы доклассической эпохи, такие как ϛ , ϟ и ϡ . Эта система пришла на смену аттической, или старо греческой, системе, которая господствовала в Греции в III веке до н. э. Необходимость сохранять порядок букв ради сохранения их числовых значений привела к относительно ранней (IV век до н. э.) стабилизации греческого алфавита.
Славянские числа
Предки нашего народа, русского – славяне для обозначения чисел употребляли буквы. Этот способ обозначения цифр называется цифирью. Но у наших предков славян буквы не только обозначали цифры, но и каждая буква имела свой смысл.
Славянские числа
Так же для обозначения больших чисел славяне придумали свой оригинальный способ, к примеру: десять тысяч – тьма, десять тем – легион, десять легионов – леорд, десять леордов – ворон, десять воронов – колода. Но Петру Великому это казалось очень неудобным (хотя я бы с ним и поспорил), и он ввёл привычные для всех нас десять цифр, которые мы используем и по сей день .
Древнекитайские цифры
Цифры Сучжоу — единственная отчасти сохранившаяся система, основанная на счёте палочками. Эта система сформировалась на базе более древней системы цифр, которые выкладывались палочками для вычислений на счётной доске, использовавшейся в Южной Сун. Долгое время расчёты велись почти только на счётной доске. На бумаге записывался результат. Сучжоуские цифры использовались в качестве скорописи в коммерции, бухгалтерии.
Древнекитайские цифры
В официальных документах использовались «формальные» китайские цифры, их сложнее перепутать при записи и чтении. В России на финансовых документах аналогичную функцию выполняет графа «сумма прописью». Цифры Сучжоу были популярны на рынках, в Гонконге они дожили до начала 1990-х, но постепенно вытесняются арабскими цифрами. Сегодня цифры Сучжоу используются только на некоторых рынках для записи цен.
Индо-арабские числа
Как принято считать числа которыми мы пишем в наши дни арабские но на самом деле они индо-арабские и придумали их в индии в 1 веке нашей эры. И выглядели они так.
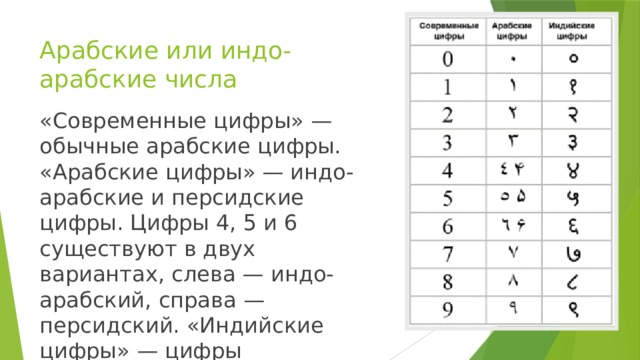
Арабские или индо-арабские числа
«Современные цифры» — обычные арабские цифры. «Арабские цифры» — индо-арабские и персидские цифры. Цифры 4, 5 и 6 существуют в двух вариантах, слева — индо-арабский, справа — персидский. «Индийские цифры» — цифры деванагари современной Индии.
Арабские числа
Арабские или современные числа всем кажутся обыденными, но что если я скажу, что их можно считать с помощью углов. Так посчитав углы, можно даже незнающему человеку понять что перед ним, за число.
Арабские числа
Но со временем углы сгладились, и цифры приобрели привычный нам вид. Вот уже много столетий весь мир пользуется арабской системой записи чисел. Этими десятью значками можно легко выразить огромные значения.
Значение чисел в современном мире
Сейчас цифры и числа имеют огромную роль в нашей жизни! Так они используются: в работе с компьютером, для оплаты товаров и услуг мы считаем сколько денег нам требуется, для оплаты налогов, и многого, многого другого!
Значение чисел в современном мире
И если вы считаете что числа в жизни вам не пригодятся, то вы глубоко заблуждаетесь! Они играют возможно лидирующую роль в современной жизни и в современном обществе, и без них никак. И из-за роста технологий значение чисел всё растёт, а они сами начинают править миром!
«Главное число» человека
Древние учёные считали, что цифры имеют таинственный, магический смысл и влияют на человека. По верованиям древних, у каждого человека есть некое число, обладающее мистической силой, влияют на характер и привычки. В нумерологии, науке о числах, используют первые 9 чисел от 1 до 9.
Значение чисел по Пифагору
Пифагор, его ученики и последователи сократили все числа до цифр от 1 до 9 включительно, так как они являются исходными числами, из которых могут быть получены все другие. Знаменитый Корнелиус Агриппа в своём труде «Оккультная философия», вышедшем в 1533 году, назвал эти числа и их значения.
Значение чисел по Пифагору
Число 1 – число цели, которое проявляется в форме агрессивности и амбиции.
Число 2 – число с крайностями. Оно поддерживает равновесие, смешивая позитивные и негативные качества.
Число 3 – означает неустойчивость. Оно объединяет талант и весёлость и символизирует приспособляемость.
Значение чисел по Пифагору
Число 4 – число означает — устойчивость и прочность.
Число 5 – символизирует риск. Это число является и самым счастливым, и самым непредсказуемым.
Число 6 – символ надёжности. Оно находится в гармонии с природой. Это идеальное число.
Значение чисел по Пифагору
Число 7 – число символизирует тайну, а так же изучение и знание.
Число 8 – число материального успеха. Оно означает надёжность, доведённую до совершенства, равновесие.
Число 9 – символ всеобщего успеха. Оно объединяет черты целой группы.
Интересные факты про числа
1. В таких странах, как Китай, Япония и Корея число «4» считается несчастливым. Поэтому этажи с номерами, которые заканчиваются на «4» отсутствуют.
Интересные факты про числа
2. Центильон – это самое большое число, которое выглядит как 1 с 600 нулями. Это число было записано еще в 1852 году.
Интересные факты про числа
3. Число «13» — во многих государствах также считается неудачным. Поэтому этаж после «12» имеет обозначение «14», «12А» или «М» (тринадцатая буква в алфавите).
Интересные факты про числа
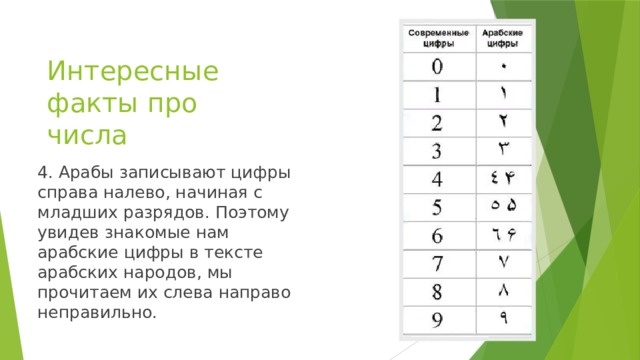
4. Арабы записывают цифры справа налево, начиная с младших разрядов. Поэтому увидев знакомые нам арабские цифры в тексте арабских народов, мы прочитаем их слева направо неправильно.
Интересные факты про числа
5. Интересные факты о числах касаются и современных технологий. Так, Google – одна из самых популярных поисковых систем. Ее придумали Сергей Брин и Ларри Пейдж. Название поисковой системы было выбрано неспроста. Так, ее создатели захотели показать то количество информации, которую система может обработать. В математике число, которое состоит из единицы и ста нулей называется «гугол». Интересно и то, что название «Google» записано неправильно (не «googol»). Но такая идея названия основателям понравилась еще больше.
Интересные факты про числа
6. 666 – это сумма всех чисел на рулетке казино.
Интересные факты про числа
7. Число «13» в Греции считается несчастливым днем только тогда, когда выпадает во вторник. В Италии опасаются пятницы 17-го. А вот статисты Нидерландов подсчитали, что именно 13-го числа случается меньше аварий и несчастных случаев, поскольку люди более осторожны и собраны.
Интересные факты про числа
8. Термин «цифра» в переводе с арабского означает «ноль». Только со временем данное слово начали использовать для обозначения любого численного символа.
Интересные факты про числа
9. Число «7» считается самым счастливым числом.
Интересные факты про числа
10. У сороконожек совсем не 40 ножек, их может быть от 30 до 400.
Вывод
Проведя это исследование я могу сказать что многие народы не зависимо друг от дуга придумали числа. Это происходило в разных точках света и в разные периоды времени но у многих никогда не встречавшихся народов очень похожие числа и системы счисления к примеру у славян и греков были алфавитные цифры а у римлян китайцев и майя были очень похожие числа записываемые с помощью палочек или чёрточек.
Вывод
И вот мы можем увидеть что всё время числа и их запись старались усовершенствовать но они до сих пор не совершенны.
Спасибо за внимание!
Просмотр содержимого презентации
«¢ ¤à âë¥ ãà ¢¥¨ï»
тема
“ Решение квадратных уравнений”
Выполнил: Оганян Егор 9Д Преподаватель: Мамасуева Татьяна Порфирьевна
Содержание.
1. Содержание
2. Цели.
3. Задачи
3.1 Основополагающий вопрос;
3.2 Проблемные вопросы;
3.3 Учебные вопросы.
- Теоретический материал.
Цели :
Знакомство с различными способами решения квадратных уравнений
Задачи
Основополагающий вопрос:
Решение квадратных уравнений.
Проблемные вопросы: Какими способами можно решать квадратные уравнения?
Учебные вопросы:
1. Что такое квадратное уравнение?
2. Какие существуют виды квадратных уравнений?
3. Что называется дискриминантом квадратного уравнения?
4. От чего зависит количество корней квадратного уравнения?
5. Каковы формулы для нахождения корней квадратного уравнения?
6. Как формулируется теорема Виета?
Определение квадратного уравнения, его виды.
Квадратным уравнением называется уравнение вида
ax 2 + bx + c = 0,
где х — переменная , а,b и с -некоторые числа, причем, а ≠ 0.
Если в квадратном уравнении ах 2 + bx + c = 0 хотя бы один из коэффициентов b или с равен нулю, то такое уравнение называют неполным квадратным уравнением . Неполные квадратные уравнения бывают трёх видов:
1) ах 2 + с = 0, где с ≠ 0;
2) ах 2 + bх = 0, где b ≠ 0;
3) ах 2 = 0.
Приведённым называют квадратное уравнение, в котором старший коэффициент равен единице. Такое уравнение может быть получено делением всего выражения на старший коэффициент a :
х 2 +px + q = 0
Различные способы решения квадратных уравнений.
1) Разложение левой части уравнения на множители.
Решим уравнение х 2 + 10х – 24 = 0.
Разложим левую часть уравнения на множители:
х 2 + 10х – 24 = х 2 + 12х – 2х – 24 = х (х + 12) – 2 (х +12) = (х + 12)(х – 2).
Следовательно, уравнение можно переписать так:
(х + 12)(х – 2) = 0.
Так как произведение равно нулю, то по крайне мере один из его множителей равен нулю. Поэтому левая часть уравнения обращается в нуль при х = 2, а также при х = — 12. это означает, что числа 2 и – 12 являются корнями уравнения х 2 + 10х – 24 = 0.
2) Метод выделения полного квадрата
Решим уравнение х 2 + 6х – 7 = 0
Выделим в левой части полный квадрат. Для этого запишем выражение
х 2 + 6х в следующем виде: х 2 + 6х = х 2 + 2· х ·3.
В полученном выражении первое слагаемое – квадрат числа х , а второе – удвоенное произведение х на 3. поэтому чтобы получить полный квадрат, нужно прибавить 3 2 , так как
х 2 + 2· х ·3 + 3 2 = (х + 3) 2 .
Преобразуем теперь левую часть уравнения
х 2 + 6х – 7 = 0,
прибавляя к ней и вычитая 3 2. Имеем:
х 2 + 6х – 7 = х 2 + 2· х ·3 + 3 2 – 3 2 – 7 = (х + 3) 2 – 9 – 7 = (х + 3) 2 – 16.
Таким образом, данное уравнение можно записать так:
(х + 3) 2 –16 = 0, т.е. (х + 3) 2 = 16.
Следовательно, х + 3 = 4, х 1 = 1, или х +3 = — 4 , х 2 = – 7.
Решение неполных квадратных уравнений.
1. Если ах 2 = 0. Уравнения такого вида решаются по алгоритму:
1) найти х 2 ;
2) найти х.
Например, 5х 2 = 0 . Разделив обе части уравнения на 5 получается:
х 2 = 0, откуда х = 0.
2. Если ах 2 + с = 0, с≠ 0 Уравнения данного вида решаются по алгоритму:
1) перенести слагаемые в правую часть;
2) найти все числа, квадраты которых равны числу с.
Например, х 2 — 5 = 0, х 2 = 5. Следовательно, надо найти все числа, квадраты которых равны числу 5. Таких чисел только два —
и
x 2 = минус корень из пяти
Таким образом, уравнение х 2 — 5 = 0 имеет два корня: x 1 = корень из 5,
и других корней не имеет.
3. Если ах 2 + bх = 0, b ≠ 0. Уравнения такого вида решаются по алгоритму:
1) вынести общий множитель за скобки;
2) найти x 1 , x 2 .
Например, х 2 — 3х = 0. Перепишем уравнение х 2 – 3х = 0 в виде
х ( х – 3 ) = 0. Это уравнение имеет, очевидно, корни x 1 = 0, x 2 = 3. Других корней оно не имеет, ибо если в него подставить вместо х любое число, отличное от нуля и 3, то в левой части уравнения х
( х – 3 ) = 0 получится число, не равное нулю.
0, т.е. В случае, когда — = m , — где m0, уравнение х 2 = m имеет два корня = = — Таким образом, неполное квадратное уравнение может иметь два корня, один корень, ни одного корня.» width=»640″
Вывод:
1) если уравнение имеет вид ах 2 = 0, то оно имеет один корень х = 0;
2) если уравнение имеет вид ах 2 + bх = 0, то используется метод разложения на множители: х (ах +b) = 0; значит, либо х = 0, либо ах + b = 0. В итоге получается два корня: x 1 = 0; x 2 = — ;
3) если уравнение имеет вид ах 2 + с = 0, то его преобразуют к виду
ах 2 = — с и далее х 2 = —
—
В случае, когда
0,уравнение х 2 =
не имеет корней (значит, не имеет корней и исходное уравнение
ах 2 +с=0).
0, т.е.
В случае, когда —
= m ,
—
где m0, уравнение х 2 = m имеет два корня
=
= —
Таким образом, неполное квадратное уравнение может иметь два корня, один корень, ни одного корня.
0, то квадратное уравнение ах 2 + bx + c = 0 имеет два корня, которые находятся по формулам: (1) ; Например, 3х 2 +8х – 11 = 0. Решение: а = 3, b = 8, с = -11. D = b 2 – 4ас = 8 2 – 4*3*(-11) = 64 + 132 = 196. Так как D 0, то данное квадратное уравнение имеет два корня. Эти корни находятся по формулам:» width=»640″
Решение полных квадратных уравнений
ах 2 + bx + c = 0, где a,b,c – заданные числа, а ≠ 0, х – неизвестное.
Рассмотриваются следующие случаи решения полных квадратных уравнений: D 0.
1. Если D
Например, 2х 2 + 4х + 7 = 0.
Решение: здесь а = 2, b = 4, с = 7.
D = b 2 – 4ас = 4 2 – 4*2*7 = 16 – 56 = — 40.
Так как D
2. Если D = 0, то квадратное уравнение ах 2 + bx + c = 0 имеет один корень, который находится по формуле
Например, 4х – 20х + 25 = 0. Решение: а = 4, b = — 20, с = 25.
D = b 2 – 4ас = (-20) 2 – 4*4*25 = 400 – 400 = 0.
Так как D = 0, то данное уравнение имеет один корень. Этот корень находится по формуле
3. Если D 0, то квадратное уравнение ах 2 + bx + c = 0 имеет два корня, которые находятся по формулам:
(1)
;
Например, 3х 2 +8х – 11 = 0. Решение: а = 3, b = 8, с = -11. D = b 2 – 4ас = 8 2 – 4*3*(-11) = 64 + 132 = 196.
Так как D 0, то данное квадратное уравнение имеет два корня. Эти корни находятся по формулам:
0, то квадратное уравнение ах 2 + bx + c = 0 имеет два корня ;» width=»640″
.
Вывод:
Если D
Если D = 0, то квадратное уравнение имеет один корень,
который находится по формуле
Если D 0, то квадратное уравнение ах 2 + bx + c = 0 имеет два корня
;
0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p . Если p0 , то оба корня отрицательные, если p , то оба корня положительны. б) Если свободный член q приведенного квадратного уравнения отрицателен ( q то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p0.» width=»640″
Решение приведенных квадратных уравнений
Теорема Виета . Сумма корней приведенного квадратного уравнения равна второму коэффициенту, взятому с противоположным знаком, а произведение корней равно свободному члену.
x 1 + x 2 = — p,
x 1 x 2 = q.
Иначе говоря, если x 1 и x 2 — корни уравнения х 2 +px + q = 0, то
Теорема, обратная теореме Виета . Если для чисел x 1 , x 2, p, q справедливы формулы то x 1 и x 2 — корни уравнения х 2 +px + q = 0 .
а) Если свободный член q
приведенного квадратного уравнения положителен ( q 0), то уравнение имеет два одинаковых по знаку корня и это зависит от второго коэффициента p .
Если p0 , то оба корня отрицательные, если p , то оба корня положительны.
б) Если свободный член q
приведенного квадратного уравнения отрицателен ( q то уравнение имеет два различных по знаку корня, причем больший по модулю корень будет положителен, если p , или отрицателен, если p0.
Свойства коэффициентов квадратного уравнения .
Пусть дано квадратное уравнение ах 2 + bх + с = 0, а ≠ 0.
1.Если а + b + с = 0 (т.е. сумма коэффициентов уравнения равна нулю),
то х 1 = 1, х 2 =
Решим уравнение 345х 2 – 137х – 208 = 0.
Решение . Так как а + b + с = 0 (345 – 137 – 208 = 0), то х 1 = 1, х 2 =
Ответ : 1; –
2. Если а — b + с = 0, или b = а + с, то х 1 = – 1, х 2 = –
Решим уравнение 132х 2 + 247х + 115 = 0
Решение. Т. к. а-b+с = 0 (132 – 247 +115=0), то
х 1 = — 1, х 2 = —
Ответ: — 1; —
Графическое решение квадратного уравнения
Если в уравнении x 2 + px + q = 0
перенести второй и третий члены в правую часть, то получим
x 2 = – px – q .
Построим графики зависимостей у = х 2 и у = – px – q .
График первой зависимости – парабола , проходящая через начало координат.
График второй зависимости – прямая .
Возможны следующие случаи: прямая и парабола могут пересекаться в двух точках, абсциссы точек пересечения являются корнями квадратного уравнения;
— прямая и парабола могут касаться (только одна общая точка),т.е. уравнение имеет одно решение;
— прямая и парабола не имеют общих точек, т.е. квадратное уравнение не имеет корней.
Решим графически уравнение х 2 – 3х – 4 = 0.
Решение. Запишем уравнение в виде
х 2 = 3х + 4
Построим параболу у = х 2 и прямую у = 3х + 4.
Прямую у = 3х + 4 можно построить по двум точкам М (0;4) и N (3;13).
Прямая и парабола пересекаются в двух точках А и B с абсциссами х 1 = – 1 и
х 2 = 4.
В
А
Решение квадратных уравнений с помощью номограммы.
Это старый и незаслуженно забытый способ решения квадратных уравнений.
Номограмма для решения уравнения z 2 + pz+ q = 0. Эта номограмма позволяет, не решая квадратного уравнения, по его коэффициентам определить корни уравнения.
Криволинейная шкала номограммы построена по формулам:
ОВ =
, АВ =
Полагая ОС = р, ЕD = q, ОЕ = а , из подобия треугольников САН и СDF получим пропорцию
откуда после подстановок и упрощений вытекает уравнение z 2 + pz + q = 0,
причем буква z означает метку любой точки криволинейной шкалы.
1. Для уравнения
z 2 – 9z + 8 = 0.
Номограмма дает корни
z 1 = 8, 0 и z 2 = 1, 0 (рис. 12).
2. Решим с помощью
номограммы уравнение 2z 2 – 9 z + 2 = 0.
Разделим коэффициенты этого
уравнения на 2,получим уравнение
z 2 – 4, 5 + 1 = 0.
Номограмма дает корни z 1 = 4 и z 2 = 0,5.
Спасибо за внимание
Просмотр содержимого презентации
«¥®à¥¬ ¨ä £®à
î娻
Проект Тема: теорема Пифагора. Предметная область: математика. Выполнил обучающийся 9Бкласса Енюхин Дмитрий Анатольевич Руководитель: Мамасуева Т.П. Курск-2018″ width=»640″
МУНИЦИПАЛЬНОЕ БЮДЖЕТНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ
УЧРЕЖДЕНИЕ
Проект
Тема: теорема Пифагора.
Предметная область: математика.
Выполнил обучающийся 9Бкласса
Енюхин Дмитрий Анатольевич
Руководитель: Мамасуева Т.П.
Курск-2018
Содержание
- Актуальность.
- Формулировка.
- Цели и задачи.
- Доказательства.
- Применение
Актуальность
Теорема Пифагора в геометрии важна не меньше, чем таблица умножения в арифметике. Решение многих геометрических задач, сводится к рассмотрению прямоугольных треугольников и применению этой замечательной теоремы. Так же большинство задач по нахождению сторон прямоугольных треугольников сводится к использованию этой теоремы.
Цели проекта
Научиться доказывать Теорему Пифагора разными способами.
Формулировка
В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
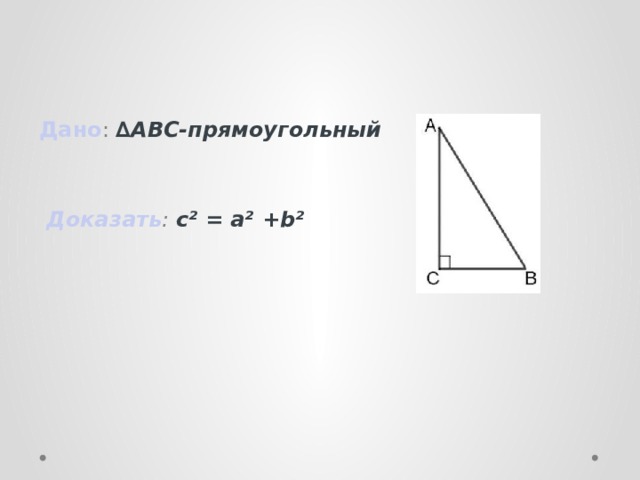
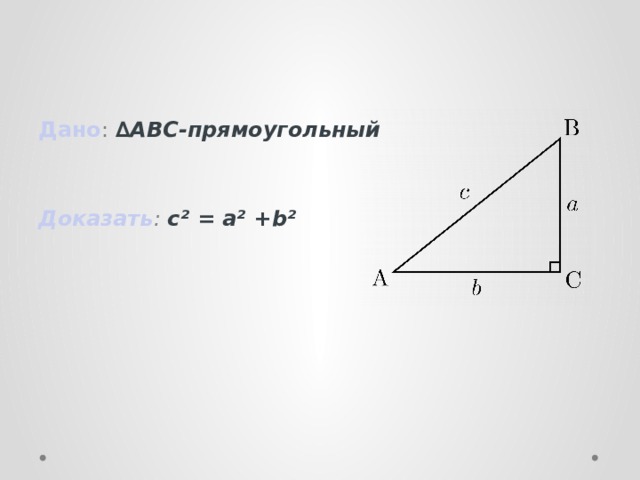
Дано : ∆ABC-прямоугольный
a,b- катеты
с-гипотенуза
Доказать : с² = а² + b²
Доказательство
1) Достроим треугольник до квадрата со стороной (a+b).
2) Sкв.=(a+b)²
3) S∆= ½·ab
4) Sкв.=4·S∆+S
5) S кв. =4·½ab+c²
6) Sкв.=2ab+c²
7) (a+b)²=2ab+c²
a²+2ab+b²=2ab+c²
9) c²=a²+b²- что и требовалось доказать
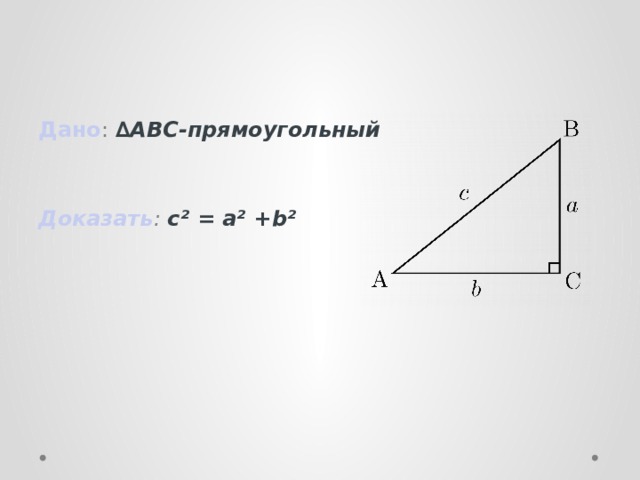
Дано : ∆ABC-прямоугольный
Доказать : с² = а² + b²
Доказательство
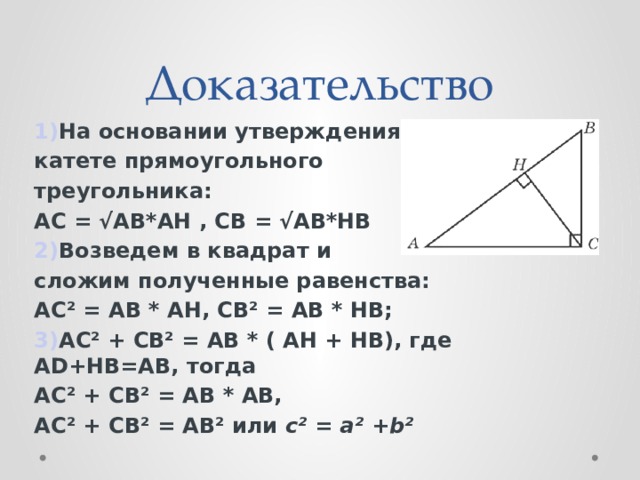
1) На основании утверждения о
катете прямоугольного
треугольника:
АС = √AB*AH , СВ = √AB*HB
2) Возведем в квадрат и
сложим полученные равенства:
АС² = АВ * АH, СВ² = АВ * HВ;
3) АС² + СВ² = АВ * ( АH + HВ), где АD+HB=AB, тогда
АС² + СВ² = АВ * АВ,
АС² + СВ² = АВ² или с² = а² + b²
Дано : ∆ABC-прямоугольный
Доказать : с² = а² + b²
Доказательство
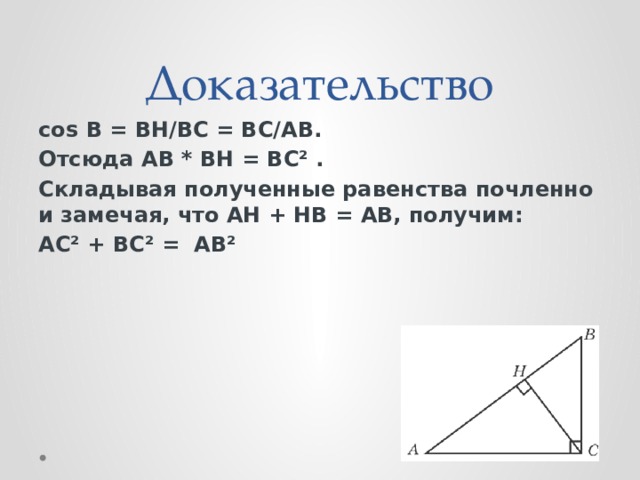
Пусть АВС – данный прямоугольный треугольник с прямым углом С. Проведем высоту СH из вершины прямого угла С.
По определению косинуса угла:
cos А = АH/АС = АС/АВ. Отсюда АВ * АD = АС²
Аналогично,
Доказательство
cos В = ВH/ВС = ВС/АВ.
Отсюда АВ * ВH = ВС² .
Складывая полученные равенства почленно и замечая, что АH + HВ = АВ, получим:
АС² + ВС² = АВ²
Дано : ∆ABC-прямоугольный
Доказать : с² = а² + b²
Доказательство
1) Расположим два равных прямоугольных треугольника так, чтобы катет одного из них был продолжением другого.
2) Площадь полученной трапеции находится как произведение полу суммы оснований на высоту
S = a+b/2*(a + b)
Доказательство
3) C другой стороны, площадь трапеции равна сумме площадей полученных треугольников:
S=2ab/2+ c²/2
4) Приравнивая данные выражения, получаем:
2ab/2+c²/2=(a+b)²/2
или c²=a²+b²
Дано : ∆ABC-прямоугольный
Доказать : с² = а² + b²
Доказательство
sin В= b/с ; cos В= a/с , то, возведя в квадрат полученные равенства, получим:
sin² В= в²/с²; cos² В = а²/с².
Сложив их, получим:
sin² В + cos² В= в²/с²+ а²/с², где sin² В + cos² В=1,
1= (в²+ а²) / с², следовательно,
с²= а² + b².
Области применения теоремы.
Широкое применение имеет при решении геометрических задач.
Именно с ее помощью, можно геометрически находить значения квадратных корней из целых чисел.
Задачи в курсе физики средней школы требуют знания теоремы Пифагора
Астрономия также широкая область для применения теоремы Пифагора
Спасибо за внимание!
Просмотр содержимого презентации
«¥®à¥¬ ¨ä £®à ®¤¥à 9 (¯à¥§¥â æ¨ï)»
Проект выполнила:
ученица 9 класса Ж
средне-образовательной школы №59
Тодер Екатерина
И всё об этом
Теорема Пифагора
Содержание
- Актуальность темы
- Цели проекта
- Задачи проекта
- Жизненный путь Пифагора
- Заслуги Пифагора
- Формулировки теоремы Пифагора
- Доказательство первое
- Доказательство второе
- Доказательство третье
- Доказательство четвертое
- Практическое применение теоремы
- Теорема, обратная теореме Пифагора
- Заключение
- Литература
Актуальность темы
Без теоремы Пифагора не обходится практически ни одна математическая задача. Эта теорема была востребована тысячелетия назад, и до сих пор не потеряла своей значимости.
Цели проекта
- Ознакомиться с жизнью Пифагора
- Узнать различные формулировки теоремы Пифагора
- Узнать новые доказательства теоремы Пифагора
- Научиться практически применять теорему Пифагора
- Рассмотреть теорему, обратную теореме Пифагора
Задачи проекта
- Найти информацию о формулировке теорем в учебнике
- Найти информацию о новых доказательствах теоремы Пифагора, пользуясь материалами Интернета
- Найти информацию о жизни и заслугах Пифагора в энциклопедиях
Жизненный путь Пифагора
Пифагор Самосский — древнегреческий философ, математик и мистик, создатель религиозно-философской школы пифагорейцев.
Его отцом был Мнесарх, родом из Тира, который получил гражданство Самоса, а матерью Партенида или Пифаида, которая была родственницей Анкея, основателя греческой колонии на Самосе.
С 18 лет Пифагор обучался у египетских жрецов и получил допуск к храмовым библиотекам.
Затем он попал в Вавилон в качестве пленника, пробыл там 12 лет и обучался у местных магов и жрецов. В 56 лет вернулся в родной Самос.
Заслуги Пифагора
В Кротоне Пифагор основал философскую школу, где пропагандировались знания и особый образ жизни. Ее ученики, или «пифагорейцы», занимались геометрией, математикой, гармонией и астрономией.
Пифагор один из первых заявил, что Земля шарообразна, а планеты имеют собственную траекторию движения.
В музыке определил, что звук зависит от длины флейты или струны.
В нумерологии Пифагор совместил числа с прогнозами на будущее.
В геометрии сформулировал теорему Пифагора, а также открыл построение отдельных многогранников и многоугольников.
Формулировки теоремы Пифагора
- Сумма площадей квадратов, опирающихся на катеты a и b, равна площади квадрата, построенного на гипотенузе c.
- Площадь квадрата, построенного на гипотенузе прямоугольного треугольника, равна сумме площадей квадратов, построенных на его катетах.
- В прямоугольном треугольнике квадрат длины гипотенузы равен сумме квадратов длин катетов.
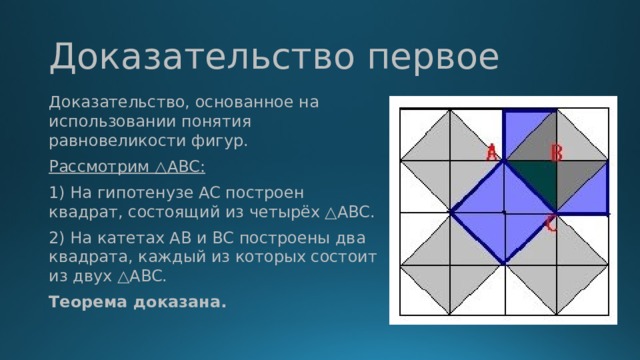
Доказательство первое
Доказательство, основанное на использовании понятия равновеликости фигур.
Рассмотрим △ABC:
1) На гипотенузе AC построен квадрат, состоящий из четырёх △ABC.
2) На катетах AB и BC построены два квадрата, каждый из которых состоит из двух △ABC.
Теорема доказана.
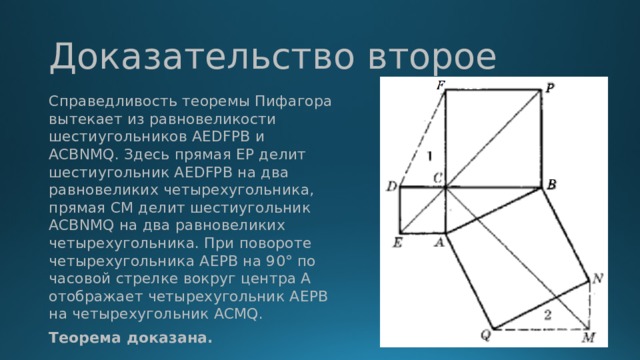
Доказательство второе
Справедливость теоремы Пифагора вытекает из равновеликости шестиугольников AEDFPB и ACBNMQ. Здесь прямая EP делит шестиугольник AEDFPB на два равновеликих четырехугольника, прямая CM делит шестиугольник ACBNMQ на два равновеликих четырехугольника. При повороте четырехугольника AEPB на 90° по часовой стрелке вокруг центра A отображает четырехугольник AEPB на четырехугольник ACMQ.
Теорема доказана.
Доказательство третье
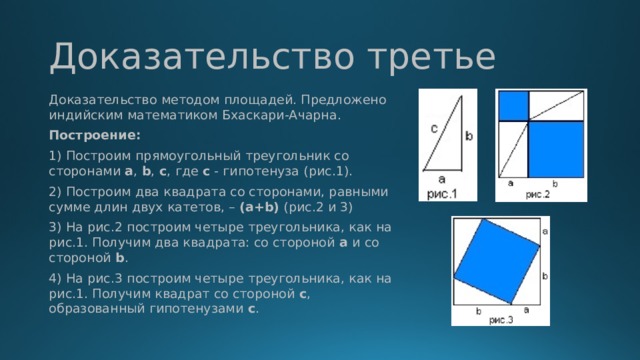
Доказательство методом площадей. Предложено индийским математиком Бхаскари-Ачарна.
Построение:
1) Построим прямоугольный треугольник со сторонами a , b , c , где с — гипотенуза (рис.1).
2) Построим два квадрата со сторонами, равными сумме длин двух катетов, – (a+b) (рис.2 и 3)
3) На рис.2 построим четыре треугольника, как на рис.1. Получим два квадрата: со стороной a и со стороной b .
4) На рис.3 построим четыре треугольника, как на рис.1. Получим квадрат со стороной c , образованный гипотенузами c .
Доказательство третье
Решение:
1) Площадь квадрата со стороной a равна a 2 , площадь квадрата со стороной b равна b 2 .
2) Площадь квадрата на рис.3 равна (a+b) 2 – 2ab .
3) Приравняем сумму площадей квадратов на рис.2 и площадь квадрата на рис.3, получим a 2 + b 2 = (a+b) 2 – 2ab .
4) Раскрыв скобки, получим a 2 + b 2 = a 2 + b 2 .
5) Площадь квадрата на рис.3 также можно записать как с 2 ; значит a 2 + b 2 = с 2 .
Теорема доказана.
Доказательство четвертое
Геометрическое доказательство, названное «Методом Гарфилда».
Дано и построение:
Дано: △ABC, ∠ A = 90 °
Доказать: ВС 2 =АС 2 +АВ 2
Дополнительные построения: продолжим катет АС и построим отрезок CD , который равен катету АВ . К AD опустим перпендикуляр ED , равный отрезку АС . Соединим точки Е и В , а также Е и С и получим чертеж, как на рисунке.
Доказательство четвертое
Чтобы доказать теорему, найдем площадь получившейся фигуры двумя способами и приравняем выражения друг к другу.
- S ABED = 2 ∙ ½(AB∙AC) + ½ВС 2 , т.к. △ ECB – равнобедренный и АВ=CD , АС=ED , ВС=СЕ.
- ABED – трапеция (AB||ED), значит S ABED = (DE+AB) ∙ ½AD.
- Приравняем выше составленные выражения: AB ∙ AC + ½BC 2 = (DE+AB) ∙ ½(AC+CD) .
- Упростим и раскроем скобки во второй части: AB ∙ AC + ½BC 2 = ½АС 2 + 2 ∙ ½(АВ*АС)+ ½АВ 2 .
- Сократим уравнение и получим: ВС 2 =АС 2 +АВ 2 .
Теорема доказана.
Практическое применение теоремы
Теорема Пифагора находит применение не только в математике, но и в архитектуре и строительстве, астрономии и даже литературе.
Рассмотрим историческую задачу Бхаскари:
Решение: По теореме Пифагора АВ 2 = ВС 2 +АС 2 ; 9+16=25, АВ=5 футов;
СD=3+5=8 футов.
Ответ: высота тополя
8 футов.
На берегу реки рос тополь одинокий. Вдруг ветра порыв его ствол надломал. Бедный тополь упал. И угол прямой С теченьем реки его ствол составлял. Запомни теперь, что в этом месте река В четыре лишь фута была широка Верхушка склонилась у края реки. Осталось три фута всего от ствола, Прошу тебя, скоро теперь мне скажи: У тополя как велика высота?
Практическое применение теоремы
Свет истины рассеется не скоро, Но, воссияв, рассеется навряд И, как тысячелетия назад, Не вызовет сомнения и спора. Мудрейшие, когда коснется взора Свет истины, богов благодарят; И сто быков, заколоты, лежат – Ответный дар счастливца Пифагора. С тех пор быки отчаянно ревут: Навеки всполошило бычье племя Событие, помянутое тут. Им кажется: вот-вот настанет время, И сызнова их в жертву принесут Какой-нибудь великой теореме.
Теорема Пифагора для многих писателей и поэтов стала и есть вдохновителем. Немецкого писателя Адельберта фон Шамиссо она вдохновила на написание сонета:
А в двадцатом веке советский писатель Евгений Велтистов в книге «Приключения Электроника» доказательствам теоремы Пифагора отвел целую главу. И еще полглавы рассказу о двухмерном мире, какой мог бы существовать, если бы теорема Пифагора стала основополагающим законом и даже религией для отдельно взятого мира. Жить в нем было бы гораздо проще, но и гораздо скучнее: например, там никто не понимает значения слов «круглый» и «пушистый».
Теорема, обратная теореме Пифагора
Ее формулировка такова : если сумма квадратов двух сторон треугольника равна квадрату третьей стороны, то такой треугольник прямоугольный. Докажем теорему.
Дано и построение:
Дано: ∆ABC, AC 2 +BС 2 =АВ 2
Доказать: ∠C=90º
Дополнительные построения: Построим прямой угол с вершиной в точке C1. Отложим на его сторонах отрезки C1A1=CA и C1B1=CB.
Теорема, обратная теореме Пифагора
Проведём отрезок A1B1. Получили ∆A1B1C1, в котором ∠C1=90º. В прямоугольном ∆A1B1C1 применим теорему Пифагора: A1C1 2 +B1С1 2 =А1В1 2 . Таким образом:
Итак, в ∆ABC и ∆A1B1C1: C1A1=CA и C1B1=CB (по построению), A1B1=AB (по доказанному). Следовательно, ∆A1B1C1=∆ABC и ∠C=∠C1=90º.
Теорема доказана.
Заключение
Несмотря на то, что теорема Пифагора была открыта множество лет назад, люди до сих пор выводят новые доказательства как ее самой, так и обратной ей.
Теорема Пифагора – действительно важный элемент математики, поскольку ее использование помогает решать не только простейшие задачи, но и задачи высшей математики, отчего она не теряет своей значимости по сей день.
Литература
Учебник:
Атанасян, Бутузов, Кадомцев: Геометрия. 7-9 классы. Учебник. ФГОС. – 2017 год, изд. «Просвещение», г.Москва.
Ссылки:
https://ru.wikipedia.org/wiki/Пифагор
http://pifagoros.blogspot.ru/p/blog-page_5067.html
http://ezop.su/pif_2/
https://ru.wikipedia.org/wiki/Теорема_Пифагора
https://www.tutoronline.ru/blog/teorema-pifagora
Спасибо за внимание!
Результаты поиска
Вы можете бесплатно и без регистрации скачать любую из 24 презентаций
Творческий проект Вышивка Апельсиновый рай Проект выполнила Ученица 9 в Гусева Мария.
Презентация: Творческий проект Вышивка Апельсиновый рай Проект выполнила Ученица 9 в Гусева Мария.
Творческий проект Вышивка Апельсиновый рай Проект выполнила Ученица 9 в Гусева Мария Обоснование выбора проекта Пэчворк-это настоящее искусство, особый стиль шитья из кусочков. Лоскутная техника- самый популярный вид рукоделия на сегодняшний день, т.к. не …
Творческий проект Автор: Каплунова Анастасия Дождикова Марина Ученица 9 класса МОУ «Иогачская средняя МОУ «Иогачская средняя образовательная школа»
Презентация: Творческий проект Автор: Каплунова Анастасия Дождикова Марина Ученица 9 класса МОУ «Иогачская средняя МОУ «Иогачская средняя образовательная школа»
Творческий проект Автор: Каплунова Анастасия Дождикова Марина Ученица 9 класса МОУ «Иогачская средняя МОУ «Иогачская средняя образовательная школа» Актуальность проблемыАктуальность проблемы На уроках технологии мы учились выполнять различные творческие …
ТВОРЧЕСКИЙ ПРОЕКТ «Анютины глазки» (батик, вышивка) СУШКЕВИЧ НАТАЛЬЯ УЧЕНИЦА 9 КЛАССА РУКОВОДИТЕЛЬ: НАУМЕНКО Р.М. МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ.
Презентация: ТВОРЧЕСКИЙ ПРОЕКТ «Анютины глазки» (батик, вышивка) СУШКЕВИЧ НАТАЛЬЯ УЧЕНИЦА 9 КЛАССА РУКОВОДИТЕЛЬ: НАУМЕНКО Р.М. МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ.
ТВОРЧЕСКИЙ ПРОЕКТ «Анютины глазки» (батик, вышивка) СУШКЕВИЧ НАТАЛЬЯ УЧЕНИЦА 9 КЛАССА РУКОВОДИТЕЛЬ: НАУМЕНКО Р.М. МУНИЦИПАЛЬНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ СРЕДНЯЯ ОБЩЕОБРАЗОВАТЕЛЬНАЯ ШКОЛА п. ДРУЖБА 2009 Батик — обобщенное название разнообразных …
Творческий проект Коллажирование Коллаж Один день в сентябре Выполнила Выполнила ученица 9 а класса ученица 9 а класса МОУ «СОШ 32» МОУ «СОШ 32» Ганьжова.
Презентация: Творческий проект Коллажирование Коллаж Один день в сентябре Выполнила Выполнила ученица 9 а класса ученица 9 а класса МОУ «СОШ 32» МОУ «СОШ 32» Ганьжова.
Творческий проект Коллажирование Коллаж Один день в сентябре Выполнила Выполнила ученица 9 а класса ученица 9 а класса МОУ «СОШ 32» МОУ «СОШ 32» Ганьжова Елена Ганьжова Елена Магнитогорск, 2010 Я всегда любила творчество. Ведь творчество- это полет …
Областной конкурс творческих проектов «Моя профессия» Профессия программист Г. Тотьма, МОУ «Тотемская СОШ 2», ученик 9А класса Тугаринов Дмитрий.
Презентация: Областной конкурс творческих проектов «Моя профессия» Профессия программист Г. Тотьма, МОУ «Тотемская СОШ 2», ученик 9А класса Тугаринов Дмитрий.
Областной конкурс творческих проектов «Моя профессия» Профессия программист Г. Тотьма, МОУ «Тотемская СОШ 2», ученик 9А класса Тугаринов Дмитрий. Сегодня наши офисы заполнены всевозможной техникой, самым важным является, конечно же, компьютер. Без этого …
Областной конкурс творческих проектов «Моя профессия» Г. Тотьма, МОУ «Тотемская СОШ 2», ученик 9А класса Дьяконов Виталий.
Областной конкурс творческих проектов «Моя профессия» Г. Тотьма, МОУ «Тотемская СОШ 2», ученик 9А класса Дьяконов Виталий.
Областной конкурс творческих проектов «Моя профессия» Г. Тотьма, МОУ «Тотемская СОШ 2», ученик 9А класса Дьяконов Виталий. 1) каждому гарантируется свобода мысли и слова; 2) не допускается пропаганда или агитация, возбуждающая социальную, расовую, …
Творческий проект на тему : на тему : ДЕКОРАТИВНАЯ КОСМЕТИКА ДЛЯ ДЕВУШЕК … ДЕКОРАТИВНАЯ КОСМЕТИКА ДЛЯ ДЕВУШЕК … Выполнила ученица 9 класса Б Выполнила.
Творческий проект на тему : на тему : ДЕКОРАТИВНАЯ КОСМЕТИКА ДЛЯ ДЕВУШЕК … ДЕКОРАТИВНАЯ КОСМЕТИКА ДЛЯ ДЕВУШЕК … Выполнила ученица 9 класса Б Выполнила.
Творческий проект на тему : на тему : ДЕКОРАТИВНАЯ КОСМЕТИКА ДЛЯ ДЕВУШЕК … ДЕКОРАТИВНАЯ КОСМЕТИКА ДЛЯ ДЕВУШЕК … Выполнила ученица 9 класса Б Выполнила ученица 9 класса Б МОУСОШ 17 МОУСОШ 17 Воляник Мария Воляник Мария Карталы 2010 год Карталы 2010 год Еще …
МОУ «Яснополянская основная общеобразовательная школа» Творческий проект: Шукшин и костёр калины красной Выполнила: Аксютина Лена, ученица 9 класса.
МОУ «Яснополянская основная общеобразовательная школа» Творческий проект: Шукшин и костёр калины красной Выполнила: Аксютина Лена, ученица 9 класса.
МОУ «Яснополянская основная общеобразовательная школа» Творческий проект: Шукшин и костёр калины красной Выполнила: Аксютина Лена, ученица 9 класса 2009 год на Алтае – объявлен годом Шукшина Тема проекта: Шукшин (вышивка крестом) Костёр калины красной ( …
Полезная и вредная пища (творческий проект) Выполнила: ученица 9 «б» класса ООШ 35 г.Сургута Петрова Мария.
Полезная и вредная пища (творческий проект) Выполнила: ученица 9 «б» класса ООШ 35 г.Сургута Петрова Мария.
Полезная и вредная пища (творческий проект) Выполнила: ученица 9 «б» класса ООШ 35 г.Сургута Петрова Мария ЭПИГРАФ Мы покупаем не то, что нравится и нужно нам, а то, что нравится всем; зачастую мы едим не то, что полезно для нашего здоровья, а то, что …
Творческий проект подготовила ученица 9б класса Садофьева Ольга Руководитель: Бойко Тамара Васильевна МОУ «Серебряно Прудская СОШ им. маршала В.И.Чуйкова»
Творческий проект подготовила ученица 9б класса Садофьева Ольга Руководитель: Бойко Тамара Васильевна МОУ «Серебряно Прудская СОШ им. маршала В.И.Чуйкова»
Творческий проект подготовила ученица 9б класса Садофьева Ольга Руководитель: Бойко Тамара Васильевна МОУ «Серебряно Прудская СОШ им. маршала В.И.Чуйкова» Творческий проект подготовила ученица 9б класса Садофьева Ольга Руководитель: Бойко Тамара …
Творческий проект «Школу будущего строим вместе» Работу выполнила Ученица 9В класса Лезова Екатерина.
Творческий проект «Школу будущего строим вместе» Работу выполнила Ученица 9В класса Лезова Екатерина.
Творческий проект «Школу будущего строим вместе» Работу выполнила Ученица 9В класса Лезова Екатерина Чтобы ребёнок был всесторонне развит, ему необходимо учиться в такой школе, где для этого созданы все условия. Идеальная школа Высоко- квалифици- рованные …
Творческий проект на тему Развивающая книжка для детей «Обслужи себя сам» Выполнила : Смелова Маргарита Ученица 9 класса « А », МОУ СОШ 16 Артемовского.
Творческий проект на тему Развивающая книжка для детей «Обслужи себя сам» Выполнила : Смелова Маргарита Ученица 9 класса « А », МОУ СОШ 16 Артемовского.
Творческий проект на тему Развивающая книжка для детей «Обслужи себя сам» Выполнила : Смелова Маргарита Ученица 9 класса « А », МОУ СОШ 16 Артемовского городского округа Развивающая книжка «Обслужи себя сам» создавалась с целью обучить ребенка основным …
Творческий проект на тему: «Русская масленица» Работу выполнила: Ученица 9 класса «Б» МОУСОШ 17 Варенникова Мария Руководитель: Королева Эрна Викторовна.
Творческий проект на тему: «Русская масленица» Работу выполнила: Ученица 9 класса «Б» МОУСОШ 17 Варенникова Мария Руководитель: Королева Эрна Викторовна.
Творческий проект на тему: «Русская масленица» Работу выполнила: Ученица 9 класса «Б» МОУСОШ 17 Варенникова Мария Руководитель: Королева Эрна Викторовна 2010г. Последовательность выполнения проекта 1.Обоснование возникшей проблемы и потребности 2. …
«Гений Гоголя до сих пор остаётся неизвестным в полной мере» И.А. Виноградов Творческий проект учащихся 9-Б класса Васильевской школы — гимназии «Сузіря».
«Гений Гоголя до сих пор остаётся неизвестным в полной мере» И.А. Виноградов Творческий проект учащихся 9-Б класса Васильевской школы — гимназии «Сузіря».
«Гений Гоголя до сих пор остаётся неизвестным в полной мере» И.А. Виноградов Творческий проект учащихся 9-Б класса Васильевской школы — гимназии «Сузіря». Руководитель: Филиппова С.П. Детство Гоголя Николай Васильевич Гоголь родился в старинной …
Творческий проект «Юбка» Выполнила: Подопригорова Екатерина, ученица 9 класса Руководитель: Ахматчина Надежда Георгиевна 2014 год ОГКОУ «Тейковская школа-интернат.
Творческий проект «Юбка» Выполнила: Подопригорова Екатерина, ученица 9 класса Руководитель: Ахматчина Надежда Георгиевна 2014 год ОГКОУ «Тейковская школа-интернат.
Творческий проект «Юбка» Выполнила: Подопригорова Екатерина, ученица 9 класса Руководитель: Ахматчина Надежда Георгиевна 2014 год ОГКОУ «Тейковская школа-интернат VIII вида» Содержание 1. Введение Выбор и обоснование проекта Цели и задачи проекта 2. …
Творческий проект по теме: «Кухонный набор» Муниципальное Образовательное Учреждение «Гимназия 1» Ученик 9 «А» класса Алтухов Николай Руководитель проекта:
Творческий проект по теме: «Кухонный набор» Муниципальное Образовательное Учреждение «Гимназия 1» Ученик 9 «А» класса Алтухов Николай Руководитель проекта:
Творческий проект по теме: «Кухонный набор» Муниципальное Образовательное Учреждение «Гимназия 1» Ученик 9 «А» класса Алтухов Николай Руководитель проекта: Сергеев И. В. г. Воскресенск, 2009-2010 год. Применение и функциональные особенности Набор …
Творческий проект «Вышивка крестом»
Творческий проект «Вышивка крестом»
Выполнила ученица 9 а класса Сашникова Елена Олеговна Руководитель Мурашова Татьяна Валентиновна Вышивка крестом Введение Вышивка крестом – это один из древнейших видов рукоделия, которым увлечено множество мужчин и женщин по всему миру. И это не …
Творческий проект «Мой профессиональный выбор» Выполнила ученица 9 А класса Баранова Лена.
Творческий проект «Мой профессиональный выбор» Выполнила ученица 9 А класса Баранова Лена.
Творческий проект «Мой профессиональный выбор» Выполнила ученица 9А класса Баранова Лена Выявление проблемы До окончания школы остается два года и уже появилась необходимость в выборе профессии. До окончания школы остается два года и уже появилась …
Творческий проект: «Разделочная доска» Выполнил ученик 9 «Б» класса МОУ «СОШ 33» п. Яйва Александровского р-на Лупенко Владимир Сергеевич.
Творческий проект: «Разделочная доска» Выполнил ученик 9 «Б» класса МОУ «СОШ 33» п. Яйва Александровского р-на Лупенко Владимир Сергеевич.
Творческий проект: «Разделочная доска» Выполнил ученик 9 «Б» класса МОУ «СОШ 33» п. Яйва Александровского р-на Лупенко Владимир Сергеевич Содержание проекта Материалы. Материалы. Древесные материалы. Древесные материалы. Образцы досок. Образцы досок. …
Творческий проект Стильная одежда Выполнила ученица 9 а класса Пономарева Мария Руководитель: Проскурина Т. А. 2011.
Творческий проект Стильная одежда Выполнила ученица 9 а класса Пономарева Мария Руководитель: Проскурина Т. А. 2011.
Творческий проект Стильная одежда Выполнила ученица 9 а класса Пономарева Мария Руководитель: Проскурина Т. А. 2011 Цели проекта 1. Познакомиться с историей вязания. 2. Обновить свой гардероб. 3. Связать стильный жилет. 4. Сэкономить семейный бюджет. …
|
МУНИЦИПАЛЬНОЕ АВТОНОМНОЕ ОБЩЕОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ «ГИМНАЗИЯ №1 Г. БЛАГОВЕЩЕНСКА» |
|
ИНДИВИДУАЛЬНЫЙ ИТОГОВЫЙ ПРОЕКТ Предметная область «Информатика и ИКТ» и «Робототехника» |
|
Тема: «Модель «умный дом» »» Выполнил: Саяпин Никита Александрович, обучающийся 9Е класса МАОУ «Гимназия №1 г. Благовещенска» Научный руководитель: Федченко Галина Михайловна, Преподаватель БГПУ; Руководитель проекта: Саяпина Маргарита Николаевна, учитель информатики и ИКТ МАОУ «Гимназия №1 г. Благовещенска» г. Благовещенск — 2016 г Содержание |
|
Введение |
3 — 4 |
|
Глава 1. Технологическая часть |
5 — 7 |
|
Глава 2. Разработка устройства |
8 — 9 |
|
Выводы |
10 |
|
Список литературы |
11 |
|
Приложение |
12 — 19 |
Введение
Само понятие «умный» дом (англ. smart house) не такое уж молодое. Оно возникло в США в начале 70-х годов прошлого века, в недрах «Института интеллектуальных зданий». На тот момент под умным домом подразумевалось «здание, обеспечивающее продуктивное и эффективное использование рабочего пространства…».
Однако годом рождения современного «умного» дома можно считать 1978-й год. В этом году в США компании Х10 USA и Leviton разработали и внедрили в производство технологию управления бытовыми приборами по проводам бытовой электросети.
Распространение эти разработки получили в то время лишь на территории Северной Америки, ибо были рассчитаны на работу при напряжении 110 В и частоту сети 60 Гц. Тем не менее, именно этим фирмам человечество обязано появлением «невероятных чудес прогресса» — автоматически открывающихся дверей, включающегося по хлопку света и прочих «фокусов», которыми состоятельные американцы удивляли своих гостей, а голливудские фильмы — весь остальной мир.
Для конца 70-х годов технология X10 (именно такое название закрепилось и сохранилось за ней и поныне) являлась, конечно, революционной. Однако она была рассчитана на поддержку всего шести управленческих команд и, в основном, использовалась для управления электроосвещением. Но людям хотелось большего. «Умный» дом должен был становиться все «умнее».
С начала нового тысячелетия человечество шагает в эпоху новых технологических открытий, одним из которых является бытовая автоматизация. Время современного человека имеет огромную ценность и такие системы автоматизации как «умный дом» существенно экономят этот жизненно-важный ресурс. Включить кондиционер, выключить свет в прихожей, активировать ночную сигнализацию — это лишь маленький перечень действий, которые можно возложить на систему «умного дома». Но такие устройства имеют один минус — большую рыночную стоимость. Поэтому разработка относительно дешевой системы, с аналогичными возможностями получает все большую актуальность.
Целью работы является разработка модуля системы «умный дом», а так же разработка и исследование алгоритмов системы, позволяющих увеличить экономию ресурсов.
Задачи проекта
Создание архитектуры аппаратных средств «умного дома»
Анализ программно-аппаратных систем управления «умным домом»
Отладка стенда
Содержание работы
Обзор систем управления зданиями
Обзор готовых программных решений
Выбор аппаратных средств
Создание архитектуры аппаратных средств «умного дома»
Разработка требований к многофункциональному программно-аппаратному стенду
Разработка структуры программно-аппаратного стенда
Экспериментальная часть
Отладка стенда
Глава 1. Технологическая часть
Arduino — это электронный конструктор и удобная платформа быстрой разработки электронных устройств для новичков и профессионалов. Платформа пользуется огромной популярностью во всем мире благодаря удобству и простоте языка программирования, а также открытой архитектуре и программному коду. Устройство программируется через USB без использования программаторов.
Arduino позволяет компьютеру выйти за рамки виртуального мира в физический и взаимодействовать с ним. Устройства на базе Arduino могут получать информацию об окружающей среде посредством различных датчиков, а также могут управлять различными исполнительными устройствами.
Микроконтроллер на плате программируется при помощи языка С++ и среды разработки Arduino. Проекты устройств, основанные на Arduino, могут работать самостоятельно, либо же взаимодействовать с программным обеспечением на компьютере (напр.: Flash, Processing, MaxMSP). Платы могут быть собраны пользователем самостоятельно или куплены в сборе. Программное обеспечение доступно для бесплатного скачивания. Исходные чертежи схем (файлы CAD) являются общедоступными, пользователи могут применять их по своему усмотрению.
В 2006 Arduino получила признание в категории Digital Communities на фестивале Ars Electronica Prix .
Аппаратная часть платформы Arduino
Существует несколько версий платформ Arduino. Последняя версия Leonardo базируется на микроконтроллере ATmega32u4.
Uno, как и предыдущая версия Duemilanove построены на микроконтроллере Atmel ATmega328.
Старые версии платформы Diecimila и первая рабочая Duemilanoves были разработаны на основе Atmel ATmega168 ,более ранние версии использовали ATmega8.
Arduino Mega2560, в свою очередь, построена на микроконтроллере ATmega2560.
Язык Arduino можно разделить на три раздела:
Глава 2. Разработка устройства
Проектирование системы можно разделить на 2 части: аппаратную и программную.
Аппаратная часть системы представлена платформой Arduino (рис.1) с расширениями и физическими модулями. Arduino – это инструмент для проектирования электронных устройств, более тесно взаимодействующих с окружающей физической средой, чем стандартные персональные компьютеры. В данной работе будет использована версия платформы Arduino UNO – самая популярная версия базовой платформы Arduino с USB-интерфейсом и возможностью подключения большого разнообразия плат расширения. Эта платформа предназначена для физических расчетов (physical computing) с открытым программным кодом, построенная на простой печатной плате с современной средой для разработки программного обеспечения .
Рисунок 1 — Внешний вид платформы Arduino MEGA
Arduino использует микроконтроллер Atmega328, который имеет 32 Кб флеш памяти. Этого будет вполне достаточно для выполнения возложенной на платформу задачи. Остальная обработка будет распределена на веб-ресурс.
Микроконтроллеры Arduino отличаются наличием предварительно прошитого в них загрузчика. С помощью этого загрузчика пользователь загружает свою программу в микроконтроллер без использования традиционных отдельных аппаратных программаторов и соединяется с компьютером через USB-интерфейс.
Программная часть системы представлена в программном коде микроконтроллера (Arduino скетч) (см. Приложение 1)
Модуль управления кроватью
Модуль управления вентилятором
Модуль управления светом
Выводы
Разрабатываемая система управления исключит вероятность того, что неиспользуемые в данный момент приборы будут потреблять электроэнергию. Это позволит улучшить энергосбережение используемого помещения и получить экономическую выгоду.
В данный момент работа не окончена. Идет стадия аппаратного проектирования системы «умный дом».
Список литературы
1. В. Архипов «Системы для «интеллектуального» здания» — «СтройМаркет», № 45 1999 г.
2. Mike Riley «Programming Your Home Automate with Arduino, Android, and Your Computer» — « The Pragmatic Bookshelf Dallas, Texas • Raleigh, North Carolina », 2012 г.
3. Информация сайта http://habrahabr.ru/post/118817/
4. Информация сайта http://ab-log.ru/
5. Информация сайта http://a-bolshakov.ru/index/0-163
6. Информация сайта https://xively.com/?from_cosm=true
7. Информация сайта http://www.tesli.com/ru/service/automation/smarthouse/
8. Информация сайта http://www.fibaro.com
Приложение 1.
#include
#include
const int
pin = 8,
DotDelay = 200;
const byte ROWS = 4; //four rows
const byte COLS = 4; //four columns
//define the cymbols on the buttons of the keypads
char hexaKeys[ROWS][COLS] = {
{‘1′,’2′,’3′,’A’},
{‘4′,’5′,’6′,’B’},
{‘7′,’8′,’9′,’C’},
{‘*’,’0′,’#’,’D’}
};
byte rowPins[ROWS] = {31,33,35,37}; //connect to the row pinouts of the keypad
byte colPins[COLS] = {39,41,43,45}; //connect to the column pinouts of the keypad
int a;
//initialize an instance of class NewKeypad
Keypad customKeypad = Keypad( makeKeymap(hexaKeys), rowPins, colPins, ROWS, COLS);
char text[]=»sos»;
Servo servo; //объявляем переменную servo типа Servo
void setup()
{
Serial.begin(9600);
pinMode(pin, OUTPUT);
servo.attach(9);
}
void dot()
{
digitalWrite(pin,HIGH);
delay(DotDelay);
digitalWrite(pin,LOW);
delay(DotDelay);
}
void dash()
{
digitalWrite(pin,HIGH);
delay(DotDelay * 3);
digitalWrite(pin,LOW);
delay(DotDelay);
}
void A()
{
dot();
dash();
}
void B()
{
dash();
dot();
dot();
dot();
}
void C()
{
dash();
dot();
dash();
dot();
}
void D()
{
dash();
dot();
dot();
}
void E()
{
dot();
}
void f()
{
dot();
dot();
dash();
dot();
}
void G()
{
dash();
dash();
dot();
}
void H()
{
dot();
dot();
dot();
dot();
}
void I()
{
dot();
dot();
}
void J()
{
dot();
dash();
dash();
dash();
}
void K()
{
dash();
dot();
dash();
}
void L()
{
dot();
dash();
dot();
}
void M()
{
dash();
dash();
}
void N()
{
dash();
dot();
}
void O()
{
dash();
dash();
dash();
}
void P()
{
dot();
dash();
dot();
}
void Q()
{
dash();
dash();
dot();
dash();
}
void R()
{
dot();
dash();
dot();
}
void S()
{
dot();
dot();
dot();
}
void T()
{
dash();
}
void U()
{
dot();
dot();
dash();
}
void V()
{
dot();
dot();
dot();
dash();
}
void W()
{
dot();
dash();
dash();
}
void X()
{
dash();
dot();
dot();
dash();
}
void Y()
{
dash();
dot();
dash();
dash();
}
void Z()
{
dash();
dash();
dot();
dot();
}
void loop()
{
char customKey = customKeypad.getKey();
char customKey1 = customKeypad.getKey();
if (customKey)
{
Serial.println(customKey);
if (customKey == ‘5’)
{
int a=0;
servo.write(180);
analogWrite(pin, 0);
delay(2000);
}
else
{
int a=1;
Serial.println(a);
servo.write(90);
analogWrite(pin, 400);
delay(1000);
morseText(text);
analogWrite(pin, 400);
delay(5000);
morseText(text);
analogWrite(pin, 400);
delay(10000);
morseText(text);
analogWrite(pin, 400);
delay(15000);
morseText(text);
analogWrite(pin, 400);
delay(20000);
morseText(text);
analogWrite(pin, 0);
delay(2000);
morseText(text);
}
}
}
void morseText(char text[])
{
int l=strlen(text);
for (int i=0; i
{
morseLetter(text[i]);
Serial.print(text[i]);
}
Serial.println();
}
void morseLetter(char letter)
{
if (letter==’ ‘) delay(DotDelay * 6);
if (letter==’a’) A();
if (letter==’b’) B();
if (letter==’c’) C();
if (letter==’d’) D();
if (letter==’e’) E();
if (letter==’f’) f();
if (letter==’g’) G();
if (letter==’h’) H();
if (letter==’i’) I();
if (letter==’g’) G();
if (letter==’k’) K();
if (letter==’l’) L();
if (letter==’m’) M();
if (letter==’n’) N();
if (letter==’o’) O();
if (letter==’p’) P();
if (letter==’q’) Q();
if (letter==’r’) R();
if (letter==’s’) S();
if (letter==’t’) T();
if (letter==’u’) U();
if (letter==’v’) V();
if (letter==’w’) W();
if (letter==’x’) X();
if (letter==’y’) Y();
if (letter==’z’) Z();
}
Свет
#define led_pin1 13
#define led_pin2 12
#define led_pin3 11
#define led_pin4 10
#define led_pin5 9
#define ldr_pin A0
#define pot_pin A1
void setup()
{
pinMode(led_pin1, OUTPUT);
pinMode(led_pin2, OUTPUT);
pinMode(led_pin3, OUTPUT);
pinMode(led_pin4, OUTPUT);
pinMode(led_pin5, OUTPUT);
}
void loop()
{
int lightness = analogRead(ldr_pin);
int threshold = analogRead(pot_pin);
boolean tooDark = (lightness < threshold);
if (tooDark)
{
digitalWrite(led_pin1, HIGH);
digitalWrite(led_pin2, HIGH);
digitalWrite(led_pin3, HIGH);
digitalWrite(led_pin4, HIGH);
digitalWrite(led_pin5, HIGH);
}
else
{
digitalWrite(led_pin1, LOW);
digitalWrite(led_pin2, LOW);
digitalWrite(led_pin3, LOW);
digitalWrite(led_pin4, LOW);
digitalWrite(led_pin5, LOW);
}
}
Профессия и её роль в жизни человека
Ученический проект по информатике «Профессия и её роль в жизни человека» содержит интересные сведения о том, как выбрать профессию своей мечты, на что нужно обращать внимание, а также указаны и изучены ошибки при выборе профессии.
Проект на тему «Лесные пожары» 9 класс
Автор:
Александрова Ксения Владимировна
В предложенном исследовательском проекте на тему «Лесные пожары» учащаяся 9 класса школы изучает основные причины возникновения лесных пожаров, дает их классификацию и предлагает способы решения этой проблемы.
Проект «Права несовершеннолетних» 9 класс
Автор:
Макулбаева Дарья Романовна
Готовая исследовательская работа «Права несовершеннолетних», которую провела ученица 9 класса школы, была создана с целью узнать о правах детей согласно нашему законодательству и донести эту информацию до своих одноклассников.
Проект «Подростковые наркозависимости»
Автор:
Селькина Александра Сергеевна
Ученическая исследовательская работа «Подростковые наркозависимости», проведенная учащейся школы, рассматривает основные признаки подростковой наркомании и устанавливает частые причины данного недуга.
Проект «Создание криптовалюты»
В предложенном исследовательском проекте на тему «Создание криптовалюты» учащийся 9 класса школы изучает историю создания и развития криптовалюты. Рассказывает о создании и продвижении криптовалюты в интернете.
Влияние рекламы на потребительские предпочтения телезрителей
Готовая исследовательская работа «Влияние рекламы на потребительские предпочтения телезрителей», которую провела ученица 9 класса школы, была создана с целью изучить проблему навязывания рекламой интересов и пробуждение желания тратить деньги на ненужные товары.
Проект «Безработица и её причины»
Автор:
Фёдорова Ксения Александровна
Ученическая исследовательская работа «Безработица и её причины», которую провела ученица 9 класса гимназии, рассматривает понятие «безработица» и определяет историю и предпосылки появления данного явления в обществе.
Влияние социальных сетей на подростков
В индивидуальном социальном проекте на тему «Влияние социальных сетей на подростков» учащаяся 9 класса рассматривает влияние социальных сетей и виртуального общения на социализацию подростков и их коммуникативные навыки в современном мире.
Проект «Школьный буллинг»
Автор:
Кузьмина Анастасия Дмитриевна
Готовая исследовательская работа «Школьный буллинг», которую провела ученица 9 класса школы, была создана с целью изучить проблему травли, психологического насилия и физической агрессии среди школьников.
Проект «Криптовалюта — деньги будущего?»
Автор:
Матвеев Владислав Владимирович
Ученическая исследовательская работа «Криптовалюта — деньги будущего?», которую провел ученик 9 класса школы, рассматривает историю возникновения криптовалюты и ее соотношение с традиционными денежными единицами.
Страницы
Новые Популярные Добавить материал
8
Чертежи, фигуры, линии и математические расчёты в кройке и шитье костюма «Снегурочки»
В ходе исследовательской работы сделан обзор материала по школьному курсу математики. Выяснено, какие математические знания необходимо применять при пошиве костюма «Снегурочки». Фигуры: 1. прямоугольник , 2. квадрат , 3. окружность,4. отрезок, 5. овал, 6. понятие симметрии. Свойства фигур: 1. равенство диагоналей прямоугольника, 2. свойства фигуры квадрат, 3. окружность (радиус, диаметр, построение окружностей), 4. равенства отрезков, сравнение отрезков, 5. осевая и центральная симметрии, сделан главный вывод: чтобы сшить костюм Снегурочки (другую одежду) необходимо изучать математику.
5
Создание радиоприёмника своими руками
Сейчас радио можно встретить в любом уголке мира. Как же хочется такой же: компактный, технологичный и мобильный. А может быть его собрать? На свой вкус, как раз и магазин электроники неподалёку…
2
Эмоциональное поведение старшеклассников в критической ситуации
Проблема эмоционального развития старшеклассников на сегодняшний день является сложной и сравнительно малоизученной. Несмотря на то, что старший школьный возраст традиционно считается одним из самых эмоциогенных и эмоциональные изменения рассматриваются в качестве главных новообразований этого периода, не существует единой, общепризнанной концепции эмоционального развития старшеклассников
13
Проектная работа
Исследовательский проект:
Агрессия и подростки
Творческая тема: Как укротить подростка
2
«Виртуальное путешествие в Кыргызстан»
Некоторые из традиций и обычаев кочевых киргизских племен остались в далеком прошлом, сохранившись лишь в памяти народной (в преданиях и эпосах), другие в неизменном или же трансформированном виде продол-жают бытовать среди киргизов и поныне. Цель этой работы – раскрыть перед слушателями все многообразие национальных обрядов и традиций, зародившихся еще в те далекие времена, когда киргизы были кочевниками.
2
Драконы:от мифа до реальности
Данная работа представляет собой проект ученицы 9 класса Веселковой Юлии. в проекте рассматриваются типы драконов, которые могли бы существовать, они оцениваются м точки зрения строения тела, крыльев, огненного дыхания. Также представлена модель дракона.
Предметы
|
Найдено 478 презентаций, для учеников 9 класса
|
Случайные
Популярные
Самые скачиваемые
|
Автор работы:
Савостьянов Тимофей Романович
Готовый исследовательский проект по химии на тему «Фосфор» рассматривает историю появления фосфора, его виды и соединения, а также области применения фосфора в медицине, промышленности и в быту.
- Подробнее о Исследовательский проект по химии: «Фосфор»
Автор работы:
Глебова Елена Александровна, Стребков Кирилл Романович
Ученический проект по биологии на тему «Перспективы селекции как решение глобальных экологических проблем» рассматривает понятие «селекция», ее задачи, методы и перспективы развития, а также приходит к выводу о том, что селекция позволяет повышать продуктивность сортов растений, пород животных и штаммов микроорганизмов, разрабатывать системы искусственного отбора, способствующие усилению и закреплению полезных для человека признаков у различных организмов.
- Подробнее о «Перспективы селекции как решение глобальных экологических проблем»
Автор работы:
Гайдай Арсений Алексеевич
В исследовательской работе и проекте по обществознанию «Семья в современном обществе» автор
выяснил значение семьи в современном обществе, выявил тенденции развития семьи и традиций.
- Подробнее о Проект «Семья в современном обществе»
Автор работы:
Гычков Пётр Алексеевич
В исследовательской работе и проекте по биологии «Насекомые в природе: медведка» автор изучил образ жизни и особенности насекомого — медведки, узнал о сокращении численности медведок на огороде.
- Подробнее о Проект «Насекомые в природе: медведка»