Презентация егэ по математике решение задач на работу

Слайд 1

Задачи на работу. Математические модели

Слайд 2

Вводят переменную, т.е. обозначают буквой х… величину, которую требуется найти по условию задачи, либо ту, которая необходима для отыскания искомых величин. Решение задачи с помощью уравнения обычно проводят в такой последовательности: 3. Решают составленное уравнение и из полученных решений отбирают те, которые подходят по смыслу задачи. 2. Используя введенную переменную, а также указанные в условии задачи конкретные значения переменных и соотношения между ними, составляют уравнение, т.е. «переводят» текст задачи на язык алгебры, составляя равенство алгебраических выражений.

Слайд 3

Это условие поможет нам составить уравнение. В другой столбик внесем Урожай, собранный каждым звеном В новом столбике можно выразить урожайность, для этого весь урожай : площадь участка х х – 2 S , га 1 2 А, ц урожайность, ц/га > на 5 ц 875 920 875 х 920 х – 2 1. Одно звено собрало со своего участка 875 ц пшеницы, а другое звено с участка, меньшего на 2 га, — 920 ц пшеницы. Сколько центнеров пшеницы собрало каждое звено с 1 га, если известно, что с 1 га во втором звене собрали на 5 ц пшеницы больше, чем в первом? 920 х – 2 – 875 х = 5 920 х – 2 = 875 х + 5 920 х – 2 – 5 875 х = 1 способ 2 способ 3 способ Из большей величины вычтем 5, уравняем с меньшей величиной  Первый столбик – площадь участков. Из большей величины вычтем меньшую, разность равна 5  К меньшей величине прибавим 5, уравняем с большей величиной  Это условие поможет ввести х …

Слайд 4

х х – 2 S , га 1 2 А, ц урожайность, ц/га > на 5 ц 875 920 875 х 920 х – 2 1. Одно звено собрало со своего участка 875 ц пшеницы, а другое звено с участка, меньшего на 2 га, — 920 ц пшеницы. Сколько центнеров пшеницы собрало каждое звено с 1 га, если известно, что с 1 га во втором звене собрали на 5 ц пшеницы больше, чем в первом? 920 х – 2 – 875 х = 5 920х – 875(х – 2) = 5х(х – 2) 920х – 875х + 1750 = 5х 2 – 10х 5х 2 – 55х – 1750 = 0 х(х – 2) : 5 х 2 – 11х – 350 = 0 х 1 = 25 х 2 = — 14 Не уд. усл. 875 х = 875 25 = 35 920 х – 2 = 920 25–2 = 40

Слайд 5

Очень часто решить задачу можно разными способами. Например, мы ввели х из условия… Одно звено собрало со своего участка 875 ц пшеницы, а другое звено с участка, меньшего на 2 га, — 920 ц пшеницы. Сколько центнеров пшеницы собрало каждое звено с 1 га, если известно, что с 1 га во втором звене собрали на 5 ц пшеницы больше, чем в первом? Это условие помогло ввести х … А можно начать «раскручивать» задачу с другого условия. Введем х иначе… Одно звено собрало со своего участка 875 ц пшеницы, а другое звено с участка, меньшего на 2 га, — 920 ц пшеницы. Сколько центнеров пшеницы собрало каждое звено с 1 га, если известно, что с 1 га во втором звене собрали на 5 ц пшеницы больше, чем в первом? Это условие поможет ввести х … Посмотрим, что получится? В этом случае мы «выйдем» сразу на ответ, ведь за х будет обозначена искомая величина.

Слайд 6

В другой столбик внесем Урожай, собранный каждым звеном Первый столбик – урожайность. Это условие поможет нам составить уравнение. х х + 5 S , га 1 2 А, ц урожайность, ц/га < на 2 га 875 920 875 х 920 х + 5 1. Одно звено собрало со своего участка 875 ц пшеницы, а другое звено с участка, меньшего на 2 га, — 920 ц пшеницы. Сколько центнеров пшеницы собрало каждое звено с 1 га, если известно, что с 1 га во втором звене собрали на 5 ц пшеницы больше, чем в первом? 875 х – 920 х+5 = 2 920 х + 5 = 875 х + 2 920 х + 5 – 2 875 х = 1 способ 2 способ 3 способ Из большей величины вычтем 2, уравняем с меньшей величиной  В новом столбике можно выразить площадь участков, для этого весь урожай : урожайность Из большей величины вычтем меньшую, разность равна 2  К меньшей величине прибавим 2, уравняем с большей величиной  Это условие поможет ввести х … Решив, любое из уравнений, мы сразу получим ответ на вопрос задачи, без дополнительных действий.

Слайд 7

Задачи на работу обычно содержат следующие величины: – время, в течение которого производится работа, – производительность труда, работа, произведенная в единицу времени (возможны и другие обозначения N, W ); – работа, произведенная за время t Уравнения, связывающее эти три величины: vt A  v A t  t A v  v A t

Слайд 8

Первый столбик – время, необходимое на выполнение работы каждым насосом отдельно. В другой столбик внесем выполненную работу – это 1 часть В новом столбике можно выразить производительность (скорость) работы, для этого работу : время х-2 х 1 2 1 1 1 х-2 2. При одновременной работе двух насосов пруд был очищен за 2 ч 55 мин. За сколько времени мог бы очистить пруд каждый насос, работая отдельно, если один из них может эту работу выполнить на 2 ч быстрее другого? справка справка справка Формула A = vt поможет нам составить уравнение  Скорость совместной работы находим сложением скоростей  Работа выполнена полностью, т.е. выполнена 1 часть  Это условие поможет ввести х … , часть/ч v , часть A , ч t 1 х t A v  1 х-2 1 х + v совм = A = 1 t = 1 х-2 1 х + = 1 35 12 Реши уравнение самостоятельно

Слайд 9

1 х-4 1 х + В новом столбике можно выразить производительность (скорость) работы, для этого работу : время = 5 Первый столбик – время, необходимое на выполнение работы каждой бригадой отдельно. В другой столбик внесем выполненную работу – это 1 часть х х- 4 1 2 1 1 1 х 3. Одна из дорожных бригад может заасфальтировать некоторый участок дороги на 4 ч быстрее, чем другая. За сколько часов может заасфальтировать участок каждая бригада, если известно, что за 24 ч совместной работы они заасфальтировали 5 таких участков? справка справка справка Формула A = vt поможет нам составить уравнение  Скорость совместной работы находим сложением скоростей  За 24ч заасфальтировали 5 участков, т.е. работа составляет 5 частей  Это условие поможет ввести х … , часть/ч v , часть A , ч t х- 4 1 t A v  1 х- 4 1 х + v совм = A = 5 t = 24 24 Реши уравнение самостоятельно

Слайд 10

В новом столбике можно выразить производительность (скорость) работы, для этого работу : время Первый столбик – время, необходимое на заполнение бассейна каждой трубе отдельно. В другой столбик внесем выполненную работу – это 1 часть х х- 5 1 2 1 1 1 х 4. Бассейн наполняется через первую трубу на 5 ч быстрее, чем через вторую. Бассейн можно наполнить, если открыть сначала первую трубу на 5 ч, а затем вторую на 7,5 ч. За сколько часов наполнится бассейн при совместной работе обеих труб? справка справка Найдем работу, которую выполнит I труба за 5 ч по формуле A = vt  Найдем работу, которую выполнит II труба за 7,5 ч по формуле A = vt  Это условие поможет ввести х … , часть/ч v , часть A , ч t х- 5 1 t A v  7,5 х A 1 = A 2 = 1 х- 5 5 1 = 1 = 1 х- 5 5 х 7,5 + Реши уравнение самостоятельно

Слайд 11

В новом столбике можно выразить производительность (скорость) работы, для этого работу : время Первый столбик – время, необходимое на выполнение всей работы каждой бригаде отдельно. В другой столбик внесем выполненную работу – это 1 часть х х- 12 1 2 1 1 1 х 5. На строительстве работали две бригады. После 5 дней совместной работы вторую бригаду перевели на другой объект. Оставшуюся часть работы первая бригада закончила через 9 дней. За сколько дней могла бы выполнить всю работу каждая бригада, работая отдельно, если известно, что второй бригаде на выполнение всей работы потребовалось бы на 12 дней меньше, чем одной первой бригаде? Это условие поможет ввести х … , часть/дн. v , часть A , дн. t х-12 1 t A v  = 1 = 1 5 справка справка справка По формуле A = vt найдем работу, выполненную за 9дн. I бригадой  Скорость совместной работы находим сложением скоростей  По формуле A = vt найдем работу, выполненную за 5дн. совместно  1 х- 12 1 х + v совм = A = A = 9 1 х- 12 1 х + 1 х + 1 х- 12 1 х + 5 1 х 9 Реши уравнение самостоятельно

Слайд 12

Задачи для самостоятельной работы. 1. Два экскаватора, работая одновременно, выполняют некоторый объем земляных работ за 3 ч 45 мин. Один экскаватор, работая отдельно, может выполнить этот объем работ на 4 ч быстрее, чем другой. Сколько времени требуется каждому экскаватору в отдельности для выполнения того же объема земляных работ? 2. Чтобы наполнить бассейн, сначала открыли одну трубу и через 2 ч, не закрывая её, открыли вторую. Через 4 ч совместной работы труб бассейн был наполнен. Одна вторая труба могла бы наполнить бассейн в 1,5 раза быстрее, чем одна первая. За сколько часов можно наполнить бассейн через каждую трубу? 3. Бригада слесарей может выполнить некоторое задание по обработке деталей на 15 ч быстрее, чем бригада учеников. Если бригада учеников отработает 18 ч, выполняя это задание, а потом бригада слесарей продолжит выполнение задания в течение 6 ч, то и тогда будет выполнено только 0,6 всего задания. Сколько времени требуется бригаде учеников для самостоятельного выполнения данного задания?

Слайд 13

Форма для поверки ответов. max 12 Задача 2. 1 насос 2 насос Задача 3. 1 бригада 2 бригада Задача 4. 1 бригада Задача 5. 1 бригада 2 бригада Задача 1. 1 экскав. 2 экскав. Задача 2. 1 труба 2 труба Задача 3. Бригада учеников Уравнения Задачи для самостоятельной работы

Слайд 14

мин., рыжий кот мин. Ответ: ч 2. Опытный дрессировщик может вымыть слона за 40 мин, а его сын – за 2 ч. За сколько времени они вымоют трех слонов, работая вместе? 1. Рыжий и серый коты вместе могут съесть миску сметаны за 6 мин. За сколько времени может съесть эту сметану каждый кот в отдельности, если рыжий кот ест сметану на 25 % быстрее, чем серый? max 5 Порой, не сразу узнаешь задачу на работу. Дополнительные задачи 3. В кинотеатре имеются две разные двери. Через обе двери зрители могут покинуть зал в течение мин. Если их выпускать через одну большую дверь, то выход из зала займет времени на 4 мин меньше, чем в том случае, если их выпускать через меньшую дверь. Сколько времени требуется, чтобы выпустить зрителей из зала через каждую дверь в отдельности? 4 3 3 Ответ: серый кот съест сметану за Ответ: через большую дверь мин, через маленькую —

1


Подготовка к ЕГЭ по математике Решение текстовых задач «на работу»

2


Результаты решения текстовых задач на ЕГЭ по математике.

3


Особенности решения задач «на работу». А=Р*t, где А-работа Р- производительность труда t- время Р=А/t t=А/Р Если в условии не дана вся работа, то её можно принять за 1 Общая производительность равна сумме производительностей.

4


Пример 1 Для наполнения плавательного бассейна водой имеются три насоса. Первому насосу для наполнения бассейна требуется времени в три раза меньше, чем второму, и на 2 ч больше, чем третьему. Три насоса, работая вместе, наполнили бы бассейн за 3ч, но по условиям эксплуатации одновременно должны работать только два насоса. Определите минимальную стоимость наполнения бассейна, если 1ч работы любого из насосов стоит 140 рублей. Решение: Эту задачу удобно решать с помощью таблицы.

5


РаботаВремя, часПроизводительность 1 насос 2 насос 3 насос ВМЕСТЕ X+2 3 X 3(х + 2) 1/X+2 1/3(X+2) 1/3 1/X

6


Алгоритм решения задачи 1. Внесем в таблицу известные величины ( работу примем за 1) 2. Одну из неизвестных величин обозначим за х. 3. Остальные неизвестные величины выразим через х, используя условие задачи или формулы.. 4Составим уравнение. 5. Решим уравнение и ответим на главный вопрос задачи.

7


Уравнение 1/х+2 + 1/3(х+2) + 1/х = 1/3 Решив уравнение, мы найдем х=6 6ч- время наполнения бассейна третьим насосом. Тогда время первого насоса 8ч, второго 24ч. Значит минимальное время работы двух насосов – это время работы 1 и3 насосов,т.е. 14ч Определим минимальную стоимость наполнения бассейна двумя насосами. 140*14=1960(руб.) Ответ: 1960 руб.

8


Реши сам! Два маляра, работая вместе, могут за 1ч покрасить стену площадью 40 кв.м. Первый маляр, работая отдельно, может покрасить 50 кв. м стены на 4ч быстрее, чем второй покрасит 90 кв.м такой же стены. За сколько часов первый маляр сможет покрасит 100 кв. м стены? Ответ: 4ч

9


Пример 2

10


Пример 3 Бак заполняют керосином за 2часа 30 минут с помощью трех насосов, работающих вместе. Производительности насосов относятся как 3:5:8. Сколько процентов объёма будет заполнено за 1час 18 минут совместной работы второго и третьего насосов?

11


Решение задачи Так как объём бака не указан, то примем объём бака за 1. Пусть коэффициент пропорциональности равен х, тогда производительности насосов соответственно равны 3х, 5х, 8х. И время наполнения бака при совместной работе всех трех насосов равно 1/3х+5х+8х = 1/ 16х или, по условию задачи, 2ч 30 мин. Решим уравнение 1/16х = 2,5 Х =1/ 40 Производительность второго насоса равна 1/ 40 * 5 = 1/ 8 Производительность третьего насоса равна 1/ 40 * 8 = 1/ 5. Совместная производительность второго и третьего насосов равна 1/ 8 + 1/ 5 =13/40 За 1ч 30мин второй и третий насосы наполнят 13/ 40 * 78/ 60 = 13/ 40 * 1,3 = 16,9/ 40 = 0,4225 объёма бака. Итак, при совместной работе 2 и 3 насосов за 1ч 18 мин будет заполнено 0,4225 *100% =42,25% объёма бака.

12


Реши сам ! Два фермера, работая вместе могут вспахать поле за 25 ч. Производительности труда первого и второго фермеров относятся как 2:5. Фермеры планируют работать поочередно. Сколько времени должен проработать второй фермер, чтобы это поле было вспахано за 45,5 ч? Ответ: 28 ч.

Подготовка к егэ

Задачи на совместную работу

Задачи на работу решаются с помощью одной-единственной формулы:

A — работа,

t — время,

P — производительность

Правила решения задач на работу

• 1. А = р∙t, из этой формулы легко найти t или p.
• 2. Если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу. Построен дом (один), покрашен забор (один), наполнен резервуар. А вот если речь идет о количестве кирпичей, количестве деталей, литрах воды —  работа как раз и равна этому количеству.
• 3. Если трудятся двое рабочих (два экскаватора, два мастера, Даша и Маша…) или трое (не важно) — их производительности складываются. Очень логичное правило.
• 4. В качестве переменной х удобно взять (в абсолютном большинстве задач) именно производительность.

Задача 1

• Заказ на 240 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?

Первый рабочий выполнил заказ на   час быстрее. Следовательно, времени он затрачивает на 1 час меньше, чем второй, то есть t 1     на 1   меньше, чем t 2 ,   значит

Очевидно, производительность рабочего не   может быть отрицательной величиной.   Значит, отрицательный корень не   подходит .

Ответ: 15

Задача 2

• На изготовление 40 деталей первый рабочий затрачивает на 6 часов  меньше, чем второй рабочий на изготовление 70 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй рабочий?

• Сравнение будем проводить по времени. Сказано, что первый затрачивает на 6 часов меньше, чем второй. Значит:

Ответ: 7

Задача 3

• Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 192 литра она заполняет на 4 минуты дольше, чем вторая труба?

• Первая труба заполняет резервуар на 4 минуты дольше, чем вторая. То есть времени уходит больше

Ответ: 12

Задача 4

• Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 19 часов. Через 1 час после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?

Сразу отметим, что производительность каждого рабочего

1/19 (заказа в час). Заказ это работа, она равна 1.

• Сумма сделанных ими объёмов работы составляет всю работу, равную 1.

Совместно рабочие работали 9 часов.

Значит, на весь заказ ушло 9 + 1 = 10 часов .

Ответ: 10

Задача 5

• Один мастер может выполнить заказ за 36 часов, а другой — за 12 часов. За сколько часов выполнят заказ оба мастера, работая вместе?

Пусть х это время, за которое мастера выполнят работу вместе.

Производительность первого 1/36 (заказа в час),

второго 1/12 (заказа в час),  этот  вывод мы сделали из условия задачи.

• При совместной работе производительности складываются:

Ответ: 9

Задача 6

• В помощь садовому насосу, перекачивающему 9 литров воды за 4 минуты, подключили второй насос, перекачивающий тот же объем воды за 6 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 30 литров воды?

Сразу,  исходя из условия, можно определить производительности насосов: 

у первого 9/4 (литра в минуту), у второго 9/6 (литра в минуту).

Пусть совместно они будут работать х  минут. 

Ответ: 8

Задача 7

• Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 12 вопросов теста, а Ваня — на 20. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 90 минут. Сколько вопросов содержит тест?

В данной задаче производительности даны:

у Пети 12 (вопросов в час), у Вани 20.

Количество вопросов это и есть работа, принимаем за её за х.

• Петя закончил свой тест на 90 минут позже Вани, то есть Петя затратил больше времени.
• Не забываем перевести минуты в часы: 90 минут это 1,5 часа.

Ответ:45

Задача 8

• Через одну трубу бассейн наполняется за 7 часов, а через другую опустошается за 8 часов. За какое время бассейн будет наполнен, если открыть обе трубы?

1 труба

p

1

2 труба

t

7

A

7

1

Вместе

1

7

?

8

1

?

1

• Сначала найдем производительность труда совместной работы обеих труб за один час. Поскольку одна труба бассейн наполняет, а другая — опустошает, производительность совместной работы равна разности производительности первой и второй труб:

Теперь найдем время, за которое бассейн будет наполнен при открытии обеих труб одновременно. Чтобы найти время работы, надо объем работы разделить на производительность труда:

Ответ:56

РЕШЕНИЕ ТЕКСТОВЫХ ЗАДАЧ
(задачи на работу)
Подготовка к ЕГЭ

• Колесникова Елена Васильевна, учитель математики
• МОУ «Борчанская СОШ» Валуйского района Белгородской области

Работу характеризуют три компонента
действия:

• Соотношение между этими величинами следующее:

• время работы — t;

• объем работы — A;

• производительность (количество произведенной работы в единицу времени) — p.

• время работы• производительность = объем работы

• t• p = A

Решение. Пусть машинистка должна печатать по норме х листов в день и выполнить работу за у дней. Заполним таблицу, используя условия задачи:

• Так как количество листов постоянно, то составим систему уравнений:
• ,

• Пример 1. Машинистка рассчитала, что если она будет печатать ежедневно на 2 листа более установленной для нее нормы, то закончит работу ранее намеченного срока на 3 дня; если же будет печатать по 4 листа сверх нормы, то окончит работу на 5 дней раньше срока. Сколько листов она должна была печатать?

• Следовательно, машинистка должна была напечатать за 15 дней 120 листов. Ответ: 120.

Пример 2. Бак заполняют керосином за 2 часа 30 минут с помощью трех насосов, работающих вместе. Производительности насосов относятся как 3:5:8. Сколько процентов объема будет заполнено за 1 час 18 минут совместной работы второго и третьего насосов?

• Решение. Так как объем бака не указан, то примем его за 1. Пусть коэффициент пропорциональности равен х, тогда производительности насосов соответственно равны 3х, 5х, 8х. И время наполнения бака при совместной работе всех трех насосов равно ,

• или, по условию задачи 2 часа 30 минут

Пример 3. Три насоса, работая вместе, заполняют цистерну нефтью за 5 часов. Производительности насосов относятся как 4:3:1. Сколько процентов объема цистерны будет заполнено за 8 часов совместной работы второго и третьего насосов?

Пример 4. Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?

Пример 5. На изготовление 475 деталей первый рабочий затрачивает на 6 часов меньше, чем второй рабочий на изготовление 550 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает первый рабочий?

Пример 6. Заказ на 110 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?

Пример 7. Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?

Пример 8. Двум сотрудникам поручили отредактировать рукопись объемом 560 страниц. Один сотрудник, отдав второму 80 страниц рукописи, взял остальные себе. Второй выполнил свою работу за время, в 8 раз меньшее, чем первый свою. Сколько страниц рукописи первый сотрудник должен был сразу отдать второму (взяв себе остальные), чтобы они, работая с прежней производительностью, выполнили свою работу за одинаковое время?

Пример 9. Два переводчика переводили рукопись. Первые 2 часа работал первый переводчик, следующие 6 часов они работали вместе. За это время было переведено 80% рукописи. Сколько часов потребовалось бы первому переводчику, чтобы перевести всю рукопись, если известно, что ему потребуется на эту работу на 4 часа меньше, чем второму?

Пример 10. Две бригады, работая вместе, ремонтировали дорогу в течение 6 дней, а затем одна вторая бригада закончила ремонт за 10 дней. За сколько дней могла бы отремонтировать дорогу одна первая бригада, если она может выполнить эту работу на 6 дней быстрее, чем одна вторая бригада?

Ресурсы

• http://nachalo4ka.ru/shkolnyie-kartinki-assorti-dlya-prezentatsiy/ картинка: геометрический набор
• http://tatyana-chulan.ucoz.ru/load/shablony_prezentacij_k_urokam_matematiki/1-1-0-1 шаблон презентации
• http://st.depositphotos.com/1000792/2981/v/450/depositphotos_29814419-Cartoon-penguin.jpg картинка
• http://crosti.ru/patterns/00/03/b5/57f1a3a2a1/picture.jpg картинка кот
• http://st.depositphotos.com/1967477/4237/v/950/depositphotos_42374805-stock-illustration-cute-mouse-cartoon.jpg картинка мышь
• http://lily-girls.ru/wp-content/2017/01/Nichego_malish_ne_znaet-_nebilici_sochinyaet_i_odet_kak_popugaj_Kto_zhe_eto-2.jpg картинка Незнайка
• https://img3.stockfresh.com/files/e/ensiferrum/m/32/449074_stock-photo-ancient-opened-book.jpg картинка книга
• http://clipart-work.net/data_gallery/clipart-cute-ape-royalty-free-vector-design-ytoIMm-clipart.jpg картинка мартышка
• http://st.depositphotos.com/2400497/2931/v/950/depositphotos_29310763-Cartoon-professor.jpg картинка ученый
• https://prikolnye-kartinki.ru/img/picture/Aug/13/65d38e443cd9cc61631dc799d8acd1dd/mini_1.jpg картинка попугай
• https://us.123rf.com/450wm/ciawitaly/ciawitaly1307/ciawitaly130700067/21186035 картинка сова
• Слонимская И.С. Математика: «Решение тестовых задач»: экспресс- репетитор для подготовки к ЕГЭ /И.С. Слонимская, Л.И. Слонимский. — М.: ACT: Астрель; Владимир: ВКТ, 2010. — 61, [3] с. — (Единый государственный экзамен).

Готовимся к ЕГЭ Несколько типов «задач на работу»

Подготовила

Учитель математики первой категориии

Гимназии №96

Бухараева Лариса Юрьевна

Задачи на работу  делятся на два типа:

• задачи, в которых  выполняется  раздельная работа  – эти задачи решаются аналогично задачам на движение.
• задачи на совместную работу.

Раздельная работа

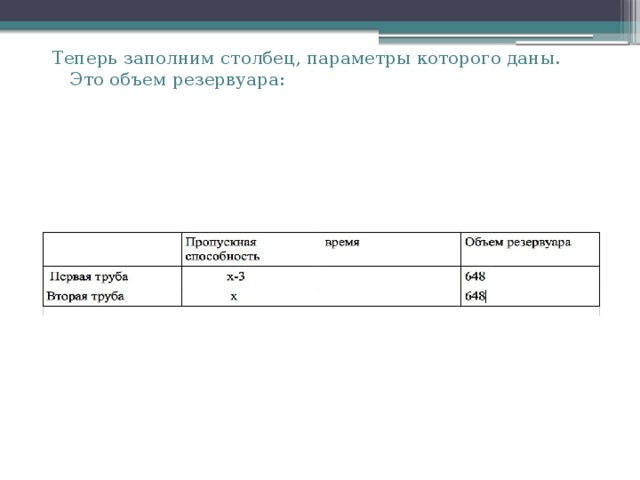
• Первая труба пропускает на 3л воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 648 л она заполняет на 3 мин. быстрее, чем первая труба?

В  задачах  мы имеем дело с тремя параметрами:

• пропускная способность трубы(А/t)  –    объем жидкости, который труба пропускает в единицу времени (л/мин);
• объем резервуара(A) , который необходимо заполнить, или, наоборот, освободить (л);
• Время(t)  (мин)

Эти параметры связаны таким соотношением:

A(работа)=A/t(производительность)*t(время)

В задаче спрашивается, сколько литров воды в минуту пропускает вторая труба – эту величину мы и примем за  . Поскольку по условию задачи первая труба пропускает на 3л воды в минуту меньше, чем вторая, то пропускную способность первой  трубы обозначим  .

Теперь заполним столбец, параметры которого даны. Это объем резервуара:

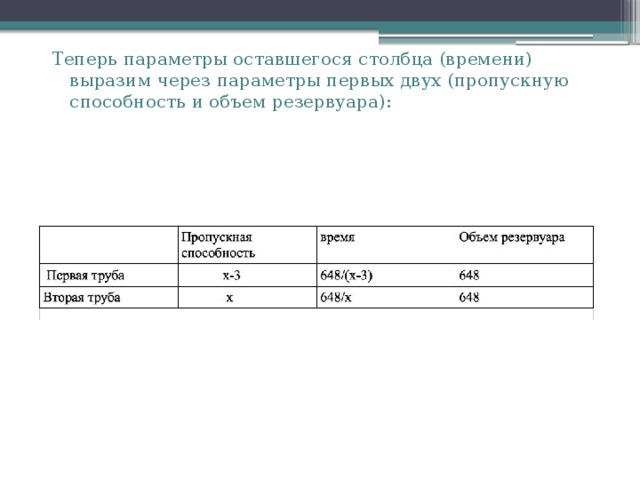
Теперь параметры оставшегося столбца (времени) выразим через параметры первых двух (пропускную способность и объем резервуара):

Составим уравнение:

Приравняем числитель к нулю, раскроем скобки и приведем подобные члены. Получим уравнение:

-24 —  не подходит по смыслу задачи.

Ответ: 27 л/мин.

Задача на совместную работу .

• Если в задаче встречаются слова «выполнили работу вместе» или слова «совместная работа», значит это  задача на совместную работу .

Объем работы , если он не указан отдельно,  принимаем равным 1 .

Вводим два неизвестных:

х – время выполнения всей работы кем-то (или  чем-то) первым

y — время выполнения всей работы кем-то (или  чем-то) вторым.

(В некоторых задачах «выгоднее» принять за неизвестные производительность)

Тогда

1/x  – производительность кого-то (или чего-то) первого

1/y  — производительность кого-то (или чего-то) второго

И в этом месте появляется параметр, которого не было в задачах на раздельную работу, а именно –  совместная производительность 

совместная производительность равна:

1/x+1/y 

Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша?

Объем работы = производительность * время.

• Про Машу нам все известно: время ее работы равно 20, следовательно, ее производительность равна 1/20.
• Пусть Даша пропалывает грядку за х минут, тогда ее производительность равна 1/x.
• Тогда  совместная производительность  равна:

1/20+1/x

Объем работы  примем равным 1.

Решим уравнение:

Классическая задача на совместную работу:

Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?

У нас 2 неизвестных, поэтому  будем составлять систему из двух уравнений.

По условию задачи,  первая труба наполняет резервуар на 6 минут дольше, чем вторая , следовательно время работы первой трубы на 6 минут больше, чем второй:

1) x=y+6

Обе трубы наполняют этот же резервуар за 4 минуты , следовательно, время совместной работы равно 4 минуты. Получаем второе уравнение системы:

2) (1/x + 1/y)*4=1

Получили систему уравнений:

-4 – не подходит по смыслу. Ответ: 6

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

• 

  2 слайд

  Задачи на работу.
  Математические модели
  «Текстовые задачи по математике», 8 класс.

• 

  3 слайд

  Устная работа.
  1. При каких значениях х имеет смысл выражения:

  х2 -4
  1

• 

  4 слайд

  2. Назовите наименьший общий знаменатель для каждой из следующих пар:

  и

  и
  5
  а-2
  15
  а-5
  5
  а2 -5а
  3а
  а+2

• 

  5 слайд

  3. Решить уравнения:
  х(х-5) =0;
  х2 -4х =0;
  х2 -4 =0;
  х2 +4 =0.

• 

  6 слайд

  Решите уравнение:

• 

  7 слайд

  Алгоритм решения дробных рациональных уравнений.

  Найти допустимые значения дробей, входящих в уравнение.
  Найти общий знаменатель дробей, входящих в уравнение.
  Умножить обе части уравнения на общий знаменатель.
  Сократить дроби.
  Решить получившееся уравнение.
  Исключить корни, не входящие в допустимые значения дробей уравнения.

• 

  8 слайд

  Решение:
  НОЗ= 6х(х+5)
  ОДЗ: х≠0; х≠-5
  6(х+5)+6х=х(х+5)

• 

  9 слайд

  6х+30+6х= х2 +5х

  Х2 +5х–6х -30-6х =0

  х2 -7х -30 =0
  D =49 +120 =169; D > 0

  х1 =10 х2 = -3
  Проверим, являются ли -3 и 10 корнями уравнения

• 

  10 слайд

  При х = -3
  6х(х +5)= -18(-3 +5) 0;
  При х =10
  6х(х +5)= 60(10 + 5) 0.

  Ответ: -3 и 10.
  ОДЗ: х≠0; х≠-5
  х1 =10
  х2 = -3
  Ответ: -3 и 10.

• 

  11 слайд

  Решение задач с помощью дробных рациональных
  уравнений

  Задачи на совместную работу
  Задачи на движение

• 

• 

• 

• 

  15 слайд

  Работа = производительность · время
  Задачи на работу обычно содержат следующие величины:
  t – время, в течение которого производится работа,

  – производительность труда, работа, произведенная в единицу времени (возможны обозначения N, v, W, Р);
  A – работа, произведенная за время t
  N·t
  A
  =
  t
  A
  N
  =

• 

  16 слайд

  Завод должен выпустить 45680 холодильников к определенному сроку…;
  Экскаватор должен выкопать траншею за месяц….;
  Тракторист вспахать 300га поля за день…;
  Бассейн наполнить водой за 10 ч….;
  Машинистка должна перепечатать рукопись за неделю…;
  Ученик решить 40 задач при подготовке к тесту за …..

  Каков объем работы?
  А= 45680 шт
  А= 1

• 

  17 слайд

  Решим задачу:
  №614

• 

  18 слайд

  Один штукатур может выполнить задание на 5 ч быстрее другого.
  Оба вместе они выполнят это задание за 6 ч. За сколько часов каждый из них выполнит это задание?
  №614
  О каком процессе идет речь в задаче?
  Какими величинами характеризуется этот процесс и как они взаимосвязаны?
  Сколько процессов в задаче?
  Что нужно узнать в задаче?

• 

  19 слайд

  1
  2
  2
  1
  1
  1
  1
  х
  Х+5
  6
  Один штукатур может выполнить задание на 5 ч быстрее другого.
  Оба вместе они выполняют это задание за 6 ч.
  Работа /время
  +
  =
  производительность совместной
  работы находим сложением производительностей

• 

  20 слайд

  Пусть все задание первый штукатур выполнит за х ч, тогда второй – за (х+5)ч.
  Принимая всю работу за 1, имеем:
  за 1 час первый штукатур выполнит
  всей работы; второй — за 1 ч всей работы.
  Тогда оба штукатура, работая вместе,
  выполняют за 1 час всей работы,

  что по условию задачи составляет всей работы. Составим и решим уравнение:
  где х > 6.

• 

  21 слайд

  Следовательно, первый штукатур выполнит задание за 10 ч, а второй за 15ч.
  Ответ : 10 ч , 15 ч

• 

  22 слайд

  Алгоритм решения задачи на совместную работу
  1. Внесем в таблицу известные величины ( работу примем за 1)
  2. Одну из неизвестных величин обозначим за х.
  3. Остальные неизвестные величины выразим через х, используя условие задачи или формулы.
  4. Составим уравнение.
  5. Решим уравнение и ответим на главный вопрос задачи.

• 

  23 слайд

  Решим задачу в группах:
  № 615

• 

  24 слайд

  Двое рабочих выполнили работу за 12 дней. За сколько дней может выполнить работу каждый рабочий, если одному из них для выполнения всей работы потребуется на 10 дней больше, чем другому?
  №615

• 

  25 слайд

  1
  2
  2
  1
  1
  1
  1
  х
  Х+10
  12
  Если одному из них для выполнения всей работы потребуется потребуется на 10 дней больше, чем другому.
  Двое рабочих выполнили работу за 12 дней.
  Работа /время
  +
  =
  производительность совместной
  работы находим сложением производительностей

• 

  26 слайд

  Умножим обе части уравнения на 12х(х+10).
  ОДЗ: х≠0; х≠-10
  12(х+10) + 12х = х(х+10)
  х2 — 14х – 120 = 0
  По обратной теореме Виета
  х1 = -6 не удовлетворяет смыслу задачи
  х2 = 20 удовлетворяет ОДЗ.
  Ответ: первому понадобится 20,
  а второму 30 дней чтобы выполнить эту работу
  самостоятельно.

• 

  27 слайд

  Итог
  Работа = производительность · время
  Задачи на работу обычно содержат следующие величины:
  – время, в течение которого производится работа,

  – производительность труда, работа, произведенная в единицу времени
  (возможны и другие обозначения N, v, W, Р);
  – работа, произведенная за время t

• 

  28 слайд

  Итог

  Если в условии не дана работа, то ее можно принять за 1.
  Общая производительность
  равна сумме производительности.

  Если в условии не дана работа, то ее можно принять за 1.
  Общая производительность
  равна сумме производительностей.

• 

  29 слайд

  Задачи, решаемые с помощью дробных рациональных уравнений, можно разделить на несколько групп:

  Задачи на движение по местности.
  Задачи на движение по воде.
  Задачи на работу.
  Задачи на покупку.
  Задачи на нахождение дробей и т.д.

• 

  30 слайд

  Есть ли сходство между процессами
  движение по местности.
  движение по воде.
  процесс на работу.
  процесс на покупку?
  Путь = скорость время
  Стоимость = цена количество
  Работа = производительность время

• 

  31 слайд

  Домашнее задание:
  № 616;617;
  746(в)

• 

  32 слайд

  1.Числитель обыкновенной дроби на 4 меньше ее знаменателя. Если к числителю этой дроби прибавить 19, а к знаменателю 28, то она увеличится на . Найдите эту дробь.
  2. Теплоход, собственная скорость которого 18 км/ч, прошел 50 км по течению реки и 8 км против течения, затратив на весь путь 3 часа. Какова скорость течения реки?
  3. Два комбайна убрали поле за 4 дня. За сколько дней мог убрать поле каждый комбайн, если одному из них для выполнения этой работы потребовалось бы на 6 дней меньше, чем другому?
  4. Моторная лодка прошла против течения 8 км и вернулась обратно, затратив на обратный путь на 30 мин меньше, чем при движении против течения. Найдите скорость лодки в неподвижной воде, если скорость течения равна 4 км/ч.
  5. Расстояние 700 км экспресс проходит на 4 часа быстрее товарного поезда, так как его скорость больше скорости товарного поезда на 20 км/ч. Определите скорость каждого из поездов, если известно, что они движутся с постоянной скоростью без остановок.

• 

  33 слайд

  6. Мастеру на выполнение заказа потребуется на 5 дней меньше, чем его ученику, но при совместной работе они выполнят заказ на 4 дня быстрее, чем мастер, работающий в одиночку. За сколько дней выполнит заказ мастер, работая в одиночку?
  7. На участке пути длиной 300 км поезд увеличил скорость на 10 км/ч, в результате чего прибыл на конечную станцию на 1 час раньше, чем планировалось по расписанию. С какой скоростью должен был идти поезд по расписанию?
  8. Прозаик хочет набрать на компьютере рукопись объемом 450 страниц. Если он будет набирать на 5 страниц в день больше, чем запланировал, то закончит работу на 3 дня раньше. Сколько страниц в день планирует набирать прозаик?
  9. Дорога между пунктами А и В состоит из подъема и спуска, а ее длина равна 19 км. Пешеход прошел путь из А в В за 5 часов. Время его движения на спуске составило 4 часа. С какой скоростью пешеход шел на спуске, если скорость его движения на подъеме меньше скорости движения на спуске на 1 км/ч?

• 

  34 слайд

  10. Велосипедист отправился с некоторой скоростью из города А в город В, расстояние между которыми равно 88 км. Возвращаясь из В в А, он ехал поначалу с той же скоростью, но через 2 часа пути вынужден был сделать остановку на 10 минут. После этого он продолжил путь в А, увеличив скорость на 2 км/ч, и в результате затратил на обратный путь столько же времени, сколько на путь из А в В. Найдите скорость велосипедиста на пути из А в В.
  11. Была куплена краска двух сортов. Краски первого сорта куплено на 3р., второго – на 2р., причем краски второго сорта куплено на 2 кг больше, чем первого, и 1кг краски второго сорта на 1р. Дешевле 1кг краски первого сорта. Сколько краски куплено первого сорта?

• 

  35 слайд

  Рефлексия
  Я работал(а) отлично, в полную силу своих возможностей, чувствовал(а) себя уверенно
  Я работал(а) хорошо, но не в полную силу, испытывал(а) чувство неуверенности, боязни, что отвечу неправильно
  У меня не было желания работать.
  Сегодня не мой день

• 

  36 слайд

  2
  2
  1
  1/2
  1/3
  1
  х
  Х
  Х+1
  Две машинистки присовместной работе затрачивают на 1 ч больше.
  Работа /время
  +
  =
  производительность совместной
  работы находим сложением производительностей
  №705(*)
  1

• 

  37 слайд

  Две бригады столяров делали стулья, причем первая бригада сделала 65 стульев, а вторая 66 стульев. Первая бригада делала за один день на два стула больше, чем вторая, но работала на один день меньше второй. Сколько стульев за один день делали две бригады вместе?

• 

  38 слайд

  65
  66
  Х+2
  Х
  2х+2
  На 1 день больше
  Первая бригада делала за 1 день на 2 стула больше, чем вторая

• 

• 

  40 слайд

  В новом столбике можно
  выразить производительность (скорость) работы,
  для этого
  работу : время
  Первый столбик – время, необходимое на выполнение всей работы каждому штукатуру отдельно.
  В другой столбик внесем выполненную работу –
  это 1 часть
  х
  Х+5
  1
  2
  1
  1
  1
  х
  Один штукатур может выполнить задание на 5 ч быстрее другого. Оба вместе они выполняют это задание за 6 ч.
  За сколько часов каждый из них выполнит задание?
  Это условие поможет ввести х …
  , часть/ч
  v
  , часть
  A
  , ч
  t
  Х+5
  1
  t
  A
  v
  =
  = 1
  = 1
  6
  справка
  справка
  Скорость совместной работы находим сложением скоростей
  
  По формуле A = vt найдем работу, выполненную за 6 ч совместно
  
  1
  1
  х
  +
  vсовм=
  A =
  A
  1
  Х+5
  1
  х
  +
  1
  Х+5
  1
  х
  +
  6
  Реши уравнение самостоятельно

• 

  41 слайд

  №614
  1
  1
  1
  х
  Х+5
  6
  Nсовм=N1 +N2

• 

  42 слайд

  Моделирование – один из ключевых видов деятельности человека.

  Проф. Н.А.Макарова

• 

  43 слайд

  А что мы понимаем под моделью?
  Что такое моделирование?
  Каковы этапы моделирования?

  Сегодня наша модель – дробные рациональные уравнение.

• 

Краткое описание документа:

Данная презентация позволяет наглядно и красочно показать ,как составить уравнение в задач на работу. эту презентацию можно использовать и для подготовки к ОГЭ и ЕГЭ.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 155 062 материала в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»

• Курс повышения квалификации «Разработка бизнес-плана и анализ инвестиционных проектов»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Страхование и актуарные расчеты»

• Курс повышения квалификации «Финансы предприятия: актуальные аспекты в оценке стоимости бизнеса»

• Курс повышения квалификации «Использование активных методов обучения в вузе в условиях реализации ФГОС»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс повышения квалификации «Мировая экономика и международные экономические отношения»

• Курс профессиональной переподготовки «Организация системы менеджмента транспортных услуг в туризме»

• Курс профессиональной переподготовки «Техническая диагностика и контроль технического состояния автотранспортных средств»