Слайд 1
Виды экономических задач на ЕГЭ и способы их решения (профильный уровень) …читал Адама Смита и был глубокий эконом, то есть умел судить о том, как государство богатеет и чем живет и почему не нужно золота ему, когда простой продукт имеет. Отец понять его не мог и земли отдавал в залог. А.С. Пушкин о герое романа « Евгений Онегин».
Слайд 3
Спецификация КИМ ЕГЭ 2021 по математике (фрагмент)
Слайд 4
Кодификатор требований к уровню подготовки выпускников образовательных организаций для проведения единого государственного экзамена по математике
Слайд 5
Кодификатор элементов содержания по МАТЕМАТИКЕ для составления контрольных измерительных материалов для проведения единого государственного экзамена
Слайд 6
Проценты
Слайд 7
Простые задачи.
Слайд 9
Кредиты
Слайд 11
Задача
Слайд 13
Задача 31 декабря 2014 года Дмитрий взял в банке 4290000 рублей в кредит под 14,5% годовых . Схема выплаты кредита следующая — 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг на 14,5%), затем Дмитрий переводит в банк Х рублей . Какой должна быть сумма Х, чтобы Дмитрий выплатил долг двумя равными платежами ( то есть за два года )?
Слайд 14
Пусть сумма кредита равна S , а годовые составляют а% . Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент равный р=1 + 0,01а. После первой выплаты сумма долга составит : S 1 = S P — X После второй выплаты сумма долга составит : S 2 = S 1P — X = ( S P — X) p -X = S P 2 — ( 1 + p)X По условию двумя выплатами Дмитрий должен погасить кредит полностью , поэтому : S P 2 — ( 1 + p)X = 0 X = S P 2 /( 1 + p) X = 4290000* 1.311025/ 2622050 Откуда при S = 4290000 и а = 14,5, получаем : р = 1,145 и Ответ : 2622050.
Слайд 15
Задача 31 декабря 2014 года Георгий взял в банке кредит 1 млн рублей в кредит . Схема выплаты кредита следующая – 31 декабря каждого года банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг на а %), затем Георгий переводит очередной транш . Георгий выплатил кредит за два транша , переведя в первый раз 570 тыс рублей , во второй599,4 тыс рублей . Под какой процент банк выдал кредит Георгию ?
Слайд 16
Пусть сумма кредита равна S, а годовые составляют а %. Тогда 31 декабря каждого года оставшаяся сумма долга умножается на коэффициент р= 1 + 0,01a. После первой выплаты сумма долга составит : S 1 = S P — X Исходя из условия после первой выплаты долг Георгия будет равен : S 1 = 430000+ 10000 a сумма долга составит S 2 = S 1 p – X или S 2 = a 2 +143a — 1694 При условии , что кредит был погашен за два транша , то это сумма должна равняться 0. Получим уравнение : a 2 +143a – 1694 = 0 Отсюда а =11%. Ответ : 11%.
Слайд 17
Задача 1 января 2015 года Александр Сергеевич взял в банке 1,1 млн рублей в кредит . Схема выплаты кредита следующая — 1 числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга ( то есть увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платёж . На какое минимальное количество месяцев Александр Сергеевич может взять кредит , чтобы ежемесячные выплаты были не более 275 тыс . рублей ?
Слайд 18
Решение. Заметим , что за 4 месяца Александр Сергеевич выплатит 275 000∙4= 1,1 млн рублей . Таким образом , он не покроет долг с процентами . Каждый месяц долг увеличивается не более , чем на 1100000∙ 0,01 = 11000 рублей . Значит , за пять месяцев Александр Сергеевич должен будет выплатить не более 1100000 + 5∙11000 = 1155000 рублей , что менее , чем 5∙ 275000 = 1375000 рублей . Таким образом , Александр Сергеевич сможет выплатить кредит за 5 месяцев . Ответ : 5.
Слайд 19
Задача.
Слайд 22
КРИТЕРИИ Содержание критерия, задание 17 Баллы Обоснованно получен верный ответ 3 Верно построена математическая модель, решение сведено к исследованию этой модели и получен результат: — неверный ответ из-за вычислительной ошибки; — верный ответ, но решение недостаточно обосновано 2 Верно построена математическая модель, решение сведено к исследованию этой модели, при этом решение может быть не завершено 1 Решение не соответствует ни одному из критериев, перечисленных выше 0 Максимальный балл 3
Слайд 23
Подробнее: 1 балл можно выставлять в тех случаях, когда сюжетное условие задачи верно сведено к решению математической (арифметической, алгебраической, функциональной, геометрической) задачи. Именно к решению, а не к отдельному равенству, набору уравнений, уравнению, задающему функцию, и т .п. Предъявленный текст должен включать и описание того, как построена модель, и направление, «продолжаемое» до верного решения. Оценка в 2 балла, разумеется, включает в себя условие выставления 1 балла, но существенно ближе к верному решению задачи. Здесь предполагается завершенное, практически полное решение соответствующей математической задачи. Типичные допустимые погрешности здесь – вычислительные ошибки (при наличии всех шагов решения) или пробелы в описании составления модели. «МЕТОДИЧЕСКИЕ РЕКОМЕНДАЦИИ ПО ОЦЕНИВАНИЮ ВЫПОЛНЕНИЯ ЗАДАНИЙ С РАЗВЕРНУТЫМ ОТВЕТОМ»
- Московская область, г. Королёв
- Учитель математики МАОУ ЛНИП:
- Ткаченко Лидия Анатольевна
ЗАДАЧИ C ЭКОНОМИЧЕСКИМ СОДЕРЖАНИЕМ в ЕГЭ
Простые проценты. Налоги.
- если величина А больше величины В на p%, то
- если величина А меньше величины В на p%, то
Сложные проценты. Вклады.
- 2) при последовательном изменении величины на в течение n периодов, она становится равной
- где величины могут быть как положительными при увеличении величины на p%, так и отрицательными при уменьшении величины на p%.
или
1) Величина S0 , увеличиваемая на p% в течение n периодов в конце n-го этапа становится равной
Кредиты
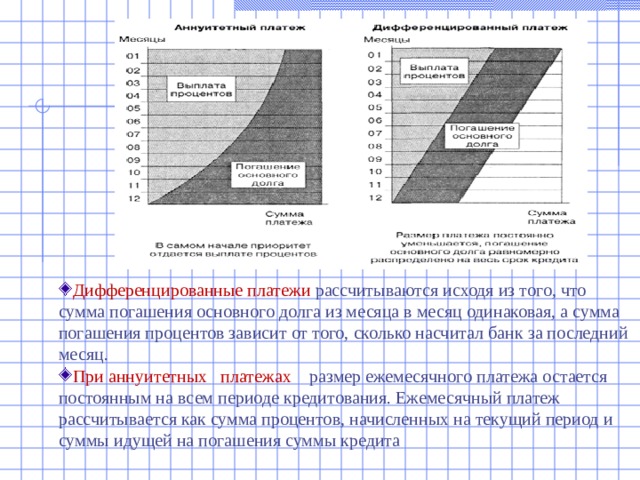
- Выбирая кредитную программу, потенциальные заемщики ориентируются на процентную ставку по кредиту. Таких методов существует два: дифференцированные платежи и аннуитетные платежи.
- Дифференцированные платежи характерны тем, что задолженность по кредиту погашается равномерно начиная с самых первых выплат, а проценты начисляются на фактический остаток. Таким образом, каждый последующий платеж меньше предыдущего.
- Аннуитет — начисление равных платежей на весь срок погашения кредита. При этом в первой половине срока погашения задолженность по кредиту практически не гасится — выплачиваются в большей части проценты. Эта особенность делает платежи относительно небольшими, но увеличивает общую сумму начисляемых процентов.
- Чтобы наглядно показать разницу в погашении кредита при разных методах начисления платежей, приведем графики погашения кредита в размере 1 000 000 руб., взятого на 20 лет при 12% годовых (серым выделена выплата процентов по кредиту, синим — выплата тела кредита).
График погашения кредита дифференцированными платежами
График погашения кредита аннуитетными платежами
Кредиты
Дифференцированные платежи дают линейную зависимость от погашения кредита: чем меньше должен — тем меньше начислили процентов.
Сумма и срок досрочного погашения ничем не ограничены.
Досрочное погашение в аннуитетной схеме лишь сокращает срок выплаты кредита: на графике «срезаются» последние платежи и отпадает необходимость платить соответствующие им проценты, которые в конце графика как раз очень малы.
Таким образом, в аннуитетной схеме досрочное погашение невыгодно.
Теорема об аннуитетных платежах
- Обобщая вышеприведенные рассуждения на случай n платежных периодов (дней, месяцев, лет), получим общие формулы, связывающие сумму кредита , коэффициент, где q% — процентная ставка за период, величину текущего долга и постоянную выплату х:
- и тогда
;
;
Теорема о дифференцированных платежах.
- Повторив решение предыдущей задачи для n месяцев, получим общие формулы для дифференцированных платежей.
- Пусть на n платежных периодов (дней, месяцев, лет) в кредит взята сумма , причем каждый платежный период долг сначала возрастет на q% по сравнению с концом предыдущего платежного периода, а затем вносится оплата так, что долг становится на одну и ту же сумму меньше долга на конец предыдущего платежного периода. Тогда величина переплаты П и полная величина выплат В за все время выплаты кредита даются формулами
1. Вклад А: 10% в год на 3 года
n — % вклада, k – количество лет, S – первоначальный взнос,
– сумма в конце k-го года
2. Вклад Б: 5% в первый год
– в конце первого года,
n % — на второй и третий год
– сумма за третий год.
Задача 1. По вкладу «А» банк начисляет 10% каждый год, а по вкладу «Б» — 5% в первый год и n % за второй и третий годы. Найдите наименьшее целое значение n, при котором за 3 года хранения вклад «Б» окажется выгоднее вклада «А» при одинаковых суммах первоначальных взносов.
Решение
По условию,
Ответ:
12,6
0
-212,6
+
—
+
Решение
Пусть в k-тый год гражданин продает бумагу и кладет средства на счет в банк.
Выгодно класть в банк, когда 10% от текущей цены бумаги будут больше 2 тысяч рублей.
- (7 + 2k) тысяч рублей ЦЕНА БУМАГИ.
2) Затем он кладет в банк под 10% годовых на (30 – k) лет:
– финальная сумма.
должна быть наибольшей,
Задача 2. Гражданин приобрел ценную бумагу за 7 тысяч рублей. Цена бумаги возрастает каждый год на 2 тысячи рублей. В любой момент гражданин может продать бумагу и положить вырученные деньги на банковский счет под 10% начислений в год. В течение какого года после покупки гражданин должен продать ценную бумагу, чтобы через 30 лет после покупки этой бумаги сумма на банковском счете была наибольшей?
— разность между двумя соседними значениями,
Если , то выгодно держать ценную бумагу на руках,
Если , то выгодно класть на счет под %.
Ответ: лет
Решение
Наибольшая выплата
Наименьшая выплата
Сумма кредита , на 9 лет разница между июлями
Каждый раз между июлями — ?
Задача 3.В июле планируется взять кредит на сумму 4,5 млн рублей сроком на 9 лет. Условия его возврата таковы:
— каждый январь долг возрастает на n % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить некоторую часть долга;
— каждый июль сумма долга должна отличаться от предыдущего на равную сумму.
Найдите целое число n, если наибольшая выплата за все время не превышает 1,4 млн рублей, а наименьшая выплата не менее 0,6 млн рублей.
Решение
июль
Январь (набегает
)
Выплаты февраль-июнь
1
2
3
4
…
8
9
Наибольшая выплата – первая, т.е.
Наименьшая выплата – последняя, т.е.
Вспомним, что
Ответ:
Решение
– сумма кредита,
– ежегодный платеж,
— годовые проценты,
– сумма долга умножается на этот коэффициент 31 декабря.
Задача 4. 31 декабря 2013г. Сергей взял в банке 9 930 000 руб. в кредит под 10% годовых.
Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т.е. увеличивает долг на 10%), затем Сергей переводит в банк определенную сумму ежегодного платежа.
Какова должна быть сумма ежегодного платежа, чтобы Сергей выплатил долг тремя равными ежегодными платежами?
Решение
остаток на счете
начисление % 31 декабря
выплаты
1
2
3
4
0
Решение
Ответ:
Задача 5.
Гражданин берет 15 января в банке кредит на 19 месяцев. Условия кредита таковы:
— 1 числа каждого месяца долг возрастает на по сравнению с концом предыдущего месяца,
— со 2 по 14 число каждого месяца необходимо выплатить часть долга,
— 15 числа каждого месяца долг должен быть на одну и ту же сумму меньше, чем долг на 15 число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите
Решение
– сумма кредита,
– сумма долга умножается на этот коэффициент 1 числа каждого месяца; в следующий раз набегает k
|
15 января |
начисление % 1 числа |
выплаты |
1
2
3
…
Решение
Но общая сумма выплат на 30% больше суммы кредита, т.е.
Суммируем и приравняем выплаты:
Гаусс
Решение
Но
Ответ:
Список литературы:
1) Математика. ЕГЭ. Задача с экономическим содержанием: учебно-методическое пособие. / под ред. Ф.ф.лысенко и с.ю.кулабухова, ростов-на-дону:легион, 2015. – 80с.
2) ЕГЭ. Математика. Профильный уровень: типовые экзаменационные варианты: 36 вариантов / под ред. и.в.ященко, издательство “национальное образование”, 2017 – 256с.
3) Д.д.гущин, курс лекций по подготовке к егэ.
Веб-страница курса с актуальными материалами: http://reshuege.ru/course?id=2610 Издание 2, дополненное. — 05.04.2016
1. «Экономическая» задача в ЕГЭ по математике (профильный уровень № 17)
Издательство «Легион»
«Экономическая» задача в ЕГЭ
по математике
(профильный уровень № 17)
Фридман Елена Михайловна
2. Задача.
2
3. Из материалов аналитического отчета ФИПИ
3
4.
Задачи на оптимальный
выбор
Банки, вклады, кредиты
Производственные
задачи
4
5.
5
6. Задача 1
Два велосипедиста равномерно движутся по
взаимно
перпендикулярным
дорогам
по
направлению к перекрестку этих дорог. Один из них
движется со скоростью 40 км/ч и находится на
расстоянии 5 км от перекрестка, второй движется со
скоростью 30 км/ч и находится на расстоянии 3 км
от перекрестка.
Через сколько минут расстояние между
велосипедистами станет наименьшим? Каково будет
это наименьшее расстояние?
6
7. Решение.
7
8.
Способ 1
Наименьшим расстояние станет
через 0,116 часа,
т.е через 6,96 минут.
Наименьшее расстояние равно 0,6.
8
9. Способ 2
9
10.
10
11.
11
12. Задача 2
У фермера есть два поля площадью 10 га. На каждом
поле можно выращивать картофель и свеклу. Поля можно
делить между этими культурами в любой пропорции.
Урожайность картофеля на первом поле составляет
300 ц/га, а на втором — 200 ц/га Урожайность свеклы на
первом поле составляет 200 ц/га, а на втором – 300 ц/га.
Фермер может продавать картофель по цене 10 000 р/ц,
а свеклу – по цене 13 000 р/ц. Какой наибольший доход
может получить фермер?
12
13. Решение.
13
14.
с=4х-19у+650. Наибольшее с — ?
Чем больше с, тем ниже прямая. Подставим координаты
точки (10;0) в уравнение прямой и найдем наибольшее
с=690, тогда
с 105 690 105 69000000 рублей.14
15. Задача 3
Предприниматель купил здание и собирается открыть в
нем отель.
В отеле могут быть стандартные номера площадью 21
квадратный метр и номера «люкс» площадью 49
квадратных метров.
Общая площадь, которую можно отвести под номера,
составляет 1099 квадратных метров.
Предприниматель может поделить эту площадь между
номерами различных типов как хочет.
Обычный номер будет приносить отелю 2000 рублей в
сутки, а номер «люкс» 4500 рублей в сутки.
Какую наибольшую сумму денег сможет заработать в
сутки на своем отеле предприниматель?
15
16. Решение.
Пусть в отеле x обычных номеров и y номеров «люкс»
21x+49y=1099.
f(x,y)= 2000x+4500y=500(4x+9y).
fнаиб- ?
1099 49 y
x
21
f ( y ) 500(4
f(y) – убывающая.
1099 49 y
4396 1
9 y ) 500(
y)
21
21 3
1099 49 y 21
y 22
Если y=1 , то x=50.
fнаиб=f(50) =2000·50+4500·1= 104500 (руб.)
16
17. Задача 4
Вкладчик положил две одинаковые суммы под
r % годовых в банки «А» и «Б».
Через год условия по вкладу «А» изменились, и
он понизил годовую ставку до 8 % годовых, в
то время как банк «Б» оставил годовую ставку
на прежнем уровне.
Найдите, при каком наименьшем целом r вклад в
банке «Б» через три года будет по крайней
мере на 16 % больше, чем вклад в банке «А».
17
18. Решение.
Вклад в банк «А»
Вклад в банк «Б»
Годы
%
Сумма в
начале года
1
r
n
2
8
r
(1
)n
100
3
8
r
8
(1
)(1
)n
100
100
Сумма в конце
года
% Сумма в
начале года
r
)n
100
r
r
8
(1
)(1
)n
100
100
r
(1
(1
r
8 2
)(1
) n
100
100
r
n
Сумма в
конце года
(1
r
)n
100
2
r
1
n
100
r
(1
)n
100
2
r
1
n
100
3
r
1
n
100
100 r 116 10,8
r 3 116
r
8 2
116 10,77
n(1
)
(1
)(1
) n
100
100
100
100
r 116 10,8 100
r 2 116
8 2
(1
)
(1
)
r 10,77 10,8 100 16,64
100
100
100
r
116
8
r = 17
(1
)
(1
)
18
100
10
100
19. Задача 5
Часть денег от суммы 400 млн. рублей
размещена в банке под 12% годовых, а другая часть
инвестирована в производство, причем через год
эффективность вложения ожидается в размере 250%
(т.е. вложенная сумма х млн. рублей оборачивается в
капитал 2,5х млн. рублей), затем отчисляются деньги
на издержки, которые задаются квадратичной
зависимостью 0,0022х2. Разность между капиталом и
издержками в производстве облагается налогом в
20%. Как распределить капитал между банком и
производством, чтобы через год получить общую
максимальную прибыль от размещения денег в банк
и вложения денег в производство? Сколько млн.
рублей составит эта прибыль?
19
20. Решение.
Производство
Банк
Вложено
x
400-x (под 12% год)
Через год
2,5x
1,12(400-x)
Издержки
0,0022 x
Налог
20 %
Итого
2
2
0,8(2,5x-0,0022 x )
1,12(400-x)
Функция прибыли
f(x)=1,12(400 – х)+0,8·(2,5х – 0,0022х2) – 400
f(x) =-0,8·0,0022х2+0,88х+48.
fнаиб = f(250) =-0,8·0,0022·2502+0,88·250+48=
= -110+220+48=158 (млн. рублей).
20
Ответ.158
21. Задача 6
21
22.
Решение.
способ 1
23.
24.
Способ 2
25.
Способ 3
26.
27. Задача 7
В банк помещён вклад 64 000 рублей под 25%
годовых. В конце каждого из первых трёх лет
(после
начисления
процентов)
вкладчик
дополнительно положил на счёт одну и ту же
фиксированную сумму. К концу четвёртого года
после начисления процентов оказалось, что он
составляет 385 000 рублей. Какую сумму (в
рублях) ежегодно добавлял вкладчик?
27
28. Решение.
Пусть x рублей вкладчик добавлял в конце каждого из
первых трёх лет. Тогда на счету в конце
1-го года 1,25·64 000+x =80 000+x рублей, в конце
2-го года – 1,25(80 000+x)+x рублей, в конце
3-го года – 1,25 (1,25(80 000+x)+x)+х рублей, в конце
4-го года – 1,25(1,25 (1,25(80 000+x)+x)+х) =385 000
рублей
28
29.
Задача 8
29
30.
30
31.
Задача 9
31
32.
32
33.
33
34. Задача 10
Семен Петрович положил 8000 рублей
в сберегательный банк. По истечении года к
его вкладу были добавлены деньги,
начисленные в качестве процентов, и,
помимо этого, Семен Петрович увеличил
свой вклад на 1360 рублей. Еще через год
он решил снять 1440 рублей, а остальные
9360 рублей положил на новый срок. Чему
равна процентная ставка в этом банке?
34
35.
35
36.
36
37.
Задача 11
38.
39.
40.
Кредиты
Задача 12
40
41.
41
42. Задача 13
Алексей взял кредит в банке на срок 17 месяцев. По
договору Алексей должен возвращать банку часть денег в
конце каждого месяца.
В конце каждого месяца к оставшейся сумме основного
долга добавляется r% этой суммы и своим ежемесячным
платежом Алексей погашает эти добавленные проценты и
уменьшает сумму долга.
Ежемесячные платежи подбираются так, чтобы сумма долга
уменьшалась на одну и ту же величину каждый месяц ( на
практике такая схема называется «схемой с
дифференцированными платежами»).
Известно, что общая сумма, выплаченная Алексеем банку за
весь срок кредитования, оказалась на 27% больше, чем
сумма, взятая им в долг. Найдите r.
42
43. Решение.
Месяц
1
Начислено
Cумма
N
Отдал
N+
N+
…
…
Должен
2
3
…
…
17
…
0
Ответ. 3
43
44. Задача 14
44
45. Задача 15
45
46.
Решение.
Ответ: 8 788 000 рублей
47.
Задача 16
47
48.
Решение.
n – срок кредита (целое число лет), 1-ая
составляющая выплат – ежегодный платеж по
кредиту x . Тогда
10
10-x
10-2x
…,
10-nx
– последовательность выплат 1-ой составляющей
по кредиту.
10-nx=0,
откуда
48
49.
Вторая составляющая — выплата процентной ставки
49
50.
31
51.
Критерии
Содержание критерия, задание 17
Баллы
Обоснованно получен верный ответ
Верно построена математическая модель, решение
сведено
к исследованию этой модели и получен результат:
— неверный ответ из-за вычислительной ошибки;
— верный ответ, но решение недостаточно обосновано
Верно построена математическая модель, решение
сведено к исследованию этой модели, при этом
решение может быть не завершено
Решение не соответствует ни одному из критериев,
перечисленных выше
Максимальный балл
3
2
1
0
3
51
52.
Оценка
эксперта:
0 баллов
52
53. Задача 17
53
54.
Решение.
Пусть S – сумма кредита.
1,04(S+0,9S+0,8S+0,7S+0,6S+0,5S)-(S+0,9S+0,8S+0,7S+0,6S+0,5S)=
=0,04(S+0,9S+0,8S+0,7S+0,6S+0,5S) = 0,04·4,5S=0,18S.
Переплата составит 18%.
Ответ. 18 %
54
55.
Задача 18
55
56.
56
57.
Задача 19
57
58.
58
59.
Книги можно заказать в нашем
интернет-магазине на сайте:
www.legionr.ru
Спрашивайте
в книжных магазинах города!
59
60. Спасибо за внимание!
60
Слайд 1Экономические задачи
Подготовка к ЕГЭ.
Задание № 17
Учитель: Шарова Светлана Геннадьевна,
МБОУ «Гимназия», г.
Урюпинск, Волгоградская область

Слайд 2Экономические задачи
Под задачами с экономическим содержанием будем понимать задачи, поставленные в области экономики,
решение которых требует использования математического аппарата.

Слайд 3В 2018 году в ЕГЭ такие задачи входят в задание под
№ 17. В спецификаторе профильного уровня в графе «примерное время выполнения» задачи повышенной сложности составляет 35 минут как на задачу с параметром. За правильно решенную задачу можно получить максимально 3 балла за обоснованный и правильный ответ, то есть эта задача считается одной из самых сложных. При любой вычислительной ошибке могут быть сняты 1 или 2 балла.

Слайд 5Анализ банка задач ЕГЭ по математике, а также демоверсии ЕГЭ 2018
года позволил выделить основные подходы к решению задач с практическим содержанием:
1. решение с помощью формул;
2. решение задач в общем виде;
3. решение задач с использованием свойства степеней;
4. решение задач с помощью математического анализа;
5. решение задач методом сравнения.

Слайд 6Все представленные в банке ЕГЭ задачи можно условно разделить
на группы
и подгруппы:
Группа I банковские задачи на вклады
1) нахождение срока вклада;
2) вычисление процентной ставки по вкладу;
3) нахождение суммы вклада;
4) нахождение ежегодной суммы пополнения вклада
Группа II банковские задачи на кредиты:
1) нахождение количества лет выплаты кредита;
2) вычисление процентной ставки по кредиту;
3) нахождение суммы кредита;
4) нахождение ежегодного транша.
Группа III задачи, не связанные с банковскими операциями.

Слайд 7В июле 2026 года планируется взять кредит в банке на три
года в размере S млн. руб., где S — целое число. Условия его возврата таковы:
— каждый январь долг увеличивается на 25% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга;
в июле каждого года долг должен составлять часть кредита в соответствии со следующей таблицей.
Найдите наибольшее значение S, при котором каждая из выплат будет меньше 4 млн. рублей.
Задача 1
Слайд 8Решение.
Долг перед банком (в млн. рублей) на июль каждого года должен
уменьшаться до нуля следующим образом:
По условию, в январе каждого года долг увеличивается на 25%, значит, долг в январе каждого года равен:
1,25S; 1,25∙0,8S; 1,25∙0,5S
Следовательно, выплаты с февраля по июнь каждого года составляют:
1,25S — 0,8S = 0,45S
1,25∙0,8S — 0,5S = 0,5S
1,25∙0,5S – 0 = 0,725S
По условию, каждая из выплат должна быть меньше 4 млн. рублей.
Это будет верно, если максимальная из выплат меньше 4 млн.рублей, т. е.
0,725S< 4;
S< 6,4
S = 6
Наибольшее целое решение этого неравенства – число 6. Значит, искомый размер кредита 6 млн. рублей.

Слайд 9Задача 2
В июле 2020 года планируется взять кредит в банке на
некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Если ежегодно выплачивать по 58 564 рубля, то кредит будет полностью погашен за 4 года, а если ежегодно выплачивать по 106 964 рубля, то кредит будет полностью погашен за 2 года. Найдите r.

Слайд 10Решение.
,
,
Пусть сумма кредита S. По условию долг увеличивается на r% по
сравнению с концом предыдущего года
,т. е. в раз.
Пусть
Долг меняется так:
Долг за 4 года погашен, значит

Слайд 11Если долг выплачен двумя платежами
,

Слайд 12Задача 3
В июле 2020 года планируется взять кредит в банке на
сумму 300 000 рублей. Условия его возврата таковы:
— каждый январь долг увеличивается на r% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Найдите r, если известно, что кредит будет полностью погашен за два года, причем в первый год будет выплачено 260000 рублей, а во второй год – 169 000 рублей.

Слайд 13Решение.
Изначально была взята сумма долга, равная 300000 рублей.
По условию задачи сначала
сумма долга увеличивается на r%, т.е. в раз, получаем сумму 300000k.
После этого вносится платеж, равный 260000 рублей.
Остаток суммы долга становится равным 300000k-260000 рублей
В следующем году остаток также увеличивается в k раз
и вносится сумма в 169000 рублей:
По условию задачи за два года долг гасится полностью, т. е. , имеем уравнение:

Слайд 14Задача 4
В июле 2020 года планируется взять кредит в банке на
некоторую сумму. Условия его возврата таковы:
— каждый январь долг увеличивается на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить одним платежом часть долга.
Сколько рублей будет выплачено банку, если известно, что кредит будет полностью погашен тремя равными платежами (то есть за три года) и общая сумма выплат после полного погашения кредита на 48 250 рублей больше суммы, взятой в кредит?

Слайд 16Задача 5
15-го января планируется взять кредит в банке на 9 месяцев.
Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. Найдите r.

Слайд 17Дифференцированный платеж-это такая система выплат, при которой сумма долга уменьшается равномерно,
т. е. на одну и ту же величину каждый год( месяц). При этом платежи каждый год разные.

Слайд 19Все выплаты:
(арифметическая прогрессия)
По условию:
Ответ: 5%

Слайд 2115-го января планируется взять кредит в банке на 9 месяцев. Условия
его возврата таковы:
— 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. Найдите r.
Решение.
Ответ: 5%
2 способ

Слайд 22Задача 6
15-го января планируется взять кредит в банке на несколько месяцев.
Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 5% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. Найдите, на сколько месяцев был взят кредит.

Слайд 2315-го января планируется взять кредит в банке на несколько месяцев. Условия
его возврата таковы:
— 1-го числа каждого месяца долг возрастает на 5% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца.
Известно, что общая сумма выплат после полного погашения кредита на 25% больше суммы, взятой в кредит. Найдите, на сколько месяцев был взят кредит.
Решение.
Ответ: 9 месяцев.

Слайд 24Задача 7
В июле планируется взять кредит в банке на сумму 5
млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн. рублей?

Слайд 25В июле планируется взять кредит в банке на сумму 5 млн.
рублей на некоторый срок (целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 20% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 7,5 млн. рублей?
Решение.
Ответ: 4 года

Слайд 26Задача 8
Взяли кредит 177 120 рублей в банке на четыре года под
25% годовых и выплатили четырьмя равными платежами. Чему будет равна общая сумма выплат после полного погашения кредита?
Решение.
Ответ: 300000 рублей

Слайд 1ЕГЭ 2020. Математика
Задачи с экономическим
содержанием
Задача 17 (профильный уровень)

Слайд 2Типы таких задач:
задачи на чтение и анализ данных, представленных
в виде графиков, диаграмм и таблиц,
простейшие текстовые арифметические задачи на
товарно-денежные отношения (в основном на оплату товаров и услуг),
арифметические текстовые задачи на проценты,
задачи о кредитовании и банковских процентах,
задачи оптимизации производства товаров или услуг (минимизации расходов или максимизации прибыли).

Слайд 3
1 процент –
часть числа.
За 100% всегда принимают то, с чем сравнивают. Если
a>b на 20%, то a=1,2b.
Отношение показывает, какую часть от числа b составляет число a.
Выражение показывает, сколько процентов от числа b составляет число a.

Слайд 4
Увеличить число S на p%.
Уменьшить число S на p%.
Число
A увеличили на 20%, то получили 1,2А.
Число A уменьшили на
20%, то получили 0,8А.

Слайд 5
На сколько процентов число a больше b (a>b)?
На сколько
процентов число b меньше a (b

Слайд 6Задачи о вкладах и кредитовании
(банковских процентах)
Проценты по вкладам (депозитам)
Проценты
по кредитам

Слайд 7В задачах на проценты по вкладам речь идёт либо
об однократном изменении величины вклада на определённое число процентов (простые
проценты), либо о последовательном изменении величины вклада через (как правило) равные промежутки времени на определённое число процентов (сложные проценты). В последнем случае каждый раз начиная со второго проценты начисляются на сумму, полученную после предыдущего начисления процентов.

Слайд 8S0—сумма вклада
r%
…
Проценты по вкладам (депозитам)

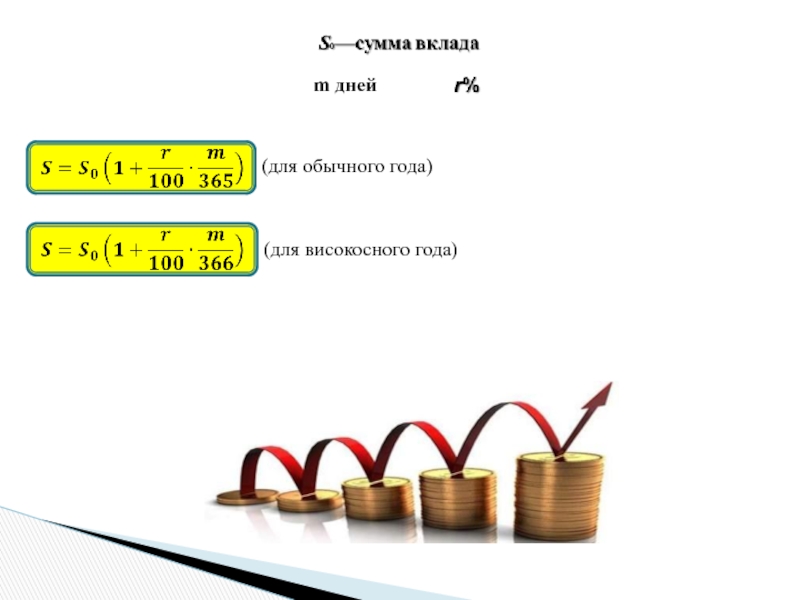
Слайд 10m дней
(для обычного года)
(для високосного года)
Слайд 11Пример 1. В не високосном году клиент открыл вклад
в банке 1 сентября сроком на 1 месяц под 12%
годовых. Сколько рублей окажется на счёте вклада 1 октября того же года, если сумма вклада равна 100 000 рублей?
S0 = 100 000
r = 12
m = 30
Решение.
Ответ. 100 986,30 руб.

Слайд 12Вклад на 3 месяца под r% годовых с последующей
автоматической пролонгацией в течение нескольких раз.
Проценты на депозит начисляются несколько
раз через равные промежутки времени и каждый раз зачисляются на вклад.

Слайд 13Решение.
S0—сумма вклада
Первый депозит
Второй депозит
Прибавка составит примерно 12,55%,
а значит, первый вклад выгоднее.
Ответ. Первый.

Слайд 14Проценты по кредитам
Дифференцированные платежи
Аннуитетные платежи
Слайд 15Дифференцированные платежи
сумма выплат
фиксированная часть
n—число платежей
проценты
Для кредита с
дифференцированными платежами процент и периодичность обязательных платежей фиксируются (например, ежегодные,
ежеквартальные или помесячные платежи), а фиксированный процент начисляется на ещё не выплаченную к моменту очередного обязательного платежа часть кредита (долга).

Слайд 16Базовая (упрощённая) задача на проценты по кредиту с дифференцированными
платежами
k%
n лет
Клиент должен вернуть банку сумму кредита (долг) и
проценты за пользование кредитом на следующих условиях: каждый год клиент возвращает банку
1/n
часть суммы долга (кредита)
проценты за пользование кредитом, начисляемые ежегодно на остаток долга

Слайд 17сумма процентов
первый год
второй год
третий год
и т. д.
последний
год
Общая сумма всех начисленных процентов (переплата)

Слайд 18Общая сумма всех выплат по кредиту равна сумме кредита
и сумме начисленных процентов

Слайд 19Пример 3. Виктор взял в банке кредит сроком на
4 года под 16% годовых. На сколько процентов сумма всех
выплат банку окажется больше суммы кредита, если досрочное погашение кредита не предполагается?
Решение.
Cумма всех выплат
окажется на 40% больше суммы кредита.

Слайд 20Аннуитетные платежи
Условия начисления процентов:
до истечения очередного платёжного периода банк
начисляет k% на оставшуюся сумму долга, т. е. увеличивает её
на k%;
после начисления процентов клиент вносит в банк (также до
истечения соответствующего платёжного периода) некоторую сумму
x—одну и ту же для каждого платежа; сумма долга при этом
уменьшается, и на эту уменьшенную на x сумму начисляются проценты до истечения следующего платёжного периода, после чего клиент вносит в банк платёж в размере той же суммы x и т. п.

Слайд 21Сумма x регулярного платежа.
По истечении последнего платёжного периода долг
равен 0.

Слайд 23Пример 4. 1 июля не високосного года Екатерина взяла
в банке кредит на сумму 109 500 рублей под 24%
годовых сроком на 6 месяцев на условиях погашения кредита ежемесячными аннуитетными (равными) платежами.
Найдите сумму всех выплат по кредиту.
Решение.

Слайд 24Пример 5. 31 декабря 2018 года бизнесмен взял в
банке кредит на 3 года под 10% годовых. Схема выплаты
кредита следующая: до 31 ноября каждого следующего года банк начисляет проценты на оставшуюся сумму долга (т. е. увеличивает долг на 10%), затем до истечения этого же платёжного периода (т. е. по 31 декабря того же года) бизнесмен переводит в банк определённую (одну и ту же для каждого года) сумму ежегодного платежа. Какой была сумма кредита (в рублях), если сумма ежегодного платежа составила 2 662 000 рублей?
Решение.
x —сумма ежегодной выплаты
Суммы долга по истечении каждого платёжного периода:
Ответ. 6 620 000.

Слайд 25Пример 5. В июле планируется взять кредит в банке
на сумму 16 млн рублей на некоторый срок (целое число
лет). Условия его возврата таковы:
• каждый январь долг возрастает на 25% по сравнению с концом предыдущего года;
• с февраля по июнь каждого года необходимо выплатить часть долга;
• в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
На сколько лет планируется взять кредит, если известно, что общая сумма выплат после его полного погашения составит 38 млн рублей?
Решение.
Пусть кредит планируется взять на n лет.
Долг перед банком (в млн рублей) по состоянию на июль должен уменьшаться до нуля равномерно, т. е. на 1/n -ю часть, поэтому суммы долга за каждый месяц (до начисления процентов) составят (в порядке убывания):
По условию каждый январь долг возрастает на 25%, поэтому последовательность размеров платежей по процентам будет следующей:

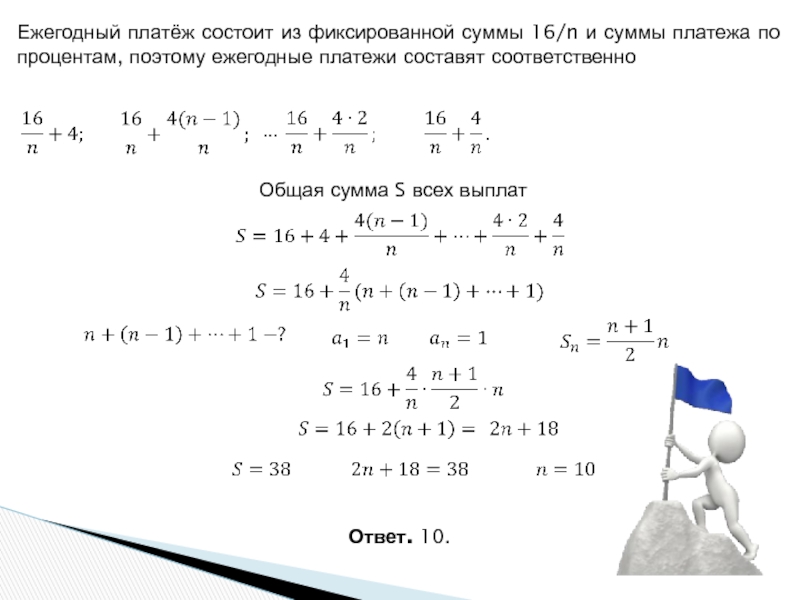
Слайд 26Ежегодный платёж состоит из фиксированной суммы 16/n и суммы
платежа по процентам, поэтому ежегодные платежи составят соответственно
Общая сумма S
всех выплат
Ответ. 10.
Слайд 27Пример 6. В июле планируется взять кредит в банке
на сумму 4,5 млн рублей на срок 9 лет. Условия
его возврата таковы:
• каждый январь долг возрастает на r% по сравнению с концом предыдущего года;
• с февраля по июнь каждого года необходимо выплатить часть долга;
• в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года.
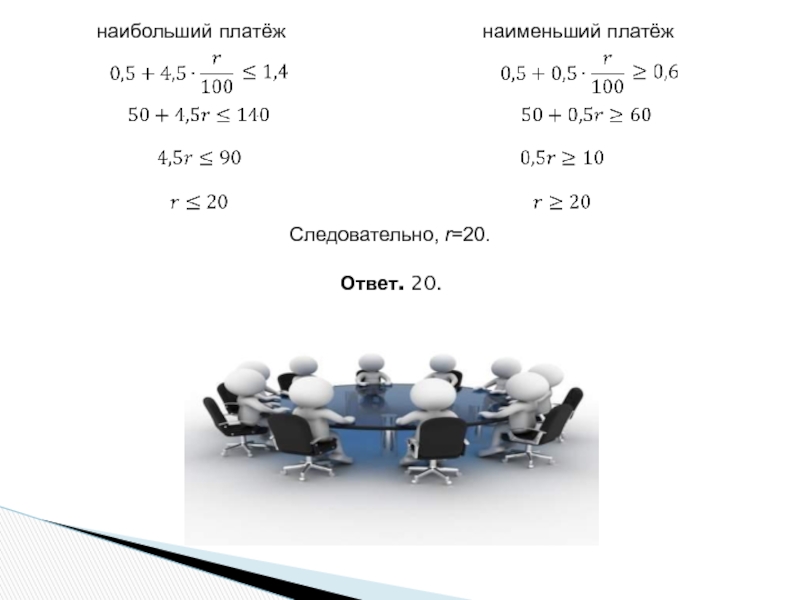
Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн рублей, а наименьший—не менее 0,6 млн рублей.
Решение.
По условию долг перед банком (в млн рублей) по состоянию на июль должен уменьшаться до нуля равномерно, т. е. на 1/9 часть, поэтому суммы долга за каждый год (до начисления процентов) составят (в порядке убывания)
4,5, 4, …, 1, 0,5.
По условию каждый январь долг возрастает на r%. Поэтому последовательность размеров платежей по процентам будет следующей:
Ежегодный платёж
фиксированная сумма
сумма платежа по процентам

Слайд 28наибольший платёж
наименьший платёж
Следовательно, r=20.
Ответ. 20.
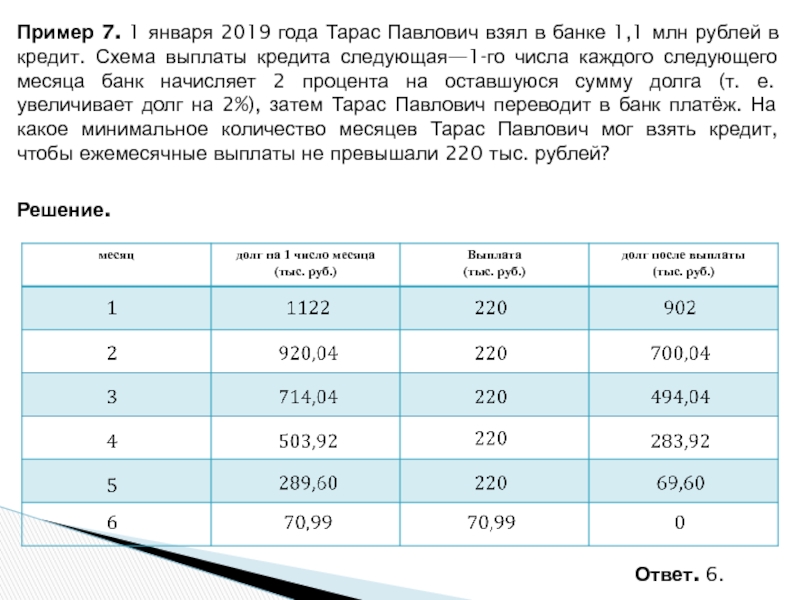
Слайд 29Пример 7. 1 января 2019 года Тарас Павлович взял
в банке 1,1 млн рублей в кредит. Схема выплаты кредита
следующая—1-го числа каждого следующего месяца банк начисляет 2 процента на оставшуюся сумму долга (т. е. увеличивает долг на 2%), затем Тарас Павлович переводит в банк платёж. На какое минимальное количество месяцев Тарас Павлович мог взять кредит, чтобы ежемесячные выплаты не превышали 220 тыс. рублей?
Решение.
Ответ. 6.
Слайд 30Пример 8. 1 января 2019 года Александр Сергеевич взял
в банке 1,1 млн рублей в кредит. Схема выплаты кредита
следующая—1-го числа каждого следующего месяца банк начисляет 1 процент на оставшуюся сумму долга (т. е. увеличивает долг на 1%), затем Александр Сергеевич переводит в банк платёж. На какое минимальное количество месяцев Александр Сергеевич мог взять кредит, чтобы ежемесячные выплаты не превышали 275 тыс. рублей?
Решение.
Александр Сергеевич
не покроет долг с процентами.
каждый месяц долг увеличивается не более чем на данную величину.
Александр Сергеевич сможет выплатить кредит за 5 месяцев.
Ответ. 5.

- Экономические задачи ЕГЭ по математике Профильный уровень Задания № 17 Солодухина Лариса Сергеевна учитель математики МКОУ «Мещовская средняя общеобразовательная школа» г. Мещовск , Калужская область
1А) Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно часов в неделю, то за эту неделю они производят 3t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно часов в неделю, то за эту неделю они производят 4t единиц товара. За каждый час работы (на каждом из заводов) Григорий платит рабочему 500 рублей. Григорий готов выделить 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Пусть, на заводе, расположенном в первом городе, рабочие трудятся часов, а на заводе, расположенном во втором городе, часов. Тогда в неделю будет произведено S =3х+4у (1) единиц товара, а затраты на оплату труда составят 500(+ 500(+ =5 000 0000, + = 10 0000 (2). Выразим из I уравнения у = = (S-3x) (3). Подставим 3 во 2 уравнение: + (-6Sx+9)=10 000, 16+-6Sx+9=160000, 25-(6S)x+(-1600000)=0, =9 -25(S-160000)= 9- 25+4000 000, -16+4 000 000
Уравнение имеет решение, если неотрицателен (2000-4S)(2000+4S)0, — + —
S =500, S=-500 -500 500
-500 500 Тем самым, наибольшее возможное значение = 3х+4у равно 500,
3х+4у=500
Покажем, что оно достигается при натуральных значениях переменных х=60, у=80.
Ответ: 500
1Б) Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно часов в неделю, то за эту неделю они производят 2t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно часов в неделю, то за эту неделю они производят 5t единиц товара. За каждый час работы (на каждом из заводов) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 580 единиц товара. Какую наименьшую сумму придется тратить еженедельно на оплату труда рабочих?
2х+5у=580 у= = (580-2х)= 116-0,4х, S(x)=500(+)=500(+ ),
(х)=500(2х+2(116-0,4х)(-0,4))=500(2х-0,8(116-0,4х)=
=500(2х-92,8+0,32х)=1000х-46400+160х=1160х-46400,
1160х-46400=0 1160х=46400 — 40 + Х=40 х=40- точка минимума S(40)=500(1600+)=500*11600=5 800 000
Ответ: 5 800 000
1В) Николай является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно часов в неделю, то за эту неделю они производят 5t единиц товара; если рабочие на заводе, расположенном во втором городе, трудятся суммарно часов в неделю, то за эту неделю они производят 12t единиц товара. За каждый час работы (на каждом из заводов) Николай платит рабочему 400 рублей. Николай готов выделить 6 760 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара сумму можно произвести за неделю на этих двух заводах?
S(x)=5х+12у, 400(=6760000, =16900
+ ( =16900
144+-(10S)x+25 =16900*144
169-(10S)x+(-2433600)=0
=25-169+411278400=411278400-144= =(20280-12S)(20280+12S), (20280-12S)(20280+12S)0
— + — =-1690, =1690
-1690 1690 Ответ: 1690
.
2. Зависимость объёма Q (в шт.) купленного у фирмы товара от товара от цены Р (в руб. за шт.) выражается формулой Q=15000 –Р, 1000 Р15000. Доход от продажи товара составляет РQ рублей. Затраты на производство Q единиц товара составляют 3000 Q + 5 000000 рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену продукции на 20 %, однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?
Q (в шт.) – объем купленного у фирмы товара, Q=1500 –Р
Р –цена в руб. за шт.
РQ(руб.) – доход от продажи товара
3000 Q + 5 000000 — затраты на производство товара
Прибыль равна разности дохода от продажи товара и затрат на его производство: f(Р)=РQ –(3000 Q+5000000)=P(15000-P)-(3000(15000-P) +5000000) = 15000P—45000000+3000P-500000 = — +18000Р-50 000 000. Пусть =0,8 цена равна 0,8.Наибольшая прибыль достигается при значении Р, для которого f(P)- парабола с ветвями, направленными вниз, поэтому максимум f(P) достигает в вершине параболы. Поскольку f(=f(0,8), вершина находится в точке =0,9. Значит, нужно увеличить цену с 0,8% до 0,9%.
100%=0,125 Ответ: 12,5%
3А) Строительство нового завода стоит 75 млн. рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны 0,5+х+7 млн. рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн. рублей) за один год составит рх — (0,5+х+7). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более чем за 3 года?
Прибыль завода (в млн. руб.) за один год рх — (0,5+х+7)= рх-0,5 -х-7=-0,5+х(р-1) -7 Это выражение квадратный трёхчлен и достигает наибольшее значение при х=р-1. Наибольшее значение равно: -0,5+(р-1)(р-1) -7=(-0,5+1) -7= -7 Строительство завода окупится не более , чем за 3 года -7 0
-1890, -630, =9 + — +
(р-9)(р+7) , -7 9
р9
Ответ : 9
3Б) Строительство нового завода стоит 78 млн. рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны 0,5+2х+6 млн. рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы (в млн. рублей) за один год составит рх — (0,5+2х+6). Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более чем за 3 года?
Прибыль завода (в млн. руб.) за один год рх — (0,5+2х+6)= рх-0,5 -2х-6= -0,5+х(р-2) -6 Это выражение квадратный трёхчлен и достигает наибольшее значение при х=р-2. Наибольшее значение равно: -0,5+(р-2)(р-2) -6=(-0,5+1) – 6= -6 Строительство завода окупится не более , чем за 3 года ; -6 0
— 600, = 10 + — +
(р-10)(р+6) , -6 10
Р
Ответ : 10
4 А) В июле планируется взять кредит в банке на сумму 28 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы: -каждый январь долг возрастает на 25% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга ; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 9 млн. рублей?
Остатки долга: 1 год -28-х; 2год-28-2х; 3год-28-3х;….;0 Найдём выплаты: 1 выплата:28-(28-х)=7+х 2 выплата: (28-х)-(28-2х)=7+0,75х 3 выплата: (28-2х)-(28-3х)=7+0,5х 4 выплата: (28-3х)-(28-4х)=7+0,25х и так далее. Наибольшая выплата в первом году: 7+х=9
х=2
Остаток долга на последний год: 28-nx=0
28-2n=0
n=14 (число лет) Выплаты составляют арифметическую прогрессию: =9, d=0,75х-1х=-0,25х=-0,252=0,5, n. Общая сумма выплат: S=14=14=80,5 млн.руб.
Ответ: 80.5 млн. руб.
4 Б) В июле планируется взять кредит в банке на сумму 9 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы: -каждый январь долг возрастает на 25% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга ; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Чему будет равна общая сумма выплат после полного погашения кредита, если наименьший годовой платёж составит 1,25 млн. рублей?
По условию долг (в млн.руб.) уменьшается :
9; 9- — = ; , 0. По условию каждый январь долг возрастает на 25%, т.е.
100%+25%=125%=1,25 9=11,25 ; ; …, ,0 .
Выплаты: 2,25+; +;…,++
=1,25,
n= =9
9+2,25(1 +++++
млн.руб.
Ответ:20,25 млн.рублей
4 В) В июле планируется взять кредит в банке на сумму 9 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы: -каждый январь долг возрастает на 10% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга ; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Чему будет равна общая сумма выплат после полного погашения кредита. Если наименьший годовой платёж составит 825 тыс. рублей?
По условию долг (в млн.руб.) уменьшается :
9; 9- — = ; , 0. По условию каждый январь долг возрастает на 10%, т.е. 100%+10%=110%=1,1 9=9,9 ; ; …, ,0 . Выплаты: 0,9+; +;…,++
=0,825,
n= =12 (число месяцев)
9+0,9(1 +++++ 9+0,9(1+5)=9+0,9=9+5,85=14, 85 млн.руб.
. Ответ: 14,85 млн.руб.
5А) В июле планируется взять кредит в банке на сумму 1 300 000 рублей на некоторый срок (целое число лет). Условия его возврата таковы: -каждый январь долг возрастает на 10% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга ; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. На какое минимально количество лет можно взять кредит при условии, что ежегодные выплаты были не более 350 000 рублей?
Первый год начисляем проценты:1300000+13000=1 430 000
Делаем выплаты: 1 430 000 – 350 000= 1 080 000
Второй год : 1 080 000+108 000=1 188 000
Выплаты: 1 188 000-350 000= 838 000
Третий год: 838 000 + 83 800= 921 800
Выплаты: 921 800 -350 000= 571 800
Четвертый год: 571 800 +57 180 = 628 980
Выплаты: 628 980 – 350 000= 278 980
Пятый год: 278 980+ 27 898 =306 878
Таким образом, выплата пятого года окажется последней.
Ответ: 5 лет
5Б) В июле планируется взять кредит в банке на сумму 16 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы: -каждый январь долг возрастает на 25% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга ; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. На сколько лет планируется взять кредит если известно, что общая сумма выплат после его полного погашения составит 38 млн. рублей?
Сначала банк начислит нам проценты на всю сумму кредита: х, но в первый же платеж мы выплатим все эти деньги и вернём ещё часть долга, равную . Тогда останемся должны х- = и уже на эту сумму банк нам начислит проценты и так далее: выплачиваем проценты и часть долга, банк начисляет проценты на оставшуюся часть , тогда в конце концов мы выплатим банку весь долг 16 млн. руб. и всю сумму процентов, всего 38 млн. руб., а сумма процентов будет ни что иное, как арифметическая прогрессия:
x+ (х+ Членов у такой прогрессии ровно столько , на сколько лет (месяцев) взять кредит, разность такой прогрессии d=- , первый член-полная сумма, взятая в долг. Сумма арифметической прогрессии:=n , n
n, х=16, сумма процентов 38-16=22.
)n)= 22,
(()n) =22,
=22:
= 88,
16n-8(n-1)=88,
16n-8n+8 =88,
8n=80,
n=10 Ответ:10 лет
5В) В июле планируется взять кредит в банке на сумму 20 млн. рублей на некоторый срок (целое число лет). Условия его возврата таковы: -каждый январь долг возрастает на 30% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга ; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. На сколько лет планируется взять кредит если известно, что общая сумма выплат после его полного погашения составит 47 млн. рублей?
n, х=20, сумма процентов 47-20=27.
)n)= 27,
(()n) =27,
=27:
= 90,
20n-10(n-1)= 90,
20n-10n+10= 90,
10n=80,
n=8 Ответ:8 лет
6А) В июле планируется взять кредит в банке на сумму 4,5 млн. рублей на срок 9 лет. Условия его возврата таковы: -каждый январь долг возрастает на r% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга ; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,4 млн. рублей, а наименьший – не менее 0,6 млн. рублей?
Кредит составляет 4,5 млн. руб. Срок возврата 9 лет. Каждый год планируется платить некоторые суммы(каждый год разные), которые состоят из двух частей: 1) r% от остатка 2) фиксированная сумма в счёт погашения основного долга 4,5 : 9=0,5 млн. руб. Наибольший платёж будет первый год, он составит 4,5 + Наименьший платёж будет последний год, он составит т (4,5- + млн. руб.
Ответ:20
6Б) В июле планируется взять кредит в банке на сумму 6 млн. рублей на срок 15 лет. Условия его возврата таковы: -каждый январь долг возрастает на r% по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга ; — в июле каждого года долг должен быть на одну и ту же сумму меньше долга на июль предыдущего года. Найдите r, если известно, что наибольший годовой платёж по кредиту составит не более 1,9 млн. рублей, а наименьший – не менее 0,5 млн. рублей?
7А) 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите г.
Пусть начальная сумма кредита тогда первая выплата за 1 месяц По условию, ежемесячный долг перед банком должен уменьшаться равномерно. Этот долг состоит из и ежемесячной выплаты процентов, равной: ; ; …, Используя формулу суммы членов арифметической прогрессии, найдем полную переплату по кредиту: (1+ + + …+ +)= 10= 1+ + + …+ +==10 По условию, общая сумма выплат на 30% больше суммы , взятой в кредит, тогда, 0,1 r= 0,3 0,1 r 0,3=0 0,1 (r-3)=0; 0,1 =0 при r=3. Ответ : 3%
7Б) 15-го января планируется взять кредит в банке на 24 месяца. Условия его возврата таковы: — 1-го числа каждого месяца долг возрастает на 2% по сравнению с концом предыдущего месяца; — со 2-го по 14-е число каждого месяца необходимо выплатить часть долга; — 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Какую сумму следует взять в кредит , чтобы общая сумма выплат после полного его погашения кредита равнялась 1 млн. рублей?
Обозначим сумму , взятую в кредит , за 24 S, тогда остаток долга уменьшается равномерно в течении 24 месяцев), будет: 23S, 22 S, …, S, 0.
Чтобы найти очередную выплату, нужно из долга, увеличенного на 2%, вычесть следующий долг. Значит, выплаты будут такими: 24 S-23S; 1,02 -22S; 1,02S-21 S;…,1,02 S-0. Они составляют арифметическую прогрессию, её сумма равна : == =2,5S S; 30 S=1 000 000; S=; 24 S= 800 000=0,8 млн. рублей
Ответ: 0,8 млн. рублей
Интернет источники 1.Открытый банк заданий ЕГЭ на сайте ФИПИ http:// www.fipi.ru/content/otkrytyy-bank-zadaniy-ege 2. Решу ЕГЭ, образовательный портал для подготовки к экзаменам http:// mathb.reshuege.ru/ 3.Открытый банк заданий по математике http://www.fipi.ru/content/otkrytyy-bank-zadaniy-ege
Цель проекта: Классифицировать и систематизировать виды экономических задач.
Научиться решать экономические задачи.
Создать методическое пособие для учащихся 10-11 классов при подготовке к ЕГЭ.
Задачи проекта:
- Изучить теоретический материал в рамках
подготовки ЕГЭ.
- Проанализировать виды экономических задач,
которые встречаются в ЕГЭ.
- Развить умение применять полученные знания
при решении экономических задач
Объект исследования: КИМы из сборников для подготовки к ЕГЭ 2015-2018 учебные года.
Предмет исследования:
экономические задачи
Методы исследования: анализ литературы, анкетирование, обобщение, синтез.
Актуальность работы заключается в том,
что благодаря грамотной классификации
и знаниям основных формул и приемов
практически каждый выпускник сможет
Решить экономическую задачу на ЕГЭ.
План работы:
- Работа с литературой
- Провести анкетирование учащихся
- Изучение видов задач на проценты
- Изучение способов решения задач
- Составить сборник экономических задач и задач на оптимизацию по математике
- Выводы
Итоги анкетирования
1.Плохое знание теоретического материала
— 7 человек
2. Недостаточность навыка решения
экономических задач
— 6 человек
3. Большая затрата времени на решение
экономических задач
-12 человек
4. Малое количество часов на изучение этой
темы в школе
— 5 человек
5.Трудность задач — 15 человек
Гипотеза:
Результаты анкетирования позволяют мне предположить, что если мне удастся изложить теоретический и практический материал, необходимый для решения экономических задач, в доступной для каждого выпускника форме, количество учащихся справившихся с этим видом задач возрастет.
Основные ошибки:
- – неверное составление модели;
- – вычислительные (арифметические);
- – прекращение решения без доведения ответа
до числового значения;
- – не доведение решения до конца из-за невнимательного прочтения вопроса;
- – решение методом подбора без обоснования;
- – применение готовых формул для задач о кредитовании, отсутствующих в учебниках
3 правила, упрощающие решение
3 правила, упрощающие решение
1. Для упрощения записей и вычислений при решении задач о вкладах, кредитах и оптимизацию производства переходить от «языка процентов» к десятичным дробям . Например, «увеличение величины на 15%» равносильно её умножению на число 1,15 (так как 100% + 15% = 115% = 1,15); «уменьшение величины на 24%» равносильно её умножению на число 0,76 (так как 100% — 24% = 76% = 0,76).
3 правила, упрощающие решение
3 правила, упрощающие решение
2. Для правильного выбора способа решения необходимо уметь выделять основные типы задач :
- задачи о вкладах;
- задачи о кредитах (аннуитетные и дифференцированные)
- задачи на оптимизацию
3 правила, упрощающие решение
3. Большинство задач следует сначала решать «в общем виде» , вводя следующие обозначения:
- S – сумма вклада или кредита;
- x – ежемесячный вклад или ежемесячная выплата;
- n – срок (количество месяцев или лет);
- r % — процентная ставка;
- – множитель для вычисления процентных начислений ;
числовые данные подставлять только по окончании всех преобразований
Предположим, кто то взял кредит на 1 млн руб под 30% годовых
Долг % Долг с %
1 000 000 + 300 000 = 1 300 000
100% 30% 130%
Если долг увеличивается на 30%, это значит, что он становится равен 130% от суммы до начисления. Значит чтобы найти сумму после начисления надо сумму до начисления умножить на 1,3
- Дифференцированные платежи рассчитываются исходя из того, что сумма погашения основного долга из месяца в месяц одинаковая, а сумма погашения процентов зависит от того, сколько насчитал банк за последний месяц.
- При аннуитетных платежах размер ежемесячного платежа остается постоянным на всем периоде кредитования. Ежемесячный платеж рассчитывается как сумма процентов, начисленных на текущий период и суммы идущей на погашения суммы кредита
Задача 1 (дифференнцированный)
- Допустим, что в банке взят кредит 1200 рублей на 12 месяцев. Причем, каждый платежный период долг сначала возрастает на 10% по сравнению с концом предыдущего платежного периода, а затем вносится оплата так, что долг становится на одну и ту же величину меньше долга на конец предыдущего платежного периода. Необходимо ответить на вопросы: Какую сумму нужно вернуть банку за весь платежный период? Какова сумма переплаты?
Долг перед банком по состоянию на конец года должен уменьшаться до нуля равномерно, то есть последовательность долгов перед банком такова:
1200;1100; 1000; 900;800; 700; 600; 500; 400; 300; 200;100.
Первого числа каждого месяца долг возрастает на 10% . Тогда последовательность долгов будет такова:
1200∙1.1; 1100∙1.1; 1000∙1.1; 900∙1.1; 800∙1.1; 700∙1.1; 600∙1.1; 500∙1.1; 400∙1.1; 300∙1.1; 200∙1.1;100∙1.1.
или
1320; 1210; 1100;990; 880; …110.
Обращаем внимание на то, разница между долговыми суммами равна 110 рублей . (1320-1210=110)
Теперь найдем ежемесячные выплаты:
1 месяц- 1320-1100=220
2 месяц- 1210-1000=210
3 месяц- 1100- 900=200
4 месяц- 990- 800=190
5 месяц – 880-700=180 и так далее. И последняя наименьшая выплата равна 110 рублей . Замечаем, что выплаты уменьшаются ежемесячно на 10 рублей .
Такова схема дифференцированного платежа.
Далее можно найти сумму всех выплат. Она равна: 220+210+200+…+110 = 1980 (рублей).
Таким образом, переплата составляет 65%. ((1980*100):1200=165%)
В общем виде задача формулируется так: 31 декабря 2014 года Андрей взял в банке S рублей в кредит под a процентов годовых. Схема выплаты кредита следующая: 1 числа каждого следующего года банк начисляет a процентов на оставшуюся сумму долга. Затем Андрей переводит в банк сумму X ежегодного платежа (транш). Весь долг Андрей должен выплатить за n лет, то есть за n равных платежей. Необходимо найти одну из неизвестных величин: S , a , X, или n .
Задача 2 (аннуитетный)
- 15-го января планируется взять кредит в банке на 1 млн рублей на 6 месяцев. Условия его возврата таковы:
-1-го числа каждого месяца долг возрастает на целое число r процентов по сравнению с концом предыдущего года.
-со 2го по 14е число каждого месяца необходимо выплатить часть долга.
-15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей
дата
15.01
Долг(млн в рублей)
15.02
1
15.03
0,6
15.04
0,4
15.05
0,3
15.06
0,2
15.07
0,1
0
- Найдите наибольшее значение r , при котором общая сумма выплат будет составлять менее 1,2 млн рублей .
Долг перед банком (в млн рублей) на 15-е число каждого месяца должен уменьшаться до нуля следующим образом: 1; 0.6; 0.4; 0.3; 0.2; 0.14; 0. Обозначим k = 1+ Тогда долг на 1-е число каждого месяца равен: 1к; 0.6к; 0.4к; 0.3к; 0.2к; 0.1к; 0к Найдем теперь выплаты со 2-е по 14-е число каждого месяца: 1к-0.6; 0.6к-0.4; 0.4к-0.3; 0.3к-0.2; 0.2к-0.1; 0.1к-0; Общая сумма выплат составляет: 1к-0.6+ 0.6к-0.4+0.4к-0.3+ 0.3к-0.2+ 0.2к-0.1+0.1к-0=2.6к-1.6 По условию, общая сумма выплат будет меньше 1,2 млн руб. Значит, составляем неравенство: 2.6к-1.6≤ 1.2 . Отсюда к ≤ Подставляя вместо k выражение 1+ и решая неравенство, получим, что r ≤ 7 Наибольшее целое решение этого неравенства – число 7. Значит, искомое число процентов — 7%.
- Предприниматель купил здание и собирается открыть в нем отель. В отеле могут быть стандартные номера площадью 21 квадратный метр и номера «люкс» площадью 49 квадратных метров . Общая площадь, которую можно отвести под номера, составляет 1099 квадратных метров . Предприниматель может поделить эту площадь между номерами различных типов как хочет. Обычный номер будет приносить отелю 2000 рублей в сутки, а номер «люкс» 4500 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своем отеле предприниматель?
1-й способ – с помощью логики и арифметических действий.
Найдем стоимость 1 номера стандартного:
2000:21=95 (рублей).
Найдем стоимость 1 номера «люкс»:
4500: 49 =91 (рублей).
Так как стоимость 1 стандартного номера дороже, то выгоднее разместить на этой площади больше номеров стандартных, и как можно меньше номеров «люкс».
Начнем перебор количества номеров «люкс» с наименьшей цифры.
Пусть номеров «люкс» будет 0. Тогда число 1099 не делится нацело на 21. Далее.
Допустим, что номеров «люкс» будет 1. Тогда: 1099- 49=1050 ;
1050: 21 = 50 (номеров стандартных). Значит, на площади 1050 можно разместить 50 стандартных номеров. Тогда в сутки отель может заработать: 50∙ 2000 + 1∙ 4500=104500 (р.)
2-й способ – с помощью составления опорной линейной функции.
Пусть х – количество стандартных номеров,
у- количество номеров «люкс».
Они занимают площадь 21х+49у.
Составим равенство: 21х+49у = 1099.
Выразим из этого равенства у = .
Составим функцию заработанных денег:
S ( x , y ) =2000∙ x + 4500∙ y .
Далее подставим в эту функцию выражение для у.
Получим S ( x ) =71 ∙х + 4500∙22 .
Это возрастающая линейная функция.
Свое наибольшее значение она принимает при наибольшем значении х и наименьшем значении у.
По условию х и у – натуральные числа.
Значит, у=1 (это наименьшее натуральное число) и х=50. Значит, S = 2000∙50 + 4500∙ 1=104500.
Заключение
В результате данной работы я:
– смогла все экономические задачи разбить на три основных группы;
– решила ряд экономических задач;
– создала методическое пособие для учащихся 10-11 классов при подготовке к ЕГЭ.
Для успешной сдачи надо помнить, что все экономические задачи в вариантах ЕГЭ вычислительные, поэтому для их успешного решения должен быть отработан аппарат стандартных вычислений.
Благодаря полученным знаниям в процессе моей работы, экономические задачи стали для меня не проблемой. Теперь я с легкостью смогу решить экономическую задачу на ЕГЭ и получить 3 балла, ведь для математики 3 балла – это очень много.
Экономические задачи – это не просто задачи из математики, это часть нашей жизни в современном мире. Умение их решать будет полезно как для проверки банковских операций, так и в простых жизненных ситуациях.
Спасибо за внимание !