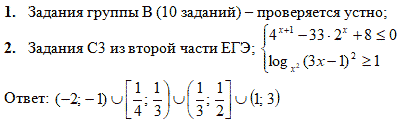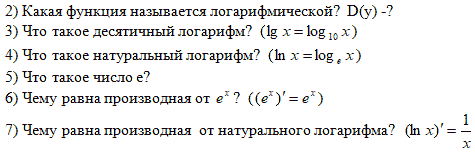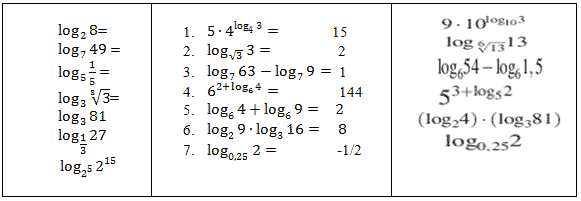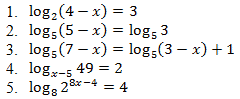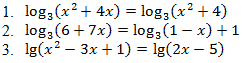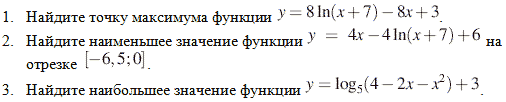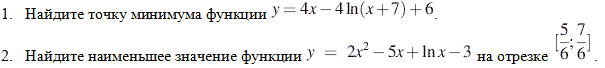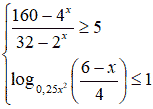Презентация логарифмы в егэ базовый уровень

Библиотека

▪Учебно-методические материалы

▪Презентации

Материал опубликовал

Вантрусов Дмитрий Евгеньевич421 Россия, Архангельская обл., город Няндома Материал размещён в группе «Презентации к уроку»

3

#11 класс #Алгебра #Учебно-методические материалы #Презентация #Учитель-предметник #Школьное образование

Скачать
презентацию

Просмотреть
презентацию

Презентация к уроку-практикуму «Логарифмы». Подготовка к ЕГЭ по математике

Опубликовано 09.04.17 в 19:40 в группе «Презентации к уроку»

Комментарии (0)

Чтобы написать комментарий необходимо авторизоваться.

Слайд 1

Готовимся к ЕГЭ «Логарифм»

Слайд 2

Содержание: Определение логарифма – слайд 3. Свойства логарифма – слайды 4-5. Графики логарифмической функции – слайды 6 — 7 . Логарифмические выражения и их преобразование – слайд 8 . Решение логарифмических уравнений – слайды 9 -1 2 Решение логарифмических неравенств – слайды 13-17

Слайд 3

Определение. Логарифмом положительного числа b по основанию а (а > 0, а ≠ 1) называется показатель степени, в который нужно возвести основание а , чтобы получить b . Обозначение: log a b. Десятичный логарифм — логарифм, основание которого равно 10. Обозначение: log 10 x = lg x . Натуральный логарифм — логарифм, основание которого равно е ≈ 2,7 . Обозначение: log е x = ln x .

Слайд 4

1

Слайд 5

Свойства логарифмов: 2

Слайд 6

График и свойства логарифмической функции. 1

Слайд 7

2 График и свойства логарифмической функции.

Слайд 8

Выражения и их преобразования.

Слайд 9

Решение логарифмических уравнений. Определение. Логарифмическим уравнением называется уравнение, в котором неизвестная находится только под знаком логарифма или в основании логарифма (или то и другое одновременно). При решении логарифмических уравнений наиболее употребительны следующие методы: 1) решение уравнений, основанное на определении логарифма; 2) решение с помощью операции потенцирования; 3) применение основного логарифмического тождества; 4) использование операции логарифмирования; 5) переход к логарифму по новому основанию; 6) введение нового неизвестного.

Слайд 10

Решение логарифмических уравнений.

Слайд 11

Решение логарифмических уравнений. Получаем: 3=3 Ответ: х = -2

Слайд 12

Решение логарифмических уравнений. Пример 3. Найдите все значения параметра а , при каждом из которых уравнение имеет два различных корня, равноудаленных от точки х = 42. Решение. Введем обозначение . Уравнение примет вид : Его корни — числа: . Следовательно , Отсюда получаем : Точка х = 42 равноудалена от точек , т.е . она является серединой отрезка с концами в этих точках. Воспользуемся формулой координаты середины отрезка Ответ : а = 1

Слайд 13

Решение логарифмических неравенств. Между методами решений логарифмических уравнений и логарифмических неравенств есть существенные отличия : 1) для решения логарифмических неравенств необходимо установить характер монотонности соответствующей логарифмической функции в зависимости от величины её основания . 2) решением неравенства , как правило, является бесконечное множество чисел , и значит, о выполнении проверки найденных решений не может быть и речи , поскольку в отличие от уравнений это просто невозможно . Поэтому при решении логарифмических неравенств особое значение приобретает умение проводить равносильные преобразования неравенств .

Слайд 14

Решение логарифмических неравенств. При решении логарифмических неравенств необходимо учитывать : 1. если а > 0, а ≠ 1, то <=> 2. если а > 0, а ≠ 1, то <=> 3. <=> 4. <=>

Слайд 15

Решение логарифмических неравенств. Имеется не менее 4 принципиально различных типов подхода к решению логарифмических неравенств: А ) перебор случаев «основание больше единицы», «основание меньше единицы»; Б ) переход к равносильным совокупностям систем неравенств , не содержащих логарифмов; В) обобщенный метод интервалов; Г) графический метод.

Слайд 16

Решение логарифмических неравенств. Пример 1. Решите неравенство В ответе укажите наименьшее целое значение. Решение . Данное неравенство равносильно следующей системе Ответ: 2 Пример 2. Решите неравенство В ответе укажите наименьшее целое значение. — 4 1 — 1,5 Решение. Представим правую часть неравенства в виде логарифма с основанием . Получим неравенство , которое равносильно следующей системе Ответ: 5

Слайд 17

Решение логарифмических неравенств. Пример 3. Решить неравенство: Решение : Данное неравенство равносильно совокупности следующих систем неравенств 1 2 1 1 2 3 6 2 0 1 2 6 Ответ:

Слайд 18

Ни пуха, ни пера!

1. Готовимся к ЕГЭ

ЛОГАРИФМЫ И
ИХ СВОЙСТВА

2. Цели урока:

• повторить определение логарифма числа,
основное логарифмическое тождество;
• закрепить основные свойства логарифмов;
• усилить практическую направленность
данной темы для качественной подготовки
к ЕГЭ;

3.

,
Определение логарифма
Логарифмом числа положительного числа в
по основанию а называется показатель
степени, в которую надо возвести число а,
чтобы получить число в.
loga b c
a b
c

4.

Основное логарифмическое
тождество

5.

Десятичный логарифм
Натуральный логарифм

6.

Возведение в степень
Логарифмирование
2

7.

Запомните эти формулы

8.

Представьте в виде степени

9.

Запомните эти формулы

10. Вычислите по определению логарифма

log 3 27 = 3
=0
= -4
=2
=1
= -1

11.

Вычислите
=5
=12
=9
=-3
=5

12. При каких значениях х существует

13. Почему не имеют смысл выражения

14.

Свойства логарифмов
Логарифм произведения
Логарифм частного
Логарифм степени

15.

Вычислите

16.

Свойства логарифмов
Логарифм произведения

17.

Свойства логарифмов
Логарифм частного

18.

Свойства логарифмов
Логарифм степени

19.

Формула перехода к новому основанию
Следствия

20.

Формула перехода к новому
основанию

21. Задачи открытого банка ЕГЭ В7

22. Задачи открытого банка ЕГЭ В7

.
Задачи открытого банка ЕГЭ
В7

23.

Вы сегодня погрузились в
логарифмы,
Безошибочно их надо вычислять.
На экзамене , конечно ,вы их
встретите,
Остается вам успехов
пожелать!

Большая часть заданий, включенных в ЕГЭ, представляет собой задания на вычисление значений числовых логарифмических выражений. При подготовке следует обратить внимание на формулу перехода к новому основанию логарифма и следствия из нее. Задачи на использование этих формул в школьных учебниках практически не встречаются.

Проверяемые элементы: Владение понятием логарифм. Знание основных свойств логарифмов. Умение выполнять тождественные преобразования логарифмических выражений.

Понравилось? Сохраните и поделитесь:

Неограниченная бесплатная загрука материала «Логарифмы в заданиях ЕГЭ» доступна всем пользователям. Разработка находится в разделе «Математика 11 класс» и представляет собой: «повторение, систематизация».

---

Конспект и презентация к уроку математики «Логарифмическая линия в ЕГЭ»

Целевая аудитория: для 11 класса

Автор: Петренко Наталья Викторовна
Место работы: МБОУ СОШ №7, ст.Воронежской, Усть-Лабинского р-на, Краснодарского края
Добавил: Ната8459

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

---

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

---

Фотографии предоставлены

Метод решения хорош, если с самого начала мы можем предвидеть –
и в последствии подтвердить это, — что, следуя этому методу, мы достигнем цели.
Г.Лейбниц

ТИП УРОКА: Закрепление и совершенствование знаний.

ЦЕЛИ:

• Дидактическая — Повторить и закрепить свойства  логарифмов; логарифмические уравнения; закрепить методы решения наибольшего и наименьшего значения функции; совершенствовать применение полученных знаний при решении задач ЕГЭ С1 и С3;
• Развивающая — Развитие логического мышления, памяти, познавательного интереса, продолжить формирование математической речи и графической культуры, вырабатывать умение анализировать;
• Воспитательная — Приучать к эстетическому оформлению записи в тетради, умению общаться, прививать аккуратность.

Оборудование: классная доска, компьютер, проектор, экран,  карточки с заданиями теста, с заданиями для работы всех обучающихся.
Формы работы: фронтальная, индивидуальная, коллективная.

ХОД УРОКА

1. ОРГАНИЗАЦИОННЫЙ МОМЕНТ

2. ПОСТАНОВКА ЦЕЛИ

3. ПРОВЕРКА ДОМАШНЕГО ЗАДАНИЯ

3. работа личных кабинетов в Интернет (просмотр результатов)

4. АКТУАЛИЗАЦИЯ ЗНАНИЙ

Проанализировать: в каких заданиях ЕГЭ встречаются логарифмы.

(В-7-простейшие логарифмические уравнения
В-11-преобразование логарифмических выражений
В-12- задачи физического содержания, связанные с логарифмами
В-15- нахождение наибольшего и наименьшего значения функции
С-1- тригонометрические уравнения, содержащие логарифм
С-3 – система неравенств, содержащая логарифмическое неравенство)

На данном этапе проводится устная работа, в ходе которой учащиеся не только вспоминают свойства логарифмов, но и выполняют простейшие задания ЕГЭ.

1) Определение логарифма. Какие вы знаете свойства логарифма? (и условия ?)

 

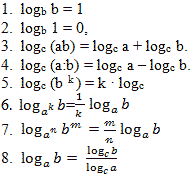
5. УСТНАЯ РАБОТА для всех обучающихся.

Вычислить устно: (задания В-11)

6. Самостоятельная деятельность учащихся по решению заданий.

В-7 с последующей проверкой

Решите уравнения (первые два уравнения проговаривают устно, а остальные решает самостоятельно  весь класс и записывает решение в тетрадь):

После проверки с места 3-5 уравнений, ребятам предлагается доказать, что уравнение не имеет решения (устно)

7. Решение В-12 (задачи физического содержания, связанные с логарифмами).

Весь класс решает задачу (у доски 2 человека: 1-й решает вместе с классом, 2-й решает аналогичную задачу самостоятельно)

8. УСТНАЯ РАБОТА (вопросы)

Вспомнить алгоритм нахождения наибольшего и наименьшего значения функции на отрезке и на промежутке.

Работа на доске и в тетради.

(прототип В15 — ЕГЭ)

(Пока ученики работают у доски, 4-м учащимся даются карточки с аналогичными заданиями)

9. Мини-тест с самоконтролем.

Тест

Ключи к тесту:

	№1	№2	№3	№4	№5	№6
Вариант №1	250	49	4	-8	3	8
Вариант №2	63	144	13	-22	7	3

Ребята меняются друг с другом работами и выступают в роли экспертов.

10. Решение заданий С1

Учащиеся выполняют задание, 1 человек работает у доски.

Подробный разбор предложенного задания на доске.

11. Выступление учащихся в роли экспертов.

Ребятам предлагается оценить работу ученика – задание С-1, выполненную на экзаменационном бланке – 0,1,2 баллами (см.презентацию)

12. ДОМАШНЕЕ ЗАДАНИЕ.

Учитель поясняет домашнее задание, обращая внимание на то, что аналогичные задания были рассмотрены на уроке. Учащиеся внимательно прослушав пояснения учителя, записывают домашнее задание.

1. ФИПИ (открытый банк заданий: раздел геометрия, 6-я страница)
2. uztest.ru (преобразование логарифмов)
3. С3 – задание второй части ЕГЭ

13. ПОДВЕДЕНИЕ  ИТОГОВ.

Сегодня на уроке мы повторили свойства логарифмов; логарифмические уравнения; закрепили методы нахождения  наибольшего и наименьшего значения функции; рассмотрели задачи физического содержания, связанные с логарифмами; решали задачи С1 и С3, которые  предлагаются на ЕГЭ по математике.

Выставление оценок.