Презентация подготовка к егэ информатика

ЕГЭ по информатике

---

ЕГЭ по русскому языку [118]	ЕГЭ по математике [89]
ЕГЭ по истории [32]	ЕГЭ по обществознанию [46]
ЕГЭ по литературе [8]	ЕГЭ по информатике [29]
ЕГЭ по физике [36]	ЕГЭ по биологии [9]
ЕГЭ по химии [10]	ЕГЭ по иностранному языку [8]
ЕГЭ по географии [3]	ЕГЭ 11 класс. Общее. [4]

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

---

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

---

Фотографии предоставлены

ЕГЭ по информатике

Фильтры         отменить

Категория ЕГЭ по информатике содержит материалов: 27

Страницы: 1 2 »

23.12.16

ПОДГОТОВКА К ЕГЭ

Лубинская Е.А.

ГБОУ СОШ №978 г. Москва

23.12.16

ИНФОРМАЦИЯ

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

A 8 КОДИРОВАНИЕ ЗВУКА.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №1

Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 24 бита. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1) 0,2 2) 2 3) 3 4) 4

• так как частота дискретизации 16 кГц, за одну секунду запоминается 16000 значений сигнала
• так как глубина кодирования – 24 бита = 3 байта, для хранения 1 секунды записи требуется
• 16000  3 байта = 48 000 байт
• (для стерео записи – в 2 раза больше)
• на 1 минуту = 60 секунд записи потребуется
• 60  48000 байта = 2 880 000 байт,
• то есть около 3 Мбайт
• таким образом, правильный ответ – 3 .

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №2

Производится одноканальная (моно) звукозапись с частотой дискретизации 64Гц. При записи использовались 32 уровня дискретизации. Запись длится 4 минуты 16 секунд, её результаты записываются в файл, причём каждый сигнал кодируется минимально возможным и одинаковым количеством битов. Какое из приведённых ниже чисел наиболее близко к размеру полученного файла, выраженному в килобайтах?

1) 10 2) 64 3) 80 4) 512

• так как частота дискретизации 64 Гц, за одну секунду запоминается 64 значения сигнала
• глубина кодирования не задана!
• используется 32 = 2 5 уровня дискретизации значения сигнала, поэтому на один отсчет приходится 5 бит
• время записи 4 мин 16 с = 4  60 + 16 = 256 с
• за это время нужно сохранить
• 256  5  64 бит = 256  5  8 байт = 5  2 Кбайт = 10 Кбайт
• таким образом, правильный ответ – 1 .

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

А9 КОДИРОВАНИЕ И ДЕКОДИРОВАНИЕ ИНФОРМАЦИИ.

• закодированное сообщение можно однозначно декодировать с начала, если выполняется условие Фано : никакое кодовое слово не является началом другого кодового слова;
• закодированное сообщение можно однозначно декодировать с конца, если выполняется обратное условие Фано : никакое кодовое слово не является окончанием другого кодового слова;
• условие Фано – это достаточное, но не необходимое условие однозначного декодирования.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №3

По каналу связи передаются сообщения, содержащие только 4 буквы: Е, Н, О, Т. Для кодирования букв Е, Н, О используются 5-битовые кодовые слова: Е — 00000, Н — 00111, О — 11011. Для этого набора кодовых слов выполнено такое свойство: любые два слова из набора отличаются не менее чем в трёх позициях. Это свойство важно для расшифровки сообщений при наличии помех. Какое из перечисленных ниже кодовых слов можно использовать для буквы Т, чтобы указанное свойство выполнялось для всех четырёх кодовых слов?

1) 11111 2) 11100 3) 00011 4) не подходит ни одно из указанных выше слов

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

легко проверить, что для заданного кода (Е — 00000, Н — 00111, О — 11011) расстояние Хэмминга равно 3; в таблице выделены отличающиеся биты, их по три в парах Е-Н и Н-О и четыре в паре Е-О:

Е – 00 000 Е – 00 0 00 Н – 001 11

Н – 00 111 О – 11 0 11 О – 110 11

теперь проверяем расстояние между известными кодами и вариантами ответа; для первого ответа 11111 получаем минимальное расстояние 1 (в паре О-Т), этот вариант не подходит:

Е – 00000 Н – 00 111 О – 11 0 11

Т — 11111 Т — 11 111 Т — 11 1 11

для второго ответа 11100 получаем минимальное расстояние 3 (в парах Е-Т и О-Т):

Е – 000 00 Н – 00 1 11 О – 11 011

Т — 111 00 Т — 11 1 00 Т — 11 100

для третьего ответа 00011 получаем минимальное расстояние 1 (в паре Н-Т) , этот вариант не подходит:

Е – 000 00 Н – 00 1 11 О – 11 011

Т — 000 11 Т — 00 0 11 Т — 00 011

таким образом, расстояние Хэмминга, равное 3, сохраняется только для ответа 2

Ответ: 2.

23.12.16

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №4

Для кодирования некоторой последовательности, состоящей из букв А, Б, В, Г и Д, решили использовать неравномерный двоичный код, позволяющий однозначно декодировать двоичную последовательность, появляющуюся на приёмной стороне канала связи. Использовали код: А–1, Б–000, В–001, Г–011. Укажите, каким кодовым словом должна быть закодирована буква Д. Длина этого кодового слова должна быть наименьшей из всех возможных. Код должен удовлетворять свойству однозначного декодирования.

1) 00 2) 01 3)11 4) 010

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

• заметим, что для известной части кода выполняется условие Фано – никакое кодовое слово не является началом другого кодового слова
• если Д = 00, такая кодовая цепочка совпадает с началом Б = 000 и В = 001, невозможно однозначно раскодировать цепочку 000000: это может быть ДДД или ББ; поэтому первый вариант не подходит
• если Д = 01, такая кодовая цепочка совпадает с началом Г = 011, невозможно однозначно раскодировать цепочку 011: это может быть ДА или Г; поэтому второй вариант тоже не подходит
• если Д = 11, условие Фано тоже нарушено: кодовое слово А = 1 совпадает с началом кода буквы Д, невозможно однозначно раскодировать цепочку 111: это может быть ДА или ААА; третий вариант не подходит
• для четвертого варианта, Д = 010, условие Фано не нарушено;
• правильный ответ – 4.

23.12.16

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №5

Для кодирования букв А, Б, В, Г решили использовать двухразрядные последовательные двоичные числа (от 00 до 11, соответственно). Если таким способом закодировать последовательность символов БАВГ и записать результат шестнадцатеричным кодом, то получится

1) 4B 16 2) 411 16 3)BACD 16 4) 1023 16

• из условия коды букв такие: A – 00, Б –01, В – 10 и Г – 11, код равномерный
• последовательность БАВГ кодируется так: 01 00 10 11 = 1001011
• разобьем такую запись на тетрады справа налево и каждую тетраду переведем в шестнадцатеричную систему (то есть, сначала в десятичную, а потом заменим все числа от 10 до 15 на буквы A, B, C, D, E, F); получаем
• 1001011 = 0100 1011 2 = 4B 16
• правильный ответ – 1.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №6

• в данном случае самое простое и надежное – просто закодировать все ответы, используя приведенную таблицу кодов, а затем сравнить результаты с заданной цепочкой
• получим

1) EBCEA – 01101100011000 2) BDDEA – 011010011000

3) BDCEA – 0110100011000 4) EBAEA – 01101000011000

• сравнивая эти цепочки с заданной, находим, что правильный ответ – 3.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №7

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

А11 ВЫЧИСЛЕНИЕ ИНФОРМАЦИОННОГО ОБЪЕМА СООБЩЕНИЯ.

• с помощью K бит можно закодировать различных вариантов (чисел)
• чтобы найти информационный объем сообщения (текста) I , нужно умножить количество символов (отсчетов) K на число бит на символ (отсчет) i :

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №8

Для регистрации на сайте некоторой страны пользователю требуется придумать пароль. Длина пароля – ровно 11 символов. В качестве символов используются десятичные цифры и 12 различных букв местного алфавита, причём все буквы используются в двух начертаниях: как строчные, так и заглавные (регистр буквы имеет значение!).

Под хранение каждого такого пароля на компьютере отводится минимально возможное и одинаковое целое количество байтов, при этом используется посимвольное кодирование и все символы кодируются одинаковым и минимально возможным количеством битов.

Определите объём памяти, который занимает хранение 60 паролей.

1) 540 байт 2) 60 0 байт 3) 66 0 б ай т 4) 720 байт

• согласно условию, в пароле можно использовать 10 цифр (0..9) + 12 заглавных букв местного алфавита + 12 строчных букв, всего 10 + 12 + 12 = 34 символа
• для кодирования 34 символов нужно выделить 6 бит памяти (5 бит не хватает, они позволяют закодировать только 2 5 = 32 варианта)
• для хранения всех 11 символов пароля нужно 11  6 = 66 бит
• поскольку пароль должен занимать целое число байт, берем ближайшее большее (точнее, не меньшее) значение, которое кратно 8: это 72 = 9  8; то есть один пароль занимает 9 байт
• тогда 60 паролей занимают 9  60 = 540 байт
• ответ: 1 .

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №9

В велокроссе участвуют 119 спортсменов. Специальное устройство регистрирует прохождение каждым из участников промежуточного финиша, записывая его номер с использованием минимально возможного количества бит, одинакового для каждого спортсмена. Каков информационный объем сообщения, записанного устройством, после того как промежуточный финиш прошли 70 велосипедистов?

1) 70 бит 2) 70 байт 3) 490 бит 4) 119 байт

• велосипедистов было 119, у них 119 разных номеров, то есть, нам нужно закодировать 119 вариантов
• по таблице степеней двойки находим, что для этого нужно минимум 7 бит (при этом можно закодировать 128 вариантов, то есть, еще есть запас); итак, 7 бит на один отсчет
• когда 70 велосипедистов прошли промежуточный финиш, в память устройства записано 70 отсчетов
• поэтому в сообщении 70*7 = 490 бит информации ( ответ 3 ).

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

B4 КОДИРОВАНИЕ СООБЩЕНИЙ. КОМБИНАТОРИКА.

• мощность алфавита M – это количество символов в этом алфавите
• если алфавит имеет мощность M , то количество всех возможных «слов» (символьных цепочек) длиной N (без учета смысла) равно
• для двоичного кодирования (мощность алфавита M – 2 символа) получаем известную формулу:

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №10

Азбука Морзе позволяет кодировать символы для сообщений по радиосвязи, задавая комбинацию точек и тире. Сколько различных символов (цифр, букв, знаков пунктуации и т. д.) можно закодировать, используя код азбуки Морзе длиной не менее четырёх и не более пяти сигналов (точек и тире)?

• согласно условию, алфавит содержит только два знака – точку и тире
• «не менее четырёх и не более пяти сигналов» означает, что нужно определить количество всех 4- и 5-буквенных слов в двоичном алфавите
• количество 4-буквенных слов равно 2 4 = 16, а количество 5-буквенных 2 5 = 32
• поэтому общее количество 4- и 5-буквенных слов равно 16 + 32 = 48

• ответ: 48.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №11

Какое наименьшее число символов должно быть в алфавите, чтобы при помощи всевозможных трехбуквенных слов, состоящих из символов данного алфавита, можно было передать не менее 9 различных сообщений?

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №12

Каждая ячейка памяти компьютера, работающего в троичной системе счисления, может принимать три различных значения (-1, 0, 1) . Для хранения некоторой величины отвели 4 ячейки памяти. Сколько различных значений может принимать эта величина?

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

B 10 ОПРЕДЕЛЕНИЕ СКОРОСТИ ПЕРЕДАЧИ ИНФОРМАЦИИ ПРИ ЗАДАННОЙ ПРОПУСКНОЙ СПОСОБНОСТИ КАНАЛА.

1 байт = 8 бит = 2 3 бит,

1 Кбайт = 1024 байта = 2 10 байта

= 2 10 · 2 3 бит = 2 13 бит,

1 Мбайт = 1024 Кбайта = 2 10 Кбайта

= 2 10 · 2 10 байта = 2 20 байта

= 2 20 · 2 3 бит = 2 23 бит.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №13

У Васи есть доступ к Интернет по высокоскоростному одностороннему радиоканалу, обеспечивающему скорость получения им информации 256 Кбит в секунду. У Пети нет скоростного доступа в Интернет, но есть возможность получать информацию от Васи по низкоскоростному телефонному каналу со средней скоростью 32 Кбит в секунду. Петя договорился с Васей, что тот будет скачивать для него данные объемом 5 Мбайт по высокоскоростному каналу и ретранслировать их Пете по низкоскоростному каналу. Компьютер Васи может начать ретрансляцию данных не раньше, чем им будут получены первые 512 Кбайт этих данных. Каков минимально возможный промежуток времени (в секундах), с момента начала скачивания Васей данных, до полного их получения Петей? В ответе укажите только число, слово «секунд» или букву «с» добавлять не нужно.

Здесь считается, что 1 Кбит = 1024 бит = 2 10 бит.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

СИСТЕМЫ СЧИСЛЕНИЯ

23.12.16

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

А1 СИСТЕМЫ СЧИСЛЕНИЯ И ДВОИЧНОЕ ПРЕДСТАВЛЕНИЕ ИНФОРМАЦИИ В ПАМЯТИ КОМПЬЮТЕРА.

• переводим в десятичную систему все ответы:
• 11011001 2 = 217, 11011100 2 = 220, 11010111 2 = 215, 11011000 2 =216
• очевидно, что между числами 215 и 217 может быть только 216
• таким образом, верный ответ – 4 .

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

B 7 КОДИРОВАНИЕ ЧИСЕЛ. СИСТЕМЫ СЧИСЛЕНИЯ.

Решите уравнение . Ответ запишите в шестеричной системе счисления. Основание системы счисления указывать не нужно.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

Запись числа 67 10 в системе счисления с основанием N оканчивается на 1 и содержит 4 цифры. Укажите основание этой системы счисления N.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

Укажите через запятую в порядке возрастания все десятичные числа, не превосходящие 25 , запись которых в системе счисления с основанием четыре оканчивается на 11 ?

• переведем 25 в четверичную систему счисления: 25 = 121 4 , все интересующие нас числа не больше этого значения
• из этих чисел выделим только те, которые заканчиваются на 11, таких чисел всего два: это 11 4 = 5 и 111 4 = 21
• таким образом, верный ответ – 5, 21 .

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

ЛОГИКА

23.12.16

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

A 3 ПОСТРОЕНИЕ ТАБЛИЦ ИСТИННОСТИ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ.

¬ A , не A (отрицание, инверсия)

A  B , A и B (логическое умножение, конъюнкция)

A  B , A или B (логическое сложение, дизъюнкция)

A → B импликация (следование)

A  B эквивалентность (равносильность)

операцию «импликация» можно выразить через «ИЛИ» и «НЕ»:

A → B = ¬ A  B или в других обозначениях A → B =

иногда для упрощения выражений полезны формулы де Моргана:

¬ (A  B) = ¬ A  ¬ B

¬ (A  B) = ¬ A  ¬ B

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №1

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №2

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

A 10 ОСНОВНЫЕ ПОНЯТИЯ МАТЕМАТИЧЕСКОЙ ЛОГИКИ.

ЗАДАЧА №3

На числовой прямой даны два отрезка: P = [10,30] и Q = [25, 55]. Определите наибольшую возможную длину отрезка A, при котором формула

( x  A ) → (( x  P )  ( x  Q ) )

тождественно истинна, то есть принимает значение 1 при любом значении переменной х.

1) 10 2) 20 3) 30 4) 45

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №4

На числовой прямой даны два отрезка: P = [14,34] и Q = [24, 44]. Выберите такой отрезок A, что формула

( x  A ) → (( x  P )  ( x  Q ) )

тождественно истинна, то есть принимает значение 1 при любом значении переменной х. Если таких отрезков несколько, укажите тот, который имеет большую длину.

1) [ 15 , 29 ] 2) [ 25 , 29 ] 3) [ 35 , 39 ] 4) [ 49 , 55 ]

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

B 12 СОСТАВЛЕНИЕ ЗАПРОСОВ ДЛЯ ПОИСКОВЫХ СИСТЕМ С ИСПОЛЬЗОВАНИЕМ ЛОГИЧЕСКИХ ВЫРАЖЕНИЙ

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №5

N 1 + N 2 + N 3 = 8700 + 7500 — 3200 = 13000

таким образом, ответ – 13000.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЗАДАЧА №6

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

ПОЛЬЗОВАТЕЛЬСКИЙ КУРС

23.12.16

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

A 2 ИСПОЛЬЗОВАНИЕ ИНФОРМАЦИОННЫХ МОДЕЛЕЙ

Между населёнными пунктами A, B, C, D, E, F построены дороги, протяжённость которых приведена в таблице. (Отсутствие числа в таблице означает, что прямой дороги между пунктами нет.)

Определите длину кратчайшего пути между пунктами A и F (при условии, что передвигаться можно только по построенным дорогам).

1) 9 2) 10 3) 11 4) 12

A

A

B

B

C

2

C

2

D

D

4

4

E

1

E

1

F

F

3

7

3

7

4

4

3

3

2

2

ответ – 1.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

A 4 ФАЙЛОВАЯ СИСТЕМА.

Определите, какое из указанных имен файлов удовлетворяет маске: ?hel*lo.c?*

1) hello.c 2) hello.cpp 3) hhelolo.cpp 4) hhelolo.c

ответ – 3.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

Каталог содержит файлы с именами

а) q.c

б) q q .cpp

в) q q .c

г) q1.c1

д) q aa .c md

е) q12. cpp

Определите, в каком порядке будут показаны файлы, если выбрана сортировка по типу (по возрастанию).

1) авгдбе 2) авгдеб 3) абвгде 4) авдбег

ответ – 2.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

Для групповых операций с файлами используются маски имен файлов. Маска представляет собой последовательность букв, цифр и прочих допустимых в именах файлов символов, в которых также могут встречаться следующие символы: Символ «?» (вопросительный знак) означает ровно один произвольный символ. Символ «*» (звездочка) означает любую последовательность символов произвольной длины, в том числе «*» может задавать и пустую последовательность.

В каталоге находятся пять файлов:

fort.docx

ford.docx

lord.doc

orsk.dat

port.doc

Определите, по какой из масок будет выбрана указанная группа файлов:

fort.docx

ford.docx

lord.doc

port.doc

1) *o?*.d?* 2) ?o*?.d* 3) *or*.doc? 4) ?or?.doc?

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

ответ – 2

23.12.16

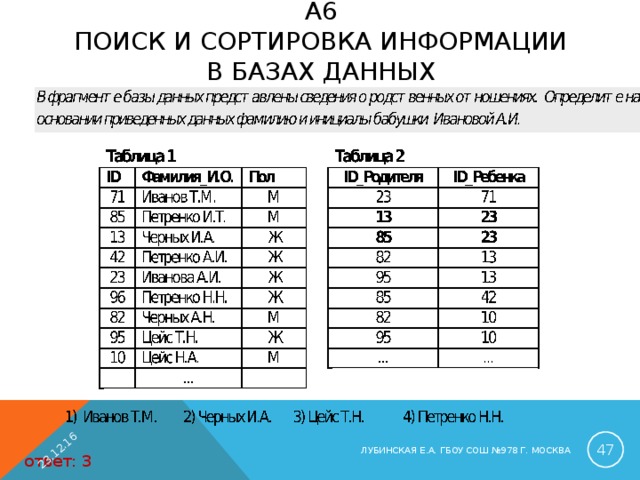
A 6 ПОИСК И СОРТИРОВКА ИНФОРМАЦИИ В БАЗАХ ДАННЫХ

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

ответ: 3

23.12.16

ответ – 1.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

A 7 ЭЛЕКТРОННЫЕ ТАБЛИЦЫ.

Дан фрагмент электронной таблицы.

A B C D

1 1 2 3

2 5 4 =$A$2+B$3

3 6 7 =A3+B3

Чему станет равным значение ячейки D1, если в неё скопировать формулу из ячейки С2?

Примечание: знак $ обозначает абсолютную адресацию.

1) 18 2) 12 3) 14 4) 17

Ответ: 1.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

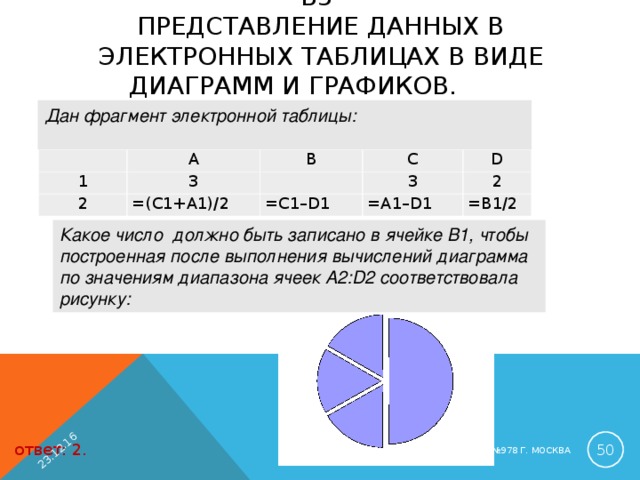
B3 ПРЕДСТАВЛЕНИЕ ДАННЫХ В ЭЛЕКТРОННЫХ ТАБЛИЦАХ В ВИДЕ ДИАГРАММ И ГРАФИКОВ.

Дан фрагмент электронной таблицы:

A

1

2

3

B

=( C 1+ A 1)/2

C

3

D

= C 1– D 1

= A 1– D 1

2

=B1/2

Какое число должно быть записано в ячейке B1, чтобы построенная после выполнения вычислений диаграмма по значениям диапазона ячеек A2:D2 соответствовала рисунку:

ответ: 2.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

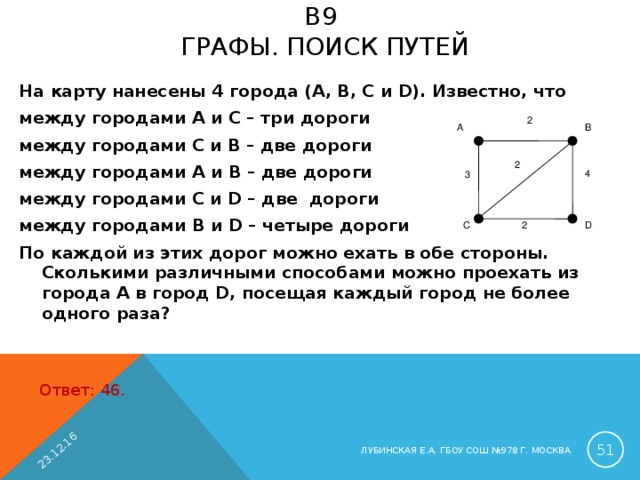
B9 ГРАФЫ. ПОИСК ПУТЕЙ

На карту нанесены 4 города (A, B, C и D). Известно, что

между городами A и С – три дороги

между городами C и B – две дороги

между городами A и B – две дороги

между городами C и D – две дороги

между городами B и D – четыре дороги

По каждой из этих дорог можно ехать в обе стороны. Сколькими различными способами можно проехать из города А в город D, посещая каждый город не более одного раза?

2

А

B

2

4

3

2

С

D

Ответ: 46.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

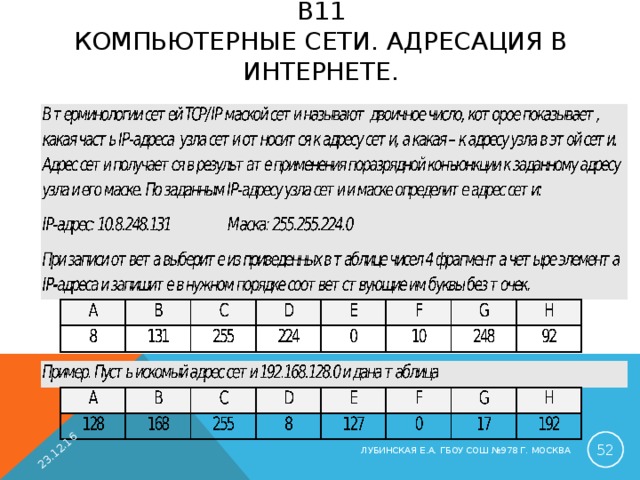
B 11 КОМПЬЮТЕРНЫЕ СЕТИ. АДРЕСАЦИЯ В ИНТЕРНЕТЕ.

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

РЕШЕНИЕ (1 СПОСОБ, ИСПОЛЬЗОВАНИЕ РАЗМЕРА ПОДСЕТИ, М. САВОСЬКИН):

нужно помнить, что каждая часть в IP-адресе (и в маске) – восьмибитное двоичное число, то есть десятичное число от 0 до 255 (поэтому каждую часть адреса и маски называют октетом )

поскольку 255 = 11111111 2 , все части IP-адреса узла, для которых маска равна 255, входят в IP-адрес сети без изменений (они полностью относятся к номеру сети)

поскольку 0 = 00000000 2 , все части IP-адреса узла, для которых маска равна 0, в IP-адресе сети заменяются нулями (они полностью относятся к номеру узла в сети)

таким образом, мы почти определили адрес сети, он равен 10.8.X.0, где X придется определять дополнительно

2) третье число в маске (соответствующее неизвестному X) – 224; в такую подсеть входят адреса, в которых третий октет (третье число IP-адреса) может принимать 256 – 224 = 32 разных значений

3) выпишем адреса, принадлежащие всем возможным подсетям такого вида (третий октет из-меняется от 0 с шагом 32):

Начальный IP-адрес (адрес сети) Конечный IP-адрес (широковещательный)

10.8.0.0 10.8.31.255

10.8.32.0 10.8.63. 255

10.8.64.0 10.8.95. 255

10.8.96.0 10.8.127. 255

10.8.128.0 10.8.159. 255

10.8.160.0 10.8.191. 255

10.8.192.0 10.8.223. 255

10.8.224.0 10.8.255. 255

4) смотрим, что нужный нам адрес 10.8.248.131 оказывается в подсети с адресом 10.8.224.0; в данном случае можно было быстрее получить ответ, если бы мы строили таблицу с конца, т.е. с последней подсети

5) по таблице находим ответ: FADE (F=10, A=8, D=224, E=0)

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

РЕШЕНИЕ (2СПОСОБ, ЛОГИЧЕСКОЕ «И» МАСКИ И НОМЕРА УЗЛА):

нужно помнить, что каждая часть в IP-адресе (и в маске) – восьмибитное двоичное число, то есть десятичное число от 0 до 255 (поэтому каждую часть адреса и маски называют октетом )

поскольку 255 = 11111111 2 , все части IP-адреса узла, для которых маска равна 255, входят в IP-адрес сети без изменений (они полностью относятся к номеру сети)

поскольку 0 = 00000000 2 , все части IP-адреса узла, для которых маска равна 0, в IP-адресе сети заменяются нулями (они полностью относятся к номеру узла в сети)

таким образом, мы почти определили адрес сети, он равен 10.8.X.0, где X придется определять дополнительно

переведем в двоичную систему третью часть IP -адреса и маски

248 = 11111000 2

224 = 11100000 2

заметим, что в маске сначала идет цепочка единиц, а потом до конца – цепочка нулей; это правильно, число где цепочка единиц начинается не с левого края (не со старшего, 8-ого бита) или внутри встречаются нули, не может быть маской; поэтому есть всего несколько допустимых чисел для последней части маски (все предыдущие должны быть равны 255):

10000000 2 = 128

11000000 2 = 192

11100000 2 = 224

11110000 2 = 240

11111000 2 = 248

11111100 2 = 252

11111110 2 = 254

11111111 2 = 255

выполним между этими числами поразрядную конъюнкцию – логическую операцию «И»; маска 224 = 11100000 2 говорит о том, что первые три бита соответствующего числа в IP-адресе относятся к номеру сети, а оставшиеся 5 – к адресу узла:

248 = 11111000 2

224 = 11100000 2

поэтому часть номера сети – это 224 = 11100000 2 , а номер узла – это 11000 2 = 24.

таким образом, полный адрес сети – 10.8.224.0

по таблице находим ответ: FADE (F=10, A=8, D=224, E=0)

Решение (1 способ, логическое «И» маски и номера узла):

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

АЛГОРИТМИЗАЦИЯ И ОСНОВЫ ПРОГРАММИРОВАНИЯ

23.12.16

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

z THEN s = s + 1 NEXT i Паскаль s:=0; z:=A[n]; for i:=0 to n do begin Си   if A[i]z then Алгоритмический язык s = 0; z = A[n]; for (i = 0; i   if (A[i] z) s:=0 z:=A[n] нцдля i от0 до n     если A[i] z то       s:=s+1     все кц     s:=s+1; end     s++; } 2 ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА » width=»640″

23.12.16

А12

В программе описан одномерный целочисленный массив с индексами от 0 до n. Ниже представлен фрагмент одной и той же программы, записанный на разных языках программирования, обрабатывающей данный массив:

Чему будет равно значение переменной s после выполнения данной программы, при любых значениях элементов массива?

1Максимальному элементу в массиве A

2Количеству элементов массива A, больших последнего элемента массива

3Индексу последнего элемента массива А, который меньше A[0]

4Количеству элементов массива A, меньших последнего элемента массива

Бейсик

s = 0

z = A(n)

FOR i = 0 TO n

  IF A(i) z THEN s = s + 1

NEXT i

Паскаль

s:=0; z:=A[n]; for i:=0 to n do begin

Си

  if A[i]z then

Алгоритмический язык

s = 0;

z = A[n];

for (i = 0; i

  if (A[i] z)

s:=0 z:=A[n] нцдля i от0 до n

    если A[i] z то

      s:=s+1     все кц

    s:=s+1;

end

    s++;

}

2

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

В программе описан одномерный целочисленный массив с индексами от 0 до n (т.е. первый элемент имеет индекс 0, последний — индекс n). Ниже представлен фрагмент одной и той же программы, записанный на разных языках программирования, обрабатывающей данный массив:

Чему будет равно значение переменной s после выполнения данной программы, при любых значениях элементов массива?

1Количеству элементов массива A, больших первого элемента массива

2Количеству элементов массива A, не превосходящих первого элемента массива

3Количеству элементов массива A, не равных первому элементу массива

4Количеству элементов массива A, равных первому элементу массива

3

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

В программе описан одномерный целочисленный массив с индексами от 0 до n (т.е. первый элемент имеет индекс 0, последний — индекс n). Ниже представлен записанный на разных языках программирования фрагмент одной и той же программы, обрабатывающей данный массив:

Чему будет равно значение переменной s после выполнения данной программы? Ответ должен быть верным при любых значениях элементов массива.

1Минимальному элементу в массиве A

2Количеству элементов массива A, равных первому элемента массива

3Сумме всех элементов массива А, равных последнему элементу массива

4Наибольшему индексу k, для которого элемент массива с индексом k равен первому элементу массива

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

Дан фрагмент программы, обрабатывающей двухмерный массив A размера n×n.

k := 1;

for i:=1 to n do begin

c := A[i,i];

A[i,i] := A[k,i];

A[k,i] := c;

end

Представим массив в виде квадратной таблицы, в которой для элемента массива A[i,j] величина i является номером строки, а величина j – номером столбца, в котором расположен элемент. Тогда данный алгоритм меняет местами

1) два столбца в таблице

2) две строки в таблице

3) элементы диагонали и k -ой строки таблицы

4) элементы диагонали и k -го столбца таблицы

3

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

Значения двух массивов A[1..100] и B[1..100] задаются с помощью следующего фрагмента программы:

for n:=1 to 100 do

A[n] := (n-80)*(n-80);

for n:=1 to 100 do

B[101-n] := A[n];

Какой элемент массива B будет наибольшим?

1) B[1] 2) B [21] 3) B [80] 4) B [100]

4

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

23.12.16

ЛИТЕРАТУРА:

• http://kpolyakov.narod.ru/school/ege.htm

ЛУБИНСКАЯ Е.А. ГБОУ СОШ №978 Г. МОСКВА

МКОУ «Рубасская СОШ» Проект На тему: « Подготовка к ЕГЭ. Тесты по темам курса «Информатика и ИКТ»»

Юнусов У.Б.

Учитель информатики и ИКТ

МКОУ «Рубасская СОШ» Дербентского района РД

с.Рубас -2017-

Цели проекта:

• Проанализировать тесты ЕГЭ по темам курса «Информатика и ИКТ»
• Рассмотреть межпреметную связь в тестах ЕГЭ.
• Выявить достоинства и недостатки тестов ЕГЭ. (срок достижения цели 17.12.2018 г.)

Тематические блоки тестов ЕГЭ.

• Информация и ее кодирование.
• Алгоритмизация и программирование.
• Моделирование и компьютерный эксперимент.
• Основы логики.
• Технологии обработки информации.
• Телекоммуникационные технологии.
• Технология программирования.

Информация и ее кодирование.

Информация и ее кодирование.

Задача 1.

• Сколько единиц в двоичной записи числа 1025?

1) 1 2) 2 3) 10 4) 11

• Решение.

1025=1024+1

1024 10 =2^10

В двоичной С.С. имеет вид: 10000000000 2

Тогда 10000000000 2 + 1 2 = 10000000001 2

Ответ: 2 единицы.

Информация и ее кодирование.

Задача 2. Сколько единиц в двоичной записи числа 1025?

1) 1 2) 2 3) 10 4) 11

• Решение.

1025=1024+1

1024 10 =2^10

В двоичной С.С. имеет вид: 10000000000 2

Тогда 10000000000 2 + 1 2 = 10000000001 2

Ответ: 2 единицы.

Информация и ее кодирование.

Задача 3. Текстовое сообщение в кодировке ASCII было переведено в кодировку Unicode. Как изменится объём этого сообщения, если оно состояло из фразы В.И. Даля:

«Язык есть вековой труд целого поколения»

• Увеличится на 41 бит 2. Уменьшится на 320 бит

• Увеличится на 40 байт 4. Уменьшится на 39 байт

Решение.

Количество символов – 40 Объём в ASCII 40 байт (1 символ 8 бит или 1 байт)

Объём в Unicode 80 байт (1 символ 16 бит или 2 байта)

Ответ: увеличится на 40 байт

Задача1. Определите значение переменной c после выполнения следующего фрагмента программы ( записанного ниже на разных языках программирования ).

a := 40;

b := 80;

b := — a — 2 * b;

if a

Ответ: 280.

Алгоритмизация и программирование.

Основы логики.

Основные логические операции:

логическое отрицание (инверсия) – « не »; ¬ ; ¯ ;

• логическое умножение (конъюнкция) – « и »; & ; ^ ; • ;
• логическое сложение (дизъюнкция) – « или »; + ;  ;
• логическое следование (импликация) –  
• логическая операция эквивалентности – ~ ;  ;  ;
• функция Вебба (отрицание дизъюнкции) – ИЛИ-НЕ ;
• функция Шеффера (отрицание конъюнкции) – И-НЕ ;
• сложение по модулю 2 (М2).

Основы логики.

Задача 1.

Укажите, какое логическое выражение равносильно выражению

A  ¬(¬B  C) 1 . ¬A  ¬B  ¬C 2. A  ¬B  ¬C

3 . A  B  ¬C 4 . A  ¬B  C

• Применим формулу де Моргана, а затем закон двойного отрицания:

A  ¬(¬B  C) =

2. Перепишем ответы в других обозначениях:

• ¬A  ¬B  ¬C = A  ¬B  ¬C = A  B  ¬C = A  ¬B  C =
• ¬A  ¬B  ¬C =
• A  ¬B  ¬C =
• A  B  ¬C =
• A  ¬B  C =

Таким образом, правильный ответ – 3 .

2)→(X 3)) ? 1) 1 2) 2 3) 3 4) 4 Решение. ) Выполняем операции для всех приведенных возможных ответов (1 обозначает истинное условие, 0 – ложное); определяем результаты сравнения в двух внутренних скобках: Ответ 3. » width=»640″

Основы логики.

Задача 2.

Для какого из указанных значений X истинно высказывание

¬((X 2)→(X 3)) ?

1) 1 2) 2 3) 3 4) 4

Решение.

) Выполняем операции для всех приведенных возможных ответов (1 обозначает истинное условие, 0 – ложное); определяем результаты сравнения в двух внутренних скобках:

Ответ 3.

Основы логики.

Задача 3. Сколько различных решений имеет уравнение

• ((K  L) → (L  M  N)) = 0

где K, L, M, N – логические переменные?

В ответе не нужно перечислять все различные наборы значений K, L, M и N, при которых выполнено данное равенство. В качестве ответа Вам нужно указать количество таких наборов

Решение. Перепишем уравнение, используя более простые обозначения операций: ((K + L) → (L · M · N)) = 0.

• Из таблицы истинности операции «импликация» следует, что это равенство верно тогда и только тогда, когда одновременно K + L = 1 и L · M · N = 0.

• Из уравнения следует, что хотя бы одна из переменных, K или L равна 1 или обе вместе; поэтому рассмотрим три случая.

K = 1 и L = 0; K = 1 и L = 1; K = 0 и L = 1.

Основы логики.

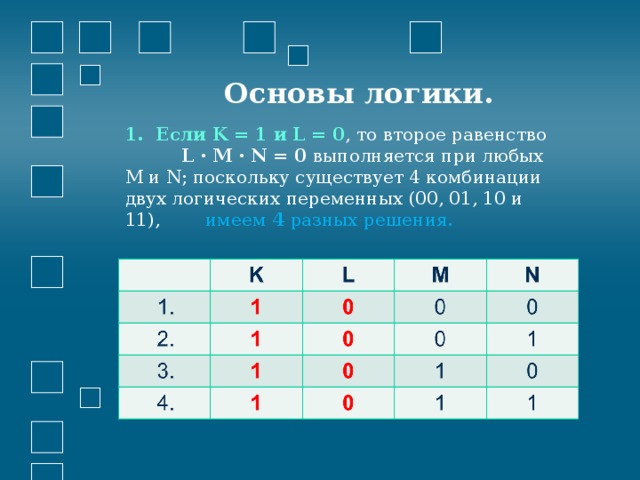
1. Если K = 1 и L = 0 , то второе равенство L · M · N = 0 выполняется при любых М и N; поскольку существует 4 комбинации двух логических переменных (00, 01, 10 и 11), имеем 4 разных решения.

Основы логики.

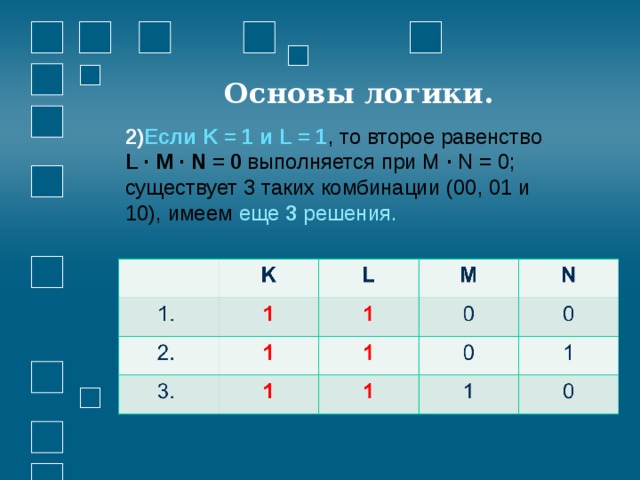
• Если K = 1 и L = 1 , то второе равенство L · M · N = 0 выполняется при М · N = 0; существует 3 таких комбинации (00, 01 и 10), имеем еще 3 решения.

Основы логики.

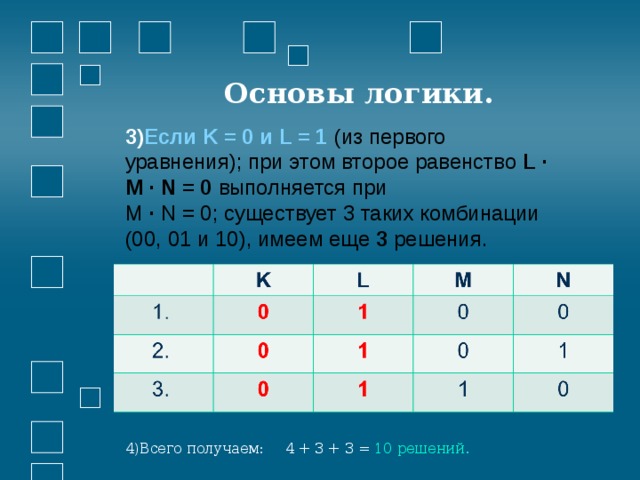
• Если K = 0 и L = 1 (из первого уравнения); при этом второе равенство L · M · N = 0 выполняется при М · N = 0; существует 3 таких комбинации (00, 01 и 10), имеем еще 3 решения.

• Всего получаем: 4 + 3 + 3 = 10 решений.

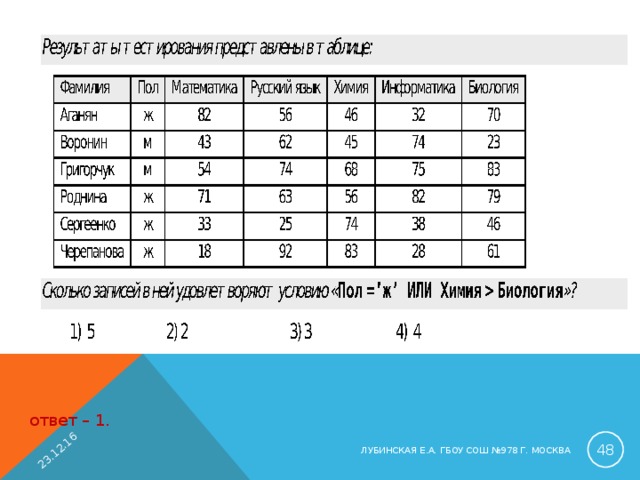
Технологии обработки информации.

Задача1. Все 5-буквенные слова, составленные из букв А,О,У, записаны в алфавитном порядке.

Вот начало списка.

• ААААА 2. ААААО 3. ААААУ 4. АААОА … .

Запишите слово, которое стоит на 240-м месте от начала списка.

Решение.

Обозначим А-0, О-1, У-2 и запишем полученное:

• 00000 2. 00001 3. 00002 4. 00010

Заметим, что коды записаны в троичной системе счисления,

Тогда на 240 месте будет стоять число 239, т. к. на 1-м месте стоит число 0. Переведем число 239 в троичную с.с.

Получим: 22212 Поэтому ответом будет УУУОУ

Ответ: УУУОУ.

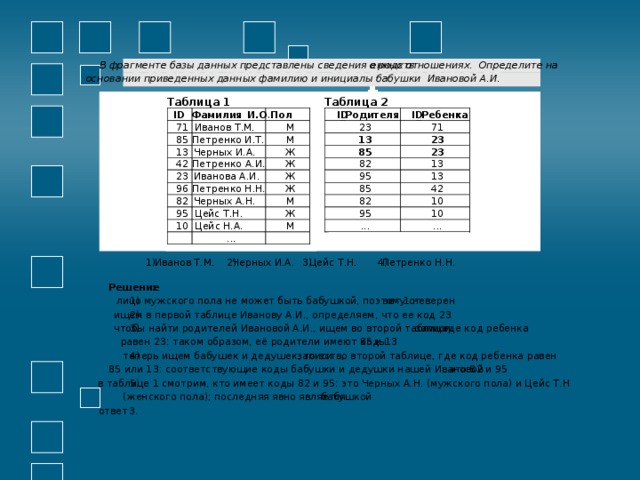
енных отношениях. Определите на

В фрагменте базы данных представлены сведения о родств

основании приведенных данных фамилию и инициалы бабушки Ивановой А.И.

Таблица 2

Таблица 1

Технологии обработки информации.

Фамилия_И.О.

Пол

_Родителя

_Ребенка

ID

ID

ID

23

М

71

Иванов Т.М.

71

М

23

85

Петренко И.Т.

13

13

23

85

Ж

Черных И.А.

82

42

Петренко А.И.

Ж

13

Ж

95

Иванова А.И.

23

13

42

Петренко Н.Н.

Ж

85

96

10

82

82

Черных А.Н.

M

Цейс Т.Н.

95

95

10

Ж

М

…

Цейс Н.А.

10

…

…

3)

4)

1)

Черных И.А.

2)

Петренко Н.Н.

Иванов Т.М.

Цейс Т.Н.

:

Решение

1)

лицо мужского пола не может быть бабушкой, поэтому от

вет 1 неверен

2)

ищем в первой таблице Иванову А.И., определяем, что ее код 23

3)

чтобы найти родителей Ивановой А.И., ищем во второй таблице

записи

, где код ребенка

85 и 13

равен 23: таком образом, её родители имеют коды

теперь ищем бабушек и дедушек, то есть,

записи во второй таблице, где код ребенка равен

4)

–

это 82 и 95

85 или 13: соответствующие коды бабушки и дедушки нашей Ивановой

в таблице 1 смотрим, кто имеет коды 82 и 95: это Черных А.Н. (мужского пола) и Цейс Т.Н

5)

(женского пола); последняя явно является

бабушкой

ответ

3.

Задача 3.

Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 24 бита. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1) 0,2 2) 2 3) 3 4) 4

Решение:

так как частота дискретизации 16 кГц, за одну секунду запоминается 16000 значений сигнала

так как глубина кодирования – 24 бита = 3 байта, для хранения 1 секунды записи требуется

16000  3 байта = 48 000 байт

(для стерео записи – в 2 раза больше)

на 1 минуту = 60 секунд записи потребуется

60  48000 байта = 2 880 000 байт,

то есть около 3 Мбайт

Таким образом, правильный ответ – 3.

• Задача 4.
• В ячейке B4 электронной таблицы записана формула = $C3*2. Какой вид приобретет формула, после того как ячейку B4 скопируют в ячейку B6? Примечание: знак $ используется для обозначения абсолютной адресации.
• 1) =$C5*4 2) =$C5*2 3) =$C3*4 4) =$C3*2
• Решение:
• ссылка $C3 – это смешанная ссылка, в которой «заблокирован» столбец C, а строка 3 – это относительный адрес;
• после того, как ячейку B4 скопировали в B6, номер строки увеличился на 2, поэтому и в ссылке $C3 номер строки (относительная часть) также увеличится на 2, ссылка превратится в $C5
• константы при копировании формул не меняются, поэтому получится =$C5*2
• таким образом, правильный ответ – 2.

Телекоммуникационные технологии.

Задача 1. Скорость передачи данных через ADSL-соединение равна 512 000 бит/c. Передача файла через это соединение заняла 1 минуту. Определить размер файла в килобайтах.

Решение:

выделим в заданных больших числах степени двойки; переведем время в секунды (чтобы «согласовать» единицы измерения), а скорость передачи – в Кбайты/с, поскольку ответ нужно получить в Кбайтах:

1 мин = 60   с = 4 · 15 с = 2 2 · 15 с

512000 бит/c = 512 · 1000 бит/с = 2 9 · 125 · 8 бит/с = 2 9 · 5 3 · 2 3 бит/с = 2 12 · 5 3 бит/с = 2 9 · 5 3 байт/с = Кбайт/с = Кбайт/с

чтобы найти время объем файла, нужно умножить время передачи на скорость передачи:

Кбайт/с Кбайт Кбайт

таким образом, ответ – 3750 Кбайт.

Телекоммуникационные технологии.

Задача 2. Производится одноканальная (моно) звукозапись с частотой дискретизации 16 кГц и глубиной кодирования 24 бита. Запись длится 1 минуту, ее результаты записываются в файл, сжатие данных не производится. Какое из приведенных ниже чисел наиболее близко к размеру полученного файла, выраженному в мегабайтах?

1) 0,2 2) 2 3) 3 4) 4

Решение:

А) так как частота дискретизации 16 кГц, за одну секунду запоминается 16000 значений сигнала

Б) так как глубина кодирования – 24 бита = 3 байта, для хранения 1 секунды записи требуется 16000  3 байта = 48 000 байт

(для стерео записи – в 2 раза больше)

В) на 1 минуту = 60 секунд записи потребуется

60  48000 байта = 2 880 000 байт, то есть около 3 Мбайт

Таким образом, правильный ответ – 3.

Технология программирования.

Выводы:

• Тесты ЕГЭ охватывают все пункты базового курса «Информатика и ИКТ»
• Во всех заданиях тестов ЕГЭ по информатике и ИКТ присутствует межпредметная связь, т.к. информационные технологии затрагивают все области наук.
• В ходе работы над проектом, замечено, что некоторые задания (исполнитель робот, количество решений логических уравнений, задачи на перебор вариантов и т.д.) содержат большой объем обрабатываемой информации и громоздкий алгоритм решения, что отрицательно сказывается в резу льтатах ЕГЭ.

Заключение:

• Необходимо упростить некоторые задачи ЕГЭ, забирающие много времени, отводимой для выполнения теста ЕГЭ.
• Уменьшить количество заданий А и В.
• Связать (учебники) программу курса «Информатика и ИКТ» с тестами заданий ЕГЭ.

Поставленные вопросы являются темами следующих проектных работ.

Литература.

1. Единый государственный экзамен: информатика: контроль. Измерит. Материалы:2009. – М.: Просвещение, СПб.: филиал изд-ва «Просвещение», 2009.-176 с.

2. Единый государственный экзамен 2009. Информатика. Универсальные материалы для подготовки учащихся/Под редакцией В.Р. Лещинера /ФИПИ. –М:Интеллект-Центр,2009 – 136 с.

4. Гусева И.Ю. ЕГЭ. Информатика: Раздаточный материал тренировочных тестов. – СПб.:Тритон,2009 – 120 с.

5. Самылкина Н.Н., Островская Е.М. ЕГЭ 2010. Информатика: Тренировочные задания. – М.: Эксмо, 2009 – 208 с.

Практические основы подготовки
учащихся к ГИА и ЕГЭ по информатике
через современные технологии
образовательной практики

Составитель:

Бадагиева Елена Зайнутдиновна,

учитель информатики

высшей квалификационной категории

МБОУ «Гимназия №26»

города Набережные Челны

для учителей информатики

Самым важным явлением в школе, самым поучительным предметом, самым живым примером для ученика является сам учитель. Он — олицетворенный метод обучения, само воплощение принципа воспитания. 

Адольф Дистервег

Теория

Тематический блок «Информация и ее кодирование» и

«Системы счисления»

Тематический блок

«Основы логики и логические основы компьютера»

Тематический блок «Пользовательский курс»

Тематический блок

«Технология обработки информации в электронных таблицах», «Технология хранения, поиска и сортировки информации в базах данных»

Тематический блок

«Алгоритмизация и программирование»

Тематический блок «Практическая часть ГИА по информатике»

Тематический блок «часть С ЕГЭ по информатике»

fipi.ru

Источники информации и средства обучения

kpolyakov.narod.ru/school/ege.htm

Источники информации и средства обучения

Источники информации и средства обучения

edu.tatar.ru

Источники информации и средства обучения

edu.ru

Источники информации и средства обучения

school-collection.edu.ru

inf.reshuege.ru

Источники информации и средства обучения

сдамгиа.рф

Источники информации и средства обучения

ПЛАН ЭКЗАМЕНАЦИОННОЙ РАБОТЫ ОГЭ ПО ИНФОРМАТИКЕ 2014 ГОДА 

Отметка по пятибалльной шкале	«2»	«3»	«4»	«5»
Общий балл	0—4	5—11	12—17	18—22

ШКАЛА ПЕРЕВОДА ОТМЕТОК

ПЛАН ЭКЗАМЕНАЦИОННОЙ РАБОТЫ ЕГЭ ПО ИНФОРМАТИКЕ 2014 ГОДА 

ШКАЛА ПЕРЕВОДА ОТМЕТОК

Первичный балл	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16	17	18	19	20	21
Тестовый балл	5	10	15	20	25	30	35	40	42	44	45	47	49	50	52	54	55	57	58	60	62

Первичный балл	22	23	24	25	26	27	28	29	30	31	32	33	34	35	36	37	38	39	40
Тестовый балл	63	65	67	68	70	71	73	75	76	78	80	81	83	84	88	91	94	97	100

Информатика и ИКТ – принципиальных изменений нет.

Оптимизирована структура экзаменационной работы: сократилось общее количество заданий (с 32 до 27);

соответственно, уменьшилось с 40 до 35 максимальное количество первичных баллов.

Уменьшение количества заданий произведено за счет укрупнения тематики заданий, сведения близких по тематике и сложности заданий в одну позицию.

Такими укрупненными стали позиции:

№3 (хранение информации в компьютере),

№6 (формальное исполнение алгоритмов),

№7 (технология вычислений и визуализации данных с помощью

электронных таблиц)

№9 (скорость передачи звуковых и графических файлов).

ПЛАН ЭКЗАМЕНАЦИОННОЙ РАБОТЫ ЕГЭ ПО ИНФОРМАТИКЕ 2015 ГОДА 

В связи с уменьшением количества частей в варианте изменилась последовательность заданий.

Часть 2 работы (задания с развернутым ответом) не изменилась, но относительный вес

баллов, полученных за выполнение заданий с развернутым ответом, увеличился за счет сокращения общего количества заданий в варианте.

ПЛАН ЭКЗАМЕНАЦИОННОЙ РАБОТЫ ЕГЭ ПО ИНФОРМАТИКЕ 2015 ГОДА 

ПЛАН ЭКЗАМЕНАЦИОННОЙ РАБОТЫ ЕГЭ ПО ИНФОРМАТИКЕ 2015 ГОДА 

ШКАЛА ПЕРЕВОДА ОТМЕТОК

	1-23	24	25	26	27	Максимальный балл
Первичный балл	1	3	2	3	4	35

Соответствие между заданиями 2014 и 2015

2015	2014
1	А9
2	А3
3	А4 или А6
4	В7
5	А2
6	А5 или В1
7	А7 или В3
8	В5
9	А8 или В10
10	В4
11	В6
12	В11
13	А11
14	А13

2015	2014
15	В9
16	—
17	В12
18	А10
19	А12
20	В8
21	В14
22	В13
23	В15
24	С1
25	С2
26	С3
27	С4

Тематический блок

«Информация и ее кодирование»

и «Системы счисления»

ГИА	ЕГЭ
1 — кодирование текстовой информации; 7 — кодирование и декодирование данных; 15 — скорость передачи информации; 13 — кодирование чисел в разных системах счисления.	A8 — кодирование звуковой информации; A9 — кодирование и декодирование данных; A11 — вычисление количества информации; B4 — кодирование, комбинаторика  B10 — скорость передачи информации; A1 — кодирование чисел в разных системах счисления; B7 — позиционные системы счисления.

задание 1

ГИА

задание 7

ГИА

задание 13

ГИА

задание 15

ГИА

задание А8

ЕГЭ

задание А9

ЕГЭ

задание А11

ЕГЭ

задание В4

ЕГЭ

задание В10

ЕГЭ

задание А1

ЕГЭ

задание В7

ЕГЭ

Меню

Тематический блок

«Основы логики и логические основы компьютера»

ГИА	ЕГЭ
— логические выражения; 18 — сложные запросы для поисковых систем.	A3 — составление таблицы истинности логической функции; A10 — проверка истинности логического выражения; B12 — сложные запросы для поисковых систем; B15 — логические уравнения.

задание 2

ГИА

задание 18

ГИА

задание В12

ЕГЭ

задание А3

ЕГЭ

задание А10

ЕГЭ

задание В15

ЕГЭ

Меню

Тематический блок

«Пользовательский курс»

ГИА	ЕГЭ
3 — анализ информационных моделей;  4 — файловая система; 11 — поиск путей в графе; 17 — адресация в Интернете.	A2 — анализ информационных моделей; A4 — файловая система; B9 — поиск путей в графе; B11 — адресация в Интернете.

задание 3

ГИА

задание 3

ГИА

задание А2

ЕГЭ

задание 4

ГИА

задание 11

ГИА

задание В9

ЕГЭ

задание 17

ГИА

задание А4

ЕГЭ

задание А4

ЕГЭ

задание В11

ЕГЭ

Меню

Тематический блок

«Технология обработки информации в электронных таблицах», «Технология хранения, поиска и сортировки информации в базах данных»

ГИА	ЕГЭ
5 — анализ диаграмм в электронных таблицах; 12 — сортировка и поиск в базах данных.	A6 — сортировка и поиск в базах данных; A7 — адресация в электронных таблицах; B3 — анализ диаграмм в электронных таблицах.

задание 5

ГИА

задание В3

ЕГЭ

задание 12

ГИА

Задание А6

ЕГЭ

задание А7

ЕГЭ

Меню

Тематический блок

«Алгоритмизация и программирование»

ГИА

ЕГЭ

6 — выполнение алгоритмов для различных исполнителей; 8 — выполнение и анализ простых алгоритмов; 9 — выполнение и анализ программ с циклами; 10 — обработка одномерных массивов; 14 — анализ и построение алгоритмов для исполнителей; 16 — выполнение алгоритма, записанного на естественном языке, обрабатывающего цепочки символов или списки.

A5 — выполнение и анализ простых алгоритмов; A12 — обработка массивов и матриц; A13 — выполнение алгоритмов для исполнителя Робот; B1 — анализ и построение алгоритмов для исполнителей; B2 — операторы присваивания и ветвления; B5 — анализ программ с циклами; B6 — рекурсивные алгоритмы; B8 — анализ программы с циклами и условными операторами; B13 — перебор вариантов, динамическое программирование; B14 — анализ программ с циклами и подпрограммами

задание 6

ГИА

задание 6

ГИА

задание А13

ЕГЭ

задание 8

ГИА

задание В2

ЕГЭ

задание 9

ГИА

задание 10

ГИА

задание А12

ЕГЭ

задание 14

ГИА

задание В1

ЕГЭ

задание 16

ГИА

задание 16

ГИА

задание А5

ЕГЭ

задание В5

ЕГЭ

задание В6

ЕГЭ

задание В8

ЕГЭ

задание В13

ЕГЭ

задание В14

ЕГЭ

Меню

Тематический блок

«Практическая часть ГИА по информатике»

задание 19

ГИА

задание 20.1

ГИА

задание 20.2

ГИА

Меню

Тематический блок

«часть С ЕГЭ по информатике»

задание С1

ЕГЭ

задание С1

ЕГЭ

задание С1

ЕГЭ

задание С1

ЕГЭ

задание С1

ЕГЭ

задание С1

ЕГЭ

задание С1

ЕГЭ

задание С1

ЕГЭ

задание С2

ЕГЭ

задание С2

ЕГЭ

задание С3

ЕГЭ

задание С3

ЕГЭ

задание С4

ЕГЭ

задание С4

ЕГЭ

Меню

Слайд 1

Учитель информатики « Моу Яснозоренская СОШ» Пронькина л.а. 2014 ЭФФЕКТИВНЫЕ ПРИЕМЫ ПОДГОТОВКИ К ГИА И ЕГЭ НА УРОКАХ ИНФОРМАТИКИ

Слайд 2

Важно не количество знаний, а качество их. Можно знать очень многое, не зная самого нужного. Л. Н. Толстой Сейчас компьютеры есть в каждом доме, ими пользуются миллионы человек, поэтому все, что с ними связано, является очень актуальным и востребованным в быстроразвивающемся мире. Единый государственный экзамен по информатике нужен тем выпускникам школы, которые планируют поступать в вузы на самые перспективные специальности, например нанотехнологии , системный анализ и управление, ракетные комплексы и космонавтика, ядерные физика и технологии и многие другие.

Слайд 3

Информатика — это один из самых быстро растущих по популярности предметов для сдачи ЕГЭ. В 2014 году экзамен сдавали почти 55,5 тысяч учащихся. Средний балл за экзамен в 2014 году составил 57,19 баллов, однако максимальный результат смогли показать лишь 38 участников. Также интересный факт, что, к всеобщему удивлению, девушки получают по информатике более высокие баллы, чем молодые люди!

Слайд 4

Изменения в КИМ ЕГЭ по информатике в 2015 году В экзамене по информатике в 2015 году появилось несколько отличий от предыдущих лет: 1. сократилось общее количество заданий, с 32 до 27; 2. Максимальный балл за выполнение всех заданий экзаменационной работы 2015 года составляет 35. Информатика – это самый продолжительный экзамен (столько же длится ЕГЭ по математике и литературе ), длительность составляет 4 часа. Количество заданий составляет 27 задач, разделенные, как и почти во всех экзаменах ЕГЭ, на две группы сложности: В1–В23 – задания повышенной сложности с предоставлением краткого ответа; С1–С4 – сложные задачи, требующие развернутого ответа. Все задания так или иначе связаны с компьютером, но на экзамене пользоваться им для написания программы в задачах группы С не разрешается. Кроме того, задачи не требуют сложных математических вычислений и калькулятором пользоваться тоже не разрешается.

Слайд 5

Демонстрационные варианты ЕГЭ по информатике Пробные тесты ЕГЭ – это материалы, специально подготовленные ФИПИ для того, чтобы ученики смогли заранее ознакомиться с предстоящей процедурой экзамена. Прохождение этих тестов позволит заранее оценить уровень готовности к экзамену и заблаговременно улучшить знания по темам, требующим дополнительного внимания.

Слайд 6

ОГЭ (ГИА ) по информатике – это необязательный экзамен при окончании 9-го класса, может сдаваться по выбору самим учеником или может быть назначен всем ученикам на региональном уровне. При сдаче ГИА по информатике ученик заранее указывает, с каким программным обеспечением он знаком и на каком языке программирования он собирается выполнять часть С. Для выполнения части С – с развернутым ответом – ученику предоставляется компьютер. Как варианты языков программирования принимаются: С или С++, Basic , Pascal или естественный язык.

Слайд 7

Общие цифры ОГЭ (ГИА) по информатике Время проведения экзамена: 150 (2,5 часа). Разрешенные материалы: для 1 и 2-й частей не используются дополнительные материалы, для 3-й части – компьютер со знакомым ученику программным обеспечением. Минимальный балл (соответствует тройке): 5. Максимальный балл: 22. Количество заданий: 20.

Слайд 8

Структура теста ГИА по информатике Все задания ГИА по информатике делятся на три группы: — группа А – 6 заданий с выбором одного правильного ответа из четырех предложенных; — группа В – 12 заданий, требующих краткого ответа на поставленный вопрос, ответом может быть слово, число или последовательность цифр; — группа С – 2 задания, требующих развернутого решения, задачи 19, 20 состоит в написании программы по одному из двух предложенных заданий.

Слайд 9

В демострационных вариантах ОГЭ (ГИА) 2015 года по информатике по сравнению с демонстрационными вариантами 2014 года содержательных изменений нет. Изменилась лишь структура самих вариантов : Каждый вариант теперь состоит из двух частей . Ответ в заданиях с выбором одного ответа записывается цифрой с номером правильного ответа (а не обводится кружком).

Слайд 10

Как вы считаете, что же является секретом успешной подготовки к сдаче ЕГЭ и ГИА? У каждого учителя есть своя стратегия. Но существуют и общие направления в стратегии подготовки. Широко распространены следующие методы подготовки к ЕГЭ: 1 способ. Школьные занятия для подготовки к ЕГЭ. Уроки, факультативы, элективы , кружки. 2 способ. Интернет. Это всевозможные тесты в режиме on-line , сайты, форумы. 3 способ. Репетитор. Большинство родителей школьников уверены: набрать максимум баллов по единому экзамену без занятий с репетитором невозможно.

Слайд 11

Я считаю, что первой скрипкой в этой подготовке должна стать все-таки школа. Подготовка как учеников, так и преподавателей к работе в новой системе оценки качества образования требует большой и кропотливой совместной работы. На мой взгляд, такая подготовка может быть связана с тщательным продумыванием учителем всей системы обучения и контроля над достигнутыми учащимися результатами освоения программного материала. Ведь не секрет, что успешность участия выпускников в итоговой аттестации связана, безусловно, с системностью подготовки к подобным испытаниям в течение всех лет обучения в школе.

Слайд 12

Для того чтобы ученику успешно сдать ЕГЭ и ГИА, во-первых, ему необходимо владеть достаточно полными знаниями по предмету, во-вторых, иметь опыт написания ЕГЭ и ГИА, в-третьих, быть психологически подготовленным к сдаче экзамена. Очевидно, выполнение всех трех критериев невозможно без помощи учителя предметника, без его системной целенаправленной работы.

Слайд 13

Главная задача учителя информатики – организовать работу с обучающимися так, чтобы их выбор предмета «информатика» на государственной итоговой аттестации был осознанным и правильным, создать условия для обеспечения качественной подготовки обучающихся и успешной сдачи ими ЕГЭ и ГИА по информатике и ИКТ.

Слайд 14

Выделю основные направления в моей системе работы по подготовке к ЕГЭ по информатике. Подробно изучаю Рекомендации по разбору отдельных заданий КИМов предыдущего года и анализу допущенных ошибок. Объективная оценка образовательного уровня ученика по предмету Раннее самоопределение или мотивация Тематическое оформление кабинета Формирование собственного банка заданий Подготовка на уроке Использование компьютерных технологий Демонстрационный вариант ЕГЭ

Слайд 15

Подготовка на уроке В плане практически каждого урока я предусмотрела время (от 5 до 10 минут) на тестирование. Объем таких мини-тестов от 5 до10 вопросов. Желательно при закреплении материала на уроке давать контрольные вопросы и задания в стандартном формате, соответству-ющем ЕГЭ. Использование систем тестового контроля не только позволит подготовить учащихся к формату письменных экзаменов, проводимых в виде тестов, но и явится несомненным подспорьем на уроках информатики. Такие тесты, умело составленные, могут выполнять не только контролирующие, но обучающие и закрепляющие функции, служить для осуществления как текущего или промежуточного, так и тематического или итогового контроля знаний.

Слайд 16

Заключение Я считаю, что хороших успехов на экзамене невозможно добиться, если не учитывать в обучении информатике и в целенаправленной подготовке к экзаменам новые требования, предъявляемые к сегодняшнему отечественному образованию, если игнорировать рекомендации экспертов, анализирующих общие результаты экзаменов по нашему предмету и обращающих особое внимание на необходимость совершенствования процесса преподавания информатики. Очень важно, чтобы каждым учителем отрабатывалась определенная система работы, благодаря которой ученики могли бы добиваться максимально предельных результатов не только в учёбе, на итоговой аттестации, но и в жизни.

Слайд 17

«Без стремления к новому нет жизни, нет развития, нет прогресса» В.Г. Белинский

Слайд 18

Источники: Examen.ru> gia – po-informatike