Скачать материал

Скачать материал


- Сейчас обучается 47 человек из 27 регионов


- Сейчас обучается 96 человек из 32 регионов


- Сейчас обучается 54 человека из 30 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Игра
“Математический поезд” -
2 слайд
Касса
www.themegallery.com
Company Logo
Чему равна площадь круга с радиусом 1?
Утверждение, принимаемое без доказательства ?
Наука ,изучающая свойства фигур в пространстве ?
Прибор для построения окружности ?
Разделите сто на половину ?
Наука , изучающая свойства фигур на плоскости ?
Как одним словом назвать сумму длин всех сторон многоугольника ?
Фигура , состоящая из всех точек плоскости, равноудаленных от одной точки?
Найдите 1 % от метра ?
Число, обращающее уравнение в верное равенство -
3 слайд
Тригонометрическая
Арифметическая
Планиметрическая
Повседневная
Стереометрическая -
4 слайд
Тригонометрическая
30
50
80
100
120 -
5 слайд
Тригонометрическая 30
www.themegallery.com
Company Logo36
-
6 слайд
www.themegallery.com
Company Logo
Тригонометрическая 50-12
-
7 слайд
www.themegallery.com
Company Logo
Тригонометрическая 80-6
-
8 слайд
www.themegallery.com
Company Logo
Тригонометрическая 100Ответ: 1.
-
9 слайд
www.themegallery.com
Company Logo
Тригонометрическая 120-3
-
10 слайд
Арифметическая
30
50
80
100
120 -
11 слайд
www.themegallery.com
Company Logo
Арифметическая 30
Найдите значение выражения
(3,9-2,4)∙8,2 =
12,3 -
12 слайд
www.themegallery.com
Company Logo
Арифметическая 502, 65
-
13 слайд
www.themegallery.com
Company Logo
Арифметическая 804
-
14 слайд
www.themegallery.com
Company Logo
Арифметическая 10027
-
15 слайд
www.themegallery.com
Company Logo
Арифметическая 1200,584
-
16 слайд
Планиметрическая
www.themegallery.com
Company Logo
30
50
80
100
120 -
17 слайд
www.themegallery.com
Company Logo
Планиметрическая 30
На клетчатой бумаге с клетками размером 1 см на 1 см изображена фигура (см. рисунок). Найдите ее площадь в квадратных сантиметрах.
12
-
18 слайд
www.themegallery.com
Company Logo
Планиметрическая 50
В треугольнике АВС. АС = ВС = 8, АВ = 8. Найдите cos A
0,5 -
19 слайд
www.themegallery.com
Company Logo
Планиметрическая 80
Основания равнобедренной трапеции равны 51 и 65. Боковые стороны равны 25. Найдите синус острого угла трапеции.
0,96 -
20 слайд
www.themegallery.com
Company Logo
Планиметрическая 100
Периметр параллелограмма равен 46. Одна сторона параллелограмма на 3 больше другой. Найдите меньшую сторону параллелограмма.
10 -
21 слайд
www.themegallery.com
Company Logo
Планиметрическая 120
Средняя линия и высота трапеции равны соответственно 3 и 2. Найдите площадь трапеции.
6 -
22 слайд
Повседневная
30
50
80
100
120 -
23 слайд
www.themegallery.com
Company Logo
Повседневная 30
Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ?
8 -
24 слайд
www.themegallery.com
Company Logo
Повседневная 50
Цена на электрический чайник была повышена на 16% и составила 3480 рублей. Сколько рублей стоил чайник до повышения цены?
3000 -
25 слайд
www.themegallery.com
Company Logo
Повседневная 80
В начале года число абонентов телефонной компании «Восток» составляло 400 тыс. человек, а в конце года их стало 480 тыс. человек. На сколько процентов увеличилось за год число абонентов этой компании?
20% -
26 слайд
www.themegallery.com
Company Logo
Повседневная 100
Аня купила проездной билет на месяц и сделала за месяц 41 поездку. Сколько рублей она сэкономила, если проездной билет стоит 580 рублей, а разовая поездка — 20 рублей?
240 -
27 слайд
www.themegallery.com
Company Logo
Повседневная 120
Участок земли для строительства санатория имеет форму прямоугольника, стороны которого равны 900 м и 400 м. Одна из бóльших сторон участка идёт вдоль моря, а три остальные стороны нужно отгородить забором. Найдите длину этого забора. Ответ дайте в метрах.1700
-
28 слайд
Стереометрическая
30
50
80
100
120 -
29 слайд
www.themegallery.com
Company Logo
Стереометрическая 30
Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.
4 -
30 слайд
www.themegallery.com
Company Logo
Стереометрическая 50
Найдите объем многогранника, изображенного на рисунке (все двугранные углы прямые).36
-
31 слайд
www.themegallery.com
Company Logo
Стереометрическая 80
Площадь поверхности куба равна 18. Найдите его диагональ.
3 -
32 слайд
www.themegallery.com
Company Logo
Стереометрическая 100
Ящик, имеющий форму куба с ребром 10 см без одной грани, нужно покрасить со всех сторон снаружи. Найдите площадь поверхности, которую необходимо покрасить. Ответ дайте в квадратных сантиметрах.
500 -
33 слайд
www.themegallery.com
Company Logo
Стереометрическая 120
Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в три раза?
9
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 155 062 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
Задачи по математике к ЕГЭ
- Учебник: «Алгебра и начала математического анализа. Базовый и углубленный уровни», Алимов А.Ш., Колягин Ю.М. и др.
- Тема: Приложение
- 11.02.2018
- 788
- 1


- 11.02.2018
- 835
- 16
Урок в коррекционном классе
- Учебник: «Алгебра», Макарычев Ю.Н., Миндюк Н.Г., Нешков К.И. и др. / Под ред. Теляковского С.А.
- Тема: 22. Формула корней квадратного уравнения
- 11.02.2018
- 777
- 0

- 11.02.2018
- 466
- 4



Вам будут интересны эти курсы:
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Управление персоналом и оформление трудовых отношений»
-
Курс профессиональной переподготовки «Организация и предоставление туристских услуг»
-
Курс повышения квалификации «Организация практики студентов в соответствии с требованиями ФГОС юридических направлений подготовки»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»
-
Курс повышения квалификации «Психодинамический подход в консультировании»
-
Курс профессиональной переподготовки «Уголовно-правовые дисциплины: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Теория и методика музейного дела и охраны исторических памятников»
-
Курс профессиональной переподготовки «Организация и управление процессом по предоставлению услуг по кредитному брокериджу»
Слайд 1
Подготовка к ЕГЭ (базовый уровень) Подготовила: Никонова С .Г., учитель математики МОУ « Колосковская СОШ»
Слайд 2
Найдите значение выражения 7,2 4,8 + = = = = = = = =
Слайд 3
Решите уравнение = 7 = -2 = 1 = 32 = = 6 — х = 3
Слайд 4
Решите задачи Вероятность того, что шариковая ручка пишет плохо или вовсе не пишет, равна 0,12. Надя не глядя берет шариковую ручку из коробки. Найдите вероятность того. Что эта ручка пишет хорошо. Фабрика выпускает сумки. В среднем из 125 сумок 6 сумок имеют скрытый дефект. Найдите вероятность того, что случайно выбранная сумка окажется с дефектом.
Слайд 5
Решите задачи В летнем лагере 195 детей и 28 воспитателей. Автобус рассчитан не более чем на 35 пассажиров. Какое наименьшее количество автобусов понадобится, чтобы за один раз перевезти всех из лагеря в город? Оптовая цена учебника 180 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 6550 рублей?
1. Подготовка к ЕГЭ по математике
Базовый уровень
2.
2
3.
3
4.
Первичные баллы базового уровня ЕГЭ по
4
математике переводятся в следующие
школьные оценки:
«2» (неудовлетворительно) — от 0 до 6 баллов
«3» (удовлетворительно) — от 7 до 11 баллов
«4» (хорошо) — от 12 до 16 баллов
«5» (отлично) — от 17 до 20 баллов
5. Задание 13
В заданиях на объёмы важно помнить, что
при увеличении всех размеров плоской фигуры в k
раз площадь увеличивается в k2 раз,
при увеличении всех размеров объёмного тела в k
раз объём увеличивается в k3 раз,
Если у фигуры два одинаковых основания
(призма, цилиндр, параллелепипед), то объём
V=Sосн*h
Если есть вершина и только 1 основание
(пирамида, конус), то объём в 3 раза меньше
V=Sосн*h/3
5
6. Задание 13
В заданиях на объёмы важно помнить, что
при увеличении всех размеров плоской фигуры в k
раз площадь увеличивается в k2 раз,
при увеличении всех размеров объёмного тела в k
раз объём увеличивается в k3 раз,
Площадь основания второй кружки больше в
22=4 раза, а высота больше в 1,5 раза, значит,
объём больше в 4*1,5= 6 раз.
Ответ. 6
6
7. Задание 13
Даны две кружки
цилиндрической
формы. Первая кружка
вдвое выше второй, а
вторая в четыре раза
шире первой. Во
сколько раз объём
второй кружки больше
объёма первой?
Ответ: 8
7
Площадь
основания
увеличилась в
42=16 раз, а высота
уменьшилась в 2
раза. Значит, объём
увеличился в
16/2=8раз
8. Задание 13
В сосуд
цилиндрической
формы была налита
вода до уровня 80 см.
Её перелили во второй
цилиндрический сосуд,
у которого радиус
основания в 4 раза
больше, чем у первого.
На каком уровне будет
вода во втором сосуде?
Ответ дайте в
сантиметрах.
8
Решение.
Так как площадь основания
увеличится в 4*4=16 раз, то
высота жидкости уменьшится
в 16 раз и станет равна
80/16=5см.
Ответ: 5
9. Задание 13
Пирамида Хеопса имеет форму
правильной
четырёхугольной
пирамиды, сторона основания
которой равна 230 м, а высота —
147 м. Сторона основания точной
музейной копии этой пирамиды
равна 23 см. Найдите высоту
музейной копии. Ответ дайте в
сантиметрах.
Ответ: 14,7
9
Основание Высота
Оригинал
230 м
147 м
Копия
23 см
x см
10. Задание 14
Это задания на
производные,
возрастание,
убывание функций
Для записи ответов
удобно заранее
построить таблицу
для ответов:
10
Функция f(x)
Производная f ’(x)
Возрастает ↗
Положительна или 0
f’(x) ≥ 0
Убывает ↘
Отрицательна или 0
f’(x) ≤ 0
А
Б
В
Г
11. Задание 14 Сравнение производных
На рисунке изображён график
функции, к которому проведены
касательные в четырёх точках.
Ниже указаны значения
производной в данных точках.
Пользуясь графиком, поставьте
в соответствие каждой точке
значение производной в ней.
ТОЧКИ
А)K
Б)L
В)M
Г)N
Ответ. 2143
11
ЗНАЧЕНИЯ
ПРОИЗВОДНОЙ
1)−4
2)3
3)2/3
4)−0,5
Производная положительна (№2 и 3),
если функция возрастает, то есть в
точках K и N.
В точке K касательная сильнее
наклонена, значит, в точке К модуль
производной больше, поэтому K=п.2)
N=п.3)
В точке L наклон круче, чем в точке M,
значит, модуль отрицательной
производной больше в точке L. Но 4>0,5,
значит, L=п.1)
12. Задание 14 Возрастание — убывание
1
12
2
3
4
Можно идти методом исключения.
А: 1 не выполнено, 2 выполнено (февраль и март) А=п.2
Б: п.1, 3 не выполнено. Б = п.4
В =п.1; Г=п.3 (последний пункт всё равно нужно проверять)
Ответ. 2413
13. Задание 14 Возрастание — убывание
13
А: п.1,2,4 не выполнены, значит, А=п.3
Б=п.4
В= п.1
Г=п.2
Ответ. 3412
14. Задание 17 Решение неравенств
Решаем в произвольном порядке.
А)
; x>1 – п.2)
Б) –x > 1;
x < –1 – п.4
В) методом интервалов
Значит, В=п.3
Г) методом интервалов
Г= п.1
14
Ответ. 2431
15. Задание 17 Округление чисел
А=п.4
1=3/3 < 4/3 < 6/3=2 Б=п.1
В=п.3
1/0,35 = 1/ (35/100) = 100 / 35 > 70/35=2
100 / 35 < 105 /35 = 3; Г=п.2
Ответ. 4132
15
16. Задание 17 Сравнение чисел
1 < m <2 (*)
1) –2< –m< –1 прибавим 6:
4<6 –m<5, значит, N=п.1
2) Все части неравенства * положительны, поэтому
1 < m2 <4 , значит, M=п.2
3) Отнимем 1 от всех частей неравенства *: 0 < m < 1, значит, L=п.3
4) 1 < 2/m < 1/2
–0,5 < – 2/m < –1 , значит, K=п.4
Ответ. 4321
16
17. Задание 18 Пересекающиеся множества (формула)
Множество
А
В
Множество
Б
Элементы не входящие ни в одно множество
Множество В – это пересечение множеств А и Б. Тогда Общее
количество элементов в множествах А и Б равно:
Кол(А+Б) = Кол (А) + Кол (Б) – Кол (В)
Различные варианты ответов получаются изменением Кол(В)
от минимально возможного до максимально возможного
17
18. Задание 18 Пересекающиеся множества (пример)
Facebook
В
Обе
сети Контакте
Элементы не входящие ни в одно множество
18
Кол(F+В) = Кол (F) + Кол (В) – Кол (обе)
10<25<30.
1) 10+25=35>30, поэтому все могут быть пользователями
2) 35 –30=5, поэтому действительно найдутся 5 человек в обоих сетях
3) 25>10, поэтому не могут все из Facebook быть Вконтакте
4) Это верно, так как Вконтакте 10 человек
Ответ. 24
19. Задание 18 Сравнение (пример)
В городе Z в 2013 г. мальчиков родилось больше, чем девочек. Мальчиков чаще всего
называли Андрей, а девочек — Мария. Выберите утверждения, которые следуют из
приведённых данных.
Среди рождённых в 2013 г. в городе Z:
1) девочек с именем Мария больше, чем с именем Светлана.
2) мальчиков с именем Николай больше, чем с именем Аристарх.
3) хотя бы одного из родившихся мальчиков назвали Андреем.
4) мальчиков с именем Андрей больше, чем девочек с именем Мария.
В ответе укажите номера выбранных утверждений без пробелов, запятых и других
дополнительных символов.
19
1) Мария самое популярное имя, значит, их больше, чем Марий. Верно.
2) Про эти имена нет информации, значит, утверждение не следует из условия.
3) Мальчиков больше, чем девочек, значит, есть мальчики и среди них Андреев
больше всего, значит, утверждение верно.
4) Это неверно, так как количество различных имён неизвестно. Например,
100 мальчиков из них 20 Андреев и по 10 других имён. При это 50 девочек,
их них 30 Марий и и по 10 других имён
Ответ. 13
20. Задание 18 Сравнение (пример)
Так как максимум 75, то утверждение верно
2) Сравнения баллов в тексте нет, так что это не
следует из условия задачи
3) Распределение баллов в тексте не описывается,
поэтому п.3 не верен
4) Минимум 36 ≥ 35, поэтому утверждение верно.
Ответ. 14
1)
20
21. Задание 18 Сравнение
П>М>Д
Д<C
1) Магнитофон и стол дороже доски, но не сказано насколько
поэтому нельзя сравнить, а, значит, утверждение неверно
2) Верно
3) Верно
4) И принтер, и стол дороже доски, но не сказано насколько,
поэтому они могут стоить одинаково. Утверждение неверно.
Ответ. 23
21
22. Задание 19 Признаки делимости
Число называется простым, если оно делится только на 1 и само на себя.
Первые простые числа нужно запомнить: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29
(все простые числа невозможно запомнить, так как их бесконечно много)
Признаки делимости на числа:
Число 2
3
4
5
Признак
Последняя
цифра –
чётная
(0,2,4,6,8)
Число
6
9
10
11
Признак
Делится
на 2 и на
3
Сумма
цифр
числа
делится
на 9
После
дняя
цифра
0
Разность суммы цифр на нечётных
местах и суммы цифр на чётных
местах делится на 11
22
Сумма
цифр
числа
делится
на 3
1) Число из последних двух цифр
делится на 4
2) Сумма числа единиц +
удвоенного числа десятков
делится на 4
Последняя
цифра 0
или 5
23. Задание 19
Приведите пример трёхзначного числа, сумма цифр которого равна 20, а сумма
квадратов цифр делится на 3, но не делится на 9.
Решение. Сумма цифр постоянна. Порядок цифр неважен. Поэтому цифры будем
брать в возрастающем порядке. Остаток от деления числа на 3 и на 9 совпадает с
остатком суммы цифр этого числа
659 не проверяем, так как цифры совпадают с 569, значит, последняя цифра не 9.
Пробуем последнюю цифру 8.
Цифры
23
Сумма
Сумма
Остаток при
квадратов делении на 3
Остаток при
делении на 9
299
20
166
1
4
389
20
154
1
1
479
20
146
2
2
569
20
142
1
7
488
20
144
0
0
578
20
138
0
Ответ: 578
Примечание. Есть ещё ответы 587, 758, 785, 857, 875.
3
24. Задание 19
Приведите пример трёхзначного натурального числа
большего 400, которое при делении на 6 и на 5 даёт равные
ненулевые остатки и первая слева цифра которого является
средним арифметическим двух других цифр. В ответе укажите
ровно одно такое число.
Если число делится на 5*6=30, то оно делится на 5 и 6.
Попробуем числа 30n+k, где k от 0 до 4.
Например 420. 4 это среднее 2 и 6, но 426 делится на 6, но не
на 5. Далее 450. 4 это среднее 5 и 3, значит, нам подойдёт 453.
Проверка. 453:5=90 (ост.3), 453:6 = 75 (ост.3)
(5+3) / 2 = 4
Ответ. 453
Примечание. Возможны также ответы 573 (ост.3), 693 (ост.3)
Есть ещё 480 (ост.0), но оно не подходит, так как в условии
говорится, что остатки ненулевые.
24
25. Задание 19 Остатки от деления
Приведите пример трёхзначного натурального
числа, большего 600, которое при делении на 4, на 5 и
на 6 даёт в остатке 3 и цифры которого расположены
в порядке убывания слева направо. В ответе укажите
ровно одно такое число.
Решение. Возьмём число на 3 меньше искомого,
оно делится на 4, 5, 6, значит, делится на их НОК
(наименьшее общее кратное), то есть 22*3*5=60,
значит, наше число 60n+3. Начинаем с 600, пока не
выполнится условие: 603, 663, 723, 783, 843 –
последнее подходит
Ответ. 843
Примечание. Ответ 963 также является верным
25
26. Задание 19
Цифры четырёхзначного числа, кратного 5, записали в обратном порядке и
получили второе четырёхзначное число. Затем из первого числа вычли второе и
получили 4536. Приведите ровно один пример такого числа.
Решение. Число кратно 5, значит, это abc0 или abc5, но 0cba – трехзначное
число, значит было число abc5, а получилось 5cba.
abc5
–
5c b a
4 536, значит, abc5 = 5cba + 4536, поэтому цифра a не меньше 9, значит a =9.
9bc5 = 5cb9 + 4536.
36+9=45, значит, с=b+4 или с = b +4 –10=b –6
Если с=b+4, то в следующий разряд ничего не переносится и получается b
=с+5, чего быть не может (с больше и меньше b одновременно)
с =b – 6 (единица переносится в следующий разряд), тогда b = c+5+1, что
совпадает с предыдущим условием. Осталось выбрать b и с, например, b = 6; c=0.
Проверка. 9605 – 5069 = 4536 верно
Ответ. 9605
Примечание. Есть ещё ответы 9715, 9825, 9935
26
27. Задание 20 На смекалку (пример 1)
Улитка за день заползает вверх по дереву на 3 м, а за ночь спускается на 2 м. Высота дерева 10 м.
Через сколько дней улитка впервые окажется на вершине дерева?
Решение. Лучше сделать таблицей, указывая все состояния (на какой высоте будет улитка после
каждого действия)
№ дня
1
2
3
4
5
6
7
8
Вечер (после дня)
3
4
5
6
7
8
9
10
Утро (после ночи)
1
2
3
4
5
6
7
9
Значит, улитка впервые окажется на вершине дерева через 8 дней.
Ответ. 8
Примечание. Популярна следующая ошибка: на 3 – 2 = 1 м в день поднимается улика, значит,
10/1=10 дней. Однако, в данном случае улитка через 10 дней СПУСТИТСЯ на вершину дерева,
значит, она должна раньше была подняться. Такое решение неверно.
27
28. Задание 20 На смекалку (пример 2)
В обменном пункте можно совершить одну из двух операций:
1) за 4 золотых монеты получить 5 серебряных и одну медную;
2) за 7 серебряных монет получить 5 золотых и одну медную.
У Николы были только серебряные монеты. После посещений обменного пункта
серебряных монет у него стало меньше, золотых не появилось, зато появилось 90
медных. На сколько уменьшилось количество серебряных монет у Николы?
1.
2.
Решение. Выделяем особые моменты:
При каждом обмене добавляется 1 медная монета, значит, всего было 90
обменов.
В итоге нет золотых монет, значит их нужно сразу разменивать, но 5 золотых не
имеет общих множителей с 4, значит нужно сначала сделать 4 обмена 2 типа:
4*7=28 серебряных монет меняется на 20 золотых и 4 медных, а затем 5 обменов
1-го типа: 20 золотых меняется на 5*5=25 серебряных и 5 медных.
В итоге за 4+5=9 обменов мы из 28 серебряных получаем 25 серебряных (на 3
меньше, чем было) и 4+5=9 медных.
Так как нужно сделать 90 обменов (см.п.1), то нужно провести 90/9=20 обменов
по п.2, тогда количество серебряных монет уменьшится на 3*10=30 монет.
Ответ: 30
28
29. Задание 20 На смекалку (пример 3)
В корзине лежат 25 грибов: рыжики и грузди.
Известно, что среди любых 11 грибов имеется хотя
бы один рыжик, а среди любых 16 грибов хотя бы
один груздь. Сколько рыжиков в корзине?
Решение. Смотрим по самому плохому варианту, так
как среди 11 точно есть один рыжик, значит, не
рыжиков (груздей) не наберётся больше 10.
Аналогично, не груздей (рыжиков) не больше 15.
р+г ≤ 25, но так как р+г=25 по условию, то г=10, р=15
Ответ. 15
29
Презентация на тему «Разбор типовых заданий ЕГЭ по математике базового уровня» 11 класс
-
Скачать презентацию (0.55 Мб)
-
117 загрузок -
0.0 оценка
Ваша оценка презентации
Оцените презентацию по шкале от 1 до 5 баллов
- 1
- 2
- 3
- 4
- 5
Комментарии
Добавить свой комментарий
Аннотация к презентации
Скачать презентацию (0.55 Мб). Тема: «Разбор типовых заданий ЕГЭ по математике базового уровня». Предмет: математика. 35 слайдов. Для учеников 11 класса. Добавлена в 2021 году.
-
Формат
pptx (powerpoint)
-
Количество слайдов
35
-
Аудитория
-
Слова
-
Конспект
Отсутствует
Содержание
-
Слайд 1
Разбор типовых заданий ЕГЭ по математике базового уровня
Геометрия
-
Слайд 2
Прикладная геометрия1. Перила лестницы дачного дома для надёжности укреплены посередине вертикальным столбом. Найдите высоту l этого столба, если наименьшая высота h1 перил равна 1,25 м, а наибольшая высота h2 равна 2,25 м. Ответ дайте в метрах.
!Алгоритм выполнения
Определить, что за фигура на рисунке.
Вспомнить определение средней линии трапеции.
Записать формулу для нахождения средней линии трапеции.
Подставить данные.
Вычислить среднюю линию трапеции. -
Слайд 3
2. План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м х 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
! Алгоритм выполнения
Определить что за фигура на рисунке.
Записать формулу нахождения площади данной фигуры.
Определить по чертежу все необходимые данные.
Вычислить площадь участка. -
Слайд 4
3. План местности разбит на клетки. Каждая клетка обозначает квадрат 1 м х 1 м. Найдите площадь участка, выделенного на плане. Ответ дайте в квадратных метрах.
! Алгоритм выполнения
Определить что за фигура на рисунке.
Записать формулу нахождения площади данной фигуры.
Определить по чертежу все необходимые данные.
Вычислить площадь участка. -
Слайд 5
4. Дачный участок имеет форму прямоугольника со сторонами 25 метров и 30 метров. Хозяин планирует обнести его забором и разделить таким же забором на две части, одна из которых имеет форму квадрата. Найдите суммарную длину забора в метрах.
!Алгоритм выполнения
Вычислить периметр прямоугольника.
Прибавить длину разделяющей части.
P = 30 м + 30 м + 25 м + 25 м = 110 м.
110 м – длина забора без перегородки.
Прибавим длину разделяющей части.
По рисунку видно, что длина разделяющей части 25 м.
110 м + 25 м = 135 м. -
Слайд 6
5. Какой угол (в градусах) образуют минутная и часовая стрелки в 16:00?
! Алгоритм выполнения
Сначала мы найдем, сколько в градусах занимает один час.
Затем найдем угол, который образуют стрелки в 16:00
Так как вся окружность — 360°, а часов 12, то один час:
360° : 12 = 30°
Значит, в четыре часа угол будет равен:
30° • 4 = 120° -
Слайд 7
6. Пожарную лестницу длиной 10 м приставили к окну дома. Нижний конец лестницы отстоит от стены на 6 м. На какой высоте находится верхний конец лестницы? Ответ дайте в метрах.
! Алгоритм выполнения
Приставленная к стене лестница образует с этой стеной и горизонтальной площадкой возле дома прямоугольный треугольник. Высота, на которой находится верхний конец лестницы, является одним из катетов этого треугольника. Следовательно, для нахождения ее величины нужно использовать теореме Пифагора. -
Слайд 8
7. Дачный участок имеет форму прямоугольника, стороны которого равны 35 и 45 м. Дом, расположенный на участке, имеет на плане форму квадрата со стороной 7 м. Найдите площадь оставшейся части участка, не занятой домом. Ответ дайте в квадратных метрах.
! Алгоритм выполнения
Находим площадь прямоугольного участка.
Находим площадь квадратного дома.
Находим разность этих площадей, отняв от большего числа меньшее.
35 · 45 = 1575 (кв.м) – площадь всего участка
7 · 7 = 49 (кв.м) – площадь дома
1575 – 49 = 1526 (кв.м) – площадь оставшейся части участка -
Слайд 9
8. На каком расстоянии (в метрах) от фонаря стоит человек ростом 1,8 м, если длина его тени равна 9 м, высота фонаря 5 м?
! Алгоритм выполнения
Рассматриваем 2 подобных треугольника. В первом стороны образуют линия фонаря и расстояние от его основания до верхней точки тени от человека. Во втором – линия роста человека и линия его тени.
Поскольку треугольники подобны, то можем соотнести соответствующие стороны и оставить из этих отношений пропорцию.
Из полученной пропорции выражаем искомую величину. Вычисляем ее.
Обозначим искомое расстояние через х.
Из рисунка имеем 2 треугольника. Один (больший) построен на сторонах 5 м и (х+9) м. Другой (меньший) – 1,8 м и 9 м. Составим пропорцию из отношений соответствующих сторон этих треугольников:
5 : 1,8 = (х + 9) : 9.
Из пропорции получим:
5 · 9 = 1,8 · (х + 9)
1,8х + 16,2 = 45
1,8х = 28,8
х = 16 (м) -
Слайд 10
Наглядная стереометрия9. Вода в сосуде цилиндрической формы находится на уровне h = 80 см. На каком уровне окажется вода, если ее перелить в другой цилиндрический сосуд, у которого радиус основания в 4 раза больше, чем у данного? Ответ дайте в сантиметрах.
! Алгоритм выполнения:
Записать формулу объема цилиндра.
Подставить значения для цилиндра с жидкостью в первом и во втором случае.
Объем жидкости не изменялся, следовательно, можно приравнять объемы.
Полученное уравнение решить относительно второй высоты h2.
Подставить данные и вычислить искомую величину.
V1 = π r1 2 h1
V2 = π r2 2 h2
Объем жидкости не изменялся, следовательно, можно приравнять объемы.
V1 = V2
π r1 2 h1 = π r2 2 h2
h2 =( π r1 2 h1)/ π r2 2
По условию площадь основания стала в 4 раза больше, то есть r2 = 4 r1 .
Подставим r2 = 4 r1 в выражение для h1.
Получим: h2 =( π r1 2 h1)/ π (4 r1) 2
Полученную дробь сократим на π, получим h2 =( r1 2 h1)/ 16 r1 2
Полученную дробь сократим на r1, получим h2 = h1/ 16.
Подставим известные данные: h2 = 80/ 16 = 5 см.
Ответ: 5. -
Слайд 11
10. Даны две коробки, имеющие форму правильной четырёхугольной призмы. Первая коробка в четыре с половиной раза выше второй, а вторая втрое шире первой. Во сколько раз объём первой коробки меньше объёма второй?
! Алгоритм выполнения:
Записать формулу, для вычисления объема правильной четырехугольной призмы.
Записать в общем виде формулу для нахождения объема в первом и втором случае.
Найти отношение объемов.
Преобразовать полученное выражение с учетом соотношения измерений первой и второй призмы.
Сократить получившуюся дробь.
V1 = a1 · b1 · c1
V2 = a2 · b2 · c2
Найдем отношение объемов.
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2)
По условию c1 = 4,5 c2 (первая коробка в четыре с половиной раза выше второй),
b2 = 3 b1 (вторая коробка втрое шире первой).
Так как это правильные четырехугольные призмы, то в основании лежит квадрат, а значит глубина второй коробки тоже втрое больше глубины первой, то есть a2 = 3 a1
Подставим эти выражения в формулу отношения объемов:
V1 / V2 = (a1 · b1 · c1)/ ( a2 · b2 · c2) = (a1 · b1 · 4,5c2)/ ( 3a1 · 3b1 · c2) = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2)
Сократим получившуюся дробь на a1 · b1 · c2. Получим:
V1 / V2 = (a1 · b1 · 4,5c2)/ ( 9a1 · b1 · c2) = 4,5/9 = ½.
Объем первой коробочки в 2 раза меньше объема второй.
Ответ: 2. -
Слайд 12
11. От деревянного кубика отпилили все его вершины (см. рис.). Сколько граней у получившегося многогранника (невидимые ребра на рисунке не изображены)?
! Сначала вспомним сколько всего граней и вершин у куба: шесть граней и восемь вершин. Теперь на месте каждой вершины образуется новая грань после отпила, значит у модифицированного в задании куба шесть родных граней и восемь новых (после отпила). Итого получаем: 6 + 8 = 14 граней.
Ответ: 14.
Если бы нас спросили, а сколько вершин у нового «куба». Очевидно, если вместо одной становится три, а их всего восемь, то получаем: 8 • 3 = 24 -
Слайд 13
12. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 2 и 6, а второго – 6 и 4. Во сколько раз объем второго цилиндра больше объема первого?
! Алгоритм выполнения
Записываем ф-лу для вычисления объема цилиндра.
Вводим обозначения для радиуса основания и высоты 1-го цилиндра. Выражаем подобным образом аналогичные параметры 2-го цилиндра.
Формируем формулы для объема 1-го и 2-го цилиндров.
Вычисляем отношение объемов.
V1=πR12H1,V2=πR22H2.
-
Слайд 14
13. В бак, имеющий форму прямой призмы, налито 5 л воды. После полного погружения в воду детали уровень воды в баке поднялся в 1,4 раза. Найдите объем детали. Ответ дайте в кубических сантиметрах, зная, что в одном литре 1000 кубических сантиметров.
! Алгоритм выполнения
Вводим обозначения для объема до погружения детали и после. Пусть это будет соответственно V1 и V2.
Фиксируем значение для V1. Выражаем V2 через V1. Находим значение V2.
Переводим результат, полученный в литрах, в куб.см.
Объем бака до погружения V1=5 (л). Т.к. после погружения детали объем стал равным V2. Согласно условию, увеличение составило 1,4 раза, поэтому V2=1,4V1.
Отсюда получаем: V2=1,4·5=7 (л).
Т.о., разница объемов, которая и составляет объем детали, равна:
V2–V1=7–5=2 (л).
2 л=2·1000=2000 (куб.см). -
Слайд 15
14. В сосуде, имеющем форму конуса, уровень жидкости достигает ½ высоты. Объем сосуда 1600 мл. Чему равен объем налитой жидкости? Ответ дайте в миллилитрах.
! Алгоритм выполнения
Доказываем, что данные в условии конусы подобны.
Определяем коэффициент подобия.
Используя свойство для объемов подобных тел, находим объем жидкости.
Если рассматривать сечение конуса по двум его противоположно расположенным образующим (осевое сечение), то видим, что полученные таким способом треугольники большого конуса и малого (образованного жидкостью) подобны. Это следует из равенства их углов. Т.е. имеем: у конусов подобны высоты и радиусы основания. Отсюда делаем вывод: т.к. линейные параметры конусов подобны, то и конусы подобны.
По условию высота малого конуса (жидкости) составляет ½ высоты конуса. Значит, коэффициент подобия малого и большого конусов равен ½.
Применяем св-во подобия тел, которое заключается в том, их объемы относятся как коэффициет подобия в кубе. Обозначим объем большого конуса V1, малого – V2. Получим:
Поскольку по условию V1=1600 мл, то V2=1600/8=200 мл. -
Слайд 16
15. Даны два шара с радиусами 4 и 1. Во сколько раз объем большего шара больше объема меньшего?
! Алгоритм выполнения
Записываем формулу для вычисления объема шара.
Адаптируем формулу для каждого из шаров. Для этого используем индексы 1 и 2.
Записываем отношение объемов, вычисляем его, подставив числовые данные из условия.
Вывод: объем большего шара в 64 раза больше. -
Слайд 17
16. Даны два цилиндра. Радиус основания и высота первого цилиндра равны соответственно 4 и 18, а второго – 2 и 3. Во сколько раз площадь боковой поверхности первого цилиндра больше площади боковой поверхности второго?
! Алгоритм выполнения
Записываем формулу для определения площади бок.поверхности цилиндра.
Переписываем ее дважды с использованием соответствующих индексов – для 1-го (большего) и 2-го (меньшего) цилиндров.
Находим отношение площадей. Вычисляем отношения, используя числовые данные из условия.
Вывод: площадь боковой поверхности 1-го цилиндра больше в 12 раз. -
Слайд 18
17. Однородный шар диаметром 3 см весит 162 грамма. Сколько граммов весит шар диаметром 2 см, изготовленный из того же материала?
! Алгоритм выполнения
Записываем формулу для определения массы большего шаров через плотность и объем.
Объем в этой формуле расписываем через ф-лу объема шара (через его радиус).
Записываем ф-лу для массы меньшего шара, расписываем объем через радиус (по аналогии с пп.1 и 2).
Поскольку оба шара изготовлены из одного и того же материала, то найденное значение для плотности можем использовать в ф-ле для массы меньшего шара. Вычисляем искомую массу.
m1=ρV1.
V1=(4/3)πR13. Отсюда получаем: m1=(4/3)πρR13
.
m2=ρV2V2=(4/3)πR23
-
Слайд 19
Планиметрия. №1518. В треугольнике ABC угол ACB равен 90°, cos A = 0,8, AC = 4. Отрезок CH – высота треугольника ABC(см. рисунок). Найдите длину отрезка AH.
! Алгоритм выполнения:
Вспомнить определение косинуса угла.
Записать выражение для нахождения косинуса угла.
Выразить неизвестную величину.
Вычислить.
cos A = АН/АС.АН = АС · cos A
АН = АС · cos A = 4 · 0,8 = 3,2
Ответ: 3,2. -
Слайд 20
19. Найдите вписанный угол, опирающийся на дугу, длина которой равна 5/18 длины окружности. Ответ дайте в градусах.
! Алгоритм выполнения:
Вспомнить соотношение величины вписанного угла и градусной меры угла, на который он опирается.
Вычислить градусную меру угла, на который опирается дуга.
Вычислить вписанный угол.
Весь круг составляет 360°, а 5/18 от его длины этоТак как вписанный угол равен половине градусной меры дуги, на которую он опирается, вписанный угол равен
100°:2 = 50°.
Ответ: 50. -
Слайд 21
20.В треугольнике АВС известно, что АВ=ВС=15, АС=24. Найдите длину медианы ВМ
! Алгоритм выполнения
Определяем вид треугольника.
Доказываем, что медиана ВМ является и высотой.
Из прямоугольного треугольника АМВ по т. Пифагора находим медиану ВМ.
Если АВ=ВС, то ∆АВС – равнобедренный.
Т.к. АМ медиана, то AM=АС:2=24:2=12. -
Слайд 22
21. На стороне ВС прямоугольника АВСD, у которого АВ=12 и АD=17, отмечена точка Е так, что треугольник АВЕ равнобедренный. Найдите ЕD.
! Алгоритм выполнения
Находим ЕС.
Определяем значение СD.
Из прямоугольного треугольника АСD по т.Пифагора
находим ЕD.
Т.к. по условию ∆АВЕ равнобедренный, то ВЕ=АВ=12.
Т.к. АВСD прямоугольник, то ВС=АD=17, СD=АВ=12.
ЕС=ВС–ВЕ=17–12=5.
∆ЕСD прямоугольный.
Тогда по т.Пифагора ЕD2=ЕC2+СD2. -
Слайд 23
22. В треугольнике АВС угол С равен 900, АВ=25, АС=24. Найдите cos B.
! Алгоритм выполнения
По т.Пифагора находим величину катета ВС.
По формуле-определению для косинуса находим cos B как отношение прилежащего катета к гипотенузе.
Из прямоугольного ∆АВС по теореме Пифагора имеем: АВ2=АС2+ВС2. -
Слайд 24
23. В равнобедренном треугольнике АВС боковая сторона АВ=25, sin A=3/5. Найдите площадь треугольника АВС.
! Алгоритм выполнения
Из вершины В проводим высоту BD к основанию ∆АВС. Получаем прямоугольного ∆ADB.
Из ∆ADB находим катет ВD, используя sin A.
Находим АD из ∆ADB по т.Пифагора. Далее определяем АС как 2AD.
Находим площадь ∆АВС по формуле S=ah/2.
В ∆ADB sin A=BD/AB → BD = AB · sin A = 25 · 3 / 5 = 15.
Из ∆ADB по т.Пифагора имеем: AB2=AD2+BD2
АС=2АD=2·20=40. -
Слайд 25
24. В треугольнике АВС угол В равен 1200. Медиана ВМ делит угол В пополам и равна 27. Найдите длину стороны АВ.
! Алгоритм выполнения
Определяем величину угла АВМ.
Доказываем, что ∆АМВ прямоугольный.
Находим АВ, используя формулу-определение для косинуса.
По условию угол АВМ равен половине угла В. Значит, угол АВМ составляет
1200:2=600.
Т.к. ВМ – медиана, опущенная на основание равнобедренного ∆АВС, то ВМ является и высотой. Поэтому ∆АМВ прямоугольный с прямым углом АМВ. -
Слайд 26
25. В равнобедренном треугольнике АВС медиана ВК=10, боковая сторона ВС=26. Найдите длину отрезка МN, если известно, что он соединяет середины боковых сторон.
! Алгоритм выполнения
Доказываем, что ∆АКВ прямоугольный.
Из ∆АКВ по т.Пифагора находим АК.
Находим АС как 2АК.
Находим МN как среднюю линию.
Из прямоугольного ∆АКВ по т.Пифагора АВ2=АК2+ВК2.
Поскольку ВК медиана, то АС=2АК=2·24=48.
Значит, MN=AC:2=48:2=24. -
Слайд 27
26. В треугольнике АВС высота АС=56, ВМ – медиана, ВН – высота, ВС=ВМ. Найдите длину отрезка АН.
! Алгоритм выполнения
Находим длину отрезков АМ и МС как половину от АС.
Доказываем, что ВН является медианой в ∆МВС.
Отсюда определяем, что МН – половина от МС.
3. Находим АН как сумму АМ и МН.
Рассмотрим ∆АВС. Т.к. ВМ медиана, то АМ=МС=АС/2=56/2=28.
МН=НС=МС/2=28/2=14.
АН=АМ+МН=28+14=42. -
Слайд 28
Стереометрия (№16)27. Радиус основания цилиндра равен 13, а его образующая 18. Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12. Найдите площадь этого сечения.
! Алгоритм выполнения:
Определить тип фигуры, образующей сечение.
Записать формулу для нахождения площади фигуры, образующей сечение.
Вычислить недостающие данные.
Вычислить искомую площадь сечения.
Сечение является прямоугольником, одна из сторон которого образующая цилиндра.
Длина прямоугольника – 18, из условия. Осталось вычислить ширину. Сделаем дополнительный чертеж цилиндра сверху: -
Слайд 29
Ширина прямоугольника – CD.
По условию «Сечение, параллельное оси цилиндра, удалено от нее на расстояние, равное 12». Расстояние от точки до прямой – это длина перпендикуляра, проведенного из этой точки на прямую. То есть на чертеже АВ = 12.
СD = СВ + ВD. СВ = ВD
Рассмотрим треугольник ВСА. Треугольник ВСА – прямоугольный.
Теорема Пифагора: квадрат гипотенузы равен сумме квадратов катетов.
В данном случае СА2 = СВ2 + АВ2
СВ2 — неизвестное слагаемое. Чтобы найти неизвестное слагаемое нужно из суммы вычесть известное слагаемое.
СВ2 = СА2 — АВ2
СВ = √(СА2 — АВ2)
СВ = √(132 — 122) = √(169 — 144) = √25 = 5
Для решения задачи необходимо знать СD = СВ + ВD = 5 + 5 = 10
Вычислим искомую площадь сечения.
10 · 18 = 180
Ответ: 180. -
Слайд 30
29. Стороны основания правильной треугольной пирамиды равны 24, а боковые рёбра равны 37. Найдите площадь боковой поверхности этой пирамиды.
! Алгоритм выполнения:
Проанализировать какие данные необходимо вычислить для ответа на вопрос задачи.
Найти площади треугольников.
Найти площадь боковой поверхности пирамиды.
В основании правильной треугольной пирамиды лежит равносторонний треугольник. Боковые ребра пирамиды, равные 37, образуют три равнобедренных треугольника, которые составляют ее боковую поверхность.
Найдем площади треугольников.Так как треугольник равнобедренный, AH=AC:2=24:2=12.Р/м треугольник АВН.АВ2 = ВН2 + АН2.ВН2 = АВ2 — АН2
Боковая поверхность пирамиды состоит из трех треугольников -
Слайд 31
30. Найдите объем правильной четырехугольной пирамиды, сторона основания которой равна 4, а боковое ребро равно √17.
Вспомним формулу площади правильной пирамиды — одна треть от произведения площади основания и высоты.
После этого перейдем к нахождению высоты. Для этого нам необходимо рассмотреть прямоугольный (так как основание перпендикулярно высоте) треугольник AMH. AH — половина диагонали квадрата, которая равна √2 его стороны, то есть в нашем случае диагональ равна 4√2, ну а половина — AH = 2√2. Зная гипотенузу и один из катетов, найдем высоту:
V = 1/3 • 16 •3 = 16
-
Слайд 32
31. Сторона основания правильной треугольной призмы АВСА1В1С1 равна 2, а высота этой призмы равна 4√3. Найдите объем призмы АВСА1В1С1.
! Алгоритм выполнения
Находим площадь основы призмы через формулу для площади правильного треугольника.
Записываем формулу для объема призмы. Подставляем в нее числовые данные, вычисляем искомую величину.
Объем призмы: V=Sh -
Слайд 33
32. Объем конуса равен 25π, а его высота равна 3. Найдите радиус основания конуса.
! Алгоритм выполнения
Записываем формулу для объема конуса. Из нее выражаем площадь основания.
Площадь основания расписываем по формуле площади круга, поскольку именно круг лежит в основании конуса.
Из этих двух формул выражаем искомую величину. Вычисляем ее.
Sосн=3V/h.
S=πR2
Поскольку в данном случае Sосн=S, то πR2=3V/h -
Слайд 34
33. Два ребра прямоугольного параллелепипеда равны 8 и 5, а объем параллелепипеда равен 280. Найдите площадь поверхности этого параллелепипеда.
! Алгоритм выполнения
Записываем формулу для объема прямоугольного параллелепипеда. Из нее выражаем 3-е (неизвестное) ребро. Вычисляем величину этого ребра.
Записываем формулу для площади поверхности. Подставляем в него числовые данные, находим искомое значение.
Объем прямоугольного параллелепипеда равен:
V=abc, где a, b, c – ребра. Будем считать, что a и b нам известны, а с – неизвестно.
Тогда: с=V/(ab).
с=280/(8·5)=7.
Площадь поверхности прямоугольного параллелепипеда вычисляется так:
S=2(ab+bc+ac).
Отсюда имеем:
S=2(8·5+5·7+8·7)=2(40+35+56)=2·131=262. -
Слайд 35
34. Объем конуса равен 24π, а радиус его основания равен 2. Найдите высоту конуса.
! Алгоритм выполнения
Записываем формулу для объема конуса. Из нее выражаем высоту.
Записываем формулу для площади круга, лежащего в основе конуса. Вычисляем эту площадь.
Подставляем числовые данные в формулу для объема, вычисляем искомую величину.
Площадь основания (как площадь круга) равна:
Sосн=πR2.
Вычисляем площадь:
Sосн=π·22=4π.
Посмотреть все слайды
Сообщить об ошибке
Похожие презентации










Спасибо, что оценили презентацию.
Мы будем благодарны если вы поможете сделать сайт лучше и оставите отзыв или предложение по улучшению.
Добавить отзыв о сайте
Задания для подготовки к ЕГЭ по математике (базовый уровень)
2015
10-11 класс
Иванова Т.В.
МБОУ СОШ №18
Г. Ростов-на-Дону
№ 1. Летом килограмм клубники стоит 80 рублей.
Маша купила
1 кг 750 гр клубники.
Сколько рублей сдачи она должна получить с 200 рублей?
1 кг 750 гр = 1,750 кг Стоимость покупки составила 80⋅1,75=140 рублей. Следовательно, Маша должна получить 200−140=60 рублей сдачи.
№ 2 Стоимость железнодорожного билета на один и тот же маршрут меняется в зависимости от даты поездки: среднегодовая цена билета умножается на коэффициент индексации. Стоимость плацкартного билета 8.12.2013 из Санкт-Петербурга в Москву составила 916 рублей, при этом коэффициент индексации в период с 5 ноября по 20 декабря
был равен 0,8.
Какова будет стоимость соответствующего билета 25 декабря, если в период с 21 декабря по 26 декабря коэффициент индексации был равен 1,1?
1259,5

Решение Пусть базовая цена равна X рублей. Тогда цена билета на 8 декабря составляет 0,8X рублей, а цена билета 25 декабря составляет 1,1X рублей. Имеем:
0,8X = 916 = X = 916/0,8 = 1145 (руб)
Значит, цена билета на 25 декабря будет 1,1· X = 1,1· 1145 = 1259,5 рублей
Ответ 1259,5
№ 3 В магазине проходит рекламная акция: при покупке пяти шоколадок «Везение» – шестая в подарок. Стоимость одной шоколадки 24 рубля. Какое наибольшее количество шоколадок «Везение» может приобрести и получить по акции покупатель, который готов потратить на них не более 400 рублей? В ответе укажите общее количество шоколадок.
Решение Чтобы узнать, сколько шоколадок можно купить, имея 400 р., делим 400 на 24 с остатком. Получим: 240:24 = 16 (ост 16). 16 шоколадок — это 3 пятерки и еще одна шоколадка (снова делим с остатком!). В результате рекламной акции пятерки превращаются в шестерки. Итого, можно приобрести 6*3+1 = 19 шоколадок. Ответ 19

№ 4 Стоимость железнодорожного билета на один и тот же маршрут меняется в зависимости от даты поездки: среднегодовая цена билета умножается на коэффициент индексации. Стоимость плацкартного билета 31.08.2013из Санкт-Петербурга в Москву составила 1374 рублей, при этом коэффициент индексации в период с 13 июля по 2сентября был равен 1,2. Какова была стоимость соответствующего билета 27 декабря, если в период с 27 декабря по 28 декабря коэффициент индексации был равен 1,15?
Решение Пусть X — среднегодовая цена билета. Тогда стоимость плацкартного билета на 31.08.2013 составляет 120% от среднегодовой цены, то есть равна 1,2*X. Имеем: 1,2 X = 1374 = X = 1374 : 1,2 = 1145 (руб) Следовательно, стоимость билета на 23 декабря равна 1,15*X = 1316,75 (рублкй) Ответ 1316,75
№ 5 В мюнхенском метрополитене продается групповой билет. По этому билету могут пройти максимум 5 взрослых человек, при этом 2 ребенка считаются за одного взрослого, т.е. этим билетом могут воспользоваться максимум 10 детей.
Сколько групповых билетов должна купить группа, состоящая из 32 детей и 9 взрослых?
Решение 32 ребенка приравниваются к 32 : 2 = 16 взрослым. Значит, в группе есть 16+9 = 25 «условных взрослых». Для них нужно 25 : 5 = 5 билетов. Ответ 5
№ 6 Саша пригласил друзей на свой день рождения, отправив SMS-сообщения 17 друзьям. Отправка одного SMS-сообщения стоит 1 рубль 50 копеек. До отправки сообщений на счету 55 рублей. Сколько рублей останется у Саши после отправки всех сообщений?
Решение Одно сообщение стоит 1,5 руб. Значит, 17 сообщения стоят 17*1,5 = 25,5 руб. В итоге у Саши останется
55 — 25,5 = 29,5 руб Ответ 29,5
№ 7 В двухдневный поход идут 23 человека. Какое наименьшее число четырёхместных палаток им нужно взять с собой?
Решение Делим 23 на 4 с остатком. Получим: 23:4 = 5 (3 ост). Значит, нужно брать 6 палаток (в последней палатке будут жить 3 человека)
Ответ 6
№ 8 Слава идет на день рождения к Свете и хочет подарить ей букет. Он знает, что в букете должно быть нечетное количество цветов. Хризантемы стоят 35 рублей за штуку. Из какого наибольшего числа хризантем Слава может купить букет, если у него 300 рублей?
№ 9 При выезде за рубеж турист должен иметь медицинскую страховку, стоимость одного дня которой составляет 120 рублей. Турист оплачивает стоимость страховки за каждый день нахождения за рубежом (в том числе и неполный). Сергей Михайлович планирует прибыть в Прагу 30 декабря, а вылететь обратно 5 января.
Какова стоимость медицинской страховки Сергея Михайловича?
Решение С.М. пробудет в Праге 31 — 30 + 1 = 2 дня декабря и 5 дней января — всего 7 дней. За страховку ему нужно уплатить 7· 120 = 840 (руб) Ответ 840
№ 10 В пачке 500 листов бумаги формата А4. За неделю в офисе расходуется 1200 листов. Какое наименьшее количество пачек бумаги нужно купить в офис на 5 недель?
Решение . На 5 недель нужно
5*1200 = 6000 листов.
Это составляет 6000 : 500 =12 пачек. Значит, нужно купить 12 пачек.
Ответ 12
№ 11 Поезд Самара-Волгоград отправляется в 19:54, а прибывает в 12:24 следующего дня (время московское).
Сколько часов поезд находится в пути?
Решение. В сутки отправления поезд был в пути
24 ч – 19 ч 54 мин = 4 ч 6 мин.
На следующий день поезд был в пути 12 ч 24 мин. Всего в пути поезд был
4 ч 6 мин + 12 ч 24 мин = 16 ч 30 мин = 16,5 часов
Ответ: 16,5
№ 12 Аня купила проездной билет на месяц и сделала за месяц 34 поездки. Сколько рублей она сэкономила, если проездной билет на месяц стоит 207 рублей, а разовая поездка — 20 рублей?
Решение. Без проездного Аня потратила бы 34*20 = 680 руб. Значит, она сэкономила 680 – 207 = 473 руб. Ответ: 473
№ 13 Таксист за месяц проехал 6000 км. Стоимость 1 литра бензина 26 рублей. Средний расход бензина на 100 км составляет 8 л. Сколько рублей потратил таксист на бензин за этот месяц?
Решение Таксист израсходовал (6000:100)*8 = 60*8 = 480 л бензина.
Этот бензин стоит 480*26 = 12480 руб Ответ: 12480
№ 14 В мюнхенском метрополитене продается групповой билет за 10 евро 50 центов. По этому билету могут пройти максимум 5 взрослых человек, при этом 2 ребенка считаются за одного взрослого, т.е. этим билетом могут воспользоваться максимум 10 детей.
Сколько евро должна заплатить группа из 26 детей и 5 взрослых, если будет покупать только групповые билеты?
Решение 26 детей приравниваются к 26 : 2 = 13 взрослым. Значит, в группе есть 13+5 = 18 «условных взрослых». Поделим 18 на 5 (это количество взрослых на 1 билет). Получим 3 и 3 в остатке. Значит, нужно купить 4 билета. Они стоят 4· 10,5 = 42 евро. Ответ: 42
№ 15 Павел Иванович купил американский автомобиль, на спидометре которого скорость измеряется в милях в час. Американская миля равна 1609 м. Какова скорость автомобиля в километрах в час, если спидометр показывает 34 мили в час? Ответ округлите до целого числа.
Решение Автомобили за час проезжает 34*1609 = 54706 м = 54.706 км. Округляя до ближайшего целого, получим 55 км. То есть, скорость автомобиля приближенно равна 55 км/ч. Ответ: 55
№ 16 Лиза каждую неделю печёт 38 вафель. На 30 вафель уходит 450 грамм муки. На сколько недель Лизе хватит 5 кг муки? Лиза каждую неделю печёт 38 вафель. На 30 вафель уходит 450 грамм муки. На сколько недель Лизе хватит 5 кг муки?
Решение На 38 вафель Лиза тратит
(450 : 30) · 38 = 15· 38 = 570 грамм муки. Делим 5 кг = 5000 г на 570 г с остатком. Получим 5000 : 570 = 8 (440 ост.) Муки хватит на 8 недель. Ответ: 8
№ 17 В летнем лагере на каждого участника полагается 40 г сахара в день.
В лагере 164 человека.
Сколько килограммовых пачек сахара понадобится на весь лагерь
на 9 дней?
Решение. На весь лагерь в день нужно
40·164 =6560 г = 6,56 кг сахара.
На 9 дней нужно 6,56·9 =59,04 кг сахара. Придется купить 60 пачек.
Ответ: 60
№ 18 Анна Павловна преподаёт математику в классе из 28 учеников. Она проверяет контрольную работу одного школьника в среднем за 7 минут, а самостоятельную — за 2 минуты. За неделю учительница провела одну контрольную работу и четыре самостоятельных. Сколько времени Анна Павловна потратит на проверку? Ответ дайте в часах.
Решение. На проверку работ одного ученика А.П. потратит 7+4·2 = 15 минут = 1/4 часа. На работы 28 учеников она потратит 28· 1/4 = 7 часов Ответ 7
Слайд 5Необходимый минимум (7 баллов)
Задание 1
Задание 2
Задание 3
Задание 4
Задание 5
Задание 6
Задание 7
Задание
9
Задание 10
Задание 11

Слайд 6Первичные баллы базового уровня ЕГЭ по математике переводятся в следующие школьные оценки:
«2»
(неудовлетворительно) — от 0 до 6 баллов
«3» (удовлетворительно) — от 7 до 11 баллов
«4» (хорошо) — от 12 до 16 баллов
«5» (отлично) — от 17 до 20 баллов

Слайд 9
Перевод обыкновенной дроби в десятичную

Слайд 19 Шоколадка в магазине стоит 25 руб. Какое наибольшее число таких
шоколадок можно приобрести на 280 рублей в магазине во время акции: покупаешь две – одна в подарок?
В школьную библиотеку привезли по 80 учебников одинакового размера на каждую параллель 1-3 классов. В библиотеке в одном шкафу по три полки, на каждую из которых помещается по 25 таких учебников. Сколько полных шкафов в библиотеке займут привезенные учебники?
Задание 6

Слайд 25Задание 10
Перефразируем вопрос используя союзы и, или

Слайд 26Задание 10
Другими словами, найти вероятность того, что он возьмет вопрос по
теме:
«Вписанная окружность» или «Тригонометрия»
Возможны два варианта: в первый раз выпал орел и во второй раз решка или
в первый раз решка и во второй орел.

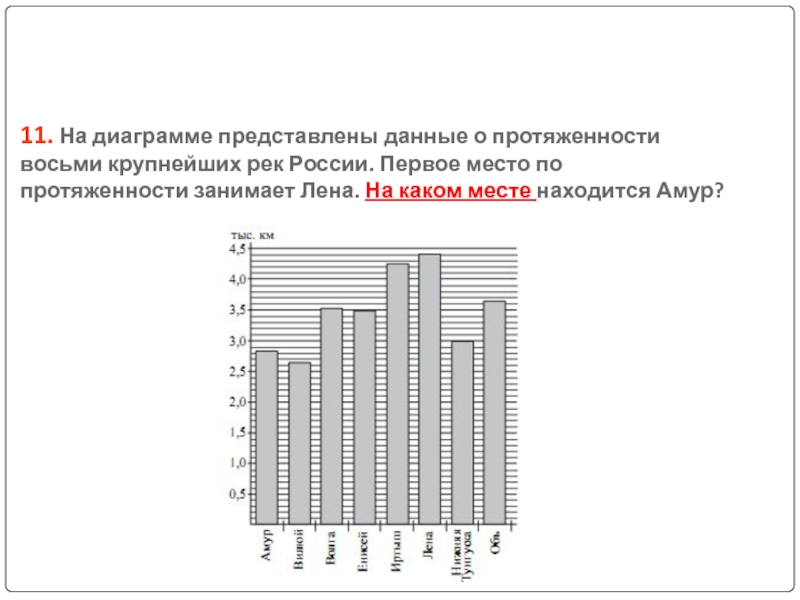
Слайд 2911. На диаграмме представлены данные о протяженности восьми крупнейших рек России.
Первое место по протяженности занимает Лена. На каком месте находится Амур?
Слайд 30Принципы работы с сайтом reshuege.ru
Базовый уровень
Профильный уровень
Слайд 314. Заходим в раздел учителю
5. Создаем тест

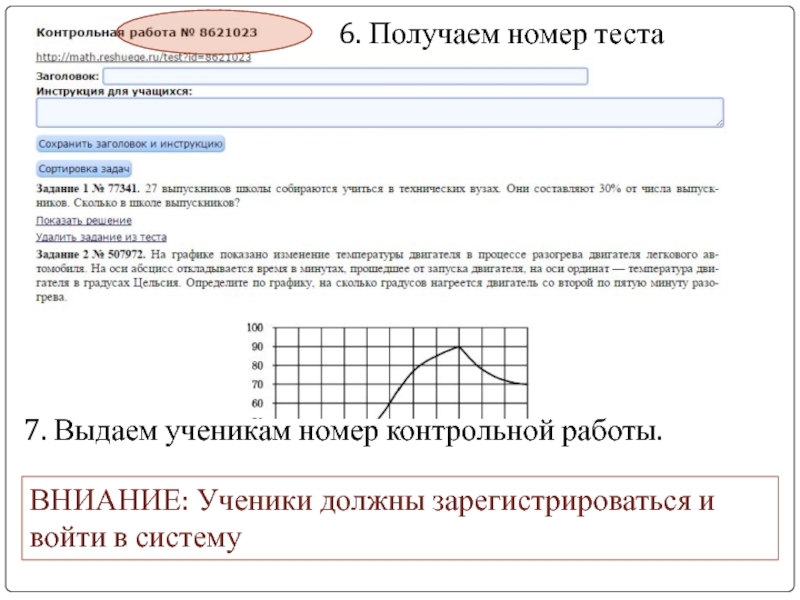
Слайд 326. Получаем номер теста
7. Выдаем ученикам номер контрольной работы.
ВНИАНИЕ: Ученики должны
зарегистрироваться и войти в систему
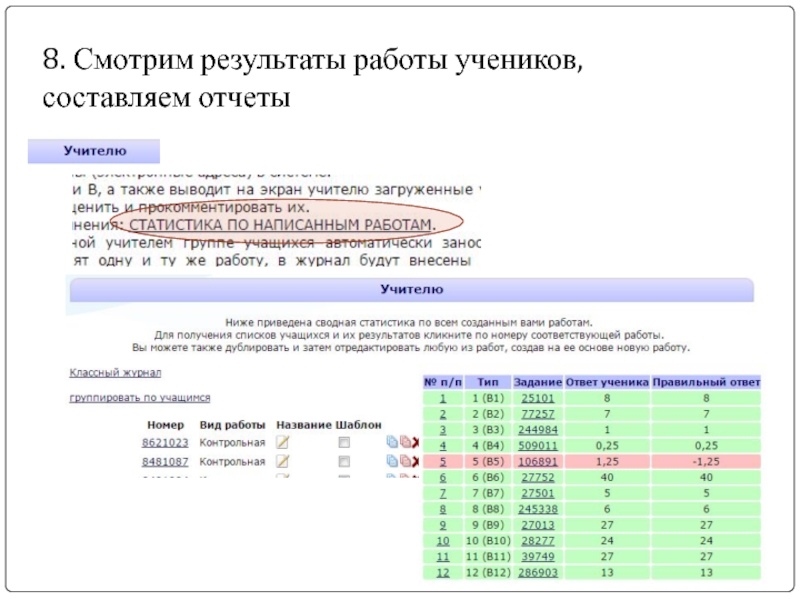
Слайд 338. Смотрим результаты работы учеников, составляем отчеты
Слайд 34Сайты для подготовки к ОГЭ и ЕГЭ по математике
http://opengia.ru
http://fipi.ru/view/sections/211/docs/471.html — демо-версия
http://alexlarin.net
— различные материалы для подготовки
http://www.egetrener.ru — видеоуроки
http://www.mathege.ru — открытый банк заданий
http://reshuege.ru/
http://matematika.egepedia.ru
http://www.mathedu.ru
http://www.ege-trener.ru
http://egeent.narod.ru/matematika/online/
http://vkontakte.ru/app1841458 — приложение ВКонтакте — отработка части В
http://matematika-ege.ru
http://uztest.ru/

Слайд 36СПАСИБО ЗА ВНИМАНИЕ!
доцент преподаватель кафедры математики и информатики дисциплин
зам. председателя предметной
комиссии
ЕГЭ по математике
Барышенский Дмитрий Сергеевич
8(861)2323747






















































































