Учиться можно только весело….
Чтобы переваривать знания, надо поглощать их с аппетитом.
« Нахождение значений тригонометрических выражений »
Разбор заданий из открытого банка заданий ЕГЭ по математике
Учитель математики МБОУ «СОШ № 34», г.Кемерово
Головина И.А.
Цель занятия:
- Выработать навыки решения заданий на нахождение значений тригонометрических выражений, выделив общую идею решения
- Обеспечить применение этих навыков на практике
Томас Пейн — англо- американский писатель , философ , публицист , прозванный « крёстным отцом США ». в своей книге « Век Разума » (1794) назвал тригонометрию «душой науки»
Что используется в ходе решения данных выражений:
формулы приведения
свойства периодичности тригонометрических функций
свойство чётности нечётности
формулы – синуса и косинуса двойного аргумента
основное тригонометри-
ческое тождество
Рекомендации:
если в выражении видите, что один угол больше другого в два раза, то смело используйте соответствующую тригонометрическую формулу двойного аргумента
если вы видите, что сумма данных углов (или их разность) составляет 90, 180, 270, 360 градусов, то применяйте формулы приведения
Найдите значение выражения :
2) Её периодичность, период равен 2 П , (360), cos(360*2+210)
- Свойство четности функции косинуса
cos(-t)=cost
3) И формулу приведения для косинуса
cos(180+30) = — cos30=
= — √3/2
4) -4√3* (- √3/2)= 6
Найдите значение выражения :
- Её периодичность, период равен П , (180),
tg(180*2+120)
- Свойство нечетности функции тангенса
tg(-t)=-tgt
3) И формулу приведения для косинуса
tg(90+30) = — ctg30=
= — √3
4) -44√3* (- √3)=132
Найдите значение выражения :
- Её периодичность, период равен 2 П , (360),
sin(360*2+60)
- Свойство нечетности функции синуса
sin(-t)=-sint
3) sin 60 = √3/2
4√3* √3/2=6
Найдите значение выражения :
Проверка:
1)
1) -5, tg(90+64),tg(180+64)
2)18
2)
3)-22
3)
4)33, cos(90-27)
4)
5)-34, sin(360-260)
5)
6)-38, cos(180-27)
6)
Найдите значение выражения :
Проверка:
1)
1) -40, sin 19=sin(90-71)
2)-7, sin270
2)
3)37, sin(180-7),sin(270-7)
3)
4) 22, tg(180-32)
4)
5) -20, sin(360+13)
5)
Решите самостоятельно :
1)
6)
2)
7)
3)

9)
4)
10)
5)
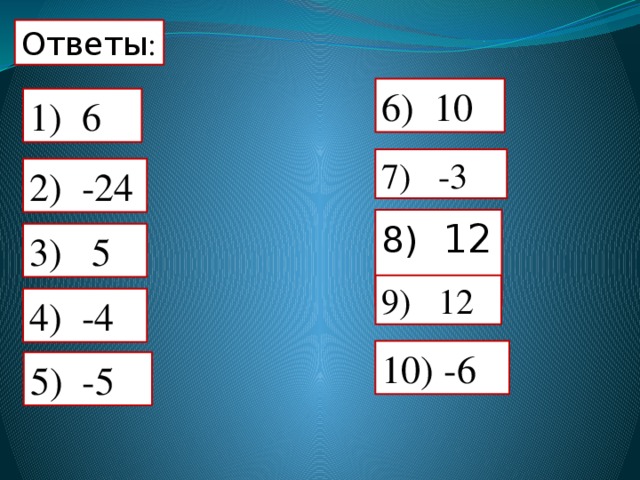
Ответы :
6) 10
1) 6
7) -3
2) -24

3) 5
9) 12
4) -4
10) -6
5) -5
Домашнее задание:
Варианты 1-20
Задание № 10
До новых встреч !
4
Презентация к уроку-практикуму «Тригонометрия»
Презентация к уроку — практикуму по теме «Тригонометрия», ЕГЭ, профильный уровень, задание №9. Презентацию можно использовать на уроках повторения, систематизации знаний при подготовке к ЕГЭ по математике. В презентации рассмотрены задачи по тригонометрии (преобразование числовых и буквенных выражений) из открытого банка заданий ЕГЭ по математике (сайт ФИПИ). В конце представлен тест для проверки знаний по теме.
Опубликовано 30.04.17 в 21:37 в группе «Математика — это интересно!»
1
В7 ТРИГОНОМЕТРИЧЕСКИЕ ВЫРАЖЕНИЯ ЕГЭ по математике
2
1) Найдите значение выражения Ответ: 6 1 способ: 2 способ: 2) Найдите значение выражения 1 способ: 2 способ: Ответ: -24
3
Ответ: 5 1 способ: 2 способ: Ответ: 2 3) Найдите значение выражения Используем формулу приведения для cos29 0 Функцию меняем Угол в 1четверти cosx >0 Используем формулу приведения для sin61 0 4) Найдите значение выражения Используем табличные значения Ответ: 36 5) Найдите значение выражения Выделим целое Угол в 1четверти cosx >0 Функцию не меняем
4
Ответ: 16 Ответ: -6 6) Найдите значение выражения sin (-x) = — sin x Подставляем найденные значения Угол в 4четверти sinx < 0 Функцию не меняем Угол в 4четверти cosx > 0 Функцию не меняем 7) Найдите значение выражения cos (-x) = cos x Выделим полные обороты =
5

6
11) Найдите значение выражения Ответ:-12 Ответ: -14 sin (-x) = — sin x cos (-x) = cos x Угол в 4 четверти sinx < 0 Функцию не меняем 10) Найдите значение выражения Используем формулу приведения: 12) Найдите значение выражения Ответ: -4 Угол в 2четверти cosx < 0
7
15) Найдите значение выражения 13) Найдите значение выражения Ответ: -5 Ответ: 14 Угол 2 четверти tgx < 0 Функцию не меняем sin = sin ( ) = sin 49 0 Угол 2четверти tgx < 0 Функцию меняем Используем формулу приведения: 14) Найдите значение выражения Выделим полный оборот Ответ: -5
8
16) Найдите значение выражения Ответ: 7 Ответ: 12 Угол 1 четверти tgx > 0 Функцию меняем sin = sin ( ) = cos 37 0 Используем формулу приведения: Ответ: 6 17) Найдите значение выражения Используем формулу приведения: 18) Найдите значение выражения Используем формулу приведения: cos = cos ( ) = — sin 23 0
9
19)20) Ответ: 1 Ответ: -1
10
21)22) Ответ: -3 Ответ: 5
11
23)24) Ответ: 22,08 Ответ: 4 1 способ: 2 способ:
12
25) Найдите значение выражения Ответ: 2 Ответ: 1 sin (-x) = — sin x Подставляем найденные значения Функцию не меняем Угол 2 четверти sinx > 0 Функцию меняем Используем формулу приведения: Угол 2 четверти cosx < 0 Угол 3 четверти cosx < 0 Функцию не меняем 26) Найдите значение выражения 1) Подставляем найденные значения
13
27) Найдите значение выражения Ответ: -28 Ответ: 0,6 Подставляем найденные значения Функцию не меняем Функцию меняем Используем формулу приведения: Угол 2 четверти tgx < 0 tg (-x) = — tg x 28) Используем формулу приведения: Угол 3 четверти sinx < 0
14
Ответ: -10 Ответ: -2,5 Подставляем найденные значения Функцию меняем Используем формулу приведения: 30) Используем формулу приведения: Угол 2 четверти tgx < 0 29) Угол 4 четверти cosx > 0
15
Ответ: 7 Ответ: -9 32)32) 31)
16
Ответ: 5 Ответ: 8 34) 33)
17
Ответ: 2.25 Ответ: 3 36) 35) Используем формулу приведения: Угол 3 четверти cosx 0 Функцию меняем
18
Ответ: 4 Ответ: -7 38) 37) sin (- ) = — sin 1 способ: 2 способ:
19
39) Найдите значение выражения Ответ: 10 Ответ: -3 Используем формулу приведения для sin 41 0 Используем формулу приведения для cos53 0 Ответ: 10 40) Найдите значение выражения41) Найдите значение выражения Используем формулу приведения
20
42) Найдите значение выражения Ответ: 2 Ответ: -1,5 43) Найдите значение выражения
21
Ответ: -1,5 44) Найдите значение выражения45) Найдите значение выражения
1. Использование преобразований тригонометрических выражений при решении заданий ЕГЭ
2. Задание 10
Найдите sin x, если cos x = 0,6 и
∏<Х<2∏
Найдите tg x , если sin x = 0,8 и
∏/2<Х<2∏
3. Известные формулы:
основные тригонометрические тождества;
формулы двойного аргумента;
синус, косинус, тангенс, котангенс суммы и
разности двух углов;
формулы понижения степени;
формулы преобразования
тригонометрических сумм в произведение.
4. Свойства тригонометрических функций:
чётность;
периодичность;
ограниченность.
5. Реши устно:
1. sin x = ∏/3
2 cos x = √3
3.
tg ∏/4 + tg x
=2
1 — tg ∏/4 + tg x
4. √2 cos2 7x — cos 7x = 0
5. 3 cos2x — sin2x — 2 sin x cos x = 0
6. Способы решения уравнений:
разложение на множители;
использование тригонометрических
формул;
замена переменной;
однородное уравнение, делением на
синус или косинус.
7. Определи способы решения уравнения:
1. (2sin x — cos x) (1+cos x)=sin2x
2. 2 cos 2x + cos x = 1
3. 4 cos4x – 3 cos 2x – 1 = 0
Найдите все корни этого уравнения,
принадлежащие интервалу
(-7∏/2;-2∏)
8. Тест
9. Решение 1 варианта
10. Решение 2 варианта
11. Работа с тестами из интернета
ЕГЭ 2015 по математике;
случайные вопросы;
режим тренировки;
С1 а;
С1 б.
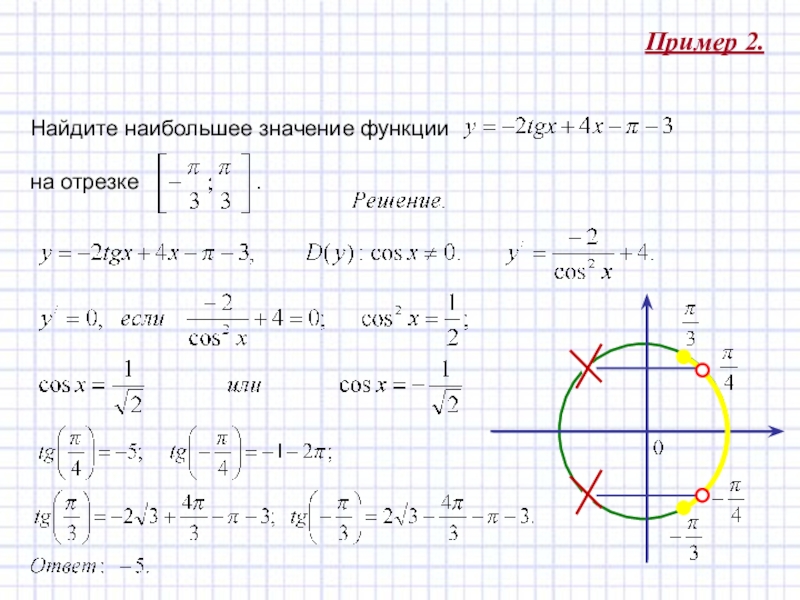
12. Пример 2
Решите уравнение
2 cos2x − 7cos(π/2+x) + 2 = 0
1
2
3
4
±π/6+2πn, n∈Z
π/6+2πn, n∈Z; 5π/6+2πk, k∈Z
−π/6+2πn, n∈Z; −5π/6+2πk, k∈Z
−π/3+2πn, n∈Z; −2π/3+2πk, k∈Z
13.
Преобразуем выражение cos(π/2+x) по формуле
косинуса суммы (или формуле приведения).
Получится cos(π/2+x) = −sinx.
Уравнение примет вид 2cos2x +7sinx + 2 = 0
Это уравнение может быть сведено к функции sinx с
помощью основного тригонометрического тождества:
2(1−sin2x) +7sinx +2 =0;
2−2sin2x +7sinx +2 = 0;
−2sin2x +7sinx +4 = 0.
Сделаем замену переменной sinx = t, при
этом t∈[−1,1]. Получим квадратное уравнение
−2t 2+7t+4=0
t1 = −1/2, t 2 =4. Корень t2 не удовлетворяет условию t
∈[−1,1].
Вернемся к переменной x при t = −1/2:
sin x = −1/2;
x= −π/6+2πn, n∈Z или x= −5π/6+2πk, k∈Z.
Ответ: x = −π/6+2πn, n∈Z;
x = −5π/6+2πk, k∈Z.
14. Найдите корни уравнения 2 cos2x − 7cos(π/2+x) + 2 = 0 принадлежащие промежутку [0;11π/6)
Найдите корни уравнения
2 cos2x − 7cos(π/2+x) + 2 = 0
принадлежащие промежутку
[0;11π/6)
1
2
3
4
5π/6
7π/6
π/3
0; π
15. Составим и решим двойное неравенство для корней первой серии x = −π/6+2πn:
Составим и решим двойное неравенство
для корней первой серии x = −π/6+2πn:
0<−π/6+2πn <11π/6 ∣:π;
0<−16+2n <11/6
∣⋅6;
0<−1+12n <11
∣+1;
1< 12n <12;
1/12< n <1.
Вспомним, что n – это целое число. Но в полученном
промежутке нет целых чисел, значит, первая серия
корней не содержит корней с заданным условием.
16. Запишем неравенство для другой серии корней x = −5π/6+2πn
0<−5π/ 6+2πn <11π/ 6 ∣:π;
0<−5/6+2n <11/6
∣⋅6;
0<−5+12n <11
∣+5;
5<12n <16;
5/12<n <16/12.
В этом промежутке имеется единственное целое
число n=1. Найдем соответствующее значение
переменной:
х = −5π/ 6+2π⋅1= −5π/ 6+12π = 7π/ 6.
Ответ: x=7π/ 6.
17. Из истории
Слово тригонометрия впервые появляется в
1505 году в заглавии книги немецкого
математика Питискуса.
Тригонометрия – слово греческое, и в
буквальном переводе означает измерение
треугольников ( trigonan – треугольник, metreo
— измеряю).
Возникновение тригонометрии было тесно
связано с землемерием, астрономией и
строительным делом.…
18. Использование тригонометрических функций в астрономии
Потребность в решении треугольников раньше всего
обнаружилась в астрономии; поэтому, в течение
долгого времени тригонометрия развивалась и
изучалась как один из разделов астрономии.
Составленные Гиппархом таблицы положений Солнца
и Луны позволили предвычислять моменты
наступления затмений (с ошибкой 1—2 ч). Гиппарх
впервые стал использовать в астрономии методы
сферической тригонометрии.
19. Использование тригонометрических функций в медицине
Американские ученые утверждают, что мозг
оценивает расстояние до объектов, измеряя угол
между плоскостью земли и плоскостью зрения.
Тригонометрия играет важную роль в медицине. С ее
помощью иранские ученые открыли формулу сердца комплексное алгебраически-тригонометрическое
равенство, состоящее из 8 выражений, 32
коэффициентов и 33 основных параметров, включая
несколько дополнительных для расчетов в случаях
аритмии.
20. Использование тригонометрических функций в биологии
Движение рыб в воде происходит по закону синуса или
косинуса, если зафиксировать точку на хвосте, а
потом рассмотреть траекторию движения.
При полёте птицы траектория взмаха крыльев
образует синусоиду.
21. Школьник в 14-15 лет не всегда знает, куда пойдет учиться и где будет работать…
Для некоторых профессий знание тригонометрии необходимо,
т.к. позволяет измерять расстояния до недалёких звёзд в
астрономии, между ориентирами в географии, контролировать
системы навигации спутников.
Принципы тригонометрии, используются и в таких областях,
как теория музыки, акустика, оптика, анализ финансовых
рынков, электроника, теория вероятностей, статистика,
биология, медицина (включая ультразвуковое исследование (УЗИ)
и компьютерную томографию), фармацевтика, химия, теория
чисел (и, как следствие, криптография), сейсмология,
метеорология, океанология, картография, многие разделы
физики, топография и геодезия, архитектура, экономика,
электронная техника, машиностроение, компьютерная графика,
кристаллография…
22. Тригонометрические уравнения
ctg 2 x cos x sin x sin x
1 sin x cos x sin x cos x 0
ctg 2 x cos x sin x sin x
23. Отметить точки:
x ( 1)
Y
x ( 1)
X
0
x
k
6
n 1
3
k , k Z
6
n, n Z
m, m Z
24. Тригонометрические уравнения
cos(arccos (4 x 9)) x2 5x 5
1.
2.
1 sin x cos x sin x cos x 0
3. ctg2x cos x sin x sin x
4.
arccos 3x 2 arcsin x
5. 11sin x 11cos x 5 sin 2x 7
2
2
cos
(
2
x
)
cos
( x) 0
6.
3
12
7. arcsin x 2arctgx
sin 2 x 5(sin x cos x) 0
8.
2
2
sin
x
sin
x
sin
2
x
sin
9.
3
3
1
2
10
(cos 2 x
)(
1
tg
2 y)(3 sin 3z ) 4
2
cos x
1
1
2
2
2
1
3
3
1
2
Преобразование тригонометрических выражений
- Разработала: Богданова Ольга Николаевна, учитель математики МКОУ «Овечкинская СОШ Завьяловского района»
- 2015 г.
- Алгебра — 10 класс
- УМК: Н.Г. Мордкович, профильный уровень
Синус и косинус разности аргументов
Пример 1
Пример 2
Пример 3
Пример 4
- II
Пример 5
- Решите уравнение:
Тангенс суммы и разности аргументов
Котангенс суммы и разности аргументов
Пример 1
Пример 2
- II
Формулы приведения
|
|
|
|
|
|
|
||||
|
||||
|
||||
|
Пример 1
Пример 2
Пример 3
Пример 4
Формулы двойного аргумента
Пример 1
Пример 2
Пример 3
Пример 4
Пример 5
- IV
Пример 6
Формулы понижения степени.
Пример 1
- II
Пример 2
- Разложение суммы и разности на множители
- Пример 1
- Пример 2
- Пример 3
- Формулы представления произведения в виде суммы
- Пример 1
- Пример 2
- Пример 3
Преобразование выражения Asinx+Bcosx к виду Csin(x+t)
- Пример 1
- Пример 2
- Пример 3
- Пример 3
- Источники
- А.Г. Мордкович, П.В. Семенов. Методическое пособие для учителя, «Алгебра и начала анализа», профильный уровень, 10 класс, «Мнемозина», М. 2013.
- http://ru.clipartlogo.com/free/pencil.html — картинка карандашей
- — А.Г. Мордкович Алгебра – 10, профильный уровень, часть 1 – учебник, М: Мнемозина, 2013
- — А.Г. Мордкович и др., Алгебра – 10, профильный уровень, часть 2 – задачник, М: Мнемозина, 2013
Презентация на тему «Урок «Использование тригонометрических преобразований при решении заданий ЕГЭ»» 10 класс
-
Скачать презентацию (0.36 Мб)
-
3 загрузки -
0.0 оценка
Ваша оценка презентации
Оцените презентацию по шкале от 1 до 5 баллов
- 1
- 2
- 3
- 4
- 5
Комментарии
Добавить свой комментарий
Аннотация к презентации
Интересует тема «Урок «Использование тригонометрических преобразований при решении заданий ЕГЭ»»? Лучшая powerpoint презентация на эту тему представлена здесь! Данная презентация состоит из 24 слайдов. Также представлены другие презентации по математике для 10 класса. Скачивайте бесплатно.
-
Формат
pptx (powerpoint)
-
Количество слайдов
24
-
Аудитория
-
Слова
-
Конспект
Отсутствует
Содержание
-
Слайд 1
Использование преобразований тригонометрических выражений при решении заданий ЕГЭ
-
Слайд 2
Задание 10
Найдите sin x, если cos x = 0,6 и ∏
-
Слайд 3
Известные формулы:
основные тригонометрические тождества;
формулы двойного аргумента;
синус, косинус, тангенс, котангенс суммы и разности двух углов;
формулы понижения степени;
формулы преобразования тригонометрических сумм в произведение. -
Слайд 4
Свойства тригонометрических функций:
чётность;
периодичность;
ограниченность. -
Слайд 5
Реши устно:
1. sin x = ∏/3
2 cos x = √3
3.tg ∏/4 + tg x = 2
1 — tg ∏/4 + tg x
4. √2 cos2 7x — cos 7x = 0
5. 3 cos2x — sin2x — 2 sin x cos x = 0 -
Слайд 6
Способы решения уравнений:
разложение на множители;
использование тригонометрических формул;
замена переменной;
однородное уравнение, делением на синус или косинус. -
Слайд 7
Определи способы решения уравнения:
1. (2sin x — cos x) (1+cos x)=sin2x
2. 2 cos 2x + cos x = 1
3. 4 cos4x – 3 cos 2x – 1 = 0
Найдите все корни этого уравнения, принадлежащие интервалу
(-7∏/2;-2∏) -
-
Слайд 9
Решение 1 варианта
-
Слайд 10
Решение 2 варианта
-
Слайд 11
Работа с тестами из интернета
ЕГЭ 2015 по математике;
случайные вопросы;
режим тренировки;
С1 а;
С1 б. -
Слайд 12
Пример 2
Решите уравнение
2 cos2x− 7cos(π/2+x) + 2 = 01 ±π/6+2πn, n∈Z
2 π/6+2πn, n∈Z; 5π/6+2πk, k∈Z
3 −π/6+2πn, n∈Z; −5π/6+2πk, k∈Z
4 −π/3+2πn, n∈Z; −2π/3+2πk, k∈Z -
Слайд 13
Преобразуем выражение cos(π/2+x) по формуле косинуса суммы (или формуле приведения). Получится cos(π/2+x) = −sinx. Уравнение примет вид 2cos2x +7sinx + 2 = 0Это уравнение может быть сведено к функции sinx с помощью основного тригонометрического тождества:2(1−sin2x) +7sinx +2 =0; 2−2sin2x +7sinx +2 = 0; −2sin2x +7sinx +4 = 0.Сделаем замену переменной sinx = t, при этом t∈[−1,1]. Получим квадратное уравнение−2t 2+7t+4=0t1 = −1/2, t 2 =4. Корень t2 не удовлетворяет условию t ∈[−1,1].Вернемся к переменной x при t = −1/2:
sin x = −1/2;x= −π/6+2πn, n∈Z или x= −5π/6+2πk, k∈Z.Ответ: x = −π/6+2πn, n∈Z;
x = −5π/6+2πk, k∈Z. -
Слайд 14
Найдите корни уравнения2 cos2x− 7cos(π/2+x) + 2 = 0принадлежащие промежутку [0;11π/6)
1 5π/6
2 7π/6
3 π/3
4 0; π -
Слайд 15
Составим и решим двойное неравенство для корней первой серии x = −π/6+2πn:
0
-
Слайд 16
Запишем неравенство для другой серии корней x = −5π/6+2πn
0
-
Слайд 17
Из истории
Слово тригонометрия впервые появляется в 1505 году в заглавии книги немецкого математика Питискуса. Тригонометрия – слово греческое, и в буквальном переводе означает измерение треугольников ( trigonan – треугольник, metreo — измеряю).Возникновение тригонометрии было тесно связано с землемерием, астрономией и строительным делом.…
-
Слайд 18
Использование тригонометрических функций в астрономии
Потребность в решении треугольников раньше всего обнаружилась в астрономии; поэтому, в течение долгого времени тригонометрия развивалась и изучалась как один из разделов астрономии.
Составленные Гиппархом таблицы положений Солнца и Луны позволили предвычислять моменты наступления затмений (с ошибкой 1—2 ч). Гиппарх впервые стал использовать в астрономии методы сферической тригонометрии.
-
Слайд 19
Использование тригонометрических функций в медицине
Американские ученые утверждают, что мозг оценивает расстояние до объектов, измеряя угол между плоскостью земли и плоскостью зрения.
Тригонометрия играет важную роль в медицине. С ее помощью иранские ученые открыли формулу сердца — комплексное алгебраически-тригонометрическое равенство, состоящее из 8 выражений, 32 коэффициентов и 33 основных параметров, включая несколько дополнительных для расчетов в случаях аритмии.
-
Слайд 20
Использование тригонометрических функций в биологии
Движение рыб в воде происходит по закону синуса или косинуса, если зафиксировать точку на хвосте, а потом рассмотреть траекторию движения.
При полёте птицы траектория взмаха крыльев образует синусоиду.
-
Слайд 21
Школьник в 14-15 лет не всегда знает, куда пойдет учиться и где будет работать…
Для некоторых профессий знание тригонометрии необходимо, т.к. позволяет измерять расстояния до недалёких звёзд в астрономии, между ориентирами в географии, контролировать системы навигации спутников.
Принципы тригонометрии, используются и в таких областях, как теория музыки, акустика, оптика, анализ финансовых рынков, электроника, теория вероятностей, статистика, биология, медицина (включая ультразвуковое исследование (УЗИ) и компьютерную томографию), фармацевтика, химия, теория чисел (и, как следствие, криптография), сейсмология, метеорология, океанология, картография, многие разделы физики, топография и геодезия, архитектура, экономика, электронная техника, машиностроение, компьютерная графика, кристаллография… -
Слайд 22
Тригонометрические уравнения
-
-
Слайд 24
Тригонометрические уравнения
1. 1
2. 1
3. 2
4. 2
5. 2
6. 1
7. 3
8. 3
9. 1
10 2
Посмотреть все слайды
Сообщить об ошибке
Похожие презентации










Спасибо, что оценили презентацию.
Мы будем благодарны если вы поможете сделать сайт лучше и оставите отзыв или предложение по улучшению.
Добавить отзыв о сайте
- Главная
- Разное
- Образование
- Спорт
- Естествознание
- Природоведение
- Религиоведение
- Французский язык
- Черчение
- Английский язык
- Астрономия
- Алгебра
- Биология
- География
- Геометрия
- Детские презентации
- Информатика
- История
- Литература
- Математика
- Музыка
- МХК
- Немецкий язык
- ОБЖ
- Обществознание
- Окружающий мир
- Педагогика
- Русский язык
- Технология
- Физика
- Философия
- Химия
- Шаблоны, фоны, картинки для презентаций
- Экология
- Экономика
Презентация, доклад Тригонометрия в заданиях ЕГЭ
Содержание
-
1.
Презентация Тригонометрия в заданиях ЕГЭ -
2.
Тригонометрия в заданиях ЕГЭ РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ -
3.
РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ ЗАДАНИЕ В7 -
4.
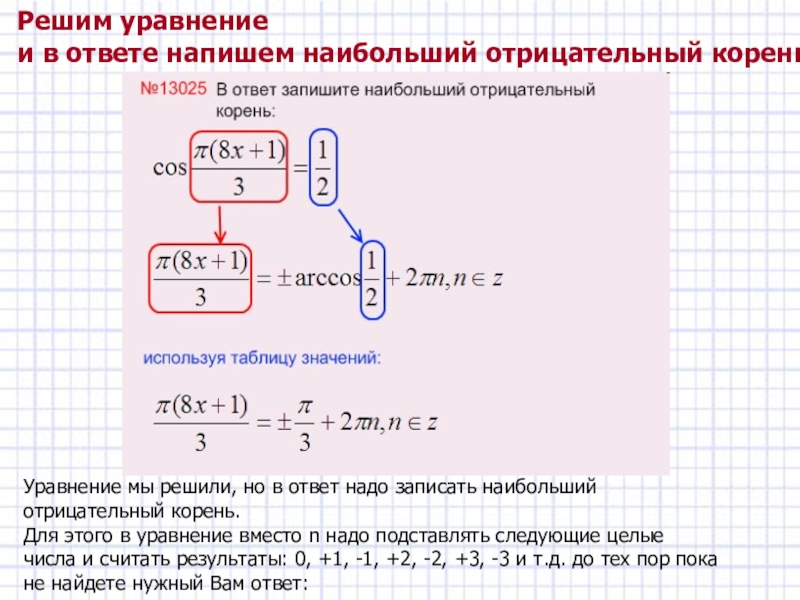
Решим уравнение и в ответе напишем наибольший отрицательный корень: -
5.
Уравнение мы решили, но в ответ надо -
6.
Наибольший отрицательный корень: -1,5. -
7.
Решим уравнение и в ответе напишем наибольший -
8.
Слайд 8 -
9.
Наибольший отрицательный корень: -0,25 -
10.
Решим уравнение и найдем наименьший положительный корень: -
11.
Наименьший положительный корень: х=6. -
12.
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ ЗАДАНИЕ В11 -
13.
Найдите значение выражения -
14.
Найдите -
15.
ПРИКЛАДНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ В ФИЗИКЕ ЗАДАНИЕ В12 -
16.
ЗадачаГруз массой 0,08 кг колеблется на пружине со -
17.
Слайд 17 -
18.
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ ЗАДАНИЕ В15 -
19.
Пример 1.Найдите точку минимума функции -
20.
Пример 2.Найдите наибольшее значение функции на отрезке
Тригонометрия в заданиях ЕГЭ РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ ЗАДАНИЕ В7 ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ ЗАДАНИЕ В11 ПРИКЛАДНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ В ФИЗИКЕ ЗАДАНИЕ В12 ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ
Слайд 1Андреева Зинаида Маркеловна,
учитель математики,
МАОУ СОШ № 41 с. Аксаково
МР Белебеевский район РБ
2017г.
Тригонометрия
в заданиях
ЕГЭ

Слайд 2Тригонометрия в заданиях ЕГЭ
РЕШЕНИЕ ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
ЗАДАНИЕ В7
ПРЕОБРАЗОВАНИЕ
ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
ЗАДАНИЕ В11
ПРИКЛАДНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ В ФИЗИКЕ
ЗАДАНИЕ В12
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ
ЗАДАНИЕ В15
Содержание

Слайд 3РЕШЕНИЕ
ПРОСТЕЙШИХ ТРИГОНОМЕТРИЧЕСКИХ УРАВНЕНИЙ
ЗАДАНИЕ В7

Слайд 4Решим уравнение
и в ответе напишем наибольший отрицательный корень:

Слайд 5Уравнение мы решили, но в ответ надо записать наибольший отрицательный корень.
Для этого в уравнение вместо n надо подставлять следующие целые числа и считать результаты: 0, +1, -1, +2, -2, +3, -3 и т.д. до тех пор пока не найдете нужный Вам ответ:

Слайд 6Наибольший отрицательный корень: -1,5.

Слайд 7Решим уравнение
и в ответе напишем наибольший отрицательный корень:
Уравнение мы
решили, но в ответ надо записать наибольший отрицательный корень.
Для этого в уравнение вместо n надо подставлять следующие целые числа и считать результаты: 0, +1, -1, +2, -2, +3, -3 и т.д. до тех пор пока не найдете нужный Вам ответ:
Слайд 9Наибольший отрицательный корень: -0,25

Слайд 10Решим уравнение
и найдем наименьший положительный корень:
Уравнение мы решили, но
в ответ надо записать наибольший отрицательный корень.
Для этого в уравнение вместо n надо подставлять следующие целые числа и считать результаты: 0, +1, -1, +2, -2, +3, -3 и т.д. до тех пор пока не найдете нужный Вам ответ:

Слайд 11Наименьший положительный корень: х=6.

Слайд 12
ПРЕОБРАЗОВАНИЕ ТРИГОНОМЕТРИЧЕСКИХ ВЫРАЖЕНИЙ
ЗАДАНИЕ В11

Слайд 15
ПРИКЛАДНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ
В ФИЗИКЕ
ЗАДАНИЕ В12

Слайд 16Задача
Груз массой 0,08 кг колеблется на пружине со скоростью, меняющейся по закону
, где t — время в секундах. Кинетическая энергия
груза, измеряемая в джоулях, вычисляется по формуле ,
где m — масса груза (в кг), v — скорость груза (в м/с). Определите, какую долю времени из первой секунды после начала движения кинетическая
энергия груза будет не менее Дж. Ответ выразите десятичной дробью, если нужно, округлите до сотых.

Слайд 18
ЭКСТРЕМАЛЬНЫЕ ЗАДАЧИ ТРИГОНОМЕТРИИ
ЗАДАНИЕ В15

Слайд 19Пример 1.
Найдите точку минимума функции
,
принадлежащую промежутку .
у’
у
0,5
0
—
+

Слайд 20Пример 2.
Найдите наибольшее значение функции
на отрезке