Презентация решение текстовых задач егэ по математике профильный уровень

Слайд 1

Алгебра Часть 1 Задачи на сплавы Преподаватель высшей категории Анисимова Оксана Михайловна ВИФК Кадетский корпус (спортивная школа)

Слайд 2

?? всего концентрация Масса вещества Было 5 14 % Добавили 5 — — стало 5+5=10 ? 0,7 Решение задач «задание 11» №1 Ответ: 7 В сосуд, содержащий 5 литров 14-процентного водного раствора некоторого вещества, добавили 5 литров воды. Сколько процентов составляет концентрация получившегося раствора?

Слайд 3

?? всего концентрация Масса вещества I x 15% 0,15x II x 17% 0,17x I+II 2x ? 0,15x + 0,17x = 0,32x Решение задач «задание 11» № 2 Ответ: 16 Смешали некоторое количество 15-процентного раствора некоторого вещества с таким же количеством 17-процентного раствора этого вещества. Сколько процентов составляет концентрация получившегося раствора?

Слайд 4

?? всего концентрация Масса вещества I 4 20% 0,2·4=0,8 II 6 35% 0,35·6=2,1 I+II 4+6=10 ? 0,8 + 2,1 = 2,9 Решение задач «задание 11» № 3 Ответ: 29 Смешали 4 литра 20-процентного водного раствора некоторого вещества с 6 литрами 35- процентного водного раствора этого же вещества. Сколько процентов составляет концентрация получившегося раствора?

Слайд 5

?? всего концентрация Масса вещества I II I+II Решение задач «задание 11» № 4 .1 Ответ: 90 Имеется два сплава. Первый содержит 10% никеля, второй — 35% никеля. Из этих двух сплавов получили третий сплав массой 150 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была меньше массы второго? ?? всего концентрация Масса вещества I x 10% 0,1x II y 35% 0,35y I+II 150 30% 0,3·150=45 0,1x+0,35y=45

Слайд 6

?? всего концентрация Масса вещества I II I+II Решение задач «задание 11» № 4 .2 Ответ: 18 Имеется два сплава. Первый содержит 20% никеля, второй — 45% никеля. Из этих двух сплавов получили третий сплав массой 90 кг, содержащий 30% никеля. На сколько килограммов масса первого сплава была больше массы второго? ?? всего концентрация Масса вещества I x 2 0% 0, 2 x II y 4 5% 0, 4 5y I+II 90 30% 0,3· 90 = 27 0, 2 x+0, 4 5y=27

Слайд 7

Первый год Второй год I II I+II Решение задач «задание 11» № 5 Ответ: 110 Численность волков в двух заповедниках составляла 210 особей. Через год обнаружили, что в первом заповеднике численность волков возросла на 10%, а во втором — на 30%. В результате общая численность волков в двух заповедниках составила 251.Сколько волков было в первом из заповедников первоначально? ?? Первый год Второй год I x x+0,1x II y y+0,3y I+II 210 251

Слайд 8

?? всего Процентное содержание Масса вещества I II I+II Решение задач «задание 11» № 6 .1 Ответ: 27 Имеется два сплава. Первый сплав содержит 5% меди, второй — 14% меди. Масса второго сплава больше массы первого на 9 кг. Из этих двух сплавов получили третий сплав, содержащий 11% меди. Найдите массу третьего сплава. Ответ дайте в килограммах. ?? всего Процентное содержание Масса вещества I x 5% 0,05x II x+9 14% 0,14(x+9) I+II 2x+9 11% 0,11(2x+9)= 0,05x+0,14(x+9)

Слайд 9

?? всего Процентное содержание Масса вещества I II I+II Решение задач «задание 11» №6.2 Ответ: 9 Имеется два сплава. Первый сплав содержит 10% меди, второй — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третье го сплава. Ответ дайте в килограммах. ?? всего Процентное содержание Масса вещества I x 10 % 0,1x II x+ 3 40 % 0,4(x+3) I+II 2x+3 30 % 0,3(2x+3)= 0,1x+0,4(x+3)

Слайд 10

Решение задач «задание 11» №7.1 Смешав 6-процентный и 74-процентный растворы кислоты и добавив 10 кг чистой воды, получили 19-процентный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50- процентного раствора той же кислоты, то получили бы 24-процентный раствор кислоты. Сколько килограммов 6-процентного раствора использовали для получения смеси? ?? всего Процент Масса вещества I x 6% 0,06x II y 74% 0,74y Добавили 1 раз 10 — — Получили 1 раз x+y+10 19% 0.19(x+y+10)= =0,06x+0,74y Добавили 2раз 10 50% 0,5·10=5 Получили 2 раз x+y+10 24% 0. 24 (x+y+10)= =0,06x+0,74y +5

Слайд 11

Решение задач «задание 11» №7.1 ?? всего Процент Масса вещества I x 6% 0,06x II y 74% 0,74y Добавили 1 раз 10 — — Получили 1 раз x+y+10 19% 0.19(x+y+10)= =0,06x+0,74y Добавили 2раз 10 50% 0,5·10=5 Получили 2 раз x+y+10 24% 0. 24 (x+y+10)= =0,06x+0,74y +5

Слайд 12

Решение задач «задание 11» №7.1 Ответ: 70

Слайд 13

Самостоятельно Сборник «4000 задач» № 1586 , № 1590 № 1587 , № 11 вариант1 №11 вариант2

Слайд 14

Алгебра Урок №11 Часть 2 Задачи на совместную работу Преподаватель высшей категории Анисимова Оксана Михайловна ВИФК Кадетский корпус (спортивная школа)

Слайд 15

Объем работы Производительность (скорость) время I II Решение задач «задание 11» №1 .1 Ответ: 6 Объем работы Производительность (скорость) время I 20 x+4 II 60 x

Слайд 16

На изготовление 16 деталей первый рабочий тратит на 6 часов меньше, чем второй рабочий на изготовление 40 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй рабочий? Объем работы Производительность (скорость) время I II Решение задач «задание 11» №1 .2 Ответ: 5 Объем работы Производительность (скорость) время I 16 x+3 II 40 x

Слайд 17

Первая труба пропускает на 1 литр воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 110 литров она заполняет на 1 минуту дольше, чем вторая труба? Объем работы Производительность (скорость) время I II Решение задач «задание 11» №1 .3 Ответ: 10 Объем работы Производительность (скорость) время I 110 x II 110 x+1

Слайд 18

Решение задач «задание 11» № 2.1 Ответ: 16 Объем работы Производительность (скорость) время I 12y·10 12y 10 24yx 12y+12y X II 21y·10 21y 10 9yx 21y-12y=9y X !!!

Слайд 19

Решение задач «задание 11» № 2.2 Ответ: 16 Объем работы Производительность (скорость) время I 16y·7=112y 16y 7 24yx 16y+8y=24y X II 25y·7=175y 25y 7 17yx 25y-8y=17y X !!! Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 16 рабочих, а во второй — 25 рабочих. Через 7 дней после начала работы в первую бригаду перешли 8 рабочих из второй бригады. В итоге оба заказа были выполнены одновременно. Найдите, сколько дней потребовалось на выполнение заказов.

Слайд 20

Самостоятельно Сборник «4000 задач» № 1639 №1652 № 1622

Слайд 21

Интернет ссылки

ЕГЭ по математике • 11 класс • повторение, систематизация , презентация 08.03.2016

Презентация содержит различные типы заданий №11 (задачи на движение, на работу, на проценты, на смеси и сплавы) из экзаменационных работ, составленных в соответствии с демонстрационным вариантом и спецификацией 2015 года с учётом проекта изменений на 2016 год. Цель: формирование умений выполнять задания №11 (текстовые задачи) из II части заданий, включаемых в итоговую аттестацию за курс средней (полной) общеобразовательной школы профильного уровня. Задачи: Образовательные: Повторить понятия: процент, производительность, скорость, средняя скорость, процентное содержание; рассмотреть основные идеи, подходы и методы решения заданий №11; систематизировать знания по данным темам, их значение в математике, связи с другими темами; развить умение проводить анализ полученных результатов. Воспитательная: формировать представление о математике как части общечеловеческой культуры; формировать осознание значения математики в повседневной жизни человека. Развивающая: формировать аналитическое мышление, развивать память, кругозор, умение преодолевать трудности при решении более сложных задач; формировать умение точно и грамотно выражать свои мысли с применением математической терминологии и символики. © Коломина Наталья Николаевна Коломина Наталья Николаевна Понравилось? Сохраните и поделитесь: По кнопке ниже вы можете скачать методическую разработку «Решение текстовых задач №11 (профильный уровень)» категории «ЕГЭ по математике» бесплатно. Будем благодарны, если вы оставите отзыв или посмотрите еще другие материалы на нашем сайте. Характеристики документа: «презентация». Загрузка началась… Понравился сайт? Получайте ссылки на лучшие материалы еженедельно! Подарок каждому подписчику!

Порядок вывода комментариев: Очень полезный ресурс для подготовки к экзаменам. Беру в работу. Спасибо, Наталья Николаевна. Наталья Николаевна,  спасибо за представленный ресурс и за различные типы заданий! Наталья Николаевна, благодарю Вас за проделанную работу. Очень вовремя. Наталья Николаевна, благодарю Вас за полезный ресурс. Беру к себе в работу. Прекрасная и нужная работа. Буду использовать в своей работе. Наталья Николаевна! Спасибо за полезный и нужный ресурс! Т Наталья Николаевна! Благодарю за Ваш труд и за то, что результатами его мы можем воспользоваться. Наталья Николаевна, спасибо! Полезный и нужный материал. Беру в копилку. М Наталья Николаевна! Спасибо за полезный и нужный материал. Буду использовать в работе

1


Решение текстовых задач 11 (профильный уровень )

2


Задачи на движение Задачи на движение Задачи на движение Задачи на движение Задачи на смеси и сплавы Задачи на смеси и сплавы Задачи на смеси и сплавы Задачи на смеси и сплавы Задачи на работу Задачи на работу Задачи на работу Задачи на работу Задачи на проценты Задачи на проценты Задачи на проценты Задачи на проценты

3

4


объекты, км/чt, чs, км 1 хs 2 32 s х + 48 = Ответ: 48 — не уд. усл.

5


Решите самостоятельно Ответ: 8 Ответ: 77 Ответ: 6

6


Ответ: 20 объекты, км/чt, чs, км автомобиль х + 80 у 50 велосипедист ку+250 = Решаем систему, получаем: х = 20 км/ч

7


Решите самостоятельно Ответ: 17 Ответ: 9 Ответ: 3

8

9


Ответ: 7 V раствораV водыV вещ-ва% вещ-ва 1 раствор 7 л 15% долили 8 л 2 раствор 7+8=15 л

10


Ответ: на 75 масса сплава масса никеля % никеля 1 сплав 5% 2 сплав 20% 3 сплав 22515%

11


Решите самостоятельно Ответ: 12

12

13


Кол-во деталей ВремяПроизводительность 1 рабочий 20 у — 8 х рабочий 60 ух Ответ: 6

14


Бригада Производитель- ность Время работы Работа 1 бригада 12 у у 12 у + 12 у = 24 ух 24 ку 2 бригада 21 у у 21 у — 12 у = 9 ух 9 ку Пусть х – количество дней, которые отработали бригады после 10 дней, у – производительность одного рабочего. == Ответ: 16

15


Решите самостоятельно Ответ: 8 Ответ: 26

16

17


Пусть стоимость куртки (у) = 100%, тогда 5 курток (5 х) = 100%-5%=95%. 5 х = 95 х = 95 : 5 х = 19% — стоимость 1 рубашки. Стоимость 6 рубашек 6 х = 6 · 19% = 114% 114% — 100% = 14% — на столько 6 рубашек дороже куртки. Ответ: 14

18


Пусть стоимость акций до подорожания – х р, в понедельник они подорожали на у%, их стоимость стала (х + ух)р. Во вторник они подешевели на у% и стали стоить (х + ух) – (у(х + ух))р. х — ((х + ух) – (у(х + ух))) = 0,49 х х – (х + ух – ух – у 2 х) = 0,49 х х – х + у 2 х = 0,49 х у 2 = 0,49 у = 0,7 = 70% Ответ: 70

19


Решите самостоятельно Ответ: 20 Ответ: 931

20

21


Эмблема СУПа: Источник заданий:

1. Текстовые задачи

ЕГЭ п математике. Профильный уровень
Текстовые задачи
1
Томск 2017

2.

2

3. Движение по реке

V
По течению
Против течения
t
S

4.

№1C31B2 Баржа прошла по течению реки 40 км и, повернув
обратно, прошла ещё 30 км, затратив на весь путь 5 часов.
Найдите собственную скорость баржи, если скорость течения
реки равна 5 км/ч.
x км/ч —
скорость баржи
V, км/ч
t, ч
S, км
По течению
40
Против течения
30

5.

5

6.

№8B32E5 Моторная лодка прошла против течения реки 77 км
и вернулась в пункт отправления, затратив на обратный путь на
2 часа меньше, чем на путь против течения. Найдите скорость
лодки в неподвижной воде, если скорость течения реки равна 4
км/ч.
x км/ч —
скорость лодки
V, км/ч
t, ч
S, км
Против течения
77
По течению
77

7.

7

8.

№03A380 Туристы проплыли на лодке от лагеря вверх по течению
реки, затем причалили к берегу и, погуляв 2 часа, вернулись обратно
через 6 часов от начала путешествия. На какое расстояние от лагеря
они отплыли, если скорость течения реки равна 3 км/ч, а собственная
скорость лодки 6 км/ч?
V, км/ч
Против течения
По течению
t, ч
S, км

9.

9

10.

№092692 Рыболов проплыл на лодке от пристани вверх по
течению реки, затем бросил якорь, 2 часа ловил рыбу и вернулся
обратно через 5 часов от начала путешествия. На какое
расстояние от пристани он отплыл, если скорость течения реки
равна 2 км/ч, а собственная скорость лодки 6 км/ч?
V, км/ч
Против течения
По течению
10
t, ч
S, км

11.

№19297D Расстояние между двумя пристанями по реке равно 24 км.
Моторная лодка прошла от одной пристани до другой, сделала стоянку на 1 ч
40 мин и вернулась обратно. Всё путешествие заняло 6 2/3 ч. Найдите
скорость течения реки, если известно, что скорость моторной лодки в
стоячей воде равна 10 км/ч.
V, км/ч
t, ч
S, км
Против течения
24
По течению
24
11

12.

12

13.

№9CD477 Расстояние между А и В равно 48 км. Из А в В по течению
реки отправился плот, а через час вслед за ним отправилась моторная
лодка, которая, прибыв в В, повернула обратно и возвратилась в А. К
этому времени плот прошёл 25 км. Найдите скорость лодки в
неподвижной воде, если скорость течения реки равна 5 км/ч.
x км/ч — скорость лодки
А
В
V, км/ч
13
t, ч
S, км
Плот
25
Моторная лодка
48
48

14.

14

15. Движение с разными скоростями

V1 км/ч
S
В
А
V2 км/ч
V, км/ч
А⟹B
B⟹А
15
t, ч
S, км

16.

№C53B94
Велосипедист выехал с постоянной скоростью из
города А в город В, расстояние между которыми равно 60 км.
Отдохнув, он отправился обратно в А, увеличив скорость на 10
км/ч. По пути он сделал остановку на 3 часа, в результате чего
затратил на обратный путь столько же времени, сколько на путь
из А в В. Найдите скорость велосипедиста на пути из А в В.
V, км/ч
1
2
16
t, ч
S, км

17.

№064788 Велосипедист выехал с постоянной скоростью из
города А в город В, расстояние между которыми равно 208 км.
Отдохнув, он отправился обратно в А, увеличив скорость на 3
км/ч. По пути он сделал остановку на 3 часа, в результате чего
затратил на обратный путь столько же времени, сколько на путь
из А в В. Найдите скорость велосипедиста на пути из В в А.
V, км/ч
17
t, ч
S, км

18.

№FF7622
Из двух городов одновременно навстречу друг другу
отправились два велосипедиста. Проехав некоторую часть пути, первый
велосипедист сделал остановку на 51 минуту, а затем продолжил движение
до встречи со вторым велосипедистом. Расстояние между городами
составляет 251 км, скорость первого велосипедиста равна 10 км/ч, скорость
второго — 20 км/ч. Определите расстояние от города, из которого выехал
второй велосипедист, до места встречи.
251 км
В
А
? км
10 км/ч
V, км/ч
1
2
18
t, ч
S, км
20 км/ч

19.

№B6E1DF
Из пункта А в пункт В, расстояние между которыми 27 км,
вышел турист. Через полчаса навстречу ему из пункта В вышел пешеход и
встретил туриста в 12 км от А. Найдите скорость туриста, если известно, что
она была на 2 км/ч меньше скорости пешехода.
12 км
А
27 км
V, км/ч
1
2
19
t, ч
S, км
В

20.

№5F17D7 Дорога между пунктами A и В состоит из подъёма и спуска, а её
длина равна 10 км. Турист прошёл путь из А в В за 4 часа, из которых спуск
занял 2 часа. С какой скоростью турист шёл на спуске, если его скорость на
подъёме меньше его скорости на спуске на 1 км/ч?
А
B
V, км/ч
Подъём
Спуск
20
t, ч
S, км

21.

№9202
Из А в В одновременно выехали два автомобилиста. Первый
проехал с постоянной скоростью весь путь. Второй проехал первую
половину пути со скоростью, меньшей скорости первого автомобилиста на 6
км/ч, а вторую половину пути проехал со скоростью 56 км/ч, в результате
чего прибыл в В одновременно с первым автомобилистом. Найдите скорость
первого автомобилиста, если известно, что она больше 45 км/ч.
x км/ч —
скорость красного автомобиля
В
А
(x — 6) км/ч
Автомобиль
1 часть пути
2 часть пути
21
V, км/ч
56 км/ч
t, ч
S, км
S = xt

22.

Расстояние между городами A и В равно 150 км. Из города А в В
город выехал автомобиль, а через 30 минут следом за ним со
скоростью 90 км/ч выехал мотоциклист, догнал автомобиль в городе С и повернул обратно. Когда он вернулся в А, автомобиль
прибыл в В. Найдите расстояние от А до С. Ответ дайте в километрах.
22

23. Средняя скорость

23

24.

№21EFE0 Первые 5 часов автомобиль ехал со скоростью 60
км/ч, следующие 3 часа — со скоростью 100 км/ч, а последние 4
часа — со скоростью 75 км/ч. Найдите среднюю скорость
автомобиля на протяжении всего пути.
1
2
3
24
V, км/ч
t, ч
60
100
75
5
3
4
S, км

25.

№A6A840 Первые 160 км автомобиль ехал со скоростью 80
км/ч, следующие 100 км — со скоростью 50 км/ч, а последние
360 км — со скоростью 90 км/ч. Найдите среднюю скорость
автомобиля на протяжении всего пути.
25

26.

№FF5333 Первую половину трассы автомобиль проехал со
скоростью 84 км/ч, а вторую — со скоростью 96 км/ч. Найдите
среднюю скорость автомобиля на протяжении всего пути.
V, км/ч
1
2
26
84
96
t, ч
S, км

27. Движение навстречу

В
А
S

28.

№4B5007 Поезд, двигаясь равномерно со скоростью 129 км/ч,
проезжает мимо пешехода, идущего параллельно путям со
скоростью 6 км/ч навстречу поезду, за 12 секунд. Найдите длину
поезда в метрах.
28

29.

№0AADB7 Поезд, двигаясь равномерно со скоростью 87 км/ч,
проезжает мимо пешехода, идущего параллельно путям со
скоростью 3 км/ч навстречу поезду, за 24 секунды. Найдите
длину поезда в метрах.
29

30.

№314605 Из пунктов А и В, расстояние между которыми 27 км,
вышли одновременно навстречу друг другу два пешехода и встретились в 15 км от А. Найдите скорость пешехода, шедшего из А,
если известно, что он шёл со скоростью, на 2 км/ч большей, чем
второй пешеход, и сделал в пути получасовую остановку.
15 км
А
30
В
27 км

31.

№3B33B9 Из городов А и В навстречу друг другу одновременно
выехали мотоциклист и велосипедист. Мотоциклист приехал в В
на 56 минут раньше, чем велосипедист приехал в А, а
встретились они через 21 минуту после выезда. Сколько часов
затратил на путь из В в А велосипедист?
А
31
В

32.

№112527 Расстояние между городами A и B равно 520 км. Из
города A в город B со скоростью 85 км/ч выехал первый
автомобиль, а через два часа после этого навстречу ему из
города B выехал со скоростью 90 км/ч второй автомобиль. На
каком расстоянии от города A автомобили встретятся? Ответ
дайте в километрах.
? км
А
32
В
520 км

33. Движение вдогонку

V1 км/ч
В
А
V2 км/ч
S

34.

№99595 Два пешехода отправляются одновременно в одном
направлении из одного и того же места на прогулку по аллее
парка. Скорость первого на 1,5 км/ч больше скорости второго.
Через сколько минут расстояние между пешеходами станет
равным 300 метрам?
x+1,5 км/ч
В
А
300 м
x км/ч
34

35.

№26579 Города А, В, С соединены прямолинейным шоссе, при
чём город В расположен меду городами А и С. Из города А в
сторону города С выехал автомобиль, и одновременно с ним из
города В в сторону города С выехал грузовик. Через сколько часов
после выезда легковой автомобиль догонит грузовик, если
скорость легкового автомобиля на 28 км/ч больше скорости
грузовика, а расстояние между городами А и В равно 112 км?
С
А
112 км
35
В

36.

№99610 По морю параллельными курсами в одном направлении
следуют два сухогруза: первый длиной 120 метров, второй — длиной 80
метров. Сначала второй сухогруз отстает от первого, и в некоторый
момент времени расстояние от кормы первого сухогруза до носа второго
составляет 400 метров. Через 12 минут после этого уже первый сухогруз
отстает от второго так, что расстояние от кормы второго сухогруза до
носа первого равно 600 метрам. На сколько километров в час скорость
первого сухогруза меньше скорости второго?
120 м
80 м
36

37.

№DD1CE4 По двум параллельным железнодорожным путям в
одном направлении следуют пассажирский и товарный поезда,
скорости которых равны соответственно 110 км/ч и 70 км/ч.
Длина товарного поезда равна 1800 метрам. Найдите длину
пассажирского поезда, если время, за которое он прошёл мимо
товарного поезда, равно 3 минутам.
37

38.

№44F50B По двум параллельным железнодорожным путям в
одном направлении следуют пассажирский и товарный поезда,
скорости которых равны соответственно 170 км/ч и 80 км/ч.
Длина товарного поезда равна 850 метрам. Найдите длину
пассажирского поезда, если время, за которое он прошёл мимо
товарного поезда, равно 1 минуте.
38

39.

№99597 Первый велосипедист выехал из поселка по шоссе со
скоростью 22 км/ч. Через час после него со скоростью 12 км/ч
из того же поселка в том же направлении выехал второй
велосипедист. а еще через час после этого — третий найдите
скорость третьего велосипедиста, если сначала он догнал
второго а через 8 часов после догнал первого.
39

40. Движение по кругу

40

41.

№167362 Из пункта А круговой трассы, длина которой равна 30 км,
одновременно в одном направлении стартовали два автомобилиста. Скорость
первого равна 92 км/ч, скорость второго – 77 км/ч. Через сколько минут
первый автомобилист будет опережать второго ровно на 1 круг?
V, км/ч
t, ч
1
92
2
77
30(x+1)

Решение задач №8,

ЕГЭ профиль.

Выполнила: Лаврова И.В.,

учитель МБОУ «Поташкинская СОШ»

15 км/ч через 1ч II 14 км/ч через 2ч III х км/ч III II I 14 15 30 III догонит I v = х – 15 = — =3 III догонит II v = x – 14 = — = 3 3 — 103 х + 840 =0 = 40/3 = 13 не удовл. ограничению = 21 Ответ: 21 » width=»640″

Задачи с тремя участниками движения. Статград 16.02.2022

Первый велосипедист выехал из посёлка по шоссе со скоростью 15 км/ч.

Через час после него со скоростью 14 км/ч из того же посёлка в том же

направлении выехал второй велосипедист, а ещё через час после этого —третий. Найдите

скорость третьего велосипедиста, если сначала он догнал второго, а через 3 часа после этого догнал первого. Ответ дайте в км/ч.

I 15 км/ч ограничения: v 15 км/ч

через 1ч II 14 км/ч

через 2ч III х км/ч

III II I

14 15 30

III догонит I v = х – 15 = — =3

III догонит II v = x – 14 =

— = 3

3 — 103 х + 840 =0

= 40/3 = 13 не удовл. ограничению = 21

Ответ: 21

Мультиурок учитель математики Лаврова Ирина Васильевна

Блог

Видео –задача с тремя участниками движения

Метод рычага

8. Смешав 38-процентный и 52-процентный растворы кислоты и добавив

10 кг чистой воды, получили 36-процентный раствор

кислоты. Если бы вместо 10 кг воды добавили 10 кг 50-процентного раствора той же кислоты, то получили бы 46-процентный раствор кислоты. Сколько килограммов 38-процентного раствора использовали для получения смеси?

38х + 52у = 36(х+у+10) (I)

38х+52у + 50∙10 = 46(х + у+ 10) (II)

10(х + у + 10) = 500

х + у + 10 = 50

х + у = 40 у=40-х, подставим в (1) х=20, у=20

Задачи на концентрацию и сплавы есть статьи :

Журналы «Математика в школе» №4, 94

«Математика в школе» №1, 97

Журнал «Математика . Всё для учителя» №2 [62] ст.Л.В.Гориной «Как перестать бояться и начать.. решать задачи на смеси и сплавы»,

стр.26

Журнал «Математика для школьников», №2, 2006,, С.Н.Олехник,

«Старинный способ решения задач на смешение веществ», стр. 56

Метод креста

12. Задание 8 №  99576

Имеется два сплава. Первый содержит 10% никеля, второй  — 30% никеля. Из этих двух сплавов получили третий сплав массой 200 кг, содержащий 25% никеля. На сколько килограммов масса первого сплава была меньше массы второго?

10% 5 частей

25%

30% 15 частей

• 15 +5 = 20(частей)-всего
• 200 : 20 = 10 г- масса 1 части
• 10 ∙5 = 50 (г) – масса 1 сплава
• 10 ∙ 15 = 150 (г) –масса 2 сплава
• 150- 50 =100 (г)
• Ответ : 100

Задание 8 №  99576

Имеется два сплава. Первый сплав содержит 10% меди, второй  — 40% меди. Масса второго сплава больше массы первого на 3 кг. Из этих двух сплавов получили третий сплав, содержащий 30% меди. Найдите массу третьего сплава. Ответ дайте в килограммах.

10% 10 частей

30%

40% 20 частей

• 20 – 10 = на 10 ( частей) больше масса 2 сплава
• 3 : 10 = 0,3 (кг) – в одной части
• 0,3 ∙10 = 3 (кг)- масса 1 сплава
• 0,3 ∙ 20 = 6 ( кг) – масса 2 сплава
• 3 + 6 = 9 (кг)

Ответ: 9 кг

№ 8. Курага получается в процессе сушки абрикосов. Сколько

килограммов абрикосов потребуется для получения 21 килограмма

кураги, если абрикосы содержат 86 % воды, а курага содержит 18 % воды?

%воды % сух. масса масса

вещ-ва сух.вещ-ва

абрикосы 86 14 % х 0,14х

курага 18 82 % 21 кг 0,82∙ 21

0,14х = 0,82 ∙ 21 14х = 82 ∙ 21

0,14х = 17,22 2х =82 ∙ 3

х = 123 х = 246 : 2

х = 123

Ответ: 123

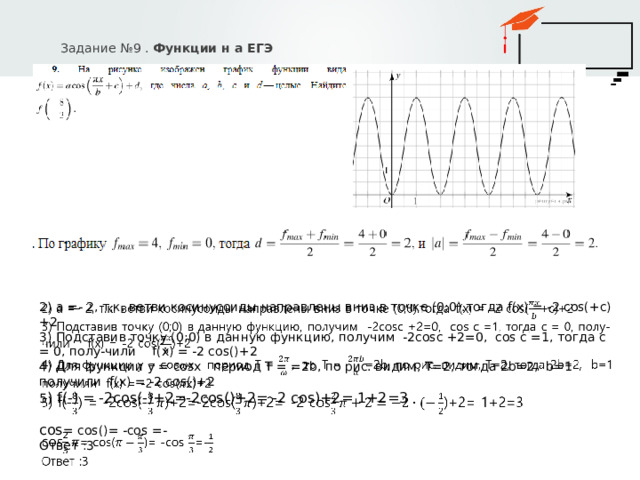
Задание №9 . Функции н а ЕГЭ

2) а =- 2, т.к. ветви косинусоиды направлены вниз в точке (0;0).тогда f(x) = -2 cos(+c)+2

3) Подставив точку (0;0) в данную функцию, получим -2cosc +2=0, сos c =1, тогда с = 0, полу-чили f(x) = -2 cos()+2

4) Для функции у = cosх период Т = =2b, по рис. видим, Т=2, тогда 2b=2, b=1

получили f(x) = -2 cos()+2

5 ) f(-) = -2cos(-)+2=-2cos()+2= -2 cos)+2= 1+2=3

cos = cos()= -cos =-

Ответ :3

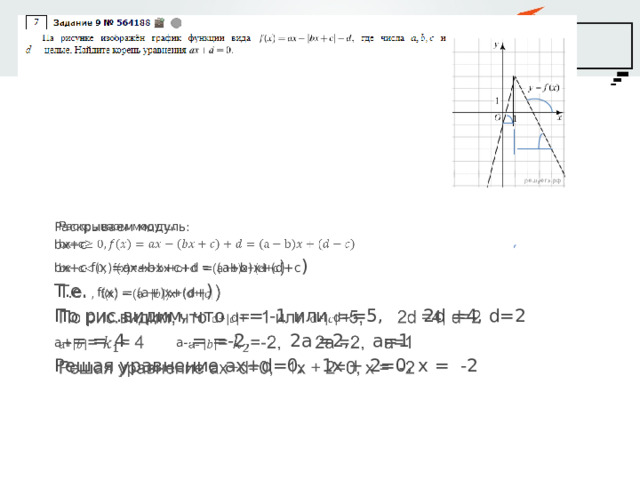
Раскрываем модуль:

bx+c

bx+c f(x)=ax+bx+c+d = (a+b)x+(d+c )

Т.е. f(x) = (a+)x+(d+ )

По рис.видим, что d+ = -1 или d+ =5, 2d =4, d=2

a+ = = 4 a- = =-2, 2a =2, a=1

Решая уравнение ax+d=0, 1x + 2=0, x = -2

Спасибо за внимание и понимание