Инфоурок
›
Математика
›Презентации›Презентация по математике подготовка к ЕГЭ и ОГЭ «Окружность и ее элементы»
Презентация по математике подготовка к ЕГЭ и ОГЭ «Окружность и ее элементы»
Скачать материал

Скачать материал


- Сейчас обучается 47 человек из 27 регионов


- Сейчас обучается 96 человек из 32 регионов


- Сейчас обучается 54 человека из 30 регионов


Описание презентации по отдельным слайдам:
-
1 слайд
Подготовка к ОГЭ и ЕГЭ
Решение задач по теме
«Окружность и её элементы»Лунёва О.А.,
учитель математики
МБОУ «Рыбинобудская СОШ» -
2 слайд
Цель:
повторить понятие окружности, её элементов;
разобрать задания по теме «Окружность»;
содействовать подготовке учащихся к сдаче ОГЭ и ЕГЭ. -
3 слайд
Основные понятия
Окружность — множество всех точек плоскости, удаленных на заданное расстояние от заданной точки (центра).
Круг — часть плоскости, ограниченная окружностью.
Радиус — отрезок, соединяющей центр окружности с какой-либо точкой окружности. -
4 слайд
Основные понятия
Хорда — отрезок, соединяющий любые две точки окружности.
Диаметр — хорда, проходящая через центр окружности.
Секущая — прямая, имеющая с окружностью две общие точки.
Касательная- прямая, имеющая с окружностью одну общую точку. -
-
6 слайд
Свойства вписанных углов
2. Вписанные углы, опирающиеся на одну и ту же дугу, равны. -
7 слайд
Свойства вписанных углов
3. Вписанный угол, опирающийся на диаметр (или полуокружность) — прямой. -
8 слайд
4. Равные дуги окружности стягиваются равными хордами.
АВ=СD, -
9 слайд
Углы, связанные с окружностью
Теорема (угол между пересекающимися хордами).
Угол между двумя пересекающимися хордами равен полусумме высекаемых ими дуг. -
10 слайд
Углы, связанные с окружностью
Теорема (угол между секущими).
Угол между двумя секущими, проведенными из одной точки, равен полуразности большей и меньшей высекаемых ими дуг. -
11 слайд
Углы, связанные с окружностью
Теорема (угол между касательной и хордой,
проведенной через точку касания).
Угол между касательной и хордой, проведенной в точку касания, равен половине дуги, стягиваемой этой хордой. -
12 слайд
Углы, связанные с окружностью
Теорема (угол между касательной и секущей).
Угол между касательной и секущей равен полуразности высекаемых ими дуг. -
13 слайд
Отрезки, связанные с окружностью
Отрезки касательных к окружности, проведенные из одной точки, равны и составляют равные углы с прямой, проходящей через эту точку и центр окружности.
<ОАВ=<ОАС, -
14 слайд
Отрезки, связанные с окружностью
Квадрат касательной равен произведению секущей на ее внешнюю часть.
-
15 слайд
Окружность, вписанная в многоугольник
Если все стороны многоугольника касаются окружности, то окружность называется вписанной в многоугольник, а многоугольник — описанным около этой окружности.
В любом описанном четырехугольнике суммы противоположных сторон равны.АВ+СД=ВС+АД
-
16 слайд
Окружность, описанная около многоугольника
Если все вершины многоугольника лежат на окружности, то окружность называется описанной около многоугольника, а многоугольник- вписанным в эту окружность.
В любом четырехугольнике, вписанном в окружность, сумма противоположных углов равна 180°.
<А+<С=180 ͦ
<В+<Д=180 ͦ -
-
-
-
-
-
-
-
-
-
-
-
-
-
-
31 слайд
СПАСИБО ЗА ВНИМАНИЕ!
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 155 062 материала в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
- 19.11.2022
- 111
- 9
- 19.11.2022
- 123
- 6


- 19.11.2022
- 96
- 0
- 19.11.2022
- 40
- 0
- 19.11.2022
- 150
- 0
- 19.11.2022
- 333
- 8
Вам будут интересны эти курсы:
-
Курс повышения квалификации «Внедрение системы компьютерной математики в процесс обучения математике в старших классах в рамках реализации ФГОС»
-
Курс повышения квалификации «Педагогическое проектирование как средство оптимизации труда учителя математики в условиях ФГОС второго поколения»
-
Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»
-
Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Специфика преподавания основ финансовой грамотности в общеобразовательной школе»
-
Курс повышения квалификации «Специфика преподавания информатики в начальных классах с учетом ФГОС НОО»
-
Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»
-
Курс профессиональной переподготовки «Теория и методика обучения информатике в начальной школе»
-
Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»
-
Курс профессиональной переподготовки «Инженерная графика: теория и методика преподавания в образовательной организации»
-
Курс повышения квалификации «Развитие элементарных математических представлений у детей дошкольного возраста»
-
Курс повышения квалификации «Методика преподавания курса «Шахматы» в общеобразовательных организациях в рамках ФГОС НОО»
-
Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»
-
Настоящий материал опубликован пользователем Лунева Оксана Анатольевна. Инфоурок является
информационным посредником и предоставляет пользователям возможность размещать на сайте
методические материалы. Всю ответственность за опубликованные материалы, содержащиеся в них
сведения, а также за соблюдение авторских прав несут пользователи, загрузившие материал на сайтЕсли Вы считаете, что материал нарушает авторские права либо по каким-то другим причинам должен быть удален с
сайта, Вы можете оставить жалобу на материал.Удалить материал
-
- На сайте: 6 лет и 3 месяца
- Подписчики: 0
- Всего просмотров: 159908
-
Всего материалов:
32
Слайд 1
Вписанные и описанные окружности.
Слайд 2
Окружность вписанная в многоугольник и описанная около него Центр окружности -точка пересечения серединных перпендикуляров Центр окружности -точка пересечения биссектрис углов многоугольника Если в трапецию вписана окружность, то Сумма оснований равна сумме боковых сторон; Радиус окружности равен половине высоты ; Если соединить вершины трапеции с центром окружности, то треугольники, прилежащие к боковым сторонам прямоугольные.
Слайд 3
Окружность вписанная в многоугольник и описанная около него Параллелограмм, вписанный в окружность- прямоугольник. Параллелограмм, описанный около окружности- ромб.
Слайд 12
Окружность вписанная в правильный многоугольник и описанная около него Правильный треугольник К вадрат Правильный шестиугольник Правильный п -угольник
Слайд 17
Задание 16 К окружности, вписанной в квадрат ABCD , проведена касательная, пересекающая стороны AB и AD в точках M и N соответственно. а) Докажите, что периметр треугольника AMN равен стороне квадрата. б) Прямая MN пересекает прямую CD в точке P . В каком отношении делит сторону BC прямая, проходящая через точку P и центр окружности, если AM : MB = 1 : 3?
Слайд 18
Вписанная и описанная окружности прямоугольного треугольника
Слайд 21
Вписанная и описанная окружности произвольного треугольника
Слайд 27
Задание 16 В треугольник ABC вписана окружность радиуса 2, касающаяся стороны AC в точке M , причём AM = 4 и CM = 6. а) Докажите, что треугольник ABC прямоугольный. б) Найдите расстояние между центрами вписанной и описанной окружностей треугольника ABC .
Слайд 28
Задание 16 Окружность проходит через вершины В и С треугольника АВС и пересекает АВ и АС в точках С 1 и В 1 соответственно. а) Докажите, что треугольник АВC подобен треугольнику АВ 1 С 1 б) Вычислите радиус данной окружности, если ВС=10 , и площадь треугольника АВ 1 С 1 в три раза меньше площади четырёхугольника ВСВ 1 С 1 .
Слайд 1Практикум № 12
по решению
планиметрических задач
УМК: любой

Слайд 2
Вписанная окружность
в заданиях ЕГЭ

Слайд 3Содержание
Задача №1
Задача №2
Задача №3
Задача №4
Задача №5
Задача №6
Задача №7
Задача №Задача №22
Задача № Задача №23
Задача № Задача №24
Задача № Задача №25
Задача № Задача №26
Задача № Задача №27
Задача №Задача №28
Задача №Задача №29
Задача № Задача №30
Задача № Задача №15
Задача № Задача №16
Задача № Задача №17
Задача № Задача №18
Задача № Задача №19
Задача № Задача №20
Задача № Задача №21
Задача №Задача №8
Задача № Задача №9
Задача № Задача №10
Задача № Задача №11
Задача № Задача №12
Задача № Задача №13
Задача № Задача №14
Задачи для самостоятельного решения

Слайд 4Задача №1
Радиус окружности, вписанной в правильный треугольник, равен 6. Найдите высоту
этого треугольника.
Высота правильного треугольника равна 3 радиусам вписанной окружности
поэтому она равна 18.

Слайд 5Задача №2
Найдите радиус окружности, вписанной в квадрат со стороной 4.
Ответ:
2.

Слайд 6Задача №3
Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну
из боковых сторон на два отрезка, длины которых равны 5 и 3, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
Ответ: 22.

Слайд 7Задача №4
Боковые стороны трапеции, описанной около окружности, равны 3 и 5.
Найдите среднюю линию трапеции.
в выпуклый четырехугольник можно вписать
окружность тогда и только тогда, когда АВ + СD = AD +CB
Средняя линия равна половине суммы оснований, значит
Равна (3+5):2=4

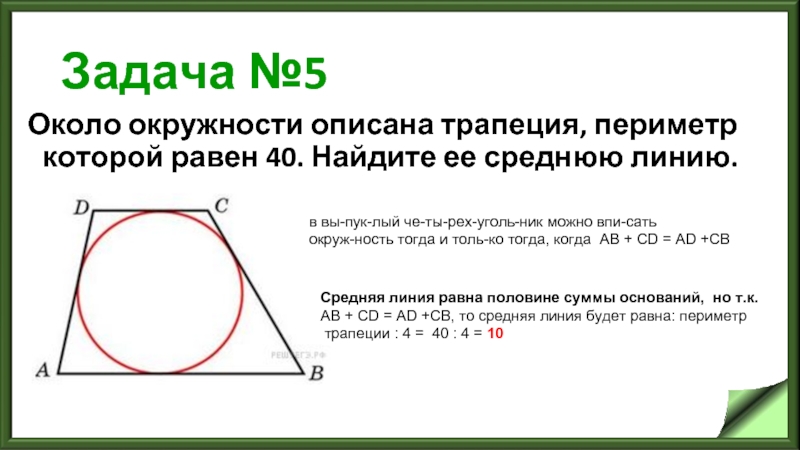
Слайд 8Задача №5
Около окружности описана трапеция, периметр которой равен 40. Найдите ее
среднюю линию.
в выпуклый четырехугольник можно вписать
окружность тогда и только тогда, когда АВ + СD = AD +CB
Средняя линия равна половине суммы оснований, но т.к.
АВ + СD = AD +CB, то средняя линия будет равна: периметр
трапеции : 4 = 40 : 4 = 10
Слайд 9Задача №6
Периметр прямоугольной трапеции, описанной около окружности, равен 22, ее большая
боковая сторона равна 7. Найдите радиус окружности.
в выпуклый четырехугольник можно вписать
окружность тогда и только тогда, когда АВ + СD = AD +CB

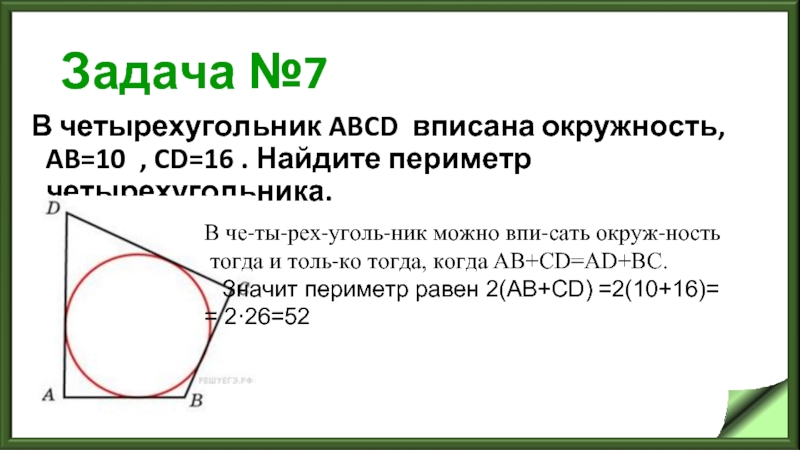
Слайд 10Задача №7
В четырехугольник ABCD вписана окружность, AB=10 , CD=16 . Найдите периметр четырехугольника.
В четырехугольник можно вписать окружность
тогда и только тогда, когда AB+CD=AD+BC.
Значит периметр равен 2(АВ+СD) =2(10+16)=
= 2·26=52
Слайд 11Задача №8
В четырехугольник ABCD вписана окружность AB=10, BC=11 и CD=15. Найдите четвертую сторону четырехугольника.
В
четырехугольник можно вписать окружность
тогда и только тогда, когда AB+CD=AD+BC.
Значит AD=(AB+CD)-DC= (10+15)-11=14

Слайд 12Задача №9
К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных
треугольников равны 6, 8, 10. Найдите периметр данного треугольника АВС.
Отрезки касательных, проведенных к окружности
из точек K,H,O,F,N,M, соответственно равны друг другу.
Поэтому

Слайд 13Задача №10
В угол C, равный 68°, вписана окружность с центром O, которая касается
сторон угла в точках A и B. Найдите угол AOB. Ответ дайте в градусах.
Острый угол между перпендикулярами к сторонам угла равен самому углу; тупой угол между ними дополняет его до 180°. Тем самым, искомый угол равен 180° − 68° = 112°.

Слайд 14Задача №11
Периметр треугольника равен 12, а радиус вписанной окружности равен 1. Найдите
площадь этого треугольника.
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
Значит S∆ =(P/2) ·r = (12 : 2) · 1 = 6

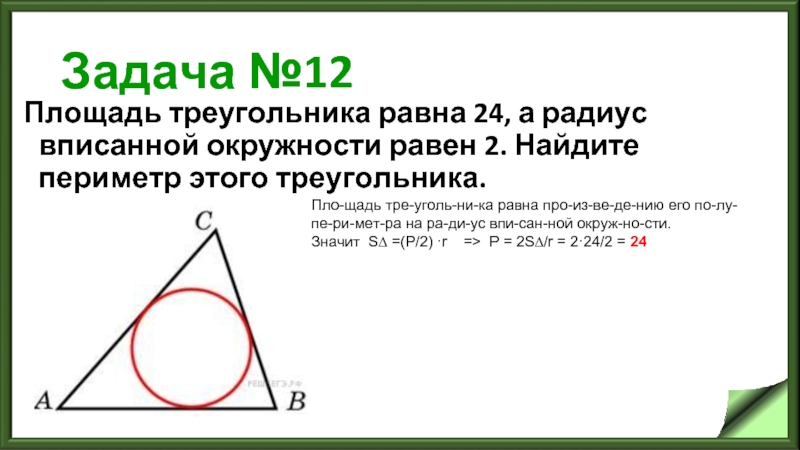
Слайд 15Задача №12
Площадь треугольника равна 24, а радиус вписанной окружности равен 2.
Найдите периметр этого треугольника.
Площадь треугольника равна произведению его полупериметра на радиус вписанной окружности.
Значит S∆ =(P/2) ·r => P = 2S∆/r = 2·24/2 = 24
Слайд 16Задача №13
Сторона правильного треугольника равна √3. Найдите радиус окружности, вписанной в
этот треугольник.
радиус вписанной в равносторонний треугольник через его сторону
Равен r = a√3 : 6 = √3·√3 : 6 = 0,5

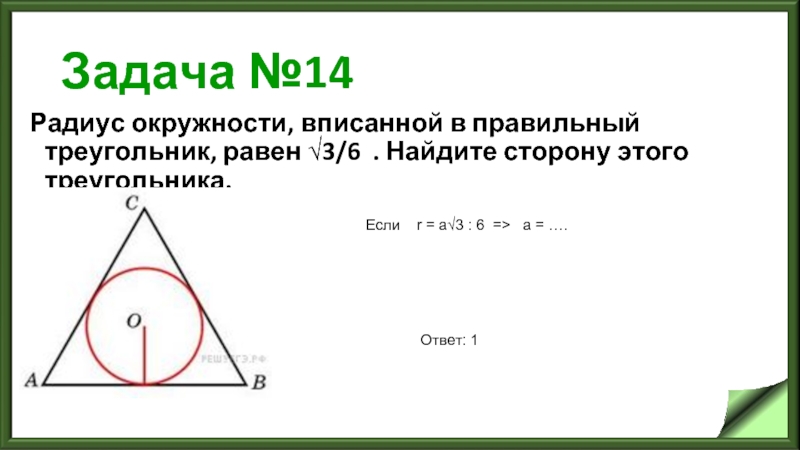
Слайд 17Задача №14
Радиус окружности, вписанной в правильный треугольник, равен √3/6 . Найдите
сторону этого треугольника.
Ответ: 1
Если r = a√3 : 6 => а = ….
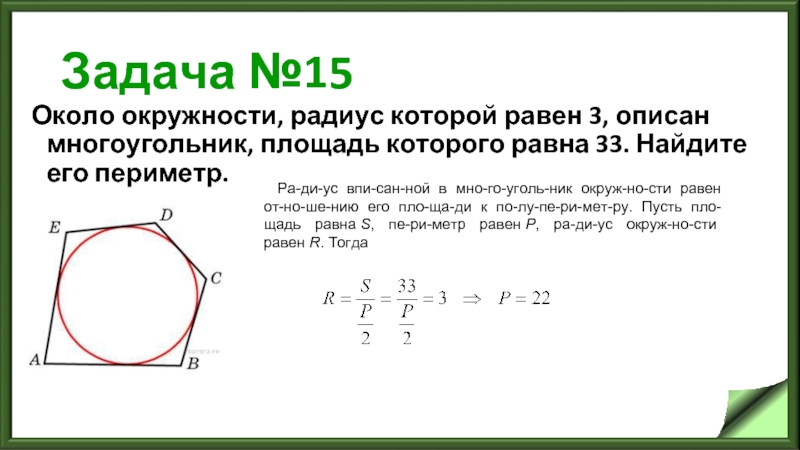
Слайд 18Задача №15
Около окружности, радиус которой равен 3, описан многоугольник, площадь которого
равна 33. Найдите его периметр.
Радиус вписанной в многоугольник окружности равен отношению его площади к полупериметру. Пусть площадь равна S, периметр равен P, радиус окружности равен R. Тогда
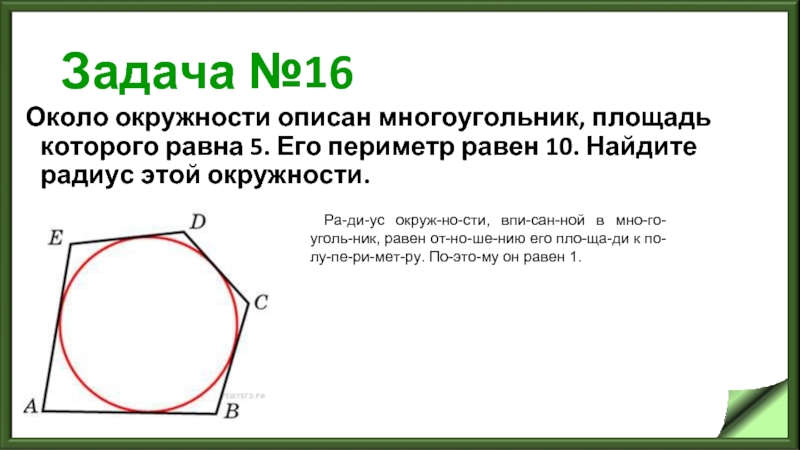
Слайд 19Задача №16
Около окружности описан многоугольник, площадь которого равна 5. Его периметр
равен 10. Найдите радиус этой окружности.
Радиус окружности, вписанной в многоугольник, равен отношению его площади к полупериметру. Поэтому он равен 1.
Слайд 20Задача №17
Катеты равнобедренного прямоугольного треугольника равны 2+√2 . Найдите радиус окружности,
вписанной в этот треугольник.
Радиус вписанной в прямоугольный треугольник окружности равен половине разности суммы катетов и гипотенузы:

Слайд 21Задача №18
В треугольнике АВС, АС=4 , ВС=3 угол равен 90°. Найдите радиус вписанной
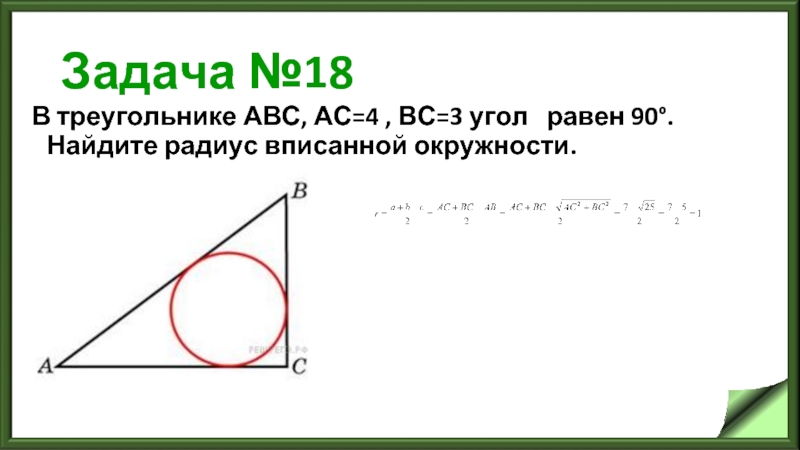
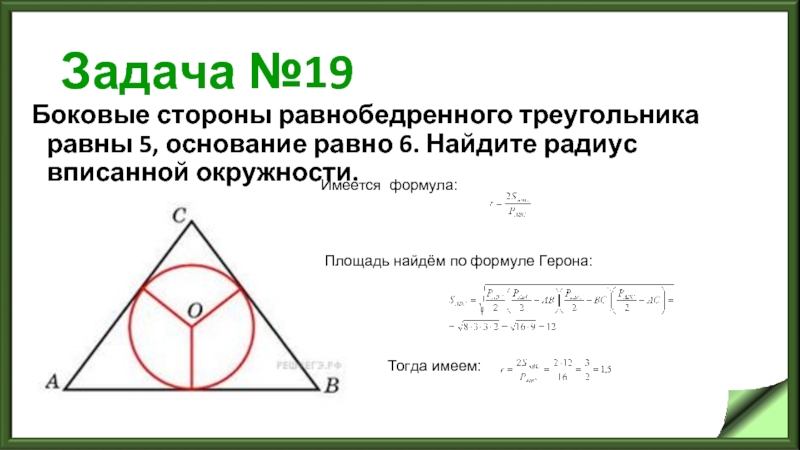
Слайд 22Задача №19
Боковые стороны равнобедренного треугольника равны 5, основание равно 6. Найдите
радиус вписанной окружности.
Имеется формула:
Площадь найдём по формуле Герона:
Тогда имеем:
Слайд 23Задача №20
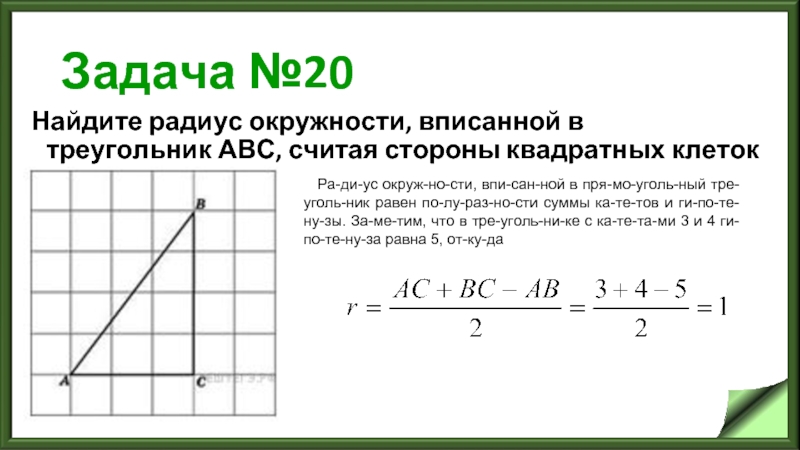
Найдите радиус окружности, вписанной в треугольник АВС, считая стороны квадратных клеток
равными 1.
Радиус окружности, вписанной в прямоугольный треугольник равен полуразности суммы катетов и гипотенузы. Заметим, что в треугольнике с катетами 3 и 4 гипотенуза равна 5, откуда
Слайд 24Задача №21
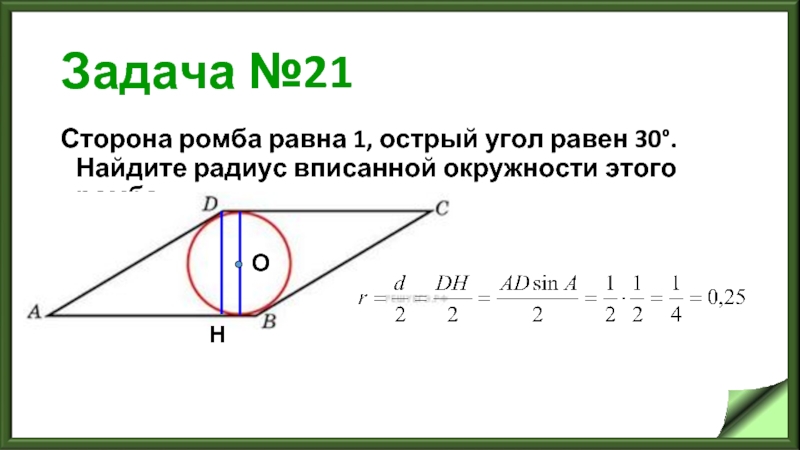
Сторона ромба равна 1, острый угол равен 30°. Найдите радиус вписанной
окружности этого ромба.
О
Н
Слайд 25Задача №22
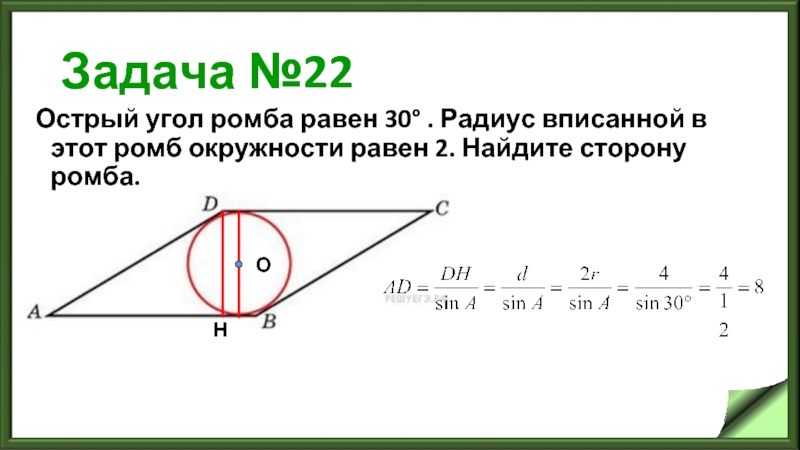
Острый угол ромба равен 30° . Радиус вписанной в этот ромб
окружности равен 2. Найдите сторону ромба.
О
Н
Слайд 26Задача №23
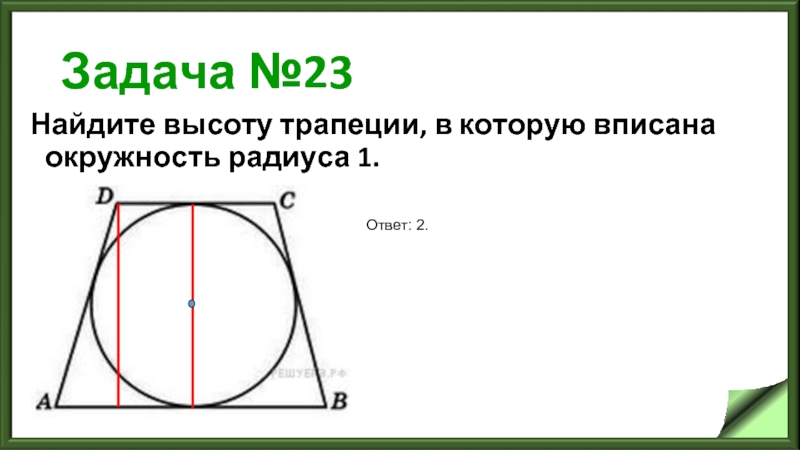
Найдите высоту трапеции, в которую вписана окружность радиуса 1.
Ответ:
2.
Слайд 27Задача №24
Периметр четырехугольника, описанного около окружности, равен 24, две его стороны
равны 5 и 6. Найдите большую из оставшихся сторон.
Пусть большая из двух оставшихся сторон имеет длину x, тогда длина четвертой стороны равна 24-5-6-х=13-х. В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда суммы длин его противоположных сторон равны.
Итак, напротив большей из первой пары смежных сторон с длинами x и 13 − x лежит меньшая из второй пары смежных сторон с длинами 5 и 6. Поскольку суммы длин противоположных сторон равны, имеем: х+5=(13-х)+6 => х=7

Слайд 28Задача №25
Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке)
как 1 : 2 : 3. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 32.
В выпуклый четырехугольник можно вписать окружность тогда и только тогда, когда AB+CD=AD+BC. Пусть меньшая сторона равна x тогда: х+3х=Р/2
4х=16
х=4
Тогда большая сторона равна 3х=3·4=12

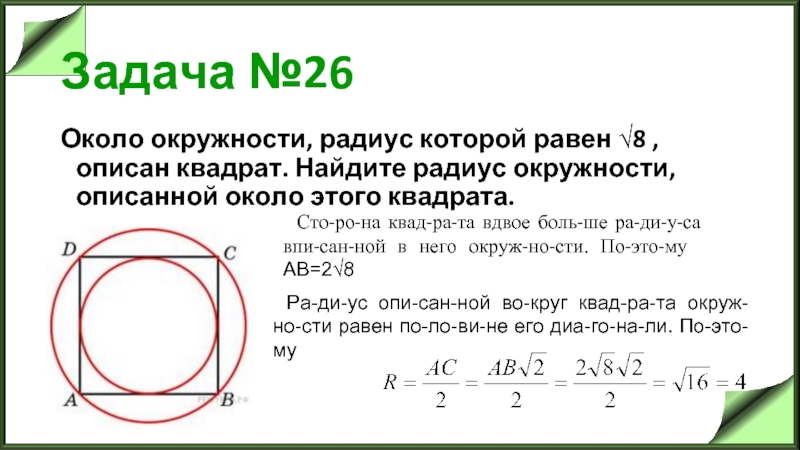
Слайд 29Задача №26
Около окружности, радиус которой равен √8 , описан квадрат. Найдите радиус
окружности, описанной около этого квадрата.
Сторона квадрата вдвое больше радиуса вписанной в него окружности. Поэтому АВ=2√8
Радиус описанной вокруг квадрата окружности равен половине его диагонали. Поэтому
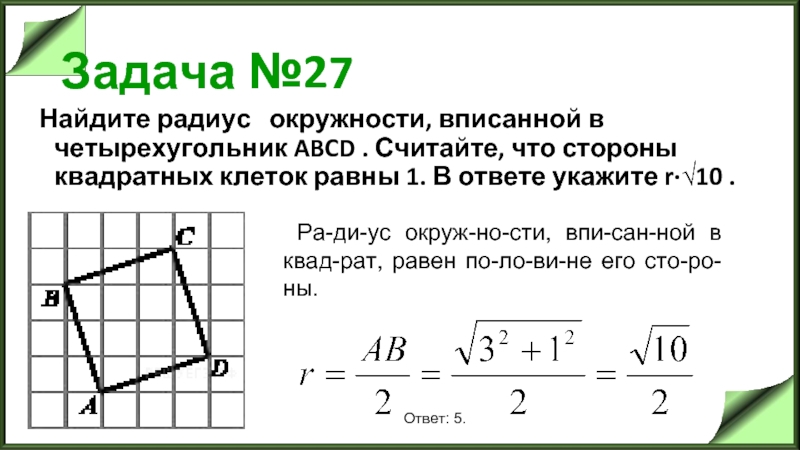
Слайд 30Задача №27
Найдите радиус окружности, вписанной в четырехугольник ABCD . Считайте, что стороны
квадратных клеток равны 1. В ответе укажите r·√10 .
Радиус окружности, вписанной в квадрат, равен половине его стороны.
Ответ: 5.
Слайд 31Задача №28
Около окружности, радиус которой равен 3, описан многоугольник, периметр которого
равен 20. Найдите его площадь.
Радиус вписанной в многоугольник окружности равен отношению его площади к полупериметру.

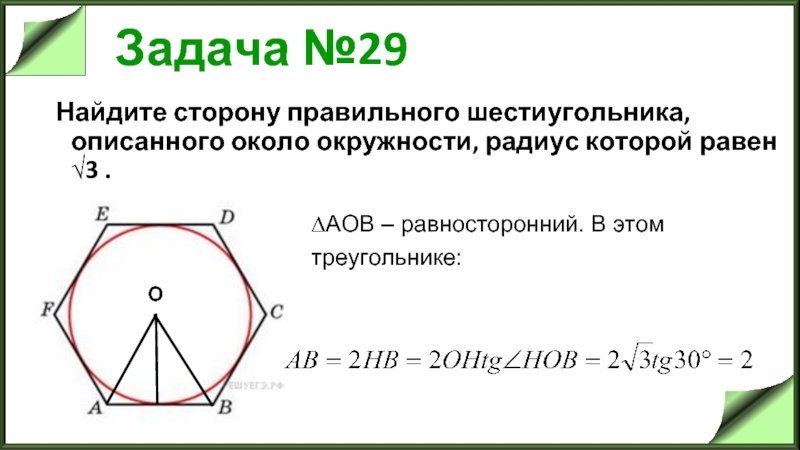
Слайд 32Задача №29
Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен
√3 .
O
∆AOB – равносторонний. В этом
треугольнике:
Слайд 33Задача №30
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной √3 .
О
Угол между сторонами правильного шестиугольника равен 120°. Рассмотрим треугольник FEA и применим теорему косинусов:

Слайд 34Задачи
для самостоятельного решения

Слайд 35Задача №1 Решите самостоятельно
Радиус окружности, вписанной в правильный треугольник, равен 31.
Найдите высоту этого треугольника.
Радиус окружности, вписанной в правильный треугольник, равен 16. Найдите высоту этого треугольника.
Радиус окружности, вписанной в правильный треугольник, равен 24. Найдите высоту этого треугольника.

Слайд 36Задача №2 Решите самостоятельно
Найдите радиус окружности, вписанной в квадрат со стороной
26.
2) Найдите радиус окружности, вписанной в квадрат со стороной 44.
3) Найдите радиус окружности, вписанной в квадрат со стороной 84.

Слайд 37Задача №3 Решите самостоятельно
1) Окружность, вписанная в равнобедренный треугольник, делит в
точке касания одну из боковых сторон на два отрезка, длины которых равны 10 и 1, считая от вершины, противолежащей основанию. Найдите периметр треугольника.
2) Окружность, вписанная в равнобедренный треугольник, делит в точке касания одну из боковых сторон на два отрезка, длины которых равны 15 и 5, считая от вершины, противолежащей основанию. Найдите периметр треугольника.

Слайд 38Задача №4 Решите самостоятельно
Боковые стороны трапеции, описанной около окружности, равны 27
и 4. Найдите среднюю линию трапеции. Ответ: 15,5
Боковые стороны трапеции, описанной около окружности, равны 1 и 11. Найдите среднюю линию трапеции.
Боковые стороны трапеции, описанной около окружности, равны 22 и 3. Найдите среднюю линию трапеции.

Слайд 39Задача №5 Решите самостоятельно
Около окружности описана трапеция, периметр которой равен 84.
Найдите ее среднюю линию.
2) Около окружности описана трапеция, периметр которой равен 32. Найдите ее среднюю линию.
3) Около окружности описана трапеция, периметр которой равен 188. Найдите ее среднюю линию.

Слайд 40Задача №6 Решите самостоятельно
Периметр прямоугольной трапеции, описанной около окружности, равен 100,
ее большая боковая сторона равна 42. Найдите радиус окружности.
2) Периметр прямоугольной трапеции, описанной около окружности, равен 64, ее большая боковая сторона равна 28. Найдите радиус окружности.

Слайд 41Задача №7 Решите самостоятельно
В четырехугольник ABCD вписана окружность, AB=22 , CD=77 . Найдите
периметр четырехугольника.
В четырехугольник ABCD вписана окружность, AB=14 , CD=60 . Найдите периметр четырехугольника.
В четырехугольник ABCD вписана окружность, AB=20 , CD=55 . Найдите периметр четырехугольника.

Слайд 42Задача №8 Решите самостоятельно
В четырехугольник ABCD вписана окружность AB=12, BC=4 и CD=46. Найдите четвертую
сторону четырехугольника. Ответ:54
2) В четырехугольник ABCD вписана окружность AB=8, BC=8 и CD=33. Найдите четвертую сторону четырехугольника.
3) В четырехугольник ABCD вписана окружность AB=7, BC=14 и CD=13. Найдите четвертую сторону четырехугольника.

Слайд 43Задача №9 Решите самостоятельно
К окружности, вписанной в треугольник ABC, проведены три касательные.
Периметры отсеченных треугольников равны 8, 23, 78. Найдите периметр данного треугольника АВС.
2) К окружности, вписанной в треугольник ABC, проведены три касательные. Периметры отсеченных треугольников равны 10, 32, 24. Найдите периметр данного треугольника АВС.

Слайд 44Задача №11 Решите самостоятельно
Периметр треугольника равен 76, а радиус вписанной окружности
равен 8. Найдите площадь этого треугольника.
2) Периметр треугольника равен 38, а радиус вписанной окружности равен 5. Найдите площадь этого треугольника.
3) Периметр треугольника равен 90, а радиус вписанной окружности равен 14. Найдите площадь этого треугольника.

Слайд 45Задача №12 Решите самостоятельно
Площадь треугольника равна 70, а радиус вписанной окружности
равен 5. Найдите периметр этого треугольника.
Площадь треугольника равна 768, а радиус вписанной окружности равен 16. Найдите периметр этого треугольника.
Площадь треугольника равна 231, а радиус вписанной окружности равен 7. Найдите периметр этого треугольника.

Слайд 46Задача №13 Решите самостоятельно
Сторона правильного треугольника равна 8√3. Найдите радиус окружности,
вписанной в этот треугольник. Ответ: 4
Сторона правильного треугольника равна 6√3. Найдите радиус окружности, вписанной в этот треугольник.
Сторона правильного треугольника равна 28√3. Найдите радиус окружности, вписанной в этот треугольник.

Слайд 47Задача №14 Решите самостоятельно
Радиус окружности, вписанной в правильный треугольник, равен 25√3/6
. Найдите сторону этого треугольника. Ответ: 25
2) Радиус окружности, вписанной в правильный треугольник, равен 46√3/6 . Найдите сторону этого треугольника.
3) Радиус окружности, вписанной в правильный треугольник, равен 11√3/6 . Найдите сторону этого треугольника.

Слайд 48Задача №15 Решите самостоятельно
Около окружности, радиус которой равен 2, описан многоугольник,
площадь которого равна 41. Найдите его периметр.
Около окружности, радиус которой равен 1, описан многоугольник, площадь которого равна 27. Найдите его периметр.
Около окружности, радиус которой равен 3, описан многоугольник, площадь которого равна 66. Найдите его периметр.

Слайд 49Задача №16 Решите самостоятельно
Около окружности описан многоугольник, площадь которого равна 27.
Его периметр равен 54. Найдите радиус этой окружности. Ответ: 1
2) Около окружности описан многоугольник, площадь которого равна 39. Его периметр равен 26. Найдите радиус этой окружности.
3) Около окружности описан многоугольник, площадь которого равна 78. Его периметр равен 39. Найдите радиус этой окружности.

Слайд 50Задача №17 Решите самостоятельно
Катеты равнобедренного прямоугольного треугольника равны 82+41√2 . Найдите
радиус окружности, вписанной в этот треугольник.
2) Катеты равнобедренного прямоугольного треугольника равны 58+29√2 . Найдите радиус окружности, вписанной в этот треугольник.
3) Катеты равнобедренного прямоугольного треугольника равны 8+4√2 . Найдите радиус окружности, вписанной в этот треугольник.

Слайд 51Задача №18 Решите самостоятельно
В треугольнике АВС, АС=37,5 , ВС=20 угол равен 90°. Найдите
радиус вписанной окружности.
2) В треугольнике АВС, АС=20 , ВС=4,5 угол равен 90°. Найдите радиус вписанной окружности.
3) В треугольнике АВС, АС=24, ВС=7 угол равен 90°. Найдите радиус вписанной окружности.

Слайд 52Задача №19 Решите самостоятельно
Боковые стороны равнобедренного треугольника равны 136, основание равно
128. Найдите радиус вписанной окружности.
2) Боковые стороны равнобедренного треугольника равны 149, основание равно 102. Найдите радиус вписанной окружности.
3) Боковые стороны равнобедренного треугольника равны 404, основание равно 792. Найдите радиус вписанной окружности.

Слайд 53Задача №21 Решите самостоятельно
1) Сторона ромба равна 20, острый угол равен 30°.
Найдите радиус вписанной окружности этого ромба.
2) Сторона ромба равна 4, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.
3) Сторона ромба равна 96, острый угол равен 30°. Найдите радиус вписанной окружности этого ромба.

Слайд 54Задача №22 Решите самостоятельно
Острый угол ромба равен 30° . Радиус вписанной в
этот ромб окружности равен 16,5. Найдите сторону ромба.
2) Острый угол ромба равен 30° . Радиус вписанной в этот ромб окружности равен 13. Найдите сторону ромба.
3) Острый угол ромба равен 30° . Радиус вписанной в этот ромб окружности равен 0,5. Найдите сторону ромба.

Слайд 55Задача №24 Решите самостоятельно
Периметр четырехугольника, описанного около окружности, равен 48, две
его стороны равны 19 и 25. Найдите большую из оставшихся сторон.
2) Периметр четырехугольника, описанного около окружности, равен 26, две его стороны равны 2 и 8. Найдите большую из оставшихся сторон.
3) Периметр четырехугольника, описанного около окружности, равен 56, две его стороны равны 15 и 21. Найдите большую из оставшихся сторон.

Слайд 56Задача №25 Решите самостоятельно
Три стороны описанного около окружности четырехугольника относятся (в
последовательном порядке) как 1 : 17 : 23. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 48.
2) Три стороны описанного около окружности четырехугольника относятся (в последовательном порядке) как 2 : 13 : 28. Найдите большую сторону этого четырехугольника, если известно, что его периметр равен 60.

Слайд 57Задача №26 Решите самостоятельно
Около окружности, радиус которой равен 45√2 , описан квадрат.
Найдите радиус окружности, описанной около этого квадрата.
2) Около окружности, радиус которой равен 32√2 , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.
3) Около окружности, радиус которой равен 50√2 , описан квадрат. Найдите радиус окружности, описанной около этого квадрата.

Слайд 58Задача №28 Решите самостоятельно
Около окружности, радиус которой равен 4, описан многоугольник,
периметр которого равен 57. Найдите его площадь.
2) Около окружности, радиус которой равен 3, описан многоугольник, периметр которого равен 62. Найдите его площадь.
3) Около окружности, радиус которой равен 1, описан многоугольник, периметр которого равен 8. Найдите его площадь.

Слайд 59Задача №29 Решите самостоятельно
Найдите сторону правильного шестиугольника, описанного около окружности, радиус
которой равен 17√3
2) Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 37√3 .
3) Найдите сторону правильного шестиугольника, описанного около окружности, радиус которой равен 40√3 .

Слайд 60Задача №30Решите самостоятельно
Найдите радиус окружности, вписанной в правильный шестиугольник со стороной 84√3
.
2) Найдите радиус окружности, вписанной в правильный шестиугольник со стороной 52√3 .
3) Найдите радиус окружности, вписанной в правильный шестиугольник со стороной 70√3 .

Слайд 61Интернет источники
https://fotki.yandex.ru/next/users/nata-komiati/album/158683/view/670127?page=3
https://img-fotki.yandex.ru/get/15541/83186431.80f/0_a2852_7a2e97ba_S
Шаблон подготовила учитель русского языка и литературы Тихонова Надежда Андреевна
«Решу ЕГЭ» Образовательный портал для подготовки к ЕГЭ и ОГЭ. Режим доступа: http://mathb.reshuege.ru
http://sch-53.ru/files/director/GIA/2016/%D0%95%D0%93%D0%AD%202016.jpg
Автор и источник заимствования неизвестен

1. Геометрические задания В6 ЕГЭ
Презентацию выполнил:
ученик 11 класса
Бальвас Андрей
Преподаватель:
Бисимбаева Любовь Бакеевна
ГБОУ СОШ «ОЦ»
с. Августовки.
2013год
1
2. Содержание
Введение
Основная часть
1. Теоретический материал
1.1 Историческая справка
1.2 Справочный материал по теме « Окружность»
2. Задания В6 ЕГЭ
2.1 Решение заданий В6
2.1.1 Центральные и вписанные углы
2.1.2 Касательная, хорда, секущая
2.1.3 Окружность, вписанная в треугольник
2.1.4 Окружность, вписанная в четырехугольник
2.1.5 Окружность, описанная вокруг треугольника
2.1.6 Окружность, описанная вокруг четырехугольника
Заключение
Источники
2
3. Введение
Вопросы инновационных
технологий в
строительстве,
космонавтике, технике
невозможны без умения
производить необходимые
чертежи и вычисления,
которые требуют знания
важных и интереснейших
свойств окружности.
3
4. Из истории.
Самая простая из всех кривых линий
— окружность. Это одна из
древнейших геометрических фигур.
Философы древности придавали ей
большое значение. Согласно
Аристотелю, небесная материя, из
которой состоят планеты и звезды,
как самая совершенная, должна
двигаться по самой совершенной
линии — окружности. Сотни лет
астрономы считали, что планеты
двигаются по окружностям. Это
ошибочное мнение было
опровергнуто лишь в XVII веке
учением Коперника, Галилея,
Кеплера и Ньютона.
5. Теоретический материал
Окружностью называется фигура,
состоящая из всех точек
плоскости, находящихся от данной
точки на данном расстоянии.
Данная точка
называется центром окружности,
а отрезок, соединяющий центр с
какой-либо точкой окружности, —
радиусом окружности. Радиус
окружности равен половине
диаметра.
6. Касательная — Прямая, имеющая с окружностью только одну общую точку, а их общая точка называется точкой касания прямой и
Касательная к окружности перпендикулярна к
радиусу, проведенному в точку касания.
Отрезки касательных к окружности,
проведенных из одной точки, равны и
составляют равные углы с прямой, проходящей
через эту точку и центр окружности.
7. Хорда — отрезок, соединяющий две точки окружности. Хорда, проходящая через центр окружности, называется диаметром.
Диаметр (радиус),
перпендикулярный к хорде,
делит эту хорду и обе
стягиваемые ею дуги пополам.
Верна и обратная теорема:
если диаметр (радиус) делит
пополам хорду, то он
перпендикулярен этой хорде.
8.
Дуги, заключенные между
параллельными хордами, равны.
Если две хорды
окружности, AB и CD пересекаются
в точке M, то произведение отрезков
одной хорды равно произведению
отрезков другой хорды: AM•MB =
CM•MD.
9. Свойства окружности
Прямая может не иметь с окружностью общих
точек; иметь с окружностью одну общую точку
(касательная); иметь с ней две общие точки
(секущая).
Через три точки, не лежащие на одной прямой,
можно провести окружность, и притом только
одну.
Точка касания двух окружностей лежит на
линии, соединяющей их центры.
10. Теорема о касательной и секущей
Если из точки, лежащей вне окружности,
проведены касательная и секущая, то квадрат
длины касательной равен произведению
секущей на ее внешнюю часть: MC2 = MA•MB.
11. Теорема о секущих
Если из точки, лежащей вне окружности,
проведены две секущие, то произведение одной
секущей на её внешнюю часть равно
произведению другой секущей на её внешнюю
часть. MA•MB = MC•MD.
12. Углы в окружности
Центральным углом в окружности
называется угол с вершиной в ее центре.
Угол, вершина которого лежит на
окружности, а стороны пересекают эту
окружность, называется вписанным углом.
Любые две точки окружности делят ее на две
части. Каждая из этих частей
называется дугой окружности. Мерой дуги
может служить мера соответствующего ей
центрального угла.
Дуга называется полуокружностью, если
отрезок, соединяющий её концы, является
диаметром.
13. Свойства углов, связанных с окружностью
Вписанный угол либо равен половине
соответствующего ему центрального угла, либо
дополняет половину этого угла до 180°.
Углы, вписанные в одну окружность и
опирающиеся на одну и ту же дугу, равны.
14.
Вписанный угол, опирающийся
на диаметр, равен 90°
Угол, образованный касательной к
окружности и секущей, проведенной
через точку касания, равен половине
дуги, заключенной между его
сторонами.
15. Длины и площади
Длина окружности C радиуса R вычисляется по
формуле: C = 2 .
Площадь S круга радиуса R вычисляется по
формуле: S = 2.
Длина дуги окружности L радиуса R с
центральным углом ,измеренным в радианах,
вычисляется по формуле: L = R
Площадь S сектора радиуса R с центральным
углом в радиан вычисляется по формуле:
2
R
R
S=
R
16. Вписанные и описанные окружности Окружность и треугольник
Центр вписанной окружности — точка
пересечения биссектрис треугольника, ее
радиус r вычисляется по формуле: r =
где S — площадь треугольника, а —
полупериметр
17.
Центр описанной окружности — точка
пересечения серединных перпендикуляров, ее
радиус R вычисляется по формуле: R =
R=
здесь a, b, c — стороны треугольника, — угол,
лежащий против стороны a, S — площадь
треугольника.
центр описанной около прямоугольного
треугольника окружности лежит на
середине гипотенузы,
центр описанной и вписанной окружностей
треугольника совпадают только в том случае,
когда этот треугольник — правильный.
18. Окружность и четырехугольники
Около выпуклого четырехугольника можно
описать окружность тогда и только тогда, когда
сумма его внутренних противоположных углов
равна 180°.
+ = + = 180°
19.
В четырехугольник можно вписать окружность
тогда и только тогда, когда у него равны суммы
противоположных сторон
a+c=b+d
20.
около параллелограмма можно описать
окружность тогда и только тогда, когда он
является прямоугольником,
около трапеции можно описать окружность
тогда и только тогда, когда эта трапеция —
равнобедренная; центр окружности лежит на
пересечении оси
симметрии трапеции с серединным
перпендикуляром к боковой стороне,
в параллелограмм можно вписать окружность
тогда и только тогда, когда он является ромбом.
21. Центральные и вписанные углы
Радиус окружности равен 1.
Найдите величину тупого
вписанного угла,
опирающегося на хорду,
равную . Ответ дайте в
градусах.
Ответ: 135.
Решение. вписанный угол
дополняет половину
центрального угла,
опирающегося на ту же хорду,
до .
22.
Центральный угол
на
больше острого
вписанного угла,
опирающегося на ту же дугу
окружности. Найдите
вписанный угол. Ответ дайте
в градусах.
Ответ: 36.
Решение. вписанный угол
равен половине центрального
угла, опирающегося на ту же
дугу окружности, значит
23.
Дуга окружности
, не
содержащая точки ,
составляет
. А дуга
окружности
, не
содержащая точки ,
составляет
. Найдите
вписанный угол
. Ответ
дайте в градусах.
Ответ: 40.
Решение.
вписанный угол равен
половине дуги, на которую он
опирается.
24.
В окружности с
центром
и
–
диаметры. Вписанный
угол
равен . Найдите
центральный угол
.
Ответ дайте в градусах.
Ответ: 104.
Решение.
вписанный угол равен
половине центрального угла,
опирающегося на ту же дугу
окружности, значит,
25.
Радиус окружности равен 1.
Найдите величину острого
вписанного угла,
опирающегося на хорду,
равную
. Ответ дайте в
градусах.
Ответ: 45.
Решение.
По теореме синусов для
треугольника ACB имеем:
Следовательно, искомый угол
равен 45°.
26.
Найдите вписанный угол,
опирающийся на дугу,
которая
составляет окружности.
Ответ дайте в градусах.
Ответ: 36.
Решение.
27.
Угол
равен .
Градусная величина
дуги
окружности, не
содержащей точек
и
равна
. Найдите
угол
. Ответ дайте в
градусах.
Ответ: 20.
Решение.
,
центральный угол равен дуге,
на которую он опирается, а
вписанный угол равен
половине дуги, на которую он
опирается, значит
28.
В окружности с
центром
и
–
диаметры. Центральный
угол
равен
.
Найдите вписанный
угол
. Ответ дайте в
градусах.
Ответ: 35.
Решение.
вписанный угол равен
половине центрального угла,
опирающегося на ту же дугу
окружности, значит
29.
Найдите угол
, если
вписанные
углы
и
опираются
на дуги окружности,
градусные величины которых
равны
соответственно
и
.
Ответ дайте в градусах.
Ответ: 40.
Решение.
Угол между двумя секущими
равен полуразности
высекаемых ими дуг:
30.
Чему равен острый
вписанный угол,
опирающийся на хорду,
равную радиусу окружности?
Ответ дайте в градусах.
Ответ: 30.
Решение.
Рассмотрим
треугольник
. Он
равносторонний, так
как
.
Тогда
равен половине
центрального угла,
опирающегося на ту же хорду,
т. е.
31. Касательная, хорда, секущая
Найдите хорду, на которую
опирается угол 30° , вписанный
в окружность радиуса 3.
Ответ: 3.
Решение.
Угол <ACB=30°, значит,
<AOB=60° , т. к. является
центральным углом,
опирающимся на ту же хорду.
Соответственно, треугольник
AOB – равносторонний, так
какAO=OB=AB=R=3 .
32.
Найдите хорду, на которую
опирается угол 120° ,
вписанный в окружность
радиуса 3 .
Ответ: 3.
Решение.
вписанный угол дополняет
половину центрального угла,
опирающегося на ту же хорду, до
180°, значит, <AOB=2(180°120°)=120°. По теореме косинусов:
33.
Найдите хорду, на которую
опирается угол 90°,
вписанный в окружность
радиуса 1.
Ответ: 2.
Решение.
вписанный угол
является прямым,
значит, он опирается
на диаметр
окружности.
D=2R=2
34.
Хорда AB делит окружность
на две части, градусные
величины которых относятся
как 5:7. Под каким углом
видна эта хорда из точки C ,
принадлежащей меньшей
дуге окружности? Ответ
дайте в градусах.
Ответ: 105.
Решение.
Из точки C хорда АВ видна
под углом АCВ. Пусть большая
часть окружности равна 7x, тогда
меньшая равна 5x.
Значит, меньшая дуга
окружности равна 150°, а
большая — 210 °
Вписанный угол равен половине
дуги, на которую он опирается,
значит, опирающийся на
большую дугу угол АCВ равен
105°
35.
Угол ACO равен 28°, где O –
центр окружности. Его
сторона CA касается
окружности. Найдите
величину меньшей дуги
AB окружности,
заключенной внутри этого
угла. Ответ дайте в градусах.
Ответ: 62.
Решение.
касательная к окружности
перпендикулярна радиусу,
центральный угол равен дуге,
на которую он опирается,
значит, треугольник OAC –
прямоугольный и
36.
Через концы A , B дуги
окружности в 62° проведены
касательные AC и BC .
Найдите угол ACB . Ответ
дайте в градусах.
Ответ: 118.
Решение.
Угол между
касательной и хордой
равен половине
заключенной между
ними дуги. В
треугольнике ABC:
37.
Найдите угол ACO, если его
сторона CA касается
окружности, O – центр
окружности, а дуга меньшая
дуга окружности AB,
заключенная внутри этого
угла, равна 64° . Ответ дайте
в градусах.
Ответ: 26.
Решение.
касательная к окружности
перпендикулярна радиусу,
центральный угол равен дуге,
на которую он опирается,
значит, треугольник OAC –
прямоугольный и
38.
Касательные CA и CB к
окружности образуют угол
ACB , равный 122°. Найдите
величину меньшей дуги AB ,
стягиваемой точками касания.
Ответ дайте в градусах.
Ответ: 58.
Решение.
угол между
касательной и хордой
равен половине дуги,
стягиваемой хордой,
рассмотрим
треугольник ABC:
39.
Хорда AB стягивает дугу
окружности в 92°. Найдите
угол ABC между этой хордой
и касательной к окружности,
проведенной через точку B .
Ответ дайте в градусах.
Ответ: 46.
Решение.
угол между касательной и
хордой равен половине дуги,
стягиваемой хордой
40.
Угол ACO равен 24° . Его
сторона CA касается
окружности. Найдите
градусную величину большей
дуги AD окружности,
заключенной внутри этого
угла. Ответ дайте в градусах.
Ответ: 114.
Решение.
Касательная к окружности
перпендикулярна радиусу,
центральный угол равен дуге,
на которую он опирается,
значит, треугольник OAC –
прямоугольный и
41. Окружность, вписанная в треугольник
Найдите радиус окружности,
вписанной в правильный
треугольник, высота которого
равна 6.
Ответ: 2.
Решение.
Радиус круга, вписанного в
равносторонний треугольник,
равен одной трети высоты.
Поэтому он равен 2.
42.
Решение.
Радиус окружности,
вписанной в правильный
треугольник, равен 3 .
6
Найдите сторону этого
треугольника.
Ответ: 1.
43.
Радиус окружности,
вписанной в правильный
треугольник, равен 6.
Найдите высоту этого
треугольника.
Решение.
значит,
Ответ: 18.
44.
Сторона правильного
треугольника равна 3.
Найдите радиус окружности,
вписанной в этот
треугольник.
Ответ: 0,5.
Решение.
Радиус вписанной в
треугольник окружности
равен отношению площади к
полупериметру:
45.
В треугольнике ABC
AC=4 , BC=3, угол C равен
90°. Найдите радиус
вписанной окружности.
Ответ: 1.
Решение.
46.
Катеты равнобедренного
прямоугольного треугольника
равны 2 2 . Найдите
радиус окружности,
вписанной в этот
треугольник.
Ответ: 1.
Решение.
47.
Боковые стороны
равнобедренного
треугольника равны 5,
основание равно 6. Найдите
радиус вписанной
окружности.
Решение.
Для нахождения площади,
воспользуемся формулой
Герона:
тогда:
Ответ: 1,5.
48.
Окружность, вписанная в
равнобедренный треугольник,
делит в точке касания одну из
боковых сторон на два
отрезка, длины которых
равны 5 и 3, считая от
вершины, противолежащей
основанию. Найдите
периметр треугольника.
Ответ: 22.
Решение.
треугольники HOB и
KOB равны, т. к. являются
прямоугольными с общей
гипотенузой и равными
катетами, значит, HB=KB=3.
49.
К окружности, вписанной в
треугольник ABC, проведены
три касательные. Периметры
отсеченных треугольников
равны 6, 8, 10. Найдите
периметр данного
треугольника.
Ответ: 24.
Решение.
Отрезки касательных,
проведенных к окружности из
точек K,H,O,F,N,M ,
соответственно равны друг
другу. Поэтому
50.
Площадь треугольника равна
24, а радиус вписанной
окружности равен 2. Найдите
периметр этого треугольника.
Ответ: 24.
Решение.
Из формулы
находим,
что периметр описанного
многоугольника равен
отношению удвоенной
площади к радиусу вписанной
окружности:
51. Окружность, вписанная в четырехугольник
Найдите сторону квадрата,
описанного около окружности
радиуса 4.
Ответ: 8.
Решение.
52.
Найдите высоту трапеции, в
которую вписана окружность
радиуса 1.
Ответ: 2.
Решение.
53.
Острый угол ромба равен
30° . Радиус вписанной в этот
ромб окружности равен 2.
Найдите сторону ромба.
Ответ: 8.
Решение.
54.
Сторона ромба равна 1,
острый угол равен 30° .
Найдите радиус вписанной
окружности этого ромба.
Ответ: 0,25.
Решение.
55.
Около окружности описана
трапеция, периметр которой
равен 40. Найдите ее
среднюю линию.
Ответ: 10.
Решение.
В выпуклый четырехугольник
можно вписать окружность
тогда и только тогда, когда
56.
Боковые стороны трапеции,
описанной около окружности,
равны 3 и 5. Найдите
среднюю линию трапеции.
Ответ: 4.
Решение.
в выпуклый четырехугольник
можно вписать окружность
тогда и только тогда, когда
57.
В
четырехугольник ABCD впис
ана окружность,AB=10 ,
CD=16 . Найдите периметр
четырехугольника.
Ответ: 52.
Решение.
В выпуклый прямоугольник
можно вписать окружность
тогда и только тогда, когда
AB+CD=BC+AD Тогда
58.
Периметр четырехугольника,
описанного около
окружности, равен 24, две его
стороны равны 5 и 6. Найдите
большую из оставшихся
сторон.
Ответ: 7.
Решение.
Пусть большая из двух
оставшихся сторон имеет
длину x, тогда длина четвертой
стороны равна 24-4-5-x=13- x. В
выпуклый четырехугольник
можно вписать окружность тогда
и только тогда, когда суммы длин
его противоположных сторон
равны. В этом случае периметр
четырехугольника вдвое больше
суммы длин противоположных
сторон, а значит, стороны
длиной x и 13 − x, как и стороны
длиной 5 и 6, не могут быть
противоположными и являются
смежными.
Итак, напротив большей из
первой пары смежных сторон с
длинами x и 13 − x лежит
меньшая из второй пары
смежных сторон с длинами 5 и 6.
Поскольку суммы длин
противоположных сторон равны,
имеем:
59.
Три стороны описанного
около окружности
четырехугольника относятся
(в последовательном порядке)
как 1:2:3. Найдите большую
сторону этого
четырехугольника, если
известно, что его периметр
равен 32.
Решение.
в выпуклый прямоугольник
можно вписать окружность
тогда и только тогда, когда
AB+CD=BC+AD. Пусть
меньшая сторона
равна x тогда
значит, четвертая сторона
равна
Тогда большая сторона равна
Ответ: 12.
60.
Около окружности, радиус
которой равен 3, описан
квадрат. Найдите радиус
окружности, описанной около
этого квадрата.
Ответ: 4.
Решение.
Сторона квадрата вдвое
больше радиуса вписанной в
него окружности.
Поэтому AB= 2 8. Радиус
описанной вокруг квадрата
окружности равен половине
его диагонали. Поэтому
61. Окружность, описанная вокруг треугольника
Точки A, B, C,
расположенные на
окружности, делят ее на три
дуги, градусные величины
которых относятся как 1:3:5.
Найдите больший угол
треугольника ABC. Ответ
дайте в градусах.
Ответ: 100.
Решение.
пусть меньшая часть
окружности равна x тогда
x+3 x +5 x =360°, x=40°
Вписанный угол равен
половине дуги, на которую он
опирается, значит,
62.
Радиус окружности,
описанной около правильного
треугольника, равен 3 .
Найдите сторону этого
треугольника.
Ответ: 3.
Решение.
треугольникABC правильный
, значит, все углы равны по
60° .
63.
Радиус окружности,
описанной около правильного
треугольника, равен 3.
Найдите высоту этого
треугольника.
Ответ: 4,5.
Решение.
треугольник ABC правильны
й, значит, все углы равны
по 60°.
64.
Сторона правильного
треугольника равна . Найдите
радиус окружности,
описанной около этого
треугольника.
Ответ: 1.
Решение.
треугольник ABC правильны
й, значит, все углы равны по
60° .
65.
Высота правильного
треугольника равна 3.
Найдите радиус окружности,
описанной около этого
треугольника.
Ответ: 2.
Решение.
треугольник ABC правильны
й, значит, все углы равны по
60°.
66.
Гипотенуза прямоугольного
треугольника равна 12.
Найдите радиус описанной
окружности этого
треугольника.
Ответ: 6.
Решение.
вписанный угол
опирающийся на диаметр
окружности, является
прямым, значит, AB –
диаметр.
67.
В треугольнике ABC BC=6 ,
угол C равен 90°. Радиус
описанной окружности этого
треугольника равен 5.
Найдите AC.
Ответ: 8.
Решение.
Гипотенуза прямоугольного
треугольника является
диаметром описанной вокруг
него окружности, поэтому ее
длина 10. Тогда по теореме
Пифагора:
68.
В треугольнике ABC
AC=4 , BC=3, угол C равен
90°. Найдите радиус
описанной окружности этого
треугольника.
Ответ: 2,5
Решение.
вписанный угол,
опирающийся на диаметр
окружности, является
прямым, значит, AB –
диаметр.
69.
Радиус окружности,
описанной около
прямоугольного
треугольника, равен 4.
Найдите гипотенузу этого
треугольника.
Ответ: 8.
Решение.
вписанный угол,
опирающийся на диаметр
окружности, является
прямым, значит, AB–
диаметр.
70.
Боковая сторона
равнобедренного
треугольника равна 1, угол
при вершине,
противолежащей основанию,
равен 120°. Найдите диаметр
описанной окружности этого
треугольника.
Ответ: 2.
Решение.
Сумма двух равных углов при
основании треугольника
равна 60°, поэтому каждый из
них равен 30°. Тогда по
теореме синусов
71. Окружность, описанная вокруг четырехугольника
Меньшая сторона
прямоугольника равна 6. Угол
между диагоналями
равен 60°. Найдите радиус
описанной окружности этого
прямоугольника.
Решение.
рассмотрим
треугольник AOD. Он
равнобедренный,
т.к. AO=OD=R;
<A=<D=60° значит,
треугольник AOD –
равносторонний, тогда
Ответ: 6.
72.
Найдите радиус окружности,
описанной около квадрата со
стороной, равной 8 .
Ответ: 2.
Решение.
угол A является прямым, он
опирается на диагональ
BD, которая является
диаметром.
73.
Найдите радиус окружности,
описанной около
прямоугольника, две стороны
которого равны 3 и 4.
Ответ: 2,5.
Решение.
угол A является прямым, он
опирается на
диагональ BD которая
является диаметром
74.
Найдите диагональ
прямоугольника, вписанного
в окружность, радиус которой
равен 5.
Ответ: 10.
Решение.
угол A является прямым, он
опирается на
диагональ BD которая
является диаметром.
75.
Найдите сторону квадрата,
вписанного в окружность
радиуса 8 .
Ответ: 4.
Решение.
угол A является прямым, он
опирается на диагональ BD,
которая является диаметром.
76.
Углы A, B и C четырехугольн
ика относятся как 1:2:3 .
Найдите угол D, если около
данного четырехугольника
можно описать окружность.
Ответ дайте в градусах.
Ответ: 90.
Решение.
так как вокруг
четырехугольника можно
описать окружность, то сумма
его противоположных углов
равна 180°.
77.
Основания равнобедренной
трапеции равны 8 и 6. Радиус
описанной окружности равен
5. Найдите высоту трапеции.
Ответ: 7.
Решение.
высота
трапеции KH=KO+OH и OH
– высоты равнобедренных
треугольников DOC и AOB .
По теореме Пифагора:
78.
Боковая сторона
равнобедренной трапеции
равна ее меньшему
основанию, угол при
основании равен 60°, большее
основание равно 12. Найдите
радиус описанной
окружности этой трапеции.
Решение.
Окружность, описанная вокруг
трапеции, описана и вокруг
треугольника . Это треугольник
равнобедренный, угол при
вершине равен 120°, углы при
основании равны 30°. Найдем его
боковую сторону:
Тогда по теореме синусов:
Ответ: 6.
79.
Около трапеции описана
окружность. Периметр
трапеции равен 22, средняя
линия равна 5. Найдите
боковую сторону трапеции.
Ответ: 6.
Решение.
трапеция ABCD –
равнобедренная, т. к. вокруг
неё описана окружность.
80.
Четырехугольник ABCD впис
ан в окружность.
Угол ABC равен 105°,
угол CAD равен 35°. Найдите
угол ABD. Ответ дайте в
градусах.
Ответ: 70.
Решение.
вписанный угол равен
половине дуги, на которую он
опирается, значит
81. Заключение
Исследование мною заданий В6 ЕГЭ
показало, что свойства окружностей часто
применяются при решении
планиметрических задач и широко
используются на практике.
82. Источники
http://www.univer.omsk.su/omsk/Edu/Rus
anova/circles.htm
http://reshuege.ru/?redir=1
1
Решение задач на окружность (планиметрия на ЕГЭ) Учебное пособие Анжеро-Судженск, 2009 Материал сопровождается эффектами анимации – Word 2007
2
ЗАДАЧИ. Окружность и её элементы. Окружность вписанная и описанная. 4. Окружность, вписанная в ромб АВСD, касается стороны АВ в точке М, причем АМ : МВ = 2 : 3. Найдите радиус окружности, если площадь ромба равна В ромб АВСD в писана окружность радиуса 12. Она касается стороны ВС в точке Р, причем СР : РВ = 9 : 16. Найдите площадь ромба. 1. Треугольник АВС вписан в окружность с центром в точке О и радиусом 4. Найдите площадь треугольника АВС, если угол В равен 40, угол С равен Средняя линия прямоугольной трапеции равна 9, а радиус вписанной в нее окружности равен 4. Найдите большее основание трапеции г 2 8. Длины боковых сторон трапеции равны 6 и 10. известно, что в трапецию можно вписать окружность, а средняя линия делит её на части, площади которых относятся как 5 : 11. Найдите длину большего основания трапеции. 6. Прямоугольная трапеция описана около окружности радиуса 2. Найдите площадь трапеции, если одно из её оснований больше другого основания на 3. (пр. 2009). 7. Около трапеции описана окружность радиуса 7,5. Её большее основание образует с боковой стороной угол, синус которого равен 2/3, а диагональ образует с меньшим основанием угол, синус которого 0,6. Найдите площадь трапеции. (пр. 2009). 9. На стороне ВА угла АВС, равного 30, взята такая точка Д, что АД = 2 и ВД = 1. Найдите радиус окружности, проходящей через точки А, Д и касающейся прямой ВС. (1 или 7) 2. Около треугольника АВС описана окружность с центром О, угол АОС равен 60. В треугольник АВС вписана окружность с центром М. Найдите угол АМС.
3
Из точки М к окружности, радиус которой равен 4, проведены касательная, касающаяся окружности в точке С, и секущая, проходящая через центр О окружности и пересекающая её в точках А и В так, что МА = ОА. Точка К – середина дуги АС окружности. Найдите площадь треугольника МОК. (8) О В А / / К ІІ М С S МОК — ? Почему ? Достаточно ли данных, чтобы найти S МОК ? По какой формуле ? Да ! S МОК = ½ ОМ · ОК · sin MOK. S = 8 Почему ? О А В С Треугольник АВС вписан в окружность с центром в точке О и радиусом 4. Найдите площадь треугольника ВОС, если угол В равен 40, угол С равен 35. S — ? Для определения площади ВОС надо знать угол ВОС. S ВОС = ½ ОВ ОС · sin ВОС. Углы АСВ и АВС вписанные, то дуги АВ и АС 70 и 80. Дуга как сумма дуг АВ и АС и центральный угол 150. S ВОС = ½ · 4 4 · sin 150, S ВОС = 8 · sin ( ), S ВОС = 8 · cos 60 = 4.
4
. 4 О М А С В Угол АВС = 30 — вписанный, опирается на дугу АС в 60. Тогда сумма углов АСВ и САВ равна 150 ( в АСВ). М — центр вписанной окружности — точка пересечения биссектрис углов АМС. Тогда в АМС искомый угол АМС равен 105. Угол АОС = 60 — центральный угол (О — центр описанной окружности около АСВ). Тогда и дуга АС содержит 60. Половина суммы углов АСВ и САВ равна 75. (в АМС). 2. Около треугольника АВС описана окружность с центром О, угол АОС равен 60. В треугольник АВС вписана окружность с центром М. Найдите угол АМС. ? 60
5
В О М А К 1)Проведём диаметр КР в точку касания, С 2) Отметим точку С. По условию АС:СВ=3:1. Р Имеем: окружность, касательная, диаметр, радиус, хорды, секущая – для решения нужны теоретические знания о них. МК — касательная, связана с данными на секущей МВ. МА = 3 – внешняя часть. Зная АВ, находим АС и СВ (из отношения) АС и СВ дают выход на хорды АВ и КР. Теорема о равенстве произведений длин отрезков, пересекающихся хорд Квадрат касательной равен произведению секущей на её внешнюю часть 5 МА = 3 3) Заметим: МВ – секущая, МК² = МВ · МА. КС·СР = АС · СВ, (А) Из точки М к окружности с центром О проведена касательная МК равная 33 и прямая, пересекающая окружность в точках А и В. Причём МА = 3. Диаметр в точку касания делит хорду АВ в точке С, как 3:1 и ОС = 13. Найдите радиус окружности. 3 к 1 к АВ = 8. АС = 3 к, СВ = 1 к. к = 2. АС = 6, СВ = 2. где КС = КО + ОС, СР = ОР — ОС, а КО = ОР = R R = 5 R — ? МА – внешняя часть секущей, КР и АВ — хорды окружности. выход на МВ и АВ Теорема. Какая ?
6
С В А Д 3. В ромб АВСD вписана окружность радиуса 12. Она касается стороны ВС в точке Р, причем СР:РВ=9:16. Найдите площадь ромба. 6 Р 12 9 к 16 к О АВСД — ромб, его свойства. Окружность вписана в ромб. Окружность касается всех сторон ромба. Стороны равны, диагонали перпендикулярны. Радиус в точку касания. Радиус перпендикулярен касательной. ВОС — прямоугольный Радиус РО – высота ВОС из вершины прямого угла. Высота из вершины прямого угла в прямоугольном. Есть среднее пропорциональное отрезков гипотенузы ОР² = СР · РВ, найдём К ! — КЛЮЧ К РЕШЕНИЮ !!! Далее легко находим СР, РВ и ВС. РТ = 2 ОР (24). S АВСД = ВС · РТ, S = 600. Пусть к приходится на одну часть, то (см. рисунок) Т
7
5. Средняя линия прямоугольной трапеции равна 9, а радиус вписанной в нее окружности равен 4. Найдите большее основание трапеции. (2009 г) R = а — 4 в — 4 а — 4 в — а а + в = 18 4 СД = (а — 4) + (в – 4), СД = а + в — 8, СД = , СД = 10. По т. Пифагора НД = 6. а + в = 18, в — а = 6. в = 12. С Д А В М N MN = ½ (а + в), 0 Т K Р Н С другой стороны, НД = в – а (см. чертёж), то НСД – прямоугольный, СН = 8, СД = 10. в — а = 6. Пусть основания а – верхнее, в – нижнее — ? Запишем по свойству средней линии трапеции: Касательные из одной точки равны: выразим СД. Чтобы найти в, надо знать а и другие отрезки на в. 2) Выразить СД можно и из условия: У четырёхугольника описанного около окружности равны суммы противоположных сторон: АВ + СД = АД + ВС, 8 + СД = а + в, СД = (а + в) — 8, СД = 10. С построения высоты СН решение то же: НСД прямоугольный. НД = 6. Построим высоту СН. Имеем… 7
8
Известны синусы двух углов и радиус описанной окружности. А В С Д 7. Около трапеции описана окружность радиуса 7,5. Её большее основание образует с боковой стороной угол, синус которого равен 2/3, а диагональ образует с меньшим основанием угол, синус которого 0,6. Найдите площадь трапеции. (пр. 2009). (48) О Н АВД и ВСД — также вписаны в эту окружность По следствию из т. СИНУСОВ: ВД : Sin ВАД = 2R, ВД = 2R Sin ВАД, ВД = 15· 2/3, ВД = 10. СД : Sin ДВС = 2R, СД = 2R Sin ДВС, СД = 15· 0.6, СД = 9 = АВ. Проведём высоту трапеции ВН. АВН По определению синуса угла А: Sin А = ВН: АВ, ВН = 2/3 9 = 6. В НВД по т. Пифагора НД = 8. Имеем высоту и нижнее основание трапеции. Нетрудно найти и верхнее основание: НД – АН, а затем и площадь трапеции. Но надо знать АН – по т. Пифагора в АВН. Приём «удачных» дополнительных построений (см. рисунок) Тогда S АВСД равна пощади прямоугольника со сторонами 6 и 8 ( АВН = ДСК), 48. К 8 Трапеция ABCD вписана в окружность. Найдите среднюю линию трапеции, если ее большее основание АD равно 15, синус угла ВАС равен 1/3, синус угла АВД равен 5/9. (12)
9
8. Длины боковых сторон трапеции равны 6 и 10. Известно, что в трапецию можно вписать окружность, а средняя линия делит её на части, площади которых относятся как 5 : 11. Найдите длину большего основания трапеции. О А В С Д М К S МВСК : S АМКД = 5 : 11 АД — ? 6 10 H Р Приём: пусть на одну часть приходится К, тогда: S МВСК = 5 к, S АМКД = 11 к, С другой стороны, площадь АВСД по формуле: ½ (ВС + АД) · РН = 16 к. Где МК = ½ (ВС + АД). МК – средняя линия ВС + АД = АВ + СД -? Четырёхугольник описан около окружности, то равны суммы противоположных сторон То ½ ·16 · РН = 16 к. Тогда высота РН = 2 к, ОН = к S АМКД = ½ (АД + МК) ОН = 11 к, Для всей трапеции АВСД: S АВСД = 16 к ½ (АД + 

10
9. На стороне ВА угла АВС, равного 30, взята такая точка Д, что АД = 2 и ВД = 1. Найдите радиус окружности, проходящей через точки А, Д и касающейся прямой ВС. (1 или 7) 10 В А С 30 Е О К Р R R R ДА = 2 ВД = 1 Д ДА — хорда. Диаметр перпендикулярный хорде АД делит её пополам, 1 1 Радиус ОК в точку касания перпендикулярен касательной ВС. Пусть ОК = R. R = ОК ОКЕ прямоугольный угол КЕО 60 где ЕО = ЕР + РО ЕР ВЕР прямоугольный угол 30, ВР = 1 РО ОДР прямоугольный ОД = R, ДР = 1 (по определению синуса ОК = ЕОsin60) (по определению тангенса ЕР = ВР·tg30) (по т. Пифагора) Р – середина (ДР = РА = 1). 60 (2tg30 + R² — 1)·sin60 = R
11
Вывод ? * Окружности 10 и 17 пересекаются в точках А и В. Найдите расстояние между центрами окружностей, если АВ = 16. R = 17 r = 10 (21, 9) А В О М А В О М К К АК = 8 КВ = 8 Задача очень проста! Почему АК = КВ ? или Почему точка К лежит на ОМ ? Вопрос лишь в том: Проведите радиусы ОВ и МВ. Что это даёт ? ДА ! Равнобедренные ВОА и ВМА. Причём с общим основанием АВ. ОК и МК и высоты, и медианы. ОК из ОАК и МАК по т. Пифагора. Но почему же два ответа ? Задача с исследованием ! Сравните чертёж… Решение то же, только МК – ОК. ОМ = 21. АВ = 16 ОМ — ?
Презентация «Планиметрические задачи на окружность на ОГЭ и ЕГЭ»
Подписи к слайдам:
Планиметрические задачи на окружность наОГЭ и ЕГЭ
- подготовила учитель математики
- МБОУ СШ №2
- Бессонова Тамара Владимировна
- — построение геометрических конструкций;
- — формулировка свойств, относящихся к данной геометрической конструкции;
- — подбор и решение ключевых задач,
- — подбор и решение сложных задач.
- Обучение решению геометрических задач при подготовке к ОГЭ и ЕГЭ включает в себя следующее:
Пересекающиеся в точка А и В окружности имеют общую хорду АВ.
- Пересекающиеся в точка А и В окружности имеют общую хорду АВ.
- Общая хорда перпендикулярна линии центров и делится ею пополам.
- Трапеция вписана в некоторую окружность тогда и только тогда, когда она является равнобедренной.
- Если два угла равны и лежат по одну сторону от прямой, соединяющей две общие точки, лежащих на сторонах угла,то около этих точек и вершин углов можно описть окружность
- «Ключевые задачи на окружность»
- А
- В
- С
- 2
- Угол А+угол С=180-уголВ
- 1
- Угол 1+угол2=90-1/2 углаВ
- О
- Угол АОС=90+1/2 угла В
- Угол между биссектрисами треугольника
- Вписанная окружность с центром О треугольника АВС касается сторон АВ и АС в точках М и N соответственно. Прямая М N пересекает биссектрису угла В в точке Р.Докажите что точки N, О, С и Р лежат на одной окружности
- А
- В
- С
- М
- N
- Р
- О
- .
- Угол ВОС=90+1/2 угла А
- Угол СОР=90-1/2угла А
- Угол МNА=углу СNР=90-1/2 угла А
- Точки N,Р,С,О лежат на одной окружности
- Угол между хордами двух касающихся окружностей
Задачи ЕГЭ
- Две окружности касаются внешним образом в точке К. Прямая АВ касается первой окружности в точке А, а второй – в точке В. Прямая ВК пересекает первую
- окружность в точке D, прямая АК пересекает вторую
- окружность в точке С.
- а) Докажите, что прямые
- AD и BC параллельны.
- б) Найдите площадь
- треугольника ABK, если
- известно,
- что радиусы окружностей
- равны 4 и 1.
Решение. а)
б)
- ΔAKD ~ΔBKC
- (по двум углам)
- AK – общая высота
- ΔAВD и ΔAKВ
- Ответ. 3,2
- Около остроугольного треугольника ABC описана окружность с центром O.
- На продолжении отрезка AO за точку O отмечена точка K так, что ∠BAC + ∠AKC = 90°.
- а) Докажите, что четырёхугольник OBKC вписанный.
- б) Найдите радиус окружности, описанной вокруг четырёхугольника OBKC, если cos∠BAC= =3/5, а BC = 48.
- Решение.
- a) Пусть ∠ВАС = х; ∠ВOС = 2∠АВС = 2х (как центральный и вписанный углы с общей дугой ВС); ∠АКС = ∠ОКС = 90° − х
- ∆ВOС – р/б; ОВ = ОС (радиусы) ⟹
- ∠ОВС = ∠ОСВ = (180° – 2х) : 2 = 90° − х
- ⟹ ∠ОКС = ∠ОВС (вписанные в окружность с общей дугой ОС)
- ОВКС – вписанный четырёхугольник.
- б)
- O
- А
- С
- В
- К
- х
- По теореме синусов:
- Биссектриса угла ADC параллелограмма ABCD пересекает прямую AB в точке E. В треугольник ADE вписана окружность, касающаяся стороны AE в точке K и стороны AD в точке T .
- а) Докажите, что прямые KT и DE параллельны.
- б) Найдите угол BAD, если известно, что AD = 6 и KT = 3.
- Решение.
- a) ∠АDE = ∠СDE = ∠АED (как накрест лежащие при параллельных прямых
- AB и DC и секущей DE)
- ∆AOT = ∆AOK (по общей гипотенузе и катетам ОТ = ОК = r) ⟹ AT = AK ⟹
- ∆ATK – р/б ⟹ ∠ATK = ∠AKT
- ∆AKT ~ ∆AED (по общему углу А и двум прилежащим сторонам) ⟹ ∠ATK =
- = ∠ADE – соответственные ⟹ KT ∥ DE
- O
- А
- С
- В
- Р
- E
- D
- T
- K
- б) ∆ADE – р/б; AD = AE = 6, АР – высота и медиана ⟹ DP = EP. Пусть АТ = АК = х, тогда TD = PD = 6 – x, т. к. ∆AKT ~ ∆AED ⟹ AT : AD = KT : ED, x : 6 = 3 : 2(6 – x) ⟹ x = 3.
- Значит, ∆AKT и ∆AED – равносторонние, ∠BAD = 60°.
- Ответ: 60.
- Окружность, вписанная в треугольник ABC, площадь которого равна 66, касается средней линии, параллельной стороне BC. Известно, что BC = 11. Найдите сторону AB.
- С
- B
- A
- N
- М
- O
- Решение.
- Пусть АВ = х, АС = у, тогда Р∆АВС = АВ + АС + ВС = х + у + 11;
- MN = 5,5 (как средняя линия ∆АВС).
- MNCB – трапеция, в которую вписана окружность ⟹
- MN + BC = MB + CN = ½ (x + y) = 5,5 + 11 = 16,5 ⟹ х + у = 33;
- P ∆АВС = 33 + 11 = 44.
- По формуле Герона:
- Получим систему:
- Ответ: 13 или 20.
- 25
- Окружность ω1 касается стороны AC и продолжений сторон AB и BC треугольника ABC за точки A и C соответственно; M − точка её касания с прямой BC. Окружность ω2 касается стороны AB и продолжений сторон AC и BC за точки A и B соответственно; N − точка её касания с прямой BC.
- a) Докажите, что BM = CN
- б) Найдите расстояние между центрами окружностей ω1 и ω2, если AC = , AB = , BC = 6.
- Решение.
- б) BC2 = AC2 + AB2 =
- Значит, ∆ABC – п/у, А = 90°.
- CL = CA + AL = + y; BS = BA + AS = + x
- Радиус вневписанной окружности:
- O2
- А
- В
- С
- O1
- r2
- М
- r1
- К
- N
- P
- L
- S
- r2
- r1
- Ответ:
- Подведем итог.
- Научить решать учащихся геометрические задачи это значит не только подготовить их к хорошей сдаче экзамена, но это значит научить учащихся логически мыслить, доказательно отстаивать свою точку зрения, уметь творчески подходить к любому делу.
В презентации использован технологический прием Г.О.Аствацатурова «Анимированные сорбонки с удалением». Для того, чтобы получить решение, надо нажать на сорбонку. Рассмотрены 7 задач с их решениями.
Понравилось? Сохраните и поделитесь:
По кнопке ниже вы можете скачать методическую разработку «Решу ЕГЭ: вписанные и описанные окружности (часть 1)» категории «ЕГЭ по математике» бесплатно. Будем благодарны, если вы оставите отзыв или посмотрите еще другие материалы на нашем сайте. Характеристики документа: «презентация».
Загрузка началась…
Понравился сайт? Получайте ссылки
на лучшие материалы еженедельно!
Подарок каждому подписчику!



































