Презентация задачи на совместную работу егэ

Подготовка к егэ

Задачи на совместную работу

Задачи на работу решаются с помощью одной-единственной формулы:

A — работа,

t — время,

P — производительность

Правила решения задач на работу

• 1. А = р∙t, из этой формулы легко найти t или p.
• 2. Если объем работы не важен в задаче и нет никаких данных, позволяющих его найти — работа принимается за единицу. Построен дом (один), покрашен забор (один), наполнен резервуар. А вот если речь идет о количестве кирпичей, количестве деталей, литрах воды —  работа как раз и равна этому количеству.
• 3. Если трудятся двое рабочих (два экскаватора, два мастера, Даша и Маша…) или трое (не важно) — их производительности складываются. Очень логичное правило.
• 4. В качестве переменной х удобно взять (в абсолютном большинстве задач) именно производительность.

Задача 1

• Заказ на 240 деталей первый рабочий выполняет на 1 час быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 1 деталь больше?

Первый рабочий выполнил заказ на   час быстрее. Следовательно, времени он затрачивает на 1 час меньше, чем второй, то есть t 1     на 1   меньше, чем t 2 ,   значит

Очевидно, производительность рабочего не   может быть отрицательной величиной.   Значит, отрицательный корень не   подходит .

Ответ: 15

Задача 2

• На изготовление 40 деталей первый рабочий затрачивает на 6 часов  меньше, чем второй рабочий на изготовление 70 таких же деталей. Известно, что первый рабочий за час делает на 3 детали больше, чем второй. Сколько деталей в час делает второй рабочий?

• Сравнение будем проводить по времени. Сказано, что первый затрачивает на 6 часов меньше, чем второй. Значит:

Ответ: 7

Задача 3

• Первая труба пропускает на 4 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает первая труба, если резервуар объемом 192 литра она заполняет на 4 минуты дольше, чем вторая труба?

• Первая труба заполняет резервуар на 4 минуты дольше, чем вторая. То есть времени уходит больше

Ответ: 12

Задача 4

• Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 19 часов. Через 1 час после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?

Сразу отметим, что производительность каждого рабочего

1/19 (заказа в час). Заказ это работа, она равна 1.

• Сумма сделанных ими объёмов работы составляет всю работу, равную 1.

Совместно рабочие работали 9 часов.

Значит, на весь заказ ушло 9 + 1 = 10 часов .

Ответ: 10

Задача 5

• Один мастер может выполнить заказ за 36 часов, а другой — за 12 часов. За сколько часов выполнят заказ оба мастера, работая вместе?

Пусть х это время, за которое мастера выполнят работу вместе.

Производительность первого 1/36 (заказа в час),

второго 1/12 (заказа в час),  этот  вывод мы сделали из условия задачи.

• При совместной работе производительности складываются:

Ответ: 9

Задача 6

• В помощь садовому насосу, перекачивающему 9 литров воды за 4 минуты, подключили второй насос, перекачивающий тот же объем воды за 6 минуты. Сколько минут эти два насоса должны работать совместно, чтобы перекачать 30 литров воды?

Сразу,  исходя из условия, можно определить производительности насосов: 

у первого 9/4 (литра в минуту), у второго 9/6 (литра в минуту).

Пусть совместно они будут работать х  минут. 

Ответ: 8

Задача 7

• Петя и Ваня выполняют одинаковый тест. Петя отвечает за час на 12 вопросов теста, а Ваня — на 20. Они одновременно начали отвечать на вопросы теста, и Петя закончил свой тест позже Вани на 90 минут. Сколько вопросов содержит тест?

В данной задаче производительности даны:

у Пети 12 (вопросов в час), у Вани 20.

Количество вопросов это и есть работа, принимаем за её за х.

• Петя закончил свой тест на 90 минут позже Вани, то есть Петя затратил больше времени.
• Не забываем перевести минуты в часы: 90 минут это 1,5 часа.

Ответ:45

Задача 8

• Через одну трубу бассейн наполняется за 7 часов, а через другую опустошается за 8 часов. За какое время бассейн будет наполнен, если открыть обе трубы?

1 труба

p

1

2 труба

t

7

A

7

1

Вместе

1

7

?

8

1

?

1

• Сначала найдем производительность труда совместной работы обеих труб за один час. Поскольку одна труба бассейн наполняет, а другая — опустошает, производительность совместной работы равна разности производительности первой и второй труб:

Теперь найдем время, за которое бассейн будет наполнен при открытии обеих труб одновременно. Чтобы найти время работы, надо объем работы разделить на производительность труда:

Ответ:56

Готовимся к ЕГЭ Несколько типов «задач на работу»

Подготовила

Учитель математики первой категориии

Гимназии №96

Бухараева Лариса Юрьевна

Задачи на работу  делятся на два типа:

• задачи, в которых  выполняется  раздельная работа  – эти задачи решаются аналогично задачам на движение.
• задачи на совместную работу.

Раздельная работа

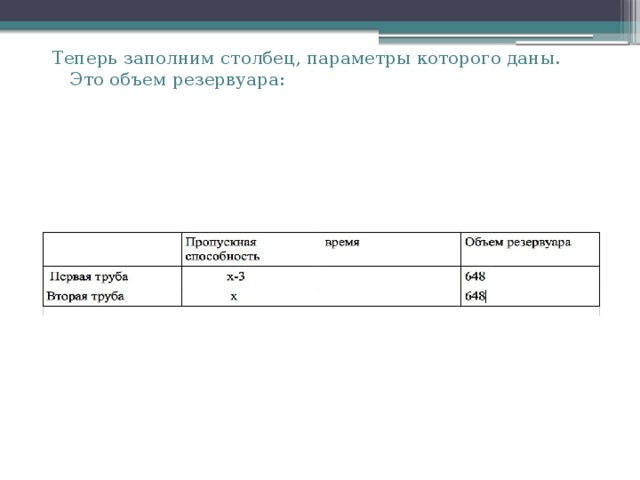
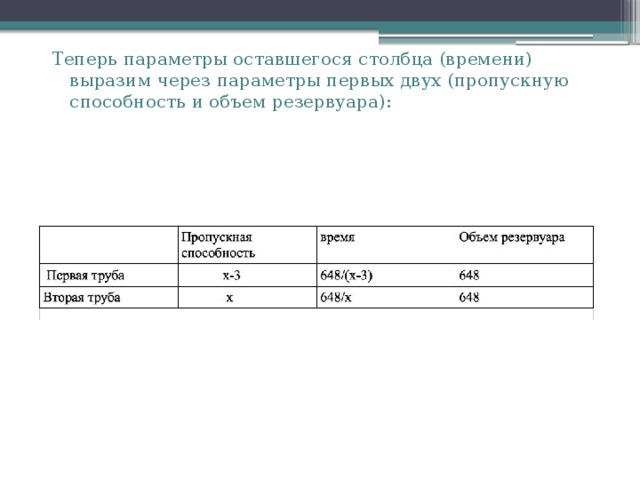
• Первая труба пропускает на 3л воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объемом 648 л она заполняет на 3 мин. быстрее, чем первая труба?

В  задачах  мы имеем дело с тремя параметрами:

• пропускная способность трубы(А/t)  –    объем жидкости, который труба пропускает в единицу времени (л/мин);
• объем резервуара(A) , который необходимо заполнить, или, наоборот, освободить (л);
• Время(t)  (мин)

Эти параметры связаны таким соотношением:

A(работа)=A/t(производительность)*t(время)

В задаче спрашивается, сколько литров воды в минуту пропускает вторая труба – эту величину мы и примем за  . Поскольку по условию задачи первая труба пропускает на 3л воды в минуту меньше, чем вторая, то пропускную способность первой  трубы обозначим  .

Теперь заполним столбец, параметры которого даны. Это объем резервуара:

Теперь параметры оставшегося столбца (времени) выразим через параметры первых двух (пропускную способность и объем резервуара):

Составим уравнение:

Приравняем числитель к нулю, раскроем скобки и приведем подобные члены. Получим уравнение:

-24 —  не подходит по смыслу задачи.

Ответ: 27 л/мин.

Задача на совместную работу .

• Если в задаче встречаются слова «выполнили работу вместе» или слова «совместная работа», значит это  задача на совместную работу .

Объем работы , если он не указан отдельно,  принимаем равным 1 .

Вводим два неизвестных:

х – время выполнения всей работы кем-то (или  чем-то) первым

y — время выполнения всей работы кем-то (или  чем-то) вторым.

(В некоторых задачах «выгоднее» принять за неизвестные производительность)

Тогда

1/x  – производительность кого-то (или чего-то) первого

1/y  — производительность кого-то (или чего-то) второго

И в этом месте появляется параметр, которого не было в задачах на раздельную работу, а именно –  совместная производительность 

совместная производительность равна:

1/x+1/y 

Даша и Маша пропалывают грядку за 12 минут, а одна Маша — за 20 минут. За сколько минут пропалывает грядку одна Даша?

Объем работы = производительность * время.

• Про Машу нам все известно: время ее работы равно 20, следовательно, ее производительность равна 1/20.
• Пусть Даша пропалывает грядку за х минут, тогда ее производительность равна 1/x.
• Тогда  совместная производительность  равна:

1/20+1/x

Объем работы  примем равным 1.

Решим уравнение:

Классическая задача на совместную работу:

Первая труба наполняет резервуар на 6 минут дольше, чем вторая. Обе трубы наполняют этот же резервуар за 4 минуты. За сколько минут наполняет этот резервуар одна вторая труба?

У нас 2 неизвестных, поэтому  будем составлять систему из двух уравнений.

По условию задачи,  первая труба наполняет резервуар на 6 минут дольше, чем вторая , следовательно время работы первой трубы на 6 минут больше, чем второй:

1) x=y+6

Обе трубы наполняют этот же резервуар за 4 минуты , следовательно, время совместной работы равно 4 минуты. Получаем второе уравнение системы:

2) (1/x + 1/y)*4=1

Получили систему уравнений:

-4 – не подходит по смыслу. Ответ: 6

Текстовые задачи
на совместную работу

Подготовка к ЕГЭ и ОГЭ

Учитель математики высшей категории

Манаенко Светлана Григорьевна

Муниципальное бюджетное общеобразовательное учреждение

«Обоянская средняя общеобразовательная школа №2»

«Решение задач – специфическое достижение разума, разум же – особый дар, которым наделён человек»
Д. Пойа

Задачи на работу — задачи на прямую или обратную зависимость

• Производительность труда, время работы и объем выполненной работы за данное время – это тройка пропорциональных величин.
• Зависимости бывают:

─ прямые – когда изменение одной величины приводит к изменению второй величины в ту же самую сторону (например, если увеличить производительность деталей, то и общий объём выполненной работы увеличится)
─ обратные – когда увеличение одной величины приводит к уменьшению другой (например, если нужно сделать определённое количество деталей, то при увеличении производительности, время, затрачиваемое на работу, уменьшится).

Задачи на работу делятся на две группы:

1) задачи, в которых выполняемый объем работы известен или его нужно определить (например, количество изготовленных деталей, количество гектар вспаханной земли, объем бассейна и т.д.);
2) задачи, в которых вообще не сказано, какая работа выполняется или эта работа задана неявно (в таких задачах зачастую задано только время).
Типы задач на работу
— задачи, в которых выполняется раздельная работа — эти задачи решаются аналогично задачам на движение;
— задачи на совместную работу.
Пример задачи на раздельную работу
№1. (из открытого банка заданий ЕГЭ -2019, ФИПИ) Первая труба пропускает на 2 литра воды в минуту меньше, чем вторая. Сколько литров воды в минуту пропускает вторая труба, если резервуар объёмом 130 литров она заполняет на 4 минуты быстрее, чем первая труба заполняет резервуар объёмом 136 литров?

	v, л/мин.	V, л	t, мин
1 труба
2 труба

№2. (из открытого банка заданий ЕГЭ -2019, ФИПИ)
На изготовление 540 деталей первый рабочий затрачивает на 12 часов меньше, чем второй рабочий на изготовление 600 деталей. Известно, что первый рабочий за час делает на 10 деталей больше, чем второй. Сколько деталей в час делает первый рабочий?
Решение:

	Р, дет/час	А, дет	t, ч
1
2

Алгоритм решения задач
на совместную работу
1. В задачах на совместную работу три параметра:
— время – t (время, за которое выполняют работу);
— объём работы – А (объем работы, выполняемый за единицу времени),
— производительность – Р (скорость работы),
Производительность труда, время работы и объем выполненной работы за данное время – это тройка пропорциональных величин.
Три величины связаны между собой, следующими формулами:
1) Работа = производительность • время, A= P • t;
2) Производительность = работа : время, P= A : t;
3) Время = работа : производительность, t = A/ P .
Алгоритм решения задач
на совместную работу
2. Если объем работы не важен и нет никаких данных, позволяющих его найти – работу принимаем за единицу. А = 1
Если трудятся два рабочих (два экскаватора и т.д.) – их производительности складываются. P= P1+ P2
В качестве переменной удобно взять производительность.

Алгоритм решения задач
на совместную работу
3. Во время решения задач на совместную работу нужно ответить на следующие вопросы (рассмотрим на примере рабочих):
― Что принято за время выполнения работы первым рабочим?
― Что принято за время выполнения работы вторым рабочим?
― Какова производительность труда первого рабочего?
― Какова производительность труда второго рабочего?
― Чему равна совместная производительность труда?
― Чему равно время, за которое выполнят задание, работая вместе?
Алгоритм решения задач на совместную работу
Объём работы принимаем равным 1.
Пусть х – время выполнения некоторой работы первым рабочим,
у – время выполнения этой же работы вторым рабочим.
Тогда 1/х – производительность труда первого рабочего,
1/у – производительность труда второго рабочего,
1/х + 1/у — совместная производительность труда.
1/(1/х+1/у) = ху/(х+у) – время, за которое они выполнят задание, работая вместе.

Рекомендации к решению задач:

Что необходимо знать?

1. Объём, выполняемой работы! (A)

3. Производительность! (P или N)

2. Время работы! (t)

Что необходимо делать?

• Задачу прочти
• Немного помолчи
• Про себя повтори
• Ещё раз прочти
• Нет объёма работы, за 1 прими
• Данные в таблицу занеси
• Уравнение запиши
• Уравнение реши!
• На вопрос задачи ответь!

Что необходимо делать?

1. Мастер, работая самостоятельно, может изго-

товить партию из 200 деталей за некоторое время. Ученик за это же время может изготовить только половину всех деталей. Работая вместе, они могут изготовить всю партию деталей за 4 ч. За какое время мастер может изготовить все детали, работая самостоятельно?

мастер

ученик

Время

(t)

х

200

Объем

работы

100

Производительность

Объем работы = производительность⋅ время.

х

4

вместе

200

Составим и решим

уравнение.

⋅

=

Ответ: 6 часов.

2.Один мастер может выполнить заказ за 12 часов, а другой – за 18 часов. За сколько часов выполнят заказ эти мастера, работая вместе?

мастер

ученик

t

12

1

А

1

N

Объем работы = производительность⋅ время.

18

х

вместе

1

⋅

=

Ответ: 7,2 часа.

Составим и решим

уравнение.

3. Первая труба и вторая, работая вместе, наполняют бассейн за 36 часов, первая и третья – за 30 часов, вторая и третья – за 20 часов. За сколько часов наполнят бассейн три трубы, работая вместе?

1 т

2 т

х

1

1

Объем работы = производительность⋅ время.

у

z

Вместе

1 и 2

1

Ответ: 18 часов.

3 т

+

36

1

Вместе

1 и 3

1

+

Вместе

2 и 3

+

1

30

20

⋅36=

+

1

+

⋅30=

1

+

⋅20=

1

А

P

t

3. Первая труба и вторая, работая вместе, наполняют бассейн за 36 часов, первая и третья – за 30 часов, вторая и третья – за 20 часов. За сколько часов наполнят бассейн три трубы, работая вместе?

2 способ решения:
Арифметический способ

Задача 4. Мастер может изготовить 360 деталей за 6 дней, а ученик — за 12 дней. За сколько дней мастер и ученик могут изготовить это количество деталей, работая одновременно?
Решение.
Сначала найдём производительность мастера и ученика по отдельности, далее, найдём их общую производительность, затем сможем найти время, за которое они вместе смогут сделать всю работу.
1) 360:6 = 60 (дет.) – производительность мастера за один день.
2) 360:12 = 30 (дет.) – производительность ученика за один день.
3) 30+60 = 90 (дет.) – производительность мастера и ученика за один день, если они будут работать вместе.
4) 360:90 = 4 (дня) – количество дней, которое нужно мастеру и ученику на совместное изготовление всего количества деталей.
Ответ: 4 дня.
Арифметический способ

Задача 5. Первый насос наполняет бак за 20 минут, второй — за 30 минут, а третий — за 1 час. За сколько минут наполнят бак три насоса, работая одновременно?
Решение:
Арифметический способ
№6. Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 13 часов. Через 5 часов после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?

№ 7. (из открытого банка ЕГЭ-2019. ФИПИ)
Плиточник должен уложить 175 м2 плитки. Если он будет укладывать на 10 м2 в день больше, чем запланировал, то закончит работу на 2 дня раньше. Сколько квадратных метров плитки в день планирует укладывать плиточник?
Задачи для самостоятельной работы

• Заказ на 140 деталей первый рабочий выполняет на 4 часа быстрее, чем второй. Сколько деталей в час делает второй рабочий, если известно, что первый за час делает на 4 детали больше?

2. Саша и Маша решают задачи. Саша может решить 20 задач за то время, за которое Маша может решить в 2 раза меньше задач. Саша и Маша вместе могут решить 20 этих задач за 2 ч. За сколько часов Саша самостоятельно может решить 20 задач?
3. Первый и второй насосы наполняют бассейн за 9 минут, второй и третий — за 14 минут, а первый и третий — за 18 минут. За сколько минут эти три насоса заполнят бассейн, работая вместе?
4. Первый насос наполняет бак за 19 минут, второй — за 57 минут, а третий — за 1 час 16 минут. За сколько минут наполнят бак три насоса, работая одновременно?
5. Каждый из двух рабочих одинаковой квалификации может выполнить заказ за 15 часов. Через 3 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?

Успехов в решении задач!!!

Приятной вам

совместной работы

при подготовке

к ОГЭ и ЕГЭ!!!

Скачать материал

Выберите документ из архива для просмотра:

Задачи на совместную работу.docx

Задачи на совместную работу.pptx

Выбранный для просмотра документ Задачи на совместную работу.docx

Скачать материал

Выбранный для просмотра документ Задачи на совместную работу.pptx

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Задачи на совместную работу
  Обобщение знаний. Решение задач.
  Учитель: Коряковцева Н.В.

• 

  2 слайд

  Задача 1
  Два каменщика, работая вместе, могут выполнить задание за 12 часов. Производительность труда первого и второго каменщика относятся как 1:3. Каменщики договорились работать поочерёдно. Сколько времени должен работать первый каменщик, чтобы задание было выполнено за 20 часов?

• 

  3 слайд

  Решение 1
  1)Условно принимаем всю работу за 1.
  Пусть х – производительность первого, тогда 3х – производительность второго.
  1 4х =12, х = 1 48 , 3х = 1 16
  2)Пусть у ч. – время I, тогда (20 – у) ч. – время II.
  1 48 у + 1 16 (20-у)=1, у=6.
  Ответ: 6 часов должен проработать первый каменщик.

• 

  4 слайд

  Задача 2.
  Отец с сыном должны вскопать огород. Производительность труда у отца в 2 раза больше, чем у сына. Работая вместе, они могут вскопать огород за 4 часа. Однако, вместе они проработали только 1 час, потом некоторое время работал один сын, а заканчивал работу один отец. Сколько часов в общей сложности проработал в огороде отец, если вся работа была выполнена за 7 часов?

• 

  5 слайд

  Решение 2
  За 4 часа сын может вскопать 1 3 огорода, отец — 2 3 .
  За 1 час сын вскопает 1 12 часть, отец — 1 6 , а вместе за час 1 4 , то есть через 1 час совместной работы останется 3 4 огорода и 6 часов работы.
  Пусть у часов – время работы отца, (6-у) часов – время сына.
  1 12 (6-у)+ 1 6 у= 3 4 , у = 3 ч.
  1+3 = 4 ч.
  Ответ: 4 часа работал отец.

• 

  6 слайд

  Задача 3
  Два плотника, работая вместе, могут выполнить задание за 36 часов. Производительность труда первого и второго плотников относятся как 3:4. Плотники договорились работать поочерёдно. Какую часть этого задания должен выполнить второй плотник, чтобы всё задание было выполнено за 69,3 часа?

• 

  7 слайд

  Решение 3
  За 36 часов первый работник выполнит 3 7 задания, а второй — 4 7 .
  За 1 час первый выполнит 1 84 , а второй — 1 63 задания.
  Пусть у часов – время работы II, (69,3-у) часов – время I.
  1 63 (69,3-у)+ 1 84 у=1, у = 25,2 ч. – время II
  25,2∙ 1 84 =0,3
  Ответ: 0,3 задания должен выполнить второй плотник.

• 

  8 слайд

  Задача 4
  Два фермера, работая вместе, могут вспахать поле за 25 часов. Производительность труда первого и второго фермеров относятся как 2:5. Фермеры планируют работать поочерёдно. Сколько времени должен проработать второй фермер, чтобы поле было вспахано за 45,5 часов?

• 

  9 слайд

  Решение 4
  За 25 часов I фермер может вспахать 2 7 поля, а II — 5 7 .
  За 1 час I фермер может вспахать 2 175 часть, а II — 1 35 .
  Пусть у часов – время работы II, (45,5-у) часов – время I.
  1 35 (45,5-у)+ 2 175 у=1,
  у = 17,5 ч.
  Ответ: 17,5 часов должен проработать второй фермер.

• 

  10 слайд

  Задача 5
  Набор химических реактивов состоит из трёх веществ. Массы первого, второго и третьего веществ в этом наборе относятся, как 3:7:10. Массу первого вещества увеличили на 8%, а второго – на 4%. На сколько процентов надо уменьшить массу третьего вещества, чтобы масса всего набора не изменилась?

• 

  11 слайд

  Решение 5
  Условно примем массу всех веществ за 1.
  Тогда масса первого вещества будет 3 20 , второго — 7 20 , а третьего 1 2
  При изменении массы:
  I — 3 20 ∙1,08
  II — 7 20 ∙1,04
  III — 1 2 х
  3 20 ∙1,08+ 7 20 ∙1,04+ 1 2 х=1,
  3∙1,08+7∙1,04+10х=20,
  3,24+7,28+10х=20,
  10х=9,48,
  х=0,948.
  1-0,948=0,052 – 5,2%
  Ответ: на 5,2% необходимо уменьшить массу третьего вещества.

• 

  12 слайд

  Задача 6
  Подарочный набор состоит из трёх сортов конфет. Массы конфет первого, второго и третьего сорта в этом наборе относятся как 1:2:8. Массу конфет первого сорта увеличили на 20%, а второго – на 6%. На сколько процентов надо уменьшить массу конфет третьего сорта, чтобы масса всего набора не изменилась?

• 

  13 слайд

  Решение 6
  Условно примем массу всего набора за 1.
  Тогда масса конфет первого сорта будет 1 11 , второго — 2 11 , а третьего 8 11
  При изменении массы:
  I — 1 11 ∙1,2
  II — 2 11 ∙1,06
  III — 8 11 х
  1 11 ∙1,2+ 2 11 ∙1,06+ 8 11 х=1,
  1∙1,08+2∙1,04+8х=11,
  1,08+2,08+8х=11,
  8х=7,84,
  х=0,98.
  1-0,98=0,02 – 2%
  Ответ: на 2% необходимо уменьшить массу третьего сорта.

• 

  14 слайд

  Задача 7
  Объём ежегодной добычи нефти первой, второй и третьей скважины относится как 7:6:5. Планируется уменьшить годовую добычу нефти из первой скважины на 4%, а из второй – на 2%. На сколько процентов нужно увеличить годовую добычу нефти из третьей скважины, чтобы суммарный объём добываемой за год нефти не изменился?

• 

  15 слайд

  Решение 7
  Условно примем объём добываемой нефти за 1.
  Тогда добыча нефти из первой скважины будет 7 18 , второй — 1 3 , а третьей 5 18
  При изменении добычи:
  I — 7 18 ∙0,96
  II — 1 3 ∙0,98
  III — 5 18 х
  7 18 ∙0,96+ 1 3 ∙0,98+ 5 18 х=1,
  7∙0,96+6∙0,98+5х=18,
  6,72+5,88+5х=11,
  5х= — 1,6,
  х= — 0,32.
  1- (- 0,32)=1,32 – 132%
  Ответ: на 32% необходимо увеличить объём добываемой нефти из третьей скважины.

• 

  16 слайд

  Задача 8
  Три насоса, работая вместе, заполняют цистерну нефтью за 5 часов. Производительность насосов относится как 4:3:1. Сколько процентов объёма цистерны будет заполнено за 8 часов совместной работы второго и третьего насосов?

• 

  17 слайд

  Решение 8
  За 5 часов первый насос наполнит 1 2 цистерны, второй — 3 8 и третий 1 8 .
  За 1 час второй наполнит 3 40 , а третий — 1 40 объёма.
  Совместно они заполнят за 1 час 1 10 объёма,
  а за 8 часов 8 10 , что составит 80%.
  Ответ: 80%.

• 

  18 слайд

  Задача 9
  Три насоса, работая вместе, заполняют бак с керосином за 2 часа 30 минут. Производительность насосов относится как 3:5:8. Сколько процентов объёма будет заполнено за 1 час 18 минут совместной работы второго и третьего насосов?

• 

  19 слайд

  Решение 9
  За 2,5 часа первый насос наполнит 3 16 бака, второй — 5 16 и третий 1 2 .
  За 1 час второй наполнит 1 8 , а третий — 1 5 объёма.
  Совместно они заполнят за 1 час: 1 8 + 1 5 = 13 40 объёма,
  а за 1 3 10 часа: 13 40 ∙ 13 40 = 169 400 = 0,4225, что составит 42,25%.
  Ответ: 42,25%.

• 

  20 слайд

  Задача 10
  Две трубы вместе наполняют бассейн за 3 часа. Одна первая труба может наполнить бассейн на 2,5 часа быстрее, чем вторая труба. За сколько часов может наполнить бассейн одна первая труба?

• 

  21 слайд

  Решение 10
  Условно обозначим объём бассейна за 1.
  Пусть х часов время наполнения бассейна первой трубой, тогда (х+2,5) ч. – время наполнения второй трубой.
  1 х — производительность I,
  1 х+2,5 — производительность II
  1 х + 1 х+2,5 = 1 3 ,
  1 х + 1 х+2,5 − 1 3 =0,
  3х+7,5+3х− х 2 −2,5х 3х(х+2,5) =0,
  х 2 -3,5х+7,5=0,
  х=5.
  Ответ: за 5 часов.

Краткое описание документа:

Текстовые задачи вызывают у выпускников из-за отсутствия достаточного опыта. Данный материал можно использовать для самостоятельной и совместной работы при подготовке к экзаменам в 11 классе. Он поможет учителю организовать практическую работу по этому разделу, содержит рекомендации по подходам к решению задач на совместную работу, примеры решений с пояснениями.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 155 062 материала в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Применение MS Word, Excel в финансовых расчетах»

• Курс повышения квалификации «Экономика: инструменты контроллинга»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Страхование и актуарные расчеты»

• Курс повышения квалификации «Финансы предприятия: актуальные аспекты в оценке стоимости бизнеса»

• Курс повышения квалификации «Организация маркетинга в туризме»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс профессиональной переподготовки «Управление сервисами информационных технологий»

• Курс профессиональной переподготовки «Корпоративная культура как фактор эффективности современной организации»

• Курс профессиональной переподготовки «Методика организации, руководства и координации музейной деятельности»

• Курс профессиональной переподготовки «Стандартизация и метрология»

Слайд 1

Текстовые задачи в ЕГЭ по математике Учитель Алипченкова В.П.

Слайд 2

Задача B14 . Каждый из двух рабочих одинаковой квалификации выполняет заказ за 16 часов. Через 4 часа после того, как один из них приступил к выполнению заказа, к нему присоединился второй рабочий, и работу над заказом они довели до конца уже вместе. Сколько часов потребовалось на выполнение всего заказа?

Слайд 3

Табл.№1 v t A 1-ый 1/16 16 1 2-ой 1/16 16 1 Вместе 1 / 16 + 1 / 16 = 1 /8 A= V ∙ t

Слайд 4

v t A 1-ый 1/16 4 1/4 Вместе 1/8 ? 1 – 1/4

Слайд 5

Решение 1) 1/16 ∙ 4= 1/4 работы за 4 часа 2 )1 – 1/4 = 3/4 работы осталось для совм.работы 3) 3/4 : 1/8 = 6 часов работали вместе 4) 4 + 6 = 10 часов всего Ответ: 10

Слайд 6

Две бригады, состоящие из рабочих одинаковой квалификации, одновременно начали выполнять два одинаковых заказа. В первой бригаде было 12 рабочих, во второй – 21. Через 10 дней совместной работы из 2-й бригады в 1-ю перешли 12 рабочих и в итоге оба заказа были выполнены одновременно. Сколько дней потребовалось на выполнение заказа?

Слайд 7

V t A 1-я бр . 12х 10 дн 120х 12 чел. 2-я бр . 21х 10 дн 210х 21 чел. После перехода рабочих 1-я бр . 24х у дн 24ху 2-я бр . 9х у дн 9ху Задание 1 бр . 120х + 24ху Задание 2 бр . 210х + 9ху

Слайд 8

Уравнение: 120х + 24 ху = 210 х+ 9 ху 120 + 24 у = 210 + 9у 15 у = 90 у = 6 6 дней работали в новом составе; 16 дней работали всего. Ответ :16

Слайд 9

Задачи на проценты Изюм получается в процессе сушки винограда. Сколько килограммов винограда потребуется для получения 54 кг изюма, если виноград содержит 90% воды, а изюм 5% ?

Слайд 10

Масса Вода Сухое вещ — во Виноград ? х кг 90% 10% Изюм 54кг 5% 95% Количество сухого в-ва одинаково 0,1х = 0,95∙ 54, 0,1 х = 51,3, х = 513. Ответ: 513

Слайд 11

Цена холодильника в магазине ежегодно уменьшается на одно и то же число процентов от предыдущей цены. Определите, на сколько процентов каждый год уменьшалась цена холодильника , если, выставленный на продажу за 20900 рублей, через два года был продан за 16929 рублей?

Слайд 12

Пусть х – число % (0,01х), на которое уменьшается число, тогда 1 – 0,01х – полученная дробь от исходного числа. Обозначим эту дробь буквой p. Имеем уравнение 20900 ∙ p ∙ p = 16929 p 2 = 16929/20900, P 2 = 0,81 , p = 0,9, 1- 0,09 = 0,01=10% Ответ: 10

Слайд 13

В понедельник акции компании подорожали на некоторое число процентов, а на следующий день подешевели на то же самое число процентов. В результате они стали стоить на 49% меньше, чем при открытии торгов в понедельник. На сколько процентов подорожали акции в понедельник?

Слайд 14

Пусть р – число % (0,01р), на которое увеличилась первоначальная стоимость акций (1), тогда 1 + 0,01р – полученная дробь от стоимости акций на понедельник, 1 – 0,001р – полученная дробь от получившейся после подорожания стоимости акций. 1(1 + 0,01р) (1 – 0,001р)= 0,51 1- 0,0001р 2 = 0,51, 0,0001р 2 = 0,49, р 2 = 4900, р = 70%. Ответ: 70.