Описание презентации по отдельным слайдам:
-
1 слайд
Задачи с параметрами
Подготовка к ЕГЭ.
Задание № 18
Учитель: Шарова Светлана Геннадьевна,
МБОУ «Гимназия», г. Урюпинск, Волгоградская область -
2 слайд
2
Математическое понятие параметра
Если в уравнении (неравенстве) некоторые коэффициенты заданы не конкретными числовыми значениями, а обозначены буквами, то они называются параметрами, а уравнение (неравенство) параметрическим.
Решить уравнение (неравенство) с параметрами – значит указать, при каких значениях параметров существуют решения и каковы они. -
3 слайд
Основные типы задач с параметрами
Задачи, которые необходимо решить для всех значений параметра или для значений параметра из заданного промежутка.
Задачи, где требуется найти количество решений в зависимости от значения параметра.
Задачи, где необходимо найти значения параметра, при которых задача имеет заданное количество решений.
Задачи, в которых необходимо найти значения параметра, при которых множество решений удовлетворяет заданным условиям.
3 -
4 слайд
Основные методы решения задач
Аналитический, т. е. с помощью алгебраических выражений.Графический, т. е. с помощью построения графиков функций.
Решение относительно параметра, т.е. в случае, когда параметр считается еще одной переменной.
4 -
5 слайд
Задание №1
Найдите все значения параметра а, при каждом из которых система неравенствимеет хотя бы одно решение на отрезке
Решение.
-
-
-
-
-
-
-
12 слайд
А
В
Хотя бы одно решение на -
13 слайд
Задание №2
Найдите все значения а, при каждом из которых система неравенствимеет хотя бы одно решение на отрезке
Решение.
-
-
-
-
-
-
-
20 слайд
Задание №3
Найдите все значения а, при каждом из которых уравнениеимеет ровно один корень на отрезке
Решение.
(1)
(2)
(1) -
-
22 слайд
Задание №4
Найдите все значения а, при каждом из которых уравнениеимеет ровно один корень на отрезке
.
Решение. -
-
24 слайд
Задание №5
Найдите все значения а, при каждом из которых уравнениеимеет ровно один корень на отрезке
Решение.
-
-
26 слайд
Задание №6
Найдите все значения а, при каждом из которых уравнениеимеет ровно один корень на отрезке
Решение. -
-
28 слайд
Задание №7
Найдите все значения а, при каждом из которых уравнениеимеет ровно один корень на отрезке
Решение.
0 -
-
Слайд 1
Учитель математики МОУ «Лицей №5» г. Железногорска Олейник Ольга Владимировна «Решение задач с параметрами»
Слайд 2
1) Найдите все значения при каждом из которых уравнение имеет ровно два различных действительных корня 2) Найдите все , при каждом из которых уравнение имеет наибольшее количество решений на отрезке это количество? 3) Найдите все , при каждом из которых уравнение имеет ровно четыре корня на промежутке 4) Для каждого допустимого значения решите неравенство:
Слайд 3
Найдите все значения при каждом из которых уравнение имеет ровно два различных действительных корня Область определения уравнения: Пусть (*) Если t = 4, то уравнение имеет одно решение Если уравнение (*) имеет два различных корня, принадлежащих промежутку , то заданное уравнение будет иметь 4 различных корня. Заданное уравнение имеет два различных действительных корня, если уравнение (*) имеет: а ) два равных корня из промежутка ; б ) два корня, один из которых принадлежит, а другой не принадлежит промежутку
Слайд 4
Найдите все значения при каждом из которых уравнение имеет ровно два различных действительных корня (*) а) б) 1) условие выполняется при 1,5 3 ,5 0 4 Ответ: при уравнение имеет ровно два действительных корня
Слайд 5
Найдите все , при каждом из которых уравнение имеет наибольшее количество решений на отрезке Чему равно это количество? Пусть ; , тогда (*) Рассмотрим, сколько решений имеет уравнение в зависимости от значений t : 1) При 2 решения 2) При 3 решения 3) При и 4 решения Таким образом, наибольшее количество решений 8 заданное уравнение будет иметь, если уравнение (*) будет иметь два различных корня, удовлетворяющих третьему условию
Слайд 6
Найдите все , при каждом из которых уравнение имеет наибольшее количество решений на отрезке Чему равно это количество? (*) при (**) Значит, возможны случаи расположения корней или Учитывая условие (**) получаем значения Ответ: при уравнение имеет наибольшее количество решений; 8 решений
Слайд 7
Найдите все , при каждом из которых уравнение имеет ровно четыре корня на промежутке ОДЗ параметра: Пусть тогда (*), ; ; ; ; — Уравнение (*) при любых значениях параметра имеет корень равный 1, а значит, исходное уравнение на будет иметь два корня. Рассмотрим, с колько решений будет иметь исходное уравнение при различных значениях
Слайд 8
Найдите все , при каждом из которых уравнение имеет ровно четыре корня на промежутке — Если , то исходное уравнение имеет два решения Если , то уравнение имеет три решения, а исходное пять решений Если , то уравнение имеет одно решение, а исходное три Если , то уравнение имеет два решения, а исходное четыре ; ;
Слайд 9
Найдите все , при каждом из которых уравнение имеет ровно четыре корня на промежутке С учетом ОДЗ параметра решаем систему + — + Ответ: при уравнение имеет ровно четыре корня на заданном промежутке
Слайд 10
Для каждого допустимого значения решите неравенство: ОДЗ параметра: Рассмотрим случаи, когда основание логарифма больше 1 или принимает значения от 0 до 1 1) 2) ; ; + — + + —
Слайд 11
Для каждого допустимого значения решите неравенство: Заданное уравнение будет равносильно совокупности следующих систем: (*) или (**) Решим систему (*) ; ; + + — + + — При
Слайд 12
Для каждого допустимого значения решите неравенство: (**) Решим систему (**) Сравнив и ; получаем при любых Сравнив и ; получаем, что при при
Слайд 13
Для каждого допустимого значения решите неравенство: а) если + + — б) если + + — Ответ: при при при
Тема:
“Задачи с параметрами в системе ЕГЭ
и методика их решения”
Выполнила: учитель математики
первой категории
ГБОУ Школа №1360
Долина Галина Владимировна
Цель:
формирование общих методов решения уравнений и неравенств, содержащих параметр, в классах линейных уравнений (неравенств) и уравнений не выше второй степени
Задачи:
1.ввести понятия уравнений(неравенств) с параметром, определить, что значит решить уравнение, содержащие параметр;
2.установить общий метод решения линейных уравнений(неравенств) и научиться его применять при решении конкурсных задач и задач ЕГЭ;
3.установить общий метод решения уравнений не выше 2 степени и использовать его при подготовке учащихся к ЕГЭ по математике;
Теоретические сведения
Определение 1
Уравнение вида F(a,x)=0 с двумя переменными х и а, называется уравнением с параметром а и переменной х, если для каждого значения переменной а = аi необходимо исследовать соответствующие частные уравнения F(ai,x)=0.
Определение 2
Уравнение вида f(a)x+g(a)=0, где f(a) и g(a) – любые выражения с параметром а и х – переменная, называется линейным уравнением стандартного вида.
Определение 3
Уравнение вида f(a)x2 +g(a)x+h(a)=0 c параметром а и переменной х называется уравнением стандартного вида не выше второй степени
Определение 4
В уравнении F(a;x)=0 функция х =f(a) называется общим решением на множестве Af значений параметра, если для каждого ai принадлежащего множеству Аf х =f(ai) – решение соответствующего частного уравнения F(ai;x)=0.
Графическое представление решения
Общий метод решения линейных уравнений с параметром:
- Найдём все значения, где параметр не определён и запишем ОДЗП.
- Выполним равносильные преобразования и запишем уравнение в виде f(a)x+g(a)=0, который является стандартным для данного класса уравнений.
- Найдём КЗП, решив уравнение f(a)=0
- Для каждого контрольного значения параметра решим соответствующее частное уравнение.
- Находим общее решение уравнения x=-g(a)/f(a) для всех значений а, кроме КЗП.
- При необходимости строим модель общих решений и записываем ответ.
Общий метод решения квадратных уравнений с параметром:
- Находим КЗП, для которых соответствующие частные уравнения не определены, записываем ОДЗП.
- На ОДЗП исходное уравнение при помощи равносильных преобразований приводим к стандартному виду f(a)x2+g(a)x+h(a)=0
- Выделяем множество КЗП, где f(a)=0 и для каждого КЗП решаем соответствующее частное уравнение, если f(a)=0 имеет конечное множество решений.
- Выделяем КЗП, для которых Д=g(a)2 — 4f(a)h(a) обращается в нуль. Соответствующие частные уравнения имеют двукратный корень x= -g(a)/2f(a)
- На каждом промежутке ОДЗП определяем знак дискриминанта и решаем частные уравнения.
- Составляем модель решений.
- Записываем ответ.
Общий метод решения линейных уравнений функционально-графическим методом:
- В уравнении находим ОДЗП.
- На ОДЗП уравнение приведем к виду
f(a)x + g(a)=F(x). - Введем функции:
- Из уравнения f(ai)=k находи КЗП, для которого график частной линейной функции y=f(ai)x+g(ai) параллелен графику y=kx+l.
- Для остальных f(ai) ≠ k, для частных линейных функций y=f(ai)x+g(ai) и y=F(x) находим число решений уравнения.
- Записываем ответ.
а) линейную с параметром вида y=f(a)x + g(a) — бесконечное множество частных функций;
б) y=F(x) — функция со строго фиксированным графиком, где F(x)=kx+l
Применение функционально-графического метода решения уравнений
С5. ЕГЭ.
Найдите значения параметра а, при которых количество корней уравнения
(2,5 – а)х3 -2х2 + х =0 равно количеству общих точек линий х2 + у2 = а и у = 3 -|х-1|
Решение:
1.Решим уравнение (2,5 — а)х3-2х2 + х =0 аналитическим методом.
х((2,5 – а)х2 – 2х + 1) =0
х = 0 или (2,5 – а)х2 – 2х + 1 =0 (1)
Решим уравнение (1).
КЗП: а = 2,5; Для остальных значений а, не равных 2,5, исследуем уравнение (1).
В зависимости от знака дискриминанта Д1 = а – 1,5 получим:
1 корень-
2 корня-
3 корня —
Число общих точек пересечения линий х2 + у2 = а и
у = 3 — |х-1| найдем графически.
1) х2 + у2 = а – это уравнение окружностей с центром в начале координат и а=R2
2) у = 3 — |х-1| — «уголок»
Заметим, что окружность будет касаться «уголка», если а = 2;8;10.
Таким образом:
1 точка –
2 точки –
3 точки –
4 точки –
Точек пересечения нет —
Модель решений:
Ответ: 2,5; 8; 10.
Методика формирования общего метода решений уравнений и неравенств с параметром
I. Рассмотреть конкретный пример и выделить все закономерности действия в решении уравнения (неравенства) с параметром
II. Выделить общий метод решения
III. Закрепить выделенный метод решения, фиксируя действия в общей схеме и проговаривая каждый этап
IV. Представить схему общего метода решения (как правило, учащиеся выполняют это самостоятельно).
СПАСИБО ЗА ВНИМАНИЕ
1. Проект «Разработка заданий и методических рекомендаций для решения задач с параметрами при подготовке к ЕГЭ по математике»
Выполнена учителем математики
МБОУ СОШ№14 г.Красногорска
Беляевской С. В.
2. Оглавление:
1. Введение
2.
3.
4.
5.
6.
7.
3
Особенности заданий с параметрами
Занятие №1
5-22
Занятие №2
23-31
Занятие №3
32-44
Заключение
45
Источники
47
4-5
3. Введение:
Известно, что в программах по математике в
неспециализированных классах задачам с параметрами
отводится незначительное место. С параметрами учащиеся
встречаются при введении линейной функции y = kx + b,
уравнения первой степени ax + b =0 и квадратного
уравнения ax^2 + bx + c = 0.
Понятие параметра позволяет решать поставленные задачи
не в частном, а в общем виде. Позволяет посмотреть на
проблему более широко.
Владение приемами решения задач с параметрами можно
считать критерием знаний основных разделов школьной
математики, уровня математического и логического
мышления.
Задачи с параметрами дают прекрасный материал для
настоящей учебно-исследовательской работы.
4. Особенности заданий с параметрами
В самом начале знакомства с параметрами у учеников
возникает психологический барьер, который обусловлен
противоречивыми характеристиками параметра. С одной
стороны, параметр следует считать величиной известной, а с
другой — конкретное значение параметра не дано. С одной
стороны, параметр является величиной постоянной, а с
другой — может принимать различные значения.
Получается, что параметр в условии — это «неизвестная
величина», «переменная постоянная». Этот «каламбур»
довольно точно отражает суть тех сложностей, которые
нужно преодолеть ученикам.
К задачам с параметрами, рассматриваемым в школьном
курсе, можно отнести, например, поиск решений линейных и
квадратных уравнений в общем виде, исследование
количества их корней в зависимости от значений
параметров.
5.
Такой небольшой класс задач многим не позволяет усвоить
главное: параметр, будучи фиксированным, но неизвестным
числом, имеет как бы двойственную природу. Во-первых,
предполагаемая известность позволяет «общаться» с
параметром как с числом, а во-вторых, — степень свободы
общения ограничивается его неизвестностью.
Основное, что нужно усвоить при работе с параметром, необходимость осторожного обращения с фиксированным , но
неизвестным числом.
Рассмотрим решение некоторых задач с параметрами на
уроках повторения, обобщения и систематизации знаний,
состоящих из трёх занятий по два часа на данную тему.
6. Занятие №1 (2 часа)
Главное, что должен усвоить школьник это то,
что параметр – это число, хоть и неизвестное, но
фиксированное, имеющее двойственную природу.
После этих вступительных слов можно спросить у
школьников встречались ли они с параметрами.
Это линейная функция y=kx+b, где x и y –
переменные, k и b – параметры; квадратное
уравнение ax2+bx+c=0, где x — переменная a, b, c,
— параметры.
Задачи надо начинать решать с очень простых,
постепенно усложняя их.
7. Пример №1. Сравнить –а и 5а
Решение:
1) если а <0, то –а>0, 5a<0, значит –
а>5a
2) если а=0, то –а=0, 5а=0, значит –
а=5а
3) если а>0, то –а<0, 5a>0, значит –
а<5a.
Ответ: если a<0, то –а>5a
если а=0, то–а=5а
если а>0, то–а<5a.
8. Пример №2. Решить уравнение ах=2
Решение:
1) если а=0, то 0х=2, решений нет
2
2) если а≠0, то х=
a
Ответ: если а=0, то решений
нет ,если а≠0, то х= 2
a
9. Пример №3 Решить уравнение (а2-9)х=а+3
Решение:
1) если а=3, то 0х=6,
решений нет
2) если а=-3, то 0х=0, х R
a 3
3) если а≠±3, то а2-9≠0, x 2
a 9
1
x
a 3
Ответ: если а=3, то
решений нет
если а=-3, то x R
если а≠±3, то x
1
a 3
10. Пример №4 Решить неравенство: ах<7
Пример №4 Решить неравенство:
ах<7
Решение:
7
1) если a>0, то x
a
7
a
3) если а=0, то 0 x 7
x R
2) если а<0, то x
7
Ответ: если а>0, то х<
a
7
x
если а<0, то
a
если а=0, то x R
11. Пример №5 Решить уравнение
Решение:
x a
0
x 3
x a
0
x 3
x a 0,
x a,
x 3 0
x 3.
Ответ: если а=-3, то решений нет
если а≠-3, то х=а.
12. Пример №6 Решить уравнение
(a 1) x 2 x 1 a 0
2
Решение:
1) если а=-1, то -2х+1+1=0; х=1
1 a
2) если а≠-1,то х=1 или x
a 1
Ответ: если а=-1, то х=1
1 a
если а≠-1,то х=1 или x
a 1
13. Пример №7 Решить уравнение
x b ( x 4) 0
Решение:
x b 0
x b
x b, b
x b ( x 4) 0 x 4 0, x 4, x 4, b 4.
x b 0
x b
Ответ: если b<-4, то x=-4 или x=b
если b=-4, то x=-4
если b>-4, то x=b.
14. Пример №8 Решить уравнение
x 2 1 a ( x 1) 0
Решение:
a ( x 1) 0,
2
a ( x 1) 0,
x 1 0,
2
2
x 1,
x 1 a ( x 1) 0
x 1 0
a ( x 1) 0
x 1 .
1) если а≠0, то х=1
2) если а=0, то x R значит х=1 или х=-1
Ответ: если а≠0, то х=1
если а=0, то х=±1
15. Пример №9 Решить неравенство
(1 b2 ) x 2 2bx 1 0.
Решение:
1
1) a) если b=1, то 2 x 1 0; x
2
1
2.
2) если b≠±1, то неравенство квадратное
б) если b=-1, то 2 x 1 0; x
D
b 2 (1 b 2 ) 2b 2 1
4
1
b
D
2
0 2b 2 1 0
,
4
b 1
2
16.
a)
1 b 2 0 b ( 1;1)
D
1
1
0 b ( ;
) (
; )
4
2
2
2
b 2b 2 1
b
2
b
1
x ;
;
2
2
1 b
1 b
1
b
D
2
0
4
b 1
2
x R
D
1 1
0 b (
; ) x R
4
2 2
17.
1 b 0 b ( ; 1) (1; )
б)
1
1
D
учитывая, что при
b ( ;
) ( ; ) 0,
2
2
то
4
b 2b 2 1 b 2b 2 1
x
;
2
2
1 b
1 b
Ответ: если b=1, то
если b=-1, то
если
2
1
x ;
2
1
x ;
2
b ( ; 1) (1; то
)
b 2b 2 1 b 2b 2 1
x
;
2
2
1
b
1
b
18.
если
1
1
b ( 1; ) ( ;1) то
2
2
2
b 2b 2 1
b
2
b
1
x ;
;
2
2
1
b
1
b
если
1 1
b
;
то x R
2 2
Рассмотренные выше задачи требовалось просто решить. В
следующих задачах будет поставлено какое-то более
«узкое», конкретное условие.
19. Пример №10 При каких а уравнение имеет единственное решение?
2
ax x 3 0
Решение:
1) если а=0, то х=3
2) если а≠0, то уравнение квадратное и оно имеет
единственное решение при D=0
D=1-12a
1
D 0 1 12a 0 a
12
1
Ответ: при а=0 или а = 12
20. Пример №11 При каких а уравнение имеет единственное решение?
(a 2) x (4 2a) x 3 0
2
Решение:
1) если а=2, то решений нет
2) если а≠2, то уравнение имеет единственное решение при
D=0
D
(2 a ) 2 (a 2)3 a 2 7 a 10
4
a 5
D
2
0 a 7 a 10 0
4
a 2
Ответ: при а=5
21. Задачи для самостоятельного домашнего решения задаются с ответами для самоконтроля
1)
При каких а уравнение имеет решения,
найти их
a 3 5 3a
ax 3
2
x 1 x 2 x x 2
14 a
(x
3a 2
при a ( ; 6) ( 6; 2 ) ( 2 ; 18 ) (18 ; ))
3
3 7
7
2) Решить уравнение:
a)
x a
x 4x 3
2
0
(при а=1 или а=3 решений нет; при а≠1 и а≠3 х=а)
22.
б)
x 2
0
x a
(при а =-2 решений нет; при а≠-2 х=2)
3) При каких а уравнение имеет ровно три корня
x 3 x a ( x 3 x)
(при a ( 1;1) )
23. Занятие №2 (2 часа)
Урок
начинается с разбора
домашнего задания. Затем учитель
предлагает решить более общую
задачу.
24. Пример №12 Выяснить, при каких значениях параметра а уравнение имеет:
Пример №12 Выяснить, при каких
значениях параметра а уравнение
5(4 a) x 2 10 x a 0 имеет:
1) два различных корня;
2) не более одного корня;
3) два корня различных знаков;
4) два положительных корня.
25.
Решение:
1) уравнение имеет два различных корня тогда и только
тогда, когда оно квадратное и D>0.
4 a 0,
a 4,
4 a 0,
a 4,
a ( 1;4) (4;5)
D
2
25 5a(4 a) 0
a ( 1;5)
a 4 a 5 0
4 0
x
2
3
2) а) если а=4, то
б)
a 4,
a 4,
a 4,
2
a ( ; 1] [5; )
D 0
a ( ; 1] [5; )
a 4a 5 0
26.
2
3) уравнение ax bx c 0 имеет два корня различных
c
0 значит
знаков тогда и только тогда, когда
a
a
0 a (0;4)
5(4 a)
4) уравнение ax bx c 0 имеет два положительных
корня тогда и только тогда, когда
2
D 0,
4 a 0,
c
0,
a
b
0
a
4 a 0,
2
a [ 1;5],
a 4a 5 0,
a 4,
a
a [ 1;0)
0
,
5(4 a)
a ( ;0) (4; ),
10
a 4
0
5(4 a)
27. Самостоятельная работа. Вариант I
1. Для всякого а решить уравнение
x 2 (2a 1) x 2a 0
Решение: Т.к. сумма коэффициентов равна 0, то х=1 или
х=2а
Ответ: 1; 2а.
2. При каких b уравнение имеет единственный корень?
Для каждого b найти этот корень.
3 x 2 bx 12 0
Решение: Квадратное уравнение имеет единственный
корень тогда и только тогда, когда D=0
28.
D b 2 144
b 12,
D 0 b 144 0
b 12
2
1) если b=12, то x
12
; x 2
6
2) если b=-12, то x
12
;x 2
6
Ответ: при b=12 x=-2
при b=-12 x=2.
29.
3. Для каждого значения параметра решить неравенство:
( x 2 4)( x b) 0.
Решение:
( x 4)( x b) 0 ( x 2)( x 2)( x b) 0
2
Решим неравенство методом интервалов, рассмотрев
функцию f(x)= ( x 2)( x 2)( x b, )
непрерывную на R, имеющую нули 2, -2, b
Рассмотрим три случая:
1)
b 2
x [b; 2] [2; )
30.
2) -2<b<2
x [ 2; b] [2; )
3)
b 2
x [ 2;2] [b; )
Ответ: если
если -2<b<2, то
если b 2 то
b то
2
x [b; 2] [2; )
x [ 2; b] [2; )
x [ 2;2] [b; )
31. Вариант II
Задания аналогичны заданиям варианта I.
1. x 2 (3a 1) x 3a 0
Ответ: -1; 3а.
2. 5 x 2 bx 20 0
Ответ: при b=20 x=-2
при b=-20 x=2.
2
(
x
1)( x a) 0
3.
Ответ: если a 1, то
если -1<a<1, то
если a 1, то
x ( ; a] [ 1;1]
x ( ; 1] [a;1]
x ( ; ; 1] [1; a]
32. Занятие №3 (2 часа)
Теперь можно приступать к решению
задач ЕГЭ с параметрами.
33. Пример№1.Найти все значения параметра p, при которых уравнение имеет хотя бы один корень.
Пример№1.Найти все значения параметра p,
при которых уравнение 7 4 cos x p(1 tg 2 x)
имеет хотя бы один корень.
Решение:
2
cos
x 0,
2
7 4 cos x p (1 tg x)
7 cos 2 x 4 cos3 x p.
cos 2 x 0,
a 0,
cos x a,
1 a 1,
7a 2 4a 3 p; 7 a 2 4a 3 p.
2
3
7
a
4
a
, определённую на
Рассмотрим функцию f(a)=
[-1;0)U(0;1] и найдём её область значений.
f(-1)=11; f(1)=3; при a 0 f (a ) 0
2
f ’(a)= 14a 12a ;
34.
a 0,
14a 12a 2 0 2a(7 6a) 0
f ’(a)=0
a 7
6
7
D( f ) то экстремумов у функции нет,
Т.к. 0 D ( f );
6
следовательно E(f)=(0;11].
2
3
Чтобы уравнение 7a 4a p, а значит и данное уравнение
имело хотя бы один корень, необходимо и достаточно,
чтобы p (0;11].
Ответ:
(0;11]
35. Пример №2. Найти все значения а, при которых область определения функции содержит ровно одно двузначное натуральное число.
Пример №2. Найти все значения а, при которых
область определения функции
y (( a ) 2 x 10 ( x 2 x ) 2 a 3 x 5 x log x a (a 2 )log2 16 ) 0,5
содержит ровно одно двузначное натуральное число.
Решение:
( a ) 2 x 10 ( x 2 x ) 2 a 3 x5 x logx a (a 2 )log2 16 0,
x 0,
x 1.
D(y):
Решим первое неравенство системы:
( a ) 2 x 10 ( x 2 x ) 2 a 3 x 5 x logx a (a 2 ) log2 16 0
a a x a x a a 0;
x
5
5
3
5
x
8
a 5 (a x a 3 ) x 5 (a x a 3 ) 0;
(a x a 3 )( a 5 x 5 ) 0;
36.
a x a 3 0,
5
5
a
x
0;
x
3
a
a
0,
a 5 x 5 0;
x
a
5
a
x
a
5
a
a3 ,
x5 ;
a3 ,
x5 ;
a x a 3 ,
a x;
x
3
a
a
,
a x.
1) если 0<a<1, то
x 3,
a x;
x 3,
a x;
x a,
x 3;
x (0; a) (3; ).
Решение не удовлетворяет условию задачи.
37.
2) если а>1, то
x 3,
a x;
x 3,
a x;
3 x a,
a x 3;
x (3; a).
Чтобы решение удовлетворяло условию задачи, необходимо
и достаточно, чтобы a (10;11].
Ответ: (10;11]
38. Пример №3. Найти все значения параметра а, при каждом из которых множество решений неравенства содержит какой-нибудь отрезок
Пример №3. Найти все значения параметра а, при
каждом из которых множество решений неравенства
4a 2
a 8a
x( x 2a 4)
x
2
содержит какой-нибудь отрезок длиной 2,но не
содержит никакого отрезка длиной 3
Решение:
4a 2
a 8a
x( x 2a 4)
x
2
4a 2
ax 2 8ax 4a 2 x3 2a 2 x 2 4 x 2
2
2
a 8a
x 2a x 4 x 0
0
x
x
a 2 ( x 4) 2ax( x 4) x 2 ( x 4)
( x 4)( x a) 2
0
0.
x
x
2
39.
Решим неравенство методом интервалов,
рассмотрев
2
функцию f ( x) ( x 4)( x a) непрерывную на R{0},
x
имеющую нули 4, а:
1) если
a 0
x (0;4-)решение содержит отрезок длиной 3, что не
удовлетворяет условию задачи.
2) если 0<a<4
x (0; a) (a;4)
Чтобы решение удовлетворяло условию задачи, необходимо
и достаточно, чтобы выполнялись условия:
40.
a 1,
a 2;
a 2,
a 3;
т.е. a [1;2) (2;3]
3) если a 4
x (0;4) — аналогично случаю 1)
Ответ: [1;2) (2;3]
41. Пример №4. Найти все значения параметра p, при которых уравнение имеет хотя бы один корень, и число различных корней этого
Пример №4. Найти все значения параметра p, при
которых уравнение
(2 p 3) x ( p 3) x 1 0
2
имеет хотя бы один корень, и число различных корней
этого уравнения равно числу различных корней
уравнения
2x 1
21 p
1)
1
x 3 3
Решение:
2x 1
21 p
1
x 3 3
Пусть x 3 =t, t 0 тогда
2 x 1 2t 2 7
42.
2t 2 7
1
;
21 p t 3
2t 3 6t 2 7t 21 21 p;
2t 3 6t 2 7t p.
Рассмотрим функцию f (t ) 2t 3 6t 2 7t :
D(f)=[0; ),
f(t)=0 t (2t 2 6t 7) 0 t =0.
E(f)=(- ;0]
f’(t)= 6t 2 12t 7 f’(t)<0 f
f (t ) 2t 3 6t 2 7иt y=p могут
Значит графики функций
иметь только одну общую точку, т.е. уравнение
2t 6t 7t pа значит и уравнение
3
2
может иметь ровно один корень при
2x 1
21 p
p 0.
1
x 3 3
43.
2) Узнаем при каких p уравнение (2 p 3) x 2 ( p 3) x 1 0
имеет ровно один корень:
3
2
p
а) если 2p+3=0 (
), то x p 3-удовлетворяет
2
2
3
условию.
2
б) если 2 p 3 0, то уравнение (2 p 3) x ( p 3) x 1 0
имеет единственный корень при D=0.
D ( p 3)2 4(2 p 3) p 2 2 p 3.
D=0
p 1,
p 2p 3 0
p 3.
2
Итак, уравнение (2 p 3) x 2 ( p 3) x 1 0 имеет ровно
один корень при
3
p ; 1;3 .
2
44.
Но уравнению 2 x 1
21 p
3
т.е. при p
2
1
x 3 3
удовлетворяют только p 0,
2x 1
21 p
1
x 3 3
и p=-1 уравнения
и
(2 p 3) x 2 ( p 3) x 1 0 имеют равное число корней, а
именно, по одному.
Ответ: 3 ; -1
2
45. Заключение
Все рассмотренные упражнения имеют дидактическую
цель — помочь учащимся составить представление о
параметре, о том, что значит решить уравнение
(неравенство) с параметром. Предложенные упражнения
помогают им осмыслить всего несколько строк
определения: «Пусть дано уравнение (неравенство)
f(x; a)=(>) 0 с переменными x, a. Если ставится задача для
каждого значения a решить это уравнение( неравенство)
относительно x, то уравнение (неравенство)
f(x;a)=(>)0 называется уравнением(неравенством) с
переменной x и параметром a. Решить уравнение
(неравенство) с параметром a — это значит для каждого
значения a найти значение x, удовлетворяющее этому
уравнению(неравенству)».
46.
Задачи с параметрами обладают большим потенциалом в
развитии интеллектуальных качеств личности, так как
развивают исследовательские способности, учат творчески
мыслить, помогают сформировать и развить творческое
мышление. Эти задачи должны включаться в школьный курс
математики начиная с 7 класса. Конечно, уровень сложности
заданий должен определяться уровнем подготовки всего
класса в целом и каждого ученика в отдельности.
В своей работе я постаралась составить версию обучения
учащихся решению уравнений и неравенств с параметрами с
подборкой основных заданий разного уровня, а также
продемонстрировать важность обучения учащихся таким
задачам, обосновать целесообразность обучения умению их
решать, проанализировать подходящие для этого задания.
Основной вывод работы-такие задачи должны составлять
самостоятельную линию обучения в математике.
47. Используемые источники:
1. Гронштейн П.И., Полонский В.Б., Якир М.С. — Задачи
с параметрами – «Илекса», «Гимназия» — МоскваХарьков,1999год.
2. Шахмейстер А.Х. – Задачи с параметрами, 1-е
издание СПб: «ЧеРо-на-Неве»,2004год.
3. Ященко И.В., Семенова А.Л. – Материалы ЕГЭ,
издательство «Экзамен» Москва,2011год.
4. Интернет сайты:
www.dvoek-net.ru
www.ege-trener.ru
Презентацию подготовила: Харитонова Л. В. ,учитель математики ГБОУ города Севастополя «СОШ № 15»
Цель работы:
- Изучить всевозможные способы решений задач с параметрами для подготовки к ЕГЭ.
- С параметрами учащиеся встречаются при введении некоторых понятий.
- Не приводя подробных определений, рассмотрим в качестве примеров следующие объекты
Функция прямая пропорциональность:
у = kx
( х и у переменные; k – параметр)
Линейная функция:
у = kx + b
- ( х и у — переменные; k и b параметры) ;
Линейное уравнение:
ах + b = 0
- ( х — переменная; а и b — параметры) ;
Уравнение первой степени:
ах + b = 0
- ( x — переменная; а и b — параметры, а ≠ 0);
Квадратное уравнение:
ах 2 + bx + с = 0
- ( x — переменная; а, b и с — параметры, а ≠ 0 ).
- К задачам с параметрами, рассматриваемым в школьном курсе, можно отнести,. например, поиск решений линейных и квадратных уравнений в общем виде, исследование количества их корней в зависимости от значений параметров.
Пример 1 .
Пример 2 .
2.1.3. Параметр и свойства решений уравнений, неравенств и их систем.
2.3. Графические приемы. Координатная плоскость (х ; у)
- Естественным продолжением знакомства с основными приемами и методами решений задач с параметрами будет обращение к наглядно-графическим интерпретациям.
- В зависимости от того какая роль параметру отводится в задаче (неравноправная или равноправная с переменной), можно соответственно выделить два основных графических приема: первый — построение графического образа на координатной плоскости (х;у), второй — на (х;а).
- Говоря о графических методах, невозможно обойти одну проблему, “рожденную” практикой конкурсного экзамена. Мы имеем в виду вопрос о строгости, а следовательно, о законности решения, основанного на графических соображениях. Несомненно, с формальной точки зрения результат, снятый с «картинки», не подкрепленный аналитически, получен нестрого. Однако кем, когда и где определен уровень строгости, которого следует придерживаться абитуриенту? Требования к уровню математической строгости для школьника должны определяться здравым смыслом.

Пример 4.
Задана функция f(x)=3x 4 -4x 3 -12x 2
Найти количество корней уравнения f(x)=a, где a
принадлежит множеству рациональных значений,
в зависимости от значения параметра a .
при а 0 , в уравнении два корня
у
-1
I
2
I
при а=0, в уравнении три корня;
x
При -5
-5
При а=-5, а также
При а -32 и a
При а=-32, в уравнении одно решение;
-32
При а
2.4. Графические приемы. Координатная плоскость (х;a)
Пример 5 .
Список использованной литературы:
- Горнштейн П.И., Полонский В.Б., Якир М.С. Задачи с параметрами.- К.: РИА “ Текст ” ; МП “ ОКО ” , 1992. -290с.
- Габович И.Г. Горнштейн П.И. Сколько корней имеет уравнение?// Квант. – 1985. -№3-С43-46
- Говоров В.М., Дыбов П.Т., Мирошин Н.В., Смирнова С.Ф. Сборник конкурсных задач по математике (с методическими указаниями и решениями) :Учеб. Посбобие. -2-е изд. – М. : Наука, 1986. – 384 с.
- Вишенський В.О., Перестюк М.О., Самойленко А.М. Задач i з математики, — К. : Вища шк., 1985. -264с.
1
Разработка заданий и методических рекомендаций для решения задач с параметрами при подготовке к ЕГЭ по математике. Выполнена учителем математики Новосадовой И.Б.
2
Оглавление: 1. Введение 3 2. Занятие Занятие Занятие Заключение Источники 44
3
Введение: Задания ЕГЭ по математике C-5-это задания с параметрами. Однако эта тема не входит в программу школьного курса за исключением классов с углублённым изучением математики. Существует мнение, что решение задачи с параметрами не выходит за пределы программы школьного курса математики. Имеется в виду, что если ученик или абитуриент владеет школьной программой, то он может самостоятельно, без специальной подготовки справится с задачей с параметрами. На самом деле решить задачу с параметрами может учащийся, который прошел специальную целенаправленную подготовку. Поэтому в школьной математике этим задачам должно уделяться внимание. В классах с углублённым изучением математики параметрам уделяется достаточно внимания, начиная с решения линейных уравнений. При изучении каждой темы «углублёнки» можно найти время для решения задач с параметрами. Чего нельзя сказать об общеобразовательных классах и классах с гуманитарным уклоном. Поэтому я предлагаю учителям, работающим в неспециализированных выпускных классах перед итоговым повторением уделить несколько часов решению задач с параметрами
4
Занятие 1 (2 часа) Главное, что должен усвоить школьник это то, что параметр – это число, хоть и неизвестное, но фиксированное, имеющее двойственную природу. После этих вступительных слов можно спросить у школьников встречались ли они с параметрами. Это линейная функция y=kx+b, где x и y – переменные, k и b – параметры; квадратное уравнение ax 2 +bx+c=0, где x — переменная a, b, c, — параметры. Главное, что должен усвоить школьник это то, что параметр – это число, хоть и неизвестное, но фиксированное, имеющее двойственную природу. После этих вступительных слов можно спросить у школьников встречались ли они с параметрами. Это линейная функция y=kx+b, где x и y – переменные, k и b – параметры; квадратное уравнение ax 2 +bx+c=0, где x — переменная a, b, c, — параметры. Задачи надо начинать решать с очень простых, постепенно усложняя их. Задачи надо начинать решать с очень простых, постепенно усложняя их.
5
Пример 1. Сравнить –а и 5а Решение: 1) если а 0, 5a 5a 2) если а=0, то –а=0, 5а=0, значит – а=5а 3) если а>0, то –а 0, значит – а 0, то –а 0, значит – а0, то–а 0, то–а
6
Пример 2. Решить уравнение ах=2 Решение: 1) если а=0, то 0х=2, решений нет 2) если а0, то х= если а=0, то решений нет, если а0, то х= Ответ: если а=0, то решений нет, если а0, то х=
7
Пример 3 Решить уравнение (а 2 -9)х=а+3 Решение: 1) если а=3, то 0х=6, решений нет 2) если а=-3, то 0х=0, х 3) если а±3, то а 2 -90, если а=3, то решений нет Ответ: если а=3, то решений нет если а=-3, то x если а±3, то
8
Пример 4 Решить неравенство: ах0, то 2) если а0, то х 0, то х< если а
9
Пример 5 Решить уравнение Решение: если а=-3, то решений нет Ответ: если а=-3, то решений нет если а-3, то х=а. если а-3, то х=а.
10
Пример 6 Решить уравнение Решение: 1) если а=-1, то -2х+1+1=0; х=1 2) если а-1,то х=1 или если а=-1, то х=1 Ответ: если а=-1, то х=1 если а-1,то х=1 или если а-1,то х=1 или
11
Пример 7 Решить уравнение Решение: если b-4, то x=b.
12
Пример 8 Решить уравнение Решение: 1) если а0, то х=1 2) если а=0, то x значит х=1 или х=-1 если а0, то х=1 Ответ: если а0, то х=1 если а=0, то х=±1 если а=0, то х=±1
13
Пример 9 Решить неравенство Решение: 1) a) если b=1, то 1) a) если b=1, то б) если b=-1, то б) если b=-1, то 2) если b±1, то неравенство квадратное
14
a)
15
б) учитывая, что при то если b=1, то Ответ: если b=1, то если b=-1, то если b=-1, то если то если то
16
если то Рассмотренные выше задачи требовалось просто решить. В следующих задачах будет поставлено какое-то более «узкое», конкретное условие.
17
Пример 10 При каких а уравнение имеет единственное решение? Решение: 1) если а=0, то х=3 2) если а0, то уравнение квадратное и оно имеет единственное решение при D=0 D=1-12a при а=0 или а = Ответ: при а=0 или а =
18
Пример 11 При каких а уравнение имеет единственное решение? Решение: 1) если а=2, то решений нет 2) если а2, то уравнение имеет единственное решение при D=0 при а=5 Ответ: при а=5
19
Задачи для самостоятельного домашнего решения задаются с ответами для самоконтроля 1) 1) При каких а уравнение имеет решения, найти их при при 2) 2) Решить уравнение:a) (при а=1 или а=3 решений нет; при а1 и а3 х=а)
20
б) (при а =-2 решений нет; при а-2 х=2) (при а =-2 решений нет; при а-2 х=2) 3) При каких а уравнение имеет ровно три корня (при )
21
Занятие 2 (2 часа) Урок начинается с разбора домашнего задания. Затем учитель предлагает решить более общую задачу. Урок начинается с разбора домашнего задания. Затем учитель предлагает решить более общую задачу.
22
Пример 12 Выяснить, при каких значениях параметра а уравнение имеет: 1 ) два различных корня; 2) не более одного корня; 3) два корня различных знаков; 4) два положительных корня.
23
Решение: 1) уравнение имеет два различных корня тогда и только тогда, когда оно квадратное и D>0. 2) а) если а=4, то б) б)
24
3) уравнение имеет два корня различных знаков тогда и только тогда, когда значит знаков тогда и только тогда, когда значит 4) уравнение имеет два положительных корня тогда и только тогда, когда
25
Самостоятельная работа. Вариант I 1. Для всякого а решить уравнение 1. Для всякого а решить уравнение Т.к. сумма коэффициентов равна 0, то х=1 или х=2а Решение: Т.к. сумма коэффициентов равна 0, то х=1 или х=2а 1; 2а. Ответ: 1; 2а. 2. При каких b уравнение имеет единственный корень? Для каждого b найти этот корень. 2. При каких b уравнение имеет единственный корень? Для каждого b найти этот корень. Квадратное уравнение имеет единственный корень тогда и только тогда, когда D=0 Решение: Квадратное уравнение имеет единственный корень тогда и только тогда, когда D=0
26
1) если b=12, то 2) если b=-12, то при b=12 x=-2 Ответ: при b=12 x=-2 при b=-12 x=2. при b=-12 x=2.
27
3. Для каждого значения параметра решить неравенство: 3. Для каждого значения параметра решить неравенство: Решение: Решим неравенство методом интервалов, рассмотрев функцию f(x)=, непрерывную на R, имеющую нули 2, -2, b Рассмотрим три случая: 1)
28
2) -2
29
Вариант II Задания аналогичны заданиям варианта I ; 3а. Ответ: -1; 3а при b=20 x=-2 Ответ: при b=20 x=-2 при b=-20 x=2. при b=-20 x= если то Ответ: если то если -1
30
Занятие 3 (2 часа) Теперь можно приступать к решению задач ЕГЭ с параметрами. Теперь можно приступать к решению задач ЕГЭ с параметрами.
31
Пример1.Найти все значения параметра p, при которых уравнение имеет хотя бы один корень. Решение: Рассмотрим функцию f(a)= определённую на [- 1;0)U(0;1] и найдём её область значений. f(-1)=11; f(1)=3; при f (a)=
32
f (a)=0 Т.к. то экстремумов у функции нет, следовательно E(f)=(0;11]. Чтобы уравнение а значит и данное уравнение имело хотя бы один корень, необходимо и достаточно, чтобы Ответ:
33
Пример 2. Найти все значения а, при которых область определения функции содержит ровно одно двузначное натуральное число. Решение: D(y): Решим первое неравенство системы:
34
1) если 0
35
2) если а>1, то Чтобы решение удовлетворяло условию задачи, необходимо и достаточно, чтобы Ответ:
36
Пример 3. Найти все значения параметра а, при каждом из которых множество решений неравенства содержит какой-нибудь отрезок длиной 2,но не содержит никакого отрезка длиной 3 Решение:
37
Решим неравенство методом интервалов, рассмотрев функцию непрерывную на R{0}, имеющую нули 4, а: 1) если — решение содержит отрезок длиной 3, что не удовлетворяет условию задачи. — решение содержит отрезок длиной 3, что не удовлетворяет условию задачи. 2) если 0
38
т.е. 3) если — аналогично случаю 1) — аналогично случаю 1) Ответ:
39
Пример 4. Найти все значения параметра p, при которых уравнение имеет хотя бы один корень, и число различных корней этого уравнения равно числу различных корней уравнения Решение:1) Пусть =t, тогда
40
Рассмотрим функцию D(f)=[0; ), f(t)=0 t =0. E(f)=(- ;0] f(t)= f(t)
41
2) Узнаем при каких p уравнение имеет ровно один корень: а) если 2p+3=0 ( ), то -удовлетворяет условию. б) если то уравнение имеет единственный корень при D=0. D=0 Итак, уравнение имеет ровно один корень при
42
Но уравнению удовлетворяют только т.е. при и p=-1 уравнения и имеют равное число корней, а именно, по одному. имеют равное число корней, а именно, по одному. ; -1 Ответ: ; -1
43
Заключение Разработаны конспекты для трех занятий, которые помогут учителю на уроках научить выпускников решать несложные задания с параметрами, постепенно переходя к заданиям ЕГЭ C5. Не является секретом,что существуют «ножницы» между требованиями школьной программы к выпускникам и требованиями, которые предъявляет к своему поступающему вуз. Задания, рассмотренные в работе, играют огромную роль в формировании логического мышления и математической культуры у школьников.
44
Используемые источники: 1. Гронштейн П.И., Полонский В.Б., Якир М.С. — Задачи с параметрами – «Илекса», «Гимназия» — Москва- Харьков,1999год. 2. Шахмейстер А.Х. – Задачи с параметрами, 1-е издание СПб: «ЧеРо-на-Неве»,2004год. 3. Ященко И.В., Семенова А.Л. – Материалы ЕГЭ, издательство «Экзамен» Москва,2011год. 4. Интернет сайты:
Математик так же, как художник или поэт, создает узоры. И если его узоры более устойчивы, то лишь потому, что они созданы из идей…
Г.Х. Харди
Подготовила: учитель математики Кужелева О. А.
При решении широкого класса задач с параметром довольно часто оказывается полезным графический метод.
Решение задач с параметром графическим методом имеет ряд особенностей. Он основан на нахождении всех точек данной плоскости, координаты которых удовлетворяют заданному в условии задачи соотношению.
Графический метод обладает целым рядом преимуществ перед аналитическим: он более нагляден и понятен в случаях, когда необходимо ответить на качественный вопрос или провести анализ множества решений. Однако следует помнить, что универсальных методов и приёмов, пригодных для любой математической задачи, не существует. Поэтому, приступая к анализу той или иной задачи, необходимо выбрать наиболее эффективный из возможных способов её решения.
Цель:
- показать применение графического метода при решении задач с параметром;
- показать наглядность использования ИКТ при решении задач с помощью «живых графиков»;
- рассмотреть решение заданий С5 для подготовки к ЕГЭ.
Движение прямой вдоль оси Оу и число решений системы.
Справочный материал
у= k х+ b – линейная функция, Г – прямая
k – угловой коэффициент, k = tg α
b – точка пересечения Г с Оу
Если х = 0, то у = b , прямая параллельная Ох
{
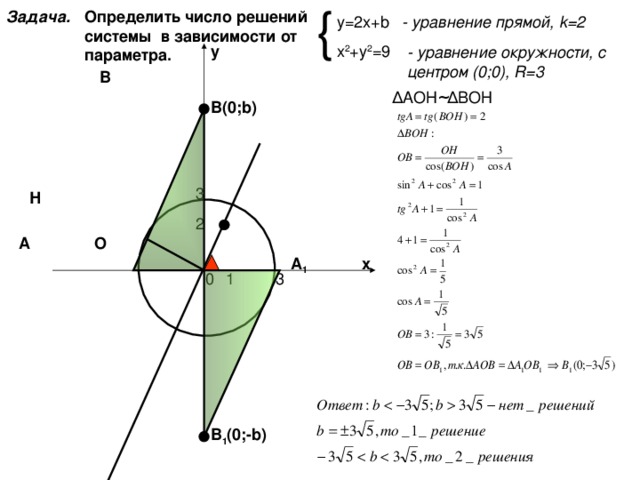
Определить число решений системы в зависимости от параметра.
Задача.
у=2х+ b
х 2 +у 2 =9
— уравнение прямой, k =2
у
— уравнение окружности, с центром (0;0), R=3
В
Δ АОН ~ Δ ВОН
В(0; b )
Н
А
О
А 1
х
В 1 (0;- b )

Угловой коэффициент прямой и число решений системы.
Справочный материал
у= k х+ b – линейная функция, Г – прямая
k – угловой коэффициент, k = tg α
Если угол острый, тогда tg α 0, следовательно k 0;
Если угол тупой, тогда tg α 0, следовательно k ;
Если α = 90 º , то tg90º — не существует, следовательно не существует k.
{
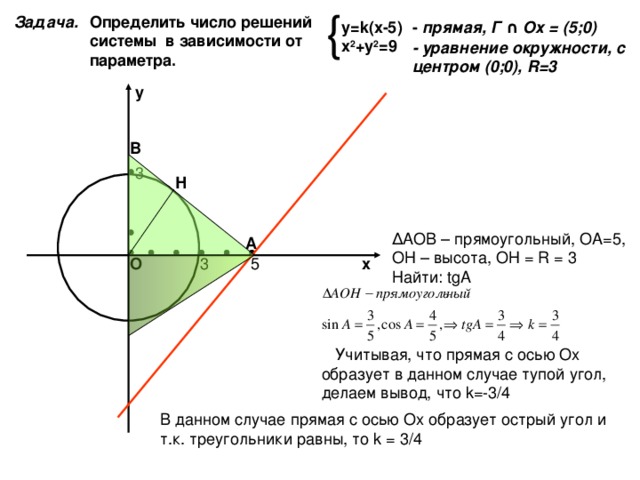
Определить число решений системы в зависимости от параметра.
Задача.
у= k( х -5)
х 2 +у 2 =9
— прямая, Г ∩ Ох = (5;0)
— уравнение окружности, с центром (0;0), R=3
у
В
Н
Δ АОВ – прямоугольный, ОА=5, ОН – высота, ОН = R = 3 Найти: tgA
А
х
О
Учитывая, что прямая с осью Ох образует в данном случае тупой угол, делаем вывод, что k=-3/4
В данном случае прямая с осью Ох образует острый угол и т.к. треугольники равны, то k = 3/4
{
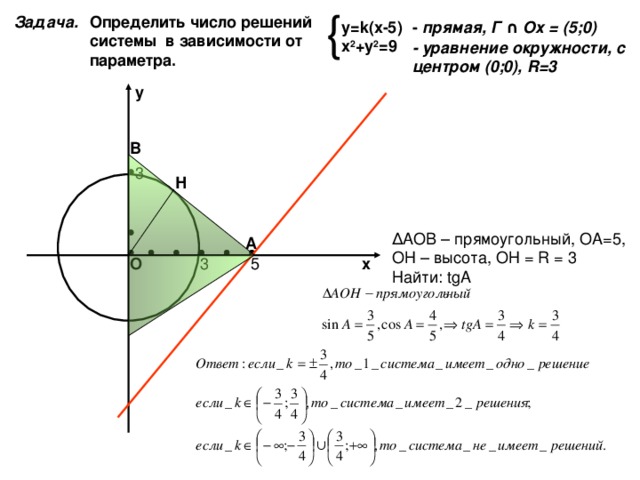
Задача.
Определить число решений системы в зависимости от параметра.
— прямая, Г ∩ Ох = (5;0)
у= k( х -5)
х 2 +у 2 =9
— уравнение окружности, с центром (0;0), R=3
у
В
Н
Δ АОВ – прямоугольный, ОА=5, ОН – высота, ОН = R = 3 Найти: tgA
А
О
х
Плавающая окружность и число решений системы.
Справочный материал.
(х – х 0 ) 2 + (у –у 0 ) 2 = R 2
(х 0 ;у 0 ) – координаты центра окружности
(х;у) – координаты точки, принадлежащей окружности
R – радиус окружности
{
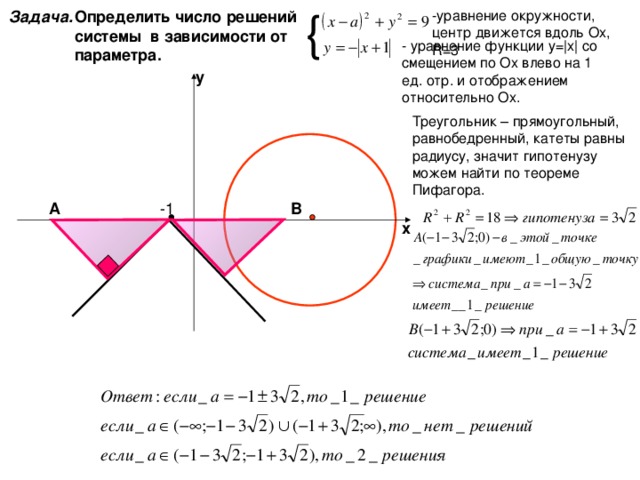
-уравнение окружности, центр движется вдоль Ох, R=3
Определить число решений системы в зависимости от параметра.
Задача.
— уравнение функции у= | х | со смещением по Ох влево на 1 ед. отр. и отображением относительно Ох.
у
Треугольник – прямоугольный, равнобедренный, катеты равны радиусу, значит гипотенузу можем найти по теореме Пифагора.
А
В
х
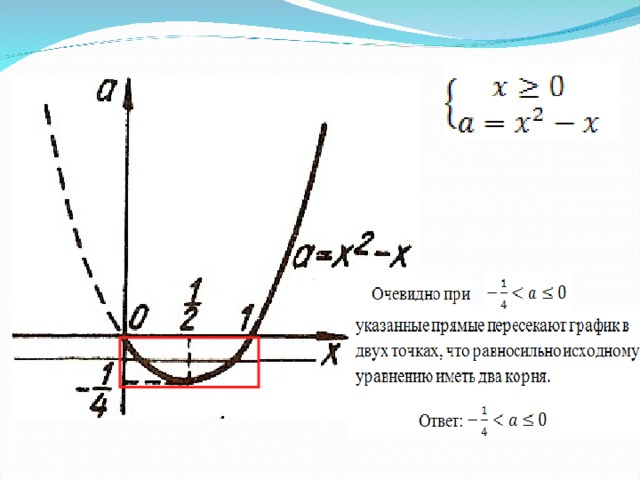
Движение параболы вдоль Оу и число решений системы
Справочный материал.
у = ах 2 + b х+с,
С помощью выделения полного квадрата получим у= k (х-х 0 ) 2 +у 0 , где (х 0 ;у 0 ) -координаты вершины параболы
{
Задача.
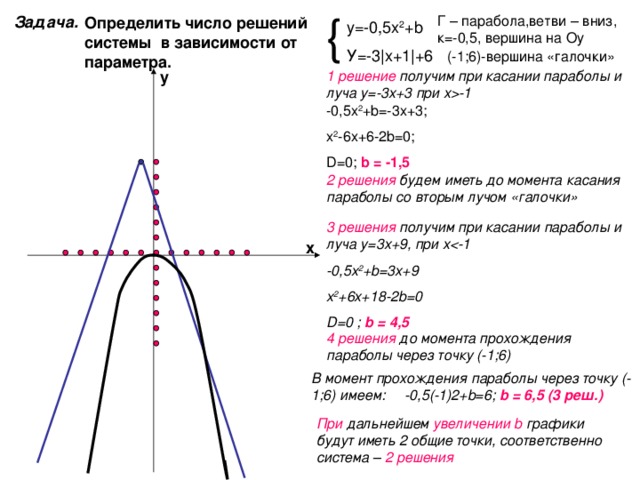
Г – парабола,ветви – вниз, к=-0,5, вершина на Оу
Определить число решений системы в зависимости от параметра.
у=-0,5х 2 + b
У=-3 | х+1 | +6
(-1;6)-вершина «галочки»
1 решение получим при касании параболы и луча у=-3х+3 при х -1 -0,5х 2 + b =-3х+3;
у
х 2 -6х+6-2 b=0 ;
D=0 ; b = -1,5
2 решения будем иметь до момента касания параболы со вторым лучом «галочки»
3 решения получим при касании параболы и луча у=3х+9, при х -1
-0,5х 2 + b=3x+9
x 2 +6x+18-2b=0
D=0 ; b = 4,5
х
4 решения до момента прохождения параболы через точку (-1;6)
В момент прохождения параболы через точку (-1;6) имеем: -0,5(-1)2+ b=6; b = 6,5 (3 реш.)
При дальнейшем увеличении b графики будут иметь 2 общие точки, соответственно система – 2 решения
График модуля меняет угловой коэффициент и число решений системы.
Справочный материал.
у = k | х-а | + b
(a;b) – координаты вершины «галочки»
k – угловой коэффициент лучей «галочки»
{
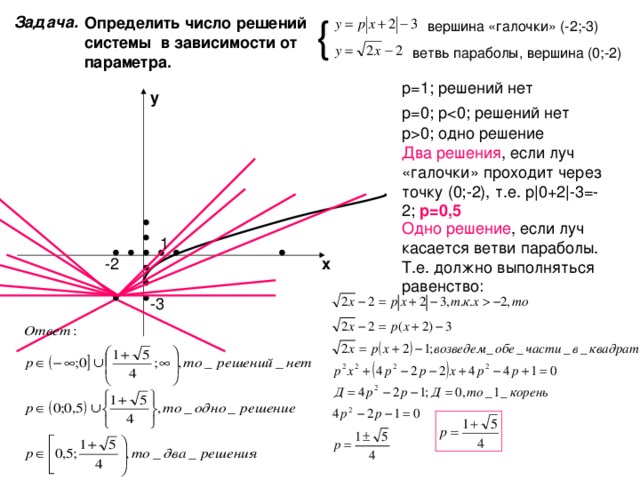
Задача.
Определить число решений системы в зависимости от параметра.
вершина «галочки» (-2;-3)
ветвь параболы, вершина (0;-2)
у
р=0; р
р 0 ; одно решение
Два решения , если луч «галочки» проходит через точку (0;-2), т.е. р | 0+2 | -3=-2; р=0,5
Одно решение
х
Окружность с фиксированным центром меняет радиус и число решений системы.
Справочный материал.
(х-а) 2 +(у- b) 2 =R 2
(a,b) -координаты центра
R — радиус
x 2 +y 2 =c 2 – уравнение окружности с центром в начале координат
(0;0) – координаты центра
R= |c| , с – принимает как положительные, так и отрицательные значения.
— ур-е окружности, (0;0) – центр, R= |c|
{
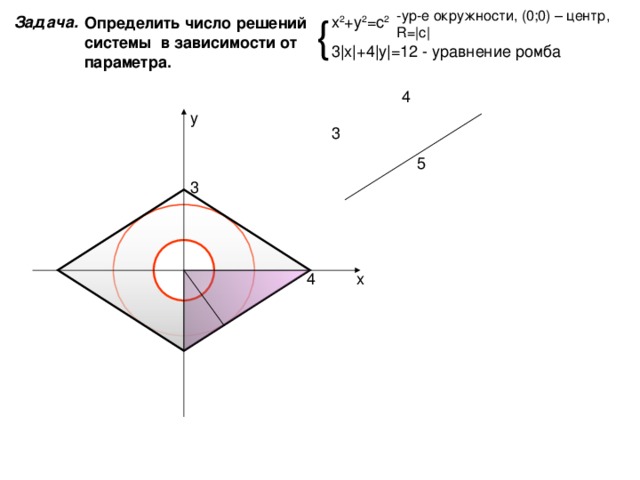
х 2 +у 2 =с 2
3 | х | +4 | у | =12
Задача.
Определить число решений системы в зависимости от параметра.
4
y
3
5
3
x
4
{
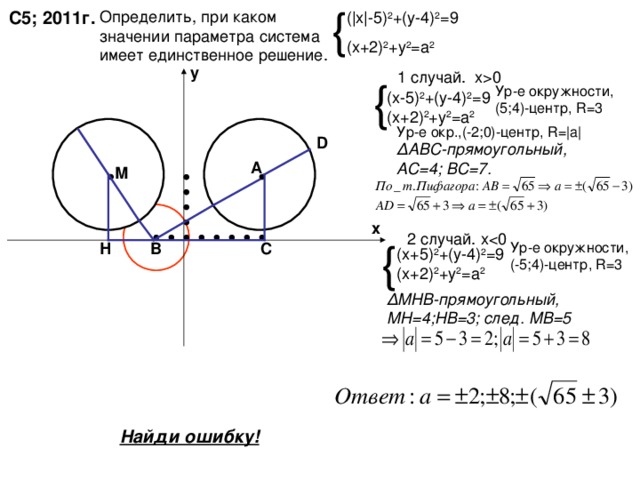
С5; 2011г.
( | х | -5) 2 +(у-4) 2 =9
(х+2) 2 +у 2 =а 2
у
1 случай. х 0
{
Ур-е окружности, (5 ; 4)- центр, R=3
2 2
2 2 2
Ур-е окр.,(-2;0)-центр, R= |a|
D
Δ АВС-прямоугольный, АС=4; ВС=7.
А
М
х
2 случай. х
{
Н
В
Ур-е окружности, (-5 ; 4)- центр, R=3
С
(х + 5) 2 +(у-4) 2 =9
(х+2) 2 +у 2 =а 2
Δ МНВ — прямоугольный, МН=4;НВ=3; след. МВ=5
Найди ошибку!
{
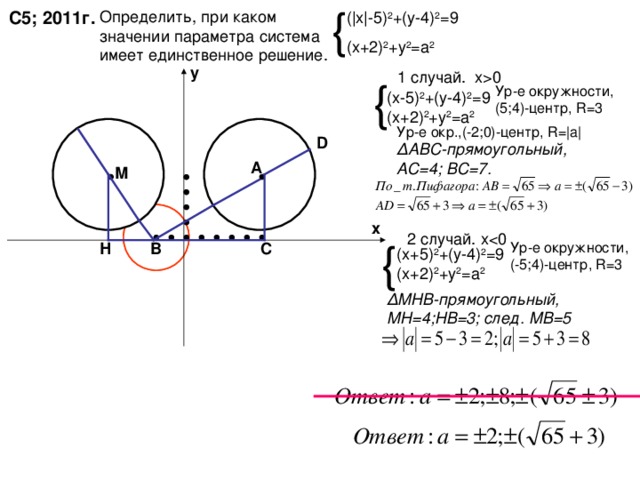
С5; 2011г.
( | х | -5) 2 +(у-4) 2 =9
(х+2) 2 +у 2 =а 2
у
1 случай. х 0
{
Ур-е окружности, (5 ; 4)- центр, R=3
2 2
2 2 2
Ур-е окр.,(-2;0)-центр, R= |a|
D
Δ АВС-прямоугольный, АС=4; ВС=7.
А
М
х
2 случай. х
{
Н
С
В
Ур-е окружности, (-5 ; 4)- центр, R=3
(х + 5) 2 +(у-4) 2 =9
(х+2) 2 +у 2 =а 2
Δ МНВ — прямоугольный, МН=4;НВ=3; след. МВ=5
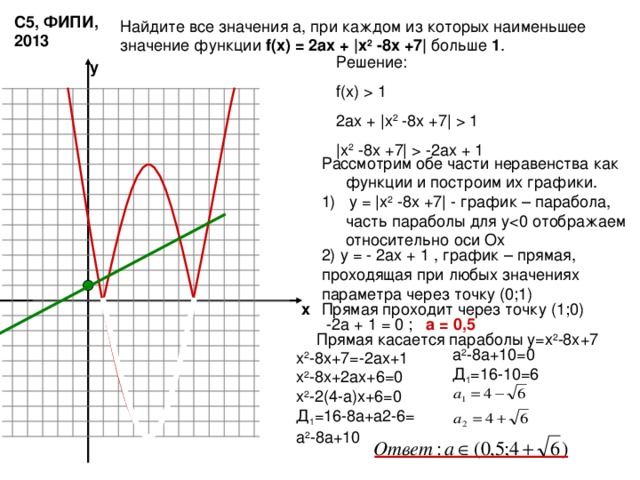
С5, ФИПИ, 2013
Найдите все значения а, при каждом из которых наименьшее значение функции f(x) = 2ax + |x 2 -8x + 7 | больше 1 .
Решение:
f(x) 1
2ax + |x 2 -8x + 7 | 1
|x 2 -8x + 7 | -2ax + 1
у
Рассмотрим обе части неравенства как функции и построим их графики.
1) у = |x 2 -8x + 7 | — график – парабола, часть параболы для у
х
а = 0,5
2
2 1
2 2 2 1 2
Вариант 1
Найдите все положительные значения параметра а, при которых система имеет единственное решение
Вариант 2
Найдите все значения параметра а, при каждом из которых система имеет ровно три различных решения
Вариант 3
Найдите все значения а, при каждом из которых наименьшее значение функции f (х) = 2ах + | х 2 – 8х + 15 | больше 1.
Ответы: