При подготовке к экзамену студент за t дней изучает 16t 2t 4

Ваня Грибоедов

09.12.2020 15:58:54

Алгебра 10-11 класс

10 баллов

При подготовке к экзамену студент за t дней изучает t/(t+k) -ю часть курса и забывает (α ⋅ t) -ю часть. Сколько дней нужно потратить на подготовку, чтобы была изучена максимальная часть курса? Решить задачу при условии, что k =1;α =1/ 16.

https://prnt.sc/vz04ou

Ирина Каминкова

09.12.2020 16:35:50

Ответ эксперта

Все предметы

Рейтинг пользователей

    • Калькуляторы
    • Словарь

    Источник

    Условие

    При подготовке к экзамену студент за t дней изучает t/(t+k)–ю часть курса, а забывает at–ю часть. Сколько дней нужно затратить на подготовку, чтобы была изучена максимальная часть курса?

    k=t/t+1 a=3t/192

    математика
    256

    Решение

    ★

    Студент за t дней изучает t/(t+k) часть курса, а забывает a*t часть.
    Здесь k = t/(t+1); a = 3t/192
    Сколько дней нужно затратить на подготовку, чтобы была изучена максимальная часть курса?
    Решение.
    Заметим, что t — это время, значит, по определению t > 0.
    Поэтому все дроби в решении имеют смысл при любом t > 0.
    Если k = t/(t+1), то:
    [m]t+k = t + frac{t}{t+1} = frac{t(t+1) +t}{t+1} = frac{t^2 + 2t}{t+1}[/m]
    Студент за t дней изучает часть курса:
    [m]f(t) = frac{t}{t+k} = frac{t(t+1)}{t^2+2t} = frac{t^2+t}{t^2+2t} = frac{t+1}{t+2}[/m]
    И забывает часть курса:
    [m]g(t) = a*t = frac{3t}{192}*t = frac{3t^2}{192}[/m]
    В итоге он за t дней выучивает:
    [m]F(t) = f(t) — g(t) = frac{t+1}{t+2} — frac{3t^2}{192} = frac{192(t+1) — 3t^2(t+2)}{192(t+2)} = frac{-3t^3 — 6t^2 + 192t + 192}{192(t+2)}[/m]
    Исследуем эту функцию на экстремум.
    Для этого найдем производную.
    [m]F'(t) = frac{(-9t^2-12t+192)*192(t+2) — (-3t^3-6t^2+192t+192)*192}{192^2(t+2)^2} = [/m]
    Сокращаем всю дробь на 192:
    [m] = frac{(-9t^2-12t+192)(t+2) — (-3t^3-6t^2+192t+192)}{192(t+2)^2} =frac{-9t^3-12t^2+192t-18t^2-24t+384 +3t^3+6t^2-192t-192}{192(t+2)^2} =frac{-6t^3-24t^2-24t+192}{192(t+2)^2}[/m]
    Получили:
    [m]F'(t) = frac{-6t^3-24t^2-24t+192}{192(t+2)^2}[/m]
    В точках экстремума производная функции должна быть равна 0.
    Знаменатель этой дроби больше 0 при любом t > 0.
    Приравниваем числитель к 0, получаем уравнение:
    -6t^3 — 24t^2 — 24t + 192 = 0
    Сокращаем на -6:
    t^3 + 4t^2 + 4t — 32 = 0
    Преобразуем так:
    t^3 — 2t^2 + 6t^2 — 12t + 16t — 32 = 0
    (t — 2)(t^2 + 6t + 16) = 0
    t = 2 — это решение.
    t^2 + 6t + 16 = 0 — действительных корней не имеет.
    Проверим, что t= 2 — точка максимума.
    При t < 2, например, при t = 1 будет:
    [m]F'(t) = frac{-6-24-24+192}{192(3)^2} = frac{138}{192*9} > 0[/m]
    Значит, на промежутке t ∈ (0; 2) функция возрастает.
    При t > 2, например, при t = 3, будет:
    [m]F'(t) = frac{-6*27-24*9-24*3+192}{192(5)^2} = frac{-162-216-72+192}{192*25} = -frac{258}{192*25} < 0[/m]
    Значит, при t > 2 функция убывает.
    Таким образом, мы доказали, что t = 2 — точка максимума.
    Ответ: через 2 дня.

    Написать комментарий

    Источник

    При подготовке к экзамену студент за t дней изучает t / t + k — ю часть курса, а забывает at — ю часть.

    Сколько дне нужно затратит на подготовку, чтобы была изучена максимальная часть курса?

    K = 1 / 2, a = 2 / 49.

    На этой странице находится вопрос При подготовке к экзамену студент за t дней изучает t / t + k — ю часть курса, а забывает at — ю часть?. Здесь же – ответы на него,
    и похожие вопросы в категории Алгебра, которые можно найти с помощью
    простой в использовании поисковой системы. Уровень сложности вопроса
    соответствует уровню подготовки учащихся 10 — 11 классов. В комментариях,
    оставленных ниже, ознакомьтесь с вариантами ответов посетителей страницы. С
    ними можно обсудить тему вопроса в режиме on-line. Если ни один из
    предложенных ответов не устраивает, сформулируйте новый вопрос в поисковой
    строке, расположенной вверху, и нажмите кнопку.

    Источник

    Условие задачи[править]

    При подготовке к экзамену студент за {displaystyle t} дней изучает {displaystyle {frac {t}{t+k}}}-ю часть курса, а забывает {displaystyle alpha t}-ю часть. Сколько дней нужно затратить на подготовку, чтобы была изучена максимальная часть курса?

    {displaystyle k=1, alpha ={frac {1}{16}}}

    Решение[править]

    Составляем функцию:

    {displaystyle S(t)={frac {t}{t+1}}-{frac {1}{16}}t.}
    {displaystyle S'(t)={frac {t+1-t}{(t+1)^{2}}}-{frac {1}{16}}={frac {1}{(t+1)^{2}}}-{frac {1}{16}}.}
    {displaystyle {frac {1}{(t+1)^{2}}}-{frac {1}{16}}=0Longrightarrow {begin{cases}t_{1}=-5,\t_{2}=3.end{cases}}}
    {displaystyle t_{1}=-5} — не удовлетворяет условию задачи.
    {displaystyle t_{2}=3} — точка минимума.

    Ответ: 3 дня.

    Источник

    доброго дня суток, у n-ю неделю мучаю себя 2-мя задачами, был бы счастлив в любой помощи, итак:

    1)При подготовке к экзамену студент за t дней изучает (t/(t+1))-ю часть курса и забывает (t/36)-ю часть. Сколько дней нужно потратить на подготовку, чтобы была изучена максимальная часть курса?
    &
    2)Тело массой m=3000 кг падает из высоты H=1280 метров и теряет массу (сгорает) про-порционально времени падения. Коэффициент пропорциональности k=100 кг/c. Считая, что начальная скорость V(0)=0, ускорение g=10 м/с, найти наибольшую кинетическую энергию тела.

    __________________
    Помощь в написании контрольных, курсовых и дипломных работ, диссертаций здесь

    Источник

    1. ;

    2. ;

    3. ;

    4. ;

    5. ;

    1. ;

    2. ;

    3. .

    Н


    айти

    Найти


    при указанном значении t.

    9),
    t=1;

    10)

    ,

    .

    §14. Производные и дифференциалы высших порядков.

    1.
    Найти

    функции у,
    если

    1)
    ; 2)

    .

    1. ;

    2. ;

    3. ;

    4. ;

    1. ;

    2. ;

    3. ;

    4. .

    2.
    Найти

    функции у,
    если

    3.
    Найти дифференциалы указанных порядков
    для заданных функций:


    1. найти

      ;


    2. найти

      ;


    3. найти

      ;


    1. найти

      ;


    2. найти

      .

    §15. Применение производной к исследованию функции.

    Основные теоремы
    дифференциального исчисления

    1.
    Определить с
    в формуле Лагранжа для функции

    на отрезке
    .

    2.
    Написать формулу Коши для функции

    и

    и определить значение с
    на отрезке [-2;1].

    1. ;

    2. ;

    3. ;

    4. ;

    5. ;

    6. ;

    8. ;

    9. ;

    10. ;

    1. ;

    2. ;

    3. ;

    4. ;

    5. ;

    6. ;

    7. ;

    8. ;

    9. ;

    10. ;

    11. ;

    1. ;

    2. ;


    3. ;

    5. ;

    6. ;

    7. ;

    8. ;

    9. ;

    10. ;

    11. .

    3



    .
    Пользуясь правилами Лопиталя, найти
    указанные пределы:

    4.
    Исследовать на монотонность и экстремум
    функции:

    1. ;

    2. ;

    3. ;

    4. ;

    5. на
      интервале (0;)
      ;

    6. ;

    7. ;

    8. ;

    9. ;

    10. ;

    1. ;

    2. ;

    3. ;

    4. ;

    5. ;

    6. ;

    7. ;

    8. ;

    9. ;


    10. на

      .

    5.
    Найти наибольшее и наименьшее значения
    функции на данном отрезке:


    1. на
      отрезке
      ;


    2. на
      отрезке
      ;


    3. на
      отрезке
      ;

    4. на
      отрезке;


    5. на
      отрезке
      ;


    1. на
      отрезке
      ;


    2. на
      отрезке


    3. на
      отрезке


    4. на
      отрезке


    5. на
      отрезке
      .

    6.
    При подготовке к экзамену студент за
    t
    дней изучает
    -ю
    часть курса, а забывает
    -ю
    часть. Сколько дней нужно затратить на
    подготовку, чтобы была изучена
    максимальная часть курса? Решить
    задачу при

    1)
    ,
    ; 2)

    ,.

    7.
    Требуется изготовить закрытый
    цилиндрический бак с заданным объемом
    V.
    Каковы должны быть размеры бака, чтобы
    его полная поверхность была наименьшей?

    8.
    В данный прямой круговой конус вписать
    цилиндр наибольшего объема.

    9.
    Данное положительное число
    а     разложить
    на два слагаемых
    так, чтобы произведение их
    было наибольшим.

    10.
    Найти точки перегиба и определить
    интервалы выпуклости кривой:

    1. ;

    2. ;

    3. ;

    1. ;

    2. ;

    3. .

    11.
    Найти асимптоты кривой:

    1. ;

    2. ;

    3. ;

    1. ;

    2. ;

    3. .

    Индивидуальное
    задание по теме: «Исследование функции
    и построение графика»

    Исследовать
    функцию и построить график.

    Исследование
    функции проводить по следующей схеме:

    1. Найти
      область определения функции;

    2. Исследовать
      функцию на непрерывность. Найти точки
      разрыва функции и ее односторонние
      пределы в этих точках;

    3. Найти
      (если можно) точки пересечения графика
      функции с осями координат;

    4. Выяснить,
      является ли функция четной, нечетной
      или общего вида;

    5. Исследовать
      на монотонность и экстремум;

    6. Найти
      интервалы выпуклости и точки перегиба
      графика функции;

    7. Найти
      асимптоты графика функции;

    8. Используя
      результаты исследования построить
      график.

    9. Найти
      наибольшее и наименьшее значения
      функции №1 на отрезке

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    ;

    .

    Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    • #
    Источник

    Сообщения без ответов | Активные темы

    используя методы дифф-го исчесления,решить физическую задачу

    Модераторы: Prokop, mad_math

    Автор Сообщение

    sl198

    Заголовок сообщения: используя методы дифф-го исчесления,решить физическую задачу

    СообщениеДобавлено: 24 янв 2012, 12:38 
    Не в сети
    Начинающий


    Зарегистрирован:
    24 янв 2012, 12:21
    Сообщений: 2
    Cпасибо сказано: 0
    Спасибо получено:
    0 раз в 0 сообщении
    Очков репутации: 1

    Добавить очки репутацииУменьшить очки репутации

    при подготовке к экзамену студент за t дней изучает (t/(t+k))-ю часть курса и забывает (a*t)-ю часть. сколько дней нужно потратить на подготовку, что бы была изучена максимальная часть курса? решить задачу при условии, что k = 1 a =1/25.
    Вернуться к началу

    Профиль  

    Cпасибо сказано 

     Похожие темы   Автор   Ответы   Просмотры   Последнее сообщение 
    Решить задачу используя интегралы

    в форуме Дифференциальные и Интегральные уравнения

    vabe1337

    0

    217

    06 дек 2016, 21:00
    Решить задачу, используя алгебру логики

    в форуме Дискретная математика, Теория множеств и Логика

    Sweet_blood

    9

    965

    21 ноя 2014, 23:24
    Ветвящиеся алгоритмы, используя конструкцию if решить задачу

    в форуме MATLAB

    BBBONESSS

    0

    314

    20 май 2020, 21:58
    Решить задачу, используя геометрический смысл производной

    в форуме Дифференциальные и Интегральные уравнения

    Natalia_vv

    1

    129

    09 апр 2020, 17:49
    Используя аппарат векторной алгебры решить задачу

    в форуме Векторный анализ и Теория поля

    chicken

    1

    525

    06 фев 2019, 10:45
    Решить задачу используя ф-лу Пуассона или локальную Муавра

    в форуме Комбинаторика и Теория вероятностей

    efinf

    2

    296

    12 июн 2016, 20:11
    Решить задачу используя классическое определение вероятности

    в форуме Теория вероятностей

    Kiryanovth

    3

    379

    10 янв 2018, 17:13
    Используя диаграммы Эйлера-Венна, решить задачу

    в форуме Дискретная математика, Теория множеств и Логика

    mailraritet

    3

    1868

    18 мар 2013, 17:45
    Как решить дифф.ур

    в форуме Дифференциальное исчисление

    Danly

    2

    264

    20 окт 2014, 19:59
    Решить дифф уравнение

    в форуме Комплексный анализ и Операционное исчисление

    kreska_g

    1

    262

    18 окт 2015, 10:20

    Кто сейчас на конференции

    Сейчас этот форум просматривают: нет зарегистрированных пользователей и гости: 6

    Вы не можете начинать темы
    Вы не можете отвечать на сообщения
    Вы не можете редактировать свои сообщения
    Вы не можете удалять свои сообщения
    Вы не можете добавлять вложения

    Powered by phpBB © 2000, 2002, 2005, 2007 phpBB Group

    Вы можете создать форум бесплатно PHPBB3 на Getbb.Ru, Также возможно сделать готовый форум PHPBB2 на Mybb2.ru

    Русская поддержка phpBB

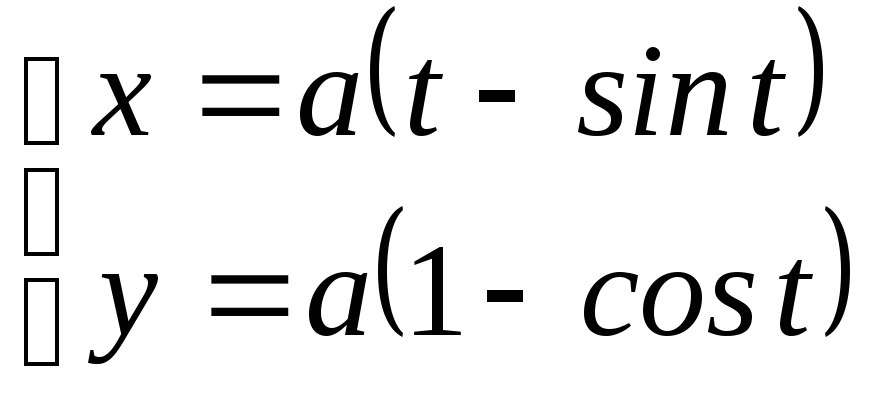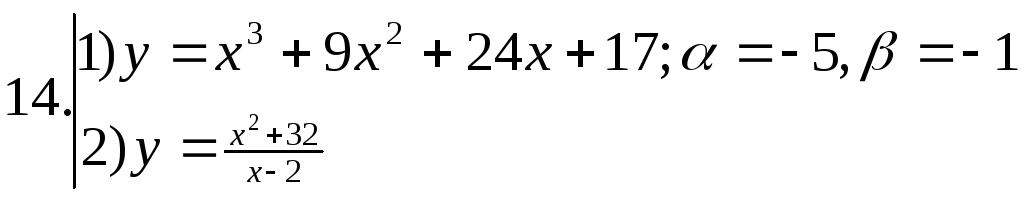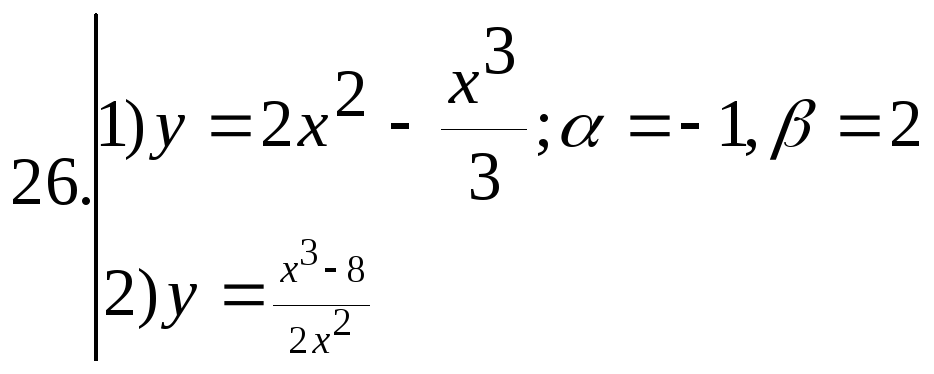    Источник

    Понравилась статья? Поделить с друзьями:
  • При подготовке к экзамену по математике митя за пять дней прорешал 150 задач
  • При заключении срочного трудового договора обязательно учитывается характер егэ
  • При гиподинамии у человека возрастает риск развития сердечно сосудистых заболеваний егэ
  • При подготовке к экзаменам я изучил много специальной литературы
  • При высокой инфляции погасить которую за короткий срок невозможно государство проводит политику егэ