Скачать материал

Скачать материал


- Сейчас обучается 96 человек из 32 регионов


- Сейчас обучается 82 человека из 34 регионов




Описание презентации по отдельным слайдам:
-
1 слайд
Презентация к уроку по алгебре 9 класс Тема урока: Формула суммы членов конечной арифметической прогрессии. Автор: учитель МБОУ СОШ № 31 г.Ижевск Павленко М.Н.
-
2 слайд
Будет ли последовательность арифметической прогрессией?
-
-
4 слайд
Задачи Найти сумму трёх членов арифме-тической прогрессии уn = — 4n + 5 . — 9 2. Найдите сумму первых пяти членов арифметической прогрессия: -5,2; -0,2; 4,8…. 24
-
5 слайд
Верно ли, что??? d = a4 – a5 an = a1 + (n – 1)d a1 = an + (n -1)d
-
6 слайд
Задачи 3.Найдите сумму двадцати четырёх членов арифметической прогрессии аn = 2n-15.
-
7 слайд
Формула Суммы Членов Конечной Арифметической Прогрессии
-
8 слайд
Задачи 4.Найдите сумму всех натуральных чисел от 1 до 100.
-
9 слайд
Легенда Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время, предложил им сосчитать сумму чисел от 1 до 100. Юный Гаусс (10 лет), ставший потом одним из самых знаменитых математиков мира, мгновенно получил результат: 5050. 1+2+3+4+5++…+97+98+99+100=? А как бы считали вы?
-
10 слайд
Гаусс Карл Фридрих (30.04.1777 — 23.02.1855) Среди ученых Карл Гаусс носит имя «Король математики».
-
11 слайд
1 + 2 + 3 + …+100 = ??? +
-
12 слайд
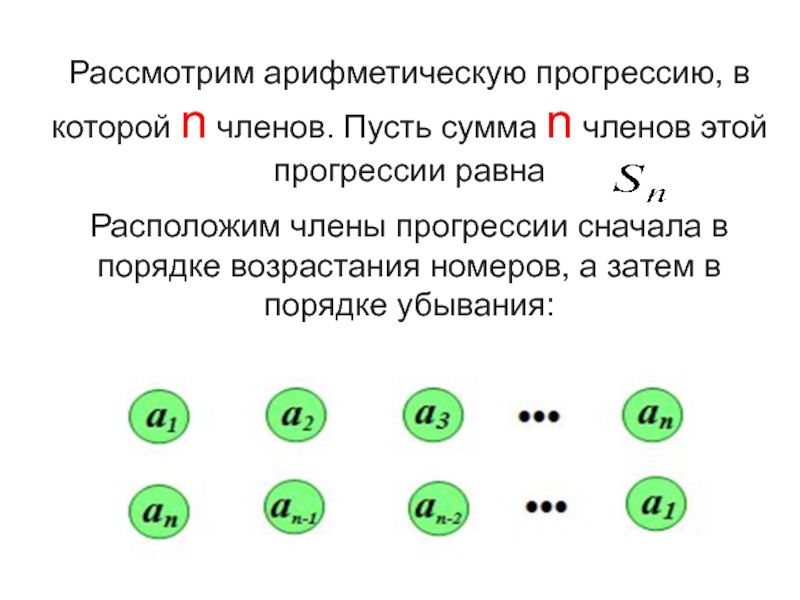
Рассмотрим арифметическую прогрессию, в которой n членов. Пусть сумма n членов этой прогрессии равна Расположим члены прогрессии сначала в порядке возрастания номеров, а затем в порядке убывания:
-
-
14 слайд
Сумма n-первых членов арифметической прогрессии:
-
15 слайд
Тренировочные упражнения-закрепления.
-
-
-
18 слайд
6. В угловом секторе стадиона в 1 ряду 7 мест, а в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в зале, если в нём 26 рядов? 7. Родители к дню рождения своего сына Коли решили купить ему новый планшет. Для этого они в первый месяц отложили 750 рублей, а в каждый последующий месяц они откладывали на 50 рублей больше, чем в предыдущий. Какая сумма будет у родителей Андрея через 10 месяцев? Задачи
-
19 слайд
8. В арифметической прогрессии а1= 3, а сумма первых семи её членов равна 0. Найдите разность арифметической прогрессии. 9. Бригада маляров красит забор длиной 400 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый день бригада покрасила 30 метров забора. Определите, сколько метров забора покрасила бригада в последний день, если вся работа была выполнена за 8 дней. Задачи
-
20 слайд
Задачи 10. Найдите сумму членов арифметической прогрессии с пятнадцатого по тридцатый включительно, если первый член равен 10 и разность равна 3. 11. При подготовке к экзамену ученик за семь дней решил 91 задачу. Каждый день он увеличивал количество решенных задач на одно и то же число. В первые четыре дня он решил 34 задачи. Сколько задач ученик решил в последний день? 12.Решить уравнение 1+3+5+…+х=307 Задачи
-
-
22 слайд
Домашнее задание Формулы Задачи № 6 – № 12 на листочках
-
23 слайд
Молодцы! Спасибо за урок!
Краткое описание документа:
Данная презентация поможет учителям математики в проведении урока по алгебре в 9 классе по теме «Формула суммы членов конечной арифметической прогрессии».
Презентация содержит материал для повторения, создание проблемной ситуации, а также тренировочные упражнения для закрепления и первичной проверки полученных знаний по новой теме, а ещё домашнее задание.
В работе представлена также легенда о юном Гаусе и физкультминутка с использованием формул арифметической прогрессии, где учащиеся молча, вставая и садясь отвечают на поставленный вопрос «Верно ли, что?». Призентация готова к применению.
Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:
6 155 066 материалов в базе
- Выберите категорию:
- Выберите учебник и тему
- Выберите класс:
-
Тип материала:
-
Все материалы
-
Статьи
-
Научные работы
-
Видеоуроки
-
Презентации
-
Конспекты
-
Тесты
-
Рабочие программы
-
Другие методич. материалы
-
Найти материалы
Другие материалы
Рейтинг:
4 из 5
- 13.02.2015
- 9187
- 593
- 13.02.2015
- 534
- 1
- 13.02.2015
- 1871
- 3
- 13.02.2015
- 1290
- 8
- 13.02.2015
- 583
- 0
- 13.02.2015
- 3148
- 1
- 13.02.2015
- 544
- 0
Слайд 1Презентация
к уроку по алгебре
9 класс
Тема урока: Формула суммы членов
конечной арифметической прогрессии.
Автор:
учитель
МБОУ СОШ № 31
г.Ижевск
Павленко М.Н.

Слайд 2Будет ли последовательность арифметической прогрессией?

Слайд 4Задачи
Найти сумму трёх членов арифме-тической прогрессии уn = — 4n
+ 5 .
— 9
2. Найдите сумму первых пяти членов арифметической прогрессия: -5,2; -0,2; 4,8….
24

Слайд 5Верно ли, что???
d = a4 – a5
an = a1 + (n – 1)d
a1
= an + (n -1)d

Слайд 6Задачи
3.Найдите сумму двадцати четырёх членов арифметической прогрессии

Слайд 7Формула Суммы Членов Конечной Арифметической Прогрессии

Слайд 8Задачи
4.Найдите сумму всех натуральных чисел от 1 до 100.

Слайд 9Легенда
Согласно легенде, школьный учитель математики, чтобы занять детей на долгое время,
предложил им сосчитать сумму чисел от 1 до 100.
Юный Гаусс (10 лет), ставший потом одним из самых знаменитых математиков мира, мгновенно получил результат: 5050.
1+2+3+4+5++…+97+98+99+100=?
А как бы считали вы?

Слайд 10Гаусс Карл Фридрих
(30.04.1777 — 23.02.1855)
Среди ученых
Карл Гаусс
носит имя «Король математики».

Слайд 12Рассмотрим арифметическую прогрессию, в которой n членов. Пусть сумма n членов
этой прогрессии равна
Расположим члены прогрессии сначала в порядке возрастания номеров, а затем в порядке убывания:
Слайд 14Сумма n-первых членов
арифметической прогрессии:

Слайд 15Тренировочные упражнения-закрепления.

Слайд 186. В угловом секторе стадиона в 1 ряду 7 мест, а
в каждом следующем на 2 больше, чем в предыдущем. Сколько мест в зале, если в нём 26 рядов?
7. Родители к дню рождения своего сына Коли решили купить ему новый планшет. Для этого они в первый месяц отложили 750 рублей, а в каждый последующий месяц они откладывали на 50 рублей больше, чем в предыдущий. Какая сумма будет у родителей Андрея через 10 месяцев?
Задачи

Слайд 198. В арифметической прогрессии а1= 3, а сумма первых семи её
членов равна 0. Найдите разность арифметической прогрессии.
9. Бригада маляров красит забор длиной 400 метров, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый день бригада покрасила 30 метров забора. Определите, сколько метров забора покрасила бригада в последний день, если вся работа была выполнена за 8 дней.
Задачи

Слайд 20Задачи
10. Найдите сумму членов арифметической прогрессии с пятнадцатого по тридцатый включительно,
если первый член равен 10 и разность равна 3.
11. При подготовке к экзамену ученик за семь дней решил 91 задачу. Каждый день он увеличивал количество решенных задач на одно и то же число. В первые четыре дня он решил 34 задачи. Сколько задач ученик решил в последний день?
12.Решить уравнение 1+3+5+…+х=307
Задачи

Слайд 22Домашнее задание
Формулы
Задачи № 6 – № 12 на листочках

Каталог заданий
Назад в каталог
Вернуться к списку прототипов этой категории
Версия для печати и копирования в MS Word
1
Тип 9 № 110603
Васе надо решить 91 задачу. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Вася решил 7 задач. Определите, сколько задач решил Вася в последний день, если со всеми задачами он справился за 7 дней.
Аналоги к заданию № 99581: 110551 110997 518909 518956 110553 110555 110557 110559 110561 110563 … Все
Кодификатор ФИПИ/Решу ЕГЭ: Задачи на прогрессии
Прототип задания
·
Предложите, как улучшить StudyLib
(Для жалоб на нарушения авторских прав, используйте
другую форму
)
Ваш е-мэйл
Заполните, если хотите получить ответ
Оцените наш проект
1
2
3
4
5
Цели урока:
обобщить и систематизировать материал по данной теме;
проверить знания основных формул арифметической прогрессии;
оценить умения решать ключевые задачи по данной теме;
рассмотреть применение формул арифметической прогрессии при решении практических задач;
развивать представления учащихся по использованию знаний об арифметической прогрессии в различных жизненных ситуациях;
способствовать развитию познавательного интереса учащихся, логического мышления, умений анализировать, выявлять закономерности, сопоставлять и обобщать полученные знания;
воспитывать культуру устной математической речи учащихся, ответственного отношения к учебному труду.
Тип урока: урок обобщения и систематизации знаний.
Этапы урока
Организационный момент.
Учитель объявляет тему и цели урока.
Исторический материал (сообщение ученика)
Первые представления об арифметической прогрессии были еще у древних народов. В клинописных вавилонских табличках и египетских папирусах встречаются задачи на прогрессии и указания, как их решать.
В древнеегипетском папирусе Ахмеса (ок. 2000 до н.э.) приводится задача: “Пусть тебе сказано: раздели 10 мер ячменя между 10 людьми так, чтобы разность мер ячменя, полученного каждым человеком и его соседом, равнялась 1/8 меры”.
Формула суммы членов арифметической прогрессии была доказана древнегреческим ученым Диофантом (в 3 веке). Формула суммы членов геометрической прогрессии дана в книге Евклида “Начала” (3 век до н.э.).
Известна интересная история о знаменитом немецком математике К. Гауссе (1777 — 1855), который в детстве обнаружил выдающиеся способности к математике. Учитель предложил учащимся сложить все натуральные числа от 1 до 100. Маленький Гаусс решил эту задачу за минуту. Сообразив, что суммы 1+100, 2+99 ит. д. равны, он умножил 101 на 50, т. е. на число таких сумм. Иначе говоря, он заметил закономерность, которая присуща арифметической прогрессии ( слайд3)
Повторение теории: ( слайд 4-9)
Чтобы успешно двигаться по всем этапам урока, давайте немного повторим.
Дайте определение арифметической прогрессии
(Арифметической прогрессией называется последовательность, каждый член которой, начиная со второго, отличается от предыдущего на одно и то же число)
Как проверить, является ли последовательность арифметической прогрессией?
(Каждый член арифметической прогрессии больше предыдущего на одно
и тоже число.)
Проверьте: является ли последовательность арифметической прогрессией:
-2; -4; -6; -8; -10;…
-13; -3; 13; 23;…
(Первая последовательность является арифметической, а вторая – нет).
— Назовите первый член этой прогрессии? (а1=-2)
— Чему равна разность этой прогрессии?(d=-2)
— Назовите шестой член этой прогрессии (а6=-12) ( слайд10)
Решить тест: (слайд11-12) – смотрите документ
Физкультминутка ( слайд13)
Эти упражнения улучшают кровообращение вашего мозга.
Ленивые восьмерки. Поставьте большой палец правой руки. Пальцем в воздухе пишем восьмерки, следим за пальцем глазами. Затем другой рукой. Обеими руками.
Сгибание шеи. Скрестив пальцы на затылке, поднять голову, смотреть вверх, согнуть шею смотреть вниз. Повторить 5 раз.
Групповое решение задач (с последующей проверкой) ( слайд14-17).
Для поливки 20 деревьев, расположенных по прямой линии на расстоянии 2 м друг от друга, садовник приносит воду для каждого отдельного дерева из колодца, находящегося на той же прямой линии в 10 м от первого дерева. Сколько всего метров пройдет садовник, чтобы полить все деревья и возвратиться к колодцу?
Компьютерная игра состоит в последовательном прохождении нескольких уровней. За прохождение каждого уровня игрок получает 50 баллов. Кроме того, начисляются и премиальные баллы по следующей схеме: 10 баллов за второй уровень и за каждый следующий уровень на 10 балов больше, чем за предыдущий. Сколько уровней надо пройти, чтобы набрать ровно 1100 баллов?
При подготовке к экзамену ученик за семь дней решил 91 задачу. Каждый день он увеличивал количество решенных задач на одно и то же число. В первые четыре дня он решил 34 задачи. Сколько задач ученик решил в последний день подготовки?
VII. Подведение итогов
Выставить и прокомментировать оценки учащихся. Отметить, с чем учащиеся справились, успешно, а на что нужно еще обратить внимание.
VIII. Домашнее задание ( слайд18)
Найти по 3 задачи, связанные с арифметической прогрессией из различных областей: физики, медицины и т. д. и решить их.
Андрей при подготовке к егэ поставил себе задачу решать каждый день на 5 задач
Первый член арифметической прогрессии: a1 = 7;
Последний член арифметической прогрессии: an = 37;
Разность арифметической прогрессии: d = 5;
Найдем количество дней n;
Общий член арифметической прогрессии равен:
An = a1 + d(n — 1);
37 = 7 + 5(n — 1);
5n = 37 — 2 = 35;
N = 7;
Общее количество решённых задач равно сумме членов арифметической прогрессии:
S7 = (a1 + an) · n / 2 = (7 + 37) · 7 / 2 = 154;
Ответ: Андрей решил 154 задачи.
- Написать правильный и достоверный ответ; Отвечать подробно и ясно, чтобы ответ принес наибольшую пользу; Писать грамотно, поскольку ответы без грамматических, орфографических и пунктуационных ошибок лучше воспринимаются.
- Списывать или копировать что-либо. Высоко ценятся ваши личные, уникальные ответы; Писать не по сути. «Я не знаю». «Думай сам». «Это же так просто» — подобные выражения не приносят пользы; Писать ответ ПРОПИСНЫМИ БУКВАМИ; Материться. Это невежливо и неэтично по отношению к другим пользователям.
Мореплаватель — имя существительное, употребляется в мужском роде. К нему может быть несколько синонимов.
1. Моряк. Старый моряк смотрел вдаль, думая о предстоящем опасном путешествии;
2. Аргонавт. На аргонавте были старые потертые штаны, а его рубашка пропиталась запахом моря и соли;
3. Мореход. Опытный мореход знал, что на этом месте погибло уже много кораблей, ведь под водой скрывались острые скалы;
4. Морской волк. Старый морской волк был рад, ведь ему предстояло отчалить в долгое плавание.
Писать грамотно, поскольку ответы без грамматических, орфографических и пунктуационных ошибок лучше воспринимаются.
Vashurok. ru
08.02.2017 13:46:10
2017-02-08 13:46:10
Источники:
Https://vashurok. ru/questions/andrey-pri-podgotovke-k-ege-postavil-sebe-zadachu-reshat-kazhdiy-den-na-5-zadach-bolshe-c
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Андрей при подготовке к егэ поставил себе задачу решать каждый день на 5 задач
Андрей при подготовке к егэ поставил себе задачу решать каждый день на 5 задач
Андрей при подготовке к егэ поставил себе задачу решать каждый день на 5 задач
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Найдите корень уравнения
В случайном эксперименте симметричную монету бросают дважды. Найдите вероятность того, что наступит исход ОР (в первый раз выпадает орёл, во второй — решка).
В треугольнике ABC угол C равен 58°, AD и BE — биссектрисы, пересекающиеся в точке O. Найдите угол AOB. Ответ дайте в градусах.
Найдите значение выражения если
Найдите объем многогранника, вершинами которого являются точки правильной шестиугольной призмы площадь основания которой равна 6, а боковое ребро равно 3.
На рисунке изображен график производной функции F(x), определенной на интервале (−10; 2). Найдите количество точек, в которых касательная к графику функции F(x) параллельна прямой Y = −2X − 11 или совпадает с ней.
Камень брошен вертикально вверх. Пока камень не упал, высота, на которой он находится, описывается формулой где H — высота в метрах, T — время в секундах, прошедшее с момента броска. Сколько секунд камень находился на высоте не менее 9 метров?
Четыре одинаковые рубашки дешевле куртки на 8%. На сколько процентов пять таких же рубашек дороже куртки?
На рисунке изображён график функции вида где числа A, B и C — целые. Найдите абсциссу вершины параболы.
Вероятность того, что новый электрический чайник прослужит больше года, равна 0,97. Вероятность того, что он прослужит больше двух лет, равна 0,89. Найдите вероятность того, что он прослужит меньше двух лет, но больше года.
Найдите точку минимума функции
А) Решите уравнение:
Б) Укажите корни этого уравнения, принадлежащие отрезку
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Дана правильная четырёхугольная пирамида SABCD с вершиной S. Точка M расположена на SD так, что SM : SD = 2 : 3. P — середина ребра AD, а Q середина ребра BC.
А) Докажите, что сечение пирамиды плоскостью MQP — равнобедренная трапеция.
Б) Найдите отношение объёмов многогранников, на которые плоскость MQP разбивает пирамиду.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Баба Валя, накопив часть своей пенсии, решила улучшить свое материальное положение. Она узнала, что в Спёрбанке от пенсионеров принимают вклады под определенный процент годовых и на этих условиях внесла свои сбережения в ближайшее отделение Спёрбанка. Но через некоторое время соседка ей рассказала, что недалеко от той местности, где проживают пенсионеры, есть коммерческий банк, в котором процент годовых для пенсионеров-вкладчиков в 20 раз выше, чем в Спёрбанке. Баба Валя не доверяла коммерческим банкам, но стремление улучшить свое материальное положение взяло верх. После долгих колебаний и ровно через год после открытия счета в Спёрбанке Баба Валя сняла половину образовавшейся суммы от ее вклада, заявив: «Такой навар меня не устраивает!» и открыла счет в том коммерческом банке, о котором говорила ее соседка, не теряя надежды на значительное улучшение своего материального благосостояния.
Надежды оправдались: через год сумма Бабы Вали в коммерческом банке превысила ее первоначальные кровные сбережения на 65%. Сожалела Баба Валя, что год назад в Спёрбанке сняла не всю сумму, а лишь половину, однако, подумала: «А где же мы не теряли. » Гендиректор коммерческого банка оказался хорошим: не оставил Бабу Валю без денег.
А каков в Спёрбанке процент годовых для пенсионеров?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Две окружности касаются внешним образом в точке K. Прямая AB касается первой окружности в точке A, а второй — в точке B. Прямая BK пересекает первую окружность в точке D, прямая AK пересекает вторую окружность в точке C.
А) Докажите, что прямые AD и BC параллельны.
Б) Найдите площадь треугольника AKB, если известно, что радиусы окружностей равны 4 и 1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Найдите все значения A, при каждом из которых модуль разности корней уравнения
Принимает наибольшее значение.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Вася и Петя решали задачи из сборника, и они оба решили все задачи этого сборника. Каждый день Вася решал на одну задачу больше, чем в предыдущий день, а Петя решал на две задачи больше, чем в предыдущий день. Они начали решать задачи в один день, при этом в первый день каждый из них решил хотя бы одну задачу.
А) Могло ли получиться так, что Вася в первый день решил на одну задачу меньше, чем Петя, а Петя решил все задачи из сборника ровно за 5 дней?
Б) Могло ли получиться так, что Вася в первый день решил на одну задачу больше, чем Петя, а Петя решил все задачи из сборника ровно за 4 дня?
В) Какое наименьшее количество задач могло быть в сборнике если каждый из ребят решал задачи более 6 дней, причем в первый день один из мальчиков решил на одну задачу больше чем другой?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
—>
Две окружности касаются внешним образом в точке K.
Math-ege. sdamgia. ru
24.01.2020 21:12:03
2020-01-24 21:12:03
Источники:
Https://math-ege. sdamgia. ru/test? id=43371230
Советы эксперта: Как сдать внутренний вступительный экзамен в МГУ. » /> » /> .keyword { color: red; } Андрей при подготовке к егэ поставил себе задачу решать каждый день на 5 задач
Советы эксперта: Как сдать внутренний вступительный экзамен в МГУ
Советы эксперта: Как сдать внутренний вступительный экзамен в МГУ
О том, как получить на внутреннем экзамене максимальный результат, «Учёбе. ру» рассказали преподаватели профильных факультетов университета.
Российские вузы принимают абитуриентов по результатам ЕГЭ, однако МГУ им. М. В. Ломоносова имеет особый статус. Университет получил право ежегодно проводить дополнительное вступительное испытание (ДВИ) на все специальности. ДВИ по каждому предмету проходит одновременно для всех факультетов, где этот экзамен присутствует в списке вступительных испытаний, по единым заданиям. Работы проверяются в зашифрованном виде и оцениваются по единым критериям. Результаты экзамена автоматически засчитываются везде, где абитуриент участвует в конкурсе.
Структура экзамена (темы, количество заданий по ним) до начала экзамена неизвестна, так же как и критерии оценки работ, их объявляют после публикации результатов. Экзамен оценивается по 100-балльной шкале.
Какие дополнительные экзамены сдают абитуриенты МГУ им. Ломоносова
ДВИ Факультеты
| Математика | Механико-математический, вычислительной математики и кибернетики, геологический, наук о материалах, экономический, биоинженерии и биоинформатики, фундаментальной физико-химической инженерии, государственного управления и др. |
| Физика | Физический |
| Химия | Химический, фундаментальной медицины, фундаментальной физико-химической инженерии |
| Биология | Биологический, биотехнологический, почвоведения, психологии |
| География | Географический |
| Литература | Филологический |
| История | Исторический, Институт стран Азии и Африки, политологии, мировой политики, глобальных процессов |
| Обществознание | Философский, юридический, социологический |
| Иностранный язык | Иностранных языков и регионоведения, глобальных процессов, Высшая школа перевода |
Математика
Самый популярный ДВИ в МГУ, его сдают абитуриенты более 10 факультетов, в том числе топовых: ВмиК, экономического, механико-математического. В последние годы поступающим предлагалось за четыре часа решить восемь задач.
«Что касается сложности экзамена, то первые две задачи из восьми, на мой взгляд, должен решать любой не троечник. Следующие четыре задания можно назвать средними. А вот последние две задачи обычно настолько сложны, что берутся за них единицы, а до ответа доходят еще меньше. Но были абитуриенты, которые решали и седьмую, и восьмую задачу. Конечно, это единичные случаи. Полной статистики у меня нет, но, по опыту моей работы в приемной комиссии, около 2% абитуриентов пытались решать эти задачи, и преуспели четверть из них, то есть 0,5% всех сдающих экзамен. Например, по условию прошлогодней задачи по стереометрии, в основании правильной пирамиды лежит шестиугольник. Даже начертить это условие, да еще со сложным сечением, уже очень непросто. А потому в этой задаче только за корректно нарисованный чертеж уже могли ставить какие-то баллы.
Я бы порекомендовал школьникам начинать готовиться к поступлению минимум за два года, то есть с 10 класса. На мой взгляд, это порочная практика — готовиться к конкретному экзамену, особенно в ситуации с ДВИ, когда ты не можешь предположить, что тебя там ждет на самом деле. Готовиться надо просто к математике, последовательно изучать все разделы, а не «натаскиваться» на конкретные типы задач. Если вам нужен невысокий балл, вы можете ограничиться «натаскиванием», но хорошего результата так не достичь.
Могу дать две рекомендации относительно плана действий на те четыре месяца, которые остались до экзамена. Первое: нужно сконцентрировать внимание на тех предметах, которые вы будете сдавать. На эти месяцы нужно отложить непрофильные предметы, все хобби и развлечения. Лучше это время провести, работая как монах, чем потом всю жизнь жалеть. Второе: необходимо повторить и держать в голове все формулы, определения и формулировки. Абитуриент, который поступает в МГУ и рассчитывает на положительную оценку по математике, должен уметь с ходу выписать любую необходимую формулу, относящуюся к любой из тем курса математики за все годы.
Что касается повторения тем и разделов, тут может быть две стратегии. Каждый абитуриент знает свои слабые места и может сосредоточиться на их «подтягивании». Или же, наоборот, если школьник видит, что в некоторых областях у него вопиющий провал, можно пожать плечами и сконцентрировать внимание на том, что он умеет хорошо, отточить задачи по этим темам до идеала.
Учитывайте, что ДВИ — это экзамен состязательный. Ваша задача — решить больше, чем конкуренты. Соответственно, можно выбрать несколько разделов и сконцентрироваться только на них. В любом случае я бы посоветовал повторить геометрию, поскольку в современной школе совсем плохо с этим предметом, особенно с доказательством теорем. Задача по планиметрии и задача по стереометрии в ДВИ обязательно будут».
Физика
Дополнительный экзамен по самому сложному школьному предмету пишут только абитуриенты физического факультета. Им предлагается решить четыре задачи.
«На экзамене традиционно дают четыре задачи примерно одинакового уровня сложности. Отличаются они по темам. Обычно первая задача — по механике, вторая — по молекулярной физике и термодинамике, третья — по электричеству и магнитным явлениям и четвертая — по оптике. Для хорошо подготовленного абитуриента все задачи решаемые.
Среди самых сложных тем для школьников прежде всего следует назвать физическую оптику. Правда, вероятность появления такой задачи на ДВИ невелика, пока она там не встречалась ни разу. Нередко вызывают затруднения задачи на движение тела по окружности, в частности, на применение законов Ньютона в этом случае. Также часто у абитуриентов есть проблемы с такой темой, как влажность. Это небольшая тема, которая находится внутри молекулярно-кинетической теории, при подготовке ей обычно уделяется мало внимания. Задача на влажность встречается редко, но тем не менее в 2014 году на ДВИ она была. Еще один непростой вопрос — это момент силы, а точнее, как определятся плечо силы. А вот среди самых беспроблемных тем, задачи по которым хорошо решаются, можно назвать законы сохранения в механике, геометрическую оптику и тепловой баланс.
ЕГЭ и ДВИ по физике — это два совершенно разных экзамена. Программа МГУ значительно шире. Есть темы и понятия, которые фигурируют в ДВИ, но их нет в ЕГЭ: например, поверхностное натяжение в жидкостях, тепловое расширение твердых тел и жидкостей, центр тяжести. В ЕГЭ большинство заданий соответствует определенной теме. В ДВИ все устроено несколько по-другому. Типичный случай — когда задача сочетает в себе несколько тем. Например, в 2013 году в третьей задаче совмещались электромагнитная индукция и динамика. Часто бывает сочетание геометрической оптики и кинематики. Плюс к этому, в ЕГЭ много типовых задач. Чтобы подготовиться, их нужно много решать, и тогда происходит узнавание. А в ДВИ задачи чаще формулируются нетипичным образом, абитуриенту нужно догадаться, каким путем идти к решению. Например, задачу по механике можно решать двумя разными путями. Это так называемые энергетический и динамический подходы. Понять, какой именно приведет к правильному результату, — вопрос не очевидный. Для ДВИ нужно не столько знать формулы, сколько понимать, какую формулу применить и в какой ситуации.
Что касается подготовки к ДВИ, в программе экзамена на сайте МГУ есть список рекомендованной литературы, в нем около 15 книг. Это основа для подготовки. Я бы посоветовал абитуриентам придерживаться следующей схемы. Сначала нужно прорешать любой из вариантов ДВИ прошлых лет, чтобы оценить свои силы. Если совсем не получается, то надо решать материал задачников из списка литературы. Если в целом получается, но есть задачи, которые вызывают сложности, нужно почитать теорию по этой теме в учебнике, освежить ее в памяти и потом еще раз вернуться к задаче.
За оставшееся до экзамена время я бы порекомендовал абитуриентам повторить геометрическую оптику, все разделы механики и электричества. В молекулярно-кинетической теории и термодинамике необходимо обратить внимание на задачи, где требуется определить изменение внутренней энергии идеального газа или совершенную им в результате некоего процесса или цикла работу».
Обществознание
Абитуриенты социологического, философского и юридического факультетов сдают экзамен по обществознанию. За четыре часа они должны в письменном виде раскрыть четыре предложенные темы. Например, в вариантах 2016 года были такие вопросы: «Предмет и метод экономической науки», «Политические институты», «Географический детерминизм в философии истории».
«Требования ДВИ обязывают членов методических комиссий, разрабатывающих задания, не выходить за рамки школьной программы. Задания составляются на основе школьных учебников, которые имеют гриф «Рекомендовано Министерством образования и науки РФ». Четыре темы экзамена относятся к разным разделам предмета. Формулировки заданий носят предметный характер и практически не отличаются от названий разделов (глав, тем) учебников. Все темы имеют одинаковый объективный уровень сложности. Это обязательная установка, которой придерживаются разработчики заданий.
Есть темы, которые, по моему опыту, вызывают наибольшие затруднения у школьников. Они связаны с изложением различных концепций и теорий из истории обществоведческой мысли. Хотя формулировки таких вопросов также берутся из учебников, их рассмотрение обычно разбросано по разным разделам, и дети не акцентируют на них внимание. К тому же, при подготовке к ЕГЭ учителя уделяют этим вопросам меньше времени, так как их практически нет в заданиях ЕГЭ. А писать эссе по философским темам вообще не рекомендуют.
В 2016 году в ДВИ было две подобные темы — «Материалистическое понимание истории» и «Теория географического детерминизма». Думающий абитуриент, немного владеющий обществоведческой терминологией, мог бы аналитически домыслить ответы на эти вопросы. Вспомнив, что такое материализм, и учитывая его специфику, отличие от идеализма, его проявление в социальном развитии, он смог бы изложить основы этой концепции. А по второму вопросу школьник мог бы вспомнить, что такое детерминизм, что он связан с поиском единого фактора-причины развития, и догадаться, что надо обратить внимание на географию (природу, ландшафт) в качестве главной причины общественного развития. Вспомнив, что древние цивилизации возникали в долинах рек и на морском побережье, он смог бы развить свою мысль. Возможно, он и не назвал бы имен хотя бы Маркса (по первой теме) и Монтескье (по второй), но какое-то количество баллов получил бы.
На экзамене может быть всякое. Никто не исключает психологический фактор. Волнение нередко приводит к неправильному пониманию проблемы. Бывает, что абитуриент пишет не по теме. Однажды на ДВИ была тема «Отличие деятельности человека от активности животных». Некоторые поступающие написали, чем отличается человек от животного. Написали хорошо, но получили «неуд» за эссе не по теме. Вообще, школьники нередко не дочитывают задание и в результате пишут ответ на другой вопрос.
Дорогие абитуриенты, если вы утвердились в своем выборе и решили, что вам надо сдавать обществознание, берите школьные учебники (прежде всего, Боголюбова) и работайте. Открывайте раздел, читайте его и пишите по нему сочинение (эссе). Не игнорируйте сноски, задания, которые приводятся после каждого раздела. В них тоже много информации, которая может вам пригодиться. Многие теории, концепции излагаются именно там».
Биология
Дополнительный экзамен по биологии предусмотрен для поступающих на биологический и биотехнологический факультеты. Также его сдают будущие психологи и почвоведы. За четыре часа абитуриентам предстоит в письменной форме раскрыть четыре темы из разных разделов биологии.
«Два или три года назад из ДВИ по биологии убрали тестовый блок и задачу по генетике. Однако это не значит, что их не будет в этом году. В последнее время экзамен состоял из четырех вопросов с развернутым ответом. Обычно в задании требуется полностью описать определенную систематическую группу, например, паукообразных: внутреннее и внешнее строение, размножение и развитие, видовое разнообразие. Есть вопросы, где нужно описать строение цветка и соцветий. Это примеры заданий из вариантов прошлого года. К подводным камням здесь стоит отнести поверхностность ответа некоторых ребят, которые дают краткую характеристику и сразу переходят к следующему вопросу.
При подготовке к таким заданиям я бы посоветовал обратить внимание на отличительные особенности строения, поведения и размножения, запомнить несколько представителей класса, отряда или семейства. Добавит баллы правильно нарисованный рисунок или схема: иллюстрация всегда засчитывается. Плюсом к ответу также будет, если вы покажете, где находится предлагаемая систематическая группа относительно представителей другого типа. Например, если вы даете характеристику класса паукообразных, нужно отметить, что они относятся к типу членистоногих, так же, как ракообразные и насекомые. А в состав класса паукообразных входят отряды скорпионов, клещей, пауков и другие.
Часто ребята при подготовке делают упор на общую биологию и генетику, забывая курс ботаники, анатомии и зоологии. А ведь эти темы чаще всего вызывают затруднения, и по ним составлена основная часть вопросов ДВИ прошлых лет. Что касается самых простых разделов биологии, то сюда относятся основы экологии, учение о биосфере и селекция.
Есть ребята, которые заблаговременно готовятся к поступлению на биологический факультет МГУ. Они учатся в профильных биологических классах, участвуют в летних школах, проходят через «сито» олимпиад. Благодаря такой подготовке многие уже в 10-11 классе становятся настоящими маститыми биологами и могут дать фору даже студентам биофака. Сейчас, за несколько месяцев до экзамена, такие абитуриенты занимаются по своему плану, который составили либо сами, либо с репетитором или школьным учителем. А вот те школьники, которые только начали готовиться к ДВИ, должны приложить огромные усилия, чтобы подойти к экзамену в лучшей форме. Я думаю, они и сами это понимают. В первую очередь, я советую им обратить внимание на ботанику высших растений, зоологию, клеточное деление (митоз, мейоз) и анатомию человека, подробно разобрать механизм работы каждой системы органов.
При хорошей подготовке ДВИ по биологии вполне реально написать на 90 и более баллов — это удается 10% поступающих. Примерно пятая часть сдающих экзамен получают крайне низкие оценки — менее 50 баллов (при том, что на тройку надо набрать 40 баллов). На 100 баллов экзамен сдать возможно. Правда, это бывает достаточно редко: менее 1% абитуриентов добиваются такого результата. 98-99 баллов встречается намного чаще».
На сайте центральной приемной комиссии МГУ можно найти подробную программу экзаменов на все факультеты, а также варианты заданий прошлых лет.
Ваша задача решить больше, чем конкуренты.
Www. ucheba. ru
02.07.2019 21:35:17
2019-07-02 21:35:17
Источники:
Https://www. ucheba. ru/article/4410
ЕГЭ–2022, математика: задания, ответы, решения. Обучающая система Дмитрия Гущина. » /> » /> .keyword { color: red; } Андрей при подготовке к егэ поставил себе задачу решать каждый день на 5 задач
Андрей при подготовке к егэ поставил себе задачу решать каждый день на 5 задач
Андрей при подготовке к егэ поставил себе задачу решать каждый день на 5 задач
Ускоренная подготовка к ЕГЭ с репетиторами Учи. Дома. Записывайтесь на бесплатное занятие!
—>
Задание 8 № 99581
Васе надо решить 434 задачи. Ежедневно он решает на одно и то же количество задач больше по сравнению с предыдущим днем. Известно, что за первый день Вася решил 5 задач. Определите, сколько задач решил Вася в последний день, если со всеми задачами он справился за 14 дней.
В первый день Вася решил задач, в последний — задач. Всего надо решить задач. Поскольку где имеем:
—>
Задание 8 № 99581
Уско рен ная под го тов ка к ЕГЭ с ре пе ти то ра ми Учи.
Ege. sdamgia. ru
22.08.2017 15:43:44
2017-08-22 15:43:44
Источники:
Http://ege. sdamgia. ru/test? pid=99581
Ответы: при подготовке к экзамену ученик решил за 7 дней 91 й день он увеличевал количество решенных задач на одно и » /> » /> .keyword { color: red; } Андрей при подготовке к егэ поставил себе задачу решать каждый день на 5 задач
При подготовке к экзамену ученик решил за 7 дней 91 й день он увеличевал количество решенных задач на одно и
При подготовке к экзамену ученик решил за 7 дней 91 задачу. каждый день он увеличевал количество решенных задач на одно и
При подготовке к экзамену ученик решил за 7 дней 91 задачу. каждый день он увеличевал количество решенных задач на одно и тоже число. впервый четыре дня он решил 34задачи. Сколько задач ученик решил в последний день подготовки?
А1 — число задач, решенных за первый день,
А2 — число задач, решенных за второй день,
.
А7 — число задач, решенных за седьмой день
Получаем арифметическую прогрессию а1, а2, ..а7
Сумма ее первых семи членов равна 91,
А сумма ее первых четырех членов равна 34
0,5(а1 + а7)*7 = 91, отсюда а1 + а7 = 26
0,5(а1 + а4)*4 = 34, отсюда а1 + а4 = 17
Тогда а7 — а4 = 26 — 17 = 9
А4 + 3d — a4 = 9, отсюда 3d = 9, d = 3
A1 + a1 + 3d = 17, подставив d = 3, получим, что 2а1 = 8, а1 = 4
Тогда а7 = а1 + 6d = 4 + 6*3 = 22
Значит, в последний день подготовки ученик решил 22 задачи
Ответ: 22 задачи.
В последний день подготовки ученик решил 22задачи, так как изначально в 1 день он решил 4 задачи, а прибавлял каждый день по 3 задачи
Сколько задач ученик решил в последний день подготовки.
Otvet. mail. ru
30.10.2019 12:12:24
2019-10-30 12:12:24
Источники:
Http://otvet. mail. ru/question/22675200
Есть Ответ: андрей при подготовке к егэ поставил себе задачу решать каждый день на 5 задач больше, чем в предыдущий. за первый день он решил 7 задач, а за последний — 37 задач. сколько всего он решил задач? (решать арифметической прогрессией) » /> » /> .keyword { color: red; } Андрей при подготовке к егэ поставил себе задачу решать каждый день на 5 задач
Андрей при подготовке к егэ поставил себе задачу решать каждый день на 5 задач больше, чем в предыдущий. за первый день он решил 7 задач, а за последний — 37 задач. сколько всего он решил задач? (решать арифметической прогрессией)
Андрей при подготовке к егэ поставил себе задачу решать каждый день на 5 задач больше, чем в предыдущий. за первый день он решил 7 задач, а за последний — 37 задач. сколько всего он решил задач?(решать арифметической прогрессией)
Андрей при подготовке к егэ поставил себе задачу решать каждый день на 5 задач больше, чем в предыдущий. за первый день он решил 7 задач, а за последний — 37 задач. сколько всего он решил задач? (решать арифметической прогрессией)
Если выразить условие задачи через арифметическую прогрессию, то: а₁=7; d=5; [latex] a_ =37[/latex] [latex] S_[/latex]-? [latex] a_ = a_+d(n-1)[/latex] 37=7+5(n-1) 5(n-1)=30 n-1=6 n=7, т. е. 37 седьмой член прогрессии [latex] S_= frac< a_+ a_> *n[/latex] [latex]S_= frac< 7+ 37> *7=154[/latex] задачи решил Андрей за все время Ответ:154 задачи
Решать арифметической прогрессией.
Cwetochki. ru
15.12.2019 0:35:22
2019-12-15 00:35:22
Источники:
Http://cwetochki. ru/question-andrey-pri-podgotovke-k-ege-postavil-sebe-zadachu-reshat-kazhdyy-den-na-5-zadach-bolshechem-v-predydushch. html
17 месяцев назад
При подготовке к экзамену ученик каждый день увеличивал количество решенных задач на одно то же число. С 3 мая по 6 мая
включительно он решил 24 задачи, а с 5 мая по 10 мая – 72 задачи. Сколько задач ученик решил с 3 по 10 мая включительно? А) 376 Б) 80 В) 76 Г) 280
Мы не размещаем вопросы, которые:
- повторяют уже опубликованные;
- содержат брань и нецензурную лексику;
- состоят из одних символов;
- не соответствуют указанному предмету;
- отсылают к картинкам/страницам учебника, которые невозможно посмотреть





























