При проведении диагностических работ по подготовке к огэ егэ следует подбирать задачи прямые аналоги - Помощь в подготовке к экзаменам и поступлению

Рекомендации по подготовке обучающихся к успешной сдаче ЕГЭ по математике.

Содержание:

Рекомендации по совершенствованию преподавания математики с учётом результатов ЕГЭ. Некоторые эффективные приёмы обучения математике. Развитие геометрических представлений. Саморегуляция и обратная связь «ученик-учитель». Завершающие рекомендации.

Лекция.

Рекомендации по совершенствованию преподавания математики с учётом результатов ЕГЭ.

В основу построения рекомендаций положены принципы развития математического образования, определение приоритетных и перспективных направлений, а также анализ наиболее типичных ошибок, допущенных в решении заданий базового и профильного экзамена.

Практика показывает, что прорешивание открытых вариантов ЕГЭ прошлых лет не даёт ожидаемого эффекта. Разобрав вариант в классе, учитель даёт аналогичный вариант для домашнего разбора. После удачного разбора в классе домашний вариант не представляет большого труда, и у обучающегося и учителя складывается ложное впечатление, что подготовка идет эффективно и цель достигнута. Многократное повторение этих манипуляций не улучшает ситуацию. Когда участник на ЕГЭ получает свой вариант, он обнаруживает, что этот вариант он с учителем не решал. Привычка повторять разобранные ранее варианты часто идет во вред обучению.

Правильным подходом является систематическое изучение материала, решение большого числа задач по каждой теме – от простых к сложным, изучение отдельных методов решения задач. Разумеется, варианты подготовительных сборников, открытые варианты можно и нужно использовать в качестве источника заданий, но их решение не должно становиться главной целью; они должны давать возможность иллюстрировать и отрабатывать те или иные методы. В любом случае, при проведении диагностических работ следует подбирать задачи, прямые аналоги которых в классе не разбирались. Только так учитель может составить верное представление об уровне знаний и умений своих учеников.

Компенсирующее обучение в старших классах.

Часто мы сталкиваемся с ситуацией, когда главенствующим методическим принципом оказывается принцип «прохождения программы», – то есть программа должна быть пройдена во что бы то ни стало, невзирая на то, что содержание этой программы может не отвечать реальным возможностям и подготовке обучающихся.

С введением нового ФГОС, реализацией Концепции развития математического образования, принятием федеральных примерных образовательных программ по математике принцип прохождения программы приобретает новый смысл – обучающийся должен участвовать в посильной интеллектуальной математической деятельности, дающей осязаемые плоды обучения.

Компенсирующая программа как вариант базовой программы для старших классов даёт возможность учителю сделать уроки математики для наименее подготовленных обучающихся осмысленными. При этом появляется реальная возможность эффективно подготовить обучающихся к базовому ЕГЭ или к решению 8 – 10 заданий профильного ЕГЭ.

Практико-ориентированная математика.

Важной частью ЕГЭ по математике и современных программ являются задачи на применение математических знаний в быту, в реальных жизненных ситуациях. Это задачи на проценты, оптимальный выбор из предложенных вариантов, чтение данных, представленных в виде диаграмм, графиков или таблиц, вычисление площадей или других геометрических величин по рисунку, задачи на вычисление по формулам и т.п.

Круг практико-ориентированных задач в ОГЭ и ЕГЭ обоих уровней постоянно расширяется; дополнительно к ним следует отнести задачи вероятностно-статистического блока.

Сложилась практика, когда к практическим задачам учитель приступает только в последний год перед сдачей ЕГЭ. К этому времени обучающиеся успели прочно забыть, как вычислять проценты, как находить площади фигур с помощью палетки или на клетчатой бумаге – все эти задачи для них оказываются новыми.

На протяжении всего периода обучения математике не следует отрываться от простых практических задач; их следует включать в блоки повторения в начале и конце учебного года, в текущий, внутришкольный контроль. Задачи на вычисление сумм налогов, процентов по банковскому вкладу или кредиту, другие задачи финансового характера должны стать постоянным инструментом на уроках математики, поскольку эти задачи связывают наш предмет с окружающим миром и повседневной жизнью.

С 2010 года удалось изменить ситуацию, когда перевод одних единиц в другие или деление с остатком вызывал затруднения у 60 – 70% участников ЕГЭ. Сейчас на практическом уровне ситуация существенно улучшилась.

Практико-ориентированные задачи по финансовой грамотности, геометрического плана, чтение таблиц и графиков нужно включать в изучение математики в средней и старшей школе. При этом характер и трудность задач могут меняться со временем, более того, это необходимо для органического вплетения практических тем в изучение теоретических вопросов. Например, задачи на вклады и кредиты органично возникают при изучении прогрессий, показательной функции и производных. Вычисление площадей по клеточкам очень часто помогает при изучении совершенно абстрактной, казалось бы, темы «первообразная и интеграл». Чтение простых графиков помогает понять и грамотно на качественном уровне применять производную.

Отдельную важную роль в сближении школьной математики с задачами окружающего мира играют вопросы вероятностей и статистики.

ТВ и статистика.

В Концепции развития математического образования ТВ и статистика названы в числе перспективных и важных направлений развития школьной математики. С 2012 года задачи по ТВ формально включаются в КИМ ОГЭ и ЕГЭ. При этом учителя понимают, что те задачи, которые сейчас есть в открытом банке заданий и те, что включены в экзамен, в большинстве случаев сводятся к перечислению равновозможных исходов.

Ясно, что роль ТВ и статистики в школьной математике будет расти. Одновременно будет расширяться круг тем, подлежащих контролю.

При обучении математике следует больше внимания уделять темам вероятности и статистики, постепенно нарабатывая опыт преподавания этих разделов, которые оказываются наиболее практически направленными. Изучение вероятности и статистики требуется вести в тесной привязке к темам алгебры и геометрии, поскольку систематический подход к вопросам ТВ требует от обучающихся знаний о свойствах геометрической прогрессии преобразованиях многочленов, корнях и степенях, площадях фигур.

Таким образом, правильно выстроенное преподавание вероятности не отнимает время, а, напротив, поддерживает изучение традиционных разделов школьной математики. В 2012 – 2014 году задачи по ТВ, появившись в экзамене, вызывали большие трудности, и выполнение этих заданий редко поднималось выше 50%. В настоящее время ситуация изменилась. На данный момент в базовом экзамене медиана выполнения задания 10 – около 70% по разным вариантам, а в профильном – около 90%.

Некоторые эффективные приёмы обучения математике.

Остановимся подробнее на некоторых приёмах обучения математике, доказавших свою эффективность.

1) При решении задач одним из эффективных приёмов является использование примеров и образцов. Скажем, ученик получает задачу и готовое решение, которое он должен разобрать самостоятельно. Решение может быть дополнено советами, комментариями трудных или «опасных» моментов, другими способами решения и т.п. Когнитивная нагрузка в данном случае получает управляющий импульс и осуществляется в заданном направлении. Важным условием является выход на стратегию, которую можно будет применить в дальнейшем при решении широкого круга задач. Следующим этапом может стать работа не с готовым решением, а с заданным алгоритмом решения, который ученик должен самостоятельно применить к данной ему задаче. После этого можно провести решение полностью самостоятельно. Покажем это (без потери общности) на простой задаче.

Условие. Каждый из двух друзей одновременно показывает на руке случайное количество пальцев от 1 до 5. С какой вероятностью в сумме получится число 8?

Решение. Общее число исходов равно: 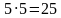. Благоприятными событию «получится в сумме число 8» будут исходы: 3 + 5, 5 + 3, 4 + 4. Вероятность события равна: 3/25 = 0,12. Ответ: 0,12.

Комментарий. Следует различать две комбинации, когда один из друзей показывает 3 пальца, а другой – 5 пальцев. Ответ можно записать как обыкновенной дробью, так и десятичной.

Задание для самостоятельного решения. Каждый из двух друзей показывает на руке случайное количество пальцев от 1 до 5. С какой вероятностью в сумме получится число 7?

Описанный приём может использоваться применительно к отдельному заданию, однако из таких заданий – с решениями и комментариями – можно составить тематическую проверочную работу, которую можно использовать и в рамках подготовки к экзамену. Решения могут быть написаны учителем самостоятельно, могут быть взяты из публикуемых сборников для подготовки к ЕГЭ, а также из материалов журнала «Математика» или других источников.

2) Весьма эффективно использование при решении задач подсказок, то есть некоторой дополнительной информации, которая дается ученику после (что важно!) того, как он начал работать над задачей. Чем определеннее подсказка, тем больше из нее можно извлечь. Фразы: «Хорошо подумай», «Внимательно прочти условие задачи», «Подумай о других способах решения» подсказками не являются, поскольку они никак не направляют ход мысли и не помогают найти решение.

Пример.

Решите уравнение .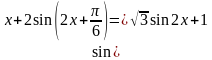

Подсказка. Можно применить формулу синуса суммы двух углов. Подсказкой может быть похожая задача, которая решалась недавно, указание на конкретный метод. Всегда полезно использовать результаты, методы уже решённых задач, а также опыт, приобретенный при решении. Это широко используется в школьном курсе геометрии, где многие важные геометрические факты, которыми целесообразно пользоваться при решении других задач, даны не в виде утверждений (теорем), а в виде задач. Кроме того, это возможность использования еще одного метода – аналогии.

При решении тригонометрических уравнений подсказкой может быть определённая формула, а при решении логарифмического уравнения – свойство логарифма. Полезно учить пользоваться подсказками, искать их самостоятельно, а также учить давать подсказки.

3) При обучении решению сложных или трудоёмких в плане вычислений и преобразований задач полезно использовать групповые формы работы, а в качестве приёма – мозговой штурм. Основные принципы мозгового штурма: на первом этапе – предложение как можно большего количества решений, без оценки их применимости, рациональности и проч., на втором – анализ и вывод о целесообразности предложенного, выбор наиболее удачных идей и предложений. Ценность приема – в стимулировании поисковой активности на первом этапе и критичности мышления на втором. Хорошо применим данный прием при поиске различных способов решения геометрических задач и тригонометрических уравнений.

4) При решении текстовых задач важным приёмом, необходимым для усвоения, является переформулирование условия, отношений, связывающих входящие в задачу величины. Ниже приводится пример такой задачи из варианта профильного экзамена.

«Задание 11. Заказ на изготовление 323 деталей первый рабочий выполняет на 2 ч быстрее, чем второй. Сколько деталей изготавливает первый рабочий, если известно, что он изготавливает на 2 детали больше второго?»

Данную задачу экзаменуемые решили существенно хуже, чем аналогичную задачу с более привычной и хорошо отработанной фабулой, связанной с движением двух велосипедистов.

Умение переформулировать условие важно и при решении нестандартных задач, то есть таких, метод решения которых ученику не известен, не изучался и не отрабатывался на уроках.

Ещё более актуально это умение при решении практико- ориентированных задач, представляющих собой некоторую ситуацию из реальной жизни, которую необходимо преобразовать и описать на языке математики (то есть самостоятельно сформулировать задачу). В самом простом случае основа задачи будет следующая: за лестницей, которую прислонили к стене дома, надо распознать прямоугольный треугольник, гипотенузой которого и будет данная лестница.

Развитие геометрических представлений

Процент выполнения экзаменующимися геометрических заданий традиционно ниже, чем процент выполнения заданий алгебраических. Одна из основных причин – недостатки в формировании пространственного мышления учащихся. Массово эта проблема проявилась с уходом из общего образования такого учебного предмета, как черчение, и вряд ли стоит ожидать его возвращения – профессия конструктора перестала быть столь массово востребованной с приходом компьютерных технологий.

Эта проблема легла на плечи учителей математики, однако решение её известно: непрерывное развитие геометрических представлений и геометрического воображения обучающихся с 1 по 11 класс; наглядная геометрия в 1–6 классах; больше внимания геометрическому моделированию и конструированию (из плоских и пространственных фигур), геометрическим чертежам, построениям, изображениям от руки и с помощью различных чертёжных инструментов, на нелинованной и клетчатой бумаге.

Это отнюдь не означает, что всю геометрию надо свести к наглядности и к работе руками. Определения и доказательства, логика и аксиоматика важны для современного человека и для изучения геометрии не менее, но надо понимать, что в развитии человека всему отводится свое время, а несформированное наглядно-образное мышление, которое должно быть основой и этапом на пути формирования логического мышления, просто мешает его формированию.

Если вернуться к этапу обучения в старшей школе, то целесообразно использовать любые приёмы и средства, которые способствовали бы визуализации предлагаемых обучающимся задач. Это не только построение чертежей по условию задачи (что непросто сделать при проблемах с пространственным воображением), это прежде всего различные предметные модели (полезно для каждой решаемой задачи иметь соответствующую ей модель-подсказку, чтобы использовать её для визуализации условия, поиска и проверки решения), компьютерные программы, позволяющие выполнять стереометрические чертежи.

Полезно выделить эту работу в отдельный тематический практикум, на котором обучающиеся тренировались бы в изображении и моделировании пространственных тел, построении чертежей по условию задачи (в различных ракурсах, выбирая наиболее удобный для поиска решения), можно также организовать данную работу в рамках проекта.

Саморегуляция и обратная связь «ученик-учитель».

Известно, что эффективность обучения возрастает в случае самооценивания, поскольку ученик самостоятельно получает информацию о своих результатах, сам её анализирует, делает выводы о своем прогрессе, корректирует цели в случае необходимости. Но для этого необходимы критерии оценивания работы, которые должны быть у ученика не просто до начала выполнения конкретной работы, но желательно и в самом начале изучения темы. К сожалению, на практике более распространена ситуация, когда работа выдаётся ученику без критериев ее выполнения.

К саморегуляции относятся также вопросы, связанные с осознанностью знания и незнания. Объяснение учителя сродни лекционной форме предъявления новых знаний. В связи с этим подчеркнём важность обратной связи. Учитель должен получать сигналы от обучающихся: «Я понимаю, могу объяснить», «Я не уверен, правильно ли я понимаю», «Я не понимаю». Учитель может прервать своё объяснение вопросом к тем, кто ещё не понял, предложением высказать свои сомнения тем, кто не уверен в понимании, предоставлением слова тем, кто всё понял.

Доказано, что обратная связь эффективна, если ученик получает сообщение о верно выполненных заданиях, а не только об ошибках, если он получает не просто маркеры, свидетельствующие о положительном результате, не просто похвалу за решённую задачу, а и некоторый содержательный комментарий. Этот комментарий может включать в себя такую оценку, как «рациональное решение», «красивое решение», «интересная идея», «грамотная запись». Может быть отмечена актуальность проверки результата, удачное прохождение «ловушек» и «опасных» мест и т.п.

Обратная связь эффективна в случае, если она конкретна, то есть связана с известными ученику результатами и действиями, подлежащими усвоению. Важное значение имеет информированность ученика относительно того, чему он должен научиться, какие задания должен научиться решать, а какие может научиться решать для того, чтобы получить желаемое количество баллов на экзамене. Если ученик фиксирует и отслеживает сам, умеет ли он выполнять требуемое задание или нет, то минимизируется время на выполнение заданий, при этом работа становится более эффективной и рациональной. Отсюда необходимость в открытости предъявляемых требований к результатам обучения, а на этапе подготовки к экзамену – в ориентации на конечный запланированный результат.

И еще об одном факторе следует упомянуть – это повторяющееся тестирование. Уже имеющийся опыт российской школы и более продолжительный зарубежный опыт не позволяют говорить о нём, как об эффективном факторе. Положительные эффекты возникают только в тех случаях, когда учитель учитывает результаты тестирования для корректировки процесса обучения и приспосабливает методы обучения к возможностям конкретного ученика, учитывая его сильные и слабые стороны, или при условии содержательной обратной связи, с которой ученик может работать самостоятельно, то есть имеет возможность учиться на тестах.

Завершающие рекомендации.

Необходимо отметить, что создание ЕГЭ по математике базового уровня и появление акцента на использование математических знаний в реальных ситуациях были неверно истолкованы некоторыми учителями в качестве генеральной идеи обучения, что привело к поверхностному освоению обучающимися программы старшей школы. В частности, это зафиксировано и результатами экзамена: результаты выполнения заданий по темам курса старшей школы ниже результатов выполнения заданий из «реальной математики».

Для того чтобы успешно сдать ЕГЭ по математике, важно пройти всю программу целиком, а не только «то, что пригодится на экзамене», повысить свою культуру вычислений, то есть минимизировать использование калькуляторов, развивать умение читать графики, правильно использовать терминологию и учить формулы.

Для учащихся, которые могут успешно освоить курс математики средней (полной) школы на базовом уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на базовом уровне. Помимо заданий базового уровня в образовательном процессе должны использоваться задания повышенного уровня. Количество часов математики должно быть не менее 5 часов в неделю.

Для учащихся, которые могут успешно освоить курс математики полной (средней) школы на профильном (повышенном) уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на профильном уровне. Количество часов математики должно быть не менее 6–7 часов в неделю.

В первую очередь нужно выработать у обучающихся быстрое и правильное выполнение заданий части 1, используя, в том числе и банк заданий экзамена базового уровня. Умения, необходимые для выполнения заданий базового уровня, должны быть под постоянным контролем.

Задания с кратким ответом (повышенного уровня) части 2 должны находить отражение в содержании математического образования, и аналогичные задания должны включаться в систему текущего и рубежного контроля.

В записи решений к заданиям с развернутым ответом нужно особое внимание обращать на построение чертежей и рисунков, лаконичность пояснений, доказательность рассуждений.

И в завершение необходимо отметить, что еще одним важным фактором является психологический климат в учебном коллективе: дружеские отношения среди одноклассников, спокойная рабочая атмосфера на уроке, методичная, прозрачная и последовательная подготовка к экзамену, доверительные отношения учителя с учениками, вера в достижение более высоких результатов и эмоциональная поддержка.

Литература:

Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2018 года по математике, подготовленные ФГБНУ «ФИПИ».
Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2017 года по математике, подготовленные ФГБНУ «ФИПИ».

Источник

ДОКЛАД

Эффективные приемы и методы подготовки учащихся к успешной сдаче ЕГЭ по математики.

Возрастание роли математики в современной жизни привело к тому, что для адаптации в современном обществе и активному участию в нем необходимо быть математически грамотным человеком. В связи со стратегическими направлениями социально — экономического развития России до 2020 года: «Приоритетной государственной задачей является обеспечение качественного базового уровня математических и естественнонаучных знаний у всех выпускниковшколы, не только будущих ученых, но и будущих квалифицированных рабочих…» Каждый школьник в процессе обучения должен иметь возможность получить полноценную подготовку к выпускным экзаменам. Формула успеха хорошо сдать экзамен ЕГЭ и ОГЭ по математике: Высокая степень восприимчивости + мотивация + компетентный педагог.

Компенсирующее обучение в старших классах.

Компенсирующая программа как вариант базовой программы для старших классов даёт возможность учителю сделать уроки математики для наименее подготовленных обучающихся осмысленными. При этом появляется реальная возможность эффективно подготовить обучающихся к решению 8 – 10 заданий профильного ЕГЭ.

Практико-ориентированная математика.

Круг практико-ориентированных задач в ЕГЭ постоянно расширяется; дополнительно к ним следует отнести задачи вероятностно-статистического блока.

Теория вероятности и статистика.

Таким образом, правильно выстроенное преподавание вероятности не отнимает время, а, напротив, поддерживает изучение традиционных разделов школьной математики. В 2012 – 2014 году задачи по ТВ, появившись в экзамене, вызывали большие трудности, и выполнение этих заданий редко поднималось выше 50%. В настоящее время ситуация изменилась. На данный момент медиана выполнения задания 4 – около 90%.

Некоторые эффективные приёмы обучения математике.

Остановимся подробнее на некоторых приёмах обучения математике, доказавших свою эффективность.

1) При решении задач одним из эффективных приёмов является использование примеров и образцов. Скажем, ученик получает задачу и готовое решение, которое он должен разобрать самостоятельно. Решение может быть дополнено советами, комментариями трудных или «опасных» моментов, другими способами решения и т.п. Когнитивная нагрузка в данном случае получает управляющий импульс и осуществляется в заданном направлении. Важным условием является выход на стратегию, которую можно будет применить в дальнейшем при решении широкого круга задач. Следующим этапом может стать работа не с готовым решением, а с заданным алгоритмом решения, который ученик должен самостоятельно применить к данной ему задаче. После этого можно провести решение полностью самостоятельно. Покажем это (без потери общности) на простой задаче.

Решение. Общее число исходов равно: 25. Благоприятными событию «получится в сумме число 8» будут исходы: 3 + 5, 5 + 3, 4 + 4. Вероятность события равна: 3/25 = 0,12. Ответ: 0,12.

2) Весьма эффективно использование при решении задач подсказок, то есть некоторой дополнительной информации, которая дается ученику после (что важно!) того, как он начал работать над задачей. Чем определеннее подсказка, тем больше из нее можно извлечь. Фразы: «Хорошо подумай», «Внимательно прочти условие задачи», «Подумай о других способах решения» подсказками не являются, поскольку они никак не направляют ход мысли и не помогают найти решение.

Пример. Решите уравнение.

3) При обучении решению сложных или трудоёмких в плане вычислений и преобразований задач полезно использовать групповые формы работы, а в качестве приёма – мозговой штурм. Основные принципы мозгового штурма: на первом этапе – предложение как можно большего количества решений, без оценки их применимости, рациональности и проч., на втором – анализ и вывод о целесообразности предложенного, выбор наиболее удачных идей и предложений. Ценность приема – в стимулировании поисковой активности на первом этапе и критичности мышления на втором. Хорошо применим данный прием при поиске различных способов решения геометрических задач и тригонометрических уравнений.

4) При решении текстовых задач важным приёмом, необходимым для усвоения, является переформулирование условия, отношений, связывающих входящие в задачу величины. Ниже приводится пример такой задачи из варианта профильного экзамена.

5).В связи с введением обязательного ЕГЭ и ОГЭ по математике возникает необходимость научить учащихся решать быстро и качественно задачи базового уровня. При этом необыкновенно возрастает роль устных

вычислений, так как на экзамене не разрешается использовать калькулятор и таблицы. Можно научить учащихся выполнять простейшие (и не очень) преобразования устно. Конечно, для этого потребуется организовать отработку такого навыка до автоматизма,

на каждом уроке необходимо отводить 5 — 7 минут для проведения упражнений устных вычислений, предусмотренных программой каждого

класса. Устные упражнения активизируют мыслительную деятельность учащихся, требуют осознанного усвоения учебного материала; при их выполнении

развивается память, речь, внимание, быстрота реакции.

Если в 5 — 6 классах устный счет – это выполнение действий с числами:

натуральные числа, обыкновенные дроби, десятичные дроби, то в старших

классах – это могут быть:

7 класс: Формулы сокращенного умножения. Решение простейших ЛУР. Действия со степенью. График линейной

функции.

8 класс: Линейные неравенства и числовые промежутки.

Решение простейших линейных неравенств. Решение КВУР с помощью

теоремы Виета и частных случаев. Решение КВУР рациональными способами. Арифметический квадратный корень и его свойства. 9 класс: Решение неравенств 2 степени. Преобразование графиков функций. Формулы приведения. Значения тригонометрических функций.

10 — 11 классах: Вычисление производных. Простейшие тригонометрические неравенства. Тригонометрические формулы. Простейшие тригонометрические уравнения. Функции, обратные тригонометрическим. Преобразование графиков функций. Вычисление первообразных. Свойства логарифмов. Простейшие показательные уравнения

умножения”) для решения более сложных задач. Учитель по математике, знающий, с чем придется столкнуться школьнику на экзамене, кроме фундамента уделяет большую часть времени на занятии отработке вопросов специфики ЕГЭ и ОГЭ. Правильность оформления заданий, тактика и стратегия решения в условиях дефицита выделенного времени на экзамене, а также банальная невнимательность. Эти и масса других особенностей составляют

суть специфики. Для эффективной подготовки к ЕГЭ и ОГЭ нужна тренировка, тренировка и еще раз тренировка. Довести решение задач до автоматизма.

Развитие геометрических представлений

Mногие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.

Работает ли эта стратегия?

Oтвет преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство (задание 15) и тем более — сложная «экономическая» задача. Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!

Cтоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.

1) Cамое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Cначала — теория. Cвойства геометрических фигур. Oпределения и теоремы. Учить наизусть.

Лучшая тренировка на этом этапе — задания №3 и №6 из первой части ЕГЭ по математике

2) Задача 16 Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. A на ЕГЭ остается только вспомнить и записать решение.

3) Oказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем.

4) Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы.

5.) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Mенелая и другую экзотику — вам это и не понадобится.

6) Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур — у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. B каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.

7) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. A это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б).

Саморегуляция и обратная связь «ученик-учитель».

Доказано, что обратная связь эффективна, если ученик получает сообщение о верно выполненных заданиях, а не только об ошибках, если он получает не просто маркеры, свидетельствующие о положительном результате, не просто похвалу за решённую задачу, а и некоторый содержательный комментарий. Этот комментарий может включать в себя такую оценку, как «рациональное решение», «интересная идея», «грамотная запись». Может быть отмечена актуальность проверки результата, удачное прохождение «ловушек» и «опасных» мест и т.п.

Завершающие рекомендации.

На занятиях стараюсь создать атмосферу комфортности,

взаимопонимания. На своих уроках я делаю установку на то, чтобы любой ребенок должен быть понят и услышан учителем и соучеником: учение должно проходить в «атмосфере непринужденности, чтобы дети и учитель свободно дышали на уроках». От учителя требуется и мастерство, и большое терпение, и любовь к учащимся. Доброжелательное отношение к ученикам снимает у них страх перед трудностями обучения: ребенок не должен бояться

ошибиться, спросить учителя, если он что то прослушал или не понял. Психологическая подготовка учащихся, может заключается в следующем:

отработка поведения в период подготовки к экзамену; обучение навыкам

саморегуляции, самоконтроля, повышение уверенности в себе, в своих силах. Методы проведения занятий по психологической подготовке учащихся разнообразны: групповая дискуссия, игровые методы, медитативные техники, Содержание занятий должно ориентироваться на следующие вопросы: как подготовиться к экзаменам, поведение на экзамене, способы снятия нервнопсихического напряжения, как противостоять стрессу.

Литература:

Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2019 года по математике, подготовленные ФГБНУ «ФИПИ».

Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2020 года по математике, подготовленные ФГБНУ «ФИПИ».

Бабанский Ю.К. Активность и самостоятельность учащихся в обучении / М.Ю. Бабанский М., Педагогика, 1989.

Беспалько В.П. Слагаемые педагогической технологии / Беспалько В.П. – М., 1989.

Красновский Э.А. Активизация учебного познания / Красновский Э.А. // Советская педагогика. – 1989. №5.

Эльконин Д. Б. Избранные педагогические труды. / Под ред. В.В. Давыдова, В.П. Зинченко.М., 1989.

Щукина Г.И. Активизация познавательной деятельности в учебном процессе/ Щукина Г.И. М., 1979.

Источник

«Из опыта работы
по подготовке учащихся к сдаче государственной итоговой аттестации по
математике»

Роль математики в современной жизни возрастает.
Человек в современном обществе должен быть математически грамотным ,чтобы
воплотить свою мечту , получить профессию , вести активную жизнь . В
связи со стратегическими направлениями социально — экономического
развития России : «Приоритетной государственной задачей
является обеспечение качественного базового уровня математических и
естественнонаучных знаний у всех выпускников школы, не только будущих ученых, но и будущих квалифицированных
рабочих…»

Ведущей целью
школьного математического образования является интеллектуальное развитие и
формирование качеств мышления учащихся, необходимых для полноценной жизни в
обществе. В школе работаю 40 лет учителем математики и каждый год проходим с
детьми государственную итоговую аттестацию в 9,11 классах (ОГЭ, ЕГЭ, ГВЭ )

Цель моей работы
– не только подготовить ученика к прохождению итоговой аттестации, но заложить
фундамент знаний по математике, необходимый для продолжения образования в 10 —
11 классах и в ВУЗе.

И приходится
делать каждый раз, когда начинаешь подготовку с очередным классом – это начать
с подготовки себя самой, составлять рабочую программу. Каждый год происходят
изменения в структуре КИМов , содержании материала В 11 классе материал
разделен на два уровня : базовый и профильный . В 9 классе добавили практико-
ориентированные задачи .Решение задач требует от учеников логического мышления
,умения представлять ситуацию ,сообразительность Плодотворно начинаем работать
с сентября месяца в 9,11 классах. А к итоговой аттестации начинаю готовиться с 7 класса Заводим тетрадь по теории и
практике В тетрадях по теории пишем алгоритмы ,приемы решений, формулы, а в
тетрадях по практике решаем задания из открытого банка и сайтов решу
ОГЭ,ЕГЭ,ГВЭ соответствующие темам из рабочей программы по математике. Эта
работа продолжается на всем протяжении обучения. Каждый урок начинается с устных
упражнений на применение таблицы умножения , вычислительных навыков и плавно
переходим к сложным заданиям. Начиная подготовку, и в процессе подготовки всем
учащимся рассказываю, как лучше организовать своё рабочее место для подготовки
к экзаменам, составить план занятий, разработать индивидуальный режим дня, с
чего начать занятие, как учитывать особенности запоминания, использовать методы
релаксации и активизации, приемы снижения экзаменационной тревожности, как
организовать день перед экзаменом, настроить свои мысли на успех, как вести
себя на экзамене, использовать полезные ссылки на Интернет-ресурсы по
подготовке. Для родителей проводим родительское собрание, где знакомим с
организацией и проведением ГИА и с тем как необходимо к экзамену подготовиться,
чтобы получить высокий результат, набрать максимальное количество баллов.

На
первом занятии знакомлю учащихся с нормативно-правовыми документами, провожу
инструктаж по правилам выполнения КИМов. Знакомимся с содержанием работ, их
особенностями В классе оформляю
стенд с заданиями из КИМов, оценивание заданий и перевод баллов Подготовка
к ЕГЭ требует индивидуального, личностно ориентированного подхода Повысить
уровень обученности, качество знаний учащихся позволяет использование
мониторинга знаний умений и навыков, применение самодиагностики, самооценки,
проведение индивидуальной работы с учениками по ликвидации пробелов в
знаниях. Хороший результат отслеживания показателей обучения каждого выпускника
дают работы которые провожу ежемесячно с ноября по апрель в 9-11 классах
Для эффективной подготовки к ЕГЭ и ОГЭ нужна тренировка, тренировка и
еще раз тренировка. Довести решение задач до автоматизма
Поэтому я решаю до 50 типов заданий по каждой теме ,но они отличаются друг от
друга Ребятам приходится думать , использовать знания не в стандартной
ситуации. Это укрепляет знания и снимает тревожность ,если задания будут не
похожие Практика показывает, что
прорешивание открытых вариантов ЕГЭ прошлых лет не даёт ожидаемого эффекта.
Разобрав вариант в классе, учитель даёт аналогичный вариант для домашнего
разбора. После удачного разбора в классе домашний вариант не представляет
большого труда, и у обучающегося и учителя складывается ложное впечатление, что
подготовка идет эффективно и цель достигнута. Многократное повторение этих
манипуляций не улучшает ситуацию. Когда участник на ЕГЭ получает свой вариант,
он обнаруживает, что этот вариант он с учителем не решал. Привычка повторять разобранные
ранее варианты часто идет во вред обучению.

Правильным подходом является систематическое изучение
материала, решение большого числа задач по каждой теме – от простых к сложным,
изучение отдельных методов решения задач. Разумеется, варианты подготовительных
сборников, открытые варианты можно и нужно использовать в качестве источника
заданий, но их решение не должно становиться главной целью; они должны давать
возможность иллюстрировать и отрабатывать те или иные методы. В любом случае,
при проведении диагностических работ следует подбирать задачи, прямые аналоги
которых в классе не разбирались. Только так учитель может составить верное
представление об уровне знаний и умений своих учеников

Этот нелёгкий
процесс более эффективен в случае, когда сами учащиеся осознанно прогнозируют
результаты своего обучения. Определив типологию
пробелов в знаниях учащихся по итогам очередной тестовой работы, я
вношу корректировку в календарно-тематическое планирование, организую уроки
разноуровнего обобщающего повторения. Сейчас издано огромное количество сборников
тестов для подготовки к ОГЭ, ЕГЭ. По таким сборникам мы работаем в течение уже
восьми лет. Предлагаю два способа использования готовых решений при подготовке.
Первый способ – изучить решение, повторить самостоятельно, осмысленно и
осознанно воспроизвести все логические шаги и вычисления. Затем взять задание
того же плана , но без решения , и еще раз воспроизвести все логические
построения и вычисления. Второй способ – изучить теорию и попробовать решить
похожую задачу . Проверить ответ. У нас в школе по учебному плану провожу
индивидуальные консультации по подготовке к итоговой аттестации.

Я работаю в сельской
средней школе, мои ученики имеют разные учебные
возможности и понятно, что без прочного
усвоения базовых знаний детьми невозможно
дальнейшее обучение. Уделяю внимание технике
выполнения экзаменационной работы: В своей работе применяю следующие принципы для эффективной

подготовки к
ОГЭ и ЕГЭ.

1. Эффективнее
выстраивать
такую подготовку, соблюдая принцип от простых
типовых заданий к сложным.
2. На этапе освоения знаний необходимо подбирать материал в виде логически
взаимосвязанной системы, где из одного следует другое.

3. На
консультациях учащимся предлагаются тренировочные
тесты, выполняя
которые дети могут оценить степень подготовленности к экзаменам.

4. На
консультациях ученик может не только
выполнить тест, но и получить
ответы на вопросы, которые вызвали затруднение.
5. Все тренировочные тесты следует проводить с ограничением времени, чтобы
учащиеся могли контролировать себя за
какое время сколько заданий они
успевают решить.

6.
Нагрузки по содержанию и по времени
для всехучащихсяодинаковы. Это необходимо, поскольку тест по своему назначению ставит всех вравные условия и предполагает объективный

контроль результатов.
Следуя этим принципам, формирую у учеников навыки самообразования,
критического мышления, самоорганизации и самоконтроля.
самостоятельной работы,
Моя цель состоит в том, чтобы помочь каждому школьнику научиться
быстро решать задачи, оформлять их чётко и компактно. Развиваю способность
мыслить свободно, без страха, творчески.

Стараюсь давать возможность

каждому
школьнику расти настолько, насколько он способен.
В связи с введением обязательного ЕГЭ и ОГЭ по математике
возникает необходимость научить учащихся решать быстро и качественно задачи
базового уровня. При этом необыкновенно возрастает роль устных

вычислений, так как на
экзамене не разрешается использовать калькулятор
и таблицы. Можно научить учащихся выполнять
простейшие преобразования устно. Конечно, для этого
потребуется организовать отработку такого
навыка до автоматизма,

на каждом уроке отвожу 5
7 минут для проведения
упражнений устных вычислений, предусмотренных
программой каждого

класса и изучение таблицы умножения на пальцах.
Устные упражнения активизируют мыслительную деятельность учащихся,
требуют
осознанного усвоения учебного материала; при их
выполнении

развивается память,
речь, внимание, быстрота реакции.

Если в 5 — 6 классах устный счет – это выполнение действий с числами:

натуральные
числа, обыкновенные дроби, десятичные дроби, то в старших

классах – это могут быть:

7 класс: Формулы
сокращенного умножения. Решение простейших линейных
уравнений. Действия со степенью. График линейной

функции.

8 класс:
Линейные неравенства и числовые промежутки.

Решение простейших линейных
неравенств. Решение квадратных уравнений с помощью
теоремы Виета и частных случаев.
Арифметический квадратный корень и его свойства.
9 класс: Решение неравенств 2 степени. Преобразование графиков функций.
Формулы приведения. Значения тригонометрических функций.

10 — 11 классах: Вычисление
производных. Простейшие тригонометрические неравенства.
Тригонометрические формулы. Простейшие тригонометрические
уравнения. Функции, обратные тригонометрическим.
Преобразование графиков функций. Вычисление первообразных.
Свойства логарифмов. Простейшие показательные
уравнения

и неравенства. Простейшие логарифмические уравнения и неравенства.
Практика показала, что систематическая работа
с устным счетом способствует значительному
повышению продуктивности вычислений и преобразований.
Сокращается время на выполнение таких
операций, что переводит их из разряда
самостоятельной задачи в разряд вспомогательной
и становится инструментом для решения более сложных
задач.
          Учитель по математике, знающий, с чем придется столкнуться школьнику на
экзамене, кроме фундамента уделяю большую
часть времени на занятии
отработке вопросов специфики ЕГЭ и ОГЭ.
Правильность оформления заданий,
тактика и стратегия решения в условиях
дефицита выделенного времени на экзамене,
а также банальная невнимательность. Эти и масса других особенностей составляют
суть специфики подготовки учащихся к итоговой аттестации. Думаю   доверительные
отношения между учителем и каждым учеником направлены на достижении главной
цели на данный период времени – успешной сдаче ОГЭ, ЕГЭ.

Источник

— Предоставить учащимся и педагогам возможность проверки (по желанию и собственной инициативе, не только в форме обязательных всероссийских контрольных работ!) уровня освоения предмета. Например, в региональных центрах оценки качества образования.

— Разработать и предложить педагогам для использования единые контрольные работы с критериями оценки на базовом и профильном уровне.

— Требования к сдаче ОГЭ и ЕГЭ не соответствуют требованиям по ФГОС. (Например, в задачнике Л.А.Кирик сократили количество задач повышенного уровня сложности. Больше стало теоретических вопросов по картинкам. На экзамене требуют знания и умения решать задачи).

— Предусмотреть критерии допуска к ЕГЭ по предмету. Выбирают ЕГЭ даже те дети, кто фактически не может сдать, и учатся на «2» и «3» на базовом уровне.

— Оценка динамики образовательных достижений обучающихся необходимо осуществлять при сравнивании результатов одних и тех же детей. Разработать на федеральном уровне и включить в концепцию единые индикаторы, критерии (объективность системы учительского оценивания).

— Мы поддерживаем переход на Федеральный программно-целевой способ решения проблемы материально-технического снабжения школ. При этом хочется добавить, что при использовании оборудования во время фронтального экспериментирования 1 часа учебного времени чаще недостаточно. При этом, если учесть что экспериментальные задания включены в КИМы ГИА, то этого времени на отработку задания точно не достаточно. Наше предложение – разрешить в расписании недельной учебной нагрузки обучающихся спаренные уроки.

— Не вводить в экзамен по физике вопросы по астрономии, т.к. это отдельный предмет.

— Сделать материалы экзаменов ЕГЭ открытыми, чтобы учащиеся знали, что их ждет на экзамене, и смогли подготовиться даже без репетиторов.

— Создать систему подготовки ОГЭ (ЕГЭ) практической части.

Выбрать на государственном уровне (производителя) поставщика комплектов (с гарантией качества) для сдачи практической части.

2. Оснастить кабинеты ОГЭ (ЕГЭ) однотипными комплектами приборов для сдачи практической части.

— Сроки сдачи экзамена по физике. (перерыв между экзаменами не менее 3-х рабочих дней ОГЭ и не менее 5-х рабочих дней ЕГЭ).

— При проверке заданий с развернутым ответом (ЕГЭ/ОГЭ) учитывать многовариантность способов решения.

— Усилить контроль за содержанием КИМов для ОГЭ и ЕГЭ, выносить на ОГЭ и ЕГЭ только тот материал, который изучается в школьном курсе.

Астрономия.

— Изучение астрономии отдельным предметом педагоги считают обоснованным, так как этот предмет демонстрирует прикладной характер физических законов, открывает для учащихся горизонты знаний. Однако, педагогической общественности стоит обсудить содержание предмета «Астрономия».

— Для учителей, которые будут преподавать этот предмет, следует организовать курсы, на которых педагог смог бы узнать о современном состоянии в области астрономии и космических исследований, ведь многие педагоги даже в школе не изучали этот предмет, а ведь речь идёт о введении вопросов астрономии в КИМы ЕГЭ. .

— Совершенно нет оборудования для проведения уроков по астрономии!!!

— Нельзя вводить астрономию за счет часов по физике;

Финансирование.

— Финансовое обеспечение учебного процесса оборудованием на должном уровне предусмотренным ФГОС необходимо осуществлять из федерального бюджета.

— Вернуть целевую систему финансирования обновления фонда оборудования: ежегодное выделение средств на приобретение оборудования для кабинета физики ОУ.

— Отказаться от подушевого финансирования. Заработная плата в профильных группах, в сельских школах, по изучению предмета «Физика», очень низкая.

— Финансирование школ необходимо производить на учебники, учебные пособия по одной статье, а на оснащение оборудованием и материальную базу – по другой.

www.pro100gia.ru

Диагностическая работа в формате ОГЭ — 2015

Инструкция по выполнению работы

Диагностическая работа состоит из 3-х частей, включающих в себя 15 заданий.

На выполнение диагностической работы по русскому языку отводится 3 часа 55 минут (235 минут). Работа состоит из 3 частей.

Часть 1 включает одно задание и представляет собой небольшую письменную работу по прослушанному тексту (сжатое изложение). Исходный текст для сжатого изложения прослушивается 2 раза. Это задание записывается в бланке ответов №2.

Часть 2 выполняется на основе прочитанного текста. Она состоит из 14 заданий (2– 14).

Ответы к заданиям 2–14 записываются в виде слова (словосочетания), числа, последовательности цифр в поле ответа в тексте работы.

В случае записи неверного ответа на задания части 2 зачеркните его и запишите рядом новый.

Приступая к части 3 работы, выберите одно из трёх предложенных заданий (15.1, 15.2 или 15.3) и дайте письменный развёрнутый аргументированный ответ. Это задание выполняется на отдельном листе (бланк ответов №2).

На экзамене разрешено пользоваться орфографическим словарём.

При выполнении заданий можно пользоваться черновиком. Записи в черновике не учитываются при оценивании работы.

Баллы, полученные Вами за все выполненные задания, суммируются. Постарайтесь выполнить как можно больше заданий и набрать как можно больше баллов.

Желаем успеха!

Вариант 1

Часть 1

Прослушайте текст и выполните задание 1 на отдельном листе.

Сначала напишите номер задания, а затем – текст сжатого изложения.

Прослушайте текст и напишите сжатое изложение.

Учтите, что Вы должны передать главное содержание как каждой микротемы, так и всего текста в целом.

Объём изложения – не менее 70 слов.

Пишите изложение аккуратно, разборчивым почерком.

Часть 2

Прочтите текст и выполните задания 2-14

Когда папа был маленьким, ему часто задавали один и тот же вопрос.

(2) Его спрашивали: «Кем ты будешь?» (3) И папа всегда, не задумываясь, отвечал на этот вопрос. (4) Но каждый раз он говорил по-другому. (5) Сначала папа хотел стать ночным сторожем. (6) Ему очень нравилось, что все спят, а сторож не спит…

(7)Но вот как-то раз маленький папа увидел на станции железной дороги удивительного человека. (8) Человек этот все время играл с вагонами и паровозами. (9) Да не с игрушечными, а с настоящими! (10) «Кто это?» – спросил папа. (11) «Это сцепщик вагонов», – ответили ему. (12) И тут маленький папа, наконец, понял, кем он будет…

(13) Но скоро он захотел стать летчиком. (14) Потом ему захотелось сделаться артистом и играть на сцене. (15) Потом он побывал с дедушкой на одном заводе и решил стать токарем.

(16) А однажды ему больше всего в жизни захотелось стать собакой. (17) Целый день он бегал на четвереньках, лаял на чужих и даже пытался укусить одну пожилую женщину, когда она захотела погладить его по голове. (18) Маленький папа научился очень хорошо лаять, но вот чесать ногой за ухом он никак не мог научиться, хотя старался изо всех сил. (19) А чтобы лучше получилось, он вышел во двор и сел рядом с Тузиком.

(20) А по улице шел незнакомый военный. (21) Он остановился и стал смотреть на папу.

(22) Смотрел, смотрел удивленно, а потом спросил:

– (23) Ты что это делаешь, мальчик?

– (24)Я хочу стать собакой, – сказал папа. (25) Тогда незнакомый военный спросил:

– (26)А человеком не хочешь быть?

– (27)А я уже давно человек! – сказал папа.

– (28) Какой же ты человек, – сказал военный, – если из тебя даже собака не получается? (29) Разве человек такой?

– (30)А какой же? – спросил папа.

– (31)Вот ты подумай! – сказал военный и ушел. (32) Он совсем не смеялся и даже не улыбался. (33) Но маленькому папе почему-то стало очень стыдно. (34) И он стал думать. (35) И чем больше он думал, тем больше стыдился. (36) Военный ему ничего не объяснил. (37) Но он сам вдруг понял: нельзя каждый день выбирать себе новую профессию. (38) А главное, он понял, что он еще маленький и что он еще сам не знает, кем он будет. (39) Когда его спросили об этом опять, он вспомнил военного и сказал:

– (40) Я буду человеком!

(41) И тут никто не засмеялся. (42) И маленький папа понял, что это самый правильный ответ. (43) Прежде всего надо быть хорошим человеком.

(По А. Раскину)

Александр Борисович Раскин – русский советский писатель, сатирик, сценарист. Автор популярного сборника прозаических миниатюр для детей «Как папа был маленьким».

Ответами к заданиям 2–14 являются число, последовательность цифр

или слово (словосочетание), которые следует записать в поле ответа

в тексте работы.

В каком варианте ответа содержится информация, необходимая для обоснования ответа на вопрос: «Почему папа, когда был маленьким, решил стать хорошим человеком?»

Он понял, что главное в жизни – быть хорошим человеком независимо от выбранной профессии.
Он понял, что он плохой человек.
Он понял, что быть хорошим человеком престижно и материально выгодно.
Он понял, что хорошим человеком необходимо стать, чтобы все тебя почитали.