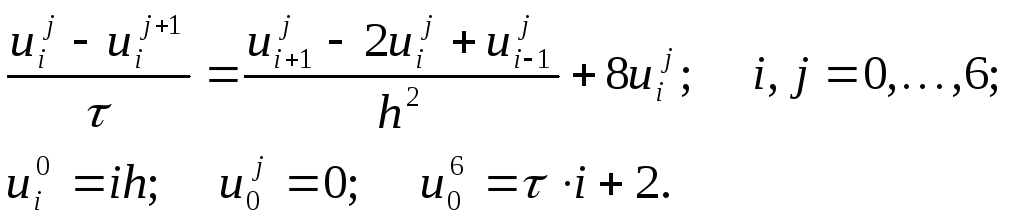Прикладная математика вопросы к экзамену

1. Математика и научно-технический прогресс.

2. Определение матрицы. Элементы матрицы.

3. Виды матриц (квадратная, диагональная, единичная).

4. Действия над матрицами. Их свойства.

5. Определители второго порядка, их вычисление.

6. Определители третьего порядка, их вычисление.

7. Определители n-го порядка, свойства определителей.

8. Понятие функции. Область определения и область значений функции.

9. Свойства функции: монотонность, четность и нечетность, ограниченность, периодичность.

10. Понятие предела функции. Основные свойства пределов.

11. Непрерывные функции и точки разрыва.

12. Предел функции. Замечательные пределы.

13. Понятие производной функции. Основные правила дифференцирования. Таблица производных.

14. Геометрический смысл производной функции.

15. Физический смысл производной функции.

16. Понятие первообразной функции. Неопределенный интеграл.

17. Основные свойства неопределенного интеграла. Основные свойства интегрирования.

18. Определенный интеграл. Формула Ньютона-Лейбница.

19. Определенный интеграл. Геометрический смысл определенного интеграла.

20. График функции. Способы задания функций. Построение графиков элементарных функций.

21. Расстояние между двумя заданными точками на плоскости.

22. Понятие уравнения линии.

23. Общее уравнение прямой.

24. Векторное и каноническое уравнения прямой.

25. Уравнение прямой в отрезках на осях.

26. Уравнение прямой с угловым коэффициентом.

27. Уравнение прямой, проходящей через данную точку в заданном направлении.

28. Уравнение прямой, проходящей через две данные точки.

29. Условие пересечения двух прямых.

30. Условие параллельности двух прямых.

31. Условие перпендикулярности двух прямых.

32. Линейные функции, их свойства и графики.

33. Квадратичные функции, их свойства и графики.

34. Обратные функции, их свойства и графики.

35. Степенные функции, их свойства и графики.

36. Дробно-линейные функции, их свойства и графики.

37. Тригонометрические функции, их свойства и графики.

38. Показательные функции, их свойства и графики.

39. Логарифмические функции, их свойства и графики.

40. Вертикальные и горизонтальные асимптоты графиков. Интервал, полуинтервал, отрезок функции.

41. Преобразования графиков функции (симметрия вдоль осей координат, сдвиг вдоль осей координат).

42. Преобразования графиков функции (растяжение и сжатие вдоль осей координат).

43. Возрастание и убывание функции. Достаточные условия существования экстремума функции. Краевые экстремумы.

44. Асимптоты. Нахождение уравнения асимптот.

45. Общая схема исследования функции.

46. Общая схема отыскания наибольшего (наименьшего) значения функции на замкнутом отрезке.

47. Направление выпуклости графика функции.

48. Достаточные условия выпуклости и вогнутости графика функции.

49. Понятие точки перегиба графика функции. Достаточные условия существования перегиба графика функции.

50. Исследование функции на выпуклость, вогнутость и точку перегиба.

51. Применение производной к исследованию функции.

52. Применение второй производной к исследованию функции.

53. Определение комплексного числа. Модуль и аргумент комплексного числа. Геометрическая интерпретация комплексных чисел на плоскости.

54. Тригонометрическая форма записи комплексных чисел.

55. Показательная форма записи комплексных чисел. Формула Эйлера.

56. Действия над комплексными числами, заданными в алгебраической форме.

57. Действия над комплексными числами, заданными в тригонометрической форме.

58. Действия над комплексными числами, заданными в показательной форме.

59. Переход от алгебраической формы записи комплексных чисел к тригонометрической и обратно.

60. Переход от алгебраической формы записи комплексных чисел к показательной и обратно.

61. Правила решения квадратных уравнений с отрицательным дискриминантом.

62. Общие сведения о системах счисления. Позиционные и непозиционные системы счисления.

63. Десятичная и двоичная системы счисления.

64. Восьмеричная и шестнадцатеричная системы счисления.

65. Перевод целых чисел из одной позиционной системы счисления в другую.

66. Перевод дробных и смешанных чисел из одной позиционной системы счисления в другую.

67. Арифметические операции над двоичными числами.

68. Форма представления чисел с фиксированной запятой.

69. Форма представления чисел с плавающей запятой.

70. Правила записи положительных и отрицательных двоичных чисел в прямом и обратном кодах.

71. Правила записи положительных и отрицательных двоичных чисел в дополнительном и модифицированном кодах.

72. Перевод чисел из двоичной в восьмеричную систему счисления и обратно. Понятие о триадах.

73. Перевод чисел из двоичной в шестнадцатеричную систему счисления и обратно. Понятие о тетрадах.

74. Математические операции (сложение и вычитание) двоичных чисел с фиксированной и плавающей запятой.

75. Переполнение разрядной сетки при математических действиях.

76. Элементы математической логики.

77. Основные понятия теории множеств.

78. Логические (булевы) функции.

79. Основные операции алгебры логики: конъюнкция, дизъюнкция, инверсия.

80. Основные законы алгебры логики.

81. Минимизация булевых функций.

82. Функциональная полнота систем булевых функций.

83. Понятие о логической переменной и функции.

84. Понятие об элементарных и комбинационных логических функциях одной и двух переменных, их функциональная запись через конъюнкцию, дизъюнкцию, инверсию.

85. Применение законов алгебры логики для записи и преобразования переключательных функций.

86. Канонические формы представления переключательных логических функций в аналитической форме.

87. Дизъюнктивные нормальные формы (ДНФ).

88. Конъюнктивные нормальные формы (КНФ).

89. Совершенные дизъюнктивные нормальные формы (СДНФ).

90. Совершенные конъюнктивные нормальные формы (СКНФ).

91. Минимизация переключательных функций.

92. Основы аналитического способа минимизации функций.

93. Основы графического (карты Карно) способа минимизации функций.

94. Методика перехода от нормальной к совершенной форме записи переключательных функций при аналитическом способе.

95. Методика перехода от нормальной к совершенной форме записи переключательных функций при графическом способе.

96. Преобразование ДНФ в СДНФ.

97. Преобразование КНФ в СКНФ.

98. Преобразование КНФ в ДНФ.

99. Преобразование ДНФ в КНФ

100. Основные понятия комбинаторики.

101. История развития комбинаторики и классические задачи.

102. Принцип комбинаторного сложения и умножения.

103. Свойства сочетаний. Треугольник Паскаля.

104. Случайный опыт и случайное событие.

105. Виды событий, их вероятности.

106. Операции над событиями.

107. Относительная частота события.

108. Классическое и статистическое определения вероятности.

109. Теорема сложения вероятностей.

110. Теорема умножения вероятностей.

111. Условная вероятность. Формула полной вероятности.

112. Независимые события. Формула Бернулли.

113. Понятие дискретной случайной величины. Закон ее распределения.

114. Математическое ожидание дискретной случайной величины, ее свойства.

115. Дисперсия дискретной случайной величины, ее свойства.

116. Понятие среднего квадратичного отклонения.

117. Понятие о законе больших чисел.

118. Задачи математической статистики.

119. Генеральная и выборочная совокупности.

120. Статистическое распределение выборки.

Кафедра Инженерная кибернетика Государственный экзамен

(междисциплинарный)

По направлению подготовки дипломированного специалиста

230401.65 «Прикладная математика» экзаменационный билет № 1

Вопрос
1. Экстремальные задачи и методы их
решения. Основные понятия оптимизации:
целевая функция, управляющие параметры,
условия ограничения.

Вопрос
2. Программный продукт, как система,
производные свойства системы.

Вопрос
3. Основные этапы построения математической
модели. Классификация математических
моделей. Основные подходы к построению
моделей. Системный подход построения
теоретической модели.

Вопрос
4. Интервальное оценивание числовых
характеристик случайных величин.
Доверительная вероятность и предельная
ошибка выборки.

Вопрос
5. Дано нелинейное уравнение
.
Отделить корни графически. Построить
блок-схему и составить программу для
уточнения одного из корней методом
бисекции с точностью до

= 0.001.

Утверждаю:

Зав. кафедрой

д.т.н.,
профессор ________________ В.Н.
Шарифуллин

(подпись)

«____»____________2009г.

Экзаменационный билет № 2

Вопрос
1. Классификация оптимизационных задач.

Вопрос
2. Жизненный
цикл программного средства.

Вопрос
3. Параметрическая идентификация модели,
принцип макси-мального правдоподобия
и критерии рассогласования.

Вопрос
4. Регрессионный анализ. Метод наименьших
квадратов.

Вопрос
5. На алгоритмическом языке составить
программу численного решения краевой
задачи:

Утверждаю:

Зав. кафедрой

д.т.н.,
профессор ________________ В.Н.
Шарифуллин

(подпись)

«____»____________2009г.

Кафедра Инженерная кибернетика Государственный экзамен

(междисциплинарный)

По направлению подготовки дипломированного специалиста

230401.65 «Прикладная математика»

Экзаменационный билет № 3

Вопрос
1. Методы безусловной минимизации
выпуклых функций многих переменных:
метод покоординатного спуска.

Вопрос
2. Характеристики Майерса для программного
модуля.

Вопрос 3. Параметрическая идентификация
модели по критерию суммы квадратов
отклонений, алгоритмы непосредственной
минимизации.

Вопрос
4. Статистическая гипотеза и общая схема
ее проверки. Проверка гипотез о равенстве
средних двух совокупностей.

Вопрос
5. Построить разностное уравнение,
аппроксимирующее данное уравнение в
частных производных и определить
точность аппроксимации:

Утверждаю:

Зав. кафедрой

д.т.н.,
профессор ________________ В.Н.
Шарифуллин

(подпись)

«____»____________2009г.

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Вопросы к зачетам и экзаменам