Каталог заданий.
Применение производной к исследованию функций
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
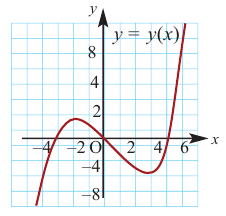
На рисунке изображен график производной функции
определенной на интервале
Найдите промежутки возрастания функции
В ответе укажите сумму целых точек, входящих в эти промежутки.
2
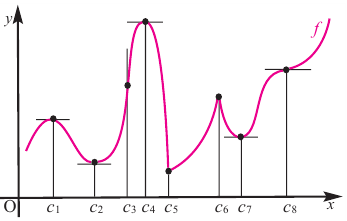
На рисунке изображен график функции y = f(x), определенной на интервале (−6; 8). Определите количество целых точек, в которых производная функции положительна.
3
На рисунке изображен график функции y = f(x), определенной на интервале (−2; 12). Найдите сумму точек экстремума функции f(x).
Источник: ЕГЭ по математике 29.06.2021. Резервная волна. Центр. Вариант 402
4
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Подмосковье
5
На рисунке изображен график производной функции f(x), определенной на интервале (−8; 4). В какой точке отрезка [−7; −3] f(x) принимает наименьшее значение?
Источник: ЕГЭ по математике 07.06.2021. Основная волна. Санкт-Петербург
Пройти тестирование по этим заданиям
Задачи из открытого банка при подготовке к ЕГЭ.
Применение производной для исследования графиков
функции
На рисунке изображен график функции , определенной на интервале (−6; 8).
Определите количество целых точек, в которых производная функции положительна.
Решение.
Производная функции положительна на тех интервалах, на которых функция
возрастает, т. е. на интервалах (−3; 0) и (4,6; 7). В них содержатся целые
точки −2, −1, 5 и 6, всего их 4.
Ответ: 4.
На рисунке изображен график функции , определенной на интервале
(−5; 5). Определите количество целых точек, в которых производная функции отрицательна.
Решение.
Производная функции отрицательна на тех интервалах, на которых функция убывает,
т. е. на интервалах (−4,1; 1,5) и (2,6; 4,2). В них содержатся целые точки −4,
−3, −2, −1, 0, 1, 3, 4. Их 8 штук.
Ответ: 8.
На рисунке изображен график функции , определенной на интервале
(−5; 5). Найдите количество точек, в которых касательная к графику функции
параллельна прямой y = 6 или совпадает с ней.
Решение.
Поскольку касательная параллельна прямой y = 6 или совпадает с
ней, их угловые коэффициенты равны 0. Угловой коэффициент касательной равен
значению производной в точке касания. Производная равна нулю в точках
экстремума функции. На заданном интервале функция имеет 2 максимума и 2
минимума, итого 4 экстремума. Таким образом, касательная к графику функции
параллельна прямой y = 6 или совпадает с ней в 4 точках.
Ответ: 4.
На рисунке изображен график функции , определенной на интервале (-2; 12).
Найдите сумму точек экстремума функции .
Решение.
Заданная функция имеет максимумы в точках 1, 4, 9, 11 и минимумы в точках 2, 7,
10. Поэтому сумма точек экстремума равна 1 + 4 + 9 + 11 + 2 + 7 + 10 = 44.
Ответ: 44.
На рисунке изображен график производной функции ,
определенной на интервале (-8; 3). В какой точке отрезка [-3; 2] принимает наибольшее значение.
Решение.
На заданном отрезке производная функции отрицательна, поэтому функция на этом
отрезке убывает. Поэтому наибольшее значение функции достигается на левой границе
отрезка, т. е. в точке −3.
Ответ: −3.
На рисунке изображен график производной функции , определенной на интервале
. В какой точке отрезка
принимает наименьшее значение.
Решение.
На заданном отрезке производная функции положительна, поэтому функция на этом
отрезке возрастает. Поэтому наименьшее значение функции достигается на левой
границе отрезка, т. е. в точке .
Ответ: −7.
На рисунке изображен график производной функции , определенной на интервале
. Найдите количество точек
максимума функции на
отрезке .
Решение.
Точки максимума соответствуют точкам смены знака производной с положительного
на отрицательный. На отрезке функция имеет одну точку максимума
Ответ: 1.
На рисунке изображен график производной функции , определенной на интервале
. Найдите количество точек
минимума функции на
отрезке .
Решение.
Точки минимума соответствуют точкам смены знака производной с отрицательного на
положительный. На отрезке функция
имеет одну точку минимума .
Ответ: 1.

функции , определенной на
интервале
(–10; 2). Найдите количество точек, в которых
касательная к графику функции параллельна прямой
или совпадает с ней.
Решение.
Значение производной в точке касания равно угловому коэффициенту касательной.
Поскольку касательная параллельна прямой или совпадает с ней, их угловые коэффициенты
равны –2. Найдем количество точек, в которых , геометрически это соответствует количеству
точек пересечения графика производной с прямой . На данном интервале таких точек 5.
Ответ: 5.
На рисунке изображен график производной функции , определенной на интервале
(–4; 8). Найдите точку экстремума функции на отрезке [–2; 6].
Решение.
Если производная в некоторой точке равна нулю, а в ее окрестности меняет знак,
то это точка экстремума. На отрезке [–2; 6] график производной пересекает ось
абсцисс, производная меняет знак с плюса на минус. Следовательно, точка является точкой экстремума.
Ответ: 4.
На рисунке изображен график функции , определенной на интервале (–5; 5).
Найдите количество точек, в которых производная функции равна 0.
Решение.
Производная изображенной на рисунке функции равна нулю в точках экстремумов: –4,3; 1,5; 2,5 и
4,2. Производная равна нулю в 4 точках.
Ответ: 4.
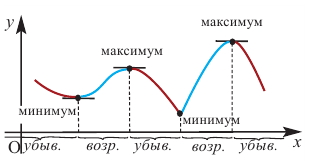
 Исследование графика функции
Исследование графика функции
x1 – точка перегиба;
x2, x4 – точки
максимума;
x3 – точка минимума.
Такие точки называются критическими.
Условие для нахождения критических точек
функции:
|
|
|
|
|
|
|
|
|
|
|
|
|
+ |
0 |
+ |
0 |
— |
0 |
+ |
0 |
— |
|
|
|
|
max |
|
min |
|
max |
|
Исследование функции

|
Область определения: |
|
|
Множество значений: |
|
|
Корни функции: |
|
|
Критические точки |
|
|
Промежутки возрастания: |
|
|
Промежутки убывания: |
|
Необходимая теория:
Производная функции
Таблица производных
Первообразная функции
Задание 7 Профильного ЕГЭ по математике — это задачи на геометрический и физический смысл производной. Это задачи о том, как производная связана с поведением функции. И еще (правда, очень редко) в этих задачах встречаются вопросы о первообразной.
Геометрический смысл производной
Вспомним, что производная — это скорость изменения функции.
Производная функции в точке
равна угловому коэффициенту касательной, проведенной к графику функции в этой точке. Производная также равна тангенсу угла наклона касательной.
1. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции
в точке
Производная функции в точке
равна тангенсу угла наклона касательной, проведенной в точке
.
Достроив до прямоугольного треугольника АВС, получим:
Ответ: 0,25.
2. На рисунке изображён график функции и касательная к нему в точке с абсциссой
Найдите значение производной функции в точке
Начнём с определения знака производной. Мы видим, что в точке функция убывает, следовательно, её производная отрицательна. Касательная в точке
образует тупой угол
с положительным направлением оси
. Поэтому из прямоугольного треугольника мы найдём тангенс угла
, смежного с углом
.
Мы помним, что тангенс угла в прямоугольном треугольнике равен отношению противолежащего катета к прилежащему: Поскольку
, имеем:
Ответ: −0, 25.
Касательная к графику функции
3. Прямая является касательной к графику функции
Найдите абсциссу точки касания.
Запишем условие касания функции и прямой
в точке
При значения выражений
и
равны.
При этом производная функции равна угловому коэффициенту касательной, то есть
.
Из второго уравнения находим или
Первому уравнению удовлетворяет только
.
Физический смысл производной
Мы помним, что производная — это скорость изменения функции.
Мгновенная скорость — это производная от координаты по времени. Но это не единственное применение производной в физике. Например, cила тока — это производная заряда по времени, то есть скорость изменения заряда. Угловая скорость — производная от угла поворота по времени.
Множество процессов в природе, экономике и технике описывается дифференциальными уравнениями — то есть уравнениями, содержащими не только сами функции, но и их производные.
4. Материальная точка движется прямолинейно по закону , где
— расстояние от точки отсчета в метрах,
— время в секундах, измеренное с начала движения. Найдите ее скорость (в м/с) в момент времени
с.
Мгновенная скорость движущегося тела является производной от его координаты по времени. Это физический смысл производной. В условии дан закон изменения координаты материальной точки, то есть расстояния от точки отсчета:
Найдем скорость материальной точки как производную от координаты по времени:
В момент времени
получим:
.
Ответ: 3.
Применение производной к исследованию функций
Каждый год в вариантах ЕГЭ встречаются задачи, в которых старшеклассники делают одни и те же ошибки.
Например, на рисунке изображен график функции — а спрашивают о производной. Кто их перепутал, тот задачу не решил.
Или наоборот. Нарисован график производной — а спрашивают о поведении функции.
И значит, надо просто внимательно читать условие. И знать, как же связана производная с поведением функции.
Если , то функция
возрастает.
Если , то функция
убывает.
В точке максимума производная равна нулю и меняет знак с «плюса» на «минус».
В точке минимума производная тоже равна нулю и меняет знак с «минуса» на «плюс».
| возрастает | точка максимума | убывает | точка минимума | возрастает | |
| 0 | 0 |
5. На рисунке изображен график функции , определенной на интервале
Найдите количество точек, в которых производная функции
равна 0.
Производная функции в точках максимума и минимума функции
Таких точек на графике 5.
Ответ: 5.
6. На рисунке изображён график — производной функции
, определённой на интервале
. В какой точке отрезка
функция
принимает наибольшее значение?
Не спешим. Зададим себе два вопроса: что изображено на рисунке и о чем спрашивается в этой задаче?
Изображен график производной, а спрашивают о поведении функции. График функции не нарисован. Но мы знаем, как производная связана с поведением функции.
На отрезке производная функции
положительна.
Значит, функция возрастает на этом отрезке. Большим значениям х соответствует большее значение
Наибольшее значение функции достигается в правом конце отрезка, то есть в точке 3.
Ответ: 3.
7. На рисунке изображён график функции , определённой на интервале
. Найдите количество точек, в которых касательная к графику функции параллельна прямой
Прямая параллельна оси абсцисс. Найдем на графике функции
точки, в которых касательная параллельна оси абсцисс, то есть горизонтальна. Таких точек на графике 7. Это точки максимума и минимума.
Ответ: 7.
8. На рисунке изображен график производной функции , определенной на интервале
Найдите количество точек максимума функции
на отрезке
Очень внимательно читаем условие задачи. Изображен график производной, а спрашивают о точках максимума функции. В точке максимума производная равна нулю и меняет знак с «плюса» на «минус». На отрезке такая точка всего одна! Это
Ответ: 1.
9. На рисунке изображен график производной функции , определенной на интервале
Найдите точку экстремума функции
на отрезке
Точками экстремума называют точки максимума и минимума функции. Если производная функции в некоторой точке равна нулю и при переходе через эту точку меняет знак, то это точка экстремума. На отрезке график производной (а именно он изображен на рисунке) пересекает ось абсцисс в точке
В этой точке производная меняет знак с минуса на плюс.
Значит, является точкой экстремума.
Первообразная и формула Ньютона-Лейбница
Функция , для которой
является производной, называется первообразной функции
Функции вида
образуют множество первообразных функции
10. На рисунке изображён график — одной из первообразных некоторой функции
, определённой на интервале
Пользуясь рисунком, определите количество решений уравнения
на отрезке
Функция для которой
является производной, называется первообразной функции
Это значит, что на графике нужно найти такие точки, принадлежащие отрезку , в которых производная функции
равна нулю. Это точки максимума и минимума функции
На отрезке
таких точек 4.
Ответ: 4.
Больше задач на тему «Первообразная. Площадь под графиком функции» — в этой статье
Первообразная функции. Формула Ньютона-Лейбница.
Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №7. Производная. Поведение функции. Первообразная u0026#8212; профильный ЕГЭ по Математике» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
Исследовать функцию — это значит установить её свойства: указать её область определения и область значений; промежутки возрастания и убывания; промежутки, на которых функция приобретает положительные значения, на которых — отрицательные; выяснить, не является ли данная функция чётной или нечётной и т. д.
Содержание:
Что такое исследование функции
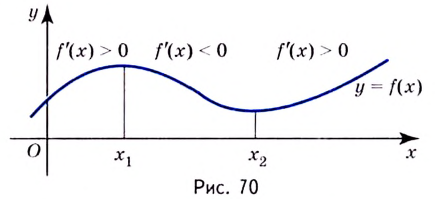
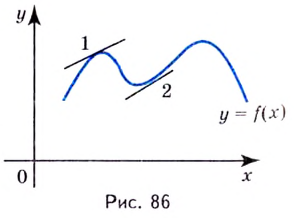
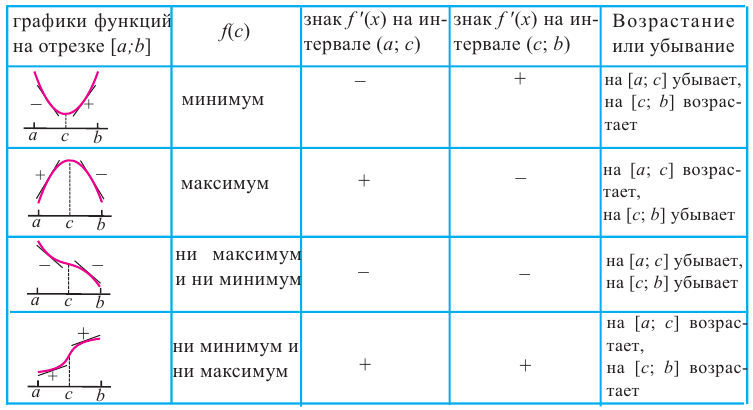
Одна из важных задач исследования функции — определение промежутков её возрастания и убывания. Как отмечалось, в тех точках, в которых функция возрастает, её производная (угловой коэффициент касательной) положительная, а в точках убывания функции её производная отрицательная {рис. 70).
Правильными будут следующие утверждения.
- Если производная функции в каждой точке некоторого промежутка положительная, то функция на этом промежутке возрастает.
- Если производная в каждой точке промежутка отрицательная, то функция на этом промежутке убывает.
- Если производная в каждой точке промежутка тождественно равна нулю, то на этом промежутке функция постоянная.
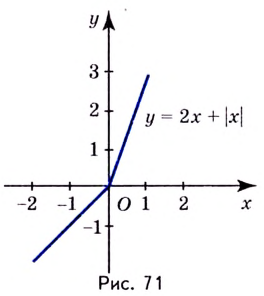
Строгое доказательство этого утверждения достаточно громоздкое, поэтому мы его не приводим. Заметим только, что в нём выражается достаточный признак возрастания или убывания функции, но не необходимый. Поэтому функция может возрастать и на промежутке, в некоторых точках которого она не имеет производной. Например, функция
Из сказанного следует, что два соседних промежутка, на одном из которых функция возрастает, а на другом — убывает, могут разделяться только такой точкой, в которой производная функции равна нулю или не существует.
Внутренние точки области определения функции, в которых её производная равна нулю или не существует, называют критическими точками функции.
Следовательно, чтобы определить промежутки возрастания и убывания функции 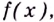
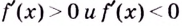
Пример:
Найдите промежутки возрастания и убывания функции
Решение:
Уравнение 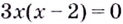
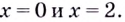
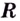
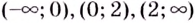
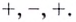
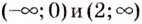
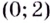
Замечание: Если функция непрерывна в каком-нибудь конце промежутка возрастания или убывания, то эту точку можно присоединить к рассматриваемому промежутку. Поскольку функция 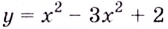
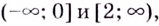
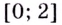
Пример:
Найдите промежутки убывания функции
Решение:
Критические точки: 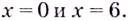
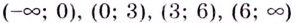
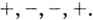
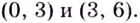
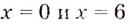
Пример:
Найдите критические точки функции 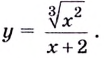
Решение:
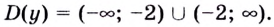
Найдём точки, в которых производная равна нулю или не существует: 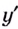
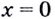
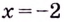

Ответ. 0 и 4.
Пример:
Докажите, что функция 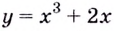
Решение:
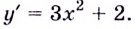
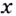
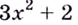
Пример:
Установите, на каком промежутке функция 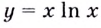
Решение:
Способ 1. 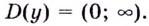
Найдём критические точки функции:
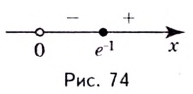
Эта точка разбивает область определения функции на два промежутка (рис. 74). Определим знак производной на каждом из них.
Следовательно, функция 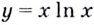
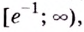
Способ 2. Решим неравенство 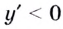
Ответ. Возрастает, если 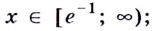
Применение второй производной к исследованию функций и построению их графиков
При помощи первой производной можно исследовать функцию на монотонность и экстремумы и схематично построить график. Оказывается, что поведение некоторых функций не всегда можно охарактеризовать, используя первую производную. Более детальное исследование проводится при помощи второй производной. Вспомним, что такое вторая производная.
Пусть функция 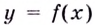
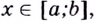
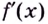
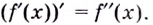
Например, найти производную 2-го порядка функции 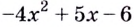
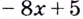
Кривая 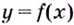
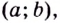
Кривая 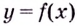
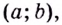
Точкой перегиба называется такая точка кривой, которая отделяет её выпуклую часть от вогнутой.
Интервалы выпуклости и вогнутости находят при помощи такой теоремы.
Теорема. Если вторая производная дважды дифференцируемой функции 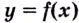
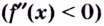
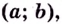
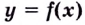
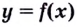
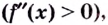
Из теоремы следует, что точками перегиба кривой 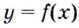
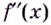
Установим до статочное условие существования точки перегиба.
Теорема. Пусть 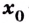
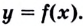
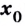
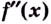
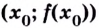
Для нахождения промежутков выпуклости и точек перегиба графика функции целесообразно пользоваться следующей схемой:
- найти область определения функции;
- найти критические точки второго рода;
- определить знак второй производной на образованных интервалах. Если
то кривая выпуклая; если
— кривая вогнутая;
- если производная
меняет знак при переходе через точку
то точка
является точкой перегиба кривой
Пример №1
Найдите интервалы выпуклости, вогнутости и точки перегиба кривой
Решение:
1) Область определения функции:
2) Найдём вторую производную: 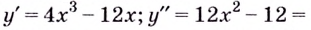
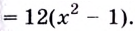
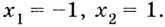
3) Разбиваем область определения на интервалы 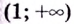
Если 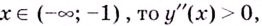
Если 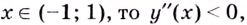
Если 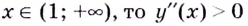
Следовательно, точки 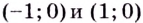
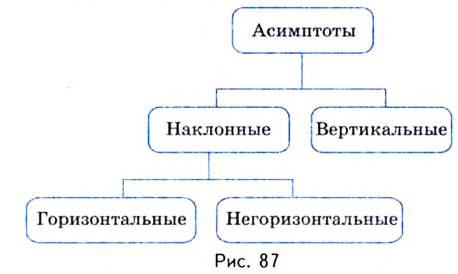
Напомним, что прямая 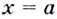
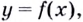
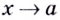
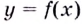
Уравнение наклонной асимптоты:
Если записанные пределы существуют, то существует наклонная асимптота; если хотя бы один из них не существует или равен 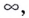
Если 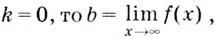
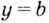
Замечание: Рассмотренные пределы могут быть односторонними, а под символом 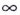
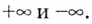
Пример №2
Найдите асимптоты кривых:
Решение:
а) 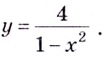
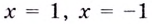
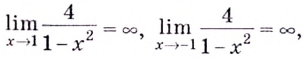
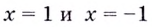
Найдём наклонную асимптоту: 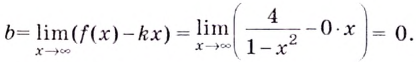
Следовательно, заданная кривая имеет три асимптоты:
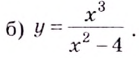
Поскольку функция не определена в точках 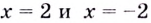
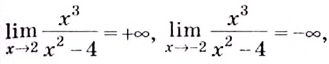
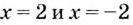
Для наклонной асимптоты
Значит прямая 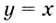
Итак, асимптоты кривой:
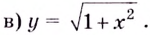
Следовательно, 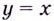
2) если 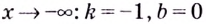

Следовательно, заданная кривая имеет две асимптоты:
Определение точек перегиба, интервалов выпуклости и асимптот существенно помогает в построении графиков различных функций.
Нахождение промежутков возрастания и убывания функции
Интервалы возрастания и убывания функции
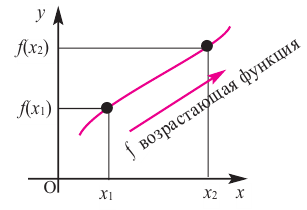
возрастающая функция
Если для любых 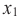
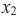
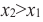
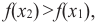
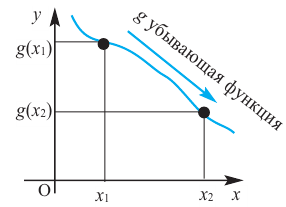
убывающая
Если для любых 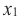
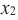
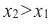
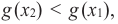
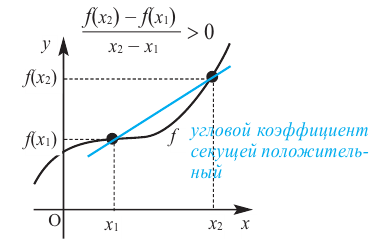
Связь промежутков возрастания и убывания функции с угловым коэффициентом секущей можно выразить следующим образом.
Если на заданном промежутке угловой коэффициент любой секущей положителен, то на этом промежутке функция 
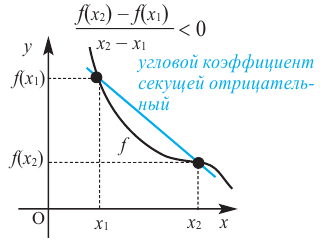
Если на заданном промежутке угловой коэффициент любой секущей отрицателен, то на этом промежутке функция 
Промежутки возрастания и убывания функции
Пусть на определенном промежутке производная функции 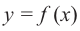
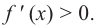
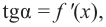
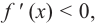
Теорема. Если функция 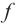
Примечание: если функция 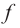
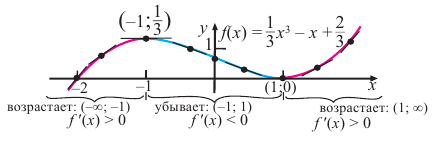
По графику функции 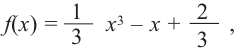
На интервалах 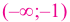
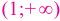
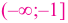
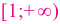
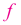
На интервале 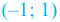
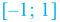
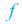
Пример №3
При помощи производной определите промежутки возрастания и убывания функции
Решение: 1. Алгебраический метод.
Найдем производную функции
Функция 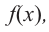
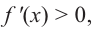
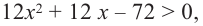
Для решения неравенства сначала надо решить соответствующее уравнение
Значит, при 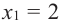
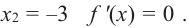
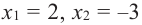
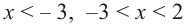
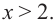
Из таблицы и непрерывности функции 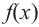
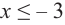
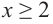
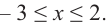
2. Промежутки возрастания и убывания функции можно определить но графику производной. На рисунке изображен график производной
График производной 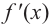
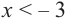
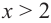
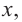
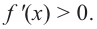
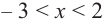
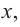
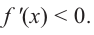
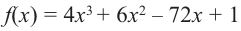
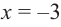
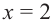
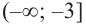
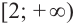
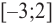
Пример №4
Изобразите схематично график непрерывной функции согласно еле дующим условиям:
a) при 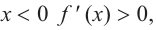
b) при 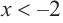
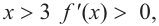
Решение:
а) при 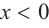
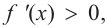
функция возрастает. При 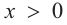
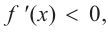
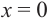
b) При 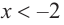
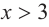
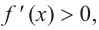
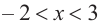
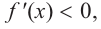
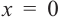
Критические точки и экстремумы функции
В некоторых точках из области определения производная функции может быть равна нулю или вообще может не существовать. Такие точки из области определения называются критическими точками функции. Покажем критические точки на графике заданной функции.
1. Для значений 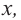
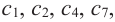
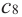
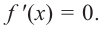
2. В точках 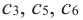
3. Для рассматриваемой нами функции критические точки 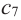
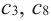
По графику видно, что в точках внутреннего экстремума(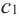
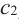
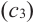
Теорема Ферма (Необходимое условие существовании экстремумов)
Во внутренних точках экстремума производная либо равна нулю, либо не существует.
Примечание. Точка, в которой производная равна нулю, может и не быть точкой экстремума. Например, в точке 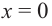
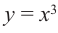
На отрезке непрерывности функция может иметь несколько критических точек, точек максимума и минимума. Существование экстремума в точке зависит от значения функции в данной точке и в точках, близких к данной, т. е. имеет смысл локального (местного) значения. Поэтому иногда используют термин локальный максимум и локальный минимум.
Достаточное условие существования экстремума
Пусть функция 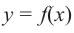
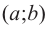
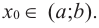
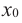
слева от точки
положительна, а справа — отрицательна, то точка
является точкой максимума.
слева от
отрицательна, а справа — положительна, то точка
является точкой минимума
с каждой стороны от точки
имеет одинаковые знаки, то точка
не является точкой экстремума.
Чтобы найти наибольшее (абсолютный максимум) или наименьшее (абсолютный минимум) значение функции, имеющей конечное число критических точек на отрезке, надо найти значение функции во всех критических точках и на концах отрезка, а затем из полученных значений выбрать наибольшее или наименьшее.
Соответствующие наибольшее и наименьшее значения функции 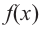
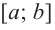
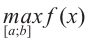
Ниже представлены примеры определения максимума и минимума в соответствии со знаком производной первого порядка.
Пример №5
Для функции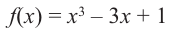
Решение: Для решения задания сначала надо найти критические точки. Для данной функции этими точками являются точки (стационарные), в которых производная равна нулю.
1. Производная функции:
2. Критические точки функции:
3. Точки 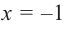
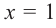
Проверим знак 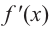
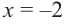
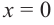
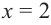

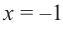
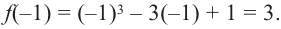
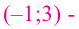
При 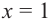
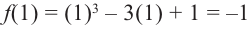
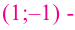
4. Используя полученные для функции 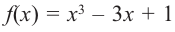
Пример №6
Найдите наибольшее и наименьшее значение функции 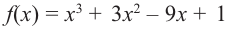
Решение: Сначала найдем критические точки.
Так как 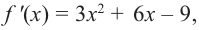
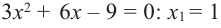
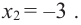
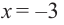
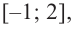
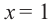
Из этих значений наименьшее — 4, наибольшее 12. Таким образом:
Пример №7
Найдите экстремумы функции
Решение: 1. Производная функции:
2. Критические точки:
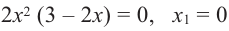
3. Интервалы, на которые критические точки делят область определения функции:
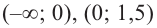
Проверим знак 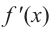
Для промежутка 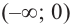
Для промежутка 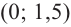
Для промежутка 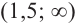
Используя полученную для функции 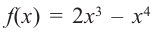
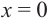
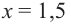
Пример №8
Найдите экстремумы функции
Решение: 1. Производная
2. Критические точки: для этого надо решить уравнение 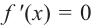
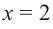
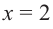
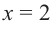
3. Промежутки, на которые критическая точка делит область определения функции: 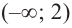
Определим знак 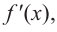
Для 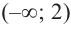
Для 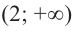
Пример №9
По графику функции производной 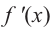
Решение:
Производная 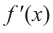
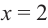
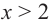
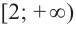
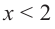
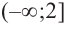
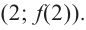
- Заказать решение задач по высшей математике
Построение графиков функции с помощью производной
Функция — многочлен определена и непрерывна на всей числовой оси.
Чтобы построить график функции- многочлен надо выполнить следующие шаги.
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания функции.
- Найдите максимумы и минимумы.
- Постройте график.
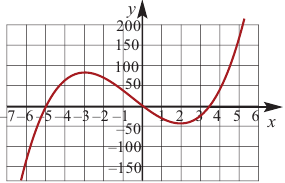
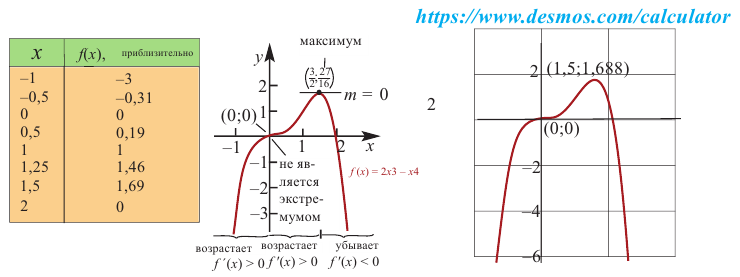
Пример:
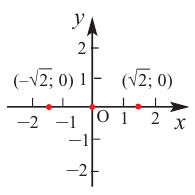
Постройте график функции
1) Точки пересечения с осями координат :
2) Критические точки ( точки, в которых производная равна нулю):
значит, точки 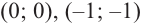
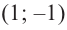
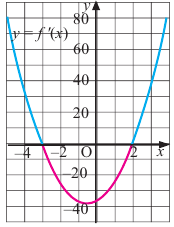
3) Промежутки возрастания и убывания. Экстремумы.
Критические точки 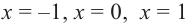
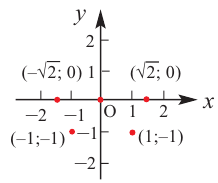
4) Используя полученную информацию, построим график функции.
Чтобы построить график рациональной функции надо выполнить следующие шаги.
- Найдите область определения.
- Найдите асимптоты (если они есть).
- Определите точки пересечения с осями координат.
- Найдите критические точки.
- Найдите промежутки возрастания и убывания и экстремумы.
- Постройте график.
Пример:
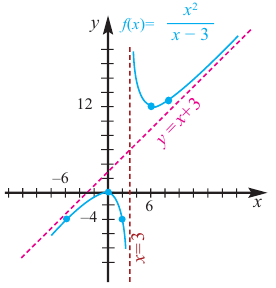
Постройте график функции
1) Область определения функции:
2) Асимптоты:
Прямая 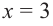
Так как степень многочлена в числителе больше степени многочлена в знаменателе, рациональная функция не имеет горизонтальной асимптоты. Однако, записав следующее:
условии 
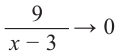
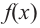
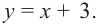
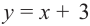
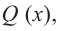
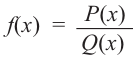
3) Точки пересечения с осями координат:
4) Критические точки:
5) Промежутки возрастания и убывания: в точке 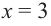
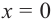
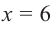
6) Построим график. Отметим на координатной плоскости точки 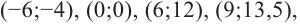
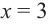
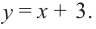
Обратите внимание! В области, близкой к точке 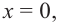
Задачи на экстремумы. Оптимизации
В реальной жизненной ситуации возникает необходимость выбора оптимального варианта и нахождения экстремумов определенной функции. Ежедневно, при решении проблем в различных областях, мы сталкиваемся с терминами наибольшая прибыль, наименьшие затраты, наибольшее напряжение, наибольший объем, наибольшая площадь и т.д. Большое экономическое значение в промышленности, при определении дизайна упаковки, имеет вопрос, как подобрать размеры упаковки с наименьшими затратами. Такого рода задания связаны с нахождением максимального или минимального значения величины. Задачи на нахождение максимального и минимального значения величины называются задачами на оптимизацию. Для решения данных задач применяется производная.
Замечание 1: На интервале 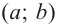
Замечание 2: В рассматриваемом интервале может быть одна стационарная точка: или точка максимума, или точка минимума. В этом случае, в точке максимума функция принимает наибольшее значение, а в точке минимума — наименьшее значение.
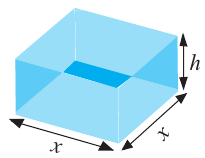
Пример 1. Максимальный объем. Фирма планирует выпуск коробки без крышки, с квадратным основанием и площадью поверхности 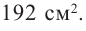
Решение:
Так как основанием коробки является квадрат, то ее объем можно вычислить по формуле 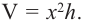
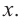
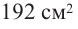
Тогда выразим 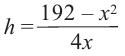
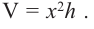
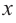
Теперь найдем область определения функции 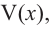
Понятно, что длина не может быть отрицательной, т. е. 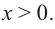
или 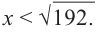
Найдем максимальное значение функции 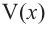
Для этого используем производную первого порядка:
При 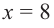
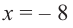
Однако. 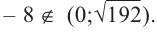
При 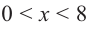
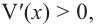
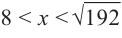
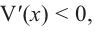
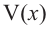
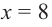
Если длина основания коробки будет 8 см, то высота будет равна
Значит, максимальный объем будет иметь коробка с размерами
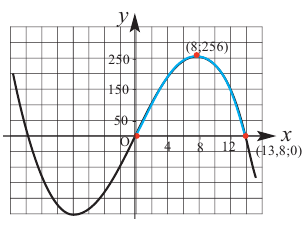
Построив при помощи графкалькулятора график функции 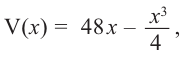
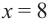
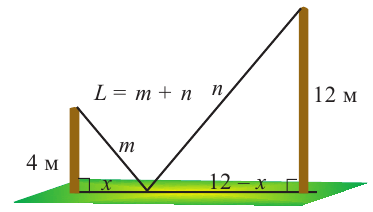
Пример 2. Минимальное потребление. Два столба высотой 4 м и 12 м находятся на расстоянии 12 м друг от друга. Самые высокие точки столбов соединены с металлической проволокой, каждая из которых, в свою очередь крепится на земле в одной точке. Выберите такую точку на земле, чтобы для крепления использовалось наименьшее количество проволоки.
Решение: 1) Изобразим рисунок, соответствующий условию задачи, и обозначим соответствующие данные на рисунке.
2) Аналитически выразим зависимость между переменными.
По теореме Пифагора:
зависимость функции 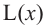
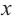
Производная функции
Найдем критические точки функции
Сравнивая значения функции 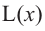
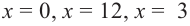
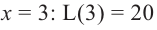
При решении задач на экстремумы обратите внимание на следующее!
1. Внимательно читайте условие. Сделайте соответствующий рисунок.
2. Задайте список соответствующих переменных и констант, которые менялись и оставались неизменными и какие единицы использовались. Если на рисунке есть размеры, обозначьте их.
3. Выберите соответствующий параметр 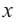
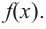
4. Полученные значения объясните экспериментально.
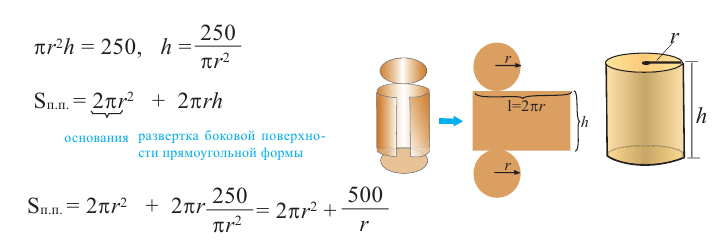
Пример: Минимальное потребление материала. Для мясных консервов планируется использовать банку в форме цилиндра объемом 250
a) Каких размеров должна быть банка, чтобы для ее изготовления использовалось как можно меньше материала?
b) Для круглого основания используется материал, цена 1 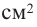
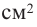
Решение: а) По условию задачи объем равен 250 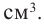
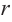
Для функции, выражающей площадь поверхности, область определения представляет собой незамкнутый интервал, и мы должны найти, при каком значении 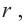
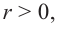
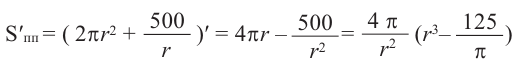
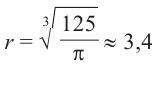
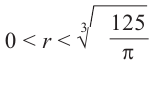
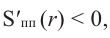
Значит,
Подставим значение 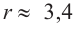
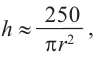
Итак, минимальные затраты на материал будет иметь банка цилиндрической формы с размерами 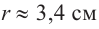
Размеры, при которых затраты на материал будут минимальными
- Приложения производной
- Производные высших порядков
- Дифференциал функции
- Дифференцируемые функции
- Касательная к графику функции и производная
- Предел и непрерывность функции
- Свойства функций, непрерывных в точке и на промежутке
- Предел функции на бесконечности
Лучшие репетиторы для сдачи ЕГЭ
Задания по теме «Применение производной к исследованию функций и построению графиков»
Открытый банк заданий по теме применение производной к исследованию функций и построению графиков. Задания B7 из ЕГЭ по математике (профильный уровень)
Геометрические фигуры на плоскости: вычисление величин с использованием углов
Геометрические фигуры в пространстве: нахождение длины, площади, объема
Задание №1163
Тип задания: 7
Тема:
Применение производной к исследованию функций и построению графиков
Условие
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (-4; 10). Найдите промежутки убывания функции f(x). В ответе укажите длину наибольшего из них.
Показать решение
Решение
Как известно, функция f(x) убывает на тех промежутках, в каждой точке которых производная f'(x) меньше нуля. Учитывая, что надо находить длину наибольшего из них естественно по рисунку выделяются три таких промежутка: (-4; -2); (0; 3); (5; 9).
Длина наибольшего из них — (5; 9) равна 4.
Ответ
4
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1162
Тип задания: 7
Тема:
Применение производной к исследованию функций и построению графиков
Условие
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (-8; 7). Найдите количество точек максимума функции f(x), принадлежащих промежутку [-6; -2].
Показать решение
Решение
Из графика видно, что производная f'(x) функции f(x) меняет знак с плюса на минус (именно в таких точках будет максимум) ровно в одной точке (между -5 и -4) из промежутка [-6; -2]. Поэтому на промежутке [-6; -2] ровно одна точка максимума.
Ответ
1
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1161
Тип задания: 7
Тема:
Применение производной к исследованию функций и построению графиков
Условие
На рисунке изображён график функции y=f(x), определённой на интервале (-2; 8). Определите количество точек, в которых производная функции f(x) равна 0.
Показать решение
Решение
Равенство нулю производной в точке означает, что касательная к графику функции, проведённая в этой точке, параллельна оси Ox. Поэтому находим такие точки, в которых касательная к графику функции параллельна оси Ox. На данном графике такими точками являются точки экстремума (точки максимума или минимума). Как видим, точек экстремума 5.
Ответ
5
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1159
Тип задания: 7
Тема:
Применение производной к исследованию функций и построению графиков
Условие
На рисунке изображён график функции y=f(x) и отмечены точки -6, -1, 1, 4 на оси абсцисс. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Показать решение
Решение
Проводим касательные к графику функции в точках с указанными абсциссами. Определяем, под каким углом они наклонены к положительному направлению оси Ox. Как известно, значение тангенса указанного угла это и есть значение производной в указанных точках.
В точках -1 и 4 касательные наклонены под острым углом, поэтому в этих точках значение производной отрицательно. Учитывая, что в точке x=-6 касательная наклонена под меньшим тупым углом (ближе к вертикальной прямой), значение производной в этой точке наименьшее.
Ответ
-6
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1154
Тип задания: 7
Тема:
Применение производной к исследованию функций и построению графиков
Условие
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (-9; 4). Найдите промежутки возрастания функции f(x). В ответе укажите длину наибольшего из них.
Показать решение
Решение
Как известно, функция f(x) возрастает на тех промежутках, в каждой точке которых производная f'(x) больше нуля. Учитывая, что надо находить длину наибольшего из них естественно по рисунку выделяются три таких промежутка: (-9; -8); (-5; -1); (1; 4).
Длина наибольшего из них (-5; -1), равна 4.
Ответ
4
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1153
Тип задания: 7
Тема:
Применение производной к исследованию функций и построению графиков
Условие
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (-8; 7). Найдите количество точек минимума функции f(x), принадлежащих промежутку [-4; 3].
Показать решение
Решение
Из графика видно, что производная f'(x) функции f(x) меняет знак с минуса на плюс (именно в таких точках будет минимум) ровно в одной точке x=2 из промежутка [-4; 3]. Поэтому на промежутке [-4; 3] ровно одна точка минимума.
Ответ
1
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1150
Тип задания: 7
Тема:
Применение производной к исследованию функций и построению графиков
Условие
На рисунке изображен график функции y=f(x) и отмечены точки -5, -4, -1, 1 на оси абсцисс. В какой из этих точек значение производной наибольшее? В ответе укажите эту точку.
Показать решение
Решение
Проводим касательные к графику функции в точках с указанными абсциссами. Определяем, под каким углом они наклонены к положительному направлению оси Ox. Как известно, значение тангенса указанного угла это и есть значение производной в указанных точках.
В точках -4 и -1 касательные наклонены под тупым углом, поэтому в этих точках значение производной отрицательно. В точках -5 и 1 касательные наклонены под острым углом, поэтому в этих точках значение производной положительно.
Учитывая, что касательная, проведённая к графику функции в точке x=1, образует больший угол с положительным направлением оси Ox, то значение производной в этой точке наибольшее.
Ответ
1
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1143
Тип задания: 7
Тема:
Применение производной к исследованию функций и построению графиков
Условие
На рисунке изображён график y=f'(x) — производной функции f(x), определённой на интервале (-7; 5). В какой точке отрезка [-6; -2] функция f(x) принимает наименьшее значение?
Показать решение
Решение
Из графика видно, что производная f'(x) функции f(x) больше нуля во всех точках промежутка [-6; -2]. Значит, на этом промежутке функция f(x) возрастает. Поэтому наименьшее значение функции будет на левом конце промежутка, то есть в точке -6.
Ответ
-6
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1142
Тип задания: 7
Тема:
Применение производной к исследованию функций и построению графиков
Условие
На рисунке изображен график функции y=f(x), определенной на интервале (-5; 7). Определите количество целых точек, в которых производная функции отрицательна.
Показать решение
Решение
Производная отрицательна в тех точках промежутков, на которых функция убывает. Рассматривая график, находим шесть таких точек с целочисленными абсциссами: -3; -2; 1; 2; 5; 6.
Ответ
6
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Задание №1140
Тип задания: 7
Тема:
Применение производной к исследованию функций и построению графиков
Условие
На рисунке изображён график функции y=f(x) и семь точек на оси абсцисс: x_1, x_2, x_3, x_4, x_5, x_6, x_7. В скольких из этих точек производная функции f(x) отрицательна?
Показать решение
Решение
Производная отрицательна в тех точках, которые принадлежат промежуткам убывания функции, если только касательные в них не горизонтальны.
Точками, удовлетворяющими сказанному, будут: x_1, x_4, x_5, x_6. Их оказалось 4.
Ответ
4
Источник: «Математика. Подготовка к ЕГЭ-2017. Профильный уровень». Под ред. Ф. Ф. Лысенко, С. Ю. Кулабухова.
Лучшие репетиторы для сдачи ЕГЭ
Сложно со сдачей ЕГЭ?
Звоните, и подберем для вас репетитора: 78007750928
09
Авг 2013
Категория: 07 Производная, ПО
07. Применение производной к исследованию функции
2013-08-09
2023-02-25
Cледующая таблица будет весьма полезна при работе с данной темой.

или ее производной
Если дан график производной, то интересовать нас будут только знаки функции и нули. Никакие «холмики» и «впадины», как в случае
не интересуют нас в принципе!
Задача 1. На рисунке изображен график функции , определенной на интервале
. Определите количество целых точек, в которых производная функции
отрицательна.
Решение: + показать
Задача 2. На рисунке изображен график функции , определенной на интервале
. Найдите количество точек, в которых касательная к графику функции параллельна прямой
или совпадает с ней.
Решение:+ показать
Задача 3. На рисунке изображен график производной функции , определенной на интервале
. Найдите количество точек, в которых касательная к графику функции
параллельна прямой
или совпадает с ней.
Решение: + показать
Задача 4. На рисунке изображен график функции , определенной на интервале
. Найдите количество точек, в которых производная функции
равна 0.
Решение: + показать
Задача 5. На рисунке изображён график функции и одиннадцать точек на оси абсцисс:
. В скольких из этих точек производная функции
отрицательна?
Решение: + показать
Задача 6. На рисунке изображен график функции , определенной на интервале
. Найдите сумму точек экстремума функции
.
Решение: + показать
Задача 7. На рисунке изображен график производной функции , определенной на интервале
. Найдите промежутки возрастания функции
. В ответе укажите сумму целых точек, входящих в эти промежутки.
Решение: + показать
Задача 8. На рисунке изображен график производной функции , определенной на интервале
. Найдите промежутки возрастания функции
. В ответе укажите длину наибольшего из них.
Решение: + показать
Задача 9. На рисунке изображен график производной функции , определенной на интервале
. В какой точке отрезка
принимает наибольшее значение.
Решение: + показать
Задача 10. На рисунке изображен график — производной функции
, определенной на интервале
. Найдите количество точек максимума функции
, принадлежащих отрезку
.
Решение: + показать
Задача 11. На рисунке изображен график функции и отмечены точки -3, 1, 6, 8. В какой из этих точек значение производной наименьшее? В ответе укажите эту точку.
Решение: + показать
Задача 12. Функция определена на промежутке
На рисунке изображен график её производной. Найдите точку
в которой функция
принимает наименьшее значение, если
Решение: + показать
Задача 13. Функция определена и непрерывна на полуинтервале
На рисунке изображен график её производной. Найдите промежутки убывания функции
В ответе укажите сумму целых точек, входящих в эти промежутки.
Решение: + показать
Вы можете пройти тест «Применение производной к исследованию функции»
Автор: egeMax |
комментариев 29
Печать страницы
























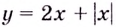
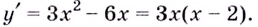
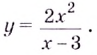
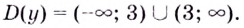
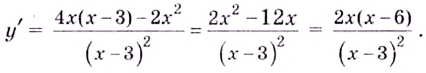
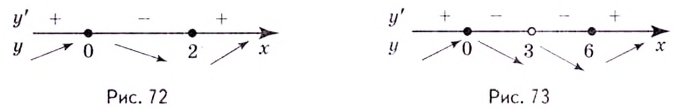
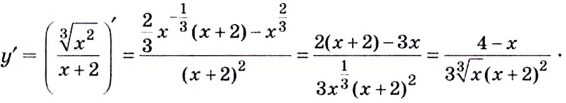
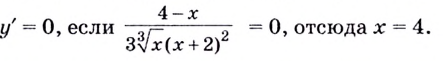
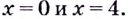
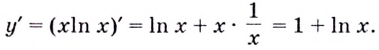
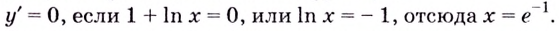
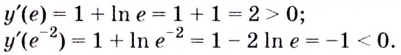
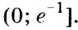
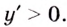
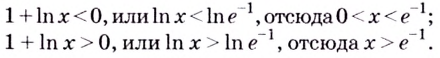
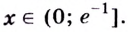
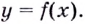
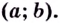
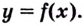
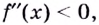 то кривая выпуклая; если
то кривая выпуклая; если 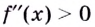 — кривая вогнутая;
— кривая вогнутая;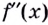 меняет знак при переходе через точку
меняет знак при переходе через точку 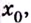 то точка
то точка 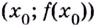 является точкой перегиба кривой
является точкой перегиба кривой 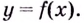
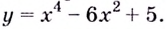
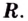
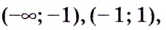
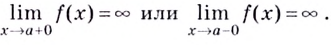
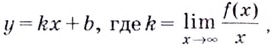
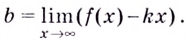
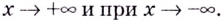
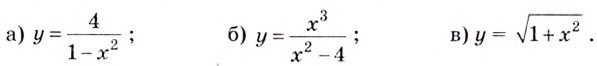
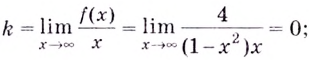
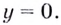
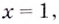
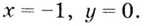
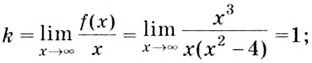
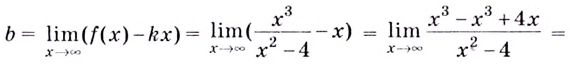
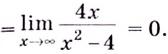
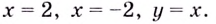
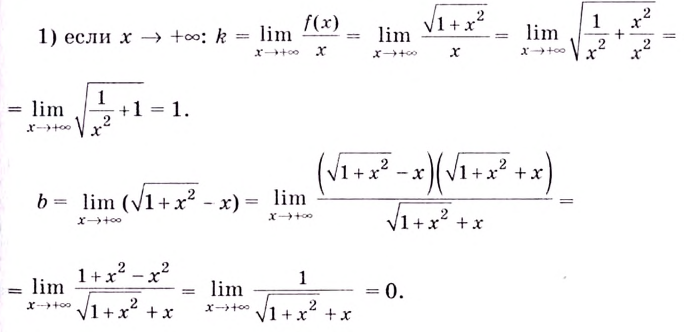
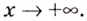
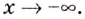
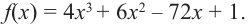
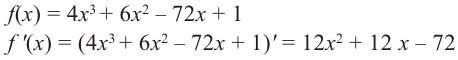
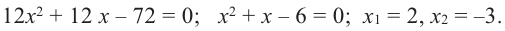

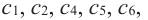
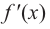 слева от точки
слева от точки 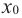 положительна, а справа — отрицательна, то точка
положительна, а справа — отрицательна, то точка 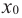 является точкой максимума.
является точкой максимума.

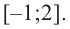
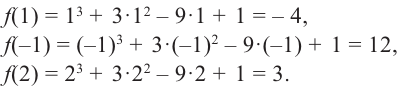
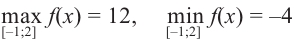
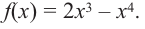
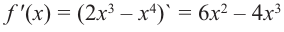
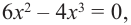
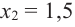

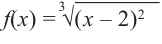
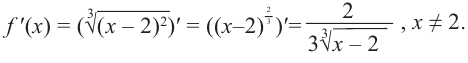
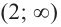
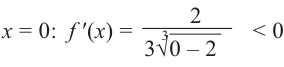

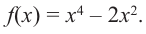
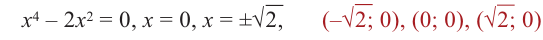
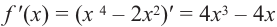
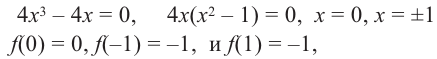

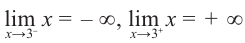
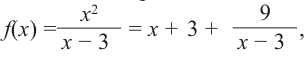
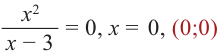
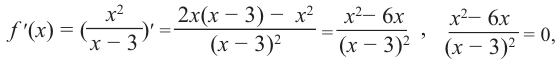
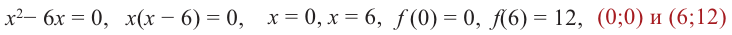

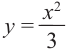
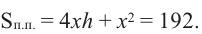
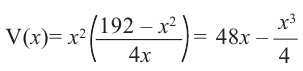
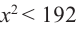
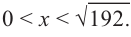
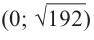
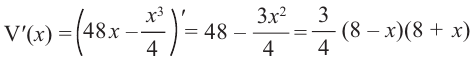
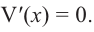
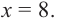
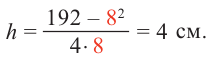
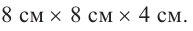
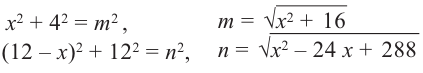
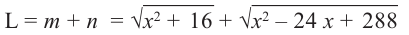
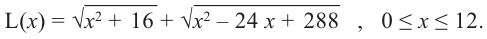
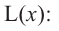
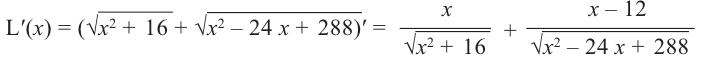
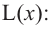
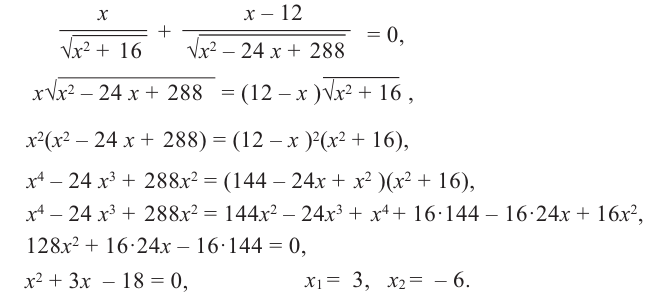
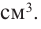
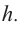
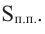
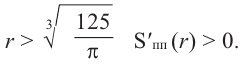
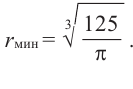
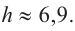
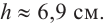
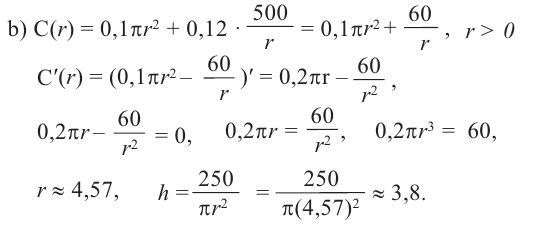
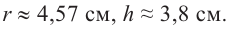

.png)


.png)


















