Применение языка программирования Python в решении задач компьютерного
ЕГЭ по информатике
Автор:
Кусточкин Александр Валерьевич
учитель
информатики, МБОУ «Поспелихинская СОШ №1»
2021
г.
Оглавление
Введение
1. Основы
языка программирования Python
2. Обзор
задач компьютерного ЕГЭ по информатике и их решение на языке Python
3. Сравнение
эффективности программ, написанных на языках Pascal,
C и Python
Заключение
Введение
Единый
государственный экзамен по информатике необходим тем, кто планирует поступать в
российские вузы на специальности, связанные с IT-технологиями. Этот экзамен
нужен тем, кто хочет стать программистом, разработчиком, специалистом по
информационным технологиям.
Единый
государственный экзамен по информатике будет проходить на компьютерах уже с
2021 года. Новая модель реализована в виде компьютерной системы тестирования, а
ее апробация прошла в нашем городе осенью 2019. Смысл новой модели состоит в
том, что все задания выпускники будут выполнять при помощи компьютеров и с
применением различных языков программирования и программного обеспечения.
В
настоящее время все большую популярность приобретает язык Python.
Одна из причин популярности Python – более простое и компактное оформление,
чем в других языках. Это самый популярный язык общего назначения: он
используется для машинного обучения, аналитике, разработке игр и в науке о
данных. В данной работе будет применение языка Pythonв
решении задач компьютерного ЕГЭ по информатике.
Объект
работы – процесс решения задач компьютерного ЕГЭ
по информатике.
Предмет
работы – средства решения задач компьютерного
ЕГЭ по информатике.
Цель
работы – провести обзор возможностей языка
программирования Pythonв
решении задач компьютерного ЕГЭ по информатике.
Задачи:
— рассмотреть
основы языка программирования Python;
— выделить
типы задач компьютерного ЕГЭ по информатике и, по возможности, решить их
средствами языка программирования Python;
— сравнить
эффективность программ, написанных на языках Pascal,
C
и Python.
1. Основы
языка программирования Python
Сценарии
исходного кода Python состоят из так называемых логических строк, каждая из которых в свою очередь
состоит из физических
строк. Для обозначения комментариев используется символ #.
Комментарии и пустые строки интерпретатор игнорирует.
Физические строки
разделяются самим символом конца строки. Для выделения блоков кода используются
исключительно отступы. Логические строки с одинаковым размером отступа
формируют блок, и заканчивается блок в том случае, когда появляется логическая
строка с отступом меньшего размера. Именно поэтому первая строка в сценарии
Python не должна иметь отступа.
Других радикальных
отличий от других языков программирования в синтаксисе Python нет. Также
используются стандартные правила для заданий идентификаторов переменных,
методов и классов – имя должно начинаться с подчеркивания или латинского символа
любого регистра и не может содержать символов @, $, %. Также не может
использоваться в качестве идентификатора только один символ подчеркивания.
Типы данных, используемых
в Python, совпадают с другими языками – целые и вещественные типы данных;
дополнительно поддерживается комплексный тип данных – с вещественной и мнимой
частью. Python поддерживает строки, которые могут быть заключены в одинарные,
двойные или тройные кавычки, при этом строки являются immutable-объектами, т.е.
не могут изменять свое значение после создания.
Есть в Python и
логический тип данных bool c двумя вариантами значения – True и False. Для
повышения читаемости кода рекомендуется использовать для логических переменных
тип bool.
В Python определены три
типа коллекций для хранения наборов данных:
—
кортеж (tuple);
—
список (list);
—
словарь (dictionary).
Кортеж представляет собой
неизменяемую упорядоченную последовательность данных. В нем могут содержаться
элементы различных типов, например другие кортежи. Кортеж определяется в круглых
скобках, а его элементы разделяются запятыми. Специальная встроенная функция
tuple() позволяет создавать кортежи из представленной последовательности
данных.
Список – это изменяемая
упорядоченная последовательность элементов. Элементы списка также разделяются
запятыми, но задаются уже в квадратных скобках. Для создания списков
предлагается функция list().
Словарь является
хеш-таблицей, сохраняющей элемент вместе с его идентификатором-ключом.
Последующий доступ к элементам выполняется тоже по ключу, поэтому единица
хранения в словаре – это пара объект-ключ и связанный с ним объект-значение.
Словарь – это изменяемая, но не упорядоченная коллекция, так что порядок
элементов в словаре может меняться со временем. Задается словарь в фигурных
скобках, ключ отделяется от значения двоеточием, а сами пары ключ/значение
разделяются запятыми. Для создания словарей доступна функция dict().
В
листинге 1 приведены примеры различных коллекций, доступных в Python.
Листинг 1. Виды коллекций, доступные в Python
|
(‘w’,‘o’,‘r’,‘l’,‘d’) (2.62,) [“test”,’me’] [ { 5:‘a’, |
Многие возможности Pythonреализованы в виде
отдельных функций; кроме того, модули расширения чаще всего делаются тоже в
виде библиотеки функций. Функции также применяются и в классах, где они по
традиции называются методами.
Синтаксис
определения функций в Python крайне простой; с учетом изложенных выше
требований (листинг 2).
Листинг 2. Виды коллекций, доступные в Python
|
def выражение выражение … |
Как
видно, необходимо использовать служебное слово def, двоеточие и отступы.
Вызвать функцию также очень просто:
Есть
только несколько моментов, специфичных для Python, которые стоит учитывать.
Параметры могут передаваться как просто по порядку перечисления, так и по
именам, в этом случае не нужно указывать при вызове те параметры, для которых
есть значения по умолчанию, а передавать только обязательные или менять порядок
параметров при вызове функции (листинг 3).
Листинг 3. Виды коллекций, доступные в Python
|
#функция, def return print print |
Функция в Python
обязательно возвращает значение – это делается либо явно с помощью оператора
return, за которым следует возвращаемое значение, либо, в случае отсутствия
оператора return, возвращается константа None, когда достигается конец функции.
Как видно из примеров объявлений функций, в Python нет необходимости указывать,
возвращается что-либо из функции или нет, однако если в функции имеется один
оператор return, возвращающей значение, то и другие операторы return в этой
функции должны возвращать значения, а если такого значения нет, то необходимо
явно прописывать return None.
Если функция очень
простая и состоит из одной строки, то ее можно определить прямо на месте
использования, в Python подобная конструкция называется лямбда-функцией
(lambda). lambda-функция – это анонимная функция (без собственного имени),
телом которой является оператор return, возвращающий значение некоторого
выражения. Такой подход может оказаться удобным в некоторых ситуациях, однако
стоит заметить, что повторное использование подобных функций невозможно.
Еще стоит описать
отношение Python к использованию рекурсии. По умолчанию глубина рекурсии
ограничена 1000 уровней, и когда этот уровень будет пройден, возникнет
исключительная ситуация, и работа программы будет остановлена. Однако при
необходимости величину этого предела можно изменить.
2. Обзор
задач компьютерного ЕГЭ по информатике и их решение на языке Python
В
проекте компьютерного ЕГЭ по информатике предлагаются десять типов заданий на
следующие темы.
1.
Вычисления
2.
Решение уравнений численными методами
3.
Перебор целых чисел. (Разбиение числа на
цифры)
4.
Перебор чисел. Проверка делимости
5.
Перебор целых чисел. Количество делителей
6.
Символьные строки. Цепочки символов
7.
Функции двух аргументов. Таблицы значений
8.
Электронные таблицы. Встроенные функции
(не решается средства Python)
9.
Рекурсия. Рекурсивные функции
10.
Исследование моделей. Оптимизация
1.
Пример задания на вычисление
С помощью программы Калькулятор или электронных
таблиц вычислите значение выражения. В ответе запишите только целую часть
результата. Можно также написать программу.
ПрограмманаязыкеPython
from math
import sqrt, cos, pi
print( sqrt(1
+ cos(3.53*pi)*10)*310 )
Ответ:
431.
Для
решения данного задания, нужно знать правила записи математических функций на
языке Python. В связи с невозможностью записи некоторых стандартных
математических функций с клавиатуры персонального компьютера в языке Python
существуют так называемые встроенные функции, с помощью которых пользователь
записывает арифметические выражения.
Основные
математические функции языка Python представлены в таблице 1. Прежде чем
использовать математические функции, необходимо в начале программы написать
инструкцию import math, однако тогда перед упоминанием каждой функции необходимо
будет добавлять имя модуля — math, например, y=math.sin(x). Другой способ,
который позволит избежать многократного вызова модуля math, — сделать следующую
запись в начале программы: from math import *.
Таблица
1. Общие математические функции модуля Math
|
Запись на Python |
Действие |
|
math.sin (x) |
Возвращает значение функции Sin от числа х |
|
math.cos (x) |
Возвращает значение функции Cos от числа х |
|
math.tan (x) или math.sin (x) / math.cos (x) |
Возвращает значение функции Tg от числа х |
|
math.cos |
Возвращает значение функции Ctg от числа х |
|
math.abs (x) |
Возвращает абсолютную величину числа х |
|
math.exp (x) |
Возвращает результат возведения числа е в степень X |
|
math.Log lp (x) |
Возвращает натуральный логарифм от х+1 |
|
math.sqrt (x) |
Возвращает результат извлечения квадратного корня |
|
math.log (x) |
Возвращает логарифм числа х по основанию 10 |
|
math.cos |
Возвращает результат возведения функции Cos х в квадрат |
|
math.acos (x) |
Возвращает значение функции арккосинус от числа х |
|
math.asin (x) |
Возвращает значение функции арксинус от числа х |
|
math.atan (x) |
Возвращает значение функции арктангенс от числа х |
|
Pi |
Возвращает 3.141592653589793 |
|
math.degrees(x) |
Преобразует радианы в градусы |
|
math.radians(x) |
Преобразует градусы в радианы |
|
math.floor(x) |
Возвращает значение, округленное до ближайшего |
|
math.ccil(x) |
Возвращает значение, округленное до ближайшего |
|
math.factorial(x) |
Возвращает факториал числа. 3 != 1 *2*3 |
В таблице2 представлены
некоторые встроенные функции для работы с числами, не требующие подключения
модуля math.
Таблица
2. Функции для работы с числами
|
Запись на Python |
Описание |
|
round(x) |
Возвращает результат округления числа х до ближайшего меньшего целого |
|
pow(x,y) другой вариант х**у |
Возвращает результат возведения числа х в степень у |
|
mах(список чисел через |
Возвращает большее значение из списка чисел |
|
min(список чисел через |
Возвращает меньшее значение из списка чисел |
|
sum(список K чисел через запятую) |
Возвращает сумму значений элементов последовательности |
|
float(число) |
Преобразует объект (например, строковое значение, целое |
2. Пример задания на решение уравнения численным
методом
Известно, что уравнение на отрезке [0; 1,5] имеет единственный корень.
Найдите его приблизительное значение с точностью не менее 0,00001 и запишите
в ответе найденное значение ровно с пятью значащими цифрами после запятой.
Программа
на языке Python:
from math
import cos, exp # подключить функции cos, exp
def
f(x): # это функция f(x)
return
0.01*exp(x) — cos(3*x)
a, b =
0, 1.5 # границыотрезка
while b-a
> 1e-6: # пока ширина отрезка >= 10^(-6)
c = (a +
b) / 2 # середина отрезка
if
f(a)*f(c) <= 0: # сдвигаем правую или левую границу
b =
c
else: a =
c
# вывод с 5
знаками в дробной части
print(
«{:.5f}».format((a + b) / 2) )
Ответ:
0.51800
3. Пример
задания на перебор целых чисел. Разбиение числа на цифры
Назовём натуральное четырёхзначное число N
(1000 £N£
9999) счастливым, если суммы двух его первых и двух последних цифр
различаются не более, чем на 3. Найдите количество таких чисел.
Программа на языке Python
count = 0
for n in
range(1000, 10000):
d0 = n %
10; n //= 10
d1 = n %
10; n //= 10
d2 = n %
10
d3 = n //
10
if
abs(d3+d2-d1-d0) <= 3:
count
+= 1
print(count)
Поскольку
заданный отрезок [1000; 9999] содержит всего 9000 чисел, можно решать задачу
простым перебором. Для этого сначала нужно разбить число на цифры с помощью
операций деления нацело и остатка от деления; цифры помещаем в переменные d0,
d1, d2, d3. Затем проверяем «счастливость» числа: число счастливое при
выполнении условияв этом случае увеличиваем счётчик найденных счастливых чисел.
Ответ:
4071.
4. Пример
задания на перебор целых чисел. Проверка делимости
Рассматривается
множество целых чисел, принадлежащих отрезку [1033;
7737], которые делятся на 5 и не делятся на 11, 17, 19 и 23. Найдите
количество таких чисел и максимальное из них. В ответе запишите два числа
через пробел: сначала количество, затем максимальное число.
Программа на языке Python
count = 0
maxGood = 0
for n in
range(1033, 7737+1):
if (n % 5
== 0) and (n % 11 != 0) and
(n %
17 != 0) and (n % 19 != 0) and (n % 23 != 0):
maxGood
= n
count += 1
print(count,
maxGood)
Поскольку
заданный отрезок [1033; 7737] содержит не так много чисел, можно решать задачу
простым перебором. Условие будем понимать так: интересующие нас числа делятся
на 5 и не делятся ни на одно из чисел 11, 17, 19 и 23. Нам выгоднее перебирать
числа в порядке возрастания, тогда последнее найдённое число – это и есть искомое
максимальное подходящее число (если требуется найти наименьшее подходящее
число, удобнее перебирать числа в порядке убывания)
Ответ:
1040 7730
Напишите программу, которая ищет среди целых
чисел, принадлежащих числовому отрезку [194455;
194500], числа, имеющие ровно 4 различных делителя. Выведите эти четыре
делителя для каждого найденного числа в порядке возрастания.
ПрограмманаязыкеPython
for n in
range(194455, 194500+1):
divs = []
for d in
range(1,n+1):
if n %
d == 0:
divs.append(d)
if
len(divs) == 4:
print(
*divs )
При
написании программы на языке Python можно поступить так
for для
всех чисел n в интервале:
divs =
массив всех делителей n
if
len(divs) == 4:
вывести
массив делителей
5. Пример
задания на работу с простыми числами
Напишите программу, которая ищет среди целых
чисел, принадлежащих числовому отрезку [3532000;
3532160], простые числа. Выведите все найденные простые числа в порядке
возрастания, слева от каждого числа выведите его номер по порядку.
ПрограмманаязыкеPython
from
math import sqrt
count
= 0
for
n in range(3532000, 3532160+1):
prime = True
for d in range(2, round(sqrt(n))):
if n % d == 0:
prime = False
break
ifprime:
count
+= 1
print(
count, n )
6. Пример
задания на работу с символьными строками
В текстовом файле k7.txt
находится цепочка из символов латинского алфавита A, B, C, D, E. Найдите
количество цепочек длины 3, удовлетворяющих следующим условиям:
·
1-й символ – один из символов B, C или D;
·
2-й символ – один из символов B, D, E, который не
совпадает с первым;
·
3-й символ – один из символов B, C, E, который не
совпадает со вторым.
Программанаязыке
Python
s =
open(‘k7.txt’).read()
count = 0
for i in
range(len(s)-2):
if s[i]
in ‘BCD’ and s[i+1] in ‘BDE’
and
s[i+2] in ‘BCE’ and s[i]!=s[i+1]
and
s[i+1]!=s[i+2]:
count
+= 1
print(count)
Решение:
1)
Считываем из файла и перебираем символы.
2)
Перебираем все тройки символов. Примем,
что переменная i будет хранить номер первого элемента в тройке, то есть, будем
рассматривать тройки (s[i], s[i+1], s[i+2]).
3)
Организуем цикл который перебирает
значения i от 1 до len(s)-2
for i in
range(len(s)-2):
…
4) Проверяем
символы в каждой тройке на соответствие условию. Проверка принадлежности
символов набору аналогична заданию 1. Дополнительно необходимо указать условия
неравенства символов, указанных в условии задачи. Если условия выполняются, то
к переменной количества прибавляется единица.
7. Пример задания на
вычисление значения функции от двух переменных
С помощью редактора
электронных таблиц создайте таблицу вещественных значений выражения для следующих вещественных
значений x и y:
x = 5,5; 6,0; …; 8,5; y
= 10,0; 10,3; …; 13,0.
Вычислите сумму
получившихся значений и запишите её целую часть в ответе.
Для выполнения этого
заданий также можно написать программу.
Решение:
1)
Чтобы написать программу, нужно
использовать вложенный цикл: в одном цикле будем перебирать значения x,
а во втором (вложенном) – значения y; учитывая, что цикл с переменной (for
… in …)
работает только с целыми последовательностями чисел, придётся использовать
циклы с условием:
s =
0 # это неправильная программа
x =
5.5 # это неправильная программа
while x
<= 8.5: # это неправильная программа
y = 10
while y
<= 13:
#
print(x, y) # отладочная печать, см. обсуждение ниже
s +=
2*x**3/(y+1)
y +=
0.3
x += 0.5
print( s )
сумма значений функции накапливается в
переменной s
2)
однако эта программа выводит неверный
ответ.
3)
Дело в том, что вещественные числа,
которые нельзя представить в виде суммы целых (в том числе и отрицательных)
степеней числа 2, в двоичной системе счисления представляют собой бесконечную
дробь и поэтому не могут быть точно записаны в памяти двоичного компьютера; при
выполнении вычислений с такими числами ошибка накапливается, и к последнему
шагу (это можно проверить с помощью отладочной печати) значение y равно
не 12,7, а чуть больше:
12.700000000000006
из-за
этого следующее значение, равное 13,000000000000006, уже больше, чем 13, и не
удовлетворяет условию работы цикла; таким образом, на каждом шаге цикла по x
мы теряем одно значение y, и соответствующее значение функции не
включается в сумму.
4)
с переменной x подобных проблем
нет, так как шаг изменения x равен 0,5 = 2–1
5)
исправить ситуацию можно так: организовать
перебор только целых значений, используя вспомогательные целочисленные
переменные x10 = x×
10 и y10
= y×
10:
s
= 0
for
x10 in range(55, 86, 5):
for y10 in range(100, 131, 3):
s
+= 2*(x10/10)**3/(y10/10+1)
print(s)
8. Пример задания на
вычисление значения рекурсивной функции
Определите
наименьшее значение n, при котором сумма чисел, которые будут выведены при
вызове F(n), будет больше 500000. Запишите в ответе сначала найденное значение
n, а затем через пробел – соответствующую сумму выведенных чисел.
def F( n ):
print(2*n)
if n > 1:
print(n-5)
F(n-1)
F(n-2)
Решение:
Первое,
что может прийти в голову – вызывать приведённую процедуру при разных значениях
параметра и увеличивать это значение до тех пор, пока сумма выведенных чисел не
превысит заданное значение 500000; это тупиковый подход, поскольку чисел очень
много и сложение займет очень много времени при низкой вероятности правильного
ответа
Можно
попробовать изменить программу так, чтобы сумма выводимых чисел считалась
автоматически: добавим в программу глобальную переменную s
и будем увеличивать её при выводе каждого числа на значение этого числа; при
этом для ускорения (значительного!) работы программы сразу закомментируем вывод
чисел на экран:
def
F( n ):
global s # если не объявить s глобальной – ошибка!
#
print(2*n)
s += 2*n
if n >
1:
#
print(n-5)
s += n — 5
F(n-1)
F(n-2)
Дальше
можно написать такую программу и запускать её при различных значениях
переменной n:
n
= 15
s
= 0
F(n)
print(
n, s )
Увеличивая
каждый раз значение n
на 1, мы в конце концов найдём первое (минимальное) значение n,
при котором сумма чисел, которые будут выведены при вызове F(n),
будет больше 500000 – это F(24) = 531864
Ответ:
24 531864.
9. Пример задания на
оптимизацию
На покупку мебели выделено 500 тыс. рублей.
Стоимость одного комплекта составляет 18 тыс. рублей. Запишите наборы
вариантов покупки максимального количества комплектов мебели, при условии,
что производитель М продает мебель упаковками по 6 комплектов в упаковке, а
производитель N – по 4 комплекта в упаковке.
Запишите в ответ пары чисел: количество упаковок
производителя М далее через пробел количество упаковок производителя N.
Каждую пару записывайте с новой строки. Пары должны быть отсортированы по
возрастанию значений в первом столбце.
Решение:
В
простейшем варианте можно просто вывести на экран все варианты сочетаний a
и b с соответствующими значениями K,
в конце программы вывести макcимальное
значение K; затем вручную найти все строки, где значение K
равно максимальному.
S0
= 500000 # доступная сумма
cost1
= 18000 # стоимость одного комплекта
packM
= 6 # количество комплектов в упаковке M
packN
= 4 # количество комплектов в упаковке N
# максимальное значение a
aMax = int(S0 /
(packM*cost1))
#
поиск максимального K по всем вариантам
maxK = 0
for a in
range(aMax+1):
Sb = S0 —
a*packM*cost1 # сумманазакупкуу N
b =
int(Sb / (packN*cost1))
K =
packM*a + packN*b # общее количество
print(a, b,
K)
if K >
maxK:
maxK = K
# новыймаксимум
print(maxK,
maxK*cost1)
3. Сравнение
эффективности программ, написанных на языках Pascal, C и Python
Сравним
программы, написанные на языках Pascal,
C
и Python
по таким критериям, как время работы и используемая память. Для примера возьмем
линейные программы, программы с циклами и программы с рекурсивными функциями.
Задача
1:дано натуральное число.
Выведите его последнюю цифру.
|
Pascal |
C |
Python |
|
var a: integer; begin readln(a); writeln(a end. |
#include main() { int x; } |
x=int(input()) print(x%10) |
|
Время Используемая |
Время работы: Используемая |
Время Используемая 360448 бит |
Как видно из таблицы, при реализации линейных
алгоритмов программа на Pythonпроигрывает во времени реализации и используемой
памяти программам на Pascalи C.
Задача2:подсчитайте количество натуральных
делителей числа x (включая
1 и само число;x2
109).
|
Pascal |
C |
Python |
|
var x, i, k: longint; begin readln(x); k:=0; for i:=1 to x do begin if (x mod i =0) then inc(k); end; writeln(k); end. |
#include #include main() { int x, i, k; scanf(«%i», k=0; for (i=1; i<=x; i++) if (x % i ==0) { k=k+1; } } printf(«%i», } |
x=int(input()) k=0 for i in range(1,x+1): if x%i==0: k+=1 print(k) |
|
Время Используемая |
Время работы: Используемая |
Время Используемая 376832 бит |
Из-за того, что значение xможет быть достаточно большим, все написанные программы не проходят все
тесты. Последние два теста не выполняются из-за того, что превышено
максимальное время работы (рис. 1).
Рис. 1. Результаты
прохождения тестов
Поэтому простым перебором данную задачу решать
нельзя. Повысим эффективность программы, идея состоит в
том, чтобы для определения количества делителей числа N
перебирать только числа до ;
если число q целое, его нужно
добавить в список делителей, а все остальные делители – парные, то есть если a
– делитель N, то b
= N
/ a
– тоже делитель N.
Таким
образом, циклом пробегаемся от 1 до (корня X)-1, и проверяем на делимость, если
делится, то увеличиваем счетчик. После цикла удваиваем наш счетчик, так как
любое число если имеет делитель до корня этого числа, то он имеет ещё один
делитель после корня этого числа. Проверяем отдельным if-ом случай для корня X,
если делится нацело, то увеличиваем на один и выводим наш счетчик, иначе просто
выводим счетчик.
|
Pascal |
C |
Python |
|
var x, i, k: longint; begin readln(x); k:=0; for i:=1 to x do begin if (x mod i =0) then inc(k); end; writeln(k); end. |
#include #include main() { int x, i, k,q; double fp,ip; scanf(«%i», k=0; if (x%2==0) { q=trunc(sqrt(x)); } else { q=trunc(sqrt(x))-1; } for (i=1; i<=q; i++) if (x % i ==0) { k=k+1; } } k=k*2; fp = modf(sqrt(x) , if(fp==0) { k=k+1; } printf(«%i», } |
import math x=int(input()) if(x%2==0): q=math.trunc(math.sqrt(x)) else: q=math.trunc(math.sqrt(x))—1 k=0 for i inrange(1,q+1): if(x%i==0): k=k+1 k=k*2 if(math.sqrt(x)%1==0): k=k+1 print(k) |
|
Время Используемая |
Время работы: Используемая |
Время Используемая 380928 бит |
Заключение
Девяносто
процентов задач компьютерного ЕГЭ по информатике решается с помощью программирования.
В
процессе выполнения работы были решены следующие задачи:
— рассмотрены
основы языка программирования Python;
— выделены
типы задач компьютерного ЕГЭ по информатике. Задачи решены средствами языка
программирования Python;
— проанализирована
эффективность программ, написанных на языках Pascal,
C
и Python.
Список литературы
1.
Сайт К. Ю. Полякова. Методические материалы и
программное обеспечение [Электронный ресурс]. Режим доступа:http://kpolyakov.spb.ru
2.
Прохоренок Н. А. Python 3. Самое
необходимое [Текст]. – Спб.: БХВ-Петербург, 2019. – 608 с.
3.
Основы Python [Электронный ресурс]. Режим доступа:
4.
Применение и основы Python [Электронный ресурс]. Режим доступа:
5.
Дистанционная подготовка к информатике [Электронный ресурс]. Режим доступа
https://informatics.mccme.ru
Автор: Губаев Максим Станиславович
Место работы/учебы (аффилиация): МАОУ Лицей №39 города Нижний Тагил Свердловской области, 11 класс
Единый государственный экзамен по информатике необходим тем, кто планирует поступать в российские вузы на специальности, связанные с IT-технологиями. Этот экзамен нужен тем, кто хочет стать программистом, разработчиком, специалистом по информационным технологиям. Единый государственный экзамен по информатике будет проходить на компьютерах уже с 2021 года. Новая модель реализована в виде компьютерной системы тестирования, а ее апробация прошла в нашем городе осенью 2019. Смысл новой модели состоит в том, что все задания выпускники будут выполнять при помощи компьютеров и с применением различных языков программирования и программного обеспечения.
В настоящее время все большую популярность приобретает язык Python. Одна из причин популярности Python – более простое и компактное оформление, чем в других языках. Это самый популярный язык общего назначения: он используется для машинного обучения, аналитике, разработке игр и в науке о данных. В данной работе будет применение языка Python в решении задач компьютерного ЕГЭ по информатике.
Объект работы – процесс решения задач компьютерного ЕГЭ по информатике.
Предмет работы – средства решения задач компьютерного ЕГЭ по информатике.
Цель работы – провести обзор возможностей языка программирования Python в решении задач компьютерного ЕГЭ по информатике.
Задачи:
- рассмотреть основы языка программирования Python;
- выделить типы задач компьютерного ЕГЭ по информатике и, по возможности, решить их средствами языка программирования Python;
- сравнить эффективность программ, написанных на языках Pascal, C и Python.
Доброго времени суток каждому жителю Хабрвилля! Давненько я не писал статей! Пора это исправить!
В сегодняшней статье поговорим о насущной для многих выпускников школ теме — ЕГЭ. Да-да-да! Я знаю, что Хабр — это сообщество разработчиков, а не начинающих айтишников, но сейчас ребятам как никогда нужна поддержка именно сообщества. Ребят опять посадили на дистант. Пока не ясно на какой период, но уже сейчас можно сказать, что ЕГЭ по информатике будет на компьютерах и его можно зарешать при помощи языка Python.
Вот я и подумал, чтобы не получилось как в песне, стоит этим заняться. Я расскажу про все задачи первой части и их решения на примере демо варианта ЕГЭ за октябрь.
Всех желающих — приглашаю ниже!
Быстрый перевод из системы в систему
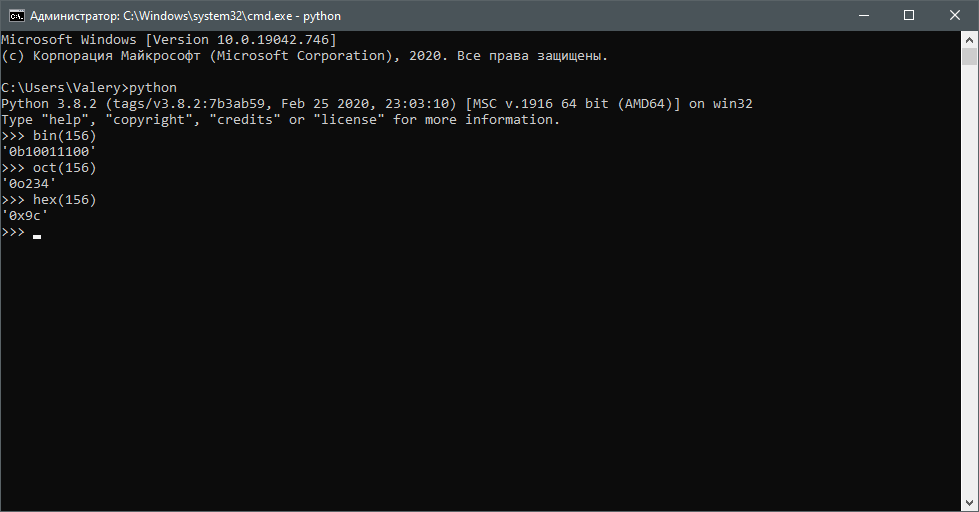
В Python есть интересные функции bin(), oct() и hex(). Работают данные функции очень просто:
bin(156) #Выводит '0b10011100'
oct(156) #Выводит '0o234'
hex(156) #Выводит '0x9c'Как вы видите, выводится строка, где 0b — означает, что число далее в двоичной системе счисления, 0o — в восьмеричной, а 0x — в шестнадцатеричной. Но это стандартные системы, а есть и необычные…
Давайте посмотрим и на них:
n = int(input()) #Вводим целое число
b = '' #Формируем пустую строку
while n > 0: #Пока число не ноль
b = str(n % 2) + b #Остатот от деления нужной системы (в нашем сл записываем слева
n = n // 2 #Целочисленное деление
print(b) #ВыводДанная программа будет работать при переводе из десятичной системы счисления в любую до 9, так как у нас нет букв. Давайте добавим буквы:
n = int(input()) #Вводим целое число
b = '' #Формируем пустую строку
while n > 0: #Пока число не ноль
if (n % 21) > 9: #Если остаток от деления больше 9...
if n % 21 == 10: #... и равен 10...
b = 'A' + b #... запишем слева A
elif n % 21 == 11:#... и равен 11...
b = 'B' + b#... запишем слева B
'''
И так далее, пока не дойдём до системы счисления -1 (я переводил в 21-ную систему и шёл до 20)
'''
elif n % 21 == 11:
b = 'B' + b
elif n % 21 == 12:
b = 'C' + b
elif n % 21 == 13:
b = 'D' + b
elif n % 21 == 14:
b = 'E' + b
elif n % 21 == 15:
b = 'F' + b
elif n % 21 == 16:
b = 'G' + b
elif n % 21 == 17:
b = 'H' + b
elif n % 21 == 18:
b = 'I' + b
elif n % 21 == 19:
b = 'J' + b
elif n % 21 == 20:
b = 'K' + b
else: #Иначе (остаток меньше 10)
b = str(n % 21) + b #Остатот от деления записываем слева
n = n // 21 #Целочисленное деление
print(b) #ВыводСпособ объёмен, но понятен. Теперь давайте используем тот же функцию перевода из любой системы счисления в любую:
def convert_base(num, to_base=10, from_base=10):
# Перевод в десятичную систему
if isinstance(num, str): # Если число - строка, то ...
n = int(num, from_base) # ... переводим его в нужную систему счисления
else: # Если же ввели число, то ...
n = int(num) # ... просто воспринять его как число
# Перевод десятичной в 'to_base' систему
alphabet = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ" # Берём алфавит
if n < to_base: # Если число меньше системы счисления в которую переводить...
return alphabet[n] # ... вернуть значения номера в алфавите (остаток от деления)
else: # Иначе...
return convert_base(n // to_base, to_base) + alphabet[n % to_base] # ... рекурсивно обратиться к функии нахождения остаткаВызвав функцию вывода print(convert_base(156, 16, 10)) мы переведём 156 из 10 в 16 систему счисления, а введя print(convert_base('23', 21, 4)) переведёт 23 из 4-ичной в 21-ичную систему (ответ: B).
Задача 2
Все задания беру из первого октябрьского варианта (он же вариант № 9325894) с сайта Решу.ЕГЭ.
Решение данной задачи совсем простое: банальный перебор.
print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы
for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1'
for x in range(2):
for z in range(2):
for w in range(2):
F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию
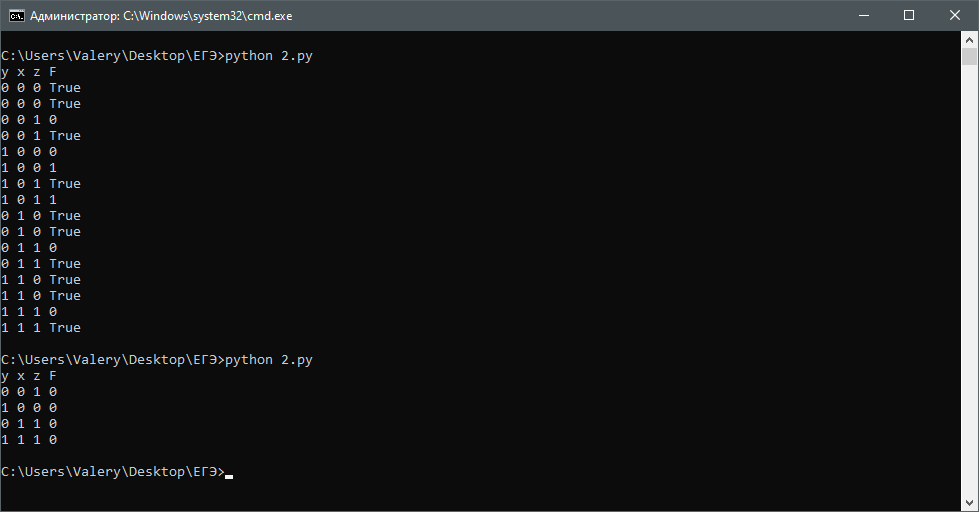
print(x, y, z, F) #Выводим результатРезультат:
Нам вывелась вся таблица истинности (1 = True, 0 = False). Но это не очень удобно. Обратите внимание, что в задании, функция равно 0, так и давайте подправим код:
print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы
for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1'
for x in range(2):
for z in range(2):
for w in range(2):
F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию
if not F:
print(x, y, z, F) #Выводим результатРезультат:
Далее — простой анализ.
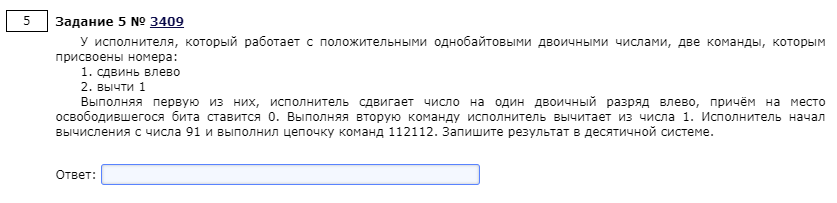
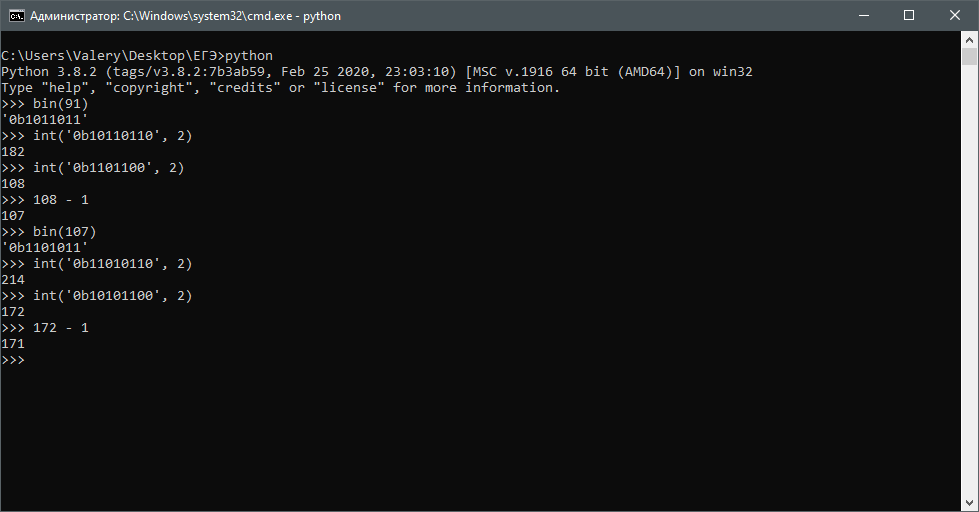
Задача 5
Данная задача легко решается простой последовательностью действий в интерпретационном режиме:
Задача 6
Перепечатали и получили ответ:
s = 0
k = 1
while s < 66:
k += 3
s += k
print(k)Задача 12
В очередной раз, просто заменим слова на код:
a = '9' * 1000
while '999' in a or '888' in a:
if '888' in a:
a = a.replace('888', '9', 1)
else:
a = a.replace('999', '8', 1)
print(a)Задача 14
Компьютер железный, он всё посчитает:
a = 4 ** 2020 + 2 ** 2017 - 15
k = 0
while a > 0:
if a % 2 == 1:
k += 1
a = a // 2
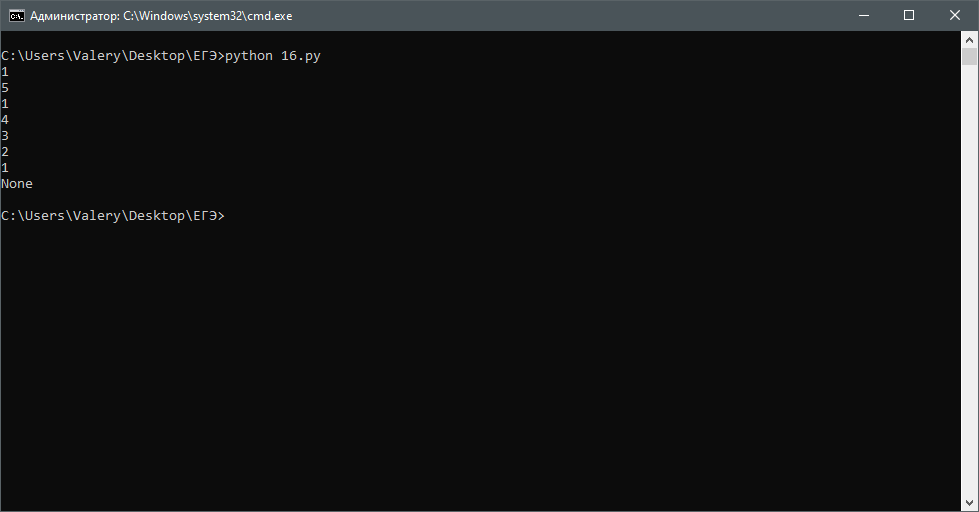
print(k)Задача 16
Опять же, просто дублируем программу в python:
def F(n):
if n > 0:
F(n // 4)
print(n)
F (n - 1)
print(F(5))Результат:
Задача 17
Задача с файлом. Самое сложное — достать данные из файла. Но где наша не пропадала?!
with open("17.txt", "r") as f: #Открыли файл 17.txt для чтения
text = f.read() #В переменную text запихнули строку целиком
a = text.split("n") #Разбили строку энтерами (n - знак перехода на новую строку)
k = 0 #Стандартно обнуляем количество
m = -20001 #Так как у нас сумма 2-ух чисел и минимальное равно -10000, то минимум по условию равен -20000, поэтому...
for i in range(len(a)): #Обходим все элементы массива
if (int(a[i - 1]) % 3 == 0) or (int(a[i]) % 3 == 0): #Условное условие
k += 1 #Счётчик
if int(a[i - 1]) + int(a[i]) > m: #Нахождение минимума
m = int(a[i - 1]) + int(a[i])
print(k, m) #ВыводНемного пояснений. Функция with() открывает файл считывает данные при помощи функции read() и закрывает файл. В остальном — задача стандартна.
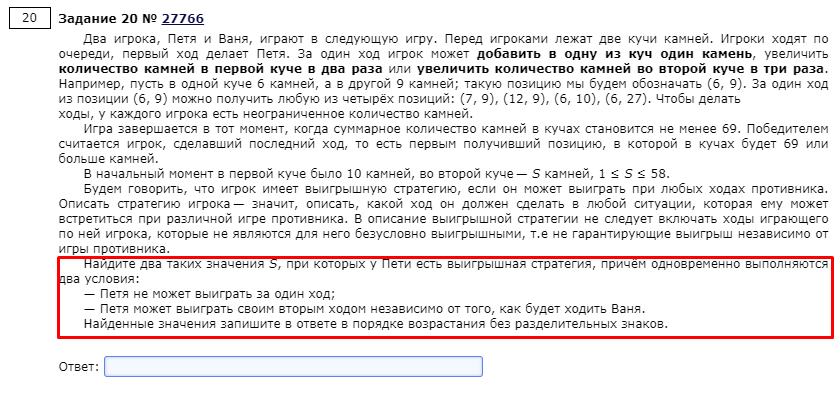
Задача 19, 20 и 21
Все три задачи — задачи на рекурсию. Задачи идентичны, а вопросы разные. Итак, первая задача:
Пишем рекурсивную функцию и цикл перебора S:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 3: #Условия завершения игры
return p == 3
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)
breakНемного пояснений. В рекурсивной функции существует 3 переменные x — число камней в первой куче, y — число камней во второй куче, p — позиция. Позиция рассчитывается по таблице:
|
Игра |
Петя |
Ваня |
Петя |
Ваня |
Петя |
|
|
p |
1 |
2 |
3 |
4 |
5 |
6 |
Далее — всё по условию задачи.
Вторая задача на теорию игр:
Все отличия в рамке. Ну и код, соответственно, не сильно отличается:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 4: #Условия завершения игры
return p == 4
if p % 2 != 0:
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
else:
return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and
f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)Отличия:
-
Выиграл Петя, соответственно, позиция 4
-
Так как Петя не может выиграть за один ход — он выигрывает за 2 хода (and, а не or на нечётных позициях (играх Пети))
-
Убрали break, так как нам нужны все S, а не единственный
Последняя вариация задачи:
Сразу код:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 5: #Условия завершения игры
return p == 3 or p == 5
if p % 2 == 0:
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
else:
return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and
f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)Ну и всего лишь 2 отличия:
-
Позиции 3 или 5, а не 4, так как выиграл Ваня
-
На второй ход выигрывает Ваня и нам нужно or и and поменять. Я заменил только кратность 2.
Задача 22
Ctrl+C, Ctrl+V — наше всё! 
for i in range(1, 100000):
x = i
L = 0
M = 0
while x > 0 :
L = L+1
if (x % 2) != 0:
M = M + x % 8
x = x // 8
if L == 3 and M == 6:
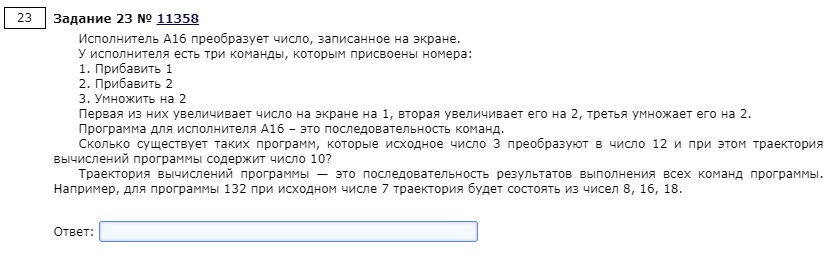
print(i)Задача 23
Итак, код:
def f(x, y):
if x > y: #Перегнали цель
return 0
if x == y: #Догнали цель
return 1
if x < y: #Догоняем цель тремя методами
return f(x + 1, y) + f(x + 2, y) + f(x * 2, y)
print(f(3, 10) * f(10, 12)) #Прошло через 10, значит догнали 10 и от де догоняем 12Так как в условии задачи мы увеличиваем число, но будем числа «догонять». Три метода описаны, ну а пройти через 10 — значит дойти до него и идти от него.
Собственно, это и есть вся первая часть ЕГЭ по информатике решённая на Python.
Ссылка на репозиторий со всеми программами:
Надеюсь, что смог помочь в своей статье выпускникам и готовящимся 
Остался один вопрос — нужен ли разбор второй части ЕГЭ по информатике на Python? Оставлю этот вопрос на ваше голосование.
Всем удачи!
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Делаю разбор второй части?
Проголосовали 106 пользователей.
Воздержались 15 пользователей.
Доброго времени суток каждому жителю Хабрвилля! Давненько я не писал статей! Пора это исправить!
В сегодняшней статье поговорим о насущной для многих выпускников школ теме — ЕГЭ. Да-да-да! Я знаю, что Хабр — это сообщество разработчиков, а не начинающих айтишников, но сейчас ребятам как никогда нужна поддержка именно сообщества. Ребят опять посадили на дистант. Пока не ясно на какой период, но уже сейчас можно сказать, что ЕГЭ по информатике будет на компьютерах и его можно зарешать при помощи языка Python.
Вот я и подумал, чтобы не получилось как в песне, стоит этим заняться. Я расскажу про все задачи первой части и их решения на примере демо варианта ЕГЭ за октябрь.
Всех желающих — приглашаю ниже!
Быстрый перевод из системы в систему
В Python есть интересные функции bin(), oct() и hex(). Работают данные функции очень просто:
bin(156) #Выводит '0b10011100'
oct(156) #Выводит '0o234'
hex(156) #Выводит '0x9c'Как вы видите, выводится строка, где 0b — означает, что число далее в двоичной системе счисления, 0o — в восьмеричной, а 0x — в шестнадцатеричной. Но это стандартные системы, а есть и необычные…
Давайте посмотрим и на них:
n = int(input()) #Вводим целое число
b = '' #Формируем пустую строку
while n > 0: #Пока число не ноль
b = str(n % 2) + b #Остатот от деления нужной системы (в нашем сл записываем слева
n = n // 2 #Целочисленное деление
print(b) #ВыводДанная программа будет работать при переводе из десятичной системы счисления в любую до 9, так как у нас нет букв. Давайте добавим буквы:
n = int(input()) #Вводим целое число
b = '' #Формируем пустую строку
while n > 0: #Пока число не ноль
if (n % 21) > 9: #Если остаток от деления больше 9...
if n % 21 == 10: #... и равен 10...
b = 'A' + b #... запишем слева A
elif n % 21 == 11:#... и равен 11...
b = 'B' + b#... запишем слева B
'''
И так далее, пока не дойдём до системы счисления -1 (я переводил в 21-ную систему и шёл до 20)
'''
elif n % 21 == 11:
b = 'B' + b
elif n % 21 == 12:
b = 'C' + b
elif n % 21 == 13:
b = 'D' + b
elif n % 21 == 14:
b = 'E' + b
elif n % 21 == 15:
b = 'F' + b
elif n % 21 == 16:
b = 'G' + b
elif n % 21 == 17:
b = 'H' + b
elif n % 21 == 18:
b = 'I' + b
elif n % 21 == 19:
b = 'J' + b
elif n % 21 == 20:
b = 'K' + b
else: #Иначе (остаток меньше 10)
b = str(n % 21) + b #Остатот от деления записываем слева
n = n // 21 #Целочисленное деление
print(b) #ВыводСпособ объёмен, но понятен. Теперь давайте используем тот же функцию перевода из любой системы счисления в любую:
def convert_base(num, to_base=10, from_base=10):
# Перевод в десятичную систему
if isinstance(num, str): # Если число - строка, то ...
n = int(num, from_base) # ... переводим его в нужную систему счисления
else: # Если же ввели число, то ...
n = int(num) # ... просто воспринять его как число
# Перевод десятичной в 'to_base' систему
alphabet = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ" # Берём алфавит
if n < to_base: # Если число меньше системы счисления в которую переводить...
return alphabet[n] # ... вернуть значения номера в алфавите (остаток от деления)
else: # Иначе...
return convert_base(n // to_base, to_base) + alphabet[n % to_base] # ... рекурсивно обратиться к функии нахождения остаткаВызвав функцию вывода print(convert_base(156, 16, 10)) мы переведём 156 из 10 в 16 систему счисления, а введя print(convert_base('23', 21, 4)) переведёт 23 из 4-ичной в 21-ичную систему (ответ: B).
Задача 2
Все задания беру из первого октябрьского варианта (он же вариант № 9325894) с сайта Решу.ЕГЭ.
Решение данной задачи совсем простое: банальный перебор.
print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы
for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1'
for x in range(2):
for z in range(2):
for w in range(2):
F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию
print(x, y, z, F) #Выводим результатРезультат:
Нам вывелась вся таблица истинности (1 = True, 0 = False). Но это не очень удобно. Обратите внимание, что в задании, функция равно 0, так и давайте подправим код:
print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы
for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1'
for x in range(2):
for z in range(2):
for w in range(2):
F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию
if not F:
print(x, y, z, F) #Выводим результатРезультат:
Далее — простой анализ.
Задача 5
Данная задача легко решается простой последовательностью действий в интерпретационном режиме:
Задача 6
Перепечатали и получили ответ:
s = 0
k = 1
while s < 66:
k += 3
s += k
print(k)Задача 12
В очередной раз, просто заменим слова на код:
a = '9' * 1000
while '999' in a or '888' in a:
if '888' in a:
a = a.replace('888', '9', 1)
else:
a = a.replace('999', '8', 1)
print(a)Задача 14
Компьютер железный, он всё посчитает:
a = 4 ** 2020 + 2 ** 2017 - 15
k = 0
while a > 0:
if a % 2 == 1:
k += 1
a = a // 2
print(k)Задача 16
Опять же, просто дублируем программу в python:
def F(n):
if n > 0:
F(n // 4)
print(n)
F (n - 1)
print(F(5))Результат:
Задача 17
Задача с файлом. Самое сложное — достать данные из файла. Но где наша не пропадала?!
with open("17.txt", "r") as f: #Открыли файл 17.txt для чтения
text = f.read() #В переменную text запихнули строку целиком
a = text.split("n") #Разбили строку энтерами (n - знак перехода на новую строку)
k = 0 #Стандартно обнуляем количество
m = -20001 #Так как у нас сумма 2-ух чисел и минимальное равно -10000, то минимум по условию равен -20000, поэтому...
for i in range(len(a)): #Обходим все элементы массива
if (int(a[i - 1]) % 3 == 0) or (int(a[i]) % 3 == 0): #Условное условие
k += 1 #Счётчик
if int(a[i - 1]) + int(a[i]) > m: #Нахождение минимума
m = int(a[i - 1]) + int(a[i])
print(k, m) #ВыводНемного пояснений. Функция with() открывает файл считывает данные при помощи функции read() и закрывает файл. В остальном — задача стандартна.
Задача 19, 20 и 21
Все три задачи — задачи на рекурсию. Задачи идентичны, а вопросы разные. Итак, первая задача:
Пишем рекурсивную функцию и цикл перебора S:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 3: #Условия завершения игры
return p == 3
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)
breakНемного пояснений. В рекурсивной функции существует 3 переменные x — число камней в первой куче, y — число камней во второй куче, p — позиция. Позиция рассчитывается по таблице:
|
Игра |
Петя |
Ваня |
Петя |
Ваня |
Петя |
|
|
p |
1 |
2 |
3 |
4 |
5 |
6 |
Далее — всё по условию задачи.
Вторая задача на теорию игр:
Все отличия в рамке. Ну и код, соответственно, не сильно отличается:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 4: #Условия завершения игры
return p == 4
if p % 2 != 0:
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
else:
return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and
f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)Отличия:
-
Выиграл Петя, соответственно, позиция 4
-
Так как Петя не может выиграть за один ход — он выигрывает за 2 хода (and, а не or на нечётных позициях (играх Пети))
-
Убрали break, так как нам нужны все S, а не единственный
Последняя вариация задачи:
Сразу код:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 5: #Условия завершения игры
return p == 3 or p == 5
if p % 2 == 0:
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
else:
return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and
f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)Ну и всего лишь 2 отличия:
-
Позиции 3 или 5, а не 4, так как выиграл Ваня
-
На второй ход выигрывает Ваня и нам нужно or и and поменять. Я заменил только кратность 2.
Задача 22
Ctrl+C, Ctrl+V — наше всё!
for i in range(1, 100000):
x = i
L = 0
M = 0
while x > 0 :
L = L+1
if (x % 2) != 0:
M = M + x % 8
x = x // 8
if L == 3 and M == 6:
print(i)Задача 23
Итак, код:
def f(x, y):
if x > y: #Перегнали цель
return 0
if x == y: #Догнали цель
return 1
if x < y: #Догоняем цель тремя методами
return f(x + 1, y) + f(x + 2, y) + f(x * 2, y)
print(f(3, 10) * f(10, 12)) #Прошло через 10, значит догнали 10 и от де догоняем 12Так как в условии задачи мы увеличиваем число, но будем числа «догонять». Три метода описаны, ну а пройти через 10 — значит дойти до него и идти от него.
Собственно, это и есть вся первая часть ЕГЭ по информатике решённая на Python.
Ссылка на репозиторий со всеми программами:
Надеюсь, что смог помочь в своей статье выпускникам и готовящимся
Остался один вопрос — нужен ли разбор второй части ЕГЭ по информатике на Python? Оставлю этот вопрос на ваше голосование.
Всем удачи!
Только зарегистрированные пользователи могут участвовать в опросе. Войдите, пожалуйста.
Делаю разбор второй части?
Проголосовали 106 пользователей.
Воздержались 15 пользователей.
Применение языка программирования Python в решении задач компьютерного
ЕГЭ по информатике
Автор:
Кусточкин Александр Валерьевич
учитель
информатики, МБОУ «Поспелихинская СОШ №1»
2021
г.
Оглавление
Введение
1. Основы
языка программирования Python
2. Обзор
задач компьютерного ЕГЭ по информатике и их решение на языке Python
3. Сравнение
эффективности программ, написанных на языках Pascal,
C и Python
Заключение
Введение
Единый
государственный экзамен по информатике необходим тем, кто планирует поступать в
российские вузы на специальности, связанные с IT-технологиями. Этот экзамен
нужен тем, кто хочет стать программистом, разработчиком, специалистом по
информационным технологиям.
Единый
государственный экзамен по информатике будет проходить на компьютерах уже с
2021 года. Новая модель реализована в виде компьютерной системы тестирования, а
ее апробация прошла в нашем городе осенью 2019. Смысл новой модели состоит в
том, что все задания выпускники будут выполнять при помощи компьютеров и с
применением различных языков программирования и программного обеспечения.
В
настоящее время все большую популярность приобретает язык Python.
Одна из причин популярности Python – более простое и компактное оформление,
чем в других языках. Это самый популярный язык общего назначения: он
используется для машинного обучения, аналитике, разработке игр и в науке о
данных. В данной работе будет применение языка Pythonв
решении задач компьютерного ЕГЭ по информатике.
Объект
работы – процесс решения задач компьютерного ЕГЭ
по информатике.
Предмет
работы – средства решения задач компьютерного
ЕГЭ по информатике.
Цель
работы – провести обзор возможностей языка
программирования Pythonв
решении задач компьютерного ЕГЭ по информатике.
Задачи:
— рассмотреть
основы языка программирования Python;
— выделить
типы задач компьютерного ЕГЭ по информатике и, по возможности, решить их
средствами языка программирования Python;
— сравнить
эффективность программ, написанных на языках Pascal,
C
и Python.
Сценарии
исходного кода Python состоят из так называемых логических строк, каждая из которых в свою очередь
состоит из физических
строк. Для обозначения комментариев используется символ #.
Комментарии и пустые строки интерпретатор игнорирует.
Физические строки
разделяются самим символом конца строки. Для выделения блоков кода используются
исключительно отступы. Логические строки с одинаковым размером отступа
формируют блок, и заканчивается блок в том случае, когда появляется логическая
строка с отступом меньшего размера. Именно поэтому первая строка в сценарии
Python не должна иметь отступа.
Других радикальных
отличий от других языков программирования в синтаксисе Python нет. Также
используются стандартные правила для заданий идентификаторов переменных,
методов и классов – имя должно начинаться с подчеркивания или латинского символа
любого регистра и не может содержать символов @, $, %. Также не может
использоваться в качестве идентификатора только один символ подчеркивания.
Типы данных, используемых
в Python, совпадают с другими языками – целые и вещественные типы данных;
дополнительно поддерживается комплексный тип данных – с вещественной и мнимой
частью. Python поддерживает строки, которые могут быть заключены в одинарные,
двойные или тройные кавычки, при этом строки являются immutable-объектами, т.е.
не могут изменять свое значение после создания.
Есть в Python и
логический тип данных bool c двумя вариантами значения – True и False. Для
повышения читаемости кода рекомендуется использовать для логических переменных
тип bool.
В Python определены три
типа коллекций для хранения наборов данных:
—
кортеж (tuple);
—
список (list);
—
словарь (dictionary).
Кортеж представляет собой
неизменяемую упорядоченную последовательность данных. В нем могут содержаться
элементы различных типов, например другие кортежи. Кортеж определяется в круглых
скобках, а его элементы разделяются запятыми. Специальная встроенная функция
tuple() позволяет создавать кортежи из представленной последовательности
данных.
Список – это изменяемая
упорядоченная последовательность элементов. Элементы списка также разделяются
запятыми, но задаются уже в квадратных скобках. Для создания списков
предлагается функция list().
Словарь является
хеш-таблицей, сохраняющей элемент вместе с его идентификатором-ключом.
Последующий доступ к элементам выполняется тоже по ключу, поэтому единица
хранения в словаре – это пара объект-ключ и связанный с ним объект-значение.
Словарь – это изменяемая, но не упорядоченная коллекция, так что порядок
элементов в словаре может меняться со временем. Задается словарь в фигурных
скобках, ключ отделяется от значения двоеточием, а сами пары ключ/значение
разделяются запятыми. Для создания словарей доступна функция dict().
В
листинге 1 приведены примеры различных коллекций, доступных в Python.
Листинг 1. Виды коллекций, доступные в Python
|
(‘w’,‘o’,‘r’,‘l’,‘d’) (2.62,) [“test”,’me’] [ { 5:‘a’, |
Многие возможности Pythonреализованы в виде
отдельных функций; кроме того, модули расширения чаще всего делаются тоже в
виде библиотеки функций. Функции также применяются и в классах, где они по
традиции называются методами.
Синтаксис
определения функций в Python крайне простой; с учетом изложенных выше
требований (листинг 2).
Листинг 2. Виды коллекций, доступные в Python
|
def выражение выражение … |
Как
видно, необходимо использовать служебное слово def, двоеточие и отступы.
Вызвать функцию также очень просто:
Есть
только несколько моментов, специфичных для Python, которые стоит учитывать.
Параметры могут передаваться как просто по порядку перечисления, так и по
именам, в этом случае не нужно указывать при вызове те параметры, для которых
есть значения по умолчанию, а передавать только обязательные или менять порядок
параметров при вызове функции (листинг 3).
Листинг 3. Виды коллекций, доступные в Python
|
#функция, def return print print |
Функция в Python
обязательно возвращает значение – это делается либо явно с помощью оператора
return, за которым следует возвращаемое значение, либо, в случае отсутствия
оператора return, возвращается константа None, когда достигается конец функции.
Как видно из примеров объявлений функций, в Python нет необходимости указывать,
возвращается что-либо из функции или нет, однако если в функции имеется один
оператор return, возвращающей значение, то и другие операторы return в этой
функции должны возвращать значения, а если такого значения нет, то необходимо
явно прописывать return None.
Если функция очень
простая и состоит из одной строки, то ее можно определить прямо на месте
использования, в Python подобная конструкция называется лямбда-функцией
(lambda). lambda-функция – это анонимная функция (без собственного имени),
телом которой является оператор return, возвращающий значение некоторого
выражения. Такой подход может оказаться удобным в некоторых ситуациях, однако
стоит заметить, что повторное использование подобных функций невозможно.
Еще стоит описать
отношение Python к использованию рекурсии. По умолчанию глубина рекурсии
ограничена 1000 уровней, и когда этот уровень будет пройден, возникнет
исключительная ситуация, и работа программы будет остановлена. Однако при
необходимости величину этого предела можно изменить.
2. Обзор
задач компьютерного ЕГЭ по информатике и их решение на языке Python
В
проекте компьютерного ЕГЭ по информатике предлагаются десять типов заданий на
следующие темы.
1.
Вычисления
2.
Решение уравнений численными методами
3.
Перебор целых чисел. (Разбиение числа на
цифры)
4.
Перебор чисел. Проверка делимости
5.
Перебор целых чисел. Количество делителей
6.
Символьные строки. Цепочки символов
7.
Функции двух аргументов. Таблицы значений
8.
Электронные таблицы. Встроенные функции
(не решается средства Python)
9.
Рекурсия. Рекурсивные функции
10.
Исследование моделей. Оптимизация
1.
Пример задания на вычисление
С помощью программы Калькулятор или электронных
таблиц вычислите значение выражения. В ответе запишите только целую часть
результата. Можно также написать программу.
ПрограмманаязыкеPython
from math
import sqrt, cos, pi
print( sqrt(1
+ cos(3.53*pi)*10)*310 )
Ответ:
431.
Для
решения данного задания, нужно знать правила записи математических функций на
языке Python. В связи с невозможностью записи некоторых стандартных
математических функций с клавиатуры персонального компьютера в языке Python
существуют так называемые встроенные функции, с помощью которых пользователь
записывает арифметические выражения.
Основные
математические функции языка Python представлены в таблице 1. Прежде чем
использовать математические функции, необходимо в начале программы написать
инструкцию import math, однако тогда перед упоминанием каждой функции необходимо
будет добавлять имя модуля — math, например, y=math.sin(x). Другой способ,
который позволит избежать многократного вызова модуля math, — сделать следующую
запись в начале программы: from math import *.
Таблица
1. Общие математические функции модуля Math
|
Запись на Python |
Действие |
|
math.sin (x) |
Возвращает значение функции Sin от числа х |
|
math.cos (x) |
Возвращает значение функции Cos от числа х |
|
math.tan (x) или math.sin (x) / math.cos (x) |
Возвращает значение функции Tg от числа х |
|
math.cos |
Возвращает значение функции Ctg от числа х |
|
math.abs (x) |
Возвращает абсолютную величину числа х |
|
math.exp (x) |
Возвращает результат возведения числа е в степень X |
|
math.Log lp (x) |
Возвращает натуральный логарифм от х+1 |
|
math.sqrt (x) |
Возвращает результат извлечения квадратного корня |
|
math.log (x) |
Возвращает логарифм числа х по основанию 10 |
|
math.cos |
Возвращает результат возведения функции Cos х в квадрат |
|
math.acos (x) |
Возвращает значение функции арккосинус от числа х |
|
math.asin (x) |
Возвращает значение функции арксинус от числа х |
|
math.atan (x) |
Возвращает значение функции арктангенс от числа х |
|
Pi |
Возвращает 3.141592653589793 |
|
math.degrees(x) |
Преобразует радианы в градусы |
|
math.radians(x) |
Преобразует градусы в радианы |
|
math.floor(x) |
Возвращает значение, округленное до ближайшего |
|
math.ccil(x) |
Возвращает значение, округленное до ближайшего |
|
math.factorial(x) |
Возвращает факториал числа. 3 != 1 *2*3 |
В таблице2 представлены
некоторые встроенные функции для работы с числами, не требующие подключения
модуля math.
Таблица
2. Функции для работы с числами
|
Запись на Python |
Описание |
|
round(x) |
Возвращает результат округления числа х до ближайшего меньшего целого |
|
pow(x,y) другой вариант х**у |
Возвращает результат возведения числа х в степень у |
|
mах(список чисел через |
Возвращает большее значение из списка чисел |
|
min(список чисел через |
Возвращает меньшее значение из списка чисел |
|
sum(список K чисел через запятую) |
Возвращает сумму значений элементов последовательности |
|
float(число) |
Преобразует объект (например, строковое значение, целое |
2. Пример задания на решение уравнения численным
методом
Известно, что уравнение на отрезке [0; 1,5] имеет единственный корень.
Найдите его приблизительное значение с точностью не менее 0,00001 и запишите
в ответе найденное значение ровно с пятью значащими цифрами после запятой.
Программа
на языке Python:
from math
import cos, exp # подключить функции cos, exp
def
f(x): # это функция f(x)
return
0.01*exp(x) — cos(3*x)
a, b =
0, 1.5 # границыотрезка
while b-a
> 1e-6: # пока ширина отрезка >= 10^(-6)
c = (a +
b) / 2 # середина отрезка
if
f(a)*f(c) <= 0: # сдвигаем правую или левую границу
b =
c
else: a =
c
# вывод с 5
знаками в дробной части
print(
«{:.5f}».format((a + b) / 2) )
Ответ:
0.51800
3. Пример
задания на перебор целых чисел. Разбиение числа на цифры
Назовём натуральное четырёхзначное число N
(1000 £N£
9999) счастливым, если суммы двух его первых и двух последних цифр
различаются не более, чем на 3. Найдите количество таких чисел.
Программа на языке Python
count = 0
for n in
range(1000, 10000):
d0 = n %
10; n //= 10
d1 = n %
10; n //= 10
d2 = n %
10
d3 = n //
10
if
abs(d3+d2-d1-d0) <= 3:
count
+= 1
print(count)
Поскольку
заданный отрезок [1000; 9999] содержит всего 9000 чисел, можно решать задачу
простым перебором. Для этого сначала нужно разбить число на цифры с помощью
операций деления нацело и остатка от деления; цифры помещаем в переменные d0,
d1, d2, d3. Затем проверяем «счастливость» числа: число счастливое при
выполнении условияв этом случае увеличиваем счётчик найденных счастливых чисел.
Ответ:
4071.
4. Пример
задания на перебор целых чисел. Проверка делимости
Рассматривается
множество целых чисел, принадлежащих отрезку [1033;
7737], которые делятся на 5 и не делятся на 11, 17, 19 и 23. Найдите
количество таких чисел и максимальное из них. В ответе запишите два числа
через пробел: сначала количество, затем максимальное число.
Программа на языке Python
count = 0
maxGood = 0
for n in
range(1033, 7737+1):
if (n % 5
== 0) and (n % 11 != 0) and
(n %
17 != 0) and (n % 19 != 0) and (n % 23 != 0):
maxGood
= n
count += 1
print(count,
maxGood)
Поскольку
заданный отрезок [1033; 7737] содержит не так много чисел, можно решать задачу
простым перебором. Условие будем понимать так: интересующие нас числа делятся
на 5 и не делятся ни на одно из чисел 11, 17, 19 и 23. Нам выгоднее перебирать
числа в порядке возрастания, тогда последнее найдённое число – это и есть искомое
максимальное подходящее число (если требуется найти наименьшее подходящее
число, удобнее перебирать числа в порядке убывания)
Ответ:
1040 7730
Напишите программу, которая ищет среди целых
чисел, принадлежащих числовому отрезку [194455;
194500], числа, имеющие ровно 4 различных делителя. Выведите эти четыре
делителя для каждого найденного числа в порядке возрастания.
ПрограмманаязыкеPython
for n in
range(194455, 194500+1):
divs = []
for d in
range(1,n+1):
if n %
d == 0:
divs.append(d)
if
len(divs) == 4:
print(
*divs )
При
написании программы на языке Python можно поступить так
for для
всех чисел n в интервале:
divs =
массив всех делителей n
if
len(divs) == 4:
вывести
массив делителей
5. Пример
задания на работу с простыми числами
Напишите программу, которая ищет среди целых
чисел, принадлежащих числовому отрезку [3532000;
3532160], простые числа. Выведите все найденные простые числа в порядке
возрастания, слева от каждого числа выведите его номер по порядку.
ПрограмманаязыкеPython
from
math import sqrt
count
= 0
for
n in range(3532000, 3532160+1):
prime = True
for d in range(2, round(sqrt(n))):
if n % d == 0:
prime = False
break
ifprime:
count
+= 1
print(
count, n )
6. Пример
задания на работу с символьными строками
В текстовом файле k7.txt
находится цепочка из символов латинского алфавита A, B, C, D, E. Найдите
количество цепочек длины 3, удовлетворяющих следующим условиям:
·
1-й символ – один из символов B, C или D;
·
2-й символ – один из символов B, D, E, который не
совпадает с первым;
·
3-й символ – один из символов B, C, E, который не
совпадает со вторым.
Программанаязыке
Python
s =
open(‘k7.txt’).read()
count = 0
for i in
range(len(s)-2):
if s[i]
in ‘BCD’ and s[i+1] in ‘BDE’
and
s[i+2] in ‘BCE’ and s[i]!=s[i+1]
and
s[i+1]!=s[i+2]:
count
+= 1
print(count)
Решение:
1)
Считываем из файла и перебираем символы.
2)
Перебираем все тройки символов. Примем,
что переменная i будет хранить номер первого элемента в тройке, то есть, будем
рассматривать тройки (s[i], s[i+1], s[i+2]).
3)
Организуем цикл который перебирает
значения i от 1 до len(s)-2
for i in
range(len(s)-2):
…
4) Проверяем
символы в каждой тройке на соответствие условию. Проверка принадлежности
символов набору аналогична заданию 1. Дополнительно необходимо указать условия
неравенства символов, указанных в условии задачи. Если условия выполняются, то
к переменной количества прибавляется единица.
7. Пример задания на
вычисление значения функции от двух переменных
С помощью редактора
электронных таблиц создайте таблицу вещественных значений выражения для следующих вещественных
значений x и y:
x = 5,5; 6,0; …; 8,5; y
= 10,0; 10,3; …; 13,0.
Вычислите сумму
получившихся значений и запишите её целую часть в ответе.
Для выполнения этого
заданий также можно написать программу.
Решение:
1)
Чтобы написать программу, нужно
использовать вложенный цикл: в одном цикле будем перебирать значения x,
а во втором (вложенном) – значения y; учитывая, что цикл с переменной (for
… in …)
работает только с целыми последовательностями чисел, придётся использовать
циклы с условием:
s =
0 # это неправильная программа
x =
5.5 # это неправильная программа
while x
<= 8.5: # это неправильная программа
y = 10
while y
<= 13:
#
print(x, y) # отладочная печать, см. обсуждение ниже
s +=
2*x**3/(y+1)
y +=
0.3
x += 0.5
print( s )
сумма значений функции накапливается в
переменной s
2)
однако эта программа выводит неверный
ответ.
3)
Дело в том, что вещественные числа,
которые нельзя представить в виде суммы целых (в том числе и отрицательных)
степеней числа 2, в двоичной системе счисления представляют собой бесконечную
дробь и поэтому не могут быть точно записаны в памяти двоичного компьютера; при
выполнении вычислений с такими числами ошибка накапливается, и к последнему
шагу (это можно проверить с помощью отладочной печати) значение y равно
не 12,7, а чуть больше:
12.700000000000006
из-за
этого следующее значение, равное 13,000000000000006, уже больше, чем 13, и не
удовлетворяет условию работы цикла; таким образом, на каждом шаге цикла по x
мы теряем одно значение y, и соответствующее значение функции не
включается в сумму.
4)
с переменной x подобных проблем
нет, так как шаг изменения x равен 0,5 = 2–1
5)
исправить ситуацию можно так: организовать
перебор только целых значений, используя вспомогательные целочисленные
переменные x10 = x×
10 и y10
= y×
10:
s
= 0
for
x10 in range(55, 86, 5):
for y10 in range(100, 131, 3):
s
+= 2*(x10/10)**3/(y10/10+1)
print(s)
8. Пример задания на
вычисление значения рекурсивной функции
Определите
наименьшее значение n, при котором сумма чисел, которые будут выведены при
вызове F(n), будет больше 500000. Запишите в ответе сначала найденное значение
n, а затем через пробел – соответствующую сумму выведенных чисел.
def F( n ):
print(2*n)
if n > 1:
print(n-5)
F(n-1)
F(n-2)
Решение:
Первое,
что может прийти в голову – вызывать приведённую процедуру при разных значениях
параметра и увеличивать это значение до тех пор, пока сумма выведенных чисел не
превысит заданное значение 500000; это тупиковый подход, поскольку чисел очень
много и сложение займет очень много времени при низкой вероятности правильного
ответа
Можно
попробовать изменить программу так, чтобы сумма выводимых чисел считалась
автоматически: добавим в программу глобальную переменную s
и будем увеличивать её при выводе каждого числа на значение этого числа; при
этом для ускорения (значительного!) работы программы сразу закомментируем вывод
чисел на экран:
def
F( n ):
global s # если не объявить s глобальной – ошибка!
#
print(2*n)
s += 2*n
if n >
1:
#
print(n-5)
s += n — 5
F(n-1)
F(n-2)
Дальше
можно написать такую программу и запускать её при различных значениях
переменной n:
n
= 15
s
= 0
F(n)
print(
n, s )
Увеличивая
каждый раз значение n
на 1, мы в конце концов найдём первое (минимальное) значение n,
при котором сумма чисел, которые будут выведены при вызове F(n),
будет больше 500000 – это F(24) = 531864
Ответ:
24 531864.
9. Пример задания на
оптимизацию
На покупку мебели выделено 500 тыс. рублей.
Стоимость одного комплекта составляет 18 тыс. рублей. Запишите наборы
вариантов покупки максимального количества комплектов мебели, при условии,
что производитель М продает мебель упаковками по 6 комплектов в упаковке, а
производитель N – по 4 комплекта в упаковке.
Запишите в ответ пары чисел: количество упаковок
производителя М далее через пробел количество упаковок производителя N.
Каждую пару записывайте с новой строки. Пары должны быть отсортированы по
возрастанию значений в первом столбце.
Решение:
В
простейшем варианте можно просто вывести на экран все варианты сочетаний a
и b с соответствующими значениями K,
в конце программы вывести макcимальное
значение K; затем вручную найти все строки, где значение K
равно максимальному.
S0
= 500000 # доступная сумма
cost1
= 18000 # стоимость одного комплекта
packM
= 6 # количество комплектов в упаковке M
packN
= 4 # количество комплектов в упаковке N
# максимальное значение a
aMax = int(S0 /
(packM*cost1))
#
поиск максимального K по всем вариантам
maxK = 0
for a in
range(aMax+1):
Sb = S0 —
a*packM*cost1 # сумманазакупкуу N
b =
int(Sb / (packN*cost1))
K =
packM*a + packN*b # общее количество
print(a, b,
K)
if K >
maxK:
maxK = K
# новыймаксимум
print(maxK,
maxK*cost1)
3. Сравнение
эффективности программ, написанных на языках Pascal, C и Python
Сравним
программы, написанные на языках Pascal,
C
и Python
по таким критериям, как время работы и используемая память. Для примера возьмем
линейные программы, программы с циклами и программы с рекурсивными функциями.
Задача
1:дано натуральное число.
Выведите его последнюю цифру.
|
Pascal |
C |
Python |
|
var a: integer; begin readln(a); writeln(a end. |
#include main() { int x; } |
x=int(input()) print(x%10) |
|
Время Используемая |
Время работы: Используемая |
Время Используемая 360448 бит |
Как видно из таблицы, при реализации линейных
алгоритмов программа на Pythonпроигрывает во времени реализации и используемой
памяти программам на Pascalи C.
Задача2:подсчитайте количество натуральных
делителей числа x (включая
1 и само число;x2
109).
|
Pascal |
C |
Python |
|
var x, i, k: longint; begin readln(x); k:=0; for i:=1 to x do begin if (x mod i =0) then inc(k); end; writeln(k); end. |
#include #include main() { int x, i, k; scanf(«%i», k=0; for (i=1; i<=x; i++) if (x % i ==0) { k=k+1; } } printf(«%i», } |
x=int(input()) k=0 for i in range(1,x+1): if x%i==0: k+=1 print(k) |
|
Время Используемая |
Время работы: Используемая |
Время Используемая 376832 бит |
Из-за того, что значение xможет быть достаточно большим, все написанные программы не проходят все
тесты. Последние два теста не выполняются из-за того, что превышено
максимальное время работы (рис. 1).
Рис. 1. Результаты
прохождения тестов
Поэтому простым перебором данную задачу решать
нельзя. Повысим эффективность программы, идея состоит в
том, чтобы для определения количества делителей числа N
перебирать только числа до ;
если число q целое, его нужно
добавить в список делителей, а все остальные делители – парные, то есть если a
– делитель N, то b
= N
/ a
– тоже делитель N.
Таким
образом, циклом пробегаемся от 1 до (корня X)-1, и проверяем на делимость, если
делится, то увеличиваем счетчик. После цикла удваиваем наш счетчик, так как
любое число если имеет делитель до корня этого числа, то он имеет ещё один
делитель после корня этого числа. Проверяем отдельным if-ом случай для корня X,
если делится нацело, то увеличиваем на один и выводим наш счетчик, иначе просто
выводим счетчик.
|
Pascal |
C |
Python |
|
var x, i, k: longint; begin readln(x); k:=0; for i:=1 to x do begin if (x mod i =0) then inc(k); end; writeln(k); end. |
#include #include main() { int x, i, k,q; double fp,ip; scanf(«%i», k=0; if (x%2==0) { q=trunc(sqrt(x)); } else { q=trunc(sqrt(x))-1; } for (i=1; i<=q; i++) if (x % i ==0) { k=k+1; } } k=k*2; fp = modf(sqrt(x) , if(fp==0) { k=k+1; } printf(«%i», } |
import math x=int(input()) if(x%2==0): q=math.trunc(math.sqrt(x)) else: q=math.trunc(math.sqrt(x))—1 k=0 for i inrange(1,q+1): if(x%i==0): k=k+1 k=k*2 if(math.sqrt(x)%1==0): k=k+1 print(k) |
|
Время Используемая |
Время работы: Используемая |
Время Используемая 380928 бит |
Заключение
Девяносто
процентов задач компьютерного ЕГЭ по информатике решается с помощью программирования.
В
процессе выполнения работы были решены следующие задачи:
— рассмотрены
основы языка программирования Python;
— выделены
типы задач компьютерного ЕГЭ по информатике. Задачи решены средствами языка
программирования Python;
— проанализирована
эффективность программ, написанных на языках Pascal,
C
и Python.
Список литературы
1.
Сайт К. Ю. Полякова. Методические материалы и
программное обеспечение [Электронный ресурс]. Режим доступа:http://kpolyakov.spb.ru
2.
Прохоренок Н. А. Python 3. Самое
необходимое [Текст]. – Спб.: БХВ-Петербург, 2019. – 608 с.
3.
Основы Python [Электронный ресурс]. Режим доступа:
4.
Применение и основы Python [Электронный ресурс]. Режим доступа:
5.
Дистанционная подготовка к информатике [Электронный ресурс]. Режим доступа
https://informatics.mccme.ru
Документация
Библиотека работает в Python 3.6+
Немного терминологии
Модуль — это файл с расширением .py, находящийся в библиотеке.
Например, модуль constants — это файл constants.py.
Модуль decorators
1. Декоратор cache
Для чего: мемоизация работы функции.
Пример использования:
from infEGE import cache @cache def fib(n): if n in {0,1}: return 1 return fib(n - 1) + fib(n - 2) fib(50)
Если убрать @cache, то вычисляться будет очень долго.
Модуль constants
Для чего: константы для использования в алгоритмах.
Содержимое:
E = 2.718281828459045 PI = 3.141592653589793 maxValue = float('inf') minValue = float('-inf')
Модуль algebra_logic
1. Функция print_true_table
Синтаксис: print_true_table(variables: str, expretion: str, value: Union[int, bool, ‘all’] = ‘all’) -> None
Для чего:
Вывод таблицы истинности лог.функции expretion от переменных variables.
Если value='all', выводятся все строки таблицы;
Если value=1 или True, выводятся строки таблицы, где функция истинна;
Если value=0 или False, выводятся строки таблицы, где функция ложна.
В качестве лог.операций можно использовать обычные операции Python
или такие эквиваленты:
{"&": " and ", "|": " or ", "~": " not ", "->": "<="}.
Пример использования #1:
from infEGE import print_true_table print_true_table("xy", "x->y", 1)
Вывод:
xy F
00 1
01 1
11 1
Внимание: в Python приоритет <= выше, чем and, or, not! Ставьте скобки!
Пример использования #2:
from infEGE import print_true_table print_true_table("xy", "x&(y|x)|y", 0)
Вывод:
xy F
00 0
Пример использования #3:
from infEGE import print_true_table print_true_table("xzy", "x or z and (y or not x)")
Вывод:
xzy F
000 0
001 0
010 1
011 1
100 1
101 1
110 1
111 1
Модуль combinatorics
1. Функция permutation_with_repeat
Синтаксис: permutation_with_repeat(seq: Union[list, tuple, str], repeat: int = 1)
Для чего:
Возвращает перестановки элкементов итерируемого
обьекта seq с repeat повторениями.
Пример использования:
from infEGE import permutation_with_repeat for el in permutation_with_repeat('123', 2): print(el)
Вывод:
('1', '1')
('1', '2')
('1', '3')
('2', '1')
('2', '2')
('2', '3')
('3', '1')
('3', '2')
('3', '3')
2. Функция permutations
Синтаксис: permutations(seq: Union[list, tuple, str]):
Для чего:
Возвращает перестановки элкементов итерируемого объекта seq.
Пример использования:
from infEGE import permutations for el in permutations('abc'): print(el)
Вывод:
abc
acb
bac
bca
cab
cba
Модуль lists_and_other
1. Функция prod
Синтаксис: prod(seq: Union[list, tuple, set]) -> Union[int, float]
Для чего:
Возввращает произведение элементов итерируемого объекта seq.
Пример использования:
from infEGE import prod print(prod([5, 8, 6, 100, 54]))
Вывод:
1296000
Модуль string
1. Функция replacing
Синтаксис: replacing(string: str, substring: str, new_string: str, mode: str = ‘обычно’, cnt: Union[int, str] = ‘all’) -> str
Для чего:
Возвращает строку string с заменённой подстрокой
substring на подстроку new_string в количестве cnt.
Режим "обычно":
замена стандартным replace
Режим "целиком":
замена подстроки substring если она не
является частью большей подстроки.
Пример использования #1:
from infEGE import replacing print(replacing("Питон плохой тон", "тон", "нот"))
Вывод:
Пинот плохой нот
Пример использования #2:
from infEGE import replacing print(replacing("Питон плохой тон", "тон", "нот", cnt=1))
Вывод:
Пинот плохой тон
Пример использования #3:
from infEGE import replacing print(replacing("Питон плохой тон", "тон", "нот", "целиком"))
Вывод:
Питон плохой нот
2. Функция index_n
Синтаксис: index_n(string: str, substring: str, n: int = 1) -> int
Для чего:
Возвращает индекс n-го вхождения СЛЕВА подстроки
substring в строку string. Если такого вхождения
нет, возвращается -1000.
Пример использования #1:
from infEGE import index_n print(index_n("01230123", "1"))
Вывод:
1
Пример использования #2:
from infEGE import index_n print(index_n("01230123", "1", 2))
Вывод:
5
Пример использования #3:
from infEGE import index_n print(index_n("01230123", "1", 3))
Вывод:
-1000
3. Функция is_number
Синтаксис: is_number(n: str) -> bool
Для чего:
Проверяет является ли строка n числом.
Если да возвращается True, иначе - False.
Пример использования #1:
from infEGE import is_number print(is_number("23"))
Вывод:
True
Пример использования #2:
from infEGE import is_number print(is_number("2n3"))
Вывод:
False
Модуль system_count
1. Функция to_base
Синтаксис: to_base(number: Union[int, str], old_base: int = 10, new_base: int = 10) -> Union[int, str]
Для чего:
Переводит число number с основанием old_base в число
с основанием new_base.
Пример использования #1:
from infEGE import to_base print(to_base(5, new_base=2))
Вывод:
101
Пример использования #2:
from infEGE import to_base print(to_base(15, new_base=16))
Вывод:
F
Пример использования #3:
from infEGE import to_base print(to_base("FA32", old_base=17, new_base=10))
Вывод:
76638
Пример использования #4:
from infEGE import to_base print(to_base("FA32", old_base=17, new_base=6))
Вывод:
1350450
Модуль mathematics
1. Функция is_prime
Синтаксис: is_prime(n: int) -> bool
Для чего:
Если n - простое, то возващается True, иначе - False.
Пример использования #1:
from infEGE import is_prime print(is_prime(5))
Вывод:
True
Пример использования #2:
from infEGE import is_prime print(is_prime(25))
Вывод:
False
Пример использования #3:
from infEGE import is_prime print(is_prime(1))
Вывод:
False
2. Функция is_even
Синтаксис: is_even(n: int) -> bool
Для чего:
Если n - чётно, то возващается True, иначе - False.
Пример использования #1:
from infEGE import is_even print(is_even(12))
Вывод:
True
Пример использования #2:
from infEGE import is_even print(is_even(25))
Вывод:
False
3. Функция is_odd
Синтаксис: is_odd(n: int) -> bool
Для чего:
Если n - нечётно, то возващается True, иначе - False.
Пример использования #1:
from infEGE import is_odd print(is_odd(12))
Вывод:
False
Пример использования #2:
from infEGE import is_odd print(is_odd(25))
Вывод:
True
4. Функция divided
Синтаксис: divided(n: int, d: int) -> bool
Для чего:
Если n нацело делится на d, то возвращается True, иначе - False.
Пример использования #1:
from infEGE import divided print(divided(12, 5))
Вывод:
False
Пример использования #2:
from infEGE import divided print(divided(121, 11))
Вывод:
True
5. Функция not_divisible
Синтаксис: not_divisible(n: int, d: int) -> bool
Для чего:
Если n не делится нацело на d, то возвращается True, иначе - False.
Пример использования #1:
from infEGE import not_divisible print(not_divisible(12, 5))
Вывод:
True
Пример использования #2:
from infEGE import not_divisible print(not_divisible(121, 11))
Вывод:
False
6. Функция factorial
Синтаксис: factorial(n: int) -> int
Для чего:
Возвращает n! (0! = 1)
Пример использования:
from infEGE import factorial print(factorial(6))
Вывод:
720
7. Функция factorize
Синтаксис: factorize(number: int) -> list
Для чего:
Возвращает разложение числа number на простые множители в list.
Пример использования #1:
from infEGE import factorize print(factorize(1))
Вывод:
[]
Пример использования #2:
from infEGE import factorize print(factorize(11))
Вывод:
[11]
Пример использования #3:
from infEGE import factorize print(factorize(55))
Вывод:
[5, 11]
8. Функция divisors
Синтаксис: divisors(n: int) -> list
Для чего:
Возвращает все натуральные делители числа n на интервале (1; n).
Пример использования #1:
from infEGE import divisors print(divisors(1))
Вывод:
[]
Пример использования #2:
from infEGE import divisors print(divisors(720))
Вывод:
[2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 30, 36, 40, 45, 48, 60, 72, 80, 90, 120, 144, 180, 240, 360]
9. Функция fib
Синтаксис: fib(n: int) -> int
Для чего:
Возвращает n-ый член последовательности Фибоначчи. Нумерация с 0.
Пример использования #1:
from infEGE import fib print(fib(0))
Вывод:
0
Пример использования #2:
from infEGE import fib print(fib(1))
Вывод:
1
Пример использования #3:
from infEGE import fib print(fib(2))
Вывод:
1
Пример использования #4:
from infEGE import fib print(fib(3))
Вывод:
2
Пример использования #5:
from infEGE import fib print(fib(2001))
Вывод:
6835702259575806647045396549170580107055408029365524565407553367798082454408054014954534318953113802726603726769523447478238192192714526677939943338306101405105414819705664090901813637296453767095528104868264704914433529355579148731044685634135487735897954629842516947101494253575869699893400976539545740214819819151952085089538422954565146720383752121972115725761141759114990448978941370030912401573418221496592822626
Примечание: Данный алгоритм работает быстрее рекурсивного! Асимптоматика: O(N)
Доброго времени суток каждому жителю Хабрвилля! Давненько я не писал статей! Пора это исправить!
В сегодняшней статье поговорим о насущной для многих выпускников школ теме — ЕГЭ. Да-да-да! Я знаю, что Хабр — это сообщество разработчиков, а не начинающих айтишников, но сейчас ребятам как никогда нужна поддержка именно сообщества. Ребят опять посадили на дистант. Пока не ясно на какой период, но уже сейчас можно сказать, что ЕГЭ по информатике будет на компьютерах и его можно зарешать при помощи языка Python.
Вот я и подумал, чтобы не получилось как в песне, стоит этим заняться. Я расскажу про все задачи первой части и их решения на примере демо варианта ЕГЭ за октябрь.
Всех желающих — приглашаю ниже!
Быстрый перевод из системы в систему
В Python есть интересные функции bin(), oct() и hex(). Работают данные функции очень просто:
bin(156) #Выводит '0b10011100'
oct(156) #Выводит '0o234'
hex(156) #Выводит '0x9c'Как вы видите, выводится строка, где 0b — означает, что число далее в двоичной системе счисления, 0o — в восьмеричной, а 0x — в шестнадцатеричной. Но это стандартные системы, а есть и необычные…
Давайте посмотрим и на них:
n = int(input()) #Вводим целое число
b = '' #Формируем пустую строку
while n > 0: #Пока число не ноль
b = str(n % 2) + b #Остатот от деления нужной системы (в нашем сл записываем слева
n = n // 2 #Целочисленное деление
print(b) #ВыводДанная программа будет работать при переводе из десятичной системы счисления в любую до 9, так как у нас нет букв. Давайте добавим буквы:
n = int(input()) #Вводим целое число
b = '' #Формируем пустую строку
while n > 0: #Пока число не ноль
if (n % 21) > 9: #Если остаток от деления больше 9...
if n % 21 == 10: #... и равен 10...
b = 'A' + b #... запишем слева A
elif n % 21 == 11:#... и равен 11...
b = 'B' + b#... запишем слева B
'''
И так далее, пока не дойдём до системы счисления -1 (я переводил в 21-ную систему и шёл до 20)
'''
elif n % 21 == 11:
b = 'B' + b
elif n % 21 == 12:
b = 'C' + b
elif n % 21 == 13:
b = 'D' + b
elif n % 21 == 14:
b = 'E' + b
elif n % 21 == 15:
b = 'F' + b
elif n % 21 == 16:
b = 'G' + b
elif n % 21 == 17:
b = 'H' + b
elif n % 21 == 18:
b = 'I' + b
elif n % 21 == 19:
b = 'J' + b
elif n % 21 == 20:
b = 'K' + b
else: #Иначе (остаток меньше 10)
b = str(n % 21) + b #Остатот от деления записываем слева
n = n // 21 #Целочисленное деление
print(b) #ВыводСпособ объёмен, но понятен. Теперь давайте используем тот же функцию перевода из любой системы счисления в любую:
def convert_base(num, to_base=10, from_base=10):
# Перевод в десятичную систему
if isinstance(num, str): # Если число - строка, то ...
n = int(num, from_base) # ... переводим его в нужную систему счисления
else: # Если же ввели число, то ...
n = int(num) # ... просто воспринять его как число
# Перевод десятичной в 'to_base' систему
alphabet = "0123456789ABCDEFGHIJKLMNOPQRSTUVWXYZ" # Берём алфавит
if n < to_base: # Если число меньше системы счисления в которую переводить...
return alphabet[n] # ... вернуть значения номера в алфавите (остаток от деления)
else: # Иначе...
return convert_base(n // to_base, to_base) + alphabet[n % to_base] # ... рекурсивно обратиться к функии нахождения остаткаВызвав функцию вывода print(convert_base(156, 16, 10)) мы переведём 156 из 10 в 16 систему счисления, а введя print(convert_base('23', 21, 4)) переведёт 23 из 4-ичной в 21-ичную систему (ответ: B).
Задача 2
Все задания беру из первого октябрьского варианта (он же вариант № 9325894) с сайта Решу.ЕГЭ.
Решение данной задачи совсем простое: банальный перебор.
print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы
for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1'
for x in range(2):
for z in range(2):
for w in range(2):
F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию
print(x, y, z, F) #Выводим результатРезультат:
Нам вывелась вся таблица истинности (1 = True, 0 = False). Но это не очень удобно. Обратите внимание, что в задании, функция равно 0, так и давайте подправим код:
print('y', 'x', 'z', 'F') #Напечатаем заголовки таблицы
for y in range(2): #Берём все переменные и меняем их в циклах '0' и '1'
for x in range(2):
for z in range(2):
for w in range(2):
F = ((not x or y) == (not z or w)) or (x and w) #Записываем функцию
if not F:
print(x, y, z, F) #Выводим результатРезультат:
Далее — простой анализ.
Задача 5
Данная задача легко решается простой последовательностью действий в интерпретационном режиме:
Задача 6
Перепечатали и получили ответ:
s = 0
k = 1
while s < 66:
k += 3
s += k
print(k)Задача 12
В очередной раз, просто заменим слова на код:
a = '9' * 1000
while '999' in a or '888' in a:
if '888' in a:
a = a.replace('888', '9', 1)
else:
a = a.replace('999', '8', 1)
print(a)Задача 14
Компьютер железный, он всё посчитает:
a = 4 ** 2020 + 2 ** 2017 - 15
k = 0
while a > 0:
if a % 2 == 1:
k += 1
a = a // 2
print(k)Задача 16
Опять же, просто дублируем программу в python:
def F(n):
if n > 0:
F(n // 4)
print(n)
F (n - 1)
print(F(5))Результат:
Задача 17
Задача с файлом. Самое сложное — достать данные из файла. Но где наша не пропадала?!
with open("17.txt", "r") as f: #Открыли файл 17.txt для чтения
text = f.read() #В переменную text запихнули строку целиком
a = text.split("n") #Разбили строку энтерами (n - знак перехода на новую строку)
k = 0 #Стандартно обнуляем количество
m = -20001 #Так как у нас сумма 2-ух чисел и минимальное равно -10000, то минимум по условию равен -20000, поэтому...
for i in range(len(a)): #Обходим все элементы массива
if (int(a[i - 1]) % 3 == 0) or (int(a[i]) % 3 == 0): #Условное условие
k += 1 #Счётчик
if int(a[i - 1]) + int(a[i]) > m: #Нахождение минимума
m = int(a[i - 1]) + int(a[i])
print(k, m) #ВыводНемного пояснений. Функция with() открывает файл считывает данные при помощи функции read() и закрывает файл. В остальном — задача стандартна.
Задача 19, 20 и 21
Все три задачи — задачи на рекурсию. Задачи идентичны, а вопросы разные. Итак, первая задача:
Пишем рекурсивную функцию и цикл перебора S:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 3: #Условия завершения игры
return p == 3
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)
breakНемного пояснений. В рекурсивной функции существует 3 переменные x — число камней в первой куче, y — число камней во второй куче, p — позиция. Позиция рассчитывается по таблице:
|
Игра |
Петя |
Ваня |
Петя |
Ваня |
Петя |
|
|
p |
1 |
2 |
3 |
4 |
5 |
6 |
Далее — всё по условию задачи.
Вторая задача на теорию игр:
Все отличия в рамке. Ну и код, соответственно, не сильно отличается:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 4: #Условия завершения игры
return p == 4
if p % 2 != 0:
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
else:
return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and
f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)Отличия:
-
Выиграл Петя, соответственно, позиция 4
-
Так как Петя не может выиграть за один ход — он выигрывает за 2 хода (and, а не or на нечётных позициях (играх Пети))
-
Убрали break, так как нам нужны все S, а не единственный
Последняя вариация задачи:
Сразу код:
def f(x, y, p): #Рекурсивная функция
if x + y >= 69 or p > 5: #Условия завершения игры
return p == 3 or p == 5
if p % 2 == 0:
return f(x + 1, y, p + 1) or f(x, y + 1, p + 1) or
f(x * 2, y, p + 1) or f(x, y * 3, p + 1) #Варианты действий
else:
return f(x + 1, y, p + 1) and f(x, y + 1, p + 1) and
f(x * 2, y, p + 1) and f(x, y * 3, p + 1) #Варианты действий
for s in range (1, 58 + 1): #Перебор S
if f(10, s, 1): #Начали с 10 камней
print(s)Ну и всего лишь 2 отличия:
-
Позиции 3 или 5, а не 4, так как выиграл Ваня
-
На второй ход выигрывает Ваня и нам нужно or и and поменять. Я заменил только кратность 2.
Задача 22
Ctrl+C, Ctrl+V — наше всё!
for i in range(1, 100000):
x = i
L = 0
M = 0
while x > 0 :
L = L+1
if (x % 2) != 0:
M = M + x % 8
x = x // 8
if L == 3 and M == 6:
print(i)Задача 23
Итак, код:
def f(x, y):
if x > y: #Перегнали цель
return 0
if x == y: #Догнали цель
return 1
if x < y: #Догоняем цель тремя методами
return f(x + 1, y) + f(x + 2, y) + f(x * 2, y)
print(f(3, 10) * f(10, 12)) #Прошло через 10, значит догнали 10 и от де догоняем 12Так как в условии задачи мы увеличиваем число, но будем числа «догонять». Три метода описаны, ну а пройти через 10 — значит дойти до него и идти от него.
Собственно, это и есть вся первая часть ЕГЭ по информатике решённая на Python.
Ссылка на репозиторий со всеми программами:
Надеюсь, что смог помочь в своей статье выпускникам и готовящимся
Остался один вопрос — нужен ли разбор второй части ЕГЭ по информатике на Python? Оставлю этот вопрос на ваше голосование.
Всем удачи!
Опубликовано Козар Виктория Анатольевна
вкл 08.06.2022 — 13:31
Автор:
Медведев Виктор
Этот проект поможет в подготовке к ЕГЭ по информатике
Скачать:
| Вложение | Размер |
|---|---|
| 1.42 МБ |
Предварительный просмотр:
Чтобы пользоваться предварительным просмотром создайте себе аккаунт (учетную запись) Google и войдите в него: https://accounts.google.com
Тигрёнок на подсолнухе
Сказка «Морозко»
Каргопольская игрушка
В Китае испытали «автобус будущего»
Рисуем тыкву
DOI: 10.18137/RNU.HET.21.11-12.P.042
УДК 371.315.7
Ильченко О.Ю., Сырицына В.Н., Кадеева О.Е.,
Дальневосточный федеральный университет, Школа педагогики
Решение задач ЕГЭ по информатике средствами языка Python
В настоящее время актуальна проблема изучения языков программирования, поскольку на них написано все программное обеспечение компьютера. Их изучение начинается со школьной скамьи на уроках информатики для каждого школьника [3]. В 2021 году экзамен по информатике включал в себя 27 заданий, из них восемь задач направлены на проверку знания обучающимися одного из языков программирования: Pascal, C++, Python. Каждый из языков программирования по-своему интересен и сложен в изучении. Поэтому ученику необходимо сделать выбор и остановиться на изучении одного из них. Для начинающих очень удобен язык Pascal. Но стоит отметить, что этот язык создали в конце прошлого столетия.
Соответственно, в наше время он считается уже устаревшим. Чтобы сдать единый государственный экзамен (далее — ЕГЭ), знания этого языка будет достаточно, но, чтобы в будущем стать востребованным специалистом, одного Pascal будет мало.
Язык Python в рейтинге TIOBE на май 2021 года занимает 2-ое место, обходя Pascal и C++, оставляя выше себя только язык C. Главными плюсами Python специалисты считают простоту, большое количество встроенных библиотек, читабельность и удобство кода, легкий синтаксис, а также большое сообщество программистов-единомышленников, использующих его. Это позволит решить любую проблему на форуме за считанные часы. Для новичков этот язык про-
сто находка. Чтобы начать его изучение, от человека потребуется средний уровень знания английского языка. Поэтому для школьника путь в IT-сферу лучше всего начинать именно с языка программирования Python [7; 8].
Python — язык программирования, который упрощен за счет ориентира не на синтаксис и структуру, как это происходит в C++ или Pascal, а на конкретное решение самой задачи. Не тратится лишнее время на размышления о том, в каком месте поставить операторные скобки и так далее. Существует множество различных программ, редакторов, с помощью которых можно начинать учиться писать код на Python. При установке языка программирования автоматически устанавливается редактор IDLE, но более продуктивными и функциональными при решении задач ЕГЭ по информатике являются такие среды разработки как Py-Charm, SublimeText, Jupiter Notebook. Поэтому при рассмотрении сложных заданий ЕГЭ по программированию мы будем ориентироваться на использование среды разработки Jupiter Notebook. Ее главное преимущество заключается в том, что она объединяет код и выводит текст, математические уравнения, визуализацию в виде единого документа [1].
Программирование — самая сложная часть ЕГЭ по информатике, но при этом самая интересная. Когда теория применяется на практике,
© Ильченко О.Ю., Сырицына В.Н., Кадеева О.Е., 2021
РЕШЕНИЕ ЗАДАЧ ЕГЭ ПО ИНФОРМАТИКЕ СРЕДСТВАМИ ЯЗЫКА PYTHON
КАДЕЕВА ОКСАНА ЕВГЕНЬЕВНА Российская Федерация, город Владивосток
кандидат философских наук, доцент Департамента теории и практики преподавания математики, информатики, естественных наук, Школа педагогики, Дальневосточный федеральный университет. Сфера научных интересов: инновационное творчество преподавателя, интерактивные методы проведения учебных занятий, математическое моделирование и программирование. Автор более 70 опубликованных научных и методических работ. Электронная почта: kadeeva.oe@dvfu.ru
OKSANA E. KADEEVA Vladivostok, Russian Federation
Ph.D. of Philosophical Sciences, Associate Professor at the Department of the Theory and Practice of Teaching Mathematics, Computer Science, Natural Sciences, School of Pedagogics, Far Eastern Federal University. Research interests: innovative creativity of the teacher, interactive methods of conducting training sessions, mathematical modeling and programming. Author of more than 70 published scientific and methodological papers. E-mail address: kadeeva.oe@dvfu.ru
СЫРИЦЫНА ВАЛЕНТИНА НИКОЛАЕВНА Российская Федерация, город Владивосток
старший преподаватель Департамента теории и практики преподавания математики, информатики, естественных наук, Школа педагогики, Дальневосточный федеральный университет. Сфера научных интересов: электронное обучение в высшей школе, инновационная деятельность преподавателя, математическое моделирование и программирование. Автор более 50 опубликованных научных и методических работ. Электронная почта: versia_2000@mail.ru
VALENTINA N. SYRITSYNA Vladivostok, Russian Federation
Senior Lecturer at the Department of the Theory and Practice of Teaching Mathematics, Informatics, Natural Sciences, School of Pedagogy, Far Eastern Federal University. Research interests: e-learning in higher education, teacher innovation, mathematical modeling and programming. Author of more than 50 published scientific and methodological papers. E-mail address: versia_2000@mail.ru
ИЛЬЧЕНКО ОЛЕГ ЮРЬЕВИЧ
Российская Федерация, город Владивосток
студент Школы педагогики, Дальневосточный федеральный университет. Сфера научных интересов: единый государственный экзамен по физике и информатике, математическое моделирование и программирование. Электронная почта: ilchenkoleg01@gmail.com
I OLEG Yu. ILCHENKO
Vladivostok, Russian Federation
Student of the School of Pedagogy, Far Eastern Federal University. Research interests: unified state exam in physics and informatics, mathematical modeling and programming. E-mail address: ilchenkoleg01@gmail.com
Аннотация. Рассматриваются предметные и методические аспекты единого государственного экзамена по информатике. Анализируются особенности решения сложной части заданий единого государственного экзамена по программированию на языке Python, приводятся примеры решения таких заданий.
Ключевые слова: единый государственный экзамен, программирование на языке Python, среда Jupiter Notebook, методический подход к заданиям единого государственного экзамена, программирование.
Abstract. Subject and methodological aspects of the unified state examination in informatics are considered. The peculiarities of solving a complex part of the exam tasks in Python programming are analyzed, examples of solving such tasks are given.
Keywords: unified state exam, Python programming, Jupiter Notebook environment, methodical approach to tasks USE, programming.
это всегда способствует развитию творчества и самостоятельности. Главное для обучающегося — научиться читать программный код, «прогонять» первые итерации цикла у себя в голове, чтобы понимать, как работает программа, как меняются переменные в ней. Понимание работы программы — это залог успешной сдачи экзамена. Задачи 6, 16, 17, 22 ЕГЭ не требуют углубленного знания языка програм-
мирования, в этих программах не содержится много ступеней ветвлений, не нужно работать с файлами. Умение работать со строками, массивами, понимание условного оператора и циклов — это тот багаж знаний, которым должен владеть обучающийся, чтобы успешно справиться с такими задачами. Задания, которые мы рассмотрим в данной статье, требуют от обучающегося знания алгоритмов
сортировки, нескольких языков программирования, высокого уровня владения навыками программирования, развитого логического мышления [2; 4].
Рассмотрим подходы к решению задач ЕГЭ по информатике при помощи языка программирования Python. В качестве примеров взяты задания из официальной демовер-сии ЕГЭ по информатике за 2021 год на сайте Федерального инсти-
тута педагогических измерений (ФИПИ) и пособия К.Ю. Полякова [5; 6].
Задача 6
Тема: Анализ работы программы с циклом.
Требования к обучающимся:
• знать основные конструкции языка Python: объявление переменных; оператор присваивания; оператор вывода; циклы;
• уметь читать программу, выполнять программу; определять переменную, от преобразования которой зависит количество шагов цикла; уметь определять по программе количество требуемых шагов цикла; различать входные и выходные данные.
Пример задачи:
Определите, при каком наибольшем введенном значении переменной $ программа выведет число 64. Для Вашего удобства программа представлена на четырех языках программирования (см. Рисунок 1).
Решение (теоретическое рассуждение):
1. Переменная $ получает свое значение путем ввода пользователем.
2. Далее переменная $ переопределяется. Как было рассмотрено ранее, операция «//» является целочисленным делением, в нашем случае $ нацело делится на число 10.
3. Переменная n получает значение 1.
4. Затем идет цикл While с условием, что переменная $ меньше 51 ($<51). На каждой итерации цикла значение переменной ¿увеличивается на величину 5, а переменная n увеличивается в два раза.
5. На вывод подается переменная n.
По условию задачи, переменная n в конце работы программы имеет значение 64, из этого следует: 64 = 26, для того чтобы получить n = 64, необходимо выполнить тело цикла 6 раз. Максимальное число, при котором цикл выполнится
последний раз — 50. А следующий шаг — 55 — уже не пройдет. Тогда ответ — 55 — 5 • 6 = 25. Так как на первом шаге берется целое от деления на 10, то третью цифру нужно взять максимально возможную — 9. Путем теоретического исследования получили ответ: наибольшее значение переменной s=259.
Решение с помощью программы на Python:
Запустим среду программирования на Python Jupyter Notebook и наберем код программы. Величину переменной s получить можно подбором, но лучше всего найти закономерность, для этого:
1. Вводим сначала 1 — на выводе получаем 2048, затем вводим 100 -на выводе получим 512, исходя из этого, можно увидеть, что при увеличении s значение n уменьшается (см. Рисунок 2).
2. Пробуем увеличить s еще в 2,5 раза, на выходе получаем 64, то есть искомое значение. Но задача состоит в том, чтобы найти наибольшее значение s, поэтому увеличивая вводимое значение на 1, выясним, что при 259 программа выводит значение 64, а при 260 -32 (см. Рисунок 3).
3. Ответ найден. Наибольшее значение переменной $, при котором n = 64, равно 259.
Задача 16
Тема: Рекурсия. Рекурсивные процедуры и функции
Требования к обучающимся:
• знать: условие окончания рекурсии, то есть значения параметров функции, для которых значение функции известно или вычисляется без рекурсивных вызовов; рекуррентную формулу (или формулы), с помощью которых значение функции для заданных значений параметров вычисляется через значение (или значения) функции для других значений параметров (то есть, с помощью рекурсивных вызовов);
• уметь реализовать рекуррентную функцию на Python^, например,
F(n) = 1 при n? 1
F(n) = n + 1 + F(n-1), при n> 1
На языке программирования это будет выглядеть так (см. Рисунок 4): Пример задачи: Алгоритм вычисления функции F(n) задан следующими соотношениями: F( n) = 1 при n = 1 F(n) = n + F(n-1), если n четно, F(n) = 2-F(n~2), если n> 1 и n нечетно.
Чему равно значение функции F (26)? Решение задачи:
Пусть известно значение n. Построим массив а, так чтобы значение элемента a[n] совпадало со значением F(n). Учитывая, что в Python нумерация элементов массива начинается с нуля, будем использовать фиктивный нулевой элемент. Согласно условию, в первый элемент нужно записать число 1 («F(n) = 1 при n = 1»): а = [0,1], затем перебираем в цикле все значения индексов элементов, начиная с 2 и до n включительно, вычисляя для каждого значение функции. Фактически сначала вычисляется F(2) и записывается в элемент массива а[2], затем находим F(3) и записываем в элемент массива а[3] и так далее (см. Рисунок 5).
Стоит заметить, что вместо рекурсивных вызовов здесь используются уже готовые значения F(n) для меньших значений n, ранее записанные в массив а. Теперь можно построить функцию, которая возвращает значение a[n], и вызвать print(F(26)) (см. Рисунок 6): Получили ответ. Задача решена.
Задача 17 Тема: Перебор целых чисел на заданном отрезке. Проверка делимости
Требования к обучающимся:
• знать основные принципы построения программы на языке программирования;
• уметь использовать простой перебор без оптимизации; уметь пользоваться электронными таблицами.
РЕШЕНИЕ ЗАДАЧ ЕГЭ ПО ИНФОРМАТИКЕ СРЕДСТВАМИ ЯЗЫКА PYTHON
Паскаль Python Алгоритмический язык
vars,n:integer;begm readln(s); s:=sdiv10; n:=1; whiles<51dobegin s:=s+5; n:=n*2end;writeln(n) end. s=int(input()) s=s//10 n=1 whiles<51: s=s+5 n =n,,,,,,,,,,,,,*2 print(n) алгнач целn,s вводs s:=div(s,10)n:=1 нцпокаs<51s:=s+5 n:=n*2 кцвыводп кон
С++
#include <iostream>usingnamespacestd; intmain() {ints,n;cin>>s; s=s/10;n=1; while(s<51){s=s+5;n=n*2;}cout<<n<<endl; return0; }
Рисунок 1. Пример программы с циклом [6]
s = int(inputQ) s = int{input())
S = S // 10 S = 5 // 10
n = 1 n = 1
while s < 51: while s < 51:
5 = 5 + 5 s = s + 5
n = n * 2 n = n * 2
print(n) print(n)
1 100
2048 512
Рисунок 2. Подбор значений
s = int(input()) S = S // 10 n = 1
while s < 51:
s = s + 5 n = n * 2 print(n)
250 64
s = int(input())
S = S // 10 n = 1
while s < 51:
s = s + 5
П = П * 2
print(n)
259 64
s — int(input()) s = s // 10 n = 1
while s < 51:
s = s + 5 л = n * 2 print(n)
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
260 32
Рисунок 3. Решение задачи 6
def F(n):
if n == 1: return 1
if n % 2 — 0:
return n + F(n-l)
else:
return 2 * F(n-2)
Рисунок 4. Рекуррентная функция
for i in range{2., n+1): if i % 2 == 0;
a.append( i + a[i-l] ) else:
a.append( 2*a[i-2] )
def F( п ) :
a = [e, 1]
for i in rarige(2, n+1):
if i % 2 == 0
a.append( i + a[i-l] )
else:
a.append( 2*a[i-2j )
return a[n]
print (F(26) )
4122
Рисунок 5. Начало программы Рисунок 6. Решение задачи
Рассмотрим задачу в общем виде. Пусть необходимо перебрать все целые числа на отрезке [а; Ъ] и определить, для скольких из них выполняется некоторое условие. Общая структура цикла перебора на языке Python записывается так, как показано на Рисунке 7.
Проверка делимости числа n на число x осуществляется при помощи операции взятия остатка от деления n на x: если остаток равен 0, число n делится на x нацело. Данная проверка в Python осуществляется так, как показано на Рисунке 8. Пример задачи: Рассматривается множество целых чисел, принадлежащих числовому отрезку(1016; 7937), которые делятся на 3 и не делятся на 7, 17, 19, 27. Найдите количество таких чисел и максимальное из них. В ответе запишите два целых числа: сначала количество, затем максимальное число. Для выполнения этого задания можно написать программу или воспользоваться редактором электронных таблиц. Решение задачи: Проанализируем условие: интересующие нас числа делятся на 3 и не делятся на такие числа, как 7, 17, 19 и 27 (это будет являться условием проверки). Перебор чисел выгоднее осуществлять в порядке возрастания, так как последнее найденное число будет являть максимальным из перебранного количества. (Это также требуется найти в задаче. В случае, когда требуется найти наименьшее число, перебор начинается в порядке убывания).
Составим программу на Python (см. Рисунок 9):
Решение найдено. 1568 — такое количество чисел удовлетворяет критерию поиска (в условном операторе if), 7935 — максимальное число из количества удовлетворяющих условию чисел. Ответ указан в Рисунке 8.
Задача 22 Тема: Анализ программы, содержащей подпрограммы, циклы и ветвления.
Требования к обучающимся:
• знать операции деления с остатком (%) и целочисленного деления (//);
• уметь выполнять работу операторов присваивания, циклов в языке программирования Python.
Пример задачи:
Ниже на четырех языках программирования записан алгоритм. Получив на вход число x, этот алгоритм печатает два числа: L и M. Укажите наибольшее число x, при вводе которого алгоритм печатает сначала 4, а потом 5 (см. Рисунок 10).
Решение задачи:
Проанализируем программу. Переменная x получает значение путем ввода пользователем. Переменным Q и L присваиваются значения 9 и 0 соответственно. Далее идет цикл While, рассмотрим его (см. Рисунок 11).
Так как переменная L изначально равна нулю, а затем с каждой итерацией в цикле увеличивается на 1, она несет функцию счетчика повторения цикла. На каждой итерации цикла из переменной Q вычитается x до тех пор, пока x не станет меньше Q. Фактически определяется, сколько раз «поместится» Q в x. Из данных рассуждений можно понять, что данный цикл — это операция деления, при этом, как только цикл завершится, переменная L будет нести значение частного, а переменная x -остаток от деления введенного значения Q.
Далее переменная M получает значение переменной x, и если M<L, то значения M и L меняются местами. Это сделано для того, чтобы значения частного и остатка (сначала L, потом M) были выведены на экран в порядке возрастания. Согласно условию задачи, нужно найти наибольшее число, при котором частное и остаток будут равны 4 и 5 соответственно. Чтобы получить наибольшее число, нужно взять как частное наибольшее из двух заданных чисел, то есть 5 (и за остаток взять 4). Так
как делили на 9, то искомое число будет равно 5 x 9 + 4 = 49. Получили ответ: при вводе числа 49 этот алгоритм печатает два числа: 4 и 5. Пробуем запустить программу (см. Рисунок 12).
Логика приведенных выше рассуждений оказалась верной, при вводе пользователем числа 49, выводятся числа 4 и 5.
Если не удалось провести анализ программы, можно найти альтернативное решение. В данном случае найдем подходящее значение перебором (или как говорят программисты «bruteforce» — методом «грубой силы»). Для этого осуществим следующее:
1. Строку, где вводится x, удаляем [x = int (input ())].
2. Введем переменную x0 и основную часть программы заключим в цикл (можно использовать цикл с параметром, если есть уверенность, что максимальное значение точно не больше, например, 500). Результат представлен на Рисунке 13.
Далее строки, в которых выводятся результаты заменяем на проверку нужного нам случая. По условию задачи должны получиться числа 4 и 5, поэтому, если должны быть выведены числа 4 и 5, выводим на экран переменную x0 (см. Рисунок 14).
В итоге получим полностью переделанную программу (см. Рисунок 15).
Если запустить данную программу, она даст результат 41 и 49, что соответствует минимальному и максимальному подходящему числу. В условиях данной задачи ответ будет 49. Задача решена.
Задача 24
Тема: Обработка символьных строк
Требования к обучающимся:
• знать конструкции языка Python; знать несколько способов решения подобных задач;
• уметь читать строку из файла (программно); уметь работать с конструкцией with — as. (см. Рисунок 16).
РЕШЕНИЕ ЗАДАЧ ЕГЭ ПО ИНФОРМАТИКЕ СРЕДСТВАМИ ЯЗЫКА PYTHON
value = в
for л in range (a, b+1): if условие выполнено: value+= 1 print (value)
# переменная, которая запоминает количество чисел
# цикл с параметром, для перебора заданного диапазона
# условный оператор, для отбора значений
# или же уа1ие^а1ие+1
# вывод количества чисел
Рисунок 7. Общая структура перебора
if л % х == 0:
рг1п1:(«Делится») else:
print («Не делится»)
#операция «%» — взятие остатка от деления п на х #если п нацело делится на х}получаем ответ
# если п нацело не делится на х, получаем ответ
Рисунок 8. Проверка делимости числа n на число x
value_sum = 0 ^переменная, служащая для записи кол-ва чисел удовлетворяющих условию
value^max = 0 ^переменная, служащая для записи максимального значения числа в диапазоне
for n in range(1016, 7937+1): #цикл с параметром, где способ range задает нужный диапазон
if (п % 3 == 0) and (п % 7 != 0) and <п % 17 != 0) and (п % 19 1= 0) and (п % 27 ]= 0): valuejnax = п
valuersurn += 1 # аналогично, что и vaLue_sum=vaLue_$um+l
print(value_sum, value_max) # вывод переменных, являющихся решением задачи
1568 7935
Рисунок 9. Решение задачи 17
С++ Python
#include <iostream>usingnamespacestd; x=int(input())
Q=9
intmain() L=0
{ whilex>=Q:
intx,L,M,Q;cin>>x; L=L+1
Q=9; x=x-Q
L=0; M=x
while(x>=Q){L=L+1; ifM<L:
x=x-Q; M=L
L=x
M=x; print(L)
if(M<L){M=L; print(M)
L=x;
cout<<L<<endl<<M<<endl;return
Алгоритмический язык Паскаль
алгнач varx,L,M,Q:integer;begin
целх^,М,Ц readln(x);Q:=9;
вводхЦ:=9 L:=0;
L:=0 whilex>=Qdobegin
нцпокаx>=QL:=L+1 L:=L+1;x:=x-Q;
x:=x-Q end;
кц M:=x;
M:=x ifM<Lthenbegin
еслиM<L M:=L;
то L:=x;
M:=LL:=x end;writeln(L);writeln(M);
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
все end.
выводL,нс,M
кон
Рисунок 10. Условие задачи 22
while x >= Q: L = L + 1 x = x — Q
Рисунок 11. Цикл While с условием x>= Q
Рисунок 12. Решение задачи 22
For х0 in rarige(lj501):
# здесь нужно поместить запись основного алгоритма
Рисунок 13. Альтернативное решение задачи 22
if L = 4 and М = S print(x0)
Рисунок 14. Условие вывода переменной x0
for х0 in range(l,500):
X = Х0
Q = 9 L = 0
while х >= Q: L = L + 1 x = x — Q M = x if M < L: M = L L = x
if L == 4 and M == 5 print(x0)
41
_49_
Рисунок 15. Решение задачи 22 перебором
with ореп( «24.txt»г» > as F:
Рисунок 16. Конструкция with-as для чтения файла 24.txt
Аргумент r при вызове функции open записывает ссылку на данный аргумент в файловую переменную F, выполняет тело блока (читает первую строку файла в переменную $) и закрывает (освобождает) файл. Кеад1те() — эта функция считывает строки из данного файла и возвращает их в виде строки.
Пример задачи:
Текстовый файл состоит не более чем из 106 символов X, Y и Z. Определите максимальное количество идущих подряд символов, среди которых каждые два соседних различны. Для выполнения этого задания следует написать программу.
Решение задачи:
Имеется файл, содержащий последовательность символов X, Y, Z. Нужно определить количество идущих подряд символов, «соседи» которых различны [5].
Для начала откроем имеющийся файл (как это сделать, рассмотрено выше). Чтобы считать длину цепочки (количество идущих подряд символов), введем два счетчика, присвоив им значение единицы:
• curLen (от англ. CurrentLength -«Текущая длина») — длина текущей цепочки (которая сейчас обрабатывается);
• maxLen (от англ. MaxLength -«Максимальная длина») — длина наибольшей на данный момент цепочки уже в обработанной части строки.
При помощи цикла с параметром будем «прогонять» текущий документ (см. Рисунок 17).
Метод rnnge задает начало и конец диапазона, в данном случае с первого символа до конца документа (len(s) — считает длину $, которая в себе содержит данные документа, то есть величина длины служит конечной границей диапазона). В тело данного цикла поместим условный оператор if с условием, которое выясняет, отличен ли текущий символ от предыдущего символа (см. Рисунок 18).
Если значение истинно (то есть символы различны), то переменную curLen увеличиваем на единицу и проверяем величины curLen и mnxLen. Если текущая длина станет больше максимальной, то последней присвоится значение текущей. Если символы одинаковые, то переменной CurLen присваиваем значение 1. В конце поставим на вывод переменную mnxLen, именно она запоминала максимальное число идущих подряд символов. Соберем всю программу и запустим (см. Рисунок 19).
Переменная maxLen в ходе выполнения программы получила значение 35. Оно является ответом задачи. То есть количество символов, у каждого из которых разный «сосед», в данном файле равняется 35.
Задача 25 Тема: Обработка целых чисел. Проверка делимости.
Требования к обучающимся:
• знать: конструкции языка Python; несколько способов решения подобных задач;
• уметь: читать строку из файла (программно); создавать собственные программы (10-20 строк) для обработки целочисленной информации; строить информационные модели объектов, систем и процессов в виде алгоритмов.
Пример задачи [6] : Напишите программу, которая ищет среди целых чисел, принадлежащих числовому отрезку (174457; 174505), числа, имеющие ровно два различных натуральных делителя, не считая единицы и самого числа. Для каждого найденного числа запишите эти два делителя в таблицу на экране с новой строки в порядке возрастания произведения этих двух делителей. Делители в строке таблицы также должны следовать в порядке возрастания. Решение задачи: Согласно условию, программа должна найти числа, которые имеют ровно два делителя, при этом сами числа и единицу в расчет брать нельзя. Следуя логике,
можно прийти к выводу, что произведение этих двух делителей должно давать само число (например, число 6 — откидываем 1 и 6 автоматически, остаются его делители — только 2 и 3, а произведение 2 и 3 дает нам само число 6). Так как условие требует записать делители в порядке возрастания, то нужно начинать перебор от меньшего числа к большему на заданном отрезке (это не обязательно, но рационально, так как исключит лишние строки кода).
Будет эффективно использовать более ускоренный перебор делителей, то есть для числа N перебирать только числа от 2 до q = VN (не включая точный квадратный корень, если он существует); все делители — парные, то есть если а -делитель N, то Ъ = N / а — тоже делитель N. Логика данной программы подходит для любого заданного количества делителей. Так как нужно выводить все делители, кроме единицы и самого числа, цикл перебора делителей начинаем с 2 и включаем q = VN Если очередной делитель d -это точный квадратный корень, добавляем в список делителей только один делитель, если нет — то добавляем пару делителей (d, x // d). Запишем полностью всю программу и запустим ее (см. Рисунок 20).
Получили ответ. Делители выведены на экран в порядке возрастания, чего и требовало условие задачи.
Задача 26
Тема: Обработка массива целых чисел из файла. Сортировка.
Требования к обучающимся:
• знать: конструкции языка Python; различные способы решения подобных задач;
• уметь читать данные из файла и понимать, как хранить их в массиве.
В Python, для того чтобы сохранить данные в массиве, используются списки (list).
На Рисунке 21 показано чтение массива данных размера N из списка dota из файла «26.txt» (данные записаны в столбик).
for i in ranged, len(s)):
Рисунок 17. Цикл for для прогонки документа
for i in range(lj len(s)): if si i] != s[i-l]: curLen += 1 if curLen > maxLen: maxLen = curLen
else:
curLen = 1
Рисунок 18. Проверка текущего и предыдущего
with open( «24.txt», «r» ) as F
s = F.readline() maxLen, curLen = 1, 1 for i in range(l, len(s)): if s[i] != s£i-lj: curLen += 1 if curLen > maxLen: maxLen = curLen
eise:
curLen = 1 print( maxLen )
135 I
Рисунок 19. Решение задачи 24
from math import sqrt
divCount =2 # нужное количество делителей
for n in range(174457j 174505+1):
divs = []
q = int(sqrtfn))
for d in range(2.,q-H):
if n % d == 0;
if d == n//d:
divs = divs +■ [d]
else:
divs = divs + [d, n//d]
if len(divs) > divCount: break #если число имеет больше двух делителей оно не будет учитывоться
if len(divs) == divCount:
print( ‘divs ) M символ * осуществляет вывод без структурных скобок списка []
3 58153
7 24923
59 2957
13 13421
149 1171
5 34897
211 827
2 87251
Рисунок 20. Решение задачи 25
data = [0]*N
with ореп(«2б.txt») as doc: for i in range(N):
data[i] = int(doc.readline())
Рисунок 21. Чтение массива данных размера N из списка data из файла 26.txt
Пример задачи [6] :
Системный администратор раз в неделю создает архив пользовательских файлов. Однако объем диска, куда он помещает архив, может быть меньше, чем суммарный объем архивируемых файлов. Известно, какой объем занимает файл каждого пользователя. По заданной информации об объеме файлов пользователей и свободном объеме на архивном диске определите максимальное число пользователей, чьи файлы можно сохранить в архиве, а также максимальный размер имеющегося файла, который может быть сохранен в архиве, при условии, что сохранены файлы максимально возможного числа пользователей.
Входные данные. В первой строке входного файла 26.txt находятся два числа: S — размер свободного места на диске (натуральное число, не превышающее 100 000) и N -количество пользователей (натуральное число, не превышающее 10 000). В следующих N строках находятся значения объемов файлов каждого пользователя (все числа натуральные, не превышающие 100), каждое в отдельной строке. Запишите в ответе два числа: сначала наибольшее число пользователей, чьи файлы могут быть помещены в архив, затем максимальный размер имеющегося файла, который может быть сохранен в архиве, при условии, что сохранены файлы максимально возможного числа пользователей. Пример входного файла: 100 4 80 30 50 40
При таких исходных данных можно сохранить файлы максимум двух пользователей. Возможные объемы этих двух файлов 30 и 40, 30 и 50 или 40 и 50. Наибольший объем файла из перечисленных пар — 50, поэтому ответ для приведенного примера: 2 50
Решение задачи:
Стоит отметить, что Python идеально подходит для решения этой задачи, так как он имеет множество встроенных методов, что значительно сократит код программы, если сравнивать с кодом на Pascal или C++.
1. Для начала нужно прочитать данные из файла; читаем все строки сразу в массив data (см. Рисунок 22).
2. Декодируем два числа из первой строки; первое записываем в переменную S, а второе записываем в переменную с именем «_»; первую строку сразу удаляем (см. Рисунок 23).
3. Преобразуем данные в целые числа и сразу сортируем (см. Рисунок 24).
4. Теперь накапливаем сумму в переменной totcA, пока она остается не больше, чем X (см. Рисунок 25).
5. Как только сумма превысила X, произойдет выход из цикла по оператору brent, а в переменной i останется количество добавленных значений. Выводим его на экран (printi).
6. Вычисляем запас, который мы можем уменьшить с помощью замены одного выбранного значения на другое (см. Рисунок 26).
iНе можете найти то, что вам нужно? Попробуйте сервис подбора литературы.
7. Теперь выбираем из массива данных те значения, которые могут быть выбраны: разность между таким значением и наибольшим выбранным элементом data[i] должна быть не больше, чем deltm (см. Рисунок 27).
8. Остается найти второй ответ -максимум из чисел-кандидатов:
(print (max(candгdates)).
9. Приведем полную программу и запустим ее (см. Рисунок 28).
Ответ получен. Задача решена.
Задача 27
Тема: Обработка данных, вводимых из файла в виде последовательности чисел.
Требования к обучающимся: • знать: конструкции языка Python; различные способы реше-
ния подобных задач; основы комбинаторики;
• уметь обрабатывать данные; выводить последовательность чисел из файла. Пример задачи [6] : Имеется набор данных, состоящий из пар положительных целых чисел.
Необходимо выбрать из каждой пары лишь одно число так, чтобы сумма всех выбранных чисел не делилась на 3 и при этом была максимально возможной. Гарантируется, что искомую сумму получить можно. Программа должна напечатать одно число — максимально возможную сумму, соответствующую условиям задачи. Входные данные: Даны два входных файла (файл A и файл B), каждый из которых содержит в первой строке количество пар N (1 < N < 100000). Каждая из следующих N строк содержит два натуральных числа, не превышающих 10 000.
Пример организации исходных данных во входном файле: 6
1 3
5 12
6 9 5 4 3 3 1 1
Для указанных входных данных значением искомой суммы должно быть число 32.
В ответе укажите два числа: сначала значение искомой суммы для файла А, затем для файла B. Решение задачи: В задачах, представленных выше, разобрались, как прочитать данные из файла. В языке Python это будет выглядеть так, как показано на Рисунке 29.
На начальном этапе не будем учитывать требование «чтобы сумма всех выбранных чисел не делилась на 3» и найдем максимальную сумму. Для этого достаточно выбрать из каждой пары максимальное число (см. Рисунок 30).
with ореп(«26.txt») as doc data = doc.readlines()
Рисунок 22. Хранение данных в массиве data
S, _ = mapCint, data[9].split()) del d3ta[e]_
Рисунок 23. Код программы
data = sortedClistCmapiintj data}))
Рисунок 24. Сортировка данных
total = e
for ij val in enumerate(data) if total + val > S: break total += val
Рисунок 25. Код программы
delta = S — total
Рисунок 26. Код программы
candidates = [х for х in data
if x-data[i-i] <= delta]
Рисунок 27. Код программы
with open(«26.txt») as doc: data = doc.readlines() 5, _ = map(int, dataje].spliti)) del datafe]
data = sortedtlistimapfint., data))) total = 9
for i, val in enumerate(data): if total + val > S: break total += val
print(i)
delta = S total candidates = [x for x in data
if x-data[i 1] <= delta] print(max(candidates))
568 50
Рисунок 28. Решение задачи 26
doc = open( «27.txt» ) N = int{Fin.readline()) for i in range(N):
a, b = map( int, doc.readline(}.split{) )
ft здесь будем робототь с переменными а и b doc.closet)
Рисунок 29. Код программы
s = e
for i in range(N):
a, b = map(int, doc.readline{),split()) s += raax(a., b) print(s)
Рисунок 30. Код программы
Если полученная сумма не делится на 3, то решение задачи найдено. Можно вводить ответ. Если же сумма не делится на 3, то в этом случае нужно заменить число в одной из пар, вместо максимального взять второе, минимальное. При этом, для того чтобы сумма получилась максимальной, нужно выбрать пару, в которой разница между числами минимальная и не делится на 3 (иначе делимость новой суммы на 3 сохранится).
Будем искать значение йМги — минимальную разницу между числами одной из пар, не делимое на 3; тогда при выводе в случае делимости суммы $ на 3 выводим $-йМт, что соответствует замене числа в одной паре (см. Рисунок 31).
Теперь соединим все части и получим полную программу (см. Рисунок 32).
Обработка файла А дает ответ 127127, а обработка файла В -ответ 399762080. Получили от-
вет: 127124 399762080. Задача решена.
На основе приведенных выше примеров заданий на уроке по информатике можно объяснять обучающимся сложные задания. Таким образом, учащиеся научатся не только решать задания из цикла ЕГЭ по информатике, но и анализировать решения задач по программированию, находить логические пути решения таких задач.
dMin = 19061 for i in range{N):
9j b = map{ intj Fin.readline().split() ) s += max( b ) d = abs( ab ) if d % 3 > 0:
dMin = min( dj dMin ) if s 3 1= 6: print{ s ) else:
print( s-dMin )
Рисунок 31. Код программы
doc = open( «27a.txt» ) N = int(doc.readline()) s, dMin = 0, 100S1 for i in range{tJ):
a, b = map(intj doc. readlineQ • split()) s += max(3j b) d = abs(a-b) if d ¡6 3 > 0:
dMin = tninfd, dMin) if s % 3 != 0:
print(s) else:
print(s-dMin)
127127
doc = open( «27b.txt» ) N = int(doc.readline()) s, dMin = 6, 10001 for i in range(N):
a, b = map(int, doc.readline().split()) s += тэх(а, Ь) d = abs(a-b) if d % 3 > 6:
dMin = min(dj dMin) if s % 3 != 0:
print(s) else:
print(s-dMin)
399762680
Рисунок 32. Решение задачи 27
ЛИТЕРАТУРА
1. Бизли Д.М. Python. URL: https://ru.pdfdrive.com/python-Подробный-справочник-e156670585.html (дата обращения 19.01.2021).
2. Кадеева О.Е., Сырицына В.Н., Репш Н.В., Белов А.Н. Краткий обзор качественной составляющей ЕГЭ по информатике в приморском крае // Ученые записки университета им. Лесгафта. СПб. ФГБОУВПО Национальный государственный Университет физической культуры, спорта и здоровья имени П.Ф. Лесгафта. Санкт-Петербург, 2019. № 12(178). С. 128-133.
3. Лейнингем И. Освой самостоятельно Python за 24 часа. URL: https://knigogid.ru/books/966155-osvoy-samostoyatelno-python-za-24-chasa (дата обращения 12.04.2021).
4. Любанович Б. Просто Python, современный стиль программирования. СПб.: Питер, 2016. 280 с.
5. МакГрат М. Программирование на Python для начинающих. М.: Эксмо, 2015. 192 с.
6. Поляков К.Ю. Преподавание, наука и жизнь: ЕГЭ по информатике 2021. URL: https://kpolyakov.spb.ru/school/ege. htm (дата обращения 17.02.2021).
7. Сваруп К. Укус питона. Подробный справочник; пер. с англ. В. Смоляр. URL: https://wombat.org.ua/AByteOfPython/ AByteofPythonRussian-2.02.pdf (дата обращения 12.04.2021).
8. Сузи Р.А. Язык программирования Python: Учебное пособие. М.: БИНОМ. Лаборатория знаний, 2006. 328 с.
REFERENCES
1. Beasley D.M. Python. Available at: https://ru.pdfdrive.com/python-noflpo6HNM-cnpaBO4HMK-e156670585.html (date of the Application: 19.01.2021). (in Russian).
2. Kadeeva O.E., Syritsyna V.N., Repsh N.V., Belov A.N. Kratkij obzor kachestvennoj sostavlyayushchej EGE po informa-tike v primorskom krae [A brief overview of the qualitative component of the exam in informatics in the coastal region]. St. Petersburg. Scientific notes of the university named after Lesgaft. 2019. No. 12(178). P. 128-133. (in Russian).
3. Lainingham I. Osvoy independently Python for 24 hours. Available at: https://knigogid.ru/books/966155-osvoy-samostoyatelno-python-za-24-chasa (date of the Application: 12.04.2021). (in Russian).
4. Lyubanovich B. Prosto Python, sovremennyj stil’ programmirovaniya [Just Python, modern programming style]. Saint-Petersburg: Piter, 2016. 280 p. (in Russian).
5. McGrath M. Programmirovanie na Python dlya nachinayushchih [Programming on Python for beginners]. Moscow: Eksmo, 2015. 192 p. (in Russian).
6. Polyakov K.Yu. Prepodavanie, nauka i zhizn’: EGE po informatike 2021 [Teaching, Science and Life]. Available at: https:// kpolyakov.spb.ru/school/ege.htm (date of the Application: 17.02.2021). (in Russian).
7. Swarup K. Ukus pitona. Podrobnyj spravochnik [Python bite = A byte of Python. Detailed reference guide]. Available at: https://wombat.org.ua/AByte0fPython/AByteofPythonRussian-2.02.pdf (date of the Application: 12.04.2021). (in Russian).
8. Suzi R.A. Yazyk programmirovaniya Python [Python Programming Language: Tutorial]. Moscow: BINOM. Laboratoriya znanij, 2006. 328 p. (in Russian).
В курсе полностью разобраны программные способы решения задач № 2, 5, 8, 12, 14, 15, 17, 22 в Python.
Теория, видеоразборы, задачи для самостоятельного решения.
Изучение Python с нуля для решения задач ЕГЭ.
What you will learn
- Получите все необходимые знания по Python для успешной сдачи КЕГЭ 2023 по информатике
- Научитесь решать № 2, 5, 8, 12, 14, 15, 17, 22 из КЕГЭ 2023
- Изучите условия, циклы, строки, работу с файлами, списки, множества, кортежи, функции и многое другое
- Овладеете базовыми алгоритмами в программировании
About this course
Данный курс является второй ступенью полной подготовки к КЕГЭ 2023 по информатике.
✅ В курсе изучается вся необходимая теория по программированию на языке Python для ЕГЭ по информатике. Особенностью курса является изучение программирования на языке Python именно на задачах КЕГЭ. Курс будет полезен и тем, кто имеет опыт написания программ на Python, и тем, кто совсем не знаком с программированием.
✅ Приведены эффективные способы решения заданий ЕГЭ с помощью написания программы в Python. Разобраны все нюансы и хитрости решения задач ЕГЭ по информатике в Python.
✅ В курсе полностью разобраны программные способы решения задач № 2, 5, 8, 12, 14, 15, 17, 22 на языке программирования Python.
❗ После покупки курса вы можете начать его прохождение в любое время. Доступ к курсу останется у вас навсегда
❗ Некоторые уроки открыты для свободного прохождения, вы можете попробовать учиться с нами бесплатно.
Данный курс является частью курсов:
- Информатика ЕГЭ 2023. Путь к 100 баллам. № 1 — 23
- Информатика ЕГЭ 2023. Путь к 100 баллам. № 1 — 27
Whom this course is for
Для тех, кто сдаёт ЕГЭ по информатике в 2023 году или в ближайшие года.
Для всех желающих, кто интересуется программированием.
Initial requirements
Курс подходит для учеников с любым уровнем начальных знаний.
Meet the Instructors
How you will learn
Курс разбит по темам на модули. Каждый модуль состоит из уроков. А каждый урок из коротких видеоразборов теории и задач, а также задач с автоматической проверкой для закрепления материала.
Course content
Certificate
Stepik certificate
Price
FAQ
Share this course
https://stepik.org/course/100936/promo