Экзаменационная работа ОГЭ по русскому языку
Общеизвестно, что чем раньше начнёшь готовиться к экзамену, тем легче будет его сдавать. Вопрос лишь в том, с чего начать? Для начала определитесь, как вы будете готовиться: самостоятельно, на подготовительных курсах или обучаться с репетитором. Здесь будет рассматриваться самостоятельная подготовка, так как на курсах вам всё расскажет преподаватель или, соответственно, репетитор.
Прежде всего надо понимать, что экзаменационная работа по русскому языку состоит из трёх частей, связанных между собой общетематической направленностью. Если первый текст (для сжатого изложения) носит обобщённо-отвлечённый характер, то второй раскрывает тему на живом, жизненном материале; если первый текст – рассуждение, то во втором могут быть представлены разные функционально-смысловые типы речи и их сочетания.
Первая часть
работы – Часть 1
– это небольшая письменная работа по прослушанному тексту, т. е. написание сжатого изложения по тексту публицистического или научного стиля.
Сжатое изложение –
это форма обработки информации исходного текста, позволяющая проверить комплекс необходимых жизненных умений:
- умение точно определять круг предметов и явлений действительности, отражённых в тексте;
- умение адекватно воспринимать авторский замысел;
- умение вычленять главное в информации;
- умение сокращать текст разными способами;
- умение правильно, точно и лаконично излагать содержание текста;
- умение находить и уместно использовать языковые средства обобщённой передачи текста.
Чтобы хорошо справиться с этим видом работы, необходимо усвоить, что любой текст содержит главную и второстепенную информацию. Главная информация – это то содержание, без которого будет неясен или искажён авторский замысел. Следовательно, нужно научиться воспринимать текст на слух так, чтобы точно понимать его общую тему, проблему, идею, видеть авторскую позицию. С этой целью следует тренироваться в определении микротем как составных частей общей темы прослушанного текста. Для хорошего сжатого пересказа нужно также научиться правильно и точно подбирать слова для передачи главного содержания текста, уместно употреблять синтаксические и грамматические конструкции, владеть связностью речи и логикой изложения.
В целом же сжатие текста предполагает в основном исключение подробностей, деталей, а также обобщение единичных явлений и фактов.
Вторая и третья части
работы выполняются на основе одного и того же прочитанного художественного или публицистического текста.
Вторая часть
экзаменационной работы – Часть 2
– это задания с кратким открытым ответом. Она состоит из 14 заданий (2 – 14). В заданиях требуется сформулировать ответ самостоятельно и записать цифрами или словами.
Задания части 2
проверяют глубину и точность понимания содержания прочитанного текста, выявляют уровень постижения школьниками его культурно-ценностных категорий: понимание основной проблемы текста, позиции автора или героя, характеристики героя, контекстуального значения ключевых слов, понимание отношений синонимии, важных для содержательного анализа; восприятие форм наименования героя, опознавание изученных средств выразительности речи.
Нужно отметить важность определения в тексте средств речевой выразительности, без умения видеть которых, понимать их роль невозможно до конца постичь авторский замысел и разобраться в смысловых акцентах, помогающих выявить авторскую позицию.
Предлагаемые задания также проверяют комплекс умений, определяющих уровень языковой и лингвистической компетенций выпускников. Все задания имеют практическую направленность, так как языковые явления, проверяемые ими, составляют необходимую лингвистическую базу владения орфографическими, пунктуационными и речевыми нормами.
Стоит обратить внимание, например, на задания, связанные с определением грамматической основы предложения (задания 8 и 11). Понятно, что неумение видеть грамматическую основу, заключающую в себе и опору грамматической структуры, и ядро смысла предложения, влечёт за собой непонимание предложения, искажение его содержания, а следовательно, и непонимание или недопонимание всего текста в целом.
Третья часть
работы – Часть 3
– это письменный развёрнутый аргументированный ответ на одно из трёх предложенных заданий (15.1, 15.2 или 15.3), направленный на самостоятельную интерпретацию смысла одного из ключевых фрагментов текста. Часть 3 выполняется на основе всё того же текста, с которым работали над заданиями части 2. Задание проверяет коммуникативную компетенцию школьников, в частности умение строить собственное высказывание в соответствии с типом речи — рассуждение. При этом не случайно особое внимание уделяется умению аргументировать свой ответ, используя прочитанный текст. Именно это умение необходимо в дальнейшей образовательной, а часто и в профессиональной деятельности.
Как лучше готовиться к ОГЭ. Советы для учащихся.
1. Хорошо подготовь
место для занятий
: убрать со стола лишние вещи,
удобно расположить нужные учебники, пособия, тетради, бумагу, карандаши и
т.п. Рабочее место должно быть хорошо освещено, в комнате должно быть тепло, но не жарко, её нужно часто проветривать.
2.Необходимо собрать
весь необходимый материал, а затем
систематизировать его. Важно проанализировать материал,
выяснить, что ты
знаешь хорошо, что недостаточно, какой материал вызывает затруднения. Это
поможет тебе организовать направления дальнейшей деятельности.
3.Нужно разбить материал на части и распределить материал
равномерно по всем дням данным
для подготовки
.
4.
Не стоит всѐ оставлять на последний день. Его лучше оставить для повторений и систематизации выученного
материала.
5. Необходимо выстроить подготовку к экзамену с учетом своих индивидуальных особенностей
. Если ты по своему темпераменту относишься к «быстрым темпераментам» (холерики и сангвиники), тебе лучше начать учить с наиболее сложного материала. Холерики и сангвиники быстро врабатываются, им не нужен большой подготовительный период, но и им быстро надоедает заниматься однообразной работой, до изучения трудного материала они могут просто не дойти, бросив занятия. Лучше учить материал блоками, делая небольшие перерывы на еду и отдых.
6. Если ты по своим индивидуальным особенностям относишься к людям
с медленными темпераментами
(флегматик и меланхолик) тебе лучше начать с более простых заданий. Они медленно врабатываются, но постепенно работоспособность и продуктивность мыслительной деятельности возрастает.
Флегматикам лучше осваивать материал большими блоками, а перерывы делать
не часто, так как из-за частых перерывов ты потратишь много времени на
включение в работу.
Меланхоликам лучше делать небольшие, частые перерывы, так как
у них быстро наступает утомление и снижается продуктивность мыслительной деятельности.
7. При подготовке к экзамену
учитывай свои природные биоритмы. Если
ты от природы «жаворонок», то максимальная работоспособность у тебя
приходится на первую половину суток. Поэтому тебе лучше встать пораньше и
приступить к подготовке к экзамену, а вторую половину дня потратьте на
повторение и систематизацию материала. Спать также лучше лечь пораньше.
8. Если ты от природы «сова
», то продуктивность мыслительной деятельности у тебя выше во второй половине дня. Поэтому тебе не стоит вставать рано,
первую половину дня потратить на повторение и систематизацию, а во второй
ударно поработать.
9. Необходимо также знать особенности работы памяти. Согласно
законам работы памяти
лучше всего запоминается начало и конец информации, поэтому самый сложный материал лучше выучить либо в самом начале, либо оставить на конец. Повторять материал лучше не сразу после заучивания, а спустя 1-1,5 часа так как процесс забывания идет постепенно и только спустя некоторое время будет ясно, что вы помните, а что нет.
10. Если у тебя преобладает зрительный тип памяти тебе лучше работать с письменными
источниками, если слуховой, что лучше читать вслух. При любом типе памяти продуктивность запоминания повышается, если составлять планы, схемы,
таблицы или другие зрительные опоры.
Обязательно
перепроверь точность запоминания фактического материала: даты, фамилии, название произведений, математические формулы и т.п.
11. Старайся соблюдать режим дня. Чтобы не страдать от бессонницы,
нужно ложиться и вставать
в одно и то же время
. Спать нужно не меньше 7,5-8 часов, если очень устаешь можно поспать 1-1,5 ч днем.
12. Чтобы мозг получал достаточное количество необходимых для
нормальной работы микроэлементов, нужно полноценное питание
. Не стоит пить слишком много кофе, чая и газированных напитков, так как это приводит к перевозбуждению нервной системы и ухудшает качество мыслительной деятельности.
13. Выполняй как можно больше различных опубликованных тестов по
этому предмету.
Эти тренировки ознакомят тебя с конструкциями тестовых
заданий.
Тренируйся с секундомером в руках, засекай время выполнения тестов (на заданиях в части А в среднем уходит по 2 минуты на задание).
14. Чтобы снять психическое и физическое напряжение
, необходимы
физические упражнения, отдых, прогулки на свежем
отдыхе. Готовясь к экзаменам, никогда не думай о том, что не справишься с заданием, а напротив,
мысленно рисуй себе картину триумфа.
15. Оставь один день перед экзаменом на то, чтобы вновь повторить все
планы ответов, еще
раз остановиться на самых трудных вопросах.
Как вести себя накануне экзамена:
1
. Не стоит тратить последнюю ночь перед экзаменом, на подготовку к нему.
Ты и так уже устал, а бессонная
ночь может привести к переутомлению.
С вечера перестань готовиться, прими душ, соверши прогулку. Выспись как
можно лучше, чтобы встать отдохнувшим, с ощущением своего здоровья, силы,
«боевого» настроя.
2.
За день до экзамена точно установите местонахождение, где будет
проводиться ОГЭ Это
важно в том случае, когда экзамен проводится в не
знакомом вам здании. Вы избавляетесь при этом от необходимости тратить
нервную энергию на поиск. За день до экзамена дважды проверьте, когда он
состоится. Почти, всегда находятся учащиеся, которые ошибаются и являются
на экзамен с опозданием.
3. В пункт сдачи экзамена ты должен явиться, не опаздывая, лучше за
полчаса до начала тестирования
. При себе нужно иметь паспорт (не
свидетельство о рождении) и несколько (про запас) гелиевых или капиллярных
ручек с черными чернилами.
4. Не забудь выложить сотовый телефон, чтобы тебя не заподозрили в
мошенничестве.
5. Если на улице холодно, не забудь тепло одеться, ведь ты будешь
сидеть на экзамене 4 часа.
6. Очень легко, но питательно позавтракай. Съешь что-нибудь полезное
для работы мозга (сыр, рыбу, мясо, творог), не злоупотребляй кофе, оно может
привести к перевозбуждению.
7. Сделай упражнение на дыхание перед входом в помещение, где
проходит экзамен. Внушайте себе следующее: «Я хорошо подготовился, я
справлюсь».
8. Избегайте тех своих одноклассников, которые склонны нагнетать панику, лучше отвлечься от происходящего, посмотреть в окно, вспомнить о чем-то хорошем, побыть в одиночестве, а не среди излишне волнующихся товарищей.
Как вести себя на экзамене
Нужно настроиться на экзамен, быть максимально собранным и уверенным в своих силах
Не стоит слишком беспокоиться и тревожиться, так от этого только ухудшается работа мышления и памяти. Нужно попытаться успокоится, вспомнить какое-то приятное событие из своей жизни, ситуацию в которой ты был успешен. Полезно убрать лишние движения (постукивание пальцем, раскручивание ручки и т.п.), так как это только невротизирует и тебя и других.
Необходимо сделать глубокий вдох, медленно выдохнуть и сказать себе: «Я
спокоен».
После вскрытия пакета с экзаменационными заданиями, внимательно
и аккуратно заполни регистрационный бланк.
После выполнения предварительной части тестирования (заполнения
бланков), когда ты прояснил все непонятные для себя моменты, постарайся
сосредоточиться и забыть про окружающих. Для тебя должны существовать
только текст заданий и часы, регламентирующие время выполнения теста.
Не бросайся сразу выполнять задания, внимательно прочитай
инструкцию, разберись в ней. Перед тем, как вписать ответ, перечитай вопрос
дважды и убедись, что ты правильно понял, что от тебя требуется. Читай
задание до конца!
Если ты боишься потерять нужную строку и поставить знак не туда
куда нужно, подложи под неѐ лист черновика.
Начни с легкого! Начни отвечать на те вопросы, в знании которых ты
не сомневаешься, не останавливаясь на тех, которые могут вызвать долгие
раздумья. Тогда ты успокоишься, голова начнет работать более ясно и четко, и
ты войдешь в рабочий ритм. Ты как бы освободишься от нервозности, и вся
твоя энергия потом будет направлена на более трудные вопросы. Лучше
выполнять задания в том порядке, в котором они даны, так как они
расположены в порядке возрастающей трудности.
Если какое-либо задание не получается, не стоит тратить на него
слишком много времени. Лучше начать делать другие задания, а к нему
вернуться позже. Пропускай! Надо научиться пропускать трудные или
непонятные задания. Помни: в тексте всегда найдутся такие вопросы, с которыми ты обязательно справишься. Просто глупо недобрать очков только потому, что ты не дошел до «своих» заданий, а застрял на тех, которые вызывают у тебя затруднения.
Если тебе кажется, что ты ничего не помнишь, то постарайся найти задание ответ, на который тебе известен, это поможет тебе успокоиться и восстановить другую информацию.
Думай только о текущем задании! Когда ты видишь новое задание, забудь все, что было в предыдущем. Как правило, задания в тестах не связаны друг с другом, поэтому знания, которые ты применил в одном (уже, допустим, решенном тобой), как правило, не помогают, а только мешают сконцентрироваться и правильно решить новое задание. Этот совет дает тебе и другой бесценный психологический эффект
Забудь о неудаче в прошлом задании (если оно оказалось тебе не по зубам). Думай только о том, что каждое новое задание -это шанс набрать очки.
Старайся выполнить как можно больше заданий, но не приноси количество в жертву качеству. Стремись выполнить все задания, но помни, что на практике это нереально. Учитывай, что тестовые задания рассчитаны на максимальный уровень трудности, и количество решенных тобой заданий вполне может оказаться достаточным для хорошей оценки.
Исключай! Многие задания можно быстрее решить, если не искать сразу правильный вариант ответа, а последовательно исключать те, которые явно не подходят. Метод исключения позволяет в итоге сконцентрировать внимание всего на одном-двух вариантах, а не на всех пяти-семи (что гораздо труднее).
Угадывай! Если ты не уверен в выборе ответа, но интуитивно можешь
предпочесть какой-то ответ другим, то интуиции следует доверять! При этом
выбирай такой вариант, который, на твой взгляд, имеет большую вероятность
Рассчитай время так, чтобы за две трети всего отведенного времени
пройтись по всем легким заданиям («первый круг»). Тогда ты успеешь набрать
максимум очков на тех заданиях, а потом спокойно вернуться и подумать над
трудными, которые тебе вначале пришлось пропустить («второй круг»).
Соблюдай все требования к оформлению заданий, так как от этого напрямую зависит твоя оценка.
Оставь время для проверки своей работы, хотя бы, чтобы успеть
пробежать глазами и заметить явные ошибки. Прочтите и проверьте то, что
написали с начала и до конца. Сотрите галочки и крестики ластиком.
Не покидайте аудиторию до окончания экзамена. Не обращайте внимания на
других учащихся, уходящих сразу по завершении своей работы. Оставайтесь на
своем месте до конца экзамена. Даже в последний момент вас может осенить
мысль, которая принесет вам один-два дополнительных балла.
Не переживай слишком серьезно из-за плохих результатов ОГЭ, помни, что ОГЭ
–это лишь экзамен, в нем всегда есть элемент случайности.
Программы курсов подготовки к ОГЭ в 9 классе ПЕРВОГО ЕГЭ-ЦЕНТРА разработаны с учетом всех требований ФИПИ и особенностей сдачи экзамена квалифицированными -экспертам ОГЭ и ЕГЭ. В течении всего учебного курса наши ученики выполняют задания контрольных измерительных материалов ОГЭ по всем предметам на оригинальных бланках ФИПИ. Большим плюсом также является то, что мы не просто обучаем правилам и формулам, мы также учим понимать саму суть изучаемого предмета.
На занятиях по каждому предмету:
- повторяется теоретический материал и объясняются правила выполнения практических заданий;
- отрабатываются навыки решения типовых заданий контрольных измерительных материалов ОГЭ;
- задаются домашние задания и обязательно разбираются на последующих занятиях;
- проводятся пробные репетиционные экзамены в формате, максимально приближенном к ОГЭ;
- ведется индивидуальная работа с каждым учащимся.
Заниматься нужно по возможности ежедневно. Для каждой дисциплины желательно отвести минимум 40 минут в день на закрепление пройденного материала, поскольку от самостоятельной работы дома зависит не меньше, чем от опыта педагога. Обратите внимание на то, чем занят ребёнок в перерывах между занятиями. Для оптимального запоминания информации нужно «подключать» все виды памяти. Важно не только впитывать материал из учебников, но и строить схемы, изучать рисунки, смотреть фильмы на заданную тему, слушать аудио лекции и т.д. Например, если предстоит подготовиться к экзаменам по биологии и изучить систему кровообращения человека, лучше запоминать ее по схеме, то есть визуально.
Как правильно подготовиться к экзаменам?
Конечно, у каждого преподавателя есть свои методики, по которым он проводит подготовку к ОГЭ в 2017/2018 учебном году. Можно проявить чудеса педагогики и подготовить ребенка за пару недель интенсивных занятий, но такой способ плох тем, что наспех полученные знания могут так же быстро и легко вылететь из головы в самый ответственный момент. Таким образом, вопрос необходимо ставить перед собой следующий: «Как сделать так, чтобы курсы подготовки к ОГЭ приносили максимальный эффект?» Если готовиться к экзамену и выбрать курсы ГИА заранее, то можно закрепить весь пройденный материал спокойно и без спешки. Для этого необходимо распланировать учебную неделю, в которой обязательно должен быть свободный день для отдыха от умственных нагрузок.
Чтобы максимально эффективно подготовиться к экзаменам, нужно:
- определить, к каким предметам следует подготовиться;
- отвести на каждый предмет 1-2 дня для подготовки и закрепления;
- выделить важное и второстепенное в каждом предмете;
- обратиться в ПЕРВЫЙ ЕГЭ-ЦЕНТР в Москве за консультацией;
- начать занятия на курсах;
- успешно сдать экзамены!
Основной Государственный Экзамен
Основной государственный экзамен (ОГЭ) -это форма обязательной государственной итоговой аттестации (ГИА) по образовательным программам основного общего образования выпускников 9 классов средних общеобразовательных организаций Российской Федерации.
Для проведения ОГЭ применяются контрольные измерительные материалы (КИМ) в виде комплекса заданий стандартизированной формы с использованием специальных бланков ФИПИ.
Обязательными предметами для сдачи ОГЭ являются русский язык и математика. Дополнительные предметы для сдачи государственного экзамена ученики выбирают в соответствии со своей профессиональной ориентацией.
Для перехода в 10 класс или поступления в учреждение среднего профессионального образования необходимы положительные оценки по экзамену. Поэтому подготовку к ОГЭ лучше начинать заранее на курсах ПЕРВОГО ЕГЭ-ЦЕНТРА.
ОГЭ – это лишь первая ступенька на пути к будущему профессиональному образованию, но не менее важная, чем ЕГЭ. Успешная сдача ОГЭ зависит от двух факторов – знания предмета и психологической подготовки учащегося.
Когда начать готовиться к ГИА?
Подготовка к ГИА в 9 классе – самое правильное решение. Безусловно, можно начать и раньше проходить сложный материал, но и за два года можно отлично подготовиться, при условии, что вы обратитесь к опытным педагогам. И многие родители выбирают именно этот путь, обращаясь к репетиторам, оказывающим помощь в подготовке ОГЭ с нуля. Почему именно 9 класс? Родителям, как и самим школьникам, бывает непросто осознать всю серьезность предстоящего экзамена, так как в 8-9 классах кажется, что времени до «дня икс» еще много. Безусловно, это впечатление обманчиво, так как время летит очень быстро, и не стоит тратить его впустую. Соберите семейный совет сегодня, чтобы решить, когда начать готовиться и вместе выберете подходящие элективные курсы. Кроме всего прочего, нужно подумать о том, как лучше распределить нагрузку, чтобы ребенок не утомлялся, и чтобы ничего не мешало ему на пути к знаниям.
До ОГЭ остается чуть
больше трех месяцев. Пора приступать к подготовке, если до сих пор не сделал
этого. Как правильно распределить время и, с чего начать, даже если очень не
хочется, узнали у экспертов центра «Феномен».
До ОГЭ три месяца:
В первую очередь надо
прорешать тесты по тем предметам, которые сдаешь. Так ты разберешься, в чем силен,
а в чем нет. Если результат неутешительный, не переживай, еще есть время
наверстать упущенное.
Составь план, в какие дни,
и что ты изучаешь. Это поможешь грамотно распределить время. Важно! Не ставь
подготовку к двум разным предметам на один день, иначе в голове произойдет путаница,
и забудешь все.
До ОГЭ два месяца:
Убери все яркое в комнате
с видных мест. Для того чтобы тебя не отвлекали резкие цвета, и ты мог спокойно
готовиться к экзамену, лучше исключить раздражители. После того, как сдашь,
достанешь все из шкафа.
Начни вести конспекты с
основной информацией по тем темам, в которых часто встречаются ошибки. Не переписывай
все. Только самое важное.
До ОГЭ месяц:
Все даты, формулы и
термины выпиши на отдельные карточки, чтобы обращаться к ним в любой момент. Кроме
того, на экзамене у тебя может сработать визуальная память, а накануне будет
удобно повторять материал.
До ОГЭ неделя:
Бегло перечитай конспекты
и внимательно изучи карточки, которые писал ранее.
Если ты все еще не готов,
можешь паниковать.
Завтра ОГЭ:
Перед сном еще раз повтори
даты, формулы и термины.
Ляг спать пораньше, а под
подушку положи конспекты и карточки.
Если ты все еще не готов,
постарайся не волноваться, а надейся на удачу.
Все прекрасно знают, насколько важно как можно лучше сдать государственную итоговую аттестацию после 9-го класса и Единый государственный экзамен после 11-го. От результатов ГИА зависит поступление в 10-й класс или учреждения среднего профессионального образования, а результаты ЕГЭ принимаются вузами как вступительные.
Когда же начинать к ним готовиться? В 9-м и 11-м классах? Нет, это очень поздно. Времени остается мало. Ведь проверяется весь объем знаний, полученный ко дню сдачи экзамена. Поэтому начинать готовиться к ним нужно намного раньше, класса с 5-6-го.
Для этого ребенок должен не только стараться качественно усваивать новый материал, но и ликвидировать имеющиеся пробелы в знаниях. Потому что перед экзаменом осилить такой огромный объем работы просто невозможно.
Откуда же берутся пробелы в знаниях? Причины разные и не всегда зависящие от детей.
Самая распространённая – пропуски уроков из-за болезни. Дома самостоятельно не всегда удается полностью понять новый материал.
Если уроков не было из-за учителя (заболел, на курсах и т.д.), пропущенная программа проходится быстрым темпом. В этом случае нет времени хорошо отработать на практических заданиях пройденное.
Кто-то из учеников не совсем понял новую тему на уроке. У многих низкая мотивация к учебе. А кто-то просто ленится, не желает напрягать свои силы, чтобы лучше учиться. Причин много.
Что же делать? Могут ли родители помочь ребенку? Да.
Прежде всего, постарайтесь обнаружить эти самые пробелы в знаниях. Как? Обратите внимание, какие ошибки ребенок допускает в диктантах, изложениях и других письменных работах, какие дополнительные задания не совсем уверенно делает (синтаксический, морфологический, фонетический разборы и т.д.)? Над этим и работайте. В конце концов, сколько же можно наступать на одни и те же грабли, допускать одни и те же ошибки и получать плохие оценки? Ведь это ведет к постоянным стрессам, неуверенности в своих силах, к ненависти к предмету.
Предложите учебный материал изучать в виде блоков, таблиц, опорных схем: усваивается быстрее и легче.
Систематически внимательно проверяйте выполнение домашней работы. Это способствует закреплению знаний, умений. Если заметили пробелы в знаниях ребенка, объясните, разберите сразу. Иначе это повлечет за собой непонимание следующего нового материала и в конце концов перерастет в большую проблему.
Уже в 5-6 классах можно выполнять проверку своих знаний в виде тестов. Купите или скачайте из интернета и решите их вместе с ребенком. Это не так и просто. Но экзамен-то обязателен для всех! И лучше потихоньку начать готовиться к нему заранее. Во-первых, такая форма самоподготовки учит школьника внимательности, собранности, аккуратности. Ведь надо не только вдумчиво прочитать вопрос, но и правильно понять, что от тебя требуется сделать, и быстро выполнить. Развивается орфографическая зоркость, вырабатывается привычка быстро выбирать нужное правило и применять его. Во-вторых, вы увидите слабые места в знаниях ребенка и, прочитав соответствующие правила и проработав их на тренировочных упражнениях, вы добьетесь безошибочного выполнения заданий. В-третьих, ребенок привыкает к такой форме проведения экзамена, и сдать его будет проще.
И, конечно же, нужно делать работу над допущенными ошибками. Не для учителя, формально, не вдумываясь, а осознанно, для себя. Раз допустил ошибку – значит, не знаешь соответствующее правило. И пока не выучишь и не потренируешься на практике его применять, эти ошибки будешь допускать.
Сына или дочь нужно как можно чаще поддерживать, подбадривать, тем самым укреплять его веру в свои силы и способности. Создать атмосферу успеха. Иначе ребенок может уйти в себя, во внутренний план. В этом случае он не слышит, что происходит в классе, не выполняет заданий, он пассивен, а учеба, приносящая одни неприятности, совсем не интересует.
Объективно относитесь к возможностям своего ребенка. Не требуйте от него больше, чем он может. Естественно, нужно как можно больше читать, тогда увеличивается словарный запас, запоминаются зрительные образы слов. Также важно воспитывать трудолюбие в ребенке, ведь умеющие трудиться дети даже при средних способностях добиваются больших положительных результатов, чем талантливые лентяи.
Нужно учить ребенка заниматься самостоятельно. Умение планировать свое время поможет выполнить все домашние работы вовремя, сходить на кружки, секции и погулять. Чтобы этому научиться, вначале можно записывать, сколько времени затрачивается на выполнение определенного задания.
Посмотрите, не перегружен ли рабочий день вашего ребенка. Помогите ему правильно распределить занятия и отдых. Кроме учебы, он еще должен и полноценно спать, бывать на воздухе и заниматься спортом.
Если занятий дома и в школе окажется все-таки мало, можно воспользоваться помощью квалифицированного репетитора и курсами в учреждениях дополнительного образования.
Методика подготовки в ОГЭ по математике
Совсем немного шагов к успеху на ОГЭ по математике в 9 классе
В данной публикации можно найти советы практикующего учителя математики по подготовке обучающихся 9 класса к успешной сдаче ОГЭ по математике.
Для успешной сдачи экзаменов девятиклассникам необходима определённая система подготовки.
При подготовке учащихся к ОГЭ учителю необходимо:
-
формировать у учащихся навыки самоконтроля;
-
формировать умения проверять ответ на правдоподобие;
-
систематически отрабатывать вычислительные навыки;
-
формировать умение переходить от словесной формулировки соотношений между величинами к математической;
-
учить проводить доказательные рассуждения при решении задач;
-
учить выстраивать аргументацию при проведении доказательства;
-
учить записывать математические рассуждения, доказательства, обращая внимание на точность и полноту проводимых обоснований.
Предлагается несколько интересных, приёмов:
Обязательные устные упражнения и правила быстрого счёта
Так как на экзамене не разрешается использовать калькулятор, то нужно научить учащихся выполнять простейшие (и не очень) преобразования устно. Конечно, для этого потребуется организовать отработку такого навыка до автоматизма.
Для достижения правильности и беглости устных вычислений необходимо в течение всех лет обучения на каждом уроке отводить 5-7 минут для проведения упражнений в устных вычислениях, предусмотренных программой каждого класса.
Устные упражнения должны соответствовать теме и цели урока и помогать усвоению изучаемого на данном уроке или ранее пройденного материала. Сокращается время на выполнение таких операций, как решение квадратных уравнений, линейных неравенств и неравенств 2-ой степени, разложение на множители, преобразования иррациональных выражений и другие. Эти операции переходят из разряда самостоятельной задачи в разряд вспомогательной и становятся инструментом («таблицей умножения») для решения более сложных задач.
Помогает в организации устных вычислений книга под редакцией Лысенко Ф.Ф., Кулабухова С.Ю. «Устные вычисления и быстрый счёт. Тренировочные упражнения за курс 7-11 классов» (Ростов-на-Дону: ЛЕГИОН-М.- 2010).
Важны также и приёмы быстрого счёта, такие как:
-
возведение в квадрат чисел, оканчивающихся на 5;
-
умножение на 25, на 9, на 11;
-
нахождение произведений двузначных чисел, у которых одинаковое число десятков, а сумма единиц составляет 10;
-
деление трёхзначных чисел, состоящих из одинаковых цифр, на число 37;
-
извлечение квадратного корня.
Возможно воспользоваться пособиями:
-
Рачинский С.А. 1001 задача для умственного счёта в школе.
-
Перельман Я. Быстрый счёт.В рамках проектной деятельности интересна работа с обучающимися по составлению справочников. Это развивает их индивидуальные способности. Использование метода проектов ведет к тому, что повторение, а значит и подготовка к экзаменам, идет постепенно, как бы «скрыто», но приводит к прочным знаниям и нужным в дальнейшей жизни навыкам.
При этом наблюдается:
Метод проектов для составления справочников.
Высокая степень самостоятельности и активности учащихся.
Перенос акцента в обучении с преподавания на учение.
С ростом уровня сложности деятельности учеников растет и уровень творчества и качества выполняемых работ.
Решая сложные задания, для которых нет определенного алгоритма, учащийся формирует собственную самостоятельность и готовность решать сложные проблемы в реальной жизни.
Важным в проектной деятельности, направленной на подготовку к ОГЭ является умение выполнять задания большого объема, требующие терпения и внимания.
Формируются такие качества, как ответственность, добросовестность, умение доводить начатое дело до конца, защищать и отстаивать собственное мнение. Эти качества всегда вызывали уважение и ценились в обществе.
Примером может быть проект по составлению справочника, объединяющего темы: «Квадратные уравнения», «Теорема Виета», «Квадратные неравенства», «Квадратичная функция».
При составлении справочников рекомендуется обратиться к пособию: Райбул С.В. «Алгебра и геометрия в таблицах и схемах».
Применение групповой работы на уроках математики при подготовке к ОГЭ
Психологи давно доказали, что люди лучше всего усваивают то, что обсуждают с другими, а лучше всего помнят то, что объясняют другим.
Учащиеся под руководством учителя создают группы по 3- 4 человека.
Алгоритм действий учащихся.
Задания обязательного уровня (1 часть)
Выполнив задания 1 части, сравнивают решения с ответами и между собой.
Делают работу над ошибками.
Получают другой вариант заданий 1 части и выполняют только те задания, в которых были допущены ошибки.Каждая группа получает задание и готовится самостоятельно. При этом учащиеся не знают, кто будет выполнять задание у доски.
Задания 2 части
Представители каждой группы решают задания по порядку, возможно, только те, которые решить смогли.
Остальные учащиеся проверяют задания, задают вопросы, оценивают. Оценку получает вся группа.Каждая группа готовится самостоятельно в течение недели. Проверку осуществляют на элективе.
Задания повышенной сложности
Задания у доски выполняют те учащиеся, которые с ним справились самостоятельно.
Остальные при этом имеют возможность разобраться в затруднениях, встретившихся при выполнении этих заданий.
Если есть несколько учащихся, решивших задание, то проверку можно осуществлять в виде математического боя.
Особое внимание геометрии
Когда в апреле провели пробный экзамен, то обнаружили много работ, в которых практически масса неудовлетворительных отметок именно по геометрии. Желательно готовить справочники по темам «Треугольники», «Четырёхугольники», «Окружность». Затем выполнить набор задач разного типа сложности по этим темам (брать задания из открытого банка)
Например, по теме «Окружность» рассматривают вопросы:
-
В экзаменационной работе 8 заданий по геометрии. Поскольку геометрию в школе проходят по остаточному принципу, поэтому приходится уделять ей особое внимание.
-
При таком подходе значительно увеличивается количество заданий, решаемых учениками и проверяемых в группе друг у друга.
-
прямые, отрезки и углы, связанные с окружностью;
-
свойства вписанных и центральных углов;
-
углы между хордами, касательными и секущими;
-
свойства хорд;
-
соотношения между длинами хорд, отрезков касательных и секущих;
-
свойства дуг и хорд, длина дуг и хорд, площадь круга и его частей;
-
взаимное расположение двух окружностей.
По теме «Треугольники» рассматривают вопросы:
-
признаки равенства треугольников;
-
неравенство треугольника;
-
определение вида треугольника;
-
4 замечательные точки треугольника;
-
теорема синусов;
-
теорема косинусов;
-
площади треугольников;
-
признаки подобия треугольников;
-
вписанные и описанные треугольники.
-
По теме «Четырёхугольники» рассматривают вопросы:
-
вписанные и описанные четырёхугольники, их свойства и площади;
-
параллелограмм и его свойства;
-
трапеция и её свойства;
-
прямоугольник, его свойства и признаки;
-
ромб, его свойства и признаки;
-
квадрат, его свойства и признаки.
Авторитет учителя
Хороший результат получается, когда учитель инсценирует «тупик» в процессе решения задачи. В этом случае учащиеся должны уметь найти место, с которого пошёл «тупиковый» вариант, чтобы, вернувшись к нему, найти другой вариант решения.
Очень эффективен приём показа учителем мыслительного поиска способа решения задачи. Учитель должен быть готов раскрыть перед учащимися ход своих мыслей, которые у него возникали, когда он готовился к уроку, даже если эти мысли были неверными. Целесообразно развернуть перед учащимися всю картину поиска решения, вплоть до показа своих черновых записей.
По этому разделу рекомендуется учебное пособие: Балаян Э.Н. «Геометрия. Задачи на готовых чертежах для подготовки к ГИА и ЕГЭ. 7-9 классы». Оно содержит теоретические сведения по геометрии за курс основной школы и упражнения в таблицах по всем темам геометрии 7-9 классов.
Если учитель планирует провести проверочное диагностическое тестирование по какой-то определённой теме (а это разумно), то должен соблюдаться следующий принцип: правильно решенное предыдущее задание готовит понимание смысла следующего.А еще хочется сказать о пробном ОГЭ в апреле, которое проводится по инициативе Управления образования, методического центра. Результаты очень низкие, поскольку знания и умения еще не стали навыками в решении математических задач. Затем начинается негативное сравнение итогов на настоящем ОГЭ и на пробном. Такое сравнение, считаю, не показателем для оценки труда учителя и нечистоплотности выполнения экзаменационных работ. До экзамена 1,5 месяца, именно в этот период, обучающиеся 9 класса стараются закрепить свои умения, настроиться на экзамен. Тем более, что это тот период, когда весь программный материал уже изучен полностью, именно в этот период сполна можно отработать индивидуально те задания, которые вызывают затруднения среди обучающихся.
Переход к комплексному тестированию разумен только в конце года (апрель-май), когда все темы изучены и у учеников накоплен запас общих подходов к основным типам заданий.
Подготовку к ОГЭ в 9 классе начинаем в начале года.
Работа с родителями.
Для обучающихся и их родителей в сентябре проводим совместное родительское собрание, на котором рассказываем об организации и проведении ОГЭ по математике в 9 классе и то, как необходимо к экзамену подготовиться, чтобы получить высокий результат, набрать максимальное количество баллов.
На первом же собрании знакомим родителей с нормативно-правовыми документами, со структурой экзамена, теми изменениями, которые произошли в этом учебном году, с порядком проведения экзамена, системой оценивания.
Родительские собрания проводим 1 раза в четверть. Со многими родителями совместно с детьми зачастую приходится встречаться и работать в индивидуальном порядке.
При подготовке к ОГЭ следует знать специфику класса и уровень знаний по предмету.
Для работы по подготовке к ОГЭ всех учащихся я разделила на 2 группы (можно и на 3), перед каждой поставила свои задачи.
|
1 группа |
2 группа |
|
Учащиеся, которые должны справиться с заданиями базового уровня и получить на экзамене «3». |
Учащиеся, которые должны справиться с заданиями базового уровня и более сложными заданиями. |
|
Задачи: |
|
|
1)должны выучить всю теорию; 2)научиться решать все типы заданий базового уровня; 3)на контрольных работах, тестах и зачетах не списывать. 4)если получена «2», то отработать(но не более 2 раз) |
1) должны выучить всю теорию; 2) научиться решать все типы заданий любой темы разными способами; 3) уметь объяснять, почему так решаешь; 4) уметь решать задачи на уравнения, проценты, прогрессии; 5) знать теорию геометрии и уметь решать задачи с параметрами. 6) если получишь «2»,«3» или «4», то отработать(но не более 1 раза); 7) посещать элективные курсы; |
Проведение дополнительных занятий по подготовке к ОГЭ:
-
консультации для слабых учащихся (решение 1 части);
-
консультации для сильных ребят (решение заданий 2 части);
-
индивидуальные консультации
На первых занятиях знакомлю учащихся с нормативно-правовыми документами, провожу инструктаж по правилам выполнения Кимов. Знакомлю с содержанием работ, их особенностями. На нескольких занятиях задания выполняем коллективно, с полным объяснением и записью на доске, прорешиваем несколько тестов (1 часть). При этом стараюсь знакомить с тем, как правильно читать задания, несколько раз прочитать вопрос задания. Стараюсь каждого ученика вызвать при этом к доске.
Систематическое включение в устную работу заданий из ОГЭ открытого банка задач части 1.
Включение в изучение текущего учебного материала заданий, соответствующих экзаменационным заданиям. На каждом уроке решаем и разбираем задания не только из учебника, но и задания, соответствующие теме задания из Кимов.
Использование в домашних заданиях материалов КИМов.
На протяжении первого полугодия домашнее задание задаю из открытого банка заданий КИМов: 4- 5 заданий из варианта. Те задания, которые вызвали затруднения, разбираем на доске.
Включение экзаменационных задач в содержание текущего контроля.
В контрольные и тестовые работы включаю задания из открытого банка задач. Обязательно добиваюсь того, чтобы ребята отработали задания, в которых допустили ошибки (иногда работу над ошибками приходиться выполнять по нескольку раз, пока задание не будет решено правильно).
Во время итогового повторения и изучения нового материала, начиная с 5 или 6 класса, ребята заполняли и использовали на уроках и дома тетрадь для правил (у каждой своей тетради), куда записывались основные формулы, правила и т.д. Она помогала при решении заданий, а при систематическом использовании в работе формулы и алгоритмы решений быстрее запоминались.
Проведение тематического повторения в течении года.
В сборниках для подготовки к ОГЭ есть много заданий по определённой теме, например, «Уравнения». Готовясь к уроку, учителю приходится искать задания по этой теме в разных источниках, что занимает много времени. Кроме того, повторять материал темы удобно, когда задания расположены в одном месте. Наиболее оптимальное решение — это тематические тесты.
Для этого из заданий открытого банка задач можно составить задания по прототипам (тематические тесты)и по результатам выполнения теста заполнять таблицу:
|
Ф.И. ученика |
Числа и вычисления |
Алгебраические выражения |
Уравнения и их системы |
Неравенства и их системы |
Функции |
Прогрессии |
Текстовые задачи |
|
теор |
прак |
теор |
прак |
теор |
прак |
теор |
и т.д. Такую же таблицу составляем по темам геометрии.
Для каждого ученика собираю папки с заданиями, в которые постепенно добавляю тематические тесты и демонстрационные варианты, работы пробного экзамена, которые писали ребята.
Повторения теоретического материала на обобщающих уроках с применением компьютерных технологий.
Уроки с применением презентаций зрелищны и эффективны в работе над информацией. Особенно, если это уроки повторения и обобщения материала определённой темы. Презентация обладает наглядностью и выразительностью, это прекрасное дидактическое и мотивационное средство, способствующее лучшему запоминанию учебного материала. При её систематическом использовании увеличивается продуктивность обучения. С помощью презентации можно повысить объём повторяемого материала и выполняемой работы. В работе использую свои презентации и презентации, созданные коллегами и представленные на различных образовательных сайтах в Интернете:
-
Интернет-сообщество учителей
-
Сеть творческих учителей
-
Фестиваль педагогических идей «Открытый урок»
-
Информационно-методический сайт
Систематическое повторение учебного материала начинаем с 4 четверти.
Итоговое повторение можно построить исключительно на отработке умений и навыков, требующихся для получения положительной отметки на экзамене.
Примерные экзаменационные работы беру из различных сборников для подготовки к ОГЭ (прошлых лет и новые с геометрическим материалом)
Кроме этого ребята могут проверить свои знания, решая примерные работы в режиме on-lain, а также работы, размещённые на сайте СтатГрада и СдамГИА.
Использование компьютерных презентаций на уроках математики и при подготовке к экзамену открывает огромные возможности:
компьютер может взять на себя функцию контроля знаний,
поможет сэкономить время на уроке для решения экзаменационных задач,
богато иллюстрировать материал,
трудные для понимания моменты показать в динамике,
повторить то, что вызвало затруднения,
дифференцировать урок в соответствии с индивидуальными особенностями учащихся,
быстро повторить теоретический материал.
Особенно эти презентации помогают при итоговом повторении теоретического материала по геометрии.1 часть работы содержит 5геометрических задания. Особенно трудно дается задания типа 13, которые содержат большой теоретический материал. Презентации помогают наглядно увидеть ответы на вопросы.
По данным исследований в памяти человека остаётся ¼ часть услышанного материала, 1/3 часть увиденного, ½ часть увиденного и услышанного, ¾ части материала, если ученик привлечён в активные действия в процессе обучения.
Систематическая работа по заполнению бланков. С заполнением бланков возникает много проблем, поэтому, чем раньше обучающиеся по ним начинают работать, тем меньше вероятность допущения ошибок в оформлении. На дополнительных занятиях разбираем все ошибки, которые были допущены при выполнении диагностических работ. Обращаю внимание на то, что каждая цифра и знак пишутся в отдельной клеточке, на правильность написания цифр, на то, что в ответах не пишут наименования, не ставят знаки %, не получают десятичную или неправильную дробь и т.д.ответы в тетрадях и на доске записываем в клеточках.
Решение большого числа тестов. С конца сентября в классе, на дополнительных занятиях и дома можно раздать для прорешивания большое количество тестов, желательно разные варианты. Ответы затем проверить и те задания, в которых была допущена ошибка, разобрать.
Подготовку решения заданий второй части можно начать со 2 четверти.
Для этого сначала можно использовать дополнительные занятия, на которые пригласить более подготовленных ребят. Можно дать домашнее задания из 2 части.
Конечно, подготовка к урокам, консультациям, проведение дополнительных занятий занимают много времени и сил, но, если правильно организовать свою деятельность и заинтересовать обучающихся в получении положительной оценки, то вся проведенная работа принесёт желаемый результат.
Лёгких путей в науку нет. Но необходимо использовать все возможности для того, чтобы дети учились с интересом, чтобы большинство подростков испытали и осознали притягательные стороны математики, её возможности в совершенствовании умственных способностей, в преодолении трудностей и успешно сдали экзамен.
Школьникам в девятом классе предстоит сдавать ОГЭ – государственные экзамены по четырем предметам. Обязательными являются русский язык и математика, а также каждый выпускник средней школы должен самостоятельно выбрать две дисциплины для сдачи. Форма этого экзамена очень напоминает ЕГЭ. Однако у девятиклассников это первый опыт сдачи серьезных экзаменов, поэтому и, дети, и родители, и учителя очень обеспокоены подготовкой. Из этой статьи вы узнаете, как наиболее эффективно подготовиться к ОГЭ.
Как подготовиться к ОГЭ с репетитором?
Многие нанимают репетиторов для подготовки к экзаменам. Действительно, дополнительные занятия могут помочь лучше усвоить школьный материал, ведь учитель в большом классе не всегда может уделить достаточно внимания каждому. Если вы решили готовиться к ОГЭ с помощью репетитора, возьмите на заметку несколько советов:
- Если хотите получить хороший результат, выбирайте в качестве репетиторов школьных учителей и преподавателей ВУЗов. Студенты или молодые специалисты, которые тоже нередко занимаются репетиторством, имеют мало навыков преподавания и зачастую не могут объяснить материал так же доступно и ясно, как более опытные специалисты. К тому же, подготовка к ОГЭ – это не просто занятия по предмету. Важно учитывать специфику данного теста, структуру вопросов и правильное заполнение бланков. Хорошо, если ваш репетитор уже готовил школьников к ОГЭ.
- Занятия с репетитором отнюдь не означают, что ребенок не должен учиться самостоятельно. Наиболее эффективные занятия с репетитором выстроены в формате консультаций по самостоятельно изученным темам – педагог может уточнить и объяснить отдельные моменты. Однако для полноценной подготовки пары часов в неделю с репетитором явно будет мало.
- Берите репетитора только по тем предметам, с которыми ребенок испытывает трудности. Если же школьник хорошо успевает по какому-то предмету самостоятельно, занятия могут только расслабить его, и он станет вкладывать меньше усилий в учебу.
- Если занятия выстроены таким образом, что репетитор просто выполняет за ученика домашние задания, это совершенно неверная тактика. Только посредством самостоятельной работы школьник приобретет глубокие знания по предмету и сможет продемонстрировать их на тесте.
Очень важно найти такого репетитора, с которым у ребенка возникнет контакт и взаимопонимание. Если ученику не будут нравиться занятия, подготовка будет менее эффективной. Хороший педагог всегда найдет способ заинтересовать в своем предмете – в этом случае результат не заставит себя долго ждать.
Как подготовиться к ОГЭ самостоятельно?
Очень многие обращаются к репетиторам из-за возрастающего ажиотажа перед экзаменами. Тем не менее, если на занятия нет лишних финансовых средств, подготовиться к ОГЭ можно и самостоятельно. Нередко такая подготовка оказывается даже более эффективной – если школьник рассчитывает только на себя, он вкладывает больше усердия задания. Если же какой-то вопрос кажется непонятным, с ним всегда можно подойти к школьному учителю. В целом же, самостоятельная подготовка может быть очень успешной. При ней важно учитывать следующие факторы:
- Самодисциплина очень важна при подготовке к ОГЭ без репетитора. Выпускники средней школы не всегда умеют грамотно распределять свое время. Поэтому родителям следует периодически следить за их подготовкой. Очень важно не откладывать все на последний месяц, а начать готовиться заблаговременно – хотя бы за год. Тогда знания будут действительно крепкими, а все пробелы за это время удастся заполнить.
- Лучше заниматься понемногу каждый день, чем по несколько часов раз в неделю. Так информация усваивается лучше. К тому же, так школьник не будет переутомляться. Иногда для обучения очень важно отвлечься на что-то другое, а затем вернуться к вопросу с новыми силами.
- У каждого из нас лучше развита та или иная форма памяти. У кого-то это визуальная память, а у кого-то – память на слух. В первом случае всю информацию важно записывать и отмечать разными маркерами, визуально разделять тему на блоки. Во втором случае следует больше проговаривать прочитанное вслух.
- Ассоциативный метод пригодится для запоминания дат, имен, терминов и формул. Например, формулу или дату можно связать с собственным днем рождения или с номером телефона, а для имени или термина придумайте рифму или визуальный образ. Весь объем информации так запомнить не получится, но это отличный способ выучить трудные для себя моменты.
Как психологически подготовиться к ОГЭ?
Первый настоящий экзамен – это серьезный стресс для школьников. Иногда даже отличники, которые хорошо знают предмет, получают низкие баллы на таком экзамене. Важны не только крепкие знания, но и правильный психологический настрой.
- Родительская поддержка очень важна. Не давите на ребенка по поводу экзамена – чаще хвалите его, напоминайте, как усердно он готовился, и выразите уверенность, что результат будет высоким.
- Очень мало школьников действительно проваливают экзамен. Зачастую баллы важны только тем, кто уходит в колледж. Тем, кто остается в школе, важно просто перейти определенный порог. Максимально высокие баллы здесь не так важны, как на ЕГЭ, поэтому не стоит волноваться – стоит воспринимать ОГЭ скорее как репетицию выпускных экзаменов.
- Многие преподаватели рекомендуют писать шпаргалки. Конечно, ими лучше не пользоваться, чтобы не отстранили от экзамена. Тем не менее, написанная информация не только позволяет лучше систематизировать знания в голове, но и придает определенное чувство спокойствия.
- Не нужно учиться в ночь перед экзаменом. Напротив, стоит отвлечься и хорошо выспаться.
ОГЭ – это первое серьезное испытание для школьников. Чтобы успешно сдать экзамены, готовиться надо начинать заранее. Подтянуть знания по предметам можно и с помощью репетитора, и самостоятельно – зачастую второй вариант оказывается даже более эффективным при должном родительском контроле. Однако главное – позитивный настрой и уверенность в своих силах. Учителям и родителям не следует паниковать по поводу экзаменов, ведь школьникам очень важна их поддержка.
Все прекрасно знают, насколько важно как можно лучше сдать государственную итоговую аттестацию после 9-го класса и Единый государственный экзамен после 11-го. От результатов ГИА зависит поступление в 10-й класс или учреждения среднего профессионального образования, а результаты ЕГЭ принимаются вузами как вступительные.
Когда же начинать к ним готовиться? В 9-м и 11-м классах? Нет, это очень поздно. Времени остается мало. Ведь проверяется весь объем знаний, полученный ко дню сдачи экзамена. Поэтому начинать готовиться к ним нужно намного раньше, класса с 5-6-го.
Для этого ребенок должен не только стараться качественно усваивать новый материал, но и ликвидировать имеющиеся пробелы в знаниях. Потому что перед экзаменом осилить такой огромный объем работы просто невозможно.
Откуда же берутся пробелы в знаниях? Причины разные и не всегда зависящие от детей.
Самая распространённая – пропуски уроков из-за болезни. Дома самостоятельно не всегда удается полностью понять новый материал.
Если уроков не было из-за учителя (заболел, на курсах и т.д.), пропущенная программа проходится быстрым темпом. В этом случае нет времени хорошо отработать на практических заданиях пройденное.
Кто-то из учеников не совсем понял новую тему на уроке. У многих низкая мотивация к учебе. А кто-то просто ленится, не желает напрягать свои силы, чтобы лучше учиться. Причин много.
Что же делать? Могут ли родители помочь ребенку? Да.
Прежде всего, постарайтесь обнаружить эти самые пробелы в знаниях. Как? Обратите внимание, какие ошибки ребенок допускает в диктантах, изложениях и других письменных работах, какие дополнительные задания не совсем уверенно делает (синтаксический, морфологический, фонетический разборы и т.д.)? Над этим и работайте. В конце концов, сколько же можно наступать на одни и те же грабли, допускать одни и те же ошибки и получать плохие оценки? Ведь это ведет к постоянным стрессам, неуверенности в своих силах, к ненависти к предмету.
Предложите учебный материал изучать в виде блоков, таблиц, опорных схем: усваивается быстрее и легче.
Систематически внимательно проверяйте выполнение домашней работы. Это способствует закреплению знаний, умений. Если заметили пробелы в знаниях ребенка, объясните, разберите сразу. Иначе это повлечет за собой непонимание следующего нового материала и в конце концов перерастет в большую проблему.
Уже в 5-6 классах можно выполнять проверку своих знаний в виде тестов. Купите или скачайте из интернета и решите их вместе с ребенком. Это не так и просто. Но экзамен-то обязателен для всех! И лучше потихоньку начать готовиться к нему заранее. Во-первых, такая форма самоподготовки учит школьника внимательности, собранности, аккуратности. Ведь надо не только вдумчиво прочитать вопрос, но и правильно понять, что от тебя требуется сделать, и быстро выполнить. Развивается орфографическая зоркость, вырабатывается привычка быстро выбирать нужное правило и применять его. Во-вторых, вы увидите слабые места в знаниях ребенка и, прочитав соответствующие правила и проработав их на тренировочных упражнениях, вы добьетесь безошибочного выполнения заданий. В-третьих, ребенок привыкает к такой форме проведения экзамена, и сдать его будет проще.
И, конечно же, нужно делать работу над допущенными ошибками. Не для учителя, формально, не вдумываясь, а осознанно, для себя. Раз допустил ошибку – значит, не знаешь соответствующее правило. И пока не выучишь и не потренируешься на практике его применять, эти ошибки будешь допускать.
Сына или дочь нужно как можно чаще поддерживать, подбадривать, тем самым укреплять его веру в свои силы и способности. Создать атмосферу успеха. Иначе ребенок может уйти в себя, во внутренний план. В этом случае он не слышит, что происходит в классе, не выполняет заданий, он пассивен, а учеба, приносящая одни неприятности, совсем не интересует.
Объективно относитесь к возможностям своего ребенка. Не требуйте от него больше, чем он может. Естественно, нужно как можно больше читать, тогда увеличивается словарный запас, запоминаются зрительные образы слов. Также важно воспитывать трудолюбие в ребенке, ведь умеющие трудиться дети даже при средних способностях добиваются больших положительных результатов, чем талантливые лентяи.
Нужно учить ребенка заниматься самостоятельно. Умение планировать свое время поможет выполнить все домашние работы вовремя, сходить на кружки, секции и погулять. Чтобы этому научиться, вначале можно записывать, сколько времени затрачивается на выполнение определенного задания.
Посмотрите, не перегружен ли рабочий день вашего ребенка. Помогите ему правильно распределить занятия и отдых. Кроме учебы, он еще должен и полноценно спать, бывать на воздухе и заниматься спортом.
Если занятий дома и в школе окажется все-таки мало, можно воспользоваться помощью квалифицированного репетитора и курсами в учреждениях дополнительного образования.
Стремительно приближается день сдачи общего обязательного экзамена для учащихся 9 классов — ГИА по математике, а значит, самое время подумать о подготовке к нему. Из этой статьи вы узнаете все о самых эффективных способах обучения — от подготовки с нуля, до различных вариантов дистанционных курсов. Учтите, что результат сдачи ГИА по математике заносится в аттестат о неполном среднем образовании, при этом необходимо получить положительную оценку («3» и выше) для перевода в 10 класс, а для того чтобы попасть в профильный физмат класс необходимо получить высокий балл. Если же ребенок собирается поступать в техникум, то при приеме будут учтены именно результаты этого тестирования. Поэтому будьте предельно серьезны в отношении общего государственного экзамена (ОГЭ). Итак, существуют следующие основные варианты подготовки к ГИА по математике:
- самостоятельная подготовка к ОГЭ (ГИА);
- обучение с репетитором;
- дистанционное обучение;
- гибридный вариант.
Как выбрать оптимальную форму обучения?
В первую очередь, следует оценить свои знания и возможности, а из проведенного анализа сделать выводы о стратегии подготовки к предстоящему ОГЭ. Рассмотрим возможность самостоятельного обучения для подготовки к сдаче ГИА по алгебре. Данный способ подходит для детей, отвечающих следующим критериям:
- отличник учебы (хотя бы по алгебре);
- наличие умения систематически и самостоятельно работать с учебными книгами по математике и онлайн материалом;
- наличие умения самостоятельно оценивать свои знания и ставить перед собой приоритетные учебные задачи.

Если вы чувствуете, что этот способ подготовки к ОГЭ (ГИА) хорошо вам подходит, то следующие 2 раздела целиком для вас. В противном случае, бегло ознакомьтесь с их содержанием и переходите к следующему.
Изучаем структуру ОГЭ (ГИА)
Во-первых, изучите структуру и правила проведения экзамена по математике (ОГЭ / ГИА). Хорошее понимание структуры позволит оптимально расставить учебные приоритеты и максимально эффективно распорядиться своим временем при самостоятельном обучении.
Все упражнения делятся на 2 части. В первой части находятся 20 задач базовой сложности, а во второй 4 повышенной и 2 — высокого уровня сложности (всего 6).
Каждое задание, в свою очередь, может относиться к одному из трех модулей: реальная математика, алгебра и геометрия. Структура частей:
- Первая часть ОГЭ представляет собой тесты базовой сложности, где экзаменуемому необходимо выбрать номер правильного варианта из перечисленных или вписать верный ответ в поле. В этой части присутствуют 8 задач из модуля «Алгебра», 5 из модуля «Геометрия» и все 7 задач из модуля «Реальная математика». На решение заданий этой части отводится 90 минут.
- Для получения максимально возможных баллов за упражнения второй части следует приводить развернутое решение вместе с правильным ответом. В этой части ОГЭ все упражнения относятся к модулям «Алгебра» и «Геометрия» по 3 варианта на каждый, среди которых по 1-ой высокого уровня и по 2 повышенной сложности, соответственно (итого 4 повышенной и 2 высокого уровня). На выполнение этой части предоставляется 150 минут.
Всего на решение всех 26 заданий отводится 4 часа реального времени.
Готовимся к основному государственному экзамену
Теперь, когда вы имеете представление о структуре ГИА по математике, следует заняться тематической подготовкой. Прорешайте несколько тестовых вариантов и десяток различных задач по алгебре 9 класса и получите представление о своих слабых и сильных сторонах по отдельным типам заданий. Начните последовательно изучать проблемные темы, уделяя больше времени самым сложным, на ваш взгляд, задачам. Напротив, когда вы будете сдавать настоящий экзамен, сначала как можно быстрее разберитесь с самыми простыми тестами и заданиями, оставляя как можно больше времени для наиболее сложных.
Одним из эффективных образовательных техник является ведение отдельной тетрадки с формулами по математике для подготовки к ГИА. Частое обращение к одним и тем же данным позволяет мозгу надолго запомнить необходимую информацию. Поэтому обязательно запишите и часто применяйте следующие формулы и таблицы, чтобы как можно лучше их усвоить (так как запрещено пользоваться любыми справочными материалами):
Для успешной подготовки выделяйте минимум 6 часов в неделю, при этом не реже 1 часа в 2 дня. Ваши когнитивные (интеллектуальные) способности всегда должны оставаться в тонусе, чтобы приобретенные знания по математике закреплялись максимально эффективно.
В целом, для самостоятельной подготовки вам достаточно будет иметь рабочий компьютер и подключение к сети Интернет. Все нужные учебные материалы по математике вы найдете на сайтах, в том числе и множество пробных заданий для самопроверки. Конечно, обычные учебники тоже будут полезны, а кому-то с ними и вовсе легче работать. Обратите внимание на сервис прохождения заданий ГИА прошлых лет от Яндекса https://ege.yandex.ru .
Подготовка со специалистом
Как правило, для большинства детей и людей вообще намного эффективнее работа со специалистом. Это может быть учитель в группе, индивидуальный репетитор или тьютор, не столько обучающий, сколько направляющий. Конечно, при выборе данного варианта услуги придется оплачивать, но зато и результат становится более прогнозируемым в лучшую сторону.
Если ребенок имеет хорошие оценки по алгебре и геометрии, понимает большинство тем, то все что ему нужно — это больше практики в решении задач и укрепление теоретических знаний по некоторым разделам. В этом случае отличным вариантом будут групповые занятия. Во-первых, они обойдутся заметно дешевле. Во-вторых, если группа подобрана не «разношерстная», а состоит из детей одного уровня математического развития, то сама среда станет хорошим мотиватором.
Вариант подбора репетитора становится единственным, если ребенок в связи с различными обстоятельствами вынужден готовиться с нуля к ОГЭ или ГИА по математике. Причем необходима именно индивидуальная траектория. Подготовка в группе малоэффективна для неуспевающих по тем или иным дисциплинам. Им нужен уникальный подход, учитывающий особенности характера и развития.
Кого и как выбрать

На сегодняшний день существует множество онлайн порталов по подбору репетиторов по математике, среди которых можно найти преподавателей и профессоров именитых вузов, и вы можете выбрать, например, репетитора работающего в том институте, куда планирует поступать ваш ребенок. На этих онлайн порталах вы можете подобрать специалиста из своего города для очных занятий или же отдать предпочтение дистанционным урокам. С точки зрения психологии детей, эффективнее будет проходить очное обучение, но, как правило, оно стоит дороже. Для дистанционных курсов подготовки к ГИА должны быть навыки опытного пользователя компьютера, регулярный доступ в интернет и вебкамера.
Внимательно изучайте резюме репетиторов размещенное на сайтах. На первой встрече с репетитором, вне зависимости от того где она проходит, в онлайне или в реальности, обязательно присутствие и ученика и родителя. Родителю важно прочувствовать, как взрослому человеку, педагогические навыки кандидата.
Обратите внимание на четкость дикции, свойства личности в личном общении и оцените общий внешний вид. Репетитор должен излучать спокойствие и уверенность в себе, как в педагоге, выглядеть опрятно и чисто.
Особенно будьте внимательны к тем, на чьем лице выражается долгая общая усталость, тревога или волнение. Человек с нерешенными личными проблемами, как правило, не может работать на полную отдачу, ведь его беспокоят другие мысли.

После встречи с репетитором спросите у сына или дочери о его впечатлениях. Очень важно, чтобы ребенок не нашел ничего отталкивающего в личности преподавателя. Личное доверие и уважение между учеником и педагогом будет залогом эффективного обучения и получения высокого балла на ОГЭ. Обобщая сказанное, еще раз отметим важные нюансы, на которые следует обратить внимание при организации процесса подготовки слушателя к важному экзамену:
- уровень начальной подготовки по математике;
- его психологические возможности к обучению. Чем меньше способность воспитанника к обучению, тем большим профессионалом должен быть учитель;
- доступная информация от знакомых о репетиторах вашего населенного пункта;
- способность обучающегося к интернет-обучению;
- способность слушателя к эффективному обучению в группе.
Найти репетитора для очных или онлайн занятий вы сможете, перейдя по следующим ссылкам:
Специализированные курсы

Проверка динамики обучения может выполняться специалистом. Для этого ребенок должен раз в неделю (или по другому графику) выполнять задания в режиме онлайн или прикреплять файл со сделанной работой на специальной форме сдачи результатов. Иногда можно получать комментарии от преподавателя по решенным задачам с указанием на темы, которые следует повторить. Цены на такие курсы чаще всего отличаются демократичностью, так как подготовка ведется в группах, а основную часть практической работы ребенок выполняет самостоятельно. Обучение ведется системно, требуется выполнение домашних работ, что создает мета-конструкцию для оптимального распределения времени и усилий.
Чтобы понять, что собой представляют универсальные курсы, рассмотрим структуру курса «Математика. Подготовка к ОГЭ (ГИА), 9 класс », который можно пройти на портале оказания образовательных услуг http://foxford.ru за разумную плату.
Как уже упоминалось выше, Фоксфорд выдает сертификат по любому из своих курсов и даже ГИА по математике не стал исключением. Этот сертификат не несет никакой функциональной пользы, так как не принимается в расчёт государственными учреждениями, но ребенку будет приятно.
Подводя итоги, следует сказать, что образование в молодом возрасте сказывается самым фундаментальным образом на развитии и успешности личности, поэтому выбирать и организовывать курсы подготовки к ОГЭ по математике для своих детей надо самым тщательнейшим образом. Учитывайте все нюансы, разбирайтесь в различных подходах в педагогике, внимательно прочувствуйте и серьезно относитесь к потребностям детей — только таким образом вы сможете помочь ему пройти первую, несамостоятельную часть его жизни.
Учащимся сегодня следует приложить немало усилий, чтобы выдержать и успешно сдать все итоговые экзамены по окончании основной школы. Хороший результат – это возможность продолжить обучение в профильных школах.
Скачать:
Предварительный просмотр:
Как подготовиться к ОГЭ?
Такой способ проверки знаний учащихся, как ЕГЭ и ОГЭ, появился сравнительно недавно. Некоторые выпускники и их родители ошибочно полагают, что единый экзамен гораздо важнее, нежели основной госэкзамен, который сдают учащиеся 9-х классов. На самом же деле итоговая оценка по русскому языку, например, выставляется в аттестат, основываясь не только на результатах итогового экзамена, но и на годовой отметке за 9 класс.
А это значит, что готовиться к ОГЭ следует не меньше, а так же серьезно, как и к ЕГЭ. Стоит отметить, что несколько последних лет ходят слухи о том, что вполне возможно введение конкурса аттестатов выпускников при поступлении в тот или иной ВУЗ.
Учащимся сегодня следует приложить немало усилий, чтобы выдержать и успешно сдать все итоговые экзамены по окончании основной школы. Хороший результат – это возможность продолжить обучение в профильных школах.
Чтобы прийти к намеченной цели с хорошими результатами, необходимо сделать следующее:
Во-первых, ученику стоит пройти тестирование по результатам обучения в 8-ом классе, чтобы объективно оценить уровень своих знаний;
Во-вторых, следует определиться со своими интересами и, учитывая результаты тестирования, выбрать то направление, в котором бы будущий выпускник хотел продолжить обучение (будь то колледж, лицей или профильная школа);
В-третьих, было бы неплохо составить для себя план подготовки к экзаменам по определенным предметам, которые необходимо сдать для поступления в профильное образовательное учреждение;
В-четвертых, следует продумать стратегию подготовки (например, можно записаться и посещать курсы подготовки)
Как же правильно самостоятельно подготовиться к сдаче ОГЭ?
Ученикам вполне могут оказаться полезными следующие советы:
Из сборника с тестовыми заданиями следует выбрать один вариант и попробовать его решить;
Над каждой ошибкой провести скрупулезную работу, повторив тему, к которой она относится;
Проштудировать все темы, по которым у ученика возникают вопросы;
Следующий шаг подготовки – это выбор из сборника заданий другого варианта с целью еще раз себя проверить;
Если с каким-то заданием справиться не удается, учащемуся следует обратиться за помощью и разъяснениями к учителю;
При подготовке не стоит сразу после прочтения задания сверяться с правильными ответами, так как запомнить их все невозможно;
В процессе повторения любой темы очень важно, чтобы ученик понимал суть материала, над которым он работает;
Не стоит тратить время на зубрежку изученного материала, вполне достаточно уловить смысл ключевых моментов.
Учащимся 9-х классов будет нелишним прислушаться и к некоторым простым рекомендациям:
1. Перед тем, как начинать работу по подготовке к экзамену, стоит расслабиться и не нервничать. Такой подход поможет лучше сосредоточиться на главном.
2. Чтобы на экзамене для выпускника не было неожиданностей, следует заранее ознакомиться с процедурой экзамена. Выполнение тренировочных заданий при подготовке поможет сориентироваться и правильно рассчитать время на выполнение того или иного задания. Учащимся стоит заранее узнать все правила по заполнению бланков.
3. При подготовке не следует перенапрягаться и подолгу заниматься однообразной и монотонной работой, так как внимание начнет довольно быстро рассеиваться. Умственную деятельность следует разбавлять двигательной активностью. Чтобы не переутомляться, неплохо делать небольшие перерывы для прогулок на свежем воздухе.
4. Пейте больше жидкости! Это способствует улучшению активной работы мозга. Полезно пить простую воду или минеральную, можно и зеленый чай. При этом не забывайте правильно питаться.
5. Если вы чувствуете, что ваши умственные нагрузки значительно увеличились, то будет неплохо увеличить и время сна (хотя бы на час).
Для получения аттестата школьнику необходимо сдать минимум 4 экзамена. Сюда относятся 2 обязательных (русский язык и математика), а также и 2 предмета на выбор из 12 предлагаемых дисциплин (литература, информатика, биология, география, физика, химия, иностранные языки и др.).
С выбором предметов затягивать не стоит, определиться лучше как можно быстрее, чтобы было больше времени для подготовки. Выбранные дисциплины будут также необходимы для обучения в 10-11 классах или в других учебно-образовательных учреждениях.
Попробовать свои силы и выполнить задания по ОГЭ ученики могут и при помощи сети Интернет, после чего необходимо проделать работу над ошибками и уделить больше внимания тем темам, по которым есть какие-то пробелы. Чтобы реально оценить уровень подготовки, ученику не стоит пользоваться подсказками на пробном тестировании.
До ОГЭ остается чуть
больше трех месяцев. Пора приступать к подготовке, если до сих пор не сделал
этого. Как правильно распределить время и, с чего начать, даже если очень не
хочется, узнали у экспертов центра «Феномен».
До ОГЭ три месяца:
В первую очередь надо
прорешать тесты по тем предметам, которые сдаешь. Так ты разберешься, в чем силен,
а в чем нет. Если результат неутешительный, не переживай, еще есть время
наверстать упущенное.
Составь план, в какие дни,
и что ты изучаешь. Это поможешь грамотно распределить время. Важно! Не ставь
подготовку к двум разным предметам на один день, иначе в голове произойдет путаница,
и забудешь все.
До ОГЭ два месяца:
Убери все яркое в комнате
с видных мест. Для того чтобы тебя не отвлекали резкие цвета, и ты мог спокойно
готовиться к экзамену, лучше исключить раздражители. После того, как сдашь,
достанешь все из шкафа.
Начни вести конспекты с
основной информацией по тем темам, в которых часто встречаются ошибки. Не переписывай
все. Только самое важное.
До ОГЭ месяц:
Все даты, формулы и
термины выпиши на отдельные карточки, чтобы обращаться к ним в любой момент. Кроме
того, на экзамене у тебя может сработать визуальная память, а накануне будет
удобно повторять материал.
До ОГЭ неделя:
Бегло перечитай конспекты
и внимательно изучи карточки, которые писал ранее.
Если ты все еще не готов,
можешь паниковать.
Завтра ОГЭ:
Перед сном еще раз повтори
даты, формулы и термины.
Ляг спать пораньше, а под
подушку положи конспекты и карточки.
Если ты все еще не готов,
постарайся не волноваться, а надейся на удачу.
До ОГЭ остается чуть
больше трех месяцев. Пора приступать к подготовке, если до сих пор не сделал
этого. Как правильно распределить время и, с чего начать, даже если очень не
хочется, узнали у экспертов центра «Феномен».
До ОГЭ три месяца:
В первую очередь надо
прорешать тесты по тем предметам, которые сдаешь. Так ты разберешься, в чем силен,
а в чем нет. Если результат неутешительный, не переживай, еще есть время
наверстать упущенное.
Составь план, в какие дни,
и что ты изучаешь. Это поможешь грамотно распределить время. Важно! Не ставь
подготовку к двум разным предметам на один день, иначе в голове произойдет путаница,
и забудешь все.
До ОГЭ два месяца:
Убери все яркое в комнате
с видных мест. Для того чтобы тебя не отвлекали резкие цвета, и ты мог спокойно
готовиться к экзамену, лучше исключить раздражители. После того, как сдашь,
достанешь все из шкафа.
Начни вести конспекты с
основной информацией по тем темам, в которых часто встречаются ошибки. Не переписывай
все. Только самое важное.
До ОГЭ месяц:
Все даты, формулы и
термины выпиши на отдельные карточки, чтобы обращаться к ним в любой момент. Кроме
того, на экзамене у тебя может сработать визуальная память, а накануне будет
удобно повторять материал.
До ОГЭ неделя:
Бегло перечитай конспекты
и внимательно изучи карточки, которые писал ранее.
Если ты все еще не готов,
можешь паниковать.
Завтра ОГЭ:
Перед сном еще раз повтори
даты, формулы и термины.
Ляг спать пораньше, а под
подушку положи конспекты и карточки.
Если ты все еще не готов,
постарайся не волноваться, а надейся на удачу.
Как известно, экзамен — не просто проверка знаний, а проверка знаний в условиях стресса. В то же время среди медиков существует точка зрения, что до 90 % всех заболеваний могут быть связаны со стрессом. Отсюда можно сделать вывод, что экзамены здоровья отнюдь не прибавляют, а даже наоборот. Действительно, многочисленные исследования показывают, что во время подготовки и сдачи экзаменов имеют место интенсивная умственная деятельность, крайнее ограничение двигательной активности, нарушение режима отдыха и сна (поверхностный, беспокойный сон), эмоциональные переживания. Все это приводит к перенапряжению нервной системы, отрицательно влияет на общее состояние и сопротивляемость растущего организма.
Сущность психофизиологической стрессовой реакции заключается в подготовительной активации, создающей готовность к физическому напряжению, а именно эта физическая деятельность исключена обстановкой экзамена.
Что же нужно принимать во внимание, для того чтобы успешно, без ущерба для здоровья преодолеть период подготовки и сдачи экзаменов?
Подготовка к экзамену
- Сначала подготовь место для занятий: убери со стола лишние вещи, удобно расположи нужные учебники, пособия, тетради, бумагу, карандаши и т.п.
- Можно ввести в интерьер комнаты желтый и фиолетовый цвета, поскольку они повышают интеллектуальную активность. Для этого бывает достаточно какой-либо картинки в этих тонах или эстампа.
- Составь план занятий. Для начала определи: кто ты — «сова» или «жаворонок», и в зависимости от этого максимально используй утренние или вечерние часы. Составляя план на каждый день подготовки, необходимо четко определить, что именно сегодня будет изучаться. Не вообще: «немного позанимаюсь», а какие именно разделы и темы.
- Начни с самого трудного, с того раздела, который знаешь хуже всего. Но если тебе трудно «раскачаться», можно начать с того материала, который тебе больше всего интересен и приятен. Возможно, постепенно войдешь в рабочий ритм, и дело пойдет.
- Чередуй занятия и отдых, скажем, 40 минут занятий, затем 10 минут — перерыв. Можно в это время помыть посуду, полить цветы, сделать зарядку, принять душ.
- Не надо стремиться к тому, чтобы прочитать и запомнить наизусть весь учебник. Полезно структурировать материал за счет составления планов, схем, причем желательно на бумаге. Планы полезны и потому, что их легко использовать при кратком повторении материала.
- Выполняй как можно больше различных опубликованных тестов по этому предмету. Эти тренировки ознакомят тебя с конструкциями тестовых заданий.
- Тренируйся с секундомером в руках, засекай время выполнения тестов (на заданиях в части А в среднем уходит по 2 минуты на задание).
- Готовясь к экзаменам, никогда не думай о том, что не справишься с заданием, а напротив, мысленно рисуй себе картину триумфа.
- Оставь один день перед экзаменом на то, чтобы вновь повторить все планы ответов, еще раз остановиться на самых трудных вопросах.
Накануне экзамена
- Многие считают: для того, чтобы полностью подготовиться к экзамену, не хватает всего одной, последней перед ним ночи. Это неправильно. Ты уже устал, и не надо себя переутомлять. Напротив, с вечера перестань готовиться, прими душ, соверши прогулку. Выспись как можно лучше, чтобы встать отдохнувшим, с ощущением своего здоровья, силы, «боевого» настроя. Ведь экзамен — это своеобразная борьба, в которой нужно проявить себя, показать свои возможности и способности.
- В пункт сдачи экзамена ты должен явиться, не опаздывая, лучше за полчаса до начала тестирования. При себе нужно иметь пропуск, паспорт (не свидетельство о рождении) и несколько (про запас) гелевых или капиллярных ручек с черными чернилами.
- Если в школе холодно, не забудь тепло одеться, ведь ты будешь сидеть на экзамене 3 часа.
Во время тестирования
- В начале тестирования вам сообщат необходимую информацию (как заполнять бланк, какими буквами писать, как кодировать номер школы и т.д.). Будь внимателен!!! От того, как ты внимательно запомнишь все эти правила, зависит правильность твоих ответов!
- Бланк ответов (область регистрации, сами ответы и пр.) ты заполняешь только печатными буквами! Обрати внимание на то, как пишутся некоторые буквы, например, буква «а». Часть информации записывается в кодированной форме, которую тебе скажут перед началом тестирования.
- Экзаменационные материалы состоят из трех частей: А, В, С:
- в заданиях части А нужно выбрать правильный ответ из нескольких предлагаемых вариантов. В первой части бланков ответов с заголовком «Номера заданий с выбором ответа из предложенных вариантов» ты должен под номером задания пометить знаком «Х» ту клеточку, номер которой соответствует номеру выбранного ответа.
- в заданиях части В ответ дается в виде одного слова или числа. В бланке ответов для таких заданий есть поля с заголовком «Краткие ответы на задания без вариантов ответа для выбора», куда ты аккуратно вписываешь свой ответ (слово или число) рядом с номером задания (печатными буквами). Запись формул или математических выражений, каких-либо словесных заголовков или комментариев не допускается.
- в заданиях части С дается развернутый ответ в виде решения задачи или краткого рассказа, которые записываются на отдельном бланке. Очень важно переписать в специальное поле в правом верхнем углу указанного бланка индивидуальный номер основного бланка ответов (розового цвета). При этом никакие дополнительные сведения о вас (фамилия, имя, класс) не пишутся.
- Исправления в бланке ответов крайне нежелательны. Если все-таки исправления неизбежны, то помни, что их можно делать только в заданиях типа А, используя резервные поля с заголовком «Отмена ошибочных меток». Исправления делаются только по инструкции организаторов. Количество допускаемых исправлений — не больше шести.
- В процедуре заполнения бланков возможны некоторые изменения, о которых вас обязательно проинформируют.
- При получении результатов тестирования ты имеешь право ознакомиться с проверенной работой и, если не согласен с оценкой, можешь подать апелляцию (в течение 3 дней после объявления результата) в конфликтную комиссию.
Приведем несколько универсальных рецептов для более успешной тактики выполнения тестирования.
- Сосредоточься! После выполнения предварительной части тестирования (заполнения бланков), когда ты прояснил все непонятные для себя моменты, постарайся сосредоточиться и забыть про окружающих. Для тебя должны существовать только текст заданий и часы, регламентирующие время выполнения теста. Торопись не спеша! Жесткие рамки времени не должны влиять на качество твоих ответов. Перед тем, как вписать ответ, перечитай вопрос дважды и убедись, что ты правильно понял, что от тебя требуется.
- Начни с легкого! Начни отвечать на те вопросы, в знании которых ты не сомневаешься, не останавливаясь на тех, которые могут вызвать долгие раздумья. Тогда ты успокоишься, голова начнет работать более ясно и четко, и ты войдешь в рабочий ритм. Ты как бы освободишься от нервозности, и вся твоя энергия потом будет направлена на более трудные вопросы.
- Пропускай! Надо научиться пропускать трудные или непонятные задания. Помни: в тексте всегда найдутся такие вопросы, с которыми ты обязательно справишься. Просто глупо недобрать очков только потому, что ты не дошел до «своих» заданий, а застрял на тех, которые вызывают у тебя затруднения.
- Читай задание до конца! Спешка не должна приводить к тому, что ты стараешься понять условия задания «по первым словам» и достраиваешь концовку в собственном воображении. Это верный способ совершить досадные ошибки в самых легких вопросах.
- Думай только о текущем задании! Когда ты видишь новое задание, забудь все, что было в предыдущем. Как правило, задания в тестах не связаны друг с другом, поэтому знания, которые ты применил в одном (уже, допустим, решенном тобой), как правило, не помогают, а только мешают сконцентрироваться и правильно решить новое задание. Этот совет дает тебе и другой бесценный психологический эффект — забудь о неудаче в прошлом задании (если оно оказалось тебе не по зубам). Думай только о том, что каждое новое задание — это шанс набрать очки.
- Исключай! Многие задания можно быстрее решить, если не искать сразу правильный вариант ответа, а последовательно исключать те, которые явно не подходят. Метод исключения позволяет в итоге сконцентрировать внимание всего на одном-двух вариантах, а не на всех пяти-семи (что гораздо труднее).
- Запланируй два круга! Рассчитай время так, чтобы за две трети всего отведенного времени пройтись по всем легким заданиям («первый круг»). Тогда ты успеешь набрать максимум очков на тех заданиях, а потом спокойно вернуться и подумать над трудными, которые тебе вначале пришлось пропустить («второй круг»).
- Проверь! Оставь время для проверки своей работы, хотя бы, чтобы успеть пробежать глазами и заметить явные ошибки.
- Угадывай! Если ты не уверен в выборе ответа, но интуитивно можешь предпочесть какой-то ответ другим, то интуиции следует доверять! При этом выбирай такой вариант, который, на твой взгляд, имеет большую вероятность.
- Не огорчайся! Стремись выполнить все задания, но помни, что на практике это нереально. Учитывай, что тестовые задания рассчитаны на максимальный уровень трудности, и количество решенных тобой заданий вполне может оказаться достаточным для хорошей оценки.
Опубликовано в
Изучение материала без помощи репетиторов и опытных учителей имеет не только ряд преимуществ, но и связано с определенными сложностями. Отказаться от репетитора целесообразно, если:
- Вы не испытываете трудностей с пониманием предмета. Возможно, некоторые темы вы просто пропускали из-за болезней, из-за чего в знаниях образовались пробелы, или часть материала пропускалась самим учителем, который давал темы на домашнее рассмотрение.
- Вы знаете предмет в целом хорошо и хотите освежить знания. Даже если в вашем табеле всегда красовались отличные отметки, не пренебрегайте подготовкой к экзамену. За несколько лет часть информации забывается, и вспомнить ее совсем не будет лишним. К тому же, сделать это самостоятельно довольно просто.
- Вам смогут помочь. Родители-учителя или преподаватели или даже одноклассники-отличники, которым не жаль потратить полчаса на объяснение сложной темы очень помогут вам. Если вы уверены, что с основной массой материала справитесь самостоятельно, а со сложными темами вам помогут, смело выбирайте самостоятельную подготовку.
Начинайте готовиться заранее, не откладывайте все на последние недели. Конец года – и без того напряженный период, вам придется писать контрольные, выполнять индивидуальные задания и многие другие виды работы, и времени на подготовку будет очень мало. Кроме того, усваивать информацию лучше небольшими частями, вникая в каждое правило и формулу.
Занимайтесь регулярно. Лучше выделять 1-2 часа каждый день, чем посвящать подготовке все выходные и просиживать за компьютером много часов подряд. Не забывайте, мозг может работать эффективно не более 40-45 минут, после чего нужно обязательно делать перерыв. Если вы попытаетесь «догнать» все пропущенные в течение недели занятия за один день, прочитанный материал забудется очень быстро.
Не забывайте о повторении. Лучше всего повторять материал дважды – через 6 часов после изучения и на следующий день. Повторяйте и вспоминайте лишь ключевые сведения, и вы не забудете их до дня экзамена.
Занимайтесь в спокойной, тихой обстановке, не отвлекайтесь на какие-либо домашние дела, сосредоточьтесь.
Как подготовиться к ОГЭ самостоятельно: какие материалы нужны?
Прежде всего, позаботьтесь о матчасти и запаситесь всеми необходимыми материалами, которыми будете пользоваться.
Не стоит сразу отправляться в библиотеку и просить учебники за прошлые года, они вряд ли вам помогут. Дело в том, что материал в них изложен с пространными объяснениями, на изучение которых будет уходить масса времени. К тому же, программа ОГЭ ежегодно меняется, некоторые тему пропускаются. В учебниках вам придется учить и повторять все подряд, даже то, что может совсем не пригодиться на экзамене.
Отличной альтернативой учебникам станут специальные пособия по подготовке. Материал в них изложен сжато, по сути, выделены основные понятия, формулы, даты, правила и другая ключевая информация. Часто текст сопровождается таблицами, диаграммами, схемами и другими графическими составляющими, которые упрощают процесс систематизации и запоминания сведений.
Кроме пособий и сборников с теоретической частью, вам понадобятся материалы для практики. Совсем не лишним будет потренироваться решать тесты и задачи, отвечать на письменные вопросы и писать сочинения, то есть выполнять такие виды заданий, с которыми придется столкнуться во время тестирования.
Полная база материалов для подготовки на сайте «сайт»
Чтобы не тратить лишние деньги и время на поиски и покупку всех необходимых пособий и сборников с тренировочными заданиями, зарегистрируйтесь на сайте «сайт». Здесь вас ждет полная база материалов, которые помогут при подготовке к ОГЭ по всем предметам:
- Русскому языку и литературе
- Английскому, испанскому, французскому, немецкому языку
- Химии
- Физике
- Биологии
- Обществознанию
- Истории
- Математике
- Географии
- Информатике
Мы собрали для своих пользователей все необходимые материалы:
- Теоретические пособия, в которых собрана текстовая информация, таблицы, схемы, диаграммы, графики, карты, изображения и многое другое.
- Практические задания, в числе которых – тесты, задачи, примеры, открытые задания с самостоятельной формулировкой правильного ответа, пересказы, сочинения и прочие.
Все материалы на сайте «сайт» разбиты на отдельные разделы, соответствующие предметам, и систематизированы по темам. Благодаря этому вы сможете легко найти нужную информацию и готовиться самостоятельно максимально эффективно.
Если вы готовитесь к ЕГЭ, предлагаем вашему вниманию онлайн подготовку — , что сэкономит вам время и деньги.
Такой способ проверки знаний учащихся, как ЕГЭ и ОГЭ, появился сравнительно недавно. Некоторые выпускники и их родители ошибочно полагают, что единый экзамен гораздо важнее, нежели основной госэкзамен, который сдают учащиеся 9-х классов. На самом же деле итоговая оценка по русскому языку, например, выставляется в аттестат, основываясь не только на результатах итогового экзамена, но и на годовой отметке за 9 класс.
А это значит, что готовиться к ОГЭ следует не меньше, а так же серьезно, как и к ЕГЭ. Стоит отметить, что несколько последних лет ходят слухи о том, что вполне возможно введение конкурса аттестатов выпускников при поступлении в тот или иной ВУЗ.
Учащимся сегодня следует приложить немало усилий, чтобы выдержать и успешно сдать все итоговые экзамены по окончании основной школы. Хороший результат — это возможность продолжить обучение в профильных школах.
Чтобы прийти к намеченной цели с хорошими результатами, необходимо сделать следующее:
Во-первых, ученику стоит пройти тестирование по результатам обучения в 8-ом классе, чтобы объективно оценить уровень своих знаний;
Во-вторых, следует определиться со своими интересами и, учитывая результаты тестирования, выбрать то направление, в котором бы будущий выпускник хотел продолжить обучение (будь то колледж, лицей или профильная школа);
В-третьих, было бы неплохо составить для себя план подготовки к экзаменам по определенным предметам, которые необходимо сдать для поступления в профильное образовательное учреждение;
В-четвертых, следует продумать стратегию подготовки (например, можно записаться и посещать курсы подготовки)
Как же правильно самостоятельно подготовиться к сдаче ЕГЭ? Ученикам вполне могут оказаться полезными следующие советы:
Из сборника с тестовыми заданиями следует выбрать один вариант и попробовать его решить;
Над каждой ошибкой провести скрупулезную работу, повторив тему, к которой она относится;
Проштудировать все темы, по которым у ученика возникают вопросы;
Следующий шаг подготовки — это выбор из сборника заданий другого варианта с целью еще раз себя проверить;
Если с каким-то заданием справиться не удается, учащемуся следует обратиться за помощью и разъяснениями к учителю;
При подготовке не стоит сразу после прочтения задания сверяться с правильными ответами, так как запомнить их все невозможно;
В процессе повторения любой темы очень важно, чтобы ученик понимал суть материала, над которым он работает;
Не стоит тратить время на зубрежку изученного материала, вполне достаточно уловить смысл ключевых моментов.
Учащимся 9-х классов будет нелишним прислушаться и к некоторым простым рекомендациям:
1. Перед тем, как начинать работу по подготовке к экзамену, стоит расслабиться и не нервничать. Такой подход поможет лучше сосредоточиться на главном.
2. Чтобы на экзамене для выпускника не было неожиданностей, следует заранее ознакомиться с процедурой экзамена. Выполнение тренировочных заданий при подготовке поможет сориентироваться и правильно рассчитать время на выполнение того или иного задания. Учащимся стоит заранее узнать все правила по заполнению бланков.
3. При подготовке не следует перенапрягаться и подолгу заниматься однообразной и монотонной работой, так как внимание начнет довольно быстро рассеиваться. Умственную деятельность следует разбавлять двигательной активностью. Чтобы не переутомляться, неплохо делать небольшие перерывы для прогулок на свежем воздухе.
4. Пейте больше жидкости! Это способствует улучшению активной работы мозга. Полезно пить простую воду или минеральную, можно и зеленый чай. При этом не забывайте правильно питаться.
5. Если вы чувствуете, что ваши умственные нагрузки значительно увеличились, то будет неплохо увеличить и время сна (хотя бы на час).
Для получения аттестата школьнику необходимо сдать минимум 4 экзамена. Сюда относятся 2 обязательных (русский язык и математика), а также и 2 предмета на выбор из 12 предлагаемых дисциплин (литература, информатика, биология, география, физика, химия, иностранные языки и др.).
С выбором предметов затягивать не стоит, определиться лучше как можно быстрее, чтобы было больше времени для подготовки. Выбранные дисциплины будут также необходимы для обучения в 10-11 классах или в других учебно-образовательных учреждениях.
Попробовать свои силы и выполнить задания по ОГЭ ученики могут и при помощи сети Интернет, после чего необходимо проделать работу над ошибками и уделить больше внимания тем темам, по которым есть какие-то пробелы. Чтобы реально оценить уровень подготовки, ученику не стоит пользоваться подсказками на пробном тестировании.
Для того чтобы продолжить обучение в школе в 10-11 классах или поступить в колледж, ученику 9 класса необходимо сдать выпускные экзамены, в том числе и ОГЭ по математике. Статистика показала, что большинство выпускников выбирают для сдачи гуманитарные предметы. Но что же делать, когда одним из обязательных предметов для сдачи экзамена является математика? Наша статья вам расскажет, как подготовиться к ОГЭ по математике. Итак, в путь, друзья.
Структура по математике
Так исторически сложилось, что год от года структура контрольно-измерительных материалов по разным предметам изменяется организаторами. Пока сложно сказать, зачем это нужно. Министерство образования решило, что в 2017 году ОГЭ по математике будет состоять из трех модулей:
- алгебра;
- геометрия;
- реальная математика.
Каждая часть разделена на уровни сложности. Чем тяжелее уровень, тем больше начисляется баллов за правильный ответ. Всего на экзамене придется решить 26 заданий. К базовому уровню относятся 20 заданий, еще 6 вопросов относятся к повышенному и высокому уровню сложности.
Таким образом, на выполнение данных заданий выпускнику отводится 235 минут или 3 часа 55 минут.
Эти особенности необходимо знать для того, чтобы понимать, как подготовиться к ОГЭ по математике. Во время подготовки необходимо правильно распределить время для выполнения тех или иных заданий.
Кто рано встает, тот легко ОГЭ сдает
Безусловно, подготовка к ОГЭ по математике в 9 классе должна начаться как можно ранее. Опытные педагоги советуют детям и родителям заблаговременно уделять внимание этому предмету, начиная с 5 класса. Первым делом необходимо посетить официальную страницу ФИПИ в сети Интернет. На сайте педагоги, родители, а также ученики найдут массу полезной информации. Оттуда же можно скачать демоверсии вариантов ОГЭ по математике.
Таким образом, вы заранее будете знать, какие темы будут на экзамене и какие разделы по математике нужно «подтянуть».
На том же сайте можно скачать документ под названием «Спецификация», в котором будут указаны задания и назначенное количество баллов за правильный ответ. Поэтому выпускник с легкостью может самостоятельно предварительно определить, сможет ли он успешно сдать экзамен.
Первый и один из важнейших критериев успешной сдачи ОГЭ — заблаговременная подготовка!
Помощь репетитора или самостоятельные занятия?
Многие задумываются: «Как подготовиться к ОГЭ по математике?» Реально ли это сделать самостоятельно или нужна помощь репетитора? Ответить на этот вопрос может только ученик, опираясь на внутренние ощущения. Но и родительский взгляд со стороны тоже будет полезен. Ведь каждый ответственный родитель знает, какие предметы его ребенку в школе даются легко, а какие с трудом.
Стоит отметить, если работа по подготовке к ОГЭ по математике будет проходить с репетитором, то это значит, что она будет систематической. Сможете ли вы без посторонней помощи также регулярно готовиться к тестированию? Подготовка к экзамену с другом — это ошибка. Все полезное время уйдет на разговоры.
Помните, что 30% заданий ОГЭ по математике будут связаны с темами, которые изучаются детьми только в 9 классе. Ученикам придется отрабатывать ранее пройденные темы, а также новый материал!
Итак, второй важный критерий — это регулярность и систематичность.
Добросовестность
Мы живем в век информационных технологий, а это говорит о том, что 80% интересующей нас информации можно с легкостью найти в интернете. Надеяться на списывание на экзамене не стоит. Чтобы успешно подготовиться к тестированию, необходимо искать необходимые данные и решать задания к ОГЭ по математике. Не обманывайте сами себя. Не списывайте. Эта ошибка дорого стоит!
Третий критерий — добросовестность.
Источники информации
Если у будущего выпускника нет возможности заниматься с репетитором, тогда у него возникает вопрос: «Как подготовиться к ЕГЭ по математике самостоятельно?» Не стоит паниковать. Все что необходимо для подготовки, вы с легкостью найдете в интернете.
Во-первых, скачивайте сборники тренировочных заданий. Во-вторых, поисковая система «Яндекс» вместе с талантливыми педагогами Москвы подготовила проект для выпускников «Яндекс ЕГЭ». Здесь дети найдут для себя вебинары и тесты, с помощью которых можно качественно подготовиться к экзамену. В-третьих, для отработки темы можно включать видеоуроки на портале YouTube, где учителя и дети выкладывают свои видеоматериалы с решением тех или иных заданий.
Как видите, сегодняшнему выпускнику гораздо легче готовиться к экзамену, ведь в интернете для подготовки есть варианты ОГЭ по математике. Этот фактор существенно облегчает участь экзаменуемого!
Четвертый критерий — полезная информация.
Наглядная информация
Всем известно, что математика и алгебра — предметы, в которых детям необходимо запоминать огромное количество формул, выражений и так далее. Вы можете выписывать необходимую информацию в специальный блокнот или приобрести специальное пособие, где за вас уже выбрали и напечатали необходимые формулы для успешной сдачи экзамена по математике. Чем чаще туда заглядывать, тем быстрее формулы запомнятся.
Пятый критерий — наглядные пособия.
Внимание родителей
Выпускные экзамены всегда являются причиной стресса у подростков. Поэтому родители должны с особым вниманием, пониманием и чуткостью относиться к детям в этот период. Соблюдайте дома тишину, когда ребёнок занимается уроками или готовится к экзамену. В вопросах о подготовке проявляйте не жёсткий контроль, а естественное любопытство. Спрашивайте о его настроениях, ощущениях и внутренних убеждениях, а также предлагайте свою посильную помощь.
Шестой критерий — забота родителей.
В заключение
Итак, мы с вами рассмотрели вопрос, как подготовиться к ОГЭ по математике. Акцентируем ваше внимание на том, что подготовка может быть самостоятельной или с помощью репетитора. Важно организовать и систематизировать эти занятия. Определить для себя сложные темы. Регулярно решать тесты, а также стараться запоминать формулы и выражения при помощи мнемотехнологий. Но это уже совсем другая статья!
ГИА по физике 9 класс. Варианты заданий с решением и ответами.
ГИА по физике для 9 класса с решением и ответами.
Задания ГИА по физике 9 класс.
1.
Используя график зависимости скорости движения тела от времени, определите скорость тела в конце 5-ой секунды, считая, что характер движения тела не изменяется.
1) 9 м/с 2) 10 м/с 3) 12 м/с 4) 14 м/с
2.
Через неподвижный блок перекинута невесомая нерастяжимая нить, к концам которой подвешены грузики равной массы m. Чему равна сила натяжения нити?
1) 0,25 mg 2) 0,5 mg 3) mg 4) 2 mg
3.
Тело, брошенное вертикально вверх с поверхности земли, достигает наивысшей точки и падает на землю. Если сопротивление воздуха не учитывать, то полная механическая энергия тела
1) максимальна в момент достижения наивысшей точки
2) максимальна в момент начала движения
3) одинакова в любые моменты движения тела
4) максимальна в момент падения на землю

На рисунке представлен график зависимости давления воздуха от координаты в некоторый момент времени при распространении звуковой волны. Длина звуковой волны равна
1) 0,4 м 2) 0,8 м 3) 1,2 м 4) 1,6 м
5.
Брусок в форме прямоугольного параллелепипеда положили на стол сначала узкой гранью (1), а затем – широкой (2). Сравните силы давления (F1 и F2) и давления (р1 и р2), производимые бруском на стол в этих случаях.
1) F 1 = F 2 ; p 1 > p 2 2) F 1 = F 2 ; p 1 3) F 1
6.
Верхняя граница частоты колебаний, воспринимаемых ухом человека, с возрастом уменьшается. Для детей она составляет 22 кГц, а для пожилых людей – 10 кГц. Скорость звука в воздухе равна 340 м/с. Звук с длиной волны 17 мм
1) услышит только ребенок 2) услышит только пожилой человек
3) услышит и ребенок, и пожилой человек 4) не услышит ни ребенок, ни пожилой человек
7.
В каком агрегатном состоянии находится вещество, если оно имеет собственные форму и объем?
1) только в твердом 2) только в жидком
3) только в газообразном 4) в твердом или в жидком

На диаграмме для двух веществ приведены значения количества теплоты, необходимого для нагревания 1 кг вещества на 10 °С и для плавления 100 г вещества, нагретого до температуры плавления. Сравните удельную теплоту плавления (?1 и?2) двух веществ.
1) ? 2 = ? 1
2) ? 2 = 1,5 ? 1
3) ? 2 = 2 ? 1
4) ? 2 =3 ? 1

На рисунке изображены одинаковые электроскопы, соединенные стержнем. Из какого материала может быть сделан этот стержень? А. Медь. Б. Сталь.
1) только А 2) только Б
3) и А, и Б 4) ни А, ни Б
10.
Чему равно общее сопротивление участка цепи, изображенного на рисунке, если R 1 = 1 Ом, R 2 = 10 Ом, R 3 = 10 Ом, R 4 = 5 Ом?

2) 11 Ом
3) 16 Ом
4) 26 Ом
11.
Две одинаковые катушки замкнуты на гальванометры. В катушку А вносят полосовой магнит, а из катушки Б вынимают такой же полосовой магнит. В каких катушках гальванометр зафиксирует индукционный ток?
1) ни в одной из катушек 2) в обеих катушках
3) только в катушке А 4) только в катушке Б
12.
На рисунке приведена шкала электромагнитных волн. Определите, к какому виду излучения принадлежат электромагнитные волны с длиной волны 0,1 мм?
1) только радиоизлучение
2) только рентгеновское излучение
3) ультрафиолетовое и рентгеновское излучение
4) радиоизлучение и инфракрасное излучение
13.
После прохождения оптического прибора, закрытого на рисунке ширмой, ход лучей 1 и 2 изменился на 1″ и 2″. За ширмой находится
1) плоское зеркало
2) плоскопараллельная стеклянная пластина
3) рассеивающая линза
4) собирающая линза
14.
В результате бомбардировки изотопа лития 3 7 Li
ядрами дейтерия образуется изотоп бериллия: 3 7 Li
+ 1 2 H
> 4 8
Be +
? Какая при этом испускается частица?
1) ?-частица 2 4 He
2) электрон -1 e
3) протон 1 1 p
4) нейтрон 1 n
15.
Необходимо экспериментально установить, зависит ли выталкивающая сила от объема погруженного в жидкость тела. Какой набор металлических цилиндров из алюминия и (или) меди можно использовать для этой цели?
1) А или Б 2) А или В
3) только А 4) только Б
Туман
При определенных условиях водяные пары, находящиеся в воздухе, частично конденсируются, в результате чего и возникают водяные капельки тумана. Капельки воды имеют диаметр от 0,5 мкм до 100 мкм.
Возьмем сосуд, наполовину заполним водой и закроем крышкой. Наиболее быстрые молекулы воды, преодолев притяжение со стороны других молекул, выскакивают из воды и образуют пар над поверхностью воды. Этот процесс называется испарением воды. С другой стороны, молекулы водяного пара, сталкиваясь друг с другом и с другими молекулами воздуха, случайным образом могут оказаться у поверхности воды и перейти обратно в жидкость. Это конденсация пара. В конце концов, при данной температуре процессы испарения и конденсации взаимно компенсируются, то есть устанавливается состояние термодинамического равновесия. Водяной пар, находящийся в этом случае над поверхностью жидкости, называется насыщенным.
Если температуру повысить, то скорость испарения увеличивается и равновесие устанавливается при большей плотности водяного пара. Таким образом, плотность насыщенного пара возрастает с увеличением температуры (см. рисунок).
Зависимость плотности насыщенного водяного пара от температуры.
Для возникновения тумана необходимо, чтобы пар стал не просто насыщенным, а пересыщенным. Водяной пар становится насыщенным (и пересыщенным) при достаточном охлаждении (процесс АВ) или в процессе дополнительного испарения воды (процесс АС). Соответственно, выпадающий туман называют туманом охлаждения и туманом испарения.
Второе условие, необходимое для образования тумана, — это наличие ядер (центров) конденсации. Роль ядер могут играть ионы, мельчайшие капельки воды, пылинки, частички сажи и другие мелкие загрязнения. Чем больше загрязненность воздуха, тем большей плотностью отличаются туманы.
16.
Из графика на рисунке видно, что при температуре 20 °С плотность насыщенного водяного пара равна 17,3 г/м 3
. Это означает, что при 20 °С
1) в 1 м 3
воздуха находится 17,3 г водяного пара
2) в 17,3 м 3
воздуха находится 1 г водяного пара
3) относительная влажность воздуха равна 17,3%
4) плотность воздуха равна 17,3 г/м 3
17.
Для каких процессов, указанных на рисунке, можно наблюдать туман испарения?
1) только АB 2) только АС 3) АB и АС 4) ни АB, ни АС
18.
Какие утверждения о туманах верны? А.
Городские туманы, по сравнению с туманами в горных районах, отличаются более высокой плотностью. Б.
Туманы наблюдаются при резком возрастании температуры воздуха.
1) верно только А 2) верно только Б 3) верны оба утверждения 4) оба утверждения неверны
19.
Установите соответствие между техническими устройствами (приборами) и физическими закономерностями, лежащими в основе принципа их действия.
20.
Установите соответствие между физическими величинами и формулами, по которым эти величины определяются.

На рисунке представлен график зависимости температуры от полученного количества теплоты в процессе нагревания металлического цилиндра массой 100 г. Определите удельную теплоемкость металла.
22.
Тележка массой 20 кг, движущаяся со скоростью 0,5 м/с, сцепляется с другой тележкой массой 30 кг, движущейся навстречу со скоростью 0,2 м/с. Чему равна скорость движения тележек после сцепки, когда тележки будут двигаться вместе?
23.
Для выполнения этого задания используйте лабораторное оборудование: источник тока (4,5 В), вольтметр, амперметр, ключ, реостат, соединительные провода, резистор, обозначенный R1. Соберите экспериментальную установку для определения электрического сопротивления резистора. При помощи реостата установите в цепи силу тока 0,5 А.
В бланке ответов: 1) нарисуйте электрическую схему эксперимента;
2) запишите формулу для расчета электрического сопротивления;
3) укажите результаты измерения напряжения при силе тока 0,5 А;
4) запишите численное значение электрического сопротивления.
24.
Две спирали электроплитки, сопротивлением по 10 Ом каждая, соединены последовательно и включены в сеть с напряжением 220 В. Через какое время на этой плитке закипит вода массой 1 кг, если ее начальная температура составляла 20 °С, а КПД процесса 80%? (Полезной считается энергия, необходимая для нагревания воды.)
25.
Тело массой 5 кг с помощью каната начинают равноускоренно поднимать вертикально вверх. Чему равна сила, действующая на тело со стороны каната, если известно, что за 3 с груз был поднят на высоту 12 м?
26.
Каким пятном (темным или светлым) кажется водителю ночью в свете фар его автомобиля лужа на неосвещенной дороге? Ответ поясните.
Пособие предназначено для подготовки к Основному государственному экзамену (ОГЭ) по физике. Оно поможет систематизировать знания по предмету, сконцентрировать внимание на наиболее важных вопросах, выносимых на итоговую аттестацию, а также правильно выстроить стратегию и тактику подготовки к ОГЭ. Пособие составлено с учётом специфики основных учебных программ по предмету и содержит краткий теоретический курс основного общего образования, представленный на основе кодификатора, разработанного Федеральным институтом педагогических измерений (ФИПИ).
Пособие содержит 14 типовых вариантов экзаменационных заданий Основного государственного экзамена по физике.
Назначение пособия — предоставить возможность обучающимся отработать навыки выполнения заданий, аналогичных заданиям, предоставленным в демонстрационной версии ОГЭ по физике.
Пособие адресовано учителям для подготовки учащихся к Основному государственному экзамену, а учащимся-девятиклассникам — для самоподготовки и самоконтроля.
Приказом № 699 Министерства образования и науки Российской Федерации учебные пособия издательства «Экзамен» допущены к использованию в общеобразовательных организациях.
Скачать и читать ОГЭ 2020, Физика, 14 вариантов, Типовые варианты экзаменационных заданий, Камзеева Е.Е.
Пособие содержит 14 типовых вариантов экзаменационных заданий Основного государственного экзамена по физике. Назначение пособия — предоставить возможность обучающимся отработать навыки выполнения заданий, аналогичных заданиям, предоставленным в демонстрационной версии ОГЭ по физике. Пособие адресовано учителям для подготовки учащихся к Основному государственному экзамену, а учащимся-девятиклассникам — для самоподготовки и самоконтроля. Приказом № 699 Министерства образования и науки Российской Федерации учебные пособия издательства «Экзамен» допущены к использованию в общеобразовательных организациях.
Скачать и читать ОГЭ 2020, Физика, 14 вариантов, Типовые варианты экзаменационных заданий, Камзеева Е.Е., 2020
Основной государственный экзамен (ОГЭ) представляет собой форму государственной итоговой аттестации, проводимой в целях определения соответствия результатов освоения обучающимися основных образовательных программ основного общего образования соответствующим требованиям федерального государственного образовательного стандарта. Для указанных целей используются контрольные измерительные материалы (КИМ), представляющие собой комплексы заданий стандартизированной формы.
Скачать и читать Спецификация контрольных измерительных материалов для проведения в 2020 году основного государственного экзамена по ФИЗИКЕ
Кодификатор проверяемых требований к результатам освоения основной образовательной программы основного общего образования и элементов содержания для проведения основного государственного экзамена по физике (далее – кодификатор) является одним из документов, определяющих структуру и содержание контрольных измерительных материалов (далее – КИМ). Кодификатор является систематизированным перечнем проверяемых требований к результатам освоения основной образовательной программы основного общего образования и элементов содержания, в котором каждому объекту соответствует определённый код.
Скачать и читать Кодификатор проверяемых требований к результатам освоения основной образовательной программы основного общего образования и элементов содержания для проведения основного государственного экзамена по ФИЗИКЕ, 2020
Демонстрационный вариант предназначен для того, чтобы дать возможность любому участнику экзамена и широкой общественности составить представление о структуре будущей экзаменационной работы, количестве и форме заданий, а также об их уровне сложности. Приведённые критерии оценивания выполнения заданий с развёрнутым ответом, включённые в этот вариант, позволят составить представление о требованиях к полноте и правильности записи развёрнутого ответа. Эти сведения дают будущим участникам экзамена возможность выработать стратегию подготовки к сдаче экзамена по физике в 2020 году.
Скачать и читать Демонстрационный вариант контрольных измерительных материалов основного государственного экзамена 2020 года по ФИЗИКЕ
Автор заданий — ведущий специалист, принимающий непосредственное участие в разработке методических материалов для подготовки к выполнению контрольных измерительных материалов ОГЭ.
В пособие включены 12 тренировочных типовых вариантов экзаменационных заданий, которые по структуре, содержанию и уровню сложности аналогичны контрольным измерительным материалам ОГЭ по физике.
Справочные данные, которые необходимы для решения всех вариантов, даются в начале сборника.
После выполнения вариантов правильность своих ответов учащийся может проверить, воспользовавшись таблицей ответов в конце книги. В пособии приводится разбор решений одного из вариантов. Для заданий части 2, требующих развёрнутого ответа, приводятся подробные решения.
Учащийся получает возможность эффективно отработать учебный материал на большом количестве заданий и самостоятельно подготовиться к экзамену.
Учителям книга будет полезна для организации различных форм подготовки к ОГЭ.
Скачать и читать ОГЭ 2020, Физика, 12 вариантов, Типовые варианты экзаменационных заданий, Камзеева Е.Е.
Показана страница 1 из 11
Государственная итоговая аттестация для выпускников девятых классов в настоящее время является добровольной, всегда можно отказаться и сдавать привычные традиционные экзамены.
Чем же привлекательнее тогда форма ОГЭ (ГИА) для выпускников 9 класса 2019 года?
Проведение непосредственно аттестации в данной новой форме позволяет получить независимую оценку подготовки школьников.
Все задания ОГЭ (ГИА) представлены в виде специальной формы, включающей в себя вопросы с выбором ответа на них.
Проводится прямая аналогия с ЕГЭ. При этом можно давать как краткие, так и развернутые ответы.
Наш сайт сайт
поможет вам отлично подготовиться и оценить реально свои шансы.
Помимо этого, тесты ГИА и ОГЭ онлайн с проверкой ответов
помогают вам определиться с дальнейшим выбором профильного класса старшей школы.
Вы сами сможете легко оценить свои знания по выбранному предмету. Для этого наш проект предлагает вам различные тесты по ряду дисциплин.
Наш сайт, посвященный подготовке к сдаче ГИА 2019 года 9 класс онлайн
, в полной мере поможет вам подготовиться к первому серьезному и ответственному испытанию в жизни.
Все материалы нашего сайта представлены в простой, доступной для понимания форме. Будь вы круглый отличник в своем классе или обычный среднестатистический ученик — всё теперь в ваших руках. Не лишним вам будет посетить наши . Здесь вы найдете ответы на все интересующие вас вопросы. Будьте подготовленным к непростому испытанию ОГЭ, ГИА и результат превзойдет все ваши ожидания.
В разработке собирается и обобщается опыт по решению задач, предлагаемых на ОГЭ по физике в 9 классе, в рамках раздела «кинематика. прямолинейное движение». Автор постарался разработать небольшой курс, в котором на примере разбора базовых простых задач формируется понимание общего принципа решения заданий по данной теме. Разработка содержит 19 уникальных
заданий с подробнейшим разбором каждого, причем на некоторые задачи указано несколько способов решения, что по мнению автора должно способствовать глубокому и полному усвоению методик решения подобных заданий. Практически все задания авторские, но в каждом из них отражены особенности задач формы ОГЭ. Подавляющее большинство заданий ориентированы на графическое представлению, что способствует формированию метапредметных навыков. Кроме того разработка содержит минимальный необходимый теоретический материал, который представляет собой «концентрацию» общей теории по данному разделу. Может использоваться учителем при подготовке к обычному уроку, при проведении дополнительных занятий, а также рассчитан и на ученика, который в самостоятельном порядке готовится к сдаче ОГЭ по физике.
Методическое пособие (презентация) «Электромагнитные колебания и волны. Подготовка к ГИА» составлена в соответствии с требованиями к Государственной итоговой аттестации (ГИА) по физике 2013 года и предназначено для подготовки выпускников основной школы к экзамену.
В разработке приведены краткие сведения по теме (в соответствии с кодификатором ГИА) и Планом демонстрационного варианта экзаменационной работы (Электромагнитные колебания и волны), сопровождаемые анимацией и видеофрагментами.
Целевая аудитория: для 9 класса
Методическое пособие (презентация) «Влажность воздуха. Подготовка к ГИА» составлена в соответствии с требованиями к Государственной итоговой аттестации (ГИА) по физике 2010 года и предназначено для подготовки выпускников основной школы к экзамену.
В разработке приведены краткие сведения по теме (в соответствии с кодификатором ГИА) и Планом демонстрационного варианта экзаменационной работы (Влажность воздуха), сопровождаемые анимацией и видеофрагментами.
Методическое пособие (презентация) «Испарение и конденсация. Кипение жидкости. Подготовка к ГИА» составлена в соответствии с требованиями к Государственной итоговой аттестации (ГИА) по физике 2010 года и предназначено для подготовки выпускников основной школы к экзамену.
В разработке приведены краткие сведения по теме (в соответствии с кодификатором ГИА) и Планом демонстрационного варианта экзаменационной работы (Испарение и конденсация. Кипение жидкости), сопровождаемые анимацией и видеофрагментами.
Краткость и наглядность изложения позволяет быстро и качественно повторить пройденный материал при повторении курса физики в 9 классе, а также на примерах демоверсий ГИА по физике 2008-2010 годов показать применение основных законов и формул в вариантах экзаменационных заданий уровня А и В.
Пособие можно использовать и для 10-11 классов при повторении соответствующих тем, что позволит сориентировать обучающихся на экзамен по выбору в выпускные годы.
В разработке приведены краткие сведения по теме (в соответствии с кодификатором ГИА) и Планом демонстрационного варианта экзаменационной работы (Механические колебания и волны. Звук), сопровождаемые анимацией и видеофрагментами.
Краткость и наглядность изложения позволяет быстро и качественно повторить пройденный материал при повторении курса физики в 9 классе, а также на примерах демоверсий ГИА по физике 2008-2010 годов показать применение основных законов и формул в вариантах экзаменационных заданий уровня А и В.
Методическое пособие составлено в помощь учителям и ученикам, сдающим ГИА по физике на основе материалов ФИПИ для подготовки к экзамену в новой форме; содержит примеры оформления экспериментальных заданий из части 3. Пособие можно использовать и на уроках физики 7 – 9 классов на лабораторных работах, т.к. описание некоторых лабораторных работ не приводится в учебнике.
Методическое пособие (презентация) «Закон Архимеда. Подготовка к ГИА» составлена в соответствии с требованиями к Государственной итоговой аттестации (ГИА) по физике 2010 года и предназначено для подготовки выпускников основной школы к экзамену.
В разработке приведены краткие сведения по теме (в соответствии с кодификатором ГИА) и Планом демонстрационного варианта экзаменационной работы (Закон Архимеда), сопровождаемые анимацией и видеофрагментами.
Краткость и наглядность изложения позволяет быстро и качественно повторить пройденный материал при повторении курса физики в 9 классе, а также на примерах демоверсий ГИА по физике 2008-2010 годов показать применение основных законов и формул в вариантах экзаменационных заданий уровня А и В.
Пособие можно использовать и для 10-11 классов при повторении соответствующих тем, что позволит сориентировать обучающихся на экзамен по выбору в выпускные годы.
Методическое пособие (презентация) «Закон Паскаля. Подготовка к ГИА» составлена в соответствии с требованиями к Государственной итоговой аттестации (ГИА) по физике 2010 года и предназначено для подготовки выпускников основной школы к экзамену.
В разработке приведены краткие сведения по теме (в соответствии с кодификатором ГИА) и Планом демонстрационного варианта экзаменационной работы (Закон Паскаля), сопровождаемые анимацией и видеофрагментами.
Краткость и наглядность изложения позволяет быстро и качественно повторить пройденный материал при повторении курса физики в 9 классе, а также на примерах демоверсий ГИА по физике 2008-2010 годов показать применение основных законов и формул в вариантах экзаменационных заданий уровня А и В.
Методическое пособие (презентация) «Давление. Атмосферное давление. Подготовка к ГИА» составлена в соответствии с требованиями к Государственной итоговой аттестации (ГИА) по физике 2010 года и предназначено для подготовки выпускников основной школы к экзамену.
В разработке приведены краткие сведения по теме (в соответствии с кодификатором ГИА) и Планом демонстрационного варианта экзаменационной работы (Давление. Атмосферное давление), сопровождаемые анимацией и видеофрагментами.
Краткость и наглядность изложения позволяет быстро и качественно повторить пройденный материал при повторении курса физики в 9 классе, а также на примерах демоверсий ГИА по физике 2008-2010 годов показать применение основных законов и формул в вариантах экзаменационных заданий уровня А и В.
Пособие можно использовать и для 10-11 классов при повторении соответствующих тем, что позволит сориентировать обучающихся на экзамен по выбору в выпускные годы.
Методическое пособие (презентация) «Простые механизмы. КПД простых механизмов. Подготовка к ГИА» составлена в соответствии с требованиями к Государственной итоговой аттестации (ГИА) по физике 2010 года и предназначено для подготовки выпускников основной школы к экзамену.
В разработке приведены краткие сведения по теме (в соответствии с кодификатором ГИА) и Планом демонстрационного варианта экзаменационной работы (Простые механизмы. КПД простых механизмов), сопровождаемые анимацией и видеофрагментами.
Краткость и наглядность изложения позволяет быстро и качественно повторить пройденный материал при повторении курса физики в 9 классе, а также на примерах демоверсий ГИА по физике 2008-2010 годов показать применение основных законов и формул в вариантах экзаменационных заданий уровня А и В.
Пособие можно использовать и для 10-11 классов при повторении соответствующих тем, что позволит сориентировать обучающихся на экзамен по выбору в выпускные годы.
Подготовка к ОГЭ и ЕГЭ
Основное общее образование
Линия УМК А. В. Перышкина. Физика (7-9)
В 9 классе школьники впервые сталкиваются с обязательными государственными экзаменами. Что это означает для учителя? Во-первых, стоит задача настроить детей на усиленную подготовку к аттестационной работе. Но самое важное: не просто дать полноценные знания по своему предмету, а объяснить, какого рода задания предстоит выполнить, разобрать типичные примеры, ошибки и дать ученикам все инструменты для успешной сдачи экзамена.
При подготовке к ОГЭ больше всего вопросов вызывает экспериментальное задание №23. Оно самое сложное, соответственно на него и отводится больше всего времени — 30 минут. А за его успешное выполнение можно получить больше всего баллов — 4. Этим заданием начинается вторая часть работы. Если заглянуть в кодификатор, мы увидим, что контролируемыми элементами содержания здесь являются механические и явления электромагнетизма. Ученики должны показать умение работать с физическими приборами и измерительными инструментами.
Существует 8 стандартных комплектов оборудования, которое может понадобится на экзамене. Какие именно будут использоваться, становится известно за несколько дней до экзамена, поэтому целесообразно провести дополнительную тренировку перед экзаменом с теми инструментами, которые будут задействованы; обязательно повторить, как снимать показания с приборов. Если экзамен проводится на территории другой школы, учитель может заранее приехать туда, чтобы посмотреть готовые для работы комплекты. Готовящий приборы к экзамену учитель должен обратить внимание на их исправность, особенно подверженных износу. Например, использование старой батарейки может привести к тому, что ученик элементарно не сможет установить требуемую силу тока.
Нужно проверить, совпадают ли приборы с указанными значениями. Если не совпадают, то в специальных бланках указываются истинные значения, а не те, которые записаны в официальных комплектах.
Учителю, ответственному за проведение экзамена может помогать технический специалист. Он же следит за соблюдением техники безопасности во время экзамена и может вмешаться в ход выполнения задания. Нужно напомнить ученикам, что если они заметят неисправность какого-либо прибора во время выполнения задания, нужно незамедлительно сообщить об этом.
Существует три типа экспериментальных заданий, встречающихся на экзамене по физике.
Тип 1. «Косвенные измерения физических величин». Включает в себя 12 тем:
- Плотность вещества
- Сила Архимеда
- Коэффициент трения скольжения
- Жесткость пружины
- Период и частота колебаний математического маятника
- Момент силы, действующей на рычаг
- Работа сила упругости при подъеме груза с помощью подвижного или неподвижного блока
- Работа силы трения
- Оптическая сила собирающей линзы
- Электрическое сопротивление резистора
- Работа электрического тока
- Мощность электрического тока.
Тип 2. «Представление экспериментальных результатов в виде таблиц или графиков и формулировка вывода на основании полученных экспериментальных данных». Включает в себя 5 тем:
- Зависимость силы упругости, возникающей в пружине, от степени деформации пружины
- Зависимость периода колебаний математического маятника от длины нити
- Зависимость силы тока, возникающей в проводнике, от напряжения на концах проводника
- Зависимость силы трения скольжения от силы нормального давления
- Свойства изображения, полученного с помощью собирающей линзы
Тип 3. «Экспериментальная проверка физических законов и следствий». Включает в себя 2 темы:
- Закон последовательного соединения резисторов для электрического напряжения
- Закон параллельного соединения резисторов для силы электрического тока
Подготовка к ОГЭ по физике: советы ученику
- Важно очень точно записывать в бланк ответа все, что требуют правила. Проверяя свою работу, стоит еще раз взглянуть, ничего ли не пропущено: схематический рисунок, формула для расчета искомой величины, результаты прямых измерений, расчеты, числовое значение искомой величины, вывод и т.д., в зависимости от условий. Отсутствие хотя бы одного показателя приведет к снижению балла.
- За дополнительные измерения, внесенные в бланк, оценка не снижается
- Рисунки должны быть выполнены очень аккуратно, небрежные схемы тоже отнимают балл. Немаловажно приучиться контролировать указание всех единиц измерения
- Записывая ответ, ученик не должен указывать погрешность, но стоит донести до него информацию, что проверяющий имеет критерии и правильный ответ уже содержит границы интервала, внутри которого может оказаться верный результат.
Подготовка к экзамену в целом и к экспериментальному заданию в частности не может быть спонтанной. Без постоянно нарабатываемого навыка работы с лабораторным оборудованием выполнить задания практически невозможно. Поэтому учителям рекомендуется ознакомится с демонстрационными вариантами экзаменационной работы и разбирать типичные задачи во время проведения лабораторных.
Подробный разбор всех типов заданий вы можете посмотреть в
вебинаре
ДОКЛАД
Эффективные приемы и методы подготовки учащихся к успешной сдаче ЕГЭ по математики.
В основу построения рекомендаций положены принципы развития математического образования, определение приоритетных и перспективных направлений, а также анализ наиболее типичных ошибок, допущенных в решении заданий базового и профильного экзамена.
Возрастание роли математики в современной жизни привело к тому, что для адаптации в современном обществе и активному участию в нем необходимо быть математически грамотным человеком. В связи со стратегическими направлениями социально — экономического развития России до 2020 года: «Приоритетной государственной задачей является обеспечение качественного базового уровня математических и естественнонаучных знаний у всех выпускниковшколы, не только будущих ученых, но и будущих квалифицированных рабочих…» Каждый школьник в процессе обучения должен иметь возможность получить полноценную подготовку к выпускным экзаменам. Формула успеха хорошо сдать экзамен ЕГЭ и ОГЭ по математике: Высокая степень восприимчивости + мотивация + компетентный педагог.
Практика показывает, что прорешивание открытых вариантов ЕГЭ прошлых лет не даёт ожидаемого эффекта. Разобрав вариант в классе, учитель даёт аналогичный вариант для домашнего разбора. После удачного разбора в классе домашний вариант не представляет большого труда, и у обучающегося и учителя складывается ложное впечатление, что подготовка идет эффективно и цель достигнута. Многократное повторение этих манипуляций не улучшает ситуацию. Когда участник на ЕГЭ получает свой вариант, он обнаруживает, что этот вариант он с учителем не решал. Привычка повторять разобранные ранее варианты часто идет во вред обучению.
Правильным подходом является систематическое изучение материала, решение большого числа задач по каждой теме – от простых к сложным, изучение отдельных методов решения задач. Разумеется, варианты подготовительных сборников, открытые варианты можно и нужно использовать в качестве источника заданий, но их решение не должно становиться главной целью; они должны давать возможность иллюстрировать и отрабатывать те или иные методы. В любом случае, при проведении диагностических работ следует подбирать задачи, прямые аналоги которых в классе не разбирались. Только так учитель может составить верное представление об уровне знаний и умений своих учеников.
Компенсирующее обучение в старших классах.
Часто мы сталкиваемся с ситуацией, когда главенствующим методическим принципом оказывается принцип «прохождения программы», – то есть программа должна быть пройдена во что бы то ни стало, невзирая на то, что содержание этой программы может не отвечать реальным возможностям и подготовке обучающихся.
С введением нового ФГОС, реализацией Концепции развития математического образования, принятием федеральных примерных образовательных программ по математике принцип прохождения программы приобретает новый смысл – обучающийся должен участвовать в посильной интеллектуальной математической деятельности, дающей осязаемые плоды обучения.
Компенсирующая программа как вариант базовой программы для старших классов даёт возможность учителю сделать уроки математики для наименее подготовленных обучающихся осмысленными. При этом появляется реальная возможность эффективно подготовить обучающихся к решению 8 – 10 заданий профильного ЕГЭ.
Практико-ориентированная математика.
Важной частью ЕГЭ по математике и современных программ являются задачи на применение математических знаний в быту, в реальных жизненных ситуациях. Это задачи на проценты, оптимальный выбор из предложенных вариантов, чтение данных, представленных в виде диаграмм, графиков или таблиц, вычисление площадей или других геометрических величин по рисунку, задачи на вычисление по формулам и т.п.
Круг практико-ориентированных задач в ЕГЭ постоянно расширяется; дополнительно к ним следует отнести задачи вероятностно-статистического блока.
Сложилась практика, когда к практическим задачам учитель приступает только в последний год перед сдачей ЕГЭ. К этому времени обучающиеся успели прочно забыть, как вычислять проценты, как находить площади фигур с помощью палетки или на клетчатой бумаге – все эти задачи для них оказываются новыми.
На протяжении всего периода обучения математике не следует отрываться от простых практических задач; их следует включать в блоки повторения в начале и конце учебного года, в текущий, внутришкольный контроль. Задачи на вычисление сумм налогов, процентов по банковскому вкладу или кредиту, другие задачи финансового характера должны стать постоянным инструментом на уроках математики, поскольку эти задачи связывают наш предмет с окружающим миром и повседневной жизнью.
Практико-ориентированные задачи по финансовой грамотности, геометрического плана, чтение таблиц и графиков нужно включать в изучение математики в средней и старшей школе. При этом характер и трудность задач могут меняться со временем, более того, это необходимо для органического вплетения практических тем в изучение теоретических вопросов. Например, задачи на вклады и кредиты органично возникают при изучении прогрессий, показательной функции и производных. Вычисление площадей по клеточкам очень часто помогает при изучении совершенно абстрактной, казалось бы, темы «первообразная и интеграл». Чтение простых графиков помогает понять и грамотно на качественном уровне применять производную.
Отдельную важную роль в сближении школьной математики с задачами окружающего мира играют вопросы вероятностей и статистики.
Теория вероятности и статистика.
В Концепции развития математического образования ТВ и статистика названы в числе перспективных и важных направлений развития школьной математики. С 2012 года задачи по ТВ формально включаются в КИМ ОГЭ и ЕГЭ. При этом учителя понимают, что те задачи, которые сейчас есть в открытом банке заданий и те, что включены в экзамен, в большинстве случаев сводятся к перечислению равновозможных исходов.
Ясно, что роль ТВ и статистики в школьной математике будет расти. Одновременно будет расширяться круг тем, подлежащих контролю.
При обучении математике следует больше внимания уделять темам вероятности и статистики, постепенно нарабатывая опыт преподавания этих разделов, которые оказываются наиболее практически направленными. Изучение вероятности и статистики требуется вести в тесной привязке к темам алгебры и геометрии, поскольку систематический подход к вопросам ТВ требует от обучающихся знаний о свойствах геометрической прогрессии преобразованиях многочленов, корнях и степенях, площадях фигур.
Таким образом, правильно выстроенное преподавание вероятности не отнимает время, а, напротив, поддерживает изучение традиционных разделов школьной математики. В 2012 – 2014 году задачи по ТВ, появившись в экзамене, вызывали большие трудности, и выполнение этих заданий редко поднималось выше 50%. В настоящее время ситуация изменилась. На данный момент медиана выполнения задания 4 – около 90%.
Некоторые эффективные приёмы обучения математике.
Остановимся подробнее на некоторых приёмах обучения математике, доказавших свою эффективность.
1) При решении задач одним из эффективных приёмов является использование примеров и образцов. Скажем, ученик получает задачу и готовое решение, которое он должен разобрать самостоятельно. Решение может быть дополнено советами, комментариями трудных или «опасных» моментов, другими способами решения и т.п. Когнитивная нагрузка в данном случае получает управляющий импульс и осуществляется в заданном направлении. Важным условием является выход на стратегию, которую можно будет применить в дальнейшем при решении широкого круга задач. Следующим этапом может стать работа не с готовым решением, а с заданным алгоритмом решения, который ученик должен самостоятельно применить к данной ему задаче. После этого можно провести решение полностью самостоятельно. Покажем это (без потери общности) на простой задаче.
Условие. Каждый из двух друзей одновременно показывает на руке случайное количество пальцев от 1 до 5. С какой вероятностью в сумме получится число 8?
Решение. Общее число исходов равно: 25. Благоприятными событию «получится в сумме число 8» будут исходы: 3 + 5, 5 + 3, 4 + 4. Вероятность события равна: 3/25 = 0,12. Ответ: 0,12.
Комментарий. Следует различать две комбинации, когда один из друзей показывает 3 пальца, а другой – 5 пальцев. Ответ можно записать как обыкновенной дробью, так и десятичной.
Задание для самостоятельного решения. Каждый из двух друзей показывает на руке случайное количество пальцев от 1 до 5. С какой вероятностью в сумме получится число 7?
Описанный приём может использоваться применительно к отдельному заданию, однако из таких заданий – с решениями и комментариями – можно составить тематическую проверочную работу, которую можно использовать и в рамках подготовки к экзамену. Решения могут быть написаны учителем самостоятельно, могут быть взяты из публикуемых сборников для подготовки к ЕГЭ, а также из материалов журнала «Математика» или других источников.
2) Весьма эффективно использование при решении задач подсказок, то есть некоторой дополнительной информации, которая дается ученику после (что важно!) того, как он начал работать над задачей. Чем определеннее подсказка, тем больше из нее можно извлечь. Фразы: «Хорошо подумай», «Внимательно прочти условие задачи», «Подумай о других способах решения» подсказками не являются, поскольку они никак не направляют ход мысли и не помогают найти решение.
Пример. Решите уравнение.
Подсказка. Можно применить формулу синуса суммы двух углов. Подсказкой может быть похожая задача, которая решалась недавно, указание на конкретный метод. Всегда полезно использовать результаты, методы уже решённых задач, а также опыт, приобретенный при решении. Это широко используется в школьном курсе геометрии, где многие важные геометрические факты, которыми целесообразно пользоваться при решении других задач, даны не в виде утверждений (теорем), а в виде задач. Кроме того, это возможность использования еще одного метода – аналогии.
При решении тригонометрических уравнений подсказкой может быть определённая формула, а при решении логарифмического уравнения – свойство логарифма. Полезно учить пользоваться подсказками, искать их самостоятельно, а также учить давать подсказки.
3) При обучении решению сложных или трудоёмких в плане вычислений и преобразований задач полезно использовать групповые формы работы, а в качестве приёма – мозговой штурм. Основные принципы мозгового штурма: на первом этапе – предложение как можно большего количества решений, без оценки их применимости, рациональности и проч., на втором – анализ и вывод о целесообразности предложенного, выбор наиболее удачных идей и предложений. Ценность приема – в стимулировании поисковой активности на первом этапе и критичности мышления на втором. Хорошо применим данный прием при поиске различных способов решения геометрических задач и тригонометрических уравнений.
4) При решении текстовых задач важным приёмом, необходимым для усвоения, является переформулирование условия, отношений, связывающих входящие в задачу величины. Ниже приводится пример такой задачи из варианта профильного экзамена.
«Задание 11. Заказ на изготовление 323 деталей первый рабочий выполняет на 2 ч быстрее, чем второй. Сколько деталей изготавливает первый рабочий, если известно, что он изготавливает на 2 детали больше второго?»
Данную задачу экзаменуемые решили существенно хуже, чем аналогичную задачу с более привычной и хорошо отработанной фабулой, связанной с движением двух велосипедистов.
Умение переформулировать условие важно и при решении нестандартных задач, то есть таких, метод решения которых ученику не известен, не изучался и не отрабатывался на уроках.
Ещё более актуально это умение при решении практико- ориентированных задач, представляющих собой некоторую ситуацию из реальной жизни, которую необходимо преобразовать и описать на языке математики (то есть самостоятельно сформулировать задачу). В самом простом случае основа задачи будет следующая: за лестницей, которую прислонили к стене дома, надо распознать прямоугольный треугольник, гипотенузой которого и будет данная лестница.
5).В связи с введением обязательного ЕГЭ и ОГЭ по математике возникает необходимость научить учащихся решать быстро и качественно задачи базового уровня. При этом необыкновенно возрастает роль устных
вычислений, так как на экзамене не разрешается использовать калькулятор и таблицы. Можно научить учащихся выполнять простейшие (и не очень) преобразования устно. Конечно, для этого потребуется организовать отработку такого навыка до автоматизма,
на каждом уроке необходимо отводить 5 — 7 минут для проведения упражнений устных вычислений, предусмотренных программой каждого
класса. Устные упражнения активизируют мыслительную деятельность учащихся, требуют осознанного усвоения учебного материала; при их выполнении
развивается память, речь, внимание, быстрота реакции.
Если в 5 — 6 классах устный счет – это выполнение действий с числами:
натуральные числа, обыкновенные дроби, десятичные дроби, то в старших
классах – это могут быть:
7 класс: Формулы сокращенного умножения. Решение простейших ЛУР. Действия со степенью. График линейной
функции.
8 класс: Линейные неравенства и числовые промежутки.
Решение простейших линейных неравенств. Решение КВУР с помощью
теоремы Виета и частных случаев. Решение КВУР рациональными способами. Арифметический квадратный корень и его свойства. 9 класс: Решение неравенств 2 степени. Преобразование графиков функций. Формулы приведения. Значения тригонометрических функций.
10 — 11 классах: Вычисление производных. Простейшие тригонометрические неравенства. Тригонометрические формулы. Простейшие тригонометрические уравнения. Функции, обратные тригонометрическим. Преобразование графиков функций. Вычисление первообразных. Свойства логарифмов. Простейшие показательные уравнения
и неравенства. Простейшие логарифмические уравнения и неравенства. Практика показала, что систематическая работа с устным счетом способствует значительному повышению продуктивности вычислений и преобразований. Сокращается время на выполнение таких операций, что переводит их из разряда самостоятельной задачи в разряд вспомогательной и становится инструментом (“таблицей
умножения”) для решения более сложных задач. Учитель по математике, знающий, с чем придется столкнуться школьнику на экзамене, кроме фундамента уделяет большую часть времени на занятии отработке вопросов специфики ЕГЭ и ОГЭ. Правильность оформления заданий, тактика и стратегия решения в условиях дефицита выделенного времени на экзамене, а также банальная невнимательность. Эти и масса других особенностей составляют
суть специфики. Для эффективной подготовки к ЕГЭ и ОГЭ нужна тренировка, тренировка и еще раз тренировка. Довести решение задач до автоматизма.
Развитие геометрических представлений
Процент выполнения экзаменующимися геометрических заданий традиционно ниже, чем процент выполнения заданий алгебраических. Одна из основных причин – недостатки в формировании пространственного мышления учащихся. Массово эта проблема проявилась с уходом из общего образования такого учебного предмета, как черчение, и вряд ли стоит ожидать его возвращения – профессия конструктора перестала быть столь массово востребованной с приходом компьютерных технологий.
Эта проблема легла на плечи учителей математики, однако решение её известно: непрерывное развитие геометрических представлений и геометрического воображения обучающихся с 1 по 11 класс; наглядная геометрия в 1–6 классах; больше внимания геометрическому моделированию и конструированию (из плоских и пространственных фигур), геометрическим чертежам, построениям, изображениям от руки и с помощью различных чертёжных инструментов, на нелинованной и клетчатой бумаге.
Это отнюдь не означает, что всю геометрию надо свести к наглядности и к работе руками. Определения и доказательства, логика и аксиоматика важны для современного человека и для изучения геометрии не менее, но надо понимать, что в развитии человека всему отводится свое время, а несформированное наглядно-образное мышление, которое должно быть основой и этапом на пути формирования логического мышления, просто мешает его формированию.
Если вернуться к этапу обучения в старшей школе, то целесообразно использовать любые приёмы и средства, которые способствовали бы визуализации предлагаемых обучающимся задач. Это не только построение чертежей по условию задачи (что непросто сделать при проблемах с пространственным воображением), это прежде всего различные предметные модели (полезно для каждой решаемой задачи иметь соответствующую ей модель-подсказку, чтобы использовать её для визуализации условия, поиска и проверки решения), компьютерные программы, позволяющие выполнять стереометрические чертежи.
Полезно выделить эту работу в отдельный тематический практикум, на котором обучающиеся тренировались бы в изображении и моделировании пространственных тел, построении чертежей по условию задачи (в различных ракурсах, выбирая наиболее удобный для поиска решения), можно также организовать данную работу в рамках проекта.
Mногие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.
Работает ли эта стратегия?
Oтвет преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство (задание 15) и тем более — сложная «экономическая» задача. Так было в 2018 году. И всё, баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!
Cтоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.
1) Cамое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Cначала — теория. Cвойства геометрических фигур. Oпределения и теоремы. Учить наизусть.
Лучшая тренировка на этом этапе — задания №3 и №6 из первой части ЕГЭ по математике
2) Задача 16 Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. A на ЕГЭ остается только вспомнить и записать решение.
3) Oказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем.
4) Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы.
5.) Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Mенелая и другую экзотику — вам это и не понадобится.
6) Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур — у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус вписанной окружности. B каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.
7) Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл. A это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б).
Саморегуляция и обратная связь «ученик-учитель».
Известно, что эффективность обучения возрастает в случае самооценивания, поскольку ученик самостоятельно получает информацию о своих результатах, сам её анализирует, делает выводы о своем прогрессе, корректирует цели в случае необходимости. Но для этого необходимы критерии оценивания работы, которые должны быть у ученика не просто до начала выполнения конкретной работы, но желательно и в самом начале изучения темы. К сожалению, на практике более распространена ситуация, когда работа выдаётся ученику без критериев ее выполнения.
К саморегуляции относятся также вопросы, связанные с осознанностью знания и незнания. Объяснение учителя сродни лекционной форме предъявления новых знаний. В связи с этим подчеркнём важность обратной связи. Учитель должен получать сигналы от обучающихся: «Я понимаю, могу объяснить», «Я не уверен, правильно ли я понимаю», «Я не понимаю». Учитель может прервать своё объяснение вопросом к тем, кто ещё не понял, предложением высказать свои сомнения тем, кто не уверен в понимании, предоставлением слова тем, кто всё понял.
Доказано, что обратная связь эффективна, если ученик получает сообщение о верно выполненных заданиях, а не только об ошибках, если он получает не просто маркеры, свидетельствующие о положительном результате, не просто похвалу за решённую задачу, а и некоторый содержательный комментарий. Этот комментарий может включать в себя такую оценку, как «рациональное решение», «интересная идея», «грамотная запись». Может быть отмечена актуальность проверки результата, удачное прохождение «ловушек» и «опасных» мест и т.п.
Обратная связь эффективна в случае, если она конкретна, то есть связана с известными ученику результатами и действиями, подлежащими усвоению. Важное значение имеет информированность ученика относительно того, чему он должен научиться, какие задания должен научиться решать, а какие может научиться решать для того, чтобы получить желаемое количество баллов на экзамене. Если ученик фиксирует и отслеживает сам, умеет ли он выполнять требуемое задание или нет, то минимизируется время на выполнение заданий, при этом работа становится более эффективной и рациональной. Отсюда необходимость в открытости предъявляемых требований к результатам обучения, а на этапе подготовки к экзамену – в ориентации на конечный запланированный результат.
И еще об одном факторе следует упомянуть – это повторяющееся тестирование. Уже имеющийся опыт российской школы и более продолжительный зарубежный опыт не позволяют говорить о нём, как об эффективном факторе. Положительные эффекты возникают только в тех случаях, когда учитель учитывает результаты тестирования для корректировки процесса обучения и приспосабливает методы обучения к возможностям конкретного ученика, учитывая его сильные и слабые стороны, или при условии содержательной обратной связи, с которой ученик может работать самостоятельно, то есть имеет возможность учиться на тестах.
Завершающие рекомендации.
Необходимо отметить, что создание ЕГЭ по математике базового уровня и появление акцента на использование математических знаний в реальных ситуациях были неверно истолкованы некоторыми учителями в качестве генеральной идеи обучения, что привело к поверхностному освоению обучающимися программы старшей школы. В частности, это зафиксировано и результатами экзамена: результаты выполнения заданий по темам курса старшей школы ниже результатов выполнения заданий из «реальной математики».
Для того чтобы успешно сдать ЕГЭ по математике, важно пройти всю программу целиком, а не только «то, что пригодится на экзамене», повысить свою культуру вычислений, то есть минимизировать использование калькуляторов, развивать умение читать графики, правильно использовать терминологию и учить формулы.
Для учащихся, которые могут успешно освоить курс математики средней (полной) школы на базовом уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на базовом уровне. Помимо заданий базового уровня в образовательном процессе должны использоваться задания повышенного уровня. Количество часов математики должно быть не менее 5 часов в неделю.
Для учащихся, которые могут успешно освоить курс математики полной (средней) школы на профильном (повышенном) уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на профильном уровне. Количество часов математики должно быть не менее 6–7 часов в неделю.
В первую очередь нужно выработать у обучающихся быстрое и правильное выполнение заданий части 1, используя, в том числе и банк заданий экзамена базового уровня. Умения, необходимые для выполнения заданий базового уровня, должны быть под постоянным контролем.
Задания с кратким ответом (повышенного уровня) части 2 должны находить отражение в содержании математического образования, и аналогичные задания должны включаться в систему текущего и рубежного контроля.
В записи решений к заданиям с развернутым ответом нужно особое внимание обращать на построение чертежей и рисунков, лаконичность пояснений, доказательность рассуждений.
И в завершение необходимо отметить, что еще одним важным фактором является психологический климат в учебном коллективе: дружеские отношения среди одноклассников, спокойная рабочая атмосфера на уроке, методичная, прозрачная и последовательная подготовка к экзамену, доверительные отношения учителя с учениками, вера в достижение более высоких результатов и эмоциональная поддержка.
На занятиях стараюсь создать атмосферу комфортности,
взаимопонимания. На своих уроках я делаю установку на то, чтобы любой ребенок должен быть понят и услышан учителем и соучеником: учение должно проходить в «атмосфере непринужденности, чтобы дети и учитель свободно дышали на уроках». От учителя требуется и мастерство, и большое терпение, и любовь к учащимся. Доброжелательное отношение к ученикам снимает у них страх перед трудностями обучения: ребенок не должен бояться
ошибиться, спросить учителя, если он что то прослушал или не понял. Психологическая подготовка учащихся, может заключается в следующем:
отработка поведения в период подготовки к экзамену; обучение навыкам
саморегуляции, самоконтроля, повышение уверенности в себе, в своих силах. Методы проведения занятий по психологической подготовке учащихся разнообразны: групповая дискуссия, игровые методы, медитативные техники, Содержание занятий должно ориентироваться на следующие вопросы: как подготовиться к экзаменам, поведение на экзамене, способы снятия нервнопсихического напряжения, как противостоять стрессу.
Литература:
Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2019 года по математике, подготовленные ФГБНУ «ФИПИ».
Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2020 года по математике, подготовленные ФГБНУ «ФИПИ».
Бабанский Ю.К. Активность и самостоятельность учащихся в обучении / М.Ю. Бабанский М., Педагогика, 1989.
Беспалько В.П. Слагаемые педагогической технологии / Беспалько В.П. – М., 1989.
Красновский Э.А. Активизация учебного познания / Красновский Э.А. // Советская педагогика. – 1989. №5.
Эльконин Д. Б. Избранные педагогические труды. / Под ред. В.В. Давыдова, В.П. Зинченко.М., 1989.
Щукина Г.И. Активизация познавательной деятельности в учебном процессе/ Щукина Г.И. М., 1979.
1. Задание
№25787
Какое из приведённых высказываний учителя является подсказкой?
«Внимательно прочти условие задачи»
«Хорошо подумай»
«Вспомни задачу, которую мы решали на прошлом уроке»
«Подумай о других способах решения»
2. Задание
№25788
Умение переформулировать условие задачи важно уметь использовать при решении:
Тригонометрических уравнений
Нестандартных задач
Трудоёмких в плане вычислений задач
Показательных неравенств
3. Задание
№25789
Рекомендуемое количество часов математики для тех, кто планирует сдавать профильный ЕГЭ, составляет:
Не менее 4-5 часов в неделю
Не менее 5-6 часов в неделю
Не менее 7-8 часов в неделю
Не менее 6-7 часов в неделю
4. Задание
№25790
Привычка повторять разобранные ранее варианты подготовки к ЕГЭ:
Оказывает положительное влияние на уровень подготовки к экзамену
Часто идёт во вред обучению
Способствует лучшему усвоению программы
Никак не влияет на уровень подготовки к экзамену
5. Задание
№25791
Практико-ориентированные задачи следует включать в изучение математики:
Только в старшей школе
Только в средней школе
Только по мере необходимости в рамках подготовки к ЕГЭ
И в средней, и в старшей школе
6. Задание
№25792
Какое задание из перечисленных не относится к практико-ориентированным?
Задача на проценты
Задача на вычисление вероятности события
Задача на вычисление площадей по рисунку
Задание на исследование функции с помощью производной
7. Задание
№25793
Ценность приёма «мозговой штурм», который можно условно разделить на два последовательных этапа, заключается:
В стимулировании критичности мышления на обоих этапах
В стимулировании поисковой активности на первом этапе и критичности мышления на втором этапе
В стимулировании поисковой активности на обоих этапах
В стимулировании критичности мышления на первом этапе и поисковой активности на втором этапе
8. Задание
№25794
При изучении какой темы курса «Алгебра и начала анализа» оказывается полезным умение вычислять площадь фигур по клеточкам?
Применение производной к исследованию функций
Первообразная и интеграл
Функционально-графический метод решения уравнений
Производная и её геометрический смысл
«Из опыта работы по подготовке учащихся к сдаче
государственной итоговой аттестации по математике»
Роль математики в современной жизни возрастает
.Человек в современном обществе должен быть математически грамотным ,чтобы
воплотить свою мечту , получить профессию , вести активную жизнь . В
связи со стратегическими направлениями социально — экономического
развития России : «Приоритетной государственной
задачей является обеспечение качественного
базового уровня математических и
естественнонаучных знаний у всех выпускников школы, не только будущих ученых, но и будущих квалифицированных
рабочих…»
Ведущей целью
школьного математического образования является интеллектуальное развитие и
формирование качеств мышления учащихся, необходимых для полноценной жизни в
обществе. В школе работаю 40 лет учителем математики и каждый год проходим с
детьми государственную итоговую аттестацию в 9,11 классах (ОГЭ, ЕГЭ,ГВЭ )
Цель моей
работы – не только подготовить ученика к прохождению итоговой аттестации, но
заложить фундамент знаний по математике, необходимый для продолжения
образования в 10 — 11 классах и в ВУЗе.
И приходится
делать каждый раз, когда начинаешь подготовку с очередным классом – это начать
с подготовки себя самой: составить рабочую программу, прорешать не один вариант
заданий. Ежегодно вводят изменения в структуру КИМов, в содержании материала. В
11 классе материал разделен на два уровня: базовый и профильный. В 9 классе
добавили практико-ориентированные задачи. Решение задач требует от учеников
логического мышления, умения представлять ситуацию, сообразительность.
Плодотворно
начинаем работать с сентября месяца в 9,11 классах. А к итоговой аттестации
начинаю готовиться с 7
класса. С учащимися ведем тетради по теории и практике. В тетрадях по теории
пишем алгоритмы, приемы решений, формулы, а в тетрадях по практике решаем
задания из открытого банка заданий ФИПИ и задания с сайтов решу ОГЭ,ЕГЭ,ГВЭ,
которые соответствуют темам из рабочей программы по математике.
Эта
работа продолжается на всем протяжении обучения. Каждый урок начинается с
устных упражнений на применение таблицы умножения, вычислительных навыков и
плавно переходим к сложным заданиям.
Начиная
подготовку, и в процессе подготовки всем учащимся рассказываю, как лучше
организовать своё рабочее место для подготовки к экзаменам, составить план
занятий, разработать индивидуальный режим дня, с чего начать занятие, как
учитывать особенности запоминания, использовать методы релаксации и
активизации, приемы снижения экзаменационной тревожности, как организовать день
перед экзаменом, настроить свои мысли на успех, как вести себя на экзамене, использовать
полезные ссылки на Интернет-ресурсы по подготовке.
Родителей
учащихся знакомлю с организацией и проведением ГИА и с тем, как необходимо к
экзамену подготовиться, чтобы получить высокий результат, набрать максимальное
количество баллов.
На первом занятии знакомлю учащихся с
нормативно-правовыми документами, провожу инструктаж по правилам выполнения
КИМов. Знакомимся с содержанием работ, их особенностями. В классе оформляю стенд, где размещаю задания из КИМов,
критерии оценивания заданий и правила перевода первичных баллов. Подготовка
к ЕГЭ требует индивидуального, личностно-ориентированного подхода.
Повысить уровень обученности и качество знаний
учащихся позволяет использование мониторинга знаний умений и навыков,
применение самодиагностики, самооценки, проведение индивидуальной работы
с учениками по ликвидации пробелов в знаниях. Хороший результат отслеживания
показателей обучения каждого выпускника дают работы (пробный экзамен), которые
провожу ежемесячно с ноября по апрель в 9-11 классах.
Для эффективной подготовки к ЕГЭ и ОГЭ нужна тренировка,
тренировка и еще раз тренировка. Важно довести решение задач до автоматизма.
Поэтому решаем до 50 типов заданий по каждой теме, но они отличаются друг от
друга. Ребятам приходится думать, использовать знания не в стандартной
ситуации. Это укрепляет знания и снимает тревожность, если задания будут не
похожие.
Практика показывает, что
прорешивание открытых вариантов ЕГЭ прошлых лет не даёт ожидаемого эффекта.
Разобрав вариант в классе, учитель даёт аналогичный вариант для домашнего
разбора. После удачного разбора в классе домашний вариант не представляет большого
труда, и у обучающегося и учителя складывается ложное впечатление, что
подготовка идет эффективно и цель достигнута. Многократное повторение этих
манипуляций не улучшает ситуацию. Когда участник на ЕГЭ получает свой вариант,
он обнаруживает, что этот вариант он с учителем не решал. Привычка повторять
разобранные ранее варианты часто идет во вред обучению.
Правильным подходом
является систематическое изучение материала, решение большого числа задач по
каждой теме – от простых к сложным, изучение отдельных методов решения задач.
Разумеется, варианты подготовительных сборников, открытые варианты можно и
нужно использовать в качестве источника заданий, но их решение не должно
становиться главной целью; они должны давать возможность иллюстрировать и
отрабатывать те или иные методы. В любом случае, при проведении диагностических
работ следует подбирать задачи, прямые аналоги которых в классе не разбирались.
Только так учитель может составить верное представление об уровне знаний и
умений своих учеников
Этот нелёгкий процесс более эффективен в случае, когда
сами учащиеся осознанно прогнозируют результаты своего обучения. Определив
типологию пробелов в знаниях учащихся по итогам очередной тестовой работы, я вношу корректировку в
календарно-тематическое планирование, организую уроки разноуровнего обобщающего
повторения. Сейчас издано огромное количество сборников тестов для подготовки к
ОГЭ, ЕГЭ. По таким сборникам мы работаем в течение уже восьми лет.
Предлагаю два способа использования готовых решений
при подготовке. Первый способ – изучить решение, повторить самостоятельно,
осмысленно и осознанно воспроизвести все логические шаги и вычисления. Затем
взять задание того же плана, но без решения и еще раз воспроизвести все
логические построения и вычисления. Второй способ – изучить теорию и
попробовать решить похожую задачу. Проверить ответ. У нас в школе по учебному
плану провожу индивидуальные консультации по подготовке к итоговой аттестации.
Я работаю в сельской средней школе, мои
ученики имеют разные учебные возможности и
понятно, что без прочного усвоения базовых
знаний детьми невозможно дальнейшее обучение.
Уделяю внимание технике выполнения экзаменационной работы:
В своей работе применяю следующие принципы для эффективной подготовки к
ОГЭ и ЕГЭ:
1.
Эффективнее
выстраивать
такую подготовку, соблюдая принцип от простых
типовых заданий к сложным. На этапе освоения знаний необходимо подбирать материал в виде логически
взаимосвязанной системы, где из одного следует другое.
2.
На
консультациях учащимся предлагаются тренировочные
тесты, выполняя которые дети могут оценить степень подготовленности к экзаменам.
3.
На
консультациях ученик может не только
выполнить тест, но и получить
ответы на вопросы, которые вызвали затруднение. Все тренировочные тесты следует проводить с ограничением времени, чтобы
учащиеся могли контролировать себя за
какое время сколько заданий они
успевают решить.
4.
Нагрузки
по содержанию и по времени для
всех учащихся одинаковы. Это необходимо, поскольку тест по своему назначению ставит
всех в равные условия и предполагает объективный контроль результатов.
Следуя этим принципам, формирую у учеников навыки самообразования,
критического мышления, самоорганизации и самоконтроля, самостоятельной
работы.
Моя цель состоит в том, чтобы помочь каждому школьнику научиться
быстро решать задачи, оформлять их чётко и компактно. Развиваю способность
мыслить свободно, без страха, творчески.
Стараюсь давать возможность каждому школьнику расти настолько, насколько он способен.
В связи с введением обязательного ЕГЭ и ОГЭ по математике
возникает необходимость научить учащихся решать быстро и качественно задачи
базового уровня.
При этом необыкновенно возрастает роль устных
вычислений, так как на экзамене не разрешается
использовать калькулятор и таблицы. Можно
научить учащихся выполнять простейшие преобразования
устно. Конечно, для этого потребуется
организовать отработку такого навыка до
автоматизма, на каждом уроке отвожу 5 7 минут для
проведения упражнений устных вычислений, предусмотренных
программой каждого класса и изучение таблицы умножения на пальцах.
Устные упражнения активизируют мыслительную деятельность учащихся,
требуют
осознанного усвоения учебного материала; при их
выполнении развивается память, речь, внимание, быстрота реакции.
·
Если в 5 и 6 классах устный счет – это выполнение действий с числами: натуральные
числа, обыкновенные дроби, десятичные дроби, то в старших
классах – это могут быть:
·
7 класс: Формулы
сокращенного умножения. Решение простейших линейных
уравнений. Действия со степенью. График линейнойфункции.
·
8 класс:
Линейные неравенства и числовые промежутки. Решение простейших линейных
неравенств. Решение квадратных уравнений с помощью
теоремы Виета и частных случаев.
Арифметический квадратный корень и его свойства.
·
9 класс: Решение неравенств 2 степени. Преобразование графиков функций.
Формулы приведения. Значения тригонометрических функций.
·
10 — 11 классах: Вычисление
производных. Простейшие тригонометрические неравенства.
Тригонометрические формулы. Простейшие тригонометрические
уравнения. Функции, обратные тригонометрическим.
Преобразование графиков функций. Вычисление первообразных.
Свойства логарифмов. Простейшие показательные
уравнения и неравенства. Простейшие логарифмические уравнения и неравенства.
Практика
показала, что систематическая работа с
устным счетом способствует значительному повышению
продуктивности вычислений и преобразований. Сокращается
время на выполнение таких операций,
что переводит их из разряда самостоятельной
задачи в разряд вспомогательной и
становится инструментом для решения более сложных
задач.
Из опыта моей
работы учителем математики знаю, с чем придется столкнуться школьнику на
экзамене, поэтому кроме создания фундамента прочных базовых
знаний, уделяю большую часть времени на
занятия по
отработке вопросов специфики ЕГЭ и ОГЭ.
Правильность оформления заданий, тактика и
стратегия решения в условиях дефицита выделенного
времени на экзамене, а также банальная
невнимательность — эти и масса других особенностей составляют
суть специфики подготовки учащихся к итоговой аттестации.
Думаю, что такая
работа по подготовке к экзаменам, а также доверительные отношения между
учителем и каждым учеником направлены на достижение главной цели на данный
период времени – успешной сдаче ОГЭ, ЕГЭ.
Рекомендации по подготовке обучающихся к успешной сдаче ЕГЭ по математике.
Содержание:
Рекомендации по совершенствованию преподавания математики с учётом результатов ЕГЭ. Некоторые эффективные приёмы обучения математике. Развитие геометрических представлений. Саморегуляция и обратная связь «ученик-учитель». Завершающие рекомендации.
Лекция.
Рекомендации по совершенствованию преподавания математики с учётом результатов ЕГЭ.
В основу построения рекомендаций положены принципы развития математического образования, определение приоритетных и перспективных направлений, а также анализ наиболее типичных ошибок, допущенных в решении заданий базового и профильного экзамена.
Практика показывает, что прорешивание открытых вариантов ЕГЭ прошлых лет не даёт ожидаемого эффекта. Разобрав вариант в классе, учитель даёт аналогичный вариант для домашнего разбора. После удачного разбора в классе домашний вариант не представляет большого труда, и у обучающегося и учителя складывается ложное впечатление, что подготовка идет эффективно и цель достигнута. Многократное повторение этих манипуляций не улучшает ситуацию. Когда участник на ЕГЭ получает свой вариант, он обнаруживает, что этот вариант он с учителем не решал. Привычка повторять разобранные ранее варианты часто идет во вред обучению.
Правильным подходом является систематическое изучение материала, решение большого числа задач по каждой теме – от простых к сложным, изучение отдельных методов решения задач. Разумеется, варианты подготовительных сборников, открытые варианты можно и нужно использовать в качестве источника заданий, но их решение не должно становиться главной целью; они должны давать возможность иллюстрировать и отрабатывать те или иные методы. В любом случае, при проведении диагностических работ следует подбирать задачи, прямые аналоги которых в классе не разбирались. Только так учитель может составить верное представление об уровне знаний и умений своих учеников.
Компенсирующее обучение в старших классах.
Часто мы сталкиваемся с ситуацией, когда главенствующим методическим принципом оказывается принцип «прохождения программы», – то есть программа должна быть пройдена во что бы то ни стало, невзирая на то, что содержание этой программы может не отвечать реальным возможностям и подготовке обучающихся.
С введением нового ФГОС, реализацией Концепции развития математического образования, принятием федеральных примерных образовательных программ по математике принцип прохождения программы приобретает новый смысл – обучающийся должен участвовать в посильной интеллектуальной математической деятельности, дающей осязаемые плоды обучения.
Компенсирующая программа как вариант базовой программы для старших классов даёт возможность учителю сделать уроки математики для наименее подготовленных обучающихся осмысленными. При этом появляется реальная возможность эффективно подготовить обучающихся к базовому ЕГЭ или к решению 8 – 10 заданий профильного ЕГЭ.
Практико-ориентированная математика.
Важной частью ЕГЭ по математике и современных программ являются задачи на применение математических знаний в быту, в реальных жизненных ситуациях. Это задачи на проценты, оптимальный выбор из предложенных вариантов, чтение данных, представленных в виде диаграмм, графиков или таблиц, вычисление площадей или других геометрических величин по рисунку, задачи на вычисление по формулам и т.п.
Круг практико-ориентированных задач в ОГЭ и ЕГЭ обоих уровней постоянно расширяется; дополнительно к ним следует отнести задачи вероятностно-статистического блока.
Сложилась практика, когда к практическим задачам учитель приступает только в последний год перед сдачей ЕГЭ. К этому времени обучающиеся успели прочно забыть, как вычислять проценты, как находить площади фигур с помощью палетки или на клетчатой бумаге – все эти задачи для них оказываются новыми.
На протяжении всего периода обучения математике не следует отрываться от простых практических задач; их следует включать в блоки повторения в начале и конце учебного года, в текущий, внутришкольный контроль. Задачи на вычисление сумм налогов, процентов по банковскому вкладу или кредиту, другие задачи финансового характера должны стать постоянным инструментом на уроках математики, поскольку эти задачи связывают наш предмет с окружающим миром и повседневной жизнью.
С 2010 года удалось изменить ситуацию, когда перевод одних единиц в другие или деление с остатком вызывал затруднения у 60 – 70% участников ЕГЭ. Сейчас на практическом уровне ситуация существенно улучшилась.
Практико-ориентированные задачи по финансовой грамотности, геометрического плана, чтение таблиц и графиков нужно включать в изучение математики в средней и старшей школе. При этом характер и трудность задач могут меняться со временем, более того, это необходимо для органического вплетения практических тем в изучение теоретических вопросов. Например, задачи на вклады и кредиты органично возникают при изучении прогрессий, показательной функции и производных. Вычисление площадей по клеточкам очень часто помогает при изучении совершенно абстрактной, казалось бы, темы «первообразная и интеграл». Чтение простых графиков помогает понять и грамотно на качественном уровне применять производную.
Отдельную важную роль в сближении школьной математики с задачами окружающего мира играют вопросы вероятностей и статистики.
ТВ и статистика.
В Концепции развития математического образования ТВ и статистика названы в числе перспективных и важных направлений развития школьной математики. С 2012 года задачи по ТВ формально включаются в КИМ ОГЭ и ЕГЭ. При этом учителя понимают, что те задачи, которые сейчас есть в открытом банке заданий и те, что включены в экзамен, в большинстве случаев сводятся к перечислению равновозможных исходов.
Ясно, что роль ТВ и статистики в школьной математике будет расти. Одновременно будет расширяться круг тем, подлежащих контролю.
При обучении математике следует больше внимания уделять темам вероятности и статистики, постепенно нарабатывая опыт преподавания этих разделов, которые оказываются наиболее практически направленными. Изучение вероятности и статистики требуется вести в тесной привязке к темам алгебры и геометрии, поскольку систематический подход к вопросам ТВ требует от обучающихся знаний о свойствах геометрической прогрессии преобразованиях многочленов, корнях и степенях, площадях фигур.
Таким образом, правильно выстроенное преподавание вероятности не отнимает время, а, напротив, поддерживает изучение традиционных разделов школьной математики. В 2012 – 2014 году задачи по ТВ, появившись в экзамене, вызывали большие трудности, и выполнение этих заданий редко поднималось выше 50%. В настоящее время ситуация изменилась. На данный момент в базовом экзамене медиана выполнения задания 10 – около 70% по разным вариантам, а в профильном – около 90%.
Некоторые эффективные приёмы обучения математике.
Остановимся подробнее на некоторых приёмах обучения математике, доказавших свою эффективность.
1) При решении задач одним из эффективных приёмов является использование примеров и образцов. Скажем, ученик получает задачу и готовое решение, которое он должен разобрать самостоятельно. Решение может быть дополнено советами, комментариями трудных или «опасных» моментов, другими способами решения и т.п. Когнитивная нагрузка в данном случае получает управляющий импульс и осуществляется в заданном направлении. Важным условием является выход на стратегию, которую можно будет применить в дальнейшем при решении широкого круга задач. Следующим этапом может стать работа не с готовым решением, а с заданным алгоритмом решения, который ученик должен самостоятельно применить к данной ему задаче. После этого можно провести решение полностью самостоятельно. Покажем это (без потери общности) на простой задаче.
Условие. Каждый из двух друзей одновременно показывает на руке случайное количество пальцев от 1 до 5. С какой вероятностью в сумме получится число 8?
Решение. Общее число исходов равно: 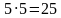
Комментарий. Следует различать две комбинации, когда один из друзей показывает 3 пальца, а другой – 5 пальцев. Ответ можно записать как обыкновенной дробью, так и десятичной.
Задание для самостоятельного решения. Каждый из двух друзей показывает на руке случайное количество пальцев от 1 до 5. С какой вероятностью в сумме получится число 7?
Описанный приём может использоваться применительно к отдельному заданию, однако из таких заданий – с решениями и комментариями – можно составить тематическую проверочную работу, которую можно использовать и в рамках подготовки к экзамену. Решения могут быть написаны учителем самостоятельно, могут быть взяты из публикуемых сборников для подготовки к ЕГЭ, а также из материалов журнала «Математика» или других источников.
2) Весьма эффективно использование при решении задач подсказок, то есть некоторой дополнительной информации, которая дается ученику после (что важно!) того, как он начал работать над задачей. Чем определеннее подсказка, тем больше из нее можно извлечь. Фразы: «Хорошо подумай», «Внимательно прочти условие задачи», «Подумай о других способах решения» подсказками не являются, поскольку они никак не направляют ход мысли и не помогают найти решение.
6
Пример.
Решите уравнение 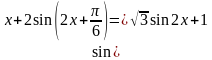
Подсказка. Можно применить формулу синуса суммы двух углов. Подсказкой может быть похожая задача, которая решалась недавно, указание на конкретный метод. Всегда полезно использовать результаты, методы уже решённых задач, а также опыт, приобретенный при решении. Это широко используется в школьном курсе геометрии, где многие важные геометрические факты, которыми целесообразно пользоваться при решении других задач, даны не в виде утверждений (теорем), а в виде задач. Кроме того, это возможность использования еще одного метода – аналогии.
При решении тригонометрических уравнений подсказкой может быть определённая формула, а при решении логарифмического уравнения – свойство логарифма. Полезно учить пользоваться подсказками, искать их самостоятельно, а также учить давать подсказки.
3) При обучении решению сложных или трудоёмких в плане вычислений и преобразований задач полезно использовать групповые формы работы, а в качестве приёма – мозговой штурм. Основные принципы мозгового штурма: на первом этапе – предложение как можно большего количества решений, без оценки их применимости, рациональности и проч., на втором – анализ и вывод о целесообразности предложенного, выбор наиболее удачных идей и предложений. Ценность приема – в стимулировании поисковой активности на первом этапе и критичности мышления на втором. Хорошо применим данный прием при поиске различных способов решения геометрических задач и тригонометрических уравнений.
4) При решении текстовых задач важным приёмом, необходимым для усвоения, является переформулирование условия, отношений, связывающих входящие в задачу величины. Ниже приводится пример такой задачи из варианта профильного экзамена.
«Задание 11. Заказ на изготовление 323 деталей первый рабочий выполняет на 2 ч быстрее, чем второй. Сколько деталей изготавливает первый рабочий, если известно, что он изготавливает на 2 детали больше второго?»
Данную задачу экзаменуемые решили существенно хуже, чем аналогичную задачу с более привычной и хорошо отработанной фабулой, связанной с движением двух велосипедистов.
Умение переформулировать условие важно и при решении нестандартных задач, то есть таких, метод решения которых ученику не известен, не изучался и не отрабатывался на уроках.
Ещё более актуально это умение при решении практико- ориентированных задач, представляющих собой некоторую ситуацию из реальной жизни, которую необходимо преобразовать и описать на языке математики (то есть самостоятельно сформулировать задачу). В самом простом случае основа задачи будет следующая: за лестницей, которую прислонили к стене дома, надо распознать прямоугольный треугольник, гипотенузой которого и будет данная лестница.
Развитие геометрических представлений
Процент выполнения экзаменующимися геометрических заданий традиционно ниже, чем процент выполнения заданий алгебраических. Одна из основных причин – недостатки в формировании пространственного мышления учащихся. Массово эта проблема проявилась с уходом из общего образования такого учебного предмета, как черчение, и вряд ли стоит ожидать его возвращения – профессия конструктора перестала быть столь массово востребованной с приходом компьютерных технологий.
Эта проблема легла на плечи учителей математики, однако решение её известно: непрерывное развитие геометрических представлений и геометрического воображения обучающихся с 1 по 11 класс; наглядная геометрия в 1–6 классах; больше внимания геометрическому моделированию и конструированию (из плоских и пространственных фигур), геометрическим чертежам, построениям, изображениям от руки и с помощью различных чертёжных инструментов, на нелинованной и клетчатой бумаге.
Это отнюдь не означает, что всю геометрию надо свести к наглядности и к работе руками. Определения и доказательства, логика и аксиоматика важны для современного человека и для изучения геометрии не менее, но надо понимать, что в развитии человека всему отводится свое время, а несформированное наглядно-образное мышление, которое должно быть основой и этапом на пути формирования логического мышления, просто мешает его формированию.
Если вернуться к этапу обучения в старшей школе, то целесообразно использовать любые приёмы и средства, которые способствовали бы визуализации предлагаемых обучающимся задач. Это не только построение чертежей по условию задачи (что непросто сделать при проблемах с пространственным воображением), это прежде всего различные предметные модели (полезно для каждой решаемой задачи иметь соответствующую ей модель-подсказку, чтобы использовать её для визуализации условия, поиска и проверки решения), компьютерные программы, позволяющие выполнять стереометрические чертежи.
Полезно выделить эту работу в отдельный тематический практикум, на котором обучающиеся тренировались бы в изображении и моделировании пространственных тел, построении чертежей по условию задачи (в различных ракурсах, выбирая наиболее удобный для поиска решения), можно также организовать данную работу в рамках проекта.
Саморегуляция и обратная связь «ученик-учитель».
Известно, что эффективность обучения возрастает в случае самооценивания, поскольку ученик самостоятельно получает информацию о своих результатах, сам её анализирует, делает выводы о своем прогрессе, корректирует цели в случае необходимости. Но для этого необходимы критерии оценивания работы, которые должны быть у ученика не просто до начала выполнения конкретной работы, но желательно и в самом начале изучения темы. К сожалению, на практике более распространена ситуация, когда работа выдаётся ученику без критериев ее выполнения.
К саморегуляции относятся также вопросы, связанные с осознанностью знания и незнания. Объяснение учителя сродни лекционной форме предъявления новых знаний. В связи с этим подчеркнём важность обратной связи. Учитель должен получать сигналы от обучающихся: «Я понимаю, могу объяснить», «Я не уверен, правильно ли я понимаю», «Я не понимаю». Учитель может прервать своё объяснение вопросом к тем, кто ещё не понял, предложением высказать свои сомнения тем, кто не уверен в понимании, предоставлением слова тем, кто всё понял.
Доказано, что обратная связь эффективна, если ученик получает сообщение о верно выполненных заданиях, а не только об ошибках, если он получает не просто маркеры, свидетельствующие о положительном результате, не просто похвалу за решённую задачу, а и некоторый содержательный комментарий. Этот комментарий может включать в себя такую оценку, как «рациональное решение», «красивое решение», «интересная идея», «грамотная запись». Может быть отмечена актуальность проверки результата, удачное прохождение «ловушек» и «опасных» мест и т.п.
Обратная связь эффективна в случае, если она конкретна, то есть связана с известными ученику результатами и действиями, подлежащими усвоению. Важное значение имеет информированность ученика относительно того, чему он должен научиться, какие задания должен научиться решать, а какие может научиться решать для того, чтобы получить желаемое количество баллов на экзамене. Если ученик фиксирует и отслеживает сам, умеет ли он выполнять требуемое задание или нет, то минимизируется время на выполнение заданий, при этом работа становится более эффективной и рациональной. Отсюда необходимость в открытости предъявляемых требований к результатам обучения, а на этапе подготовки к экзамену – в ориентации на конечный запланированный результат.
И еще об одном факторе следует упомянуть – это повторяющееся тестирование. Уже имеющийся опыт российской школы и более продолжительный зарубежный опыт не позволяют говорить о нём, как об эффективном факторе. Положительные эффекты возникают только в тех случаях, когда учитель учитывает результаты тестирования для корректировки процесса обучения и приспосабливает методы обучения к возможностям конкретного ученика, учитывая его сильные и слабые стороны, или при условии содержательной обратной связи, с которой ученик может работать самостоятельно, то есть имеет возможность учиться на тестах.
Завершающие рекомендации.
Необходимо отметить, что создание ЕГЭ по математике базового уровня и появление акцента на использование математических знаний в реальных ситуациях были неверно истолкованы некоторыми учителями в качестве генеральной идеи обучения, что привело к поверхностному освоению обучающимися программы старшей школы. В частности, это зафиксировано и результатами экзамена: результаты выполнения заданий по темам курса старшей школы ниже результатов выполнения заданий из «реальной математики».
Для того чтобы успешно сдать ЕГЭ по математике, важно пройти всю программу целиком, а не только «то, что пригодится на экзамене», повысить свою культуру вычислений, то есть минимизировать использование калькуляторов, развивать умение читать графики, правильно использовать терминологию и учить формулы.
Для учащихся, которые могут успешно освоить курс математики средней (полной) школы на базовом уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на базовом уровне. Помимо заданий базового уровня в образовательном процессе должны использоваться задания повышенного уровня. Количество часов математики должно быть не менее 5 часов в неделю.
Для учащихся, которые могут успешно освоить курс математики полной (средней) школы на профильном (повышенном) уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на профильном уровне. Количество часов математики должно быть не менее 6–7 часов в неделю.
В первую очередь нужно выработать у обучающихся быстрое и правильное выполнение заданий части 1, используя, в том числе и банк заданий экзамена базового уровня. Умения, необходимые для выполнения заданий базового уровня, должны быть под постоянным контролем.
Задания с кратким ответом (повышенного уровня) части 2 должны находить отражение в содержании математического образования, и аналогичные задания должны включаться в систему текущего и рубежного контроля.
В записи решений к заданиям с развернутым ответом нужно особое внимание обращать на построение чертежей и рисунков, лаконичность пояснений, доказательность рассуждений.
И в завершение необходимо отметить, что еще одним важным фактором является психологический климат в учебном коллективе: дружеские отношения среди одноклассников, спокойная рабочая атмосфера на уроке, методичная, прозрачная и последовательная подготовка к экзамену, доверительные отношения учителя с учениками, вера в достижение более высоких результатов и эмоциональная поддержка.
Литература:
-
Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2018 года по математике, подготовленные ФГБНУ «ФИПИ».
-
Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2017 года по математике, подготовленные ФГБНУ «ФИПИ».
4
Роль методов повторения на уроках при подготовке к ОГЭ по математике
- 19.04.2018
- 4271 Просмотр
- Обсудить
Берсенева Татьяна Алексеевна, преподаватель
Нязепетровский филиал ГБПОУ «Каслинский промышленно-гуманитарный техникум»
г. Нязепетровск, Челябинская область
Аннотация. Любой учитель, работающий в 9 классе, с тревогой и волнением ожидает успешной сдачи основного государственного экзамена каждым выпускником. При этом было бы хорошо, чтобы результаты основного государственного экзамена соответствовали потенциальным возможностям выпускников основной школы. Я думаю, что с этим мнением согласны и обучающиеся и их родители.
Как и прежде, содержание и структура экзаменационной работы предусматривают проверку наличия у учащихся базовой математической компетентности и математической подготовки повышенного уровня.
Введение государственной итоговой аттестации по математике в новой форме (ОГЭ) в 9 классе вызывает необходимость изменения в методах и формах работы учителя.
Данная необходимость обусловлена тем, что изменились требования к знаниям, умениям и навыкам учащихся в материалах экзамена по математике. Существенно сместился акцент к требованиям умений и навыкам. Изменилась формулировка вопросов: вопросы стали нестандартными, задаются в косвенной форме, ответ на вопрос требует детального анализа задачи. И это всё в первой части экзамена, которая предусматривает обязательный уровень знаний. Содержание задач изобилует математическими тонкостями, на отработку которых в общеобразовательной программе не отводится достаточное количество часов. В обязательную часть включаются задачи, которые либо изучались давно, либо на их изучение отводилось малое количество времени (проценты, стандартный вид числа, свойства числовых неравенств, задачи по статистике, чтение графиков функций), а также задачи, требующие знаний по другим предметам, например, по физике.
К сожалению, научно-методические службы не всегда могут обеспечить школы новыми, соответствующими современным требованиям, учебно-методическими комплексами, поэтому учителям приходится самим находить пути решения данной проблемы. И здесь уже однозначного решения нет, так как подготовленность детей разная, уровень классов разный.
В общеобразовательных классах основное внимание нужно уделить отработке первой части экзамена по математике, так как только первая часть обеспечивает удовлетворительную отметку.
Подготовка к основному государственному экзамену существенно отличается от традиционной. В ОГЭ введено много прикладных, «жизненных» задач и ученикам, привыкшим к традиционным школьным контрольным работам или диктантами, иногда бывает поначалу совсем непросто.
Ключевые слова: ОГЭ, математика, экзамен, школа, мотивация.
В связи с внедрением ОГЭ в практику школы, становится актуальной проблема подготовки школьников к экзамену. Поскольку основные проблемы были выявлены в подготовке слабых учащихся и учащихся, желающих получить отличные отметки, необходимо всесторонне развивать разноуровневое обучение и обобщающее повторение.
Роль методов повторения на уроках при подготовке к ОГЭ по математике велика, так как повторение обеспечивает прочность усвоения знаний. Умственное развитие при повторении обеспечивается его вариативностью. Обычно повторение проводится на новых примерах, в ином порядке с применением новых способов деятельности.
Каждый учитель сталкивается с проблемой повторения и закрепления материала. Решение этой проблемы начинается с обеспечения положительной мотивации учащихся на повторение ранее изученного и усвоенного материала, раскрывается перспектива учебной деятельности, устанавливается связь учебного материала, предназначенного для повторения, с идеями, которые предстоит освоить, ученики убеждаются, что эти идеи интересны и важны [1, с. 36].
Одним из важнейших направлений совершенствования процесса обучения математике является целенаправленная систематическая работа учителя по организации повторения, эффективность которого определяется следующими принципами: целенаправленности, сознательности, активности и самостоятельности, регулярности и систематичности, проблемности, прочности и системности, доступности, дифференциации и индивидуализации.
Необходимость повторения обусловлена задачами обучения, требующими прочного и сознательного овладения ими.
Повторение учебного материала по математике осуществляется во всей системе учебного процесса: при актуализации знаний – на этапе подготовки и изучения нового материала, при формировании учителем новых понятий, при закреплении изученного ранее, при организации самостоятельных работ различных видов, при проверке знаний учащихся. А также, основная подготовка к ОГЭ осуществляется на уроках математики. Особую роль при новой форме проведения выпускного экзамена приобретает организация итогового повторения.
Методы и приемы повторения должны находиться в тесной связи с видами повторения. При повторении необходимо применять различные приемы и методы, сделать повторение интересным, путем внесения, как в повторяемый материал, так и в методы изучения некоторых элементов новизны. По поводу полезности многообразия методов и приемов весьма удачно выразился немецкий математик-педагог Керр: «Лучше одну теорему разобрать десятью способами, чем десять теорем одним способом». К сожалению, этому хорошему принципу следуют далеко еще не все преподаватели математики [5, с. 58].
Организация повторения в процессе обучения математике представляет собой довольно сложную в методическом отношении проблему предполагающую решение нескольких частных задач. Это и выбор учебного материала для повторения, и определение наиболее эффективных приемов и форм организации деятельности учащихся на уроках и дома, и выделение места для уроков повторения в структуре учебного процесса. В связи с этим решению данной проблемы был посвящен целый ряд исследований в области теории и методики обучения математике, а также психолого-педагогической науки. Причем она решалась в русле следующего направления.
Она реализовалось в рамках исследований, раскрывающих методику организации итогового повторения учебного материала в различных курсах [2, с. 98]. Исследуются возможности реорганизации учебного материала на заключительном этапе изучения математики 5-6 классов, геометрии 7-9 классов, алгебры 7-9 классов, начал стереометрии, а также систематизации заданного материала. Предлагается распределять материал по методическим линиям.
Я считаю, что для успешности повторения ранее изученного материала необходимо соблюдать следующие условия:
— повторять надо в течение всего учебного года,
— должна быть четкая целеустремленность в работе, сознательное отношение учащихся к повторению,
— тщательно отбирать материал и продумывать планирование его при повторении,
— стимулировать самостоятельность и активность в процессе повторения,
— правильно дозировать и распределять материал повторения во времени,
— органически связывать и продумывать сочетание отдельных видов повторения.
При повторении математики значительную часть времени приходится уделять теории, так как у учащихся возникает много вопросов, требующих более полного и глубокого освещения.
Уроки повторения должны быть продуманы как с точки зрения содержания, так и организации их. Постановка самих вопросов и разбор упражнений по своей форме и характеру должны заставлять несколько по-иному осмысливать прежний материал.
Ниже представлена классификация видов повторения. Я считаю ее наиболее подходящей и продуманной.
1. Повторение в начале учебного года.
2. Текущее повторение всего, ранее пройденного, а повторение пройденного в связи с изучением нового материала сопутствующее повторение б повторение пройденного вне связи с новым материалом.
3. Тематическое повторение, обобщающее повторение законченных тем и разделов программы.
4. Систематическое повторение учебного материала.
5. Заключительное повторение, организуемое при окончании прохождения большого раздела программы или в конце учебного года.
В качестве основных средств обобщения и систематизации знаний используются систематизирующие схемы и таблицы, решение задач разными способами, выполнение упражнении на классификацию понятий, воспроизведение и анализ теоретических положений и т. д.
Анализ учебно-методической и психологической литературы показал, что система уроков по повторению обеспечивает преподавание математики на должном уровне, а знания учащихся становятся достаточно полными и прочными.
Определены основные требования к организации повторения.
Однако, несмотря на это, можно отметить многие важные вопросы, связанные с повторением, которые не были до конца исследованы. В частности, организация итогового повторения осуществлялась в отрыве от других его видов: от повторения в начале учебного года и текущего. В то время как самими авторами не раз отмечалось, что эффективность заключительного повторения во многом определяется успешностью организации всех его видов. Но исследование, включающее в себя методику организации повторения на различных его этапах, до сих пор отсутствует. Это отрицательно сказывается на эффективности повторения в практике обучения математике в школе. Методика организации повторения должна наиболее оптимальным образом быть направлена на разрешение как можно большего числа задач в обучении математике, стоящих перед повторением. Оно должно выступать и как средство реализации внутрипредметных связей учебного материала, как способ предупреждения забывания знаний школьниками, и как один из путей реализации прикладной направленности обучения.
Библиографический список
1. Васильева И. В. Технология обобщения знаний учащихся в контексте ведущего понятия «Алгебраическая структура» // Актуальные проблемы обучения математике: Материалы Всероссийской научно-практической конференции.—т.2. —Орёл: Изд-во ОГУ, 2002. -С.24-28
2. Зайкин М. И. Методика обобщающего повторения при изучении математики в 9-10 классах средней школы: Дисс. канд. пед. наук. — Московский госпединститут им. В.И. Ленина —1984. —176с.
3. Суворова М. Математика в школе 1986 2. М Ройтман П. 10. 20.
4. http://nauka-pedagogika.com/pedagogika-13-00-02/dissertaciya-teoriya-i-praktika-povtoreniya-v-obuchenii-matematike-uchaschihsya-osnovnoy-shkoly#ixzz48ycP9pxg
5. http://www.telenir.net/psihologija/pedagogika_konspekt_lekcii/index.php
- 1
- 2
- 3
- 4
- 5
21.02.2022
ТЕМА: «ОБЕСПЕЧЕНИЕ ПОВЫШЕНИЯ КАЧЕСТВА ПОДГОТОВКИ УЧАЩИХСЯ К СДАЧЕ ОГЭ И ЕГЭ, К УЧАСТИЮ В ОЛИМПИАДАХ»
Возрастание роли математики в современной жизни привело к тому, что
для адаптации в современном обществе и активному участию в нем необходимо быть математически грамотным человеком. Приоритетной государственной задачей является обеспечение качественного базового уровня математических и естественнонаучных знаний у всех выпускников школы, не только будущих ученых, но и будущих. квалифицированных рабочих…»
Каждый школьник в процессе обучения должен иметь возможность получить полноценную подготовку к выпускным экзаменам.
Оценить
212
Содержимое разработки
ДОКЛАД
ТЕМА:
«ОБЕСПЕЧЕНИЕ ПОВЫШЕНИЯ
КАЧЕСТВА ПОДГОТОВКИ
УЧАЩИХСЯ К СДАЧЕ ОГЭ И
ЕГЭ,
К УЧАСТИЮ В ОЛИМПИАДАХ»
УЧИТЕЛЬ СЛАНОВА Л.Г.
В основу построения рекомендаций положены принципы развития математического образования, определение приоритетных и перспективных направлений, а также анализ наиболее типичных ошибок, допущенных в решении заданий базового и профильного экзамена.
Возрастание роли математики в современной жизни привело к тому, что
для адаптации в современном обществе и активному участию в нем необходимо быть математически грамотным человеком. Приоритетной государственной задачей является обеспечение качественного базового уровня математических и естественнонаучных знаний у всех выпускников школы, не только будущих ученых, но и будущих. квалифицированных рабочих…»
Каждый школьник в процессе обучения должен иметь возможность получить полноценную подготовку к выпускным экзаменам.
Формула успеха хорошо сдать экзамен ЕГЭ и ОГЭ по математике:
Высокая степень восприимчивости + мотивация + компетентный педагог.
Практика показывает, что прорешивание открытых вариантов ЕГЭ прошлых лет не даёт ожидаемого эффекта. Разобрав вариант в классе, учитель даёт аналогичный вариант для домашнего разбора. После удачного разбора в классе домашний вариант не представляет большого труда, и у обучающегося и учителя складывается ложное впечатление, что подготовка идет эффективно и цель достигнута. Многократное повторение этих манипуляций не улучшает ситуацию. Когда участник на ЕГЭ получает свой вариант, он обнаруживает, что этот вариант он с учителем не решал. Привычка повторять разобранные ранее варианты часто идет во вред обучению.
Правильным подходом является систематическое изучение материала, решение большого числа задач по каждой теме — от простых к сложным, изучение отдельных методов решения задач. Разумеется, варианты подготовительных сборников, открытые варианты можно и нужно использовать в качестве источника заданий, но их решение не должно становиться главной целью; они должны давать возможность иллюстрировать и отрабатывать те или иные методы. В любом случае, при проведении диагностических работ следует подбирать задачи, прямые аналоги которых в классе не разбирались. Только так/учитель может составить верное представление об уровне знаний и умений своих учеников.
Компенсирующее обучение в старших классах.
Часто мы сталкиваемся с ситуацией, когда главенствующим методическим принципом. Оказывается принцип «прохождения программы», — то есть программа должна быть пройдена во что бы то ни стало, невзирая на то, что содержание этой программы может не отвечать реальным возможностям и подготовке обучающихся.
С введением нового ФГОС, реализацией Концепции развития математического образования. принятием федеральных примерных образовательных программ по математике принцип прохождения программы приобретает новый смысл — обучающийся должен участвовать в посильной интеллектуальной математической деятельности, дающей Осязаемые плоды обучения.
Компенсирующая программа как вариант базовой программы для старших классов даёт возможность учителю сделать уроки математики для наименее подготовленных обучающихся осмысленными. При этом появляется реальная возможность эффективно подготовить обучающихся к решению 8 — 10 заданий профильного ЕГЭ.
Практико-ориентированная математика.
Важной частью ЕГЭ по математике и современных программ являются задачи на применение математических знаний в быту, в реальных жизненных ситуациях. Это задачи на, проценты, оптимальный выбор из предложенных вариантов, чтение данных, представленных в виде диаграмм, графиков или таблиц, вычисление площадей или других геометрических величин по рисунку, задачи на вычисление по формулам и т.п.
Круг Практико-ориентированных задач в ЕГЭ постоянно расширяется; дополнительно к ним следует отнести задачи вероятностно-статистического блока.
Сложилась практика, когда к практическим задачам учитель приступает только в последний год перед сдачей ЕГЭ. К этому времени обучающиеся успели прочно забыть, как вычислять проценты, как находить площади фигур с помощью палетки или на клетчатой бумаге — все эти задачи для них оказываются новыми.
На протяжении всего периода обучения математике не следует отрываться от простых практических задач; их следует включать в блоки повторения в начале и конце учебного года, в текущий, внутришкольный контроль. Задачи на вычисление сумм налогов, процентов по банковскому вкладу или кредиту, другие задачи финансового характера должны стать постоянным инструментом на уроках математики, поскольку эти задачи связывают наш предмет с окружающим миром и повседневной жизнью.
Практико-ориентированные задачи по финансовой грамотности, геометрического плана, чтение таблиц и графиков нужно включать в изучение математики в средней и старшей школе. При этом характер и трудность задач могут меняться со временем, более того, это необходимо для органического вплетения практических тем в изучение теоретических вопросов. Например, задачи на вклады и кредиты органично возникают при изучении прогрессий, показательной функции и производных. Вычисление площадей по клеточкам Очень часто помогает при изучении совершенно абстрактной, казалось бы, темы «первообразная и интеграл». Чтение простых графиков помогает понять и грамотно на качественном уровне применять производную.
Отдельную важную роль в сближении школьной математики с задачами окружающего мира играют вопросы вероятностей и статистики.
Теория.вероятности и статистика.
В- Концепции развития математического образования ТВ и статистика названы в числе перспективных и важных направлений развития школьной математики. С 2012 года задачи по ТВ формально включаются в КИМ ОГЭ и ЕГЭ. При этом учителя понимают, что те задачи, которое сейчас есть в открытом банке заданий и те, что включены в экзамен, в большинстве. случаев сводятся к перечислению равновозможных исходов.
Ясно, что роль ТВ и статистики в школьной математике будет расти. Одновременно будет расширяться круг тем, подлежащих контролю.
При обучении математике следует больше внимания уделять темам вероятности и статистики, постепенно нарабатывая опыт преподавания этих разделов, которые оказываются наиболее практически направленными. Изучение вероятности и статистики требуется вести в тесной привязке к темам алгебры и геометрии, поскольку систематический подход к вопросам ТВ требует от обучающихся знаний о свойствах геометрической прогрессии преобразованиях многочленов, корнях и степенях, площадях фигур.
Таким образом, правильно выстроенное преподавание вероятности не отнимает время, а, напротив’, поддерживает изучение традиционных разделов школьной математики. В 2012 -2014 году задачи по ТВ, появившись в экзамене, вызывали большие трудности, и выполнение этих заданий редко поднималось выше 50%. В настоящее время ситуация изменилась. На данный момент медиана выполнения задания 4 — около 90%.
Некоторые эффективные приёмы обучения математике.
Остановимся подробнее на некоторых приёмах обучения математике, доказавших свою эффективность.
-
При решении задач одним из эффективных приёмов является использование примеров и образцов. Скажем, ученик получает задачу и готовое решение, которое он должен разобрать самостоятельно. Решение может быть дополнено советами, комментариями трудных, или «опасных» моментов, другими способами решения и т.п. Когнитивная нагрузка в данном; случае получает управляющий импульс и осуществляется в заданном направлении. Важным условием является выход на стратегию, которую можно будет применить в дальнейшем при решении широкого круга задач. Следующим этапом может стать работа не с готовым решением, а с заданным алгоритмом решения, который ученик должен самостоятельно: применить к данной ему задаче. После этого можно провести решение полностью самостоятельно. Покажем это (без потери общности) на простой задаче:
Условие: Каждый из двух друзей одновременно показывает на руке случайное количество пальцев от 1 до 5. С какой вероятностью в сумме получится число 8?
Решение. Общее число исходов равно: 25. Благоприятными событию «получится в сумме число 8» будут исходы: 3 + 5, 5 + 3, 4 + 4. Вероятность события равна: 3/25 = 0,12. Ответ: 0,12,
Комментарий. Следует различать две комбинации, когда один из друзей показывает 3 пальца, а другой — 5 пальцев. Ответ можно записать как обыкновенной дробью, так и десятичной.
Задание для .самостоятельного решения. Каждый из двух друзей показывает на руке случайное количество пальцев от 1 до 5. С какой вероятностью в сумме получится число 7?
Описанный.приём может использоваться применительно к отдельному заданию, однако из таких заданий с решениями и комментариями — можно составить тематическую проверочную работу, которую можно использовать и в рамках подготовки к экзамену. Решения могут быть написаны учителем самостоятельно, могут быть взяты из публикуемых сборников для подготовки к ЕГЭ, а также из материалов журнала «Математика» или других источников.
-
Весьма эффективно использование при решении задач подсказок, то есть некоторой дополнительной информации, которая дается ученику после (что важно!) того, как он начал работать над задачей. Чем определеннее подсказка, тем больше из нее можно извлечь. Фразы: «Хорошо подумай», «Внимательно прочти условие задачи», «Подумай о других способах решения» подсказками не являются, поскольку они никак не направляют ход мысли и не помогают найти решение.
Пример. Решите уравнение
sinх + 2 sin (2х + 

Подсказка. Можно, применить формулу синуса суммы двух углов. Подсказкой может быть похожая задача, которая решалась недавно, указание на конкретный метод. Всегда полезно использовать результаты, методы уже решённых задач, а. также опыт, приобретенный при решении. Это широко используется в школьном курсе геометрии, где Многие важные геометрические факты, которыми целесообразно пользоваться при решении других задач, даны не в виде утверждений (теорем), а в виде задач. Кроме того, это возможность использования еще одного метода — аналогии.
При решении тригонометрических уравнений подсказкой может быть определённая формула, при решений логарифмического уравнения — свойство логарифма. Полезно учить пользоваться подсказками, искать их самостоятельно, а также учить давать подсказки.
-
При обучении решению сложных или трудоёмких в плане вычислений и преобразований задач полезно использовать групповые формы работы, а в качестве приёма, мозговой штурм. Основные принципы мозгового штурма: на первом этапе — предложение как можно большего количества решений, без оценки их применимости, рациональности и проч., на втором — анализ и вывод о целесообразности предложенного, выбор наиболее удачных идей и предложений. Ценность приема — в стимулировании поисковой активности на первом этапе и критичности мышления на втором. Хорошо применим данный прием при поиске различных способов решения геометрических задач и тригонометрических уравнений.
-
При решении текстовых задач важным приёмом, необходимым для усвоения, является переформулирование условия, отношений, связывающих входящие в задачу величины! Ниже приводится пример такой задачи из варианта профильного экзамена.
‘
«Задание 1.1. Заказ на. изготовление 323 деталей первый рабочий выполняет на 2 ч быстрее, чём второй. Сколько деталей изготавливает первый рабочий, если известно, что он изготавливает на 2 детали больше второго?»
Данную задачу экзаменуемые решили существенно хуже, чем аналогичную задачу с более привычной и хорошо отработанной фабулой, связанной с движением двух велосипедистов.
Умение переформулировать условие важно и при решении нестандартных задач, то есть таких, метод решения которых ученику не известен, не изучался и не отрабатывался на уроках.
Ещё более актуально. это умение при решении практике- ориентированных задач, представляющих собой некоторую ситуацию из реальной жизни, которую необходимо преобразовать и описать на языке математики (то есть самостоятельно сформулировать задачу. В самом простом случае основа задачи будет следующая: за лестницей, которую прислонили к стене дома, надо распознать прямоугольный треугольник, гипотенузой которого и будет данная лестница.
-
В связи с введением обязательного ЕГЭ и ОГЭ по математике
возникает, необходимость научить учащихся решать быстро и качественно задачи базового уровня. При этом необыкновенно возрастает роль устных вычислений, так как на экзамене не разрешается использовать калькулятор и таблицы. Можно, научить учащихся выполнять простейшие (и не очень) преобразования устно. Конечно, для этого потребуется организовать отработку такого навыка до автоматизма, на каждом уроке необходимо отводить 5-7 минут для проведения упражнений устных вычислений, предусмотренных программой каждого класса. Устные упражнения активизируют мыслительную деятельность учащихся, требуют осознанного усвоения учебного материала; при их выполнении развивается память, речь, внимание, быстрота реакции. Если в 5-6 классах устный счет — это выполнение действий с числами: (натуральные числа,/обыкновенные дроби, десятичные дроби, то в старших классах — -это могут быть:
7 класс. Формулы сокращенного умножения. Решение простейших ЛУР. Действия со степенью. График линейной функции.
8 класс: Линейные неравенства и числовые промежутки.
Решение простейших линейных неравенств. Решение КВУР с помощью
теоремы Виета и частных случаев. Решение КВУР рациональными способами. Арифметический, квадратный кореньи его свойства.
9 Г класс: Решение неравенств 2 степени. Преобразование графиков функций.
Формулы приведения. Значения тригонометрических функций.
10 — 11 классах: Вычисление производных. Простейшие тригонометрические неравенства. Тригонометрические формулы. Простейшие тригонометрические уравнения. Функции,- обратные тригонометрическим. Преобразование графиков функций. Вычисление первообразных. Свойства логарифмов. Простейшие показательные уравнения и неравенства: Простейшие логарифмические уравнения и неравенства. Практика показала, что у систематическая работа с устным счетом способствует значительному повышению продуктивности вычислений и преобразований. Сокращается время на выполнение таких операций, что переводит их из разряда. самостоятельной задачи в разряд вспомогательной и становится инструментом (“таблицей умножения») для решения более сложных задач.
Учитель по математике, знающий, с чем придется столкнуться школьнику на экзамене, кроме фундамента уделяет большую часть времени на занятии отработке вопросов специфики ЕГЭ и ОГЭ.Правильность оформления заданий, тактика и стратегия решения в условиях дефицита выделенного времени на экзамене, также банальная невнимательность. Эти и масса других особенностей составляют суть специфики.
Для эффективной подготовки к ЕГЭ и ОГЭ нужна тренировка, тренировка иеще раз тренировка. Довести решение задач до автоматизма.
Развитие геометрических представлений
Процент выполнения экзаменующимися геометрических заданий традиционно ниже, чем процент, выполнения заданий алгебраических. Одна из основных причин — недостатки в формировании пространственного мышления учащихся. Массово эта проблема проявилась с уходом из общего образования такого учебного предмета, как черчение, и вряд ли стоит ожидать его возвращения — профессия конструктора перестала быть столь массово востребованной с приходом компьютерных технологий.
Эта проблема легла на плечи учителей математики, однако решение её известно: непрерывное развитие. геометрических представлений и геометрического воображения обучающихся с 1 по 11 класс; наглядная геометрия в 1- 6 классах; больше внимания геометрическому моделированию и конструированию (из плоских и пространственных фигур), геометрическим чертежам, построениям, изображениям от руки и с помощью различных чертёжных инструментов, на нелинованной и клетчатой бумаге.
Это отнюдь не означает, что всю геометрию надо свести к наглядности и к работе руками. Определения и доказательства, логика и аксиоматика важны для современного человека и для изучения геометрии не менее, но надо понимать, что в развитии человека всему отводится своё время, а несформированное наглядно-образное мышление, которое должно быть основой и этапом на пути формирования логического мышления, просто мешает его формированию.
Если вернуться к этапу обучения в старшей школе, то целесообразно использовать любые приёмы и средства, которые способствовали бы визуализации предлагаемых обучающимся задач. Это не только построение чертежей по условию задачи (что непросто сделать при проблемах с пространственным воображением), это прежде всего различные предметные модели (полезно для каждой решаемой задачи иметь соответствующую ей модель-подсказку, чтобы использовать её для визуализации условия, поиска и проверки решения), компьютерные программы, позволяющие выполнять стереометрические чертежи.
Полезно выделить эту работу в отдельный тематический практикум, на котором обучающиеся тренировались бы в изображении и моделировании пространственных тел, построении чертежей по условию задачи (в различных ракурсах, выбирая наиболее удобный для поиска решения), можно также организовать данную работу в рамках проекта.
Многие старшеклассники считают, что могут обойтись без знания планиметрии. Что, занимаясь только алгеброй, смогут сдать ЕГЭ на высокие баллы и поступить в выбранный вуз.
Работает ли эта стратегия?
Ответ преподавателей-экспертов: нет, не работает. На ЕГЭ вам может встретиться сложное неравенство, (задание 15) и тем более — сложная «экономическая» задача. Так было в 2018 году. И всё. баллов фатально не хватает! Тех самых баллов, которые можно было легко получить за планиметрическую задачу, не хватает для поступления!
Стоит учесть, что задачи вариантов ЕГЭ по планиметрии и стереометрии бывают намного проще, чем по алгебре.
) Самое важное — правильная методика подготовки. Не нужно начинать с реальных задач ЕГЭ. Сначала — теория. Свойства геометрических фигур. Определения и теоремы. Учить наизусть.
Лучшая: тренировка этом этапе — задания №3 и № 6 из первой части ЕГЭ по математике .
-
Задача 16.Профильного ЕГЭ по математике оценивается в 3 первичных балла и состоит из. двух пунктов. Первый пункт — доказательство. Здесь нам помогут наши «домашние заготовки» — полезные факты, которые мы учимся доказывать задолго до экзамена. А на ЕГЭ; остается только вспомнить и записать решение.
3); Оказывается, многие задачи по планиметрии строятся по одной из так называемых классических схем.
-
Есть такие теоремы, которые вроде и входят в школьную программу — а попробуй их найди в учебнике. Например, теорема о секущей и касательной или свойство биссектрисы.
-
Любая задача из варианта ЕГЭ решается без сложных формул. И если вы не помните теорему Чевы, теорему Менелая и другую экзотику — вам это и не понадобится.
-
Геометрия, конечно, это не алгебра, и готовых алгоритмов здесь намного меньше. Зато, когда вы отлично знаете все теоремы, формулы, свойства геометрических фигур —у вас в голове выстраивается цепочка ассоциаций. Например, в условии задачи дан радиус, вписанной окружности. В каких формулах он встречается? — Правильно, в теореме синусов и в одной из формул для площади треугольника.
-
Если вы вдруг не можете решить пункт (а), но решили пункт (б), вы получите за него один балл: А это лучше, чем ничего. Но вообще пункт (а), как правило, бывает простым. Иногда вопрос в пункте (а) очень простой. И это не только для того, чтобы вы получили «утешительный» балл. Помните, что пункт (а) часто содержит подсказку, идею для решения пункта (б)..
Саморегуляции и обратная связь «ученик-учитель».
Известно, что эффективность обучения возрастает в случае самооценивания, поскольку ученик самостоятельно получает информацию о своих результатах, сам её анализирует, делает выводы о своем прогрессе, корректирует цели в случае необходимости. Но для этого необходимы критерии оценивания работы, которые должны быть у ученика не просто до начала выполнения конкретной работы, но желательно и в самом начале изучения темы. К сожалению, на практике более распространена ситуация, когда работа выдаётся ученику без критериев ее выполнения.
К саморегуляции относятся также вопросы, связанные с осознанностью знания и незнания. Объяснение учителя сродни лекционной форме предъявления новых знаний. В Связи с этим подчеркнём важность обратной связи. Учитель должен получать сигналы от обучающихся: «Я понимаю, могу объяснить», «Я не уверен, правильно ли я понимаю», «Я не понимаю». Учитель может прервать своё объяснение вопросом к тем, кто ещё не Понял,, .предложением высказать свои сомнения тем, кто не уверен в понимании, предоставлением слова тем, кто всё понял.
Доказано, что обратная связь эффективна, если ученик получает сообщение о верно выполненных заданиях, а не только об ошибках, если он получает не просто маркеры, свидетельствующие о положительном результате, не просто похвалу за решённую задачу, а .и некоторый содержательный комментарий. Этот комментарий может включать в себя такую оценку,, как «рациональное решение», «интересная идея», «грамотная запись». Может быть: отмечена актуальность проверки результата, удачное прохождение «ловушек» и «опасных», мест и т.п.
Обратная связь эффективна в случае, если она конкретна, то есть связана с известными ученику результатами и действиями, подлежащими усвоению. Важное значение имеет информированность ученика относительно того, чему он должен научиться, какие задания должен научиться решать, а какие может научиться решать для того, чтобы получить желаемое количество баллов на экзамене. Если ученик фиксирует и отслеживает сам, умеет ли он выполнять требуемое задание или нет. то минимизируется время на выполнение ‘заданий, при этом работа становится более эффективной и рациональной. Отсюда необходимость в открытости предъявляемых требований к результатам обучения, а на этапе подготовки к экзамену — в ориентации на конечный запланированный результат,.
И еще об одном; факторе следует упомянуть — это повторяющееся тестирование. Уже имеющийся опыт российской школы и более продолжительный зарубежный опыт не позволяют говорить о нём, как об эффективном факторе. Положительные эффекты возникают только/в тех случаях, когда учитель учитывает результаты тестирования для корректировки- процесса обучения и приспосабливает методы обучения к возможностям конкретного ученика, учитывая его сильные и слабые стороны, или при условии содержательной обратной связи, с которой ученик может работать самостоятельно, то есть имеет возможность учиться на тестах.
Завершающие рекомендации.
Необходимо ‘отметить, что создание ЕГЭ по математике базового уровня и появление акцента использование математических знаний в реальных ситуациях были неверно истолкованы некоторыми учителями в качестве генеральной идеи обучения, что привело к поверхностному освоению обучающимися программы старшей школы. В частности, это зафиксировано и результатами экзамена: результаты выполнения заданий по темам курса старшей школы ниже, результатов выполнения заданий из «реальной математики».
Для того чтобы успешно сдать ЕГЭ по математике, важно пройти всю программу целиком, а не только «то. что пригодится на экзамене», повысить свою культуру вычислений, то есть минимизировать использование калькуляторов, развивать умение читать графики, правильно использовать терминологию и учить формулы.
Для учащихся, которые могут успешно освоить курс математики средней (полной) школы на, .базовом уровне, образовательный акцент должен быть сделан на полное изучение традиционных курсов алгебры и начал анализа и геометрии на базовом уровне. Помимо заданий, базового уровня в образовательном процессе должны использоваться задания повышенного уровня. Количество часов математики должно быть не менее 5 часов в неделю.
Для учащихся, которые могут успешно освоить курс математики полной (средней) школы на профильном (повышенном) уровне, образовательный акцент должен быть сделан на полное, изучение традиционных курсов алгебры и начал анализа и геометрии на профильном уровне. Количество часов математики должно быть не менее 6-7 часов в неделю.
-
первую очередь нужно выработать у обучающихся быстрое и правильное выполнение Заданий части Г, используя, в том числе и банк заданий экзамена базового уровня. Умения,, необходимые для выполнения заданий базового уровня, должны быть под постоянным контролем.
Задания с кратким ответом (повышенного уровня) части 2 должны находить отражение в содержании математического образования, и аналогичные задания должны включаться в систему текущего и рубежного контроля.
В записи решений с заданиям с развернутым ответом нужно особое внимание обращать на построение чертежей и рисунков, лаконичность пояснений, доказательность рассуждений.
И в завершение необходимо отметить, что еще одним важным фактором является психологический климат в учебном коллективе: дружеские отношения среди одноклассников, спокойная рабочая атмосфера на уроке, методичная, прозрачная и последовательная подготовка к экзамену, доверительные отношения учителя с учениками, вера в достижение более высоких результатов и эмоциональная поддержка.
На занятиях стараюсь создать атмосферу комфортности, взаимопонимания. На своих уроках я делаю установку на то, чтобы любой ребенок должен быть понят и услышан учителем и соучеником: учение должно проходить в «атмосфере непринужденности, чтобы дети и учитель свободно дышали на уроках». От учителя требуется и мастерство, и большое терпение, и любовь к учащимся. Доброжелательное отношение к ученикам снимает у них страх перед трудностями обучения: ребенок не должен бояться
Ошибиться, спросить учителя, если он что-то прослушал или не понял.
Психологическая подготовка учащихся может заключается в следующем:
отработка поведения в период подготовки к экзамену: обучение навыкам
саморегуляции, самоконтроля, повышение уверенности в себе, в своих силах.
Методы проведения занятий по психологической подготовке учашихся
разнообразны:
групповая дискуссия, игровые методы, медитативные техники, Содержание занятий- должно ориентироваться на следующие вопросы: как подготовиться к экзаменам, поведение на экзамене. способы снятия нервнопсихического напряжения, как противостоять стрессу.
Литература:
Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок у частников ЕГЭ 2019 года по математике, подготовленные ФГБНУ «ФИЛИ».
Методические рекомендации для учителей, подготовленные на основе анализа типичных ошибок участников ЕГЭ 2020 года по математике, подготовленные ФГБНУ «ФИЛИ»,
БабанскийIO.K. Активность и самостоятельность учащихся в обучении / М.Ю. Бабанский М., Педагогика. 1989.
Беспалько В.П. Слагаемые педагогической технологии / Беспалько В.П. — М., 1989.
Красновский Э.А. Активизация учебного познания / Красновский Э.А. // Советская педаго гика.-1989. №5.
Эльконин Д. Б. Избранные педагогические труды. / Под ред. В.В. Давыдова, В.П. Зинченк о.М.. 1989.
Щукина Г.И. Активизация познавательной деятельности в учебном процессе/ Щукина Г.И . М„ .1979,
Адрес публикации: https://www.prodlenka.org/metodicheskie-razrabotki/484984-tema-obespechenie-povyshenija-kachestva-podgo

«Свидетельство участника экспертной комиссии»
Оставляйте комментарии к работам коллег и получите документ
БЕСПЛАТНО!




































