Призма на егэ по математике презентация

Слайд 1

Призма в задачах ЕГЭ Тема урока:

Слайд 2

Задача № 1 В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 известно, что D 1 B = , BB 1 = 3, A 1 D 1 = 4. Найдите длину ребра A 1 B 1 . Ответ: 1

Слайд 3

Задача № 2 В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 известно, что DC = , BB 1 = 1, A 1 D 1 = 3. Найдите длину диагонали AC 1 . Ответ: 13

Слайд 4

Задача № 3 Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объём параллелепипеда. Ответ: 48

Слайд 5

Задача № 4 Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба. Ответ: 6

Слайд 6

Задача № 5 Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите площадь его поверхности. Ответ: 22

Слайд 7

Задача № 6 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 4. диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда. Ответ: 64

Слайд 8

Задача № 7 Диагональ куба равна 3. Найдите площадь его поверхности. Ответ: 18

Слайд 9

Задача № 8 Диагональ куба равна . Найдите его объём. Ответ: 8

Слайд 10

Задача № 9 Если каждое ребро куба увеличить на 1, то его объём увеличиться на 19. Найдите ребро куба. Ответ: 2

Слайд 11

Задача № 10 Диагональ куба равна 1. Найдите площадь его поверхности. Ответ: 2

Слайд 12

Задача № 11 Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в два раза? Ответ: 4

Слайд 13

Задача № 12 Объём одного куба в 8 раз больше объёма другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба? Ответ: 4

Слайд 14

Задача № 13 В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь её поверхности равна 248. Найдите боковое ребро этой призмы. Ответ: 10

Слайд 15

Задача № 14 Найдите площадь поверхности прямой призмы с боковым ребром, равным 5, в основании которой лежит ромб с диагоналями, равными 3 и 4. Ответ: 62

Слайд 16

Задача № 15 В сосуд, имеющий форму правильной треугольной призмы, налили 1900 см 3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 20 см до отметки 22 см. Найдите объём детали. Ответ выразите в см 3 . Ответ: 190

Слайд 17

Задача № 16 Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы. Ответ: 24

Слайд 18

Задача № 17 Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объём отсеченной треугольной призмы равна 5. Найдите объём исходной призмы. Ответ: 20

Слайд 19

Задача № 18 Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8 . площадь её поверхности равна 288. Найдите высоту призмы. Ответ: 10

Слайд 20

Задача № 19 Найдите объём правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны . Ответ: 4,5

Слайд 21

Задача № 20 Найдите площадь поверхности правильной шестиугольной призмы, стороны основания которой равны 3, а высота – 6. Ответ: 108

Слайд 22

Задача № 21 Найдите объём параллелепипеда ABCDA 1 B 1 C 1 D 1 , если объём треугольной пирамиды ABDA 1 равен 3. Ответ: 18

Слайд 23

Задача № 22 Объём параллелепипеда ABCDA 1 B 1 C 1 D 1 равен 1,8. Найдите объём треугольной пирамиды ABC В 1 . Ответ: 0,3

Слайд 24

Задача № 23 От призмы АВСА 1 В 1 С 1 , объём которой равен 6, отсечена треугольная пирамида С 1 АВС. Найдите объём оставшейся части. Ответ : 4

Слайд 25

Спасибо за внимание!

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  ПРИЗМА
  Учитель: Бондарева В.В.
  Экономический лицей ФГБОУ ВО РЭУ им. Г.В.Плеханова
  ПОДГОТОВКА К ЕГЭ

• 

  2 слайд

  Какие из следующих утверждений верны?
  1. Поверхность, составленную из многоугольников называют многогранником.

  2.Высота прямой призмы равна ее боковому ребру.
  3. Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы.

• 

  3 слайд

  Какие из следующих утверждений верны?
  1. Многогранник, составленный из двух многоугольников расположенных в параллельных плоскостях называется призмой.

  2. Площадью полной поверхности призмы называется сумма площадей оснований.
  3.Площадь боковой поверхности призмы равна сумме площадей боковых граней.

• 

  4 слайд

  Какие из следующих утверждений верны?
  1. Многогранник называется выпуклым, если он не плоский.

  3. Призма называется правильной, если ее основания — правильные многоугольники
  2.Если боковые ребра перпендикулярны к основаниям, то призма называется прямой

• 

  5 слайд

  Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, называют многогранной поверхностью или многогранником.

• 

  6 слайд

  Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.

• 

  7 слайд

  Невыпуклый многогранник

• 

  8 слайд

  Виды многогранников

• 

  9 слайд

  Призма
  А1
  А2
  Аn
  B1
  B2
  Bn
  B3
  А3
  Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.

  n-угольная призма.

  Многоугольники
  А1А2…Аn и В1В2…Вn – основания призмы.

  Параллелограммы А1В1В2А2, А2В2В3А3 и т.д. боковые грани призмы

• 

  10 слайд

  Призма
  А1
  А2
  Аn
  B1
  B2
  Bn
  B3
  А3
  Отрезки А1В1, А2В2 и т.д. —
  боковые ребра призмы

  Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

• 

  11 слайд

  Если боковые ребра перпендикулярны к основаниям, то призма называется прямой, в противном случае наклонной.
  Высота прямой призмы равна ее боковому ребру.

• 

  12 слайд

  Прямая призма называется правильной, если ее основания — правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.

• 

  13 слайд

  Площадью полной поверхности призмы называется сумма площадей всех граней, а площадью боковой поверхности призмы – сумма площадей ее боковых граней.
  h
  h
  Pocн

• 

  14 слайд

  Задача №1
  Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 2, а высота – 3.

• 

  15 слайд

  Задача №2
    Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 12 и 16, и боковым ребром, равным 8.

• 

  16 слайд

  Задача №3
  Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 15, а площадь поверхности равна 1050.

• 

  17 слайд

  Задача №4
  Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 12. Найдите площадь ее поверхности.

• 

  18 слайд

  Задача №6
  Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза?

• 

  19 слайд

  Задача №6
  Сторона основания правильной треугольной призмы ABCA1B1C1 равна 3, а высота этой призмы равна 4√3.   Найдите площадь полной поверхности призмы ABCA1B1C1.

• 

  20 слайд

  Задача №7
  В правильной шестиугольной призме  ABCDEFA1B1C1D1E1F1  все ребра равны 1. Найдите расстояние между точками В и Е.

• 

  21 слайд

  Задача №8
  В правильной шестиугольной призме  ABCDEFA1B1C1D1E1F1  все ребра равны 1. Найдите угол DАВ. Ответ дайте в градусах.

• 

  22 слайд

  Задача №9
  В правильной шестиугольной призме  ABCDEFA1B1C1D1E1F1  все ребра равны 8. Найдите угол между прямыми FA и D1E1. Ответ дайте в градусах.

• 

  23 слайд

  Задача №10
  В правильной треугольной призме АВСА1В1С1 , все ребра которой равны 3, найдите угол между прямыми АА1 и ВС1. Ответ дайте в градусах.

• 

  24 слайд

  Задача №11

  В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1  все ребра равны 1. Найдите расстояние между точками А и Е1.

• 

  25 слайд

  Задача №12
  В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1  все ребра равны 1. Найдите тангенс угла АD1D.

• 

  26 слайд

  Задача №13
  Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 36, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.

• 

  27 слайд

  Задача №14
  Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 155 066 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Формирование компетенций межкультурной коммуникации в условиях реализации ФГОС»

• Курс повышения квалификации «Экономика: инструменты контроллинга»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс профессиональной переподготовки «Организация деятельности секретаря руководителя со знанием английского языка»

• Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»

• Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»

• Курс повышения квалификации «Финансовые инструменты»

• Курс повышения квалификации «Информационная этика и право»

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Бобель Юлия Анатольевна,

учитель математики высшей квалификационной категории.

ГБОУ №313 Фрунзенского района, Санкт-Петербурга

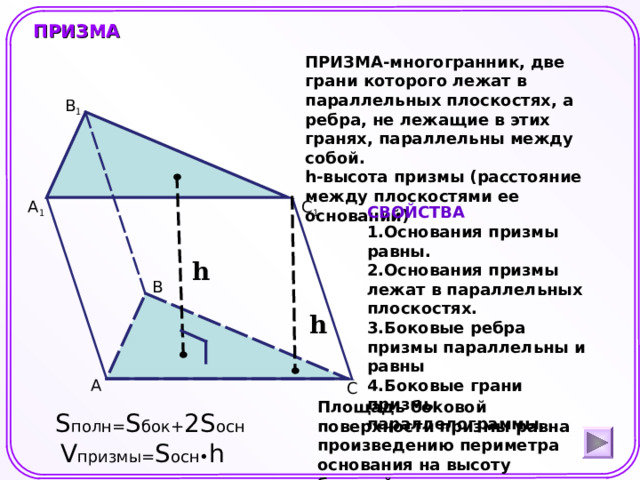
ПРИЗМА

ПРИЗМА-многогранник, две грани которого лежат в параллельных плоскостях, а ребра, не лежащие в этих гранях, параллельны между собой.

h- высота призмы (расстояние между плоскостями ее оснований)

B 1

А 1

C 1

СВОЙСТВА

• Основания призмы равны.
• Основания призмы лежат в параллельных плоскостях.
• Боковые ребра призмы параллельны и равны
• Боковые грани призмы параллелограммы.

h

B

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

h

А

C

Площадь боковой поверхности призмы равна произведению периметра основания на высоту боковой грани

S полн= S бок + 2S осн

V призмы= S осн• h

2

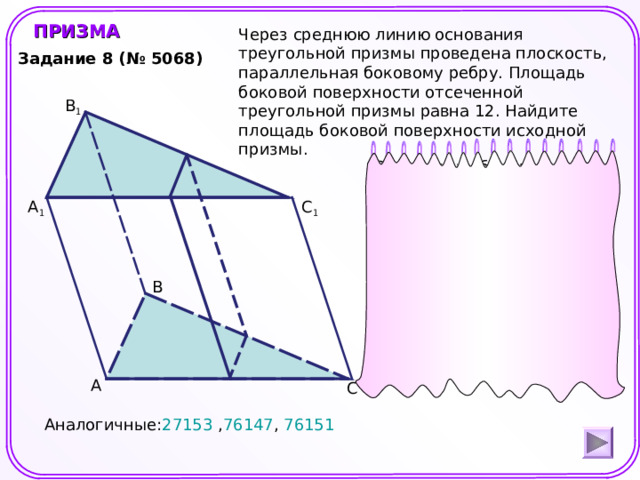
ПРИЗМА

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.

Задание 8 (№ 5068)

B 1

S 1 – площадь боковой поверхности отсеченной призмы.

S 2 — площадь боковой поверхности исходной призмы.

h- высота боковой грани.

C 1

А 1

B

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

А

C

Аналогичные: 27153 , 76147 , 76151

3

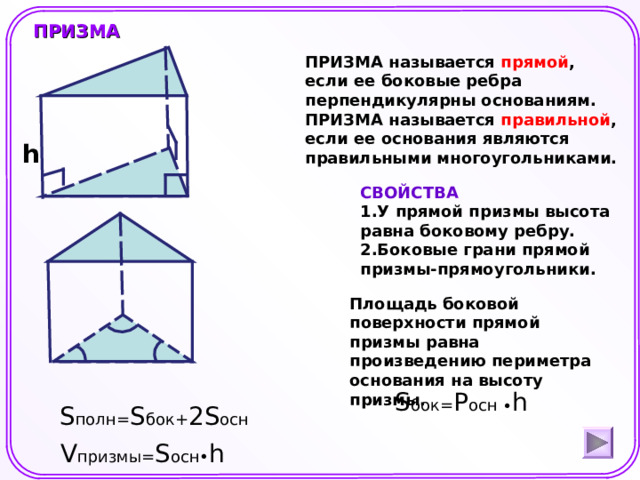
ПРИЗМА

ПРИЗМА называется прямой , если ее боковые ребра перпендикулярны основаниям.

ПРИЗМА называется правильной , если ее основания являются правильными многоугольниками.

h

СВОЙСТВА

• У прямой призмы высота равна боковому ребру.
• Боковые грани прямой призмы-прямоугольники.

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

S бок= P осн ∙ h

S полн= S бок + 2S осн

V призмы= S осн• h

4

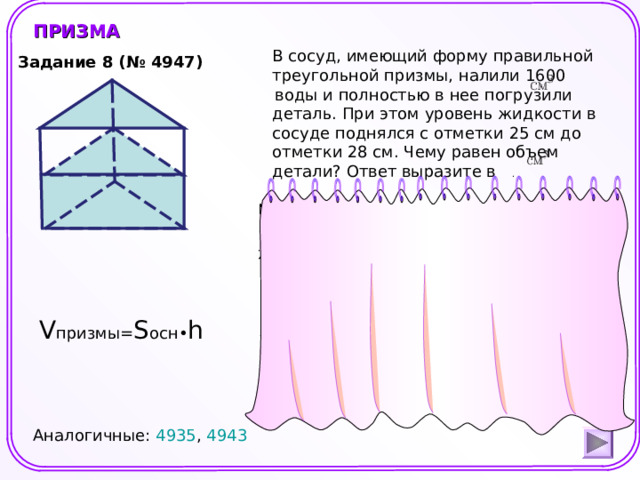
В сосуд, имеющий форму правильной треугольной призмы, налили 1600     воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 28 см. Чему равен объем детали? Ответ выразите в .

ПРИЗМА

Задание 8 (№ 4947)

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

V призмы= S осн• h

Аналогичные: 4935 , 4943

5

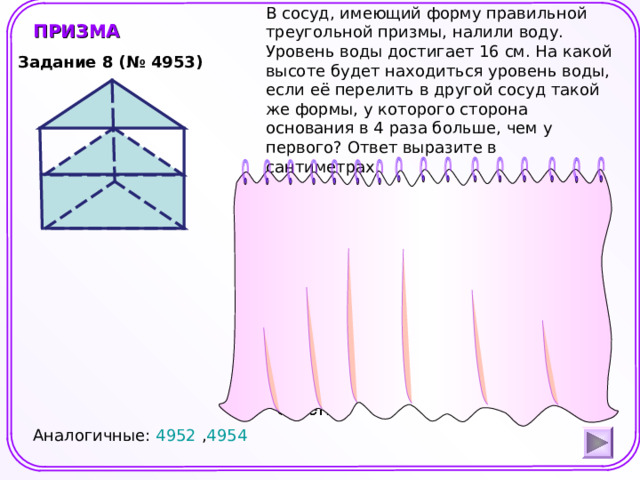
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд такой же формы, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в сантиметрах.

ПРИЗМА

Задание 8 (№ 4953)

V призмы= S осн• h

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Аналогичные: 4952 , 4954

6

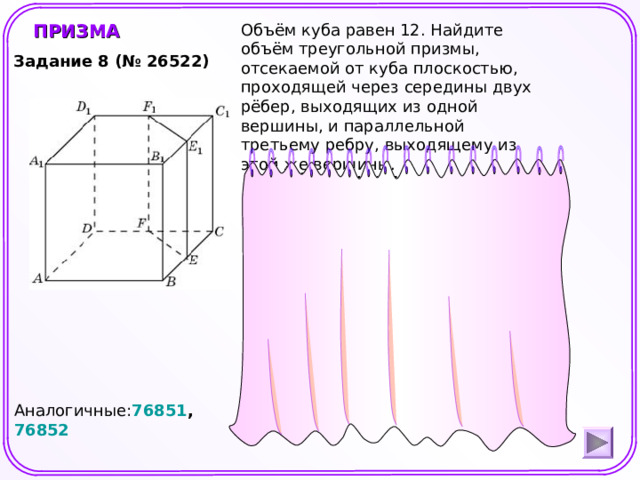
Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.

ПРИЗМА

Задание 8 (№ 26522)

Решение:

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Ответ: 1,5

Аналогичные: 76851 , 76852

7

ЛИТЕРАТУРА И ИНТЕРНЕТ РЕСУРСЫ

1. источник шаблона: сайт http://pedsovet.su

2. Открытый банк задач ЕГЭ по математике http://mathege.ru/or/ege/Main.html?view=Pos

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

7

1


Готовимся к ЕГЭ. Прототипы В9, В11. Призма. В создании презентации принимали участие ученики 10А класса. Научный руководитель: Шахова Татьяна Александровна год

2

3


3

4


4 Объем призмы равен произведению площади основания на высоту. h h

5


В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите расстояние между точками A и E 1. Никифорова Екатерина 10А Рассмотрим прямоугольный треугольник По теореме Пифагора: В треугольнике угол между сторонами правильного треугольника равен По теореме косинусов: Значит Ответ : 2 1

6


В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите расстояние между точками B и E. 2 Ответ: Богданов Владимир 10А 2 AB C D E F A1B1 C1 D1E1 F1 1 BE является большой диагональю правильного шестиугольника BЕ в два раза больше стороны шестиугольника. BE = 2

7


В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 5. Найдите расстояние между точками B и E 1. 3 BE является большой диагональю правильного шестиугольника => в два раза больше его стороны. Шахова Татьяна 10АБВ Ответ: 5

8


В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите тангенс угла AD 1 D. Ответ: 4 Гречуха Валерия 10А ВА C D E F F1F1 F1F1 B1B1 A1A1 C1C1 D1D1 E1E1 D D1D1 A 1 A D 2 Тангенс угла AD 1 D равен отношению противолежащего катета AD к прилежащему DD 1 Большая диагональ правильного шестиугольника в два раза больше его стороны 2 2

9


В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах. AD-биссектриса угла BAF Ответ: 60 5 Гурьева Дарья 10А А BC D EF В правильном шестиугольнике углы равны 120˚ DAB = 0,5·BAF=60˚ A1A1 B1B1 C1C1 D1D1 E1E1 F1F1

10


В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите угол AC 1 C. Ответ дайте в градусах. Ответ: 60 6 Карагяур Лилия 10А 1 А ВС D EF A1 B1C1 D1 E1F1 C1 C A ? 1 B AC x По теореме косинусов:

11


В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, все ребра которой равны 8, найдите угол между прямыми FA и D 1 E 1. Ответ дайте в градусах. 7 АF параллельна C 1 D 1 => угол между АF и Е 1 D 1 =углу между C 1 D 1 и Е 1 D 1 Угол правильного шестиугольника = Ответ: 120 Шахова Татьяна 10АБВ

12


Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза? 8 Ответ: 54 Гречуха Валерия 10А h a 3h 3a Разделим 1 ое на 2 ое Оснований – два + три прямоугольника

13


В правильной четырёхугольной призме ABCDA 1 B 1 C 1 D 1 известно, что AC 1 =2BC. Найдите угол между диагоналями BD 1 и CA 1. Ответ дайте в градусах. Ответ: 60 9 Гурьева Дарья 10А A BC D A1A1 B1B1 C1C1 D1D1 K K A1A1 B C D1D1 Диагонали прямоугольного параллелепипеда равны. Диагональное сечение является прямоугольником. Правильная четырехугольная призма является прямоугольным параллелепипедом. AC 1 =2BC=>A 1 C=2BC=> B C A1A1 Угол A 1 =30 0 Угол К = 60 0 Угол С=60 0 CB K 60 0 ? Треуг. КСВ – р/б

14


В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см 3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в см 3. Ответ: 10 Богданов Владимир 10А 184 Разделим первое на второе Объем детали =

15


В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см. 11 а 4 а Шахова Татьяна 10АБВ 80 h Объемы равны. Приравняем правые части. Ответ: 5

16


Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота 10. Ответ: 12 Смирнова Анастасия 10 А Площадь боковой поверхности фигуры равна сумме площадей всех боковых граней Все боковые грани – равные прямоугольники со сторонами 5 и 10.

17


Никифорова Екатерина 10А Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10. Найдем сторону ромба: Найдем площадь ромба: Тогда Ответ:

18


Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна =800+80x 80x=960 x=1212 Ответ: 20 Карагяур Лилия 10А Пусть боковое ребро х. 20 х Боковые грани – равные прямоугольники со Сторонами = х и 20, основания – квадраты со стороной = 20 14

19


Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы Ответ: 120 Шахова Татьяна 10АБВ

20


Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро. 17 Рассмотрим прямоугольный треугольник — площадь основания Ответ: Смирнова Анастасия 10 А 4

21


Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро. Ответ: 17 Коваль Дмитрий 10А А1А1 В1В1 С1С1 А В С А В С 3 5 h Боковое ребро прямой призмы является высотой 4

22


Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны Ответ: 4,5 18 Коваль Дмитрий 10А Найдем площадь основания. Составлено из шести равносторонних треугольников 1

23


Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы. 19 A1 B C N1 M M1 C1 A B1 N Шахова Татьяна 10АБВ Высоты равны. Сравним площади оснований. A C B M N Треугольники подобны с коэффициентом подобия= ½ => их площади относятся как ¼. Разделим первое на второе. Ответ: 1,25

24


Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны и наклонены к плоскости основания под углом Ответ: 20 Хачатрян Нателла 10А Найдем площадь основания. 18 Составлено из шести равносторонних треугольников 2 h Найдем высоту h

25


Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности S 1 =? 6 8 Гипотенуза= 10 S 2 =24 S 1 =24 S 3 =610=60 S 4 =810=80 S 5 =1010=100 S= =288 Ответ: 288 Хачатрян Нателла 10А

26


Николаева Ксения 10А В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы. 2) Найдем площадь боковых граней: Ответ: 10 1) Найдем площадь ромба: 3) Найдем площадь одной грани: 4) Из треугольника ВНС найдём ВС: св-во параллелограмма 5) Найдём боковое ребро призмы: 23

27


Николаева Ксения 10А В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы. Ответ: Покажем расстояния от АА 1 до других боковых ребер. Угол К – линейный угол двугранного прямого угла. КМL – перпендикулярное сечение призмы. Площадь боковой поверхности призмы равна произведению бокового ребра на периметр перпендикулярного сечения.

28


Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы. 25 Шахова Татьяна 10АБВ Площадь поверхности состоит из площадей оснований и площадей боковых граней, которые являются прямоугольниками. Ответ: 10

29


Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы. Сравним соответствующие грани Ответ: 26 Привалова Анастасия 10А A1 B C N1 M M1 C1 A B1 N Т.о. S всех боковых граней большой призмы больше S граней маленькой призмы в 2 раза => 16

30


Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины Сравним S осн.куба и S осн.пр Ответ: 1,5 27 Привалова Анастасия 10А a A B C D F E Разделим 1 е на 2 е

31


В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 3, найдите угол между прямыми AA 1 и BC 1. Ответ дайте в градусах. Ответ: Самошкин Даниил 10А В АА 1 и ВС 1 – скрещивающиеся. А С В1В1 С1С1 А1А1 АА 1 параллельна ВВ 1 => угол между АА 1 и ВС 1 = углу между ВВ 1 и ВС 1 Треугольник ВВ 1 С 1 –прямоугольный и равнобедренный так как призма прямая и все ребра равны. => Угол ВВ 1 С 1 =45 0

32


Спасибо за работу!

1. Призма в задачах ЕГЭ

Тема урока:
Призма в задачах
ЕГЭ
Е.В.Акчурина

2. Задача № 1

В
  прямоугольном параллелепипеде ABCDA1B1C1D1
известно, что D1B = , BB1 = 3, A1D1 = 4. Найдите
длину ребра A1B1.
Ответ: 1
Е.В.Акчурина

3. Задача № 2

В
  прямоугольном параллелепипеде ABCDA1B1C1D1
известно, что DC = , BB1 = 1, A1D1 = 3. Найдите
длину диагонали AC1.
Ответ: 13
Е.В.Акчурина

4. Задача № 3

Площадь грани прямоугольного параллелепипеда
равна 12. Ребро, перпендикулярное этой грани,
равно 4. Найдите объём параллелепипеда.
Ответ: 48
Е.В.Акчурина

5. Задача № 4

Три ребра прямоугольного параллелепипеда,
выходящие из одной вершины, равны 4, 6, 9.
Найдите ребро равновеликого ему куба.
Ответ: 6
Е.В.Акчурина

6. Задача № 5

Ребра прямоугольного параллелепипеда,
выходящие из одной вершины, равны 1, 2, 3.
Найдите площадь его поверхности.
Ответ: 22
Е.В.Акчурина

7. Задача № 6

Два ребра прямоугольного параллелепипеда,
выходящие из одной вершины, равны 2 и 4.
диагональ параллелепипеда равна 6. Найдите
площадь поверхности параллелепипеда.
Ответ: 64
Е.В.Акчурина

8. Задача № 7

Диагональ куба равна 3. Найдите площадь его
поверхности.
Ответ: 18
Е.В.Акчурина

9. Задача № 8

 Диагональ куба равна . Найдите его объём.
Ответ: 8
Е.В.Акчурина

10. Задача № 9

Если каждое ребро куба увеличить на 1, то его
объём увеличиться на 19. Найдите ребро куба.
Ответ: 2
Е.В.Акчурина

11. Задача № 10

Диагональ куба равна 1. Найдите площадь его
поверхности.
Ответ: 2
Е.В.Акчурина

12. Задача № 11

Во сколько раз увеличится площадь поверхности
куба, если его ребро увеличить в два раза?
Ответ: 4
Е.В.Акчурина

13. Задача № 12

Объём одного куба в 8 раз больше объёма другого
куба. Во сколько раз площадь поверхности первого
куба больше площади поверхности второго куба?
Ответ: 4
Е.В.Акчурина

14. Задача № 13

В основании прямой призмы лежит ромб с
диагоналями, равными 6 и 8. Площадь её
поверхности равна 248. Найдите боковое ребро
этой призмы.
Ответ: 10
Е.В.Акчурина

15. Задача № 14

Найдите площадь поверхности прямой призмы с
боковым ребром, равным 5, в основании которой
лежит ромб с диагоналями, равными 3 и 4.
Ответ: 62
Е.В.Акчурина

16. Задача № 15

В сосуд, имеющий форму
правильной треугольной
призмы, налили 1900 см3
воды и погрузили в воду
деталь. При этом уровень
воды поднялся с отметки 20
см до отметки 22 см.
Найдите объём детали.
Ответ выразите в см3.
Ответ: 190
Е.В.Акчурина

17. Задача № 16

Через среднюю линию
основания треугольной
призмы проведена
плоскость, параллельная
боковому ребру.
Площадь боковой
поверхности отсеченной
треугольной призмы
равна 12. Найдите
площадь боковой
поверхности исходной
призмы.
Ответ: 24
Е.В.Акчурина

18. Задача № 17

Через среднюю линию
основания треугольной
призмы проведена
плоскость, параллельная
боковому ребру. Объём
отсеченной треугольной
призмы равна 5. Найдите
объём исходной призмы.
Ответ: 20
Е.В.Акчурина

19. Задача № 18

Основанием прямой треугольной призмы служит
прямоугольный треугольник с катетами 6 и 8.
площадь её поверхности равна 288. Найдите высоту
призмы.
Ответ: 10
Е.В.Акчурина

20. Задача № 19

Найдите

 
объём правильной шестиугольной призмы,
стороны основания которой равны 1, а боковые
ребра равны .
Ответ: 4,5
Е.В.Акчурина

21. Задача № 20

Найдите площадь поверхности правильной
шестиугольной призмы, стороны основания которой
равны 3, а высота – 6.
Ответ: 108
Е.В.Акчурина

22. Задача № 21

Найдите объём параллелепипеда ABCDA1B1C1D1, если
объём треугольной пирамиды ABDA1 равен 3.
Ответ: 18
Е.В.Акчурина

23. Задача № 22

Объём параллелепипеда ABCDA1B1C1D1 равен 1,8.
Найдите объём треугольной пирамиды ABCВ1.
Ответ: 0,3
Е.В.Акчурина

24. Задача № 23

От призмы АВСА1В1С1,
объём которой равен 6,
отсечена треугольная
пирамида С1АВС. Найдите
объём оставшейся части.
Ответ: 4
Е.В.Акчурина

25. Спасибо за внимание!

Е.В.Акчурина

---

Задачи на готовых чертежах для подготовки к ЕГЭ. «Расстояние от точки до прямой. Правильная треугольная призма»

Целевая аудитория: для 10 класса

Автор: Каратанова Марина Николаевна
Место работы: МБОУ СОШ №256 ГО ЗАТО Фокино Приморский край
Добавил: KarMaN

© 2007 — 2023 Сообщество учителей-предметников «Учительский портал»
Свидетельство о регистрации СМИ: Эл № ФС77-64383 выдано 31.12.2015 г. Роскомнадзором.
Территория распространения: Российская Федерация, зарубежные страны.
Учредитель / главный редактор: Никитенко Е.И.

---

Сайт является информационным посредником и предоставляет возможность пользователям размещать свои материалы на его страницах.
Публикуя материалы на сайте, пользователи берут на себя всю ответственность за содержание этих материалов и разрешение любых спорных вопросов с третьими лицами.
При этом администрация сайта готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием сайта.
Если вы обнаружили, что на сайте незаконно используются материалы, сообщите администратору через форму обратной связи — материалы будут удалены.

Все материалы, размещенные на сайте, созданы пользователями сайта и представлены исключительно в ознакомительных целях. Использование материалов сайта возможно только с разрешения администрации портала.

---

Фотографии предоставлены

Слайды презентации