Призма подготовка к егэ по математике

Задача 1. Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна а площадь поверхности равна

Решение: + показать

---

Задача 2. В правильной четырёхугольной призме  известно, что   Найдите угол между диагоналями   и Ответ дайте в градусах.

Решение: + показать

---

Задача 3. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и боковое ребро равно Найдите объем призмы.

Решение: + показать

---

Задача 4.  Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и высота призмы равна Найдите площадь ее поверхности.

Решение: + показать

---

Задача 5. Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами и Площадь ее поверхности равна . Найдите высоту призмы.

Решение: + показать

---

Задача 6.  Площадь поверхности правильной треугольной призмы равна Какой будет площадь поверхности призмы, если все ее ребра увеличить в два раза?

Решение: + показать

---

Задача 7.  В правильной треугольной призме , все ребра которой равны найдите угол между прямыми  и . Ответ дайте в градусах.

Решение: + показать

---

Задача 8. Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными и и боковым ребром, равным

Решение: + показать

---

Задача 9. Гранью параллелепипеда является ромб со стороной и острым углом Одно из ребер параллелепипеда составляет с этой гранью угол в  и равно Найдите объем параллелепипеда.

Решение: + показать

---

Задача 10. Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна а высота —

 Решение: + показать

---

Задача 11.  Найдите объем правильной шестиугольной призмы, стороны основания которой равны а боковые ребра равны

Решение: + показать

---

Задача 12. В правильной шестиугольной призме   все ребра равны . Найдите расстояние между точками   и .

Решение: + показать

---

Задача 13. В правильной шестиугольной призме   все ребра равны Найдите угол . Ответ дайте в градусах.

Решение: + показать

---

Задача 14. В правильной шестиугольной призме  , все ребра которой равны найдите угол между прямыми    и . Ответ дайте в градусах.

Решение: + показать

---

Задача 15. В правильной шестиугольной призме   все ребра равны Найдите тангенс угла

Решение: + показать

---

Задача 16. В сосуд, имеющий форму правильной треугольной призмы, налили см воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки см до отметки см. Найдите объем детали. Ответ выразите в см

Решение: + показать

---

Задача 17. В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает  см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в раза больше, чем у первого? Ответ выразите в сантиметрах.

Решение: + показать

---

Задача 18. Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 26, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.

Решение: + показать

---

Задача 19. Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен Найдите объем исходной призмы.

Решение: + показать

---

Задача 20.  Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.

---

Задача 21. Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами а боковые ребра равны   и наклонены к плоскости основания под углом

Решение: + показать

---

Задача 22. В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно и отстоит от других боковых ребер на и Найдите площадь боковой поверхности этой призмы.

Решение: + показать

---

Задача 23.  В правильной треугольной призме  стороны оснований равны  боковые рёбра равны Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер , и и точку

Решение: + показать

---

Задача 24. В правильной треугольной призме стороны оснований равны боковые рёбра равны Найдите площадь сечения призмы плоскостью, проходящей через середины рёбер и

Решение: + показать

---

Задача 25.  Объём куба равен Построено сечение проходящее через середины рёбер  и и параллельное ребру Найдите объём треугольной призмы

Решение: + показать

---

Задача 26.  Найдите объем многогранника, вершинами которого являются точки   правильной треугольной призмы  площадь основания которой равна а боковое ребро равно

Решение: + показать

Задача 27.  Найдите объем многогранника, вершинами которого являются точки   правильной треугольной призмы  площадь основания которой равна а боковое ребро равно

Решение: + показать

---

Задача 28. Найдите объем многогранника, вершинами которого являются точки  правильной шестиугольной призмы  площадь основания которой равна а боковое ребро равно

Решение: + показать

---

Задача 29. Найдите объём многогранника, вершинами которого являются точки правильной шестиугольной призмы   площадь основания которой равна а боковое ребро равно

Решение: + показать

---

Вы можете пройти тест «Призма»

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Пройти тестирование по этим заданиям

Призма

$С_1Н$ — высота

Если боковые ребра призмы перпендикулярны к основаниям, то призма называется прямой, в противном случае – наклонной. Высота прямой призмы равна ее боковому ребру.

Формулы вычисления объема и площади поверхности призмы:

Чтобы были понятны формулы, введем обозначения:

$P_{осн}$ — периметр основания;

$S_{осн}$ — площадь основания;

$S_{бок}$ — площадь боковой поверхности;

$S_{п.п}$ — площадь полной поверхности;

$h$ — высота призмы.

$S_{бок}=P_{осн}·h$

$S_{п.п}=S_{бок}+2S_{осн}$

$V=S_{осн}·h$

В основании призмы могут лежать различные многоугольники, рассмотрим площади некоторых из них.

В основании лежит треугольник.

1. $S={a·h_a}/{2}$, где $h_a$ — высота, проведенная к стороне $а$
2. $S={a·b·sin⁡α}/{2}$, где $a,b$ — соседние стороны, $α$ — угол между этими соседними сторонами.
3. Формула Герона $S=√{p(p-a)(p-b)(p-c)}$, где $р$ — это полупериметр $p={a+b+c}/{2}$
4. $S=p·r$, где $r$ — радиус вписанной окружности
5. $S={a·b·c}/{4R}$, где $R$ — радиус описанной окружности
6. Для прямоугольного треугольника $S={a·b}/{2}$, где $а$ и $b$ — катеты прямоугольного треугольника.

В основании лежит четырехугольник

1. Прямоугольник

$S=a·b$, где $а$ и $b$ — смежные стороны.

2. Ромб

$S={d_1·d_2}/{2}$, где $d_1$ и $d_2$ — диагонали ромба

$S=a^2·sin⁡α$, где $а$ — длина стороны ромба, а $α$ — угол между соседними сторонами.

3. Трапеция

$S={(a+b)·h}/{2}$, где $а$ и $b$ — основания трапеции, $h$ — высота трапеции.

Прямая призма называется правильной, если ее основания – правильные многоугольники.

Рассмотрим площади правильных многоугольников:

1. Для равностороннего треугольника $S={a^2√3}/{4}$, где $а$ — длина стороны.

2. Квадрат

$S=a^2$, где $а$ — сторона квадрата.

3. Правильный шестиугольник

Шестиугольник разделим на шесть правильных треугольников и найдем площадь как:

$S=6·S_{треугольника}={6·a^2√3}/{4}={3·a^2√3}/{2}$, где $а$ — сторона правильного шестиугольника.

Цилиндр — это та же призма, в основании которой лежит круг.

$S_{бок}=P_{осн}·h=2πRh$

$S_{п.п}=S_{бок}+2S_{осн}=2πRh+2πR^2=2πR(h+R)$

$V=S_{осн}·h=πR^2 h$

Подобные призмы: при увеличении всех линейных размеров призмы в $k$ раз, её объём увеличится в $k^3$ раз.

Средняя линия треугольника параллельна основанию и равна его половине.

$MN$ — средняя линия, так как соединяет середины соседних сторон.

$MN {//} AC, MN = {AC}/{2}$

Подобие треугольников

Два треугольника называются подобными, если их углы соответственно равны, а стороны одного треугольника больше сходственных сторон другого треугольника в некоторое число раз.

Число $k$ — коэффициент подобия (показывает во сколько раз стороны одного треугольника больше сторон другого треугольника.)

1. Периметры подобных треугольников и их линейные величины (медианы, биссектрисы, высоты) относятся друг к другу как коэффициент подобия $k$.
2. Отношение площадей двух подобных треугольников равно квадрату коэффициента подобия.

Прямоугольный треугольник и его свойства:

В прямоугольном треугольнике катетами называются две стороны треугольника, которые образуют прямой угол. Гипотенузой называется сторона, лежащая напротив прямого угла.

Некоторые свойства прямоугольного треугольника:

1. Сумма острых углов в прямоугольном треугольнике равна $90$ градусов.
2. Катет прямоугольного треугольника, лежащий напротив угла в $30$ градусов, равен половине гипотенузы. (Этот катет называется малым катетом.)

Теорема Пифагора

В прямоугольном треугольнике сумма квадратов катетов равна квадрату гипотенузы.

$AC^2+BC^2=AB^2$

Соотношение между сторонами и углами в прямоугольном треугольнике:

В прямоугольном треугольнике $АВС$, с прямым углом $С$

Для острого угла $В: АС$ — противолежащий катет; $ВС$ — прилежащий катет.

Для острого угла $А: ВС$ — противолежащий катет; $АС$ — прилежащий катет.

1. Синусом (sin) острого угла прямоугольного треугольника называется отношение противолежащего катета к гипотенузе.
2. Косинусом (cos) острого угла прямоугольного треугольника называется отношение прилежащего катета к гипотенузе.
3. Тангенсом (tg) острого угла прямоугольного треугольника называется отношение противолежащего катета к прилежащему.
4. Котангенсом (ctg) острого угла прямоугольного треугольника называется отношение прилежащего катета к противолежащему.
5. В прямоугольном треугольнике синус одного острого угла равен косинусу другого острого угла.
6. Синусы, косинусы, тангенсы и котангенсы острых равных углов равны.
7. Синусы смежных углов равны, а косинусы, тангенсы и котангенсы отличаются знаками: для острых углов положительные значения, для тупых углов отрицательные значения

Значения тригонометрических функций некоторых углов:

$α$	$30$	$45$	$60$
$sinα$	${1}/{2}$	${√2}/{2}$	${√3}/{2}$
$cosα$	${√3}/{2}$	${√2}/{2}$	${1}/{2}$
$tgα$	${√3}/{3}$	$1$	$√3$
$ctgα$	$√3$	$1$	${√3}/{3}$

Теорема синусов

Во всяком треугольнике стороны относятся как синусы противолежащих углов:

${a}/{sinα}={b}/{sinβ}={c}/{sinγ}=2R$, где $R$ — радиус описанной около треугольника окружности.

Теорема косинусов

Квадрат одной из сторон треугольника равен сумме квадратов двух других сторон минус удвоенное произведение этих сторон на косинус угла между ними:

$a^2=b^2+c^2-2·b·c·cosα;$

$b^2=a^2+c^2-2·a·c·cos⁡β;$

$c^2=b^2+a^2-2·b·a·cosγ.$

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  ПРИЗМА
  Учитель: Бондарева В.В.
  Экономический лицей ФГБОУ ВО РЭУ им. Г.В.Плеханова
  ПОДГОТОВКА К ЕГЭ

• 

  2 слайд

  Какие из следующих утверждений верны?
  1. Поверхность, составленную из многоугольников называют многогранником.

  2.Высота прямой призмы равна ее боковому ребру.
  3. Площадь боковой поверхности призмы равна произведению периметра основания на высоту призмы.

• 

  3 слайд

  Какие из следующих утверждений верны?
  1. Многогранник, составленный из двух многоугольников расположенных в параллельных плоскостях называется призмой.

  2. Площадью полной поверхности призмы называется сумма площадей оснований.
  3.Площадь боковой поверхности призмы равна сумме площадей боковых граней.

• 

  4 слайд

  Какие из следующих утверждений верны?
  1. Многогранник называется выпуклым, если он не плоский.

  3. Призма называется правильной, если ее основания — правильные многоугольники
  2.Если боковые ребра перпендикулярны к основаниям, то призма называется прямой

• 

  5 слайд

  Поверхность, составленную из многоугольников и ограничивающую некоторое геометрическое тело, называют многогранной поверхностью или многогранником.

• 

  6 слайд

  Многогранник называется выпуклым, если он расположен по одну сторону от плоскости каждой его грани.

• 

  7 слайд

  Невыпуклый многогранник

• 

  8 слайд

  Виды многогранников

• 

  9 слайд

  Призма
  А1
  А2
  Аn
  B1
  B2
  Bn
  B3
  А3
  Многогранник, составленный из двух равных многоугольников А1А2…Аn и В1В2…Вn, расположенных в параллельных плоскостях, и n параллелограммов, называется призмой.

  n-угольная призма.

  Многоугольники
  А1А2…Аn и В1В2…Вn – основания призмы.

  Параллелограммы А1В1В2А2, А2В2В3А3 и т.д. боковые грани призмы

• 

  10 слайд

  Призма
  А1
  А2
  Аn
  B1
  B2
  Bn
  B3
  А3
  Отрезки А1В1, А2В2 и т.д. —
  боковые ребра призмы

  Перпендикуляр, проведенный из какой-нибудь точки одного основания к плоскости другого основания, называется высотой призмы.

• 

  11 слайд

  Если боковые ребра перпендикулярны к основаниям, то призма называется прямой, в противном случае наклонной.
  Высота прямой призмы равна ее боковому ребру.

• 

  12 слайд

  Прямая призма называется правильной, если ее основания — правильные многоугольники. У такой призмы все боковые грани – равные прямоугольники.

• 

  13 слайд

  Площадью полной поверхности призмы называется сумма площадей всех граней, а площадью боковой поверхности призмы – сумма площадей ее боковых граней.
  h
  h
  Pocн

• 

  14 слайд

  Задача №1
  Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 2, а высота – 3.

• 

  15 слайд

  Задача №2
    Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 12 и 16, и боковым ребром, равным 8.

• 

  16 слайд

  Задача №3
  Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 15, а площадь поверхности равна 1050.

• 

  17 слайд

  Задача №4
  Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 5 и 12, высота призмы равна 12. Найдите площадь ее поверхности.

• 

  18 слайд

  Задача №6
  Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза?

• 

  19 слайд

  Задача №6
  Сторона основания правильной треугольной призмы ABCA1B1C1 равна 3, а высота этой призмы равна 4√3.   Найдите площадь полной поверхности призмы ABCA1B1C1.

• 

  20 слайд

  Задача №7
  В правильной шестиугольной призме  ABCDEFA1B1C1D1E1F1  все ребра равны 1. Найдите расстояние между точками В и Е.

• 

  21 слайд

  Задача №8
  В правильной шестиугольной призме  ABCDEFA1B1C1D1E1F1  все ребра равны 1. Найдите угол DАВ. Ответ дайте в градусах.

• 

  22 слайд

  Задача №9
  В правильной шестиугольной призме  ABCDEFA1B1C1D1E1F1  все ребра равны 8. Найдите угол между прямыми FA и D1E1. Ответ дайте в градусах.

• 

  23 слайд

  Задача №10
  В правильной треугольной призме АВСА1В1С1 , все ребра которой равны 3, найдите угол между прямыми АА1 и ВС1. Ответ дайте в градусах.

• 

  24 слайд

  Задача №11

  В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1  все ребра равны 1. Найдите расстояние между точками А и Е1.

• 

  25 слайд

  Задача №12
  В правильной шестиугольной призме ABCDEFA1B1C1D1E1F1  все ребра равны 1. Найдите тангенс угла АD1D.

• 

  26 слайд

  Задача №13
  Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 36, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.

• 

  27 слайд

  Задача №14
  Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 155 066 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Формирование компетенций межкультурной коммуникации в условиях реализации ФГОС»

• Курс повышения квалификации «Экономика: инструменты контроллинга»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс профессиональной переподготовки «Организация деятельности секретаря руководителя со знанием английского языка»

• Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»

• Курс профессиональной переподготовки «Политология: взаимодействие с органами государственной власти и управления, негосударственными и международными организациями»

• Курс повышения квалификации «Финансовые инструменты»

• Курс повышения квалификации «Информационная этика и право»

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Бобель Юлия Анатольевна,

учитель математики высшей квалификационной категории.

ГБОУ №313 Фрунзенского района, Санкт-Петербурга

ПРИЗМА

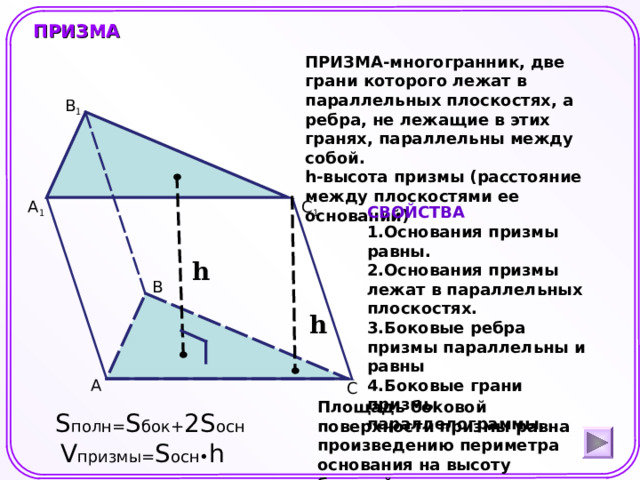
ПРИЗМА-многогранник, две грани которого лежат в параллельных плоскостях, а ребра, не лежащие в этих гранях, параллельны между собой.

h- высота призмы (расстояние между плоскостями ее оснований)

B 1

А 1

C 1

СВОЙСТВА

• Основания призмы равны.
• Основания призмы лежат в параллельных плоскостях.
• Боковые ребра призмы параллельны и равны
• Боковые грани призмы параллелограммы.

h

B

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

h

А

C

Площадь боковой поверхности призмы равна произведению периметра основания на высоту боковой грани

S полн= S бок + 2S осн

V призмы= S осн• h

2

ПРИЗМА

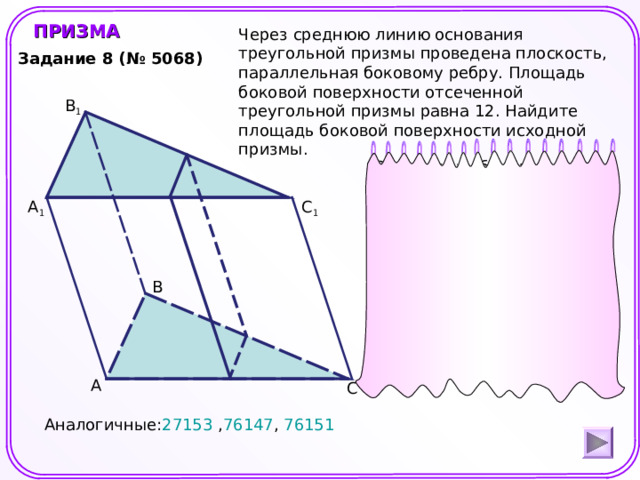
Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.

Задание 8 (№ 5068)

B 1

S 1 – площадь боковой поверхности отсеченной призмы.

S 2 — площадь боковой поверхности исходной призмы.

h- высота боковой грани.

C 1

А 1

B

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

А

C

Аналогичные: 27153 , 76147 , 76151

3

ПРИЗМА

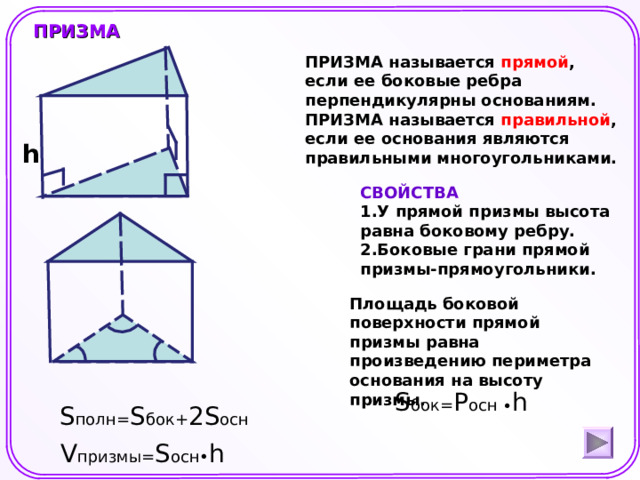
ПРИЗМА называется прямой , если ее боковые ребра перпендикулярны основаниям.

ПРИЗМА называется правильной , если ее основания являются правильными многоугольниками.

h

СВОЙСТВА

• У прямой призмы высота равна боковому ребру.
• Боковые грани прямой призмы-прямоугольники.

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

S бок= P осн ∙ h

S полн= S бок + 2S осн

V призмы= S осн• h

4

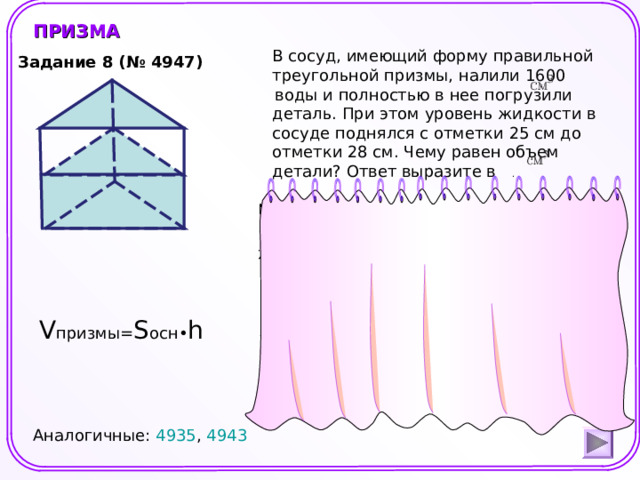
В сосуд, имеющий форму правильной треугольной призмы, налили 1600     воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 28 см. Чему равен объем детали? Ответ выразите в .

ПРИЗМА

Задание 8 (№ 4947)

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

V призмы= S осн• h

Аналогичные: 4935 , 4943

5

В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд такой же формы, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в сантиметрах.

ПРИЗМА

Задание 8 (№ 4953)

V призмы= S осн• h

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Аналогичные: 4952 , 4954

6

Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.

ПРИЗМА

Задание 8 (№ 26522)

Решение:

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Ответ: 1,5

Аналогичные: 76851 , 76852

7

ЛИТЕРАТУРА И ИНТЕРНЕТ РЕСУРСЫ

1. источник шаблона: сайт http://pedsovet.su

2. Открытый банк задач ЕГЭ по математике http://mathege.ru/or/ege/Main.html?view=Pos

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

7

Напомним,
что призмой называется многогранник, у которого две грани – равные -угольники,
лежащие в параллельных плоскостях (эти грани называются основаниями
призмы), а остальные  граней
– параллелограммы.

Эти
параллелограммы называются боковыми гранями, а их стороны, не лежащие на
основаниях призмы, называются боковыми рёбрами призмы.

Боковые
рёбра призмы параллельны и равны.

Высотой
призмы называется расстояние между основаниями.

Площадью
боковой поверхности призмы называется сумма площадей её
боковых граней.

Площадью
полной поверхности призмы – сумма площадей её боковых граней
и двух площадей оснований.

Объём
призмы равен произведению площади основания на высоту.

Призма,
в зависимости от того, какой многоугольник лежит в основании, имеет своё
название.

Рассмотрим
наклонную призму. Здесь основания – равные многоугольники,
лежащие в параллельных плоскостях. Боковые грани – параллелограммы. Высота
призмы – перпендикуляр, опущенный из любой точки верхнего основания на
плоскость нижнего. Боковые рёбра призмы равны и параллельны. Диагональ
призмы соединяет две вершины, не лежащие в одной грани. Диагональное сечение
проходит через два боковых ребра, не лежащих в одной грани, и является
параллелограммом. Площадь боковой поверхности призмы равна сумме
площадей боковых граней. Площадь полной поверхности равна сумме площади
боковой поверхности и двух площадей оснований.

Рассмотрим
прямую призму. Здесь боковые рёбра перпендикулярны основаниям. Боковые
грани – прямоугольники. Высота равна боковому ребру. Площадь
боковой поверхности прямой призмы равна произведению периметра основания на
высоту (на боковое ребро).

И
рассмотрим ещё правильную призму. Здесь в основании лежит
правильный многоугольник. Боковые рёбра перпендикулярны основанию. Боковые
грани – равные прямоугольники.

Основные
моменты мы с вами повторили, а теперь давайте перейдём к практической части
занятия.

Задача
первая. В основании прямой четырёхугольной призмы лежит
четырёхугольник со сторонами  см,
 см,
 см
и  см.
Высота призмы равна  см.
Найдите площадь боковой поверхности призмы.

Решение.

Задача
вторая. Дана шестиугольная наклонная призма с боковым ребром
 см.
Периметр сечения призмы плоскостью, перпендикулярной боковому ребру, равен  см.
Найдите площадь боковой поверхности призмы.

Решение.

Задача
третья. Дана прямая пятиугольная призма, в основание которой
вписана окружность с радиусом  см.
Площадь основания призмы равна  см²,
боковое ребро призмы равно  см.
Найдите площадь боковой поверхности призмы.

Решение.

Задача
четвёртая. Дана прямая четырёхугольная призма  В
основании призмы лежит прямоугольная трапеция с основаниями  см,
 см
и ,
в которую можно вписать окружность. Диагональное сечение   призмы
является квадратом. Найдите площадь полной поверхности призмы.

Решение.

Задача
пятая. Диагональ правильной четырёхугольной призмы равна ,
диагональ боковой грани равна .
Найдите площадь полной поверхности призмы.

Решение.

Задача
шестая. Площадь боковой поверхности правильной
четырёхугольной призмы равна  см².
Диагональ боковой грани равна  см.
Найдите наибольший возможный объём призмы, задаваемой этими условиями.

Решение.

Объем призмы и другие ее характеристики

Перед вами иллюстрированный гид о призме.

В картинках. С пояснениями к формулам. С примерами.

Определение, виды призм, высота, площадь, объем призмы – все, все, все!

Читайте и делитесь впечатлениями в комментариях!

Призма – коротко о главном

Определение призмы:

Призма – это многогранник, две грани которого (основания) – равные многоугольники, лежащие в параллельных плоскостях, а боковые грани – параллелограммы.

Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.

Виды призм:

Параллелепипед – это призма, основанием которой является параллелограмм.

Прямая призма – это призма, у которой боковые ребра перпендикулярны плоскости основания. Другие призмы называются наклонными.

Правильная призма – это прямая призма, основанием которой является правильный многоугольник. Боковые грани правильной призмы – равные прямоугольники.

Объем призмы

Главная формула объема призмы:
( displaystyle V=S{{ }_{основания}}cdot text{H}),
где ( {{text{S}}_{основания}}) – площадь основания,
( H) – высота.

Необычная формула объема призмы:
( text{V}={{text{S}}_{bot }}cdot l),
где ( {{text{S}}_{bot }}) – площадь сечения, перпендикулярного боковому ребру,
( l) – длина бокового ребра.

Площадь призмы

Площадь полной поверхности призмы – сумма площадей всех граней.
( displaystyle {{text{S}}_{полн. пов.}}={{text{S}}_{боков.пов.}}+2cdot {{text{S}}_{text{основания}.}})

А теперь чуть подробнее…

Что такое призма

Давай ответим сперва картинками:

Смотри: у призмы сверху и снизу два одинаковых многоугольника – они называются основаниями.

Остальные грани называются боковыми.

Плоскости оснований параллельный. Боковые грани – параллелограммы.

Рисуем еще раз.

А теперь рёбра.

Смотри: бывают рёбра основания и боковые рёбра.

Важно знать, что:

Все боковые рёбра призмы равны и параллельны.

А еще:

• Если в основании призмы лежит треугольник, то призма называется треугольной, если четырёхугольник, то четырёхугольной и т.д.;
• Бывают и десятиугольные, и двадцатиугольные призмы, но, к счастью, не в твоих задачах;
• А тебе будут встречаться чаще всего треугольные, четырёхугольные и шестиугольные призмы.

Думаю, теперь мы можем дать более строгое определение призмы.

Определение призмы

Призма — многогранник, две грани которого (основания) — равные многоугольники, лежащие в параллельных плоскостях, а боковые грани — параллелограммы.

Виды призм

Призма, основанием которой является параллелограмм, называется параллелепипедом.

Прямая призма – это призма, у которой боковые ребра перпендикулярны плоскости основания.

Другие призмы называются наклонными.

Высота призмы

Высота призмы – перпендикуляр, опущенный из одной из вершин призмы на плоскость противоположного основания.

И ясно, что та же самая высота получится, если опустить перпендикуляр из любой точки на верхней плоскости.

Согласен?

Объем призмы

Главная формула объема призмы

( displaystyle V=S{{ }_{основания}}cdot text{H}),где ( {{text{S}}_{основания}}) — площадь основания,
( H) — высота.

Необычная формула объема призмы

( text{V}={{text{S}}_{bot }}cdot l),
где ( {{text{S}}_{bot }}) – площадь сечения, перпендикулярного боковому ребру,
( l) – длина бокового ребра.

Площадь призмы

Площадь полной поверхности призмы – сумма площадей всех граней.
( displaystyle {{text{S}}_{полн. пов.}}={{text{S}}_{боков.пов.}}+2cdot {{text{S}}_{text{основания}.}})

Прямая призма

Если боковые рёбра призмы перпендикулярны основанию, то призма называется прямой.

Свойства прямой призмы:

• Все боковые грани прямоугольники;
• Все сечения, проходящие через боковые рёбра, – прямоугольники;
• Даже сечения, проходящие только через одно боковое ребро, – прямоугольники;
• У прямой призмы высота совпадает с боковым ребром.

Правильная призма

Если боковые рёбра призмы перпендикулярны основанию, а в основании лежит правильный многоугольник, то призма называется правильной.

То есть правильная призма – это прямая призма, у которой в основании правильный многоугольник.

Тебе, скорее всего, может встретиться:

Правильная треугольная призма – в основании правильный треугольник, боковые грани – прямоугольники.

Правильная четырёхугольная призма – это ещё и разновидность прямоугольного параллелепипеда – в основании квадрат, боковые грани – прямоугольники.

Правильная шестиугольная призма – в основании правильный шестиугольник, боковые грани – прямоугольники.

Главная формула объема призмы

( displaystyle V=S{{ }_{основания}}cdot text{H})

( {{text{S}}_{основания}}) – площадь основания

( H) – высота

Эта формула верна для любой призмы, но если призма прямая, то ( H) «превращается» в боковое ребро. И тогда

( displaystyle V=S{{ }_{основания}}cdot text{H})

– то же самое, что

( displaystyle V=S{{ }_{основания}}cdot боковое ребро)

Необычная формула объёма призмы

Представь себе, есть ещё одна, «перевёрнутая» формула для объёма призмы:

( Large text{V}={{text{S}}_{bot }}cdot l)

( {{text{S}}_{bot }}) – площадь сечения, перпендикулярного боковому ребру,

( l) – длина бокового ребра

Используется ли эта формула в задачах? Честно говоря, довольно редко, так что можешь ограничиться знанием основной формулы объёма.

Давай теперь для упражнения посчитаем объём самых популярных призм.

Объем правильной треугольной призмы

Пусть дано, что сторона основания равна ( a), а боковое ребро равно ( b).

Найдем объем:

( text{V}={{text{S}}_{Основания}}cdot text{H}={{text{S}}_{text{ABC}}}cdot text{b})

Вспомним, как находить площадь правильного треугольника:

( {{text{S}}_{text{ABC}}}=frac{1}{2}text{a}cdot text{h})

( text{h}=sqrt{{{text{a}}^{2}}-frac{{{text{a}}^{2}}}{4}}=frac{sqrt{3}}{2}text{a})

( {{text{S}}_{text{ABC}}}=frac{1}{2}text{a}cdot frac{sqrt{3}}{2}text{a}=frac{{{text{a}}^{2}}sqrt{3}}{4})

Подставляем в формулу объёма:

( text{V}={{text{S}}_{text{ABC}}}cdot text{b}=frac{{{text{a}}^{2}}text{b}sqrt{3}}{4}).

Объем правильной четырёхугольной призмы

Опять дано: сторона основания равна ( a), боковое ребро равно ( b).

( text{V}={{text{S}}_{text{основания}}}cdot text{H}={{text{S}}_{text{ABC}}}cdot text{b})

Ну, площадь квадрата долго искать не надо:

( displaystyle {{text{S}}_{text{ABCD}}}={{text{a}}^{2}})

Значит, ( displaystyle text{V}={{text{S}}_{text{ABCD}}}cdot text{b}={{text{a}}^{2}}text{b}).

Объем правильной шестиугольной призмы

Площадь поверхности призмы

Площадь боковой поверхности призмы – сумма площадей всех боковых граней.

Есть ли общая формула?

Нет, в общем случае нет. Просто нужно искать площади боковых граней и суммировать их.

Площадь полной поверхности призмы – сумма площадей всех граней.

( displaystyle {{text{S}}_{полн. пов.}}={{text{S}}_{боков.пов.}}+2cdot {{text{S}}_{text{основания}.}})

Формулу можно написать для прямой призмы:

( displaystyle {{text{S}}_{боков.}}=text{H}cdot text{P}), где ( displaystyle P) – периметр основания.

( displaystyle {{text{S}}_{text{полной}}}=text{H}cdot text{P}+2{{text{S}}_{основания}}).

Но всё-таки гораздо проще в каждом конкретном случае сложить все площади, чем запоминать дополнительные формулы.

Для примера посчитаем полную поверхность правильной шестиугольной призмы

Пусть сторона основания равна ( displaystyle a), а боковое ребро равно ( displaystyle b).

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

Алексей Шевчук – ведущий мини-групп

математика, информатика, физика

+7 (905) 541-39-06 – WhatsApp/Телеграм для записи

alexei.shevchuk@youclever.org – email для записи

• тысячи учеников, поступивших в лучшие ВУЗы страны
• автор понятного всем учебника по математике ЮКлэва (с сотнями благодарных отзывов);
• закончил МФТИ, преподавал на малом физтехе;
• репетиторский стаж – c 2003 года;
• в 2021 году сдал ЕГЭ (математика 100 баллов, физика 100 баллов, информатика 98 баллов – как обычно дурацкая ошибка:);
• отзыв на Профи.ру: “Рейтинг: 4,87 из 5. Очень хвалят. Такую отметку получают опытные специалисты с лучшими отзывами”.