Призма в задачах егэ презентация

Слайд 1

Призма в задачах ЕГЭ Тема урока:

Слайд 2

Задача № 1 В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 известно, что D 1 B = , BB 1 = 3, A 1 D 1 = 4. Найдите длину ребра A 1 B 1 . Ответ: 1

Слайд 3

Задача № 2 В прямоугольном параллелепипеде ABCDA 1 B 1 C 1 D 1 известно, что DC = , BB 1 = 1, A 1 D 1 = 3. Найдите длину диагонали AC 1 . Ответ: 13

Слайд 4

Задача № 3 Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объём параллелепипеда. Ответ: 48

Слайд 5

Задача № 4 Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба. Ответ: 6

Слайд 6

Задача № 5 Ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2, 3. Найдите площадь его поверхности. Ответ: 22

Слайд 7

Задача № 6 Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 4. диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда. Ответ: 64

Слайд 8

Задача № 7 Диагональ куба равна 3. Найдите площадь его поверхности. Ответ: 18

Слайд 9

Задача № 8 Диагональ куба равна . Найдите его объём. Ответ: 8

Слайд 10

Задача № 9 Если каждое ребро куба увеличить на 1, то его объём увеличиться на 19. Найдите ребро куба. Ответ: 2

Слайд 11

Задача № 10 Диагональ куба равна 1. Найдите площадь его поверхности. Ответ: 2

Слайд 12

Задача № 11 Во сколько раз увеличится площадь поверхности куба, если его ребро увеличить в два раза? Ответ: 4

Слайд 13

Задача № 12 Объём одного куба в 8 раз больше объёма другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба? Ответ: 4

Слайд 14

Задача № 13 В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь её поверхности равна 248. Найдите боковое ребро этой призмы. Ответ: 10

Слайд 15

Задача № 14 Найдите площадь поверхности прямой призмы с боковым ребром, равным 5, в основании которой лежит ромб с диагоналями, равными 3 и 4. Ответ: 62

Слайд 16

Задача № 15 В сосуд, имеющий форму правильной треугольной призмы, налили 1900 см 3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 20 см до отметки 22 см. Найдите объём детали. Ответ выразите в см 3 . Ответ: 190

Слайд 17

Задача № 16 Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы. Ответ: 24

Слайд 18

Задача № 17 Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объём отсеченной треугольной призмы равна 5. Найдите объём исходной призмы. Ответ: 20

Слайд 19

Задача № 18 Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8 . площадь её поверхности равна 288. Найдите высоту призмы. Ответ: 10

Слайд 20

Задача № 19 Найдите объём правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны . Ответ: 4,5

Слайд 21

Задача № 20 Найдите площадь поверхности правильной шестиугольной призмы, стороны основания которой равны 3, а высота – 6. Ответ: 108

Слайд 22

Задача № 21 Найдите объём параллелепипеда ABCDA 1 B 1 C 1 D 1 , если объём треугольной пирамиды ABDA 1 равен 3. Ответ: 18

Слайд 23

Задача № 22 Объём параллелепипеда ABCDA 1 B 1 C 1 D 1 равен 1,8. Найдите объём треугольной пирамиды ABC В 1 . Ответ: 0,3

Слайд 24

Задача № 23 От призмы АВСА 1 В 1 С 1 , объём которой равен 6, отсечена треугольная пирамида С 1 АВС. Найдите объём оставшейся части. Ответ : 4

Слайд 25

Спасибо за внимание!

Скачать материал

Скачать материал

Описание презентации по отдельным слайдам:

• 

  1 слайд

  Решение задач из ЕГЭ по теме: «Призма»
  19 ноября 2021г
  Составила:
  Пименова Мария Юрьевна,
  Учитель математики первой категории
  МБОУ «Шалинской СОШ №45»
  Задания взяты с сайта «РешуЕГЭ»

• 

  2 слайд

  Площадь боковой поверхности призмы
  Площадь боковой поверхности призмы равна сумме площадей всех ее боковых граней
  Задания взяты с сайта «РешуЕГЭ»

• 

  3 слайд

  Площадь полной поверхности призмы
  Площадь полной поверхности призмы равна сумме площадей всех ее боковых граней и оснований
  Задания взяты с сайта «РешуЕГЭ»

• 

  4 слайд

  Пример
  Прямая треугольная призма
  Состоит из 2 треугольников и 3 прямоугольников
  Тогда, площадь боковой поверхности равна сумме площадей трех прямоугольников, а площадь полной поверхности равна сумме площадей двух треугольников и трех прямоугольников
  Задания взяты с сайта «РешуЕГЭ»

• 

  5 слайд

  Задача №1
  Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10
  Задания взяты с сайта «РешуЕГЭ»

• 

  6 слайд

  Задача №1. Решение
  Площадь боковой поверхности призмы равна сумме площадей всех ее боковых граней:

  Задания взяты с сайта «РешуЕГЭ»

• 

  7 слайд

  Задача №2
  Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, а боковое ребро призмы равно 10
  Задания взяты с сайта «РешуЕГЭ»

• 

  8 слайд

  Задача №2. Решение
  По Т. Пифагора находим сторону ромба (либо через Египетский треугольник), сторона равна 5
  4
  3
  ?
  Задания взяты с сайта «РешуЕГЭ»

• 

  9 слайд

  Задача №2. Решение
  Найдем площадь ромба
  4
  3
  5
  5
  10
  Задания взяты с сайта «РешуЕГЭ»

• 

  10 слайд

  Задача №3
  Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна 1760
  Задания взяты с сайта «РешуЕГЭ»

• 

  11 слайд

  Задача №3. Решение
  Правильная четырехугольная призма состоит из 6 четырехугольников: 2 квадрата (основания) и 4 прямоугольника (боковые грани)
  Задания взяты с сайта «РешуЕГЭ»

• 

  12 слайд

  Задача №3. Решение
  Площадь поверхности правильной четырехугольной призмы выражается через сторону ее основания a и боковое ребро H формулой:
  Задания взяты с сайта «РешуЕГЭ»

• 

  13 слайд

  Задача №3. Решение
  Задания взяты с сайта «РешуЕГЭ»

• 

  14 слайд

  Задача №4
  Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности
  Задания взяты с сайта «РешуЕГЭ»

• 

  15 слайд

  Задача №4. Решение
  Третья сторона треугольника в основании равна 10 (по Т. Пифагора)
  Тогда,
  Задания взяты с сайта «РешуЕГЭ»

• 

  16 слайд

  Задача №4. Решение
  Площадь боковой поверхности призмы
  𝑆=10∙ 6+8+10 =10∙24=240 
  Полная площадь поверхности:
  Задания взяты с сайта «РешуЕГЭ»

• 

  17 слайд

  Задача №5
  В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы
  Задания взяты с сайта «РешуЕГЭ»

• 

  18 слайд

  Задача №5. Решение
  По Т. Пифагора находим сторону ромба (либо через Египетский треугольник), сторона равна 5
  4
  3
  ?
  Задания взяты с сайта «РешуЕГЭ»

• 

  19 слайд

  Задача №5. Решение
  Найдем площадь ромба
  4
  3
  5
  5
  ???
  Тогда боковое ребро найдем из выражения для площади поверхности:
  Задания взяты с сайта «РешуЕГЭ»

• 

  20 слайд

  Объем призмы
  Объём призмы равен произведению её высоты на площадь основания
  Задания взяты с сайта «РешуЕГЭ»

• 

  21 слайд

  Задача №6
  В сосуд, имеющий форму правильной треугольной призмы, налили 2300  см 3 воды и погрузили в воду деталь. При этом уровень воды поднялся с отметки 25 см до отметки 27 см. Найдите объем детали. Ответ выразите в см 3
  Задания взяты с сайта «РешуЕГЭ»

• 

  22 слайд

  Задача №6. Решение
  Объём детали равен объёму вытесненной ею жидкости. Объём вытесненной жидкости равен 2/25 исходного объёма:
  Задания взяты с сайта «РешуЕГЭ»

• 

  23 слайд

  Задача №7
  Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы
  Задания взяты с сайта «РешуЕГЭ»

• 

  24 слайд

  Задача №7. Решение
  Объем прямой призмы равен 𝑉=𝑆ℎ где S – площадь основания, а h – боковое ребро. Тогда объем равен:
  Задания взяты с сайта «РешуЕГЭ»

• 

  25 слайд

  Задача №8
  Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины
  Задания взяты с сайта «РешуЕГЭ»

• 

  26 слайд

  Задача №8. Решение
  Вид сверху
  Задания взяты с сайта «РешуЕГЭ»

• 

  27 слайд

  Задача №8. Решение
  Вид сверху
  Высота куба равна высоте призмы.
  Площадь основания построенной призмы в 8 раз меньше площади основания исходной, поэтому искомый объем призмы равен 12 : 8 = 1,5
  Задания взяты с сайта «РешуЕГЭ»

• 

  28 слайд

  Задача №8. Решение №2
  Вид сверху
  Задания взяты с сайта «РешуЕГЭ»

• 

  29 слайд

  Задача №9
  В правильной шестиугольной призме 𝐴𝐵𝐶𝐷𝐸𝐹 𝐴 1 𝐵 1 𝐶 1 𝐷 1 𝐸 1 𝐹 1 все ребра равны 1. Найдите∠𝐷𝐴𝐵
  Задания взяты с сайта «РешуЕГЭ»

• 

  30 слайд

  Задача №9. Решение
  В правильном шестиугольнике углы между сторонами равны 120° (т.к. сумма углов многоугольника (𝑛−2)∙180°, а угол правильного 𝑛 – угольника равен (𝑛−2)∙180° 𝑛 )

  Задания взяты с сайта «РешуЕГЭ»

• 

  31 слайд

  Задача №9. Решение
  В правильном шестиугольнике углы между сторонами равны 120° (т.к. сумма углов многоугольника (𝑛−2)∙180°, а угол правильного 𝑛 – угольника равен (𝑛−2)∙180° 𝑛 ).
  ∠ 𝐷𝐴𝐵= 120°:2=60°

  Задания взяты с сайта «РешуЕГЭ»

Найдите материал к любому уроку, указав свой предмет (категорию), класс, учебник и тему:

6 155 066 материалов в базе

• Выберите категорию:

• Выберите учебник и тему

• Выберите класс:

• Тип материала:

  • Все материалы

  • Статьи

  • Научные работы

  • Видеоуроки

  • Презентации

  • Конспекты

  • Тесты

  • Рабочие программы

  • Другие методич. материалы

Найти материалы

Вам будут интересны эти курсы:

• Курс повышения квалификации «Изучение вероятностно-стохастической линии в школьном курсе математики в условиях перехода к новым образовательным стандартам»

• Курс профессиональной переподготовки «Экономика: теория и методика преподавания в образовательной организации»

• Курс повышения квалификации «Основы управления проектами в условиях реализации ФГОС»

• Курс повышения квалификации «Особенности подготовки к сдаче ОГЭ по математике в условиях реализации ФГОС ООО»

• Курс профессиональной переподготовки «Математика и информатика: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Управление ресурсами информационных технологий»

• Курс повышения квалификации «Методика обучения математике в основной и средней школе в условиях реализации ФГОС ОО»

• Курс повышения квалификации «Источники финансов»

• Курс профессиональной переподготовки «Черчение: теория и методика преподавания в образовательной организации»

• Курс профессиональной переподготовки «Управление сервисами информационных технологий»

• Курс повышения квалификации «Учебная деятельность по предметной области «Черчение»: основы предмета и реализация обучения в условиях ФГОС»

• Курс профессиональной переподготовки «Риск-менеджмент организации: организация эффективной работы системы управления рисками»

• Курс профессиональной переподготовки «Осуществление и координация продаж»

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Бобель Юлия Анатольевна,

учитель математики высшей квалификационной категории.

ГБОУ №313 Фрунзенского района, Санкт-Петербурга

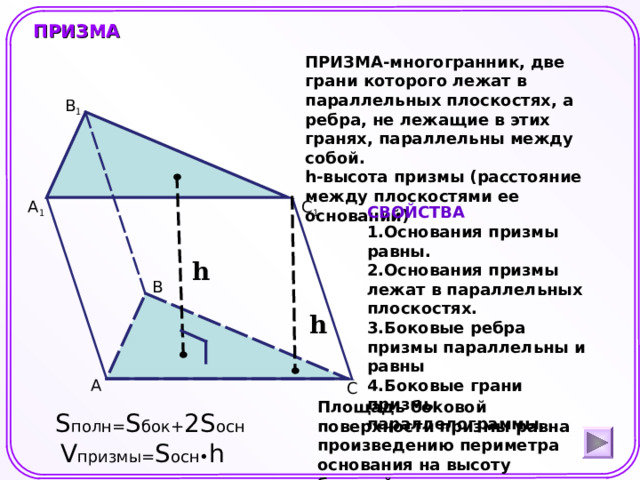
ПРИЗМА

ПРИЗМА-многогранник, две грани которого лежат в параллельных плоскостях, а ребра, не лежащие в этих гранях, параллельны между собой.

h- высота призмы (расстояние между плоскостями ее оснований)

B 1

А 1

C 1

СВОЙСТВА

• Основания призмы равны.
• Основания призмы лежат в параллельных плоскостях.
• Боковые ребра призмы параллельны и равны
• Боковые грани призмы параллелограммы.

h

B

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

h

А

C

Площадь боковой поверхности призмы равна произведению периметра основания на высоту боковой грани

S полн= S бок + 2S осн

V призмы= S осн• h

2

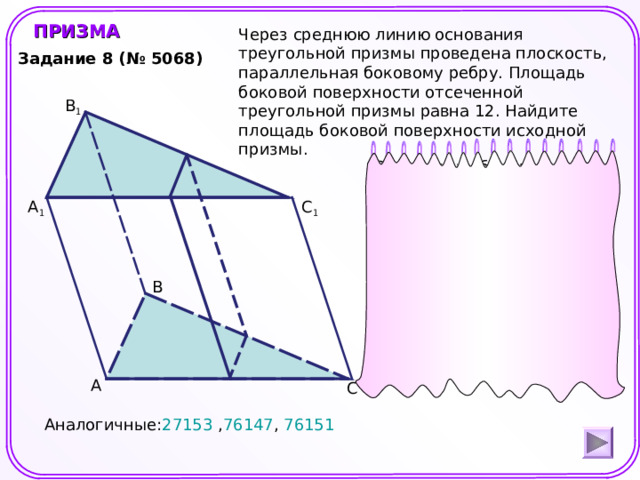
ПРИЗМА

Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 12. Найдите площадь боковой поверхности исходной призмы.

Задание 8 (№ 5068)

B 1

S 1 – площадь боковой поверхности отсеченной призмы.

S 2 — площадь боковой поверхности исходной призмы.

h- высота боковой грани.

C 1

А 1

B

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

А

C

Аналогичные: 27153 , 76147 , 76151

3

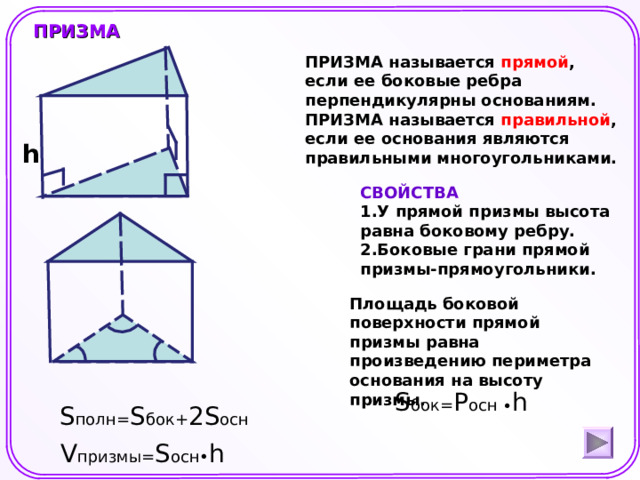
ПРИЗМА

ПРИЗМА называется прямой , если ее боковые ребра перпендикулярны основаниям.

ПРИЗМА называется правильной , если ее основания являются правильными многоугольниками.

h

СВОЙСТВА

• У прямой призмы высота равна боковому ребру.
• Боковые грани прямой призмы-прямоугольники.

Площадь боковой поверхности прямой призмы равна произведению периметра основания на высоту призмы.

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

S бок= P осн ∙ h

S полн= S бок + 2S осн

V призмы= S осн• h

4

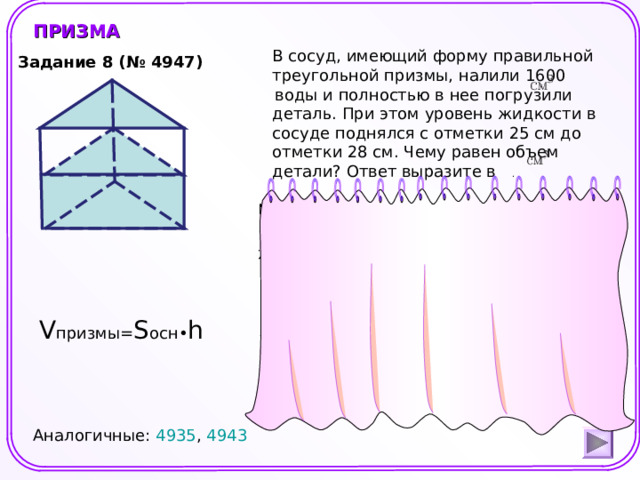
В сосуд, имеющий форму правильной треугольной призмы, налили 1600     воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 28 см. Чему равен объем детали? Ответ выразите в .

ПРИЗМА

Задание 8 (№ 4947)

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

V призмы= S осн• h

Аналогичные: 4935 , 4943

5

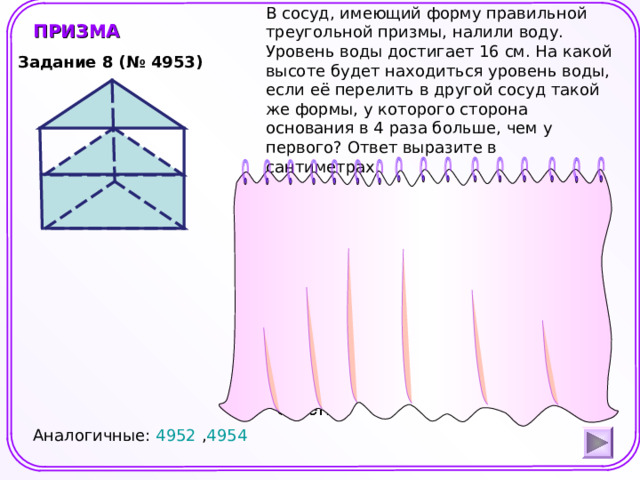
В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 16 см. На какой высоте будет находиться уровень воды, если её перелить в другой сосуд такой же формы, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в сантиметрах.

ПРИЗМА

Задание 8 (№ 4953)

V призмы= S осн• h

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Аналогичные: 4952 , 4954

6

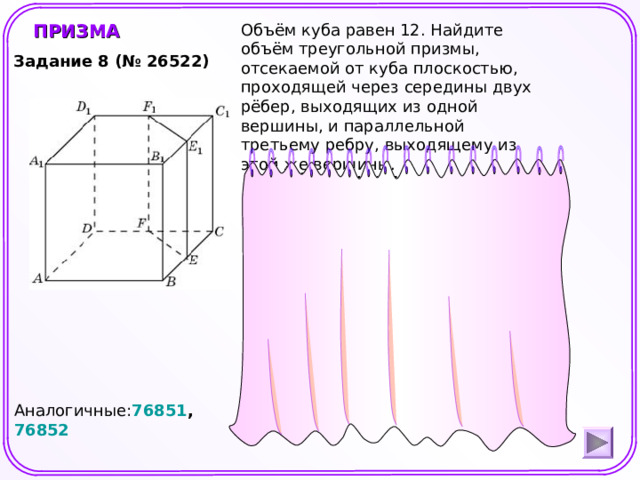
Объём куба равен 12. Найдите объём треугольной призмы, отсекаемой от куба плоскостью, проходящей через середины двух рёбер, выходящих из одной вершины, и параллельной третьему ребру, выходящему из этой же вершины.

ПРИЗМА

Задание 8 (№ 26522)

Решение:

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

Ответ: 1,5

Аналогичные: 76851 , 76852

7

ЛИТЕРАТУРА И ИНТЕРНЕТ РЕСУРСЫ

1. источник шаблона: сайт http://pedsovet.su

2. Открытый банк задач ЕГЭ по математике http://mathege.ru/or/ege/Main.html?view=Pos

Шаблон для создания презентаций к урокам математики. Савченко Е.М.

7

1. Призма в задачах ЕГЭ

Тема урока:
Призма в задачах
ЕГЭ
Е.В.Акчурина

2. Задача № 1

В
  прямоугольном параллелепипеде ABCDA1B1C1D1
известно, что D1B = , BB1 = 3, A1D1 = 4. Найдите
длину ребра A1B1.
Ответ: 1
Е.В.Акчурина

3. Задача № 2

В
  прямоугольном параллелепипеде ABCDA1B1C1D1
известно, что DC = , BB1 = 1, A1D1 = 3. Найдите
длину диагонали AC1.
Ответ: 13
Е.В.Акчурина

4. Задача № 3

Площадь грани прямоугольного параллелепипеда
равна 12. Ребро, перпендикулярное этой грани,
равно 4. Найдите объём параллелепипеда.
Ответ: 48
Е.В.Акчурина

5. Задача № 4

Три ребра прямоугольного параллелепипеда,
выходящие из одной вершины, равны 4, 6, 9.
Найдите ребро равновеликого ему куба.
Ответ: 6
Е.В.Акчурина

6. Задача № 5

Ребра прямоугольного параллелепипеда,
выходящие из одной вершины, равны 1, 2, 3.
Найдите площадь его поверхности.
Ответ: 22
Е.В.Акчурина

7. Задача № 6

Два ребра прямоугольного параллелепипеда,
выходящие из одной вершины, равны 2 и 4.
диагональ параллелепипеда равна 6. Найдите
площадь поверхности параллелепипеда.
Ответ: 64
Е.В.Акчурина

8. Задача № 7

Диагональ куба равна 3. Найдите площадь его
поверхности.
Ответ: 18
Е.В.Акчурина

9. Задача № 8

 Диагональ куба равна . Найдите его объём.
Ответ: 8
Е.В.Акчурина

10. Задача № 9

Если каждое ребро куба увеличить на 1, то его
объём увеличиться на 19. Найдите ребро куба.
Ответ: 2
Е.В.Акчурина

11. Задача № 10

Диагональ куба равна 1. Найдите площадь его
поверхности.
Ответ: 2
Е.В.Акчурина

12. Задача № 11

Во сколько раз увеличится площадь поверхности
куба, если его ребро увеличить в два раза?
Ответ: 4
Е.В.Акчурина

13. Задача № 12

Объём одного куба в 8 раз больше объёма другого
куба. Во сколько раз площадь поверхности первого
куба больше площади поверхности второго куба?
Ответ: 4
Е.В.Акчурина

14. Задача № 13

В основании прямой призмы лежит ромб с
диагоналями, равными 6 и 8. Площадь её
поверхности равна 248. Найдите боковое ребро
этой призмы.
Ответ: 10
Е.В.Акчурина

15. Задача № 14

Найдите площадь поверхности прямой призмы с
боковым ребром, равным 5, в основании которой
лежит ромб с диагоналями, равными 3 и 4.
Ответ: 62
Е.В.Акчурина

16. Задача № 15

В сосуд, имеющий форму
правильной треугольной
призмы, налили 1900 см3
воды и погрузили в воду
деталь. При этом уровень
воды поднялся с отметки 20
см до отметки 22 см.
Найдите объём детали.
Ответ выразите в см3.
Ответ: 190
Е.В.Акчурина

17. Задача № 16

Через среднюю линию
основания треугольной
призмы проведена
плоскость, параллельная
боковому ребру.
Площадь боковой
поверхности отсеченной
треугольной призмы
равна 12. Найдите
площадь боковой
поверхности исходной
призмы.
Ответ: 24
Е.В.Акчурина

18. Задача № 17

Через среднюю линию
основания треугольной
призмы проведена
плоскость, параллельная
боковому ребру. Объём
отсеченной треугольной
призмы равна 5. Найдите
объём исходной призмы.
Ответ: 20
Е.В.Акчурина

19. Задача № 18

Основанием прямой треугольной призмы служит
прямоугольный треугольник с катетами 6 и 8.
площадь её поверхности равна 288. Найдите высоту
призмы.
Ответ: 10
Е.В.Акчурина

20. Задача № 19

Найдите

 
объём правильной шестиугольной призмы,
стороны основания которой равны 1, а боковые
ребра равны .
Ответ: 4,5
Е.В.Акчурина

21. Задача № 20

Найдите площадь поверхности правильной
шестиугольной призмы, стороны основания которой
равны 3, а высота – 6.
Ответ: 108
Е.В.Акчурина

22. Задача № 21

Найдите объём параллелепипеда ABCDA1B1C1D1, если
объём треугольной пирамиды ABDA1 равен 3.
Ответ: 18
Е.В.Акчурина

23. Задача № 22

Объём параллелепипеда ABCDA1B1C1D1 равен 1,8.
Найдите объём треугольной пирамиды ABCВ1.
Ответ: 0,3
Е.В.Акчурина

24. Задача № 23

От призмы АВСА1В1С1,
объём которой равен 6,
отсечена треугольная
пирамида С1АВС. Найдите
объём оставшейся части.
Ответ: 4
Е.В.Акчурина

25. Спасибо за внимание!

Е.В.Акчурина

1


Готовимся к ЕГЭ. Прототипы В9, В11. Призма. В создании презентации принимали участие ученики 10А класса. Научный руководитель: Шахова Татьяна Александровна год

2

3


3

4


4 Объем призмы равен произведению площади основания на высоту. h h

5


В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите расстояние между точками A и E 1. Никифорова Екатерина 10А Рассмотрим прямоугольный треугольник По теореме Пифагора: В треугольнике угол между сторонами правильного треугольника равен По теореме косинусов: Значит Ответ : 2 1

6


В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите расстояние между точками B и E. 2 Ответ: Богданов Владимир 10А 2 AB C D E F A1B1 C1 D1E1 F1 1 BE является большой диагональю правильного шестиугольника BЕ в два раза больше стороны шестиугольника. BE = 2

7


В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 5. Найдите расстояние между точками B и E 1. 3 BE является большой диагональю правильного шестиугольника => в два раза больше его стороны. Шахова Татьяна 10АБВ Ответ: 5

8


В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите тангенс угла AD 1 D. Ответ: 4 Гречуха Валерия 10А ВА C D E F F1F1 F1F1 B1B1 A1A1 C1C1 D1D1 E1E1 D D1D1 A 1 A D 2 Тангенс угла AD 1 D равен отношению противолежащего катета AD к прилежащему DD 1 Большая диагональ правильного шестиугольника в два раза больше его стороны 2 2

9


В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите угол DAB. Ответ дайте в градусах. AD-биссектриса угла BAF Ответ: 60 5 Гурьева Дарья 10А А BC D EF В правильном шестиугольнике углы равны 120˚ DAB = 0,5·BAF=60˚ A1A1 B1B1 C1C1 D1D1 E1E1 F1F1

10


В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1 все ребра равны 1. Найдите угол AC 1 C. Ответ дайте в градусах. Ответ: 60 6 Карагяур Лилия 10А 1 А ВС D EF A1 B1C1 D1 E1F1 C1 C A ? 1 B AC x По теореме косинусов:

11


В правильной шестиугольной призме ABCDEFA 1 B 1 C 1 D 1 E 1 F 1, все ребра которой равны 8, найдите угол между прямыми FA и D 1 E 1. Ответ дайте в градусах. 7 АF параллельна C 1 D 1 => угол между АF и Е 1 D 1 =углу между C 1 D 1 и Е 1 D 1 Угол правильного шестиугольника = Ответ: 120 Шахова Татьяна 10АБВ

12


Площадь поверхности правильной треугольной призмы равна 6. Какой будет площадь поверхности призмы, если все ее ребра увеличить в три раза? 8 Ответ: 54 Гречуха Валерия 10А h a 3h 3a Разделим 1 ое на 2 ое Оснований – два + три прямоугольника

13


В правильной четырёхугольной призме ABCDA 1 B 1 C 1 D 1 известно, что AC 1 =2BC. Найдите угол между диагоналями BD 1 и CA 1. Ответ дайте в градусах. Ответ: 60 9 Гурьева Дарья 10А A BC D A1A1 B1B1 C1C1 D1D1 K K A1A1 B C D1D1 Диагонали прямоугольного параллелепипеда равны. Диагональное сечение является прямоугольником. Правильная четырехугольная призма является прямоугольным параллелепипедом. AC 1 =2BC=>A 1 C=2BC=> B C A1A1 Угол A 1 =30 0 Угол К = 60 0 Угол С=60 0 CB K 60 0 ? Треуг. КСВ – р/б

14


В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см 3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в см 3. Ответ: 10 Богданов Владимир 10А 184 Разделим первое на второе Объем детали =

15


В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см. 11 а 4 а Шахова Татьяна 10АБВ 80 h Объемы равны. Приравняем правые части. Ответ: 5

16


Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота 10. Ответ: 12 Смирнова Анастасия 10 А Площадь боковой поверхности фигуры равна сумме площадей всех боковых граней Все боковые грани – равные прямоугольники со сторонами 5 и 10.

17


Никифорова Екатерина 10А Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10. Найдем сторону ромба: Найдем площадь ромба: Тогда Ответ:

18


Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 20, а площадь поверхности равна =800+80x 80x=960 x=1212 Ответ: 20 Карагяур Лилия 10А Пусть боковое ребро х. 20 х Боковые грани – равные прямоугольники со Сторонами = х и 20, основания – квадраты со стороной = 20 14

19


Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, боковое ребро равно 5. Найдите объем призмы Ответ: 120 Шахова Татьяна 10АБВ

20


Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро. 17 Рассмотрим прямоугольный треугольник — площадь основания Ответ: Смирнова Анастасия 10 А 4

21


Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро. Ответ: 17 Коваль Дмитрий 10А А1А1 В1В1 С1С1 А В С А В С 3 5 h Боковое ребро прямой призмы является высотой 4

22


Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны Ответ: 4,5 18 Коваль Дмитрий 10А Найдем площадь основания. Составлено из шести равносторонних треугольников 1

23


Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы. 19 A1 B C N1 M M1 C1 A B1 N Шахова Татьяна 10АБВ Высоты равны. Сравним площади оснований. A C B M N Треугольники подобны с коэффициентом подобия= ½ => их площади относятся как ¼. Разделим первое на второе. Ответ: 1,25

24


Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны и наклонены к плоскости основания под углом Ответ: 20 Хачатрян Нателла 10А Найдем площадь основания. 18 Составлено из шести равносторонних треугольников 2 h Найдем высоту h

25


Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности S 1 =? 6 8 Гипотенуза= 10 S 2 =24 S 1 =24 S 3 =610=60 S 4 =810=80 S 5 =1010=100 S= =288 Ответ: 288 Хачатрян Нателла 10А

26


Николаева Ксения 10А В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы. 2) Найдем площадь боковых граней: Ответ: 10 1) Найдем площадь ромба: 3) Найдем площадь одной грани: 4) Из треугольника ВНС найдём ВС: св-во параллелограмма 5) Найдём боковое ребро призмы: 23

27


Николаева Ксения 10А В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы. Ответ: Покажем расстояния от АА 1 до других боковых ребер. Угол К – линейный угол двугранного прямого угла. КМL – перпендикулярное сечение призмы. Площадь боковой поверхности призмы равна произведению бокового ребра на периметр перпендикулярного сечения.

28


Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы. 25 Шахова Татьяна 10АБВ Площадь поверхности состоит из площадей оснований и площадей боковых граней, которые являются прямоугольниками. Ответ: 10

29


Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы. Сравним соответствующие грани Ответ: 26 Привалова Анастасия 10А A1 B C N1 M M1 C1 A B1 N Т.о. S всех боковых граней большой призмы больше S граней маленькой призмы в 2 раза => 16

30


Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины Сравним S осн.куба и S осн.пр Ответ: 1,5 27 Привалова Анастасия 10А a A B C D F E Разделим 1 е на 2 е

31


В правильной треугольной призме ABCA 1 B 1 C 1, все ребра которой равны 3, найдите угол между прямыми AA 1 и BC 1. Ответ дайте в градусах. Ответ: Самошкин Даниил 10А В АА 1 и ВС 1 – скрещивающиеся. А С В1В1 С1С1 А1А1 АА 1 параллельна ВВ 1 => угол между АА 1 и ВС 1 = углу между ВВ 1 и ВС 1 Треугольник ВВ 1 С 1 –прямоугольный и равнобедренный так как призма прямая и все ребра равны. => Угол ВВ 1 С 1 =45 0

32


Спасибо за работу!

Слайды презентации

Слайды и текст к этой презентации: