Вариант №2 пробного ЕГЭ Профиль Санкт-Петербург, 2021 с ответами и критериями.
- 27.09.2022
Второй тренировочный вариант ЕГЭ 2023 по математике базового уровня на основе демоверсии ЕГЭ 2023 от ФИПИ.
В 2023 году были изменения по некоторым предметам, поэтому обязательно ознакомьтесь со списком изменений, если еще не смотрели.
- Посмотреть демоверсию 2023 по базовой математике + изменения
Тестовый вариант создан по кодификатору и спецификации ФИПИ ЕГЭ 2023 и в полном соответствии со всеми изменениями демоверсии ЕГЭ 2023. В конце варианта указаны ответы ко всем задания первой и второй части теста. Вариант был опубликован и проводился 19 сентября 2022 года.
Автор-составитель: Проект ЕГЭ 100 БАЛЛОВ https://vk.com/ege100ballov
- Другие тренировочные варианты ЕГЭ по базовой математике
Есть вопросы? Пишите в комментариях ниже!
Некоторые задания из тренировочной работы №2
Задание 5
В чемпионате по гимнастике участвуют 50 спортсменок: 17 из России, 22 из США, остальные – из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Задание 15
После уценки телевизора его новая цена составила 0,96 от старой цены. На сколько процентов уменьшилась цена телевизора в результате уценки?
Задание 17
2(3−2𝑥)−7=−3𝑥+8.
Смотреть в PDF:
Или прямо сейчас: cкачать в pdf файле.
Пробный ЕГЭ № 2 по математике. 11 класс Вариант 1, Вариант 2, Вариант 3, Вариант 4. Ответы.
Скачать:
Предварительный просмотр:
МБОУ «Апраксинская СОШ»
ЕГЭ по МАТЕМАТИКЕ №2
Профильный уровень. 2022г.
Вариант 1
Часть 1
1. Решите уравнение 
. Если корней окажется несколько, то в ответе запишите наименьший из них.
Ответ: ___________________
2. Вероятность того. Что мотор холодильника прослужит более 1 года, равна 0,85, а вероятность того, что он прослужит более 2 лет, равна 0,63. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?
Ответ: ___________________
3. В ромбе АВСD угол DВА равен 160. Найдите угол ВСD. Ответ дайте в градусах.
Ответ: ___________________
4. Найдите 
, если 
.
Ответ: ___________________
5. Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 
1:3, считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 128?
Ответ: ___________________
6. На рисунке изображены график функции 
и касательная к нему в точке с абсциссой х0. Найдите значение производной функции 
в точке х0?
Ответ: ___________________
7. Локатор батискафа, равномерно погружается вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отраженного от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны отношением
, где с=1500м/с – скорость звука в воде, f0 – частота испускаемого сигнала (в МГц), f – частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГЦ), если батискаф погружается со скоростью 2м/с.
Ответ: ___________________
8. Автомобиль, движущийся с постоянной скоростью 80км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 60км/ч. каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона?
Ответ: ___________________
9. На рисунке изображён график функции вида 
, где числа а, b и с – целые. Найдите 
.
Ответ: ___________________
10. Симметричную игральную кость бросали 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события хотя бы раз выпало 2 очка?
Ответ: ___________________
11. Найдите точку минимума функции 
.
Ответ: ___________________
Часть 2
12. а) Решите уравнение: 
.
б) Укажите корни этого уравнения, принадлежащие отрезку 
.
13. Все ребра правильной треугольной призмы АВСА1В1С1 имеют длину 6. Точки М и N – середины рёбер АА1 и А1С1 соответственно.
а) Докажите, что прямые ВМ и МN перпендикулярны.
б) Найдите угол между плоскостями ВМN и АВВ1.
14. Решите неравенство
.
15. 15-го января планируется взять кредит в банке на 6 месяцев в размере 1 млн. рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг (в млн рублей) |
1,0 |
0,6 |
0,4 |
0,3 |
0,2 |
0,1 |
0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
16. Две окружности касаются внешним образом в точке К. Прямая АВ касается первой окружности в точке А, а второй – в точке В. Прямая ВК пересекает первую окружность в точке D, прямая АК пересекает вторую окружность в точке С.
а) Докажите, что прямые АD и ВС параллельны.
б) Найдите площадь треугольника АКВ, если известно, что радиусы окружностей равны 4 и 1.
17. Найдите все положительные значения a, при каждом из которых система 
имеет единственное решение
18. В школах №1 и №2 учащиеся писали тест. В каждой школе тест писали. по крайней мере, 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешел изи школы №1 в школу №2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе №1 уменьшиться в 10 раз?
б) Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе №2 равняться 7?
в) Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе №2.
Предварительный просмотр:
МБОУ «Апраксинская СОШ»
ЕГЭ по МАТЕМАТИКЕ №2
Профильный уровень. 2022г.
Вариант 2
Часть 1
1. Решите уравнение 
. Если корней окажется несколько, то в ответе запишите наименьший из них.
Ответ: ___________________
2. Вероятность того. Что мотор холодильника прослужит более 1 года, равна 0,83, а вероятность того, что он прослужит более 2 лет, равна 0,69. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?
Ответ: ___________________
3. В ромбе АВСD угол DВА равен 210. Найдите угол ВСD. Ответ дайте в градусах.
Ответ: ___________________
4. Найдите 
, если 
.
Ответ: ___________________
5. Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 
1:4, считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 250?
Ответ: ___________________
6. На рисунке изображены график функции 
и касательная к нему в точке с абсциссой х0. Найдите значение производной функции 
в точке х0?
Ответ: ___________________
7. Локатор батискафа, равномерно погружается вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отраженного от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны отношением
, где с=1500м/с – скорость звука в воде, f0 – частота испускаемого сигнала (в МГц), f – частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГЦ), если батискаф погружается со скоростью 2м/с.
Ответ: ___________________
8. Автомобиль, движущийся с постоянной скоростью 80км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 50км/ч. каким будет расстояние (в километрах) между этими автомобилями через 20 минут после обгона?
Ответ: ___________________
9. На рисунке изображён график функции вида 
, где числа а, b и с – целые. Найдите 
.
Ответ: ___________________
10. Симметричную игральную кость бросали 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события хотя бы раз выпало 4 очка?
Ответ: ___________________
11. Найдите точку минимума функции 
.
Ответ: ___________________
Часть 2
12. а) Решите уравнение: 
.
б) Укажите корни этого уравнения, принадлежащие отрезку 
.
13. Все ребра правильной треугольной призмы АВСА1В1С1 имеют длину 6. Точки М и N – середины рёбер АА1 и А1С1 соответственно.
а) Докажите, что прямые ВМ и МN перпендикулярны.
б) Найдите угол между плоскостями ВМN и АВВ1.
14. Решите неравенство
.
15. 15-го января планируется взять кредит в банке на 6 месяцев в размере 1 млн. рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг (в млн рублей) |
1,0 |
0,6 |
0,4 |
0,3 |
0,2 |
0,1 |
0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
16. Две окружности касаются внешним образом в точке К. Прямая АВ касается первой окружности в точке А, а второй – в точке В. Прямая ВК пересекает первую окружность в точке D, прямая АК пересекает вторую окружность в точке С.
а) Докажите, что прямые АD и ВС параллельны.
б) Найдите площадь треугольника АКВ, если известно, что радиусы окружностей равны 4 и 1.
17. Найдите все положительные значения a, при каждом из которых система 
имеет единственное решение
18. В школах №1 и №2 учащиеся писали тест. В каждой школе тест писали. по крайней мере, 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешел изи школы №1 в школу №2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе №1 уменьшиться в 10 раз?
б) Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе №2 равняться 7?
в) Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе №2.
Предварительный просмотр:
МБОУ «Апраксинская СОШ»
ЕГЭ по МАТЕМАТИКЕ №2
Профильный уровень. 2022г.
Вариант 3
Часть 1
1. Решите уравнение 
. Если корней окажется несколько, то в ответе запишите наименьший из них.
Ответ: ___________________
2. Вероятность того. Что мотор холодильника прослужит более 1 года, равна 0,84, а вероятность того, что он прослужит более 2 лет, равна 0,69. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?
Ответ: ___________________
3. В ромбе АВСD угол DВА равен 170. Найдите угол ВСD. Ответ дайте в градусах.
Ответ: ___________________
4. Найдите 
, если 
.
Ответ: ___________________
5. Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 
1:2, считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 81?
Ответ: ___________________
6. На рисунке изображены график функции 
и касательная к нему в точке с абсциссой х0. Найдите значение производной функции 
в точке х0?
Ответ: ___________________
7. Локатор батискафа, равномерно погружается вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отраженного от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны отношением
, где с=1500м/с – скорость звука в воде, f0 – частота испускаемого сигнала (в МГц), f – частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГЦ), если батискаф погружается со скоростью 2м/с.
Ответ: ___________________
8. Автомобиль, движущийся с постоянной скоростью 90км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 45км/ч. каким будет расстояние (в километрах) между этими автомобилями через 20 минут после обгона?
Ответ: ___________________
9. На рисунке изображён график функции вида 
, где числа а, b и с – целые. Найдите 
.
Ответ: ___________________
10. Симметричную игральную кость бросали 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события хотя бы раз выпало 3 очка?
Ответ: ___________________
11. Найдите точку минимума функции 
.
Ответ: ___________________
Часть 2
12. а) Решите уравнение: 
.
б) Укажите корни этого уравнения, принадлежащие отрезку 
.
13. Все ребра правильной треугольной призмы АВСА1В1С1 имеют длину 6. Точки М и N – середины рёбер АА1 и А1С1 соответственно.
а) Докажите, что прямые ВМ и МN перпендикулярны.
б) Найдите угол между плоскостями ВМN и АВВ1.
14. Решите неравенство
.
15. 15-го января планируется взять кредит в банке на 6 месяцев в размере 1 млн. рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг (в млн рублей) |
1,0 |
0,6 |
0,4 |
0,3 |
0,2 |
0,1 |
0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
16. Две окружности касаются внешним образом в точке К. Прямая АВ касается первой окружности в точке А, а второй – в точке В. Прямая ВК пересекает первую окружность в точке D, прямая АК пересекает вторую окружность в точке С.
а) Докажите, что прямые АD и ВС параллельны.
б) Найдите площадь треугольника АКВ, если известно, что радиусы окружностей равны 4 и 1.
17. Найдите все положительные значения a, при каждом из которых система 
имеет единственное решение
18. В школах №1 и №2 учащиеся писали тест. В каждой школе тест писали. по крайней мере, 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешел изи школы №1 в школу №2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе №1 уменьшиться в 10 раз?
б) Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе №2 равняться 7?
в) Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе №2.
Предварительный просмотр:
МБОУ «Апраксинская СОШ»
ЕГЭ по МАТЕМАТИКЕ №2
Профильный уровень. 2022г.
Вариант 4
Часть 1
1. Решите уравнение 
. Если корней окажется несколько, то в ответе запишите наименьший из них.
Ответ: ___________________
2. Вероятность того. Что мотор холодильника прослужит более 1 года, равна 0,83, а вероятность того, что он прослужит более 2 лет, равна 0,65. Какова вероятность того, что мотор прослужит более 1 года, но не более 2 лет?
Ответ: ___________________
3. В ромбе АВСD угол DВА равен 180. Найдите угол ВСD. Ответ дайте в градусах.
Ответ: ___________________
4. Найдите 
, если 
.
Ответ: ___________________
5. Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 
1:3, считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 192?
Ответ: ___________________
6. На рисунке изображены график функции 
и касательная к нему в точке с абсциссой х0. Найдите значение производной функции 
в точке х0?
Ответ: ___________________
7. Локатор батискафа, равномерно погружается вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отраженного от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны отношением
, где с=1500м/с – скорость звука в воде, f0 – частота испускаемого сигнала (в МГц), f – частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГЦ), если батискаф погружается со скоростью 2м/с.
Ответ: ___________________
8. Автомобиль, движущийся с постоянной скоростью 80км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40км/ч. каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона?
Ответ: ___________________
9. На рисунке изображён график функции вида 
, где числа а, b и с – целые. Найдите 
.
Ответ: ___________________
10. Симметричную игральную кость бросали 3 раза. Известно, что в сумме выпало 6 очков. Какова вероятность события хотя бы раз выпало 1 очко?
Ответ: ___________________
11. Найдите точку минимума функции 
.
Ответ: ___________________
Часть 2
12. а) Решите уравнение: 
.
б) Укажите корни этого уравнения, принадлежащие отрезку 
.
13. Все ребра правильной треугольной призмы АВСА1В1С1 имеют длину 6. Точки М и N – середины рёбер АА1 и А1С1 соответственно.
а) Докажите, что прямые ВМ и МN перпендикулярны.
б) Найдите угол между плоскостями ВМN и АВВ1.
14. Решите неравенство
.
15. 15-го января планируется взять кредит в банке на 6 месяцев в размере 1 млн. рублей. Условия его возврата таковы:
– 1-го числа каждого месяца долг увеличивается на r процентов по сравнению с концом предыдущего месяца, где r – целое число;
– со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
– 15-го числа каждого месяца долг должен составлять некоторую сумму в соответствии со следующей таблицей.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг (в млн рублей) |
1,0 |
0,6 |
0,4 |
0,3 |
0,2 |
0,1 |
0 |
Найдите наибольшее значение r, при котором общая сумма выплат будет меньше 1,2 млн рублей.
16. Две окружности касаются внешним образом в точке К. Прямая АВ касается первой окружности в точке А, а второй – в точке В. Прямая ВК пересекает первую окружность в точке D, прямая АК пересекает вторую окружность в точке С.
а) Докажите, что прямые АD и ВС параллельны.
б) Найдите площадь треугольника АКВ, если известно, что радиусы окружностей равны 4 и 1.
17. Найдите все положительные значения a, при каждом из которых система 
имеет единственное решение
18. В школах №1 и №2 учащиеся писали тест. В каждой школе тест писали. по крайней мере, 2 учащихся, а суммарно тест писали 9 учащихся. Каждый учащийся, писавший тест, набрал натуральное количество баллов. Оказалось, что в каждой школе средний балл за тест был целым числом. После этого один из учащихся, писавших тест, перешел изи школы №1 в школу №2, а средние баллы за тест были пересчитаны в обеих школах.
а) Мог ли средний балл в школе №1 уменьшиться в 10 раз?
б) Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Мог ли первоначальный средний балл в школе №2 равняться 7?
в) Средний балл в школе №1 уменьшился на 10%, средний балл в школе №2 также уменьшился на 10%. Найдите наименьшее значение первоначального среднего балла в школе №2.
Предварительный просмотр:
МБОУ «Апраксинская СОШ»
ЕГЭ по МАТЕМАТИКЕ №1
Профильный уровень. 2022г.
Ответы
Часть 1
Вариант 1
1) 5; 2) 0,22; 3) 148; 4) –0,96; 5) 126; 6) –1,75; 7) 751 
5; 9) 33; 10) 0,7; 11) –14.
Вариант 2
1) 2; 2) 0,14; 3) 138; 4) 0,96; 5) 248; 6) –1,75; 7) 751 10; 9) 22; 10) 0,3; 11) 15.
Вариант 3
1) 3; 2) 0,15; 3) 146; 4) –0,96; 5) 78; 6) –1,75; 7) 751 15; 9) 13; 10) 0,6; 11) 12.
Вариант 4
1) 4; 2) 0,18; 3) 144; 4) 0,96; 5) 189; 6) –1,75; 7) 751 10; 9) 66; 10) 0,9; 11) 11.
Часть 2
12) а) 
. 13) 
.
14) 
; 
15) 7. 16) 3,2. 17) 
. 18) а) да; б) нет; в) 5.
По теме: методические разработки, презентации и конспекты
- Мне нравится
Новый тренировочный вариант №2 ЕГЭ 2023 по математике 11 класс базовый уровень с ответами и решением по новой демоверсии ЕГЭ 2023 года от ФИПИ для подготовки на 100 баллов, задания взяты из банка заданий ФИПИ и с экзамена прошлых лет, сложность варианта уровня ЕГЭ. Ниже вы можете скачать вариант или решать онлайн на сайте.
Скачать вариант №2 с ответами
Скачать вариант №1 с ответами
Пробный вариант состоит из двух частей, включающих в себя 25 заданий. Часть 1 содержит 19 заданий, часть 2 содержит 6 заданий с развёрнутым ответом. На выполнение экзаменационной работы по математике отводится 3 часа 55 минут (235 минут)
Решать вариант №2 ЕГЭ 2023 база по математике 11 класс
вариант2-егэ2023-база-математика-ответы
1)Таксист за месяц проехал 9000 км. Цена бензина 30 рублей за литр. Средний расход бензина на 100 км составляет 8 литров. Сколько рублей потратил таксист на бензин за этот месяц?
Ответ: 21600
3)На графике изображена зависимость атмосферного давления от высоты над уровнем моря. На горизонтальной оси отмечена высота над уровнем моря в километрах, на вертикальной – давление в миллиметрах ртутного столба. Определите по графику, чему равно атмосферное давление на высоте 6,5 км. Ответ дайте в миллиметрах ртутного столба.
Ответ: 320
4)В фирме «Эх, прокачу!» стоимость поездки на такси длительностью меньше 5 минут составляет 150 рублей. Если поездка длится 5 минут или более, то её стоимость (в рублях) рассчитывается по формуле 𝐶 = 150 + 11(𝑡 − 5), где 𝑡 − длительность поездки, выраженная в минутах (𝑡 ≥ 5). Пользуясь этой формулой, рассчитайте стоимость 10-минутной поездки. Ответ укажите в рублях.
Ответ: 205
5)В чемпионате по гимнастике участвуют 50 спортсменок: 17 из России, 22 из США, остальные – из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
Ответ: 0,22
6)На соревнованиях по прыжкам в воду судьи выставили оценки от 0 до 10 трём спортсменам. Результаты приведены в таблице. Итоговый балл вычисляется следующим образом: две наибольшие и две наименьшие оценки отбрасываются, а три оставшиеся складываются, и их сумма умножается на коэффициент сложности. В ответе укажите номера спортсменов, итоговый балл которых больше 140, без пробелов, запятых и других дополнительных символов.
Ответ: 13
7)На графике изображена зависимость температуры от времени в процессе разогрева двигателя легкового автомобиля. На горизонтальной оси отмечено время в минутах, прошедшее с момента запуска двигателя, на вертикальной оси – температура двигателя в градусах Цельсия. Пользуясь графиком, поставьте в соответствие каждому интервалу времени характеристику температуры.
Ответ: 3412
8)Среди тех, кто зарегистрирован в «ВКонтакте», есть школьники из Твери. Среди школьников из Твери есть те, кто зарегистрирован в «Одноклассниках». Выберите утверждения, которые верны при указанных условиях.
- 1) Все школьники из Твери не зарегистрированы ни в «ВКонтакте», ни в «Одноклассниках».
- 2) Среди школьников из Твери нет тех, кто зарегистрирован в «ВКонтакте».
- 3) Среди школьников из Твери есть те, кто зарегистрирован в «ВКонтакте».
- 4) Хотя бы один из пользователей «Одноклассников» является школьником из Твери.
Ответ: 34
9)На клетчатой бумаге с размером клетки 1 × 1 изображён треугольник. Найдите его площадь.
Ответ: 9
10)Диагональ прямоугольного телевизионного экрана равна 80 см, а ширина экрана – 64 см. Найдите высоту экрана. Ответ дайте в сантиметрах.
Ответ: 48
11)Плоскость, проходящая через точки 𝐴, 𝐵 и 𝐶 (см. рис.), разбивает правильную треугольную призму на два многогранника. Сколько вершин у получившегося многогранника с меньшим числом граней?
Ответ: 6
12)На окружности по разные стороны от диаметра 𝐴𝐵 взяты точки 𝐷 и 𝐶. Известно, что ∠𝐷𝐵𝐴 = 41°. Найдите угол 𝐷𝐶𝐵. Ответ дайте в градусах.
Ответ: 49
13)Через точку, делящую высоту конуса в отношении 1:4, считая от вершины, проведена плоскость, параллельная основанию. Найдите объём этого конуса, если объём конуса, отсекаемого от данного конуса проведённой плоскостью, равен 8.
Ответ: 1000
15)После уценки телевизора его новая цена составила 0,96 от старой цены. На сколько процентов уменьшилась цена телевизора в результате уценки?
Ответ: 4
17)Найдите корень уравнения 2(3 − 2𝑥) − 7 = −3𝑥 + 8.
Ответ: -9
19)Найдите чётное трёхзначное натуральное число, сумма цифр которого на 1 меньше их произведения. В ответе укажите какое-нибудь одно такое число.
Ответ: 412
20)Из одной точки круговой трассы, длина которой равна 12 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 101 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Ответ: 65
21)В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 103, во втором – 97, в третьем – 93, а сумма чисел в каждой строке больше 21, но меньше 24. Сколько всего строк в таблице?
Ответ: 13
ПОДЕЛИТЬСЯ МАТЕРИАЛОМ
Пробный вариант ЕГЭ по математике 18.03.21 Санкт-Петербург. Вариант №2
При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.
Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.
Версия для печати и копирования в MS Word
1
В квартире установлен прибор учёта расхода горячей воды (счётчик). Показания на 1 марта составляли 748 м3 воды, а 1 апреля — 756 м3. Сколько нужно заплатить за горячую воду за март, если стоимость 1 м3 горячей воды составляет 191 руб. 50 коп.?
Ответ:
2
На диаграмме показана среднемесячная температура воздуха в городе N за каждый месяц 2019 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, какова разница между наибольшей и наименьшей среднемесячной температурой в 2019 году. Ответ дайте в градусах.
Ответ:
3
На клетчатой бумаге с размером клетки 1 × 1 отмечены две точки A и B. Найдите длину отрезка AB.
Ответ:
4
Перед началом турнира по шахматам участников случайным образом разбивают на пары с помощью жребия. Всего зарегистрировано 46 шахматистов, среди которых 19 спортсменов из Санкт-Петербурга, в том числе и Алексей Журавлёв. Найдите вероятность, что Алексей Журавлёв будет играть с шахматистом из Санкт-Петербурга.
Ответ:
5
Найдите корень уравнения: 
Ответ:
6
В треугольнике ABC угол B — тупой, AB = 7, BC = 8. Найдите величину угла, противолежащего стороне AC, если площадь треугольника равна 
Ответ дайте в градусах.
Ответ:
7
Прямая y = −3x + 2 параллельна касательной к графику функции y = x2 + 7x + 3. Найдите абсциссу точки касания.
Ответ:
8
Во сколько раз увеличится объём конуса, если радиус его основания увеличится в 3 раза, а высота останется прежней?
Ответ:
9
Вычислите 
Ответ:
10
11
Из пункта А и пункт В, расстояние между которыми 90 км, одновременно выехали мотоциклист и велосипедист. Известно, что за час мотоциклист проезжает на 16 км больше, чем велосипедист. Найдите скорость велосипедиста, если известно, что он прибыл в пункт В на 2 часа позже мотоциклиста. Ответ дайте в км/ч.
Ответ:
12
Найдите точку минимума функции 
Ответ:
13
а) Решите уравнение 
б) Найдите все корни этого уравнения, принадлежащие отрезку 
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
14
В правильной треугольной призме ABCA1B1C1 сторона основания равна 6, а боковое ребро равно 4. На ребрах BB1 и BC выбраны точки D и E соответственно так, что B1D = BE = 1.
а) Докажите, что прямые A1D и DE перпендикулярны.
б) Найдите угол между плоскостями A1DE и BCC1.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
15
Решите неравенство 
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
16
В треугольнике MPK биссектриса угла K пересекает сторону MP в точке A. Окружность, описанная около треугольника AMK пересекает сторону PK в точке B.
а) Докажите, что треугольник ABM равнобедренный.
б) Найдите площадь треугольника ABM, если MK = 9, PK = 6, MP = 5.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
17
В январе 2020 года Василий взял кредит в банке на сумму 3 300 000 рублей. По договору с банком Василий должен был погасить долг двумя равными платежами в феврале 2021 года и феврале 2022 года, при условии, что в январе 2021 года и январе 2022 года сумма оставшегося долга увеличивается на 20%. В феврале 2021 года Василий сделал первую выплату в соответствии с договором. После этого ему удалось договориться с банком о рефинансировании кредита и уменьшить процент, на который сумма долга вырастет в январе 2022 года, до 16%. Какую сумму сэкономит Василий на рефинансировании своего кредита?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
18
Найдите все значения параметра a, при каждом из которых уравнение
имеет хотя бы одно решение.
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
19
Полина записала несколько различных натуральных чисел, все цифры которых нечетны, после чего нашла сумму этих чисел и обозначила ее через S.
а) Может ли сумма цифр числа S быть нечетным числом, если Полина записала ровно четыре числа?
б) Может ли произведение цифр числа S быть нечетным числом, если S > 1000?
в) Пусть десятичная запись числа S состоит из 2021 цифры. Какое наименьшее натуральное значение может принимать произведение цифр числа S?
Решения заданий с развернутым ответом не проверяются автоматически.
На следующей странице вам будет предложено проверить их самостоятельно.
Завершить тестирование, свериться с ответами, увидеть решения.
ЕГЭ 2023. Экзаменационная работа включает в себя 21 задание. На выполнение работы отводится 3 часа (180 минут). Ответы к заданиям записываются по приведённым ниже образцам в виде числа или последовательности цифр. Сначала запишите ответы к заданиям в поле ответа в тексте работы, а затем перенесите их в бланк ответов № 1 справа от номера соответствующего задания.
Пробный вариант составлен на основе официальной демоверсии от ФИПИ за 2023 год.
В конце варианта приведены правильные ответы ко всем заданиям. Вы можете свериться с ними и найти у себя ошибки.
Скачать тренировочный вариант ЕГЭ: Скачать
Решать работу: Онлайн
Интересные задания
1. Таксист за месяц проехал 9000 км. Цена бензина 30 рублей за литр. Средний расход бензина на 100 км составляет 8 литров. Сколько рублей потратил таксист на бензин за этот месяц?
4. В фирме «Эх, прокачу!» стоимость поездки на такси длительностью меньше 5 минут составляет 150 рублей. Если поездка длится 5 минут или более, то её стоимость (в рублях) рассчитывается по формуле 𝐶 = 150 + 11(𝑡 − 5), где 𝑡 − длительность поездки, выраженная в минутах (𝑡 ≥ 5). Пользуясь этой формулой, рассчитайте стоимость 10-минутной поездки. Ответ укажите в рублях.
5. В чемпионате по гимнастике участвуют 50 спортсменок: 17 из России, 22 из США, остальные – из Китая. Порядок, в котором выступают гимнастки, определяется жребием. Найдите вероятность того, что спортсменка, выступающая первой, окажется из Китая.
8. Среди тех, кто зарегистрирован в «ВКонтакте», есть школьники из Твери. Среди школьников из Твери есть те, кто зарегистрирован в «Одноклассниках». Выберите утверждения, которые верны при указанных условиях.
1) Все школьники из Твери не зарегистрированы ни в «ВКонтакте», ни в «Одноклассниках».
2) Среди школьников из Твери нет тех, кто зарегистрирован в «ВКонтакте».
3) Среди школьников из Твери есть те, кто зарегистрирован в «ВКонтакте».
4) Хотя бы один из пользователей «Одноклассников» является школьником из Твери.
В ответе запишите номера выбранных утверждений без пробелов, запятых и других дополнительных символов.
11. Плоскость, проходящая через точки 𝐴, 𝐵 и 𝐶 (см. рис.), разбивает правильную треугольную призму на два многогранника. Сколько вершин у получившегося многогранника с меньшим числом граней?
15. После уценки телевизора его новая цена составила 0,96 от старой цены. На сколько процентов уменьшилась цена телевизора в результате уценки?
19. Найдите чётное трёхзначное натуральное число, сумма цифр которого на 1 меньше их произведения. В ответе укажите какое-нибудь одно такое число.
20. Из одной точки круговой трассы, длина которой равна 12 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 101 км/ч, и через 20 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
21. В таблице три столбца и несколько строк. В каждую клетку таблицы вписали по натуральному числу так, что сумма всех чисел в первом столбце равна 103, во втором – 97, в третьем – 93, а сумма чисел в каждой строке больше 21, но меньше 24. Сколько всего строк в таблице?
Вам будет интересно:
ЕГЭ по математике (база) 11 класс 2023. Новый тренировочный вариант №1 — №220912 (задания и ответы)
* Олимпиады и конкурсы
* Готовые контрольные работы
* Работы СтатГрад
* Официальные ВПР
Поделиться:
- Математика
- Информатика
- Математика
- Русский язык
- Английский
- Математика
- Русский язык
- Английский
- Математика
- Русский язык
- Английский
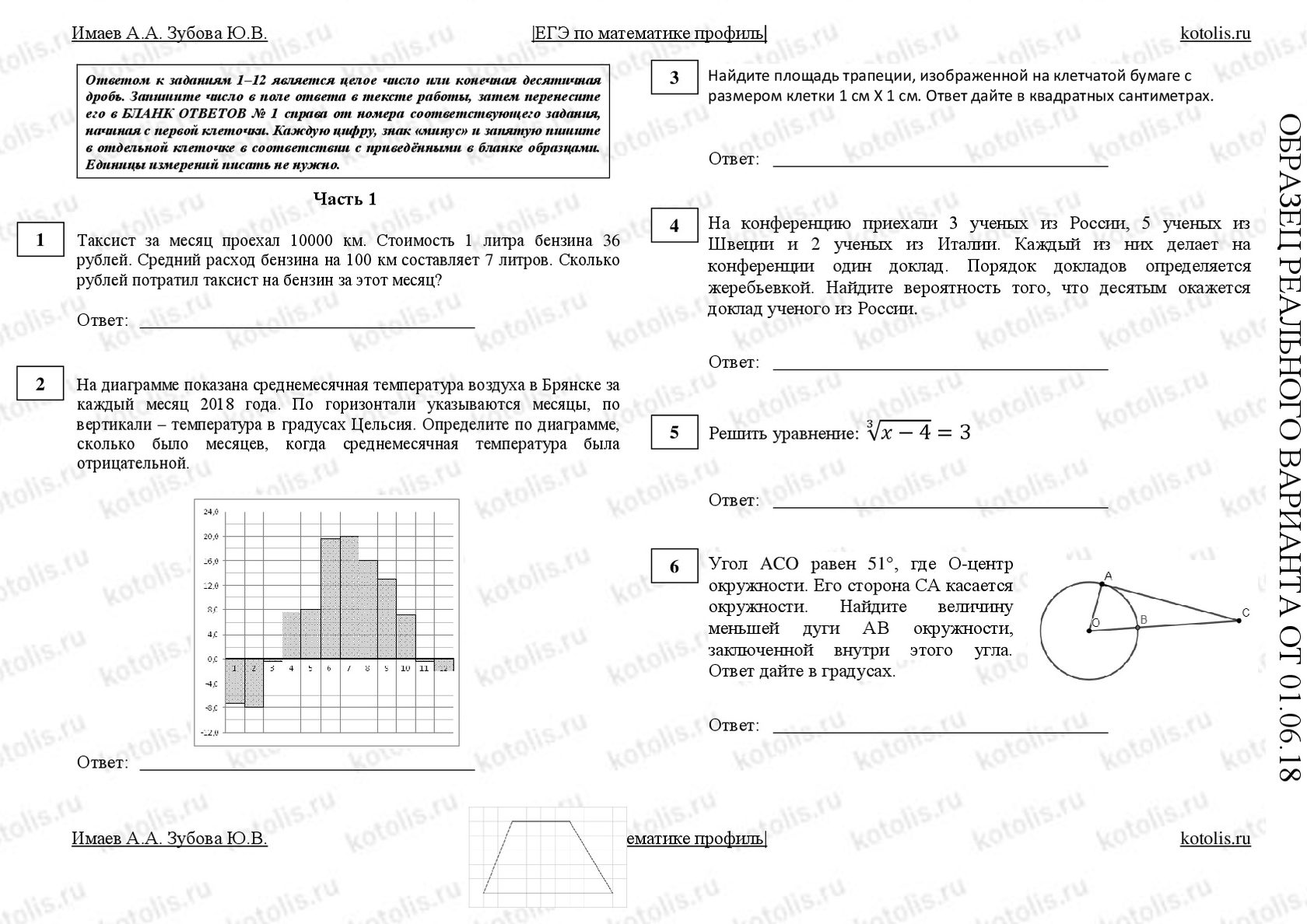
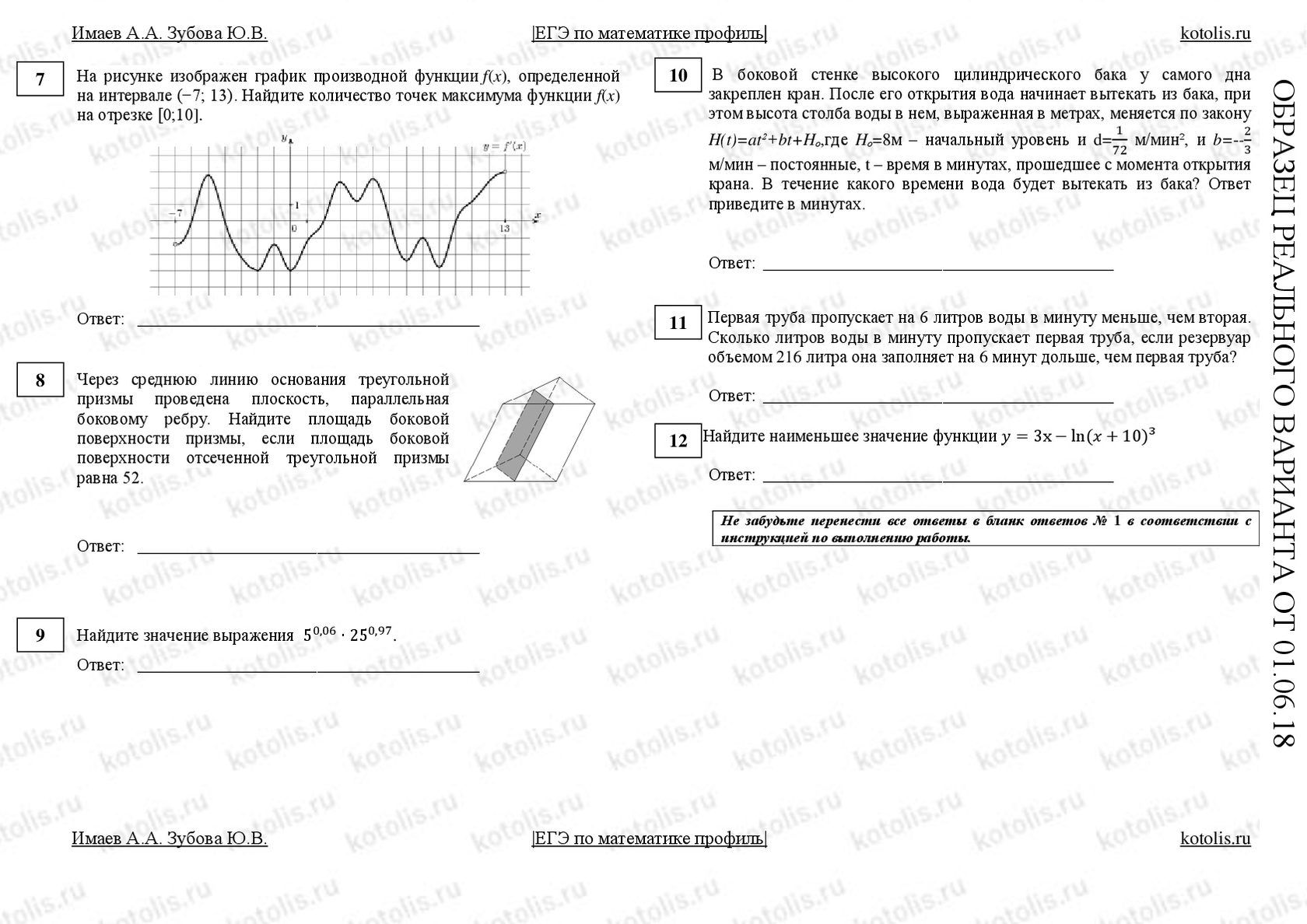
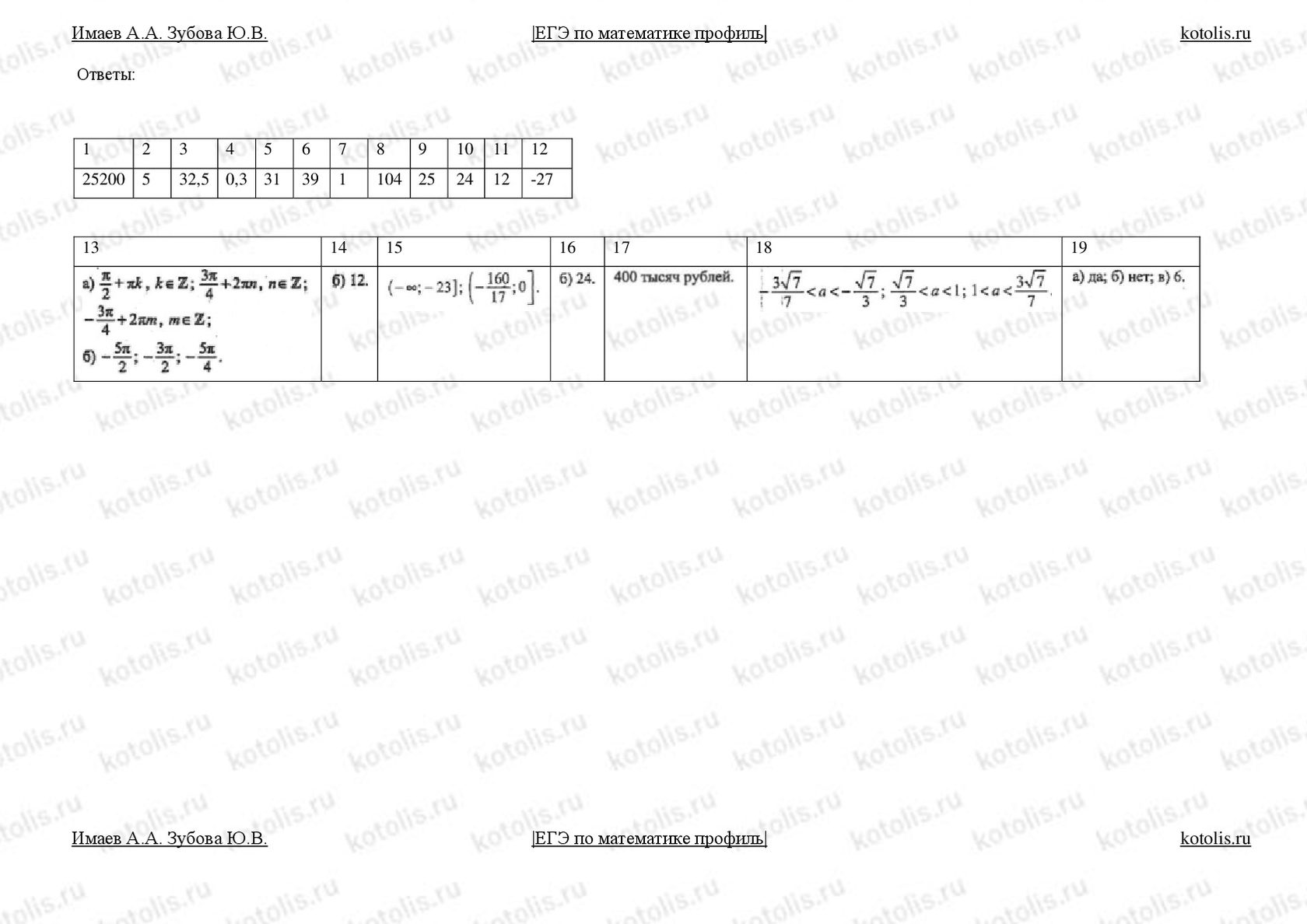
Вариант №2 реального ЕГЭ по математике от 01.06.2018
С ответами для всех заданий и официальными решениями для 2 части
Ответы и решения
Полезное
Реальные варианты ЕГЭ по математике
Перейти
Вариант №3 с решением
Перейти