Пробный экзамен по математике 2016

Пробный экзамен по профильной математике Санкт-Петербург 05.04.2016. Вариант 1.

При выполнении заданий с кратким ответом впишите в поле для ответа цифру, которая соответствует номеру правильного ответа, или число, слово, последовательность букв (слов) или цифр. Ответ следует записывать без пробелов и каких-либо дополнительных символов. Дробную часть отделяйте от целой десятичной запятой. Единицы измерений писать не нужно.

Если вариант задан учителем, вы можете вписать или загрузить в систему ответы к заданиям с развернутым ответом. Учитель увидит результаты выполнения заданий с кратким ответом и сможет оценить загруженные ответы к заданиям с развернутым ответом. Выставленные учителем баллы отобразятся в вашей статистике.

Для просмотра этого варианта необходимо авторизоваться.

• Главная

  
  

• Пробные и реальные тесты ЕГЭ

  
  

• ЕГЭ по профильной математике

  
  

• 
  Пробный ЕГЭ 2016 по математике с ответами и критериями

01.09.2015

Представляем вам первый пробный вариант ЕГЭ по математике в 2016 году (профильного уровня).

Вариант полностью оформлен как настоящий КИМ ЕГЭ по математике. Поэтому может использоваться для проведения пробных ЕГЭ в классе и школе.

В конце варианта содержатся не только ответы, но и критерии проверки к части 2.

Смотреть в PDF:

Или прямо сейчас: cкачать в pdf файле.

Сохранить ссылку:

Комментарии (0)
Добавить комментарий

Добавить комментарий

Комментарии без регистрации. Несодержательные сообщения удаляются.

Имя (обязательное)

E-Mail

Подписаться на уведомления о новых комментариях

Отправить

2015-08-25
2018-08-30

2016

Пробный вариант 1 математика 2016.

1. Най­ди­те зна­че­ние вы­ра­же­ния 6,4 − 7 · (−3,3).

Ре­ше­ние.

Найдём зна­че­ние вы­ра­же­ния:

Ответ: 29,5.

Ответ: 29,5

341401

29,5

Источник: СтатГрад: Тре­ни­ро­воч­ная ра­бо­та по ма­те­ма­ти­ке 07.04.2015 ва­ри­ант МА90704.

2. Из­вест­но, что число от­ри­ца­тель­ное. На каком из ри­сун­ков точки с ко­ор­ди­на­та­ми рас­по­ло­же­ны на ко­ор­ди­нат­ной пря­мой в пра­виль­ном по­ряд­ке?

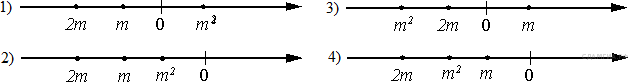
В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1) 1

2) 2

3) 3

4) 4

Ре­ше­ние.

По­сколь­ку , имеем: По­сколь­ку имеем:

Пра­виль­ный ответ ука­зан под но­ме­ром: 1.

Ответ: 1

337346

1

3. Какое из сле­ду­ю­щих чисел за­клю­че­но между чис­ла­ми и

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1) 0,8

2) 0,9

3) 1

4) 1,1

Ре­ше­ние.

При по­мо­щи де­ле­ния «в стол­бик» пе­ре­ведём обык­но­вен­ные дроби в де­ся­тич­ные с точ­но­стью до вто­ро­го знака после за­пя­той:

Сле­до­ва­тель­но,

Пра­виль­ный ответ ука­зан под но­ме­ром: 4.

Ответ: 4

337335

4

4. Ре­ши­те урав­не­ние   .

Если кор­ней не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

Ре­ше­ние.

По тео­ре­ме, об­рат­ной тео­ре­ме Виета — сумма кор­ней равна −7, а их про­из­ве­де­ние равно −18

Тем самым, это числа −9 и 2.

Ответ: −9; 2.

Ответ: -9; 2

311438

-9; 2

Источник: ГИА-2013. Математика. Экзамен. Ва­ри­ант 1

5. На ри­сун­ке изоб­ра­же­ны гра­фи­ки функ­ций вида y = kx + b. Уста­но­ви­те со­от­вет­ствие между гра­фи­ка­ми функ­ций и зна­ка­ми ко­эф­фи­ци­ен­тов k и b.

Гра­фи­ки

Ко­эф­фи­ци­ен­ты

1) k b 0

2) k 0, b 0

3) k b

4) k 0, b

За­пи­ши­те в ответ цифры, рас­по­ло­жив их в по­ряд­ке, со­от­вет­ству­ю­щем бук­вам:

А	Б	В

Ре­ше­ние.

Если пря­мая за­да­на урав­не­ни­ем то при функ­ция воз­рас­та­ет, при — убы­ва­ет. Зна­че­нию со­от­вет­сву­ет зна­че­ние функ­ции в точке Таким об­ра­зом, гра­фи­ку A со­от­вет­ству­ют ко­эфи­ци­ен­ты 2, Б − 1, В − 4.

Ответ: 214.

Ответ: 214

341325

214

Источник: СтатГрад: Тре­ни­ро­воч­ная ра­бо­та по ма­те­ма­ти­ке 07.04.2015 ва­ри­ант МА90701.

6. Дана ариф­ме­ти­че­ская про­грес­сия (a_n), раз­ность ко­то­рой равна −8,5, a₁ = −6,8. Най­ди­те a₁₁.

Ре­ше­ние.

Член ариф­ме­ти­че­ской про­грес­сии с но­ме­ром можно найти по фор­му­ле Тре­бу­ет­ся найти

Ответ: −91,8.

Ответ: -91,8

341190

-91,8

Источник: Банк за­да­ний ФИПИ

7. Упро­сти­те вы­ра­же­ние , най­ди­те его зна­че­ние при ; . В ответ за­пи­ши­те по­лу­чен­ное число.

Ре­ше­ние.

Упро­стим вы­ра­же­ние:

  (при  и  ).

Найдём зна­че­ние вы­ра­же­ния при ,  :

Ответ: 4,6.

Ответ: 4,6

114

4,6

Источник: ГИА по ма­те­ма­ти­ке 28.05.2013. Ос­нов­ная волна. Ва­ри­ант 1309.

8. Ре­ши­те си­сте­му не­ра­венств

На каком ри­сун­ке изоб­ра­же­но мно­же­ство её ре­ше­ний?

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

Ре­ше­ние.

Решим си­сте­му не­ра­венств:

Ре­ше­ние не­ра­вен­ства изоб­ра­же­но под но­ме­ром 4.

Ответ: 4

333109

4

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 17.04.2014 ва­ри­ант МА90605

9. Четырёхуголь­ник ABCD впи­сан в окруж­ность. Угол ABC равен 80°, угол CAD равен 54°. Най­ди­те угол ABD. Ответ дайте в гра­ду­сах.

Ре­ше­ние.

Угол CAD и угол CBD — впи­сан­ные углы, опи­ра­ю­щи­е­ся на одну дугу, а зна­чит, они равны 54°. Сле­до­ва­тель­но:

Ответ: 26.

Ответ: 26

316319

26

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 01.10.2013 ва­ри­ант МА90103.

10. В окруж­но­сти с цен­тром O AC и BD — диа­мет­ры. Цен­траль­ный угол AOD равен 130°. Най­ди­те впи­сан­ный угол ACB. Ответ дайте в гра­ду­сах.

Ре­ше­ние.

Смеж­ные углы BOA и AOD об­ра­зу­ют развёрну­тый угол, по­это­му их сумма равна 180°, от­ку­да ∠AOB = 180° − 130° = 50°. Угол AOB — цен­траль­ный, сле­до­ва­тель­но, он равен дуге, на ко­то­рую опи­ра­ет­ся, угол ACB — впи­сан­ный, сле­до­ва­тель­но, он равен по­ло­ви­не дуги, на ко­то­рую опи­ра­ет­ся. По­сколь­ку углы AOB и ACB опи­ра­ют­ся на одну и ту же дугу, угол ACB равен по­ло­ви­не угла AOB, то есть 25°.

Ответ: 25.

Ответ: 25

339473

25

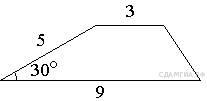
11. Бо­ко­вая сто­ро­на тра­пе­ции равна 5, а один из при­ле­га­ю­щих к ней углов равен 30°. Най­ди­те пло­щадь тра­пе­ции, если её ос­но­ва­ния равны 3 и 9.

Ре­ше­ние.

Пло­щадь тра­пе­ции вы­чис­ля­ет­ся по фор­му­ле

где и — ос­но­ва­ния, а — вы­со­та тра­пе­ции. Найдём вы­со­ту: сле­до­ва­тель­но,

Ответ: 15.

Ответ: 15

314876

15

Источник: Банк за­да­ний ФИПИ

12. На ри­сун­ке изоб­ра­жен ромб . Ис­поль­зуя ри­су­нок, най­ди­те .

Ре­ше­ние.

Тан­генс угла в пря­мо­уголь­ном тре­уголь­ни­ке — от­но­ше­ние про­ти­во­ле­жа­ще­го ка­те­та к при­ле­жа­ще­му. Тре­уголь­ник OBC — пря­мо­уголь­ный, по­это­му .

Ответ: 0,75.

Ответ: 0,75

311333

0,75

Источник: 9 класс. Математика. Кра­е­вая диагностическая работа. Крас­но­дар (вар. 2)

13. Ука­жи­те но­ме­ра не­вер­ных утвер­жде­ний.

1) При пе­ре­се­че­нии двух па­рал­лель­ных пря­мых тре­тьей пря­мой сумма на­крест ле­жа­щих углов равна 180°.

2) Диа­го­на­ли ромба пер­пен­ди­ку­ляр­ны.

3) Цен­тром окруж­но­сти, опи­сан­ной около тре­уголь­ни­ка, яв­ля­ет­ся точка пе­ре­се­че­ния его бис­сек­трис.

Если утвер­жде­ний не­сколь­ко, за­пи­ши­те их через точку с за­пя­той в по­ряд­ке воз­рас­та­ния.

Ре­ше­ние.

Про­ве­рим каж­дое из утвер­жде­ний.

1) «При пе­ре­се­че­нии двух па­рал­лель­ных пря­мых тре­тьей пря­мой сумма на­крест ле­жа­щих углов равна 180°» — не­вер­но, на­крест ле­жа­щие углы равны.

2) «Диа­го­на­ли ромба пер­пен­ди­ку­ляр­ны» — верно, по свой­ству ромба.

3) «Цен­тром окруж­но­сти, опи­сан­ной около тре­уголь­ни­ка, яв­ля­ет­ся точка пе­ре­се­че­ния его бис­сек­трис» — не­вер­но,вер­ным будет утвер­жде­ние: «Цен­тром окруж­но­сти, опи­сан­ной около тре­уголь­ни­ка, яв­ля­ет­ся точка пе­ре­се­че­ния его­се­ре­дин­ных пер­пен­ди­ку­ля­ров».

Ответ: 1; 3.

Ответ: 1;3

316349

1;3

Источник: МИОО: Тре­ни­ро­воч­ная ра­бо­та по ма­те­ма­ти­ке 19.02.2014 ва­ри­ант МА90501.

14. На диа­грам­ме по­ка­за­но ко­ли­че­ство по­са­жен­ных де­ре­вьев и ку­стар­ни­ков в г. Сочи за пе­ри­од с 2009 по 2012 гг. Опре­де­ли­те, сколь­ко всего было по­са­же­но зелёных на­саж­де­ний за 2011 г. и 2012 г.?

В от­ве­те ука­жи­те номер пра­виль­но­го ва­ри­ан­та.

1) 10 000

2) 4 000

3) 12 000

4) 8 000

Ре­ше­ние.

Зе­ле­ные на­саж­де­ния, по­са­жен­ные в 2011 году со­от­вет­ству­ют на диа­грам­ме столб­цу 3, в 2012 году — столб­цу 4. Из диа­грам­мы мы видно, что в 2011 было по­са­же­но 8 тысяч, в 2012 году — 4 ты­ся­чи зелёных на­саж­де­ний. Таким об­ра­зом, за 2011 и 2012 года было по­са­же­но 12 000 зелёных на­саж­де­ний.

Пра­виль­ный ответ ука­зан под но­ме­ром 3.

Ответ: 3

311298

3

Источник: 9 класс. Математика. Кра­е­вая диагностическая работа. Крас­но­дар (вар. 3)

15. На гра­фи­ке изоб­ра­же­на за­ви­си­мость ат­мо­сфер­но­го дав­ле­ния (в мил­ли­мет­рах ртут­но­го стол­ба) от вы­со­ты мест­но­сти над уров­нем моря (в ки­ло­мет­рах). На сколь­ко мил­ли­мет­ров ртут­но­го стол­ба ат­мо­сфер­ное дав­ле­ние на вы­со­те Эве­ре­ста ниже ат­мо­сфер­но­го дав­ле­ния на вы­со­те Мунку-Сар­ды­ка?

Ре­ше­ние.

Из гра­фи­ка видно, что дав­ле­ние на вы­со­те Эве­ре­ста мень­ше дав­ле­ния на вы­со­те Мунку-Сар­ды­ка на мм. рт. ст.

Ответ: 240.

Ответ: 240

341334

240

Источник: СтатГрад: Тре­ни­ро­воч­ная ра­бо­та по ма­те­ма­ти­ке 07.04.2015 ва­ри­ант МА90701.

16. За 20 минут ве­ло­си­пе­дист про­ехал 7 ки­ло­мет­ров. Сколь­ко ки­ло­мет­ров он про­едет за 35 минут, если будет ехать с той же ско­ро­стью?

Ре­ше­ние.

Ско­рость ве­ло­си­пе­ди­ста со­став­ля­ет: Зна­чит, за 35 минут он про­едет

Ответ: 12,25.

Ответ: 12,25

317927

12,25

17. Лест­ни­ца со­еди­ня­ет точки A и B и со­сто­ит из 20 сту­пе­ней. Вы­со­та каж­дой сту­пе­ни равна 16,5 см, а длина — 28 см. Най­ди­те рас­сто­я­ние между точ­ка­ми A и B(в мет­рах).

Ре­ше­ние.

За­да­ча сво­дит­ся к на­хож­де­нию ги­по­те­ну­зы пря­мо­уголь­но­го тре­уголь­ни­ка. Вы­со­та лест­ни­цы со­став­ля­ет 20 · 16,5 = 330 см = 3,3 м. А длина по го­ри­зон­та­ли со­став­ля­ет 20 · 28 = 560 см = 5,6 м. По тео­ре­ме Пи­фа­го­ра найдём рас­сто­я­ние между точ­ка­ми A и B:

Ответ: 6,5.

Ответ: 6,5

322886

6,5

18. На диа­грам­ме пред­став­ле­но рас­пре­де­ле­ние ко­ли­че­ства поль­зо­ва­те­лей не­ко­то­рой со­ци­аль­ной сети по стра­нам мира. Всего в этой со­ци­аль­ной сети 12 млн поль­зо­ва­те­лей.

Какое из сле­ду­ю­щих утвер­жде­ний не­вер­но?

1) Поль­зо­ва­те­лей из Укра­и­ны боль­ше, чем поль­зо­ва­те­лей из Литвы.

2) Поль­зо­ва­те­лей из Укра­и­ны мень­ше чет­вер­ти об­ще­го числа поль­зо­ва­те­лей.

3) Поль­зо­ва­те­лей из Бе­ла­ру­си боль­ше 3 мил­ли­о­нов.

4) Поль­зо­ва­те­лей из Рос­сии боль­ше, чем из всех осталь­ных стран, вме­сте взя­тых.

Ре­ше­ние.

Про­ве­рим каж­дое утвер­жде­ние:

1) Из диа­грам­мы видно, что поль­зо­ва­те­лей из Укра­и­ны боль­ше чем поль­зо­ва­те­лей из «дру­гих стран», а зна­чит, и боль­ше, чем поль­зо­ва­те­лей из Литвы. Пер­вое утвер­жде­ние верно.

2) Из диа­грам­мы видно, что поль­зо­ва­те­лей из Укра­и­ны мень­ше чет­вер­ти об­ще­го числа поль­зо­ва­те­лей. Вто­рое утвер­же­дние верно.

3) Из диа­грам­мы видно, что поль­зо­ва­те­лей из Бе­ла­ру­си мень­ше чет­вер­ти от об­ще­го числа поль­зо­ва­те­лей. Всего поль­зо­ва­те­лей 12 млн, зна­чит поль­зо­ва­те­лей из Бе­ла­ру­си менее 3 млн. Тре­тье утвер­жде­ние не­вер­но.

2) Из диа­грам­мы видно, что поль­зо­ва­те­лей из Росии около двух тре­тей от об­ще­го числа поль­зо­ва­те­лей, зна­чит, поль­зо­ва­те­лей из Рос­сии боль­ше, чем из всех осталь­ных стран вме­сте взя­тых. Четвёртое утвер­жде­ние верно.

Не­вер­ным яв­ля­ет­ся утвер­жде­ние под но­ме­ром 3.

Ответ: 3

315175

3

Источник: Банк за­да­ний ФИПИ

19. Иг­раль­ную кость бро­са­ют два­жды. Най­ди­те ве­ро­ят­ность того, что оба раза вы­па­ло число, мень­шее 4.

Ре­ше­ние.

При бро­са­нии ку­би­ка рав­но­воз­мож­ны шесть раз­лич­ных ис­хо­дов. Со­бы­тию «вы­па­дет мень­ше четырёх очков» удо­вле­тво­ря­ют три слу­чая: когда на ку­би­ке вы­па­да­ет 1, 2, или 3 очка. По­это­му ве­ро­ят­ность того, что на ку­би­ке вы­па­дет мень­ше четрёх очков равна Таким об­ра­зом, при одном бро­са­нии ку­би­ка с оди­на­ко­вой ве­ро­ят­но­стью ре­а­ли­зу­ет­ся либо со­бы­тие А — вы­па­ло число, мень­шее 4, либо со­бы­тие Б — вы­па­ло число не мень­ше 4. То есть рав­но­ве­ро­ят­но ре­а­ли­зу­ют­ся че­ты­ре со­бы­тия: А-А, А-Б, Б-А, Б-Б. По­это­му ве­ро­ят­ность того, что хотя бы раз вы­па­ло число, мень­шее 4 равна

Ответ: 0,25.

Ответ: 0,25

325492

0,25

20. Закон Мен­де­ле­е­ва-Кла­пей­ро­на можно за­пи­сать в виде PV = νRT, где P — дав­ле­ние (в пас­ка­лях), V — объём (в м³), ν — ко­ли­че­ство ве­ще­ства (в молях), T — тем­пе­ра­ту­ра (в гра­ду­сах Кель­ви­на), а R — уни­вер­саль­ная га­зо­вая по­сто­ян­ная, рав­ная 8,31 Дж/(К⋅моль). Поль­зу­ясь этой фор­му­лой, най­ди­те тем­пе­ра­ту­ру T (в гра­ду­сах Кель­ви­на), если ν = 68,2 моль, P = 37 782,8 Па, V = 6 м³.

Ре­ше­ние.

Вы­ра­зим тем­пе­ра­ту­ру из за­ко­на Кла­пей­ро­на-Мен­де­ле­е­ва: Под­став­ляя, по­лу­ча­ем:

Ответ: 400.

Ответ: 400

338296

400

21. Ре­ши­те не­ра­вен­ство

Ре­ше­ние.

Умно­жим на 12, при­ведём по­доб­ные сла­га­е­мые и раз­ло­жим на мно­жи­те­ли:

Про­из­ве­де­ние двух со­мно­жи­те­лей будет мень­ше нуля, если со­мно­жи­те­ли имеют раз­ный знак (см. ри­су­нок). Таким об­ра­зом, по­лу­ча­ем ответ:

Ответ:

Источник: Банк за­да­ний ФИПИ

22. Поезд, дви­га­ясь рав­но­мер­но со ско­ро­стью 63 км/ч, про­ез­жа­ет мимо иду­ще­го в том же на­прав­ле­нии па­рал­лель­но путям со ско­ро­стью 3 км/ч пе­ше­хо­да за 57 се­кунд. Най­ди­те длину по­ез­да в мет­рах.

Ре­ше­ние.

Пусть длина по­ез­да l м . Ско­рость по­ез­да от­но­си­тель­но пе­ше­ход равна 63-3=60 км/ч, или м/с. Сле­до­ва­тель­но, поезд про­ез­жа­ет мимо иду­ще­го в том же на­прав­ле­нии па­рал­лель­но путям пе­ше­хо­да за l : се­кунд.

Со­ста­вим и решим урав­не­ние:

; .

Длина по­ез­да со­став­ля­ет 950 м.

Ответ: 950 м.

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 17.04.2014 ва­ри­ант МА90601

23. По­строй­те гра­фик функ­ции и най­ди­те все зна­че­ния k, при ко­то­рых пря­мая имеет с гра­фи­ком дан­ной функ­ции ровно одну общую точку.

Ре­ше­ние.

Рас­кры­вая мо­ду­ли, по­лу­ча­ем, что при функ­ция при­ни­ма­ет вид при функ­ция при­ни­ма­ет вид а при функ­ция при­ни­ма­ет вид

Гра­фик функ­ции изоб­ражён на ри­сун­ке.

Пря­мая имеет с гра­фи­ком дан­ной функ­ции ровно одну общую точку при при­над­ле­жа­щем мно­же­ству

Ответ:

Источник: МИОО: Ди­а­гно­сти­че­ская ра­бо­та по ма­те­ма­ти­ке 01.10.2013 ва­ри­ант МА90106.

24. Най­ди­те ве­ли­чи­ну угла   , если   — бис­сек­три­са угла   ,   — бис­сек­три­са угла   .

Ре­ше­ние.

Имеем:   = 2 · 25° = 50°;   = 180° − 50° = 130°;   = 130° : 2 = 65°.

Ответ: 65°.

Источник: ГИА-2013. Математика. Ди­а­гно­сти­че­ская работа № 1. (вар. 1) 02.10.2012г.

25. В па­рал­ле­ло­грам­ме ABCD диа­го­на­ли AC и BD пе­ре­се­ка­ют­ся в точке O. До­ка­жи­те, что пло­щадь па­рал­ле­ло­грам­ма ABCD в че­ты­ре раза боль­ше пло­ща­ди тре­уголь­ни­ка COD.

Ре­ше­ние.

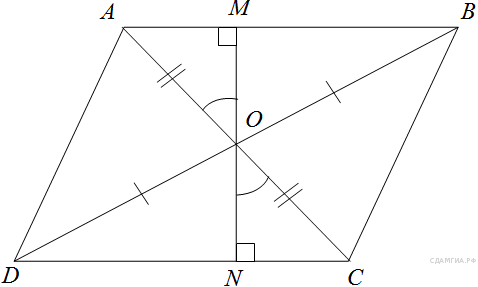
Про­ведём вы­со­ту так, чтобы она про­хо­ди­ла через точку Углы и равны друг другу как вер­ти­каль­ные. Вспом­ним также, что диа­го­на­ли де­лят­ся точ­кой пе­ре­се­че­ния по­по­лам, сле­до­ва­тель­но, Рас­смот­рим тре­уголь­ни­ки и , они пря­мо­уголь­ные, имеют рав­ные углы и рав­ные ги­по­те­ну­зы, сле­до­ва­тель­но эти тре­уголь­ни­ки равны, а зна­чит равны от­рез­ки и . Таким об­ра­зом,

Пло­щадь па­рал­ле­ло­грамм равна а пло­щадь тре­уголь­ни­ка

Источник: Банк за­да­ний ФИПИ

26. Бо­ко­вые сто­ро­ны AB и CD тра­пе­ции ABCD равны со­от­вет­ствен­но 20 и 25, а ос­но­ва­ние BC равно 5. Бис­сек­три­са угла ADC про­хо­дит через се­ре­ди­ну сто­ро­ны AB. Най­ди­те пло­щадь тра­пе­ции.

10 апреля 2016

В закладки

Обсудить

Жалоба

Задания с экзамена + решения + критерии оценки.

Источник: alexlarin.net.