Простейшие математические модели егэ

Текстовые задачи — это одни из самых нелюбимых заданий, особенно у учеников старших классов, потому что чем дальше, тем запутаннее становится условие, тем сложнее становится составить уравнение и верно решить задачу. Но, как и в любой теме в математике, чтобы уверенно решать сложные задачи, необходимо разобраться с самыми основными приемами.

Разберем эти задачи с самого начала. Текстовая задача состоит из условия, в котором описана некоторая ситуация, и вопроса, на который нужно дать ответ.

Пример:

Решение любой текстовой задачи можно разделить на несколько основных этапов:

• Работа с условием
• Составление математической модели
• Проверка ответа

Работа с условием

Для облегчения работы с условием полезно использовать иллюстрацию или моделирование. Это может быть краткая запись условия математически или словесно. Также это может быть дополнительный рисунок или таблица.

Пример: Петя выше Коли, Сережа ниже Коли. Кто выше?

Иллюстрация:

Из рисунка сразу понятен ответ: Петя выше всех.

Пример.

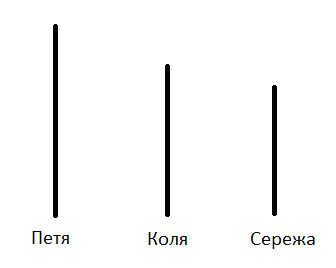
Два поезда идут навстречу друг другу. Скорость одного из них 45 км/ч, скорость другого — 55 км/ч. Сейчас между ними 200 км. Через сколько часов они встретятся?

Иллюстрация:

Пусть х часов — время движения обоих поездов, тогда по рисунку видно, что первый проедет 45х км, а второй — 55х км.

Составим математическую модель:

45х + 55х = 200

100х = 200

х = 2 ч

Ответ: 2 ч.

Для составления уравнения по условию задачи используются различные приемы, в зависимости от данной в условии зависимости величин.

Математическая модель

Математика, в частности, занимается тем, что описывает различные реальные ситуации на математическом языке. В таблице приведены различные ситуации и их математические модели.

x — число девочек

y — число мальчиков

Реальная ситуация	Математическая модель
В классе поровну мальчиков и девочек	$ { x=y} $
Девочек на 5 больше, чем мальчиков	$ { x=y+5, ; или; x-y=5,; или; x-5=y} $
Мальчиков в 2 раза больше, чем девочек	$ { y=2x, ; или; frac{y}{2}=x,; или; frac{y}{x}=2} $
Если в класс перейдут 3 мальчика, то девочек станет в два раза больше	$ { y=2(y+3)} $

Алгебраическая зависимость

Такая зависимость выражается в словах: выше/ниже, больше/меньше, дороже/дешевле, длиннее/короче и т. д.

При составлении уравнения особое значение играют используемые предлоги: «в» и «на».

Пример: Петя выше Коли на 20 см, Сережа ниже Коли на 10 см. На сколько см Петя выше Сережи?

Решение: Пусть П — рост Пети, К — рост Коли, С — рост Сережи.

Кстати, обратите внимание на этот приём — выбирать «говорящие» переменные, а не безликие иксы и игреки, чтобы не запутаться при работе с уравнением.

Выразим рост мальчиков.

Петя выше Коли на 20 см: П – 20 = К

Сережа ниже Коли на 10 см: К = С + 10

Подставим в первое уравнение рост Коли: П – 20 = С + 10

Нам нужно найти, на сколько см Петя выше Сережи: П – С

П – 20 = С + 10

П – С = 20 + 10

П – С = 30

Получаем, что Петя выше Сережи на 30 см.

Пример: На уроке труда ученики делали снежинки. Всего было сделано 12 снежинок. Маша сделала в два раза больше снежинок, чем Коля. Коля сделал на 4 снежинки меньше, чем Рома. Сколько снежинок сделала Маша?

Решение:

Пусть М — количество снежинок, которое сделала Маша, К — снежинки Коли, Р — снежинки Ромы.

Маша сделала в два раза больше снежинок, чем Коля: К = М/2

Коля сделал на 4 снежинки меньше, чем Рома: Р = К + 4 = М/2 + 4

Вместе ребята сделали 12 снежинок: М + К + Р = 12

Подставим все выраженные через М значения: М + М/2 + М/2 + 4 = 12

М = 4.

Маша сделала 4 снежинки.

Процентная зависимость

С процентами нам постоянно приходиться сталкиваться в повседневной жизни. “Скидка 30%”, “Кредит без процентов за 5 минут”, “Арендная плата выросла на 12%” — со всех сторон на нас сыпятся рекламные слоганы и призывы. Но что же значит это таинственное слово “проценты”? И как ими оперировать?

Сегодня мы с вами дадим определение процентов, поймём, как находится процент от некоторого числа, как можно найти одно количество процентов, уже зная другое. И, конечно, рассмотрим каждый из этих случаев на конкретном примере.

Как кирка у каменщика, камертон у настройщика или световой меч у Джедая, в математике тоже существуют свои инструменты, нужные для выполнения тех или иных операций. И проценты как раз и являются таким удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби. И действительно, проценты очень тесно связаны с дробями, по сути, основываясь на них.

Так что же такое один процент?

Процент — это всегда доля какого-то числа.

100% — все число

50% — половина

25% — четверть

Чтобы найти 1%, необходимо поделить всё число на 100.

Пример:

Есть 100 яблок.

$ 1% ;от ;всех ;яблок; –frac{100}{100} = 1 ;яблоко. $

Есть 200 груш

$ 1% ;от ;всех ;груш; –frac{200}{100} = 2 ;груши. $

Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом — соответствующие проценты.

Пример:

200 груш — 100 %

2 груши — 1 %

Пропорция отражает зависимость величин. По-другому это можно записать в виде двух дробей.

$ frac{200}{2}=frac{100}{1} $

Исходя из правил работы с дробями, получаем правила работы с пропорцией.

1. Внутри одной дроби можно сокращать значения.

2. Произведение накрест лежащих значений равно: 200 · 1 = 2 · 100

Эту тему мы еще подробно пройдем на курсе.

Рассмотрим несколько примеров работы с процентами в текстовых задачах.

Ситуация при работе с процентами усложняется, когда изначально нам известен не 1%, а несколько — например, 20. А требуют найти какое-нибудь неудобное число процентов

Пример: 38% населения деревни — это 76 человек. Сколько человек составляет 15% от общего населения?

Так как мы не можем сразу найти 15%, то нам вначале понадобится сделать промежуточный шаг — найти 1%. Если 38% — это 76 человек, то, разделив на 38, мы получим так нужный нам 1%. 38% = 76 человек ⇒1% = 2 человека. Тогда 15% = 30 человек

Но неугомонные математики не остановились и на этом. Что будет, если мы возьмём процент от какого-то числа, вычтем или прибавим к начальному числу, а затем снова возьмём то же количество процентов?

Пример: В 2010 дом стоял 2 тысячи рублей. В 2011 его цена увеличилась на 20%, а в 2012 — ещё на 20%. Сколько дом стоил к концу 2012 года?

На примере этой задаче мы посмотрим не только на то, как нужно брать проценты от разных величин, но и как переводить проценты в дроби. Решим её двумя способами:

Способ 1 Для начала давайте выясним, сколько стоил дом в 2011. Его стоимость увеличилась на 20%, т.е. на 400 рублей (1% = 2000:100 = 20, 20% = 400) и стала, соответственно, равна 2400. Теперь нам нужно узнать, сколько он стал стоить в 2012. Важно! Сейчас мы будем брать 20% от новой цены, т.е. той, которая была на дом в 2011 году. Если 1% = 2400:100 = 24, то 20% = 480, то есть новая цена в 2012 году — 2400 + 480 = 2880

Способ 2 Если 1% — это 0,01 от чего-то, то 20% — это 0,2. Тогда 20% от первоначальной цены это 2000⋅0,2 = 400, и цена на дом в 2011 году стала 2400. Теперь находим 20% от новой стоимости 2400⋅0,2 = 480 и итоговую стоимость в 2012 году: 2400 + 480 = 2880

Отлично! Итак, мы не только узнали, что такое проценты, как можно с ними обращаться, но и выяснили, как можно брать проценты от разных величин и как сопоставлять проценты с дробями. Больше интересных фактов и приёмов работы с процентами вы узнаете в процессе курса.

Также текстовые задачи могут быть посвящены прогрессиям, производительности, темпу — обо всем этом мы поговорим на нашем курсе. А сейчас приступайте к задачам для тренировки.

ЕГЭ по математике Профиль. Задание 8: Уметь строить и исследовать простейшие математические модели. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

ЕГЭ Профиль. Задание № 8

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 8 определяет умение строить и исследовать простейшие математические модели, решать текстовые задачи на сложные проценты, использование арифметической и геометрической прогрессии, различные виды движения, вычисление работы.

Задание состоит из текстовой задачи с описанием различных жизненных ситуаций. Как правило, решение требует составления уравнения или системы уравнении. В ответе следует записать целое число или конечную десятичную дробь.

План выполнения:

1. Внимательно прочитайте условие задачи.
2. Сделайте краткую запись.
3. Составьте выражение, уравнение или систему уравнений.
4. Выполните решение на черновике. При получении двух корней в уравнении оставьте корень, подходящий по смыслу к условию задачи. Ответьте на вопрос задачи.
5. Запишите полученное число в поле ответа КИМ и бланк ответов N 1.

При подготовке необходимо повторить правила решения задач с использованием следующих величин и понятий:

• Сложные проценты, где процент вычисляется несколько раз. При подготовке необходимо повторить понятие процента от числа и правила нахождения процента от числа, числа по его проценту, процента по числу.
• Концентрация смесей и сплавов. Концентрация — процентное отношение чистого вещества к смеси (сплаву, раствору). Такие задачи решаются с помощью процентов или пропорции.
• Движение по прямой. Из курса физики следует повторить формулы для нахождения скорости, закон сложения скоростей.
• Движение по окружности. Такие задачи в большинстве случаев решаются составлением уравнений или систем уравнений.
• Движение по течению и против течения. Подобные задачи также решаются составлением уравнения или системы уравнений.
• Работа и совместная работа. Для решения применяются уравнения или системы уравнений.
• Арифметическая и геометрическая прогрессии. При подготовке необходимо повторить определения прогрессий, формулы для вычисления отдельных членов арифметической и геометрической прогрессии, суммы членов.

Задачи с ответами и решениями:

Задача № 8 (1). В октябре цена на яблоки была снижена на 10% по отношению к цене в сентябре. В ноябре октябрьская цена повысилась на 10%. Сколько процентов составляет ноябрьская цена по отношению к сентябрьской?

Решение: Пусть х — цена на яблоки в сентябре, тогда в октябре цена составила 90% от сентябрьской и равна 0,9х. После повышения в ноябре на 10% цена составила 110% от октябрьской и равна 1,1 • (0,9х) = 0,99х. Значит, в ноябре цена составила 0,99 от цены в сентябре, то есть 99%.
Ответ: 99.
ПРИМЕЧАНИЕ: Процент означает сотую часть чего–либо. 1 % от числа означает 0,01 этого числа. В ходе решения удобно сразу переводить проценты в десятичные дроби.
Часто учащиеся пишут в ответе 0, объясняя это тем, что если цена была снижена на 10%, а затем повысилась на 10%, то конечная цена не изменилась.

Задача № 8 (2). Имеется кусок сплава меди с оловом общей массой 12 кг, содержащий 45% меди. Сколько чистого олова надо добавить к этому куску сплава, чтобы получившийся новый сплав содержал 40% меди?

Решение: Пусть х кг олова надо добавить к сплаву. Так как процентное содержание меди в сплаве равно 45%, масса меди в первоначальном сплаве m = 0,45 • 12 = 5,4 (кг). Тогда 12 + х — масса нового сплава. Поскольку масса меди в первоначальном сплаве равна 5,4 кг, то 5,4/(12+х) –  концентрация меди в новом сплаве. По условию 5,4/(12+х) = 0,4. Решая уравнение, получаем: х = 1,5 (кг)
Ответ: 1,5.
ПРИМЕЧАНИЕ: Концентрация меди в новом сплаве равна отношению массы меди к общей массе нового сплава.

Задача № 8 (3). В сосуд, содержащий 4 л 14%–ного водного раствора некоторого вещества, добавили 6 л воды. Сколько процентов составляет концентрация получившегося раствора?

Решение: Концентрация раствора равна р = V_в–ва/V_р–ра • 100%. Объём вещества в исходном растворе равен 0,14 • 4 = 0,56 (л). При добавлении 6 л воды общий объём раствора стал 10 л, а объём растворённого вещества остался прежним. Таким образом, концентрация полученного раствора равна 0,56/10 • 100% = 5,6%.
Ответ: 5,6.
ПРИМЕЧАНИЕ: Концентрация раствора равна отношению массы растворённого вещества к массе раствора, а также отношению их объёмов.
При решении задач на смешивание удобно пользоваться формулой m₁с₂ + m₂с₂ = (m₁ + m₂)с₃, где m₁, m₂ — массы смешиваемых растворов, с₁, с₂, с₃ — концентрации растворов до и после смешивания.

Задача № 8 (4). Два мотоциклиста стартуют одновременно в одном направлении из двух диаметрально противоположных точек круговой трассы, длина которой равна 12 км. Через сколько часов мотоциклисты поравняются в первый раз, если скорость одного из них на 3 км/ч больше скорости другого?

Решение: Пусть v км/ч — скорость первого мотоциклиста, тогда скорость второго мотоциклиста равна v + 3 км/ч.
Пусть первый раз мотоциклисты поравняются через t ч. Для того чтобы мотоциклисты поравнялись, более быстрый должен преодолеть изначально разделяющее их расстояние, равное половине длины трассы. Поэтому (v + 3)t – vt = 6, отсюда t = 2. Таким образом, мотоциклисты поравняются через 2 ч.
Ответ: 2.
ПРИМЕЧАНИЕ: Движение по окружности определяется теми же формулами, что и движение по прямой: S = vt; v =S/t; t = S/v.

Задача №  (5). Бригада маляров красит забор длиной 360 м, ежедневно увеличивая норму покраски на одно и то же число метров. Известно, что за первый и последний день в сумме бригада покрасила 80 м забора. Определите, сколько дней бригада маляров красила весь забор.

Решение: Пусть бригада в первый день покрасила а₁ м забора, во второй — а₂, … , в последний — а_n м забора. Тогда а₁ + а_n = 80 (м), а за n дней было покрашено S_n = (а₁ + а_n)/2 • n = 80n/2 = 40n (м). Поскольку всего было покрашено 360 м забора, имеем: 40n = 360; n = 9. Таким образом, бригада красила забор в течение 9 дней.
Ответ: 9.
ПРИМЕЧАНИЕ: Поскольку ежедневно бригада увеличивала норму на а м забора, следует использовать формулу суммы арифметической прогрессии.

Тренировочные задания с самопроверкой

№ 8.1. Из двух городов А и В, расстояние между которыми равно 360 км, навстречу друг другу одновременно выехали два автомобиля и встретились через 3 часа на расстоянии 135 км от города В. За сколько часов автомобиль, выехавший из города А, доедет до города В?

№ 8.2. Первые два часа теплоход шёл со скоростью 20 км/ч, следующий час – со скоростью 30 км/ч, а затем четыре часа – со скоростью 28 км/ч. Найдите среднюю скорость теплохода на протяжении всего пути. Ответ дайте в км/ч.

№ 8.3. Скоростной поезд, двигаясь равномерно со скоростью 150 км/ч, проезжает мимо семафора за 15 секунд. Найдите длину поезда в метрах.

№ 8.4. В помощь насосу, перекачивающему 200 литров воды за 4 минуты, подключили второй насос, который перекачивает тот же объём воды за 6 минут. За сколько минут два эти насоса перекачают 5000 литров воды, работая вместе?

№ 8.5. В мае в магазине продали товаров на 325000 рублей. В июне сумма продаж возросла на 12%, а в июле – снизилась на 10% по сравнению с июнем. На сколько рублей продал магазин товаров в июле?

---

Вы смотрели: ЕГЭ по математике Профиль. Задание 8: Уметь строить и исследовать простейшие математические модели. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

Просмотров:
23 081

Чаще всего математические модели используются в физике: тебе ведь наверняка приходилось запоминать десятки физических формул.

А формула – это и есть математическое представление ситуации.

В ОГЭ и ЕГЭ есть задачи как раз на эту тему. В ЕГЭ (профильном) это задача номер 11. В ОГЭ – задача номер 20.

Содержание этих задач таково: дано описание какого-то процесса или явления, приведена соответствующая формула. Также даны значения некоторых физических величин, входящих в эту формулу.

Задание – выразить из формулы неизвестную величину и найти ее значение.

Схема решения очевидна:

1) Из текста условия необходимо «вычленить» полезную информацию – то, что в задачах по физике мы пишем под словом «Дано». Этой полезной информацией являются:

• Формула
• Известные физические величины

То есть каждой букве из формулы нужно поставить в соответствие определенное число.

2) Берешь все известные величины и подставляешь в формулу. Неизвестная величина так и остается в виде буквы. Теперь нужно только решить уравнение (обычно, довольно простое), и ответ готов.

Понятие математической модели

Математическая модель – это представление реальной ситуации с помощью математического языка

Начнем с простого: Число ( displaystyle a) больше числа ( displaystyle b) на ( displaystyle 3). Нам нужно записать это, не используя слов, а только язык математики.

Если ( displaystyle a) больше ( displaystyle b) на ( displaystyle 3), то получается, что если мы из ( displaystyle a) вычтем ( displaystyle b), то останется та самая разность этих чисел равная ( displaystyle 3). Т.е. ( displaystyle a-b=3) или ( displaystyle a-3=b).

Суть понял?

Теперь посложнее, сейчас будет текст, который ты должен попробовать представить в виде математической модели, пока не читай, как это сделаю я, попробуй сам!

Есть четыре числа: ( displaystyle a), ( displaystyle b), ( displaystyle c) и ( displaystyle d). Произведение ( displaystyle a) и ( displaystyle b) больше произведения ( displaystyle c) и ( displaystyle d) в два раза.

Что получилось?

В виде математической модели выглядеть это будет так:

( displaystyle frac{ab}{cd}=frac{2}{1}), т.е. произведение ( displaystyle ab) относится к ( displaystyle cd) как два к одному, но это можно еще упросить:

Математическая модель на практике

Задача 1

После дождя уровень воды в колодце может повыситься. Мальчик измеряет время ( displaystyle t) падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле ( displaystyle h=5{{t}^{2}}), где — ( displaystyle h) расстояние в метрах, ( displaystyle t) — время падения в секундах.

До дождя время падения камешков составляло ( displaystyle 0,5) с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на ( displaystyle 0,1) с? Ответ выразите в метрах.

Решение:

О, ужас! Какие формулы, что за колодец, что происходит, что делать? Я прочел твои мысли?

Расслабься, в задачах этого типа условия бывают и пострашнее, главное помнить, что тебя в этой задаче интересуют формулы и отношения между переменными, а что все это обозначает в большинстве случаев не очень важно. Что ты тут видишь полезного?

Я лично вижу ( displaystyle h=5{{t}^{2}}).

Принцип решения этих задач следующий: берешь все известные величины и подставляешь. НО задумываться иногда надо!

Последовав моему первому совету и подставив все известные в уравнение, получим:

( displaystyle h=5cdot {{0,5}^{2}})

Теперь прислушайся ко второму совету и задумайся, в вопросе уточняется, «на сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на ( displaystyle 0,1) с».

Сразу надо прикинуть, тааак, после дождя уровень воды повышается, значит, время падения камня до уровня воды меньше и тут витиеватая фраза «чтобы измеряемое время изменилось» приобретает конкретный смысл: время падения не увеличивается, а сокращается на указанные ( displaystyle 0,1) секунды.

Это означает, что в случае броска после дождя, нам просто нужно из начального времени ( displaystyle 0,5) c вычесть ( displaystyle 0,1) с, и получим уравнение высоты, которую камень пролетит после дождя:

Как видишь, ничего сложного нет, главное, особо не заморачивайся, откуда такое непонятное и порой сложное уравнение в условиях взялось и что все в нем означает, поверь на слово, большинство этих уравнений взяты из физики, а там дебри похлеще, чем в алгебре.

Мне иногда кажется, что эти задачи придуманы, чтоб запугать ученика на ЕГЭ обилием сложных формул и терминов, а в большинстве случаев не требуют почти никаких знаний. Просто внимательно читай условие и подставляй известные величины в формулу!

Вот еще задача, уже не по физике, а из мира экономической теории, хотя знаний наук кроме математики тут опять не требуется.

Задача 2

Зависимость объёма спроса ( displaystyle q) (единиц в месяц) на продукцию предприятия-монополиста от цены ( displaystyle p) (тыс. руб.) задаётся формулой ( displaystyle q=100-10p). Выручка предприятия за месяц ( displaystyle r) (в тыс. руб.) вычисляется по формуле ( r(p)=qcdot p). Определите наибольшую цену ( displaystyle p), при которой месячная выручка ( displaystyle r(p)) составит не менее ( displaystyle 240) тыс. руб. Ответ приведите в тыс. руб.

Решение:

Угадай, что сейчас сделаю? Ага, начну подставлять то, что нам известно, но, опять же, немного подумать все же придется.

Пойдем с конца, нам нужно найти ( displaystyle p) при котором ( displaystyle r(p)ge 240). Так, ( displaystyle 240) есть, равно какому-то ( displaystyle r(p)), находим, чему еще равно это ( displaystyle r(p)), а равно оно ( displaystyle qcdot p), так и запишем ( displaystyle qcdot p=240).

Как ты видишь, я особо не заморачиваюсь о смысле всех этих величин, просто смотрю из условий, что чему равно, так тебе поступать и нужно.

Вернемся к задаче, у тебя уже есть ( displaystyle qcdot p=240), но как ты помнишь из одного уравнения с двумя переменными ни одну из них не найти, что же делать? Ага, у нас еще в условии осталась неиспользованная частичка ( displaystyle q=100-10p).

[thrive_lead_lock id=’9335′]

Вот, уже два уравнения и две переменных, значит, теперь обе переменные можно найти – отлично!

( displaystyle left{ begin{array}{l}qcdot p=240\q=100-10pend{array} right.)– такую систему решить сможешь?

Решаем подстановкой, у нас ( displaystyle q) уже выражена, значит, подставим ее в первое уравнение и упростим.

А вот тебе и устрашающая физика, а точнее еще одна задачка:

Задача 3

Для определения эффективной температуры звёзд используют закон Стефана–Больцмана, согласно которому ( displaystyle P=sigma S{{T}^{4}}), где ( displaystyle P) — мощность излучения звезды, ( displaystyle sigma =-5,7cdot {{10}^{-8}}cdot frac{Bт}{{{м}^{2}}cdot {{K}^{ 4}}}) — постоянная, ( displaystyle S) — площадь поверхности звезды, а ( displaystyle T) — температура.

Известно, что площадь поверхности некоторой звезды равна ( displaystyle frac{1}{125}cdot {{10}^{20}}{{M}^{2}}), а мощность её излучения равна ( displaystyle 4,56cdot {{10}^{26}})Вт. Найдите температуру этой звезды в градусах Кельвина.

Решение:

Жуууть! Ищем подход. Я рекомендую для начала выписать себе на бумажке все формулы, которые ты тут видишь. Я вот в таком виде записал:

Смотри как все просто: есть формула ( displaystyle P=sigma S{{T}^{4}}) и в ней известны ( displaystyle S), ( displaystyle P) и ( sigma )(это греческая буква «сигма». Вообще, физики любят греческие буквы, привыкай).

А неизвестна температура ( displaystyle T). Давай выразим ее в виде формулы. Как это делать, надеюсь, знаешь? Такие задания на ГИА в 9 классе обычно дают:

Продолжаем мучить задачки по физике.

Задача 4

Высота над землей подброшенного вверх мяча меняется по закону ( displaystyle h(t)=1,6+8t-{{t}^{2}}), где ( displaystyle h) — высота в метрах, ( displaystyle t) — время в секундах, прошедшее с момента броска.

Сколько секунд мяч будет находиться на высоте не менее трех метров?

Решение:

То были всё уравнения, а вот здесь надо определить, сколько мяч находился на высоте не менее трех метров, это значит на высоте ( displaystyle ge3). Что мы составлять будем?

Нас интересует промежуток, где знак минус, поскольку неравенство принимает там отрицательные значения, это от ( displaystyle 0,2) до ( displaystyle 1,4) оба включительно.

А теперь включаем мозг и тщательно думаем: для неравенства мы применяли уравнение, описывающее полет мяча, он так или иначе летит по параболе, т.е. он взлетает, достигает пика и падает, как понять, сколько времени он будет находиться на высоте не менее ( displaystyle 3) метров?

Мы нашли 2 переломные точки, т.е. момент, когда он взмывает выше ( displaystyle 3) метров и момент, когда он, падая, достигает этой же отметки, эти две точки выражены у нас в виде времени.

То есть мы знаем на какой секунде полета он вошел в интересующую нас зону (выше ( displaystyle 3) метров) и в какую вышел из нее (упал ниже отметки в ( displaystyle 3) метра). Сколько секунд он находился в этой зоне?

Логично, что мы берем время выхода из зоны и вычитаем из него время вхождения в эту зону. Соответственно: ( displaystyle 1,4text{ }-text{ }0,2=1,2~~) – столько он находился в зоне выше ( displaystyle 3) метров, это и есть ответ.

Так уж тебе повезло, что больше всего примеров по этой теме можно взять из разряда задачек по физике, так что лови еще одну, она заключительная, так что поднапрягись, осталось совсем чуть-чуть!

Задача 5

Для нагревательного элемента некоторого прибора экспериментально была получена зависимость температуры от времени работы:

( displaystyle Tleft( t right)text{ }=text{ }{{T}_{0}}+text{ }bttext{ }+text{ }a{{t}^{2}}), где ( displaystyle t) — время в минутах, ( displaystyle {{T}_{0}}=text{ }1450text{ }K), ( displaystyle a=-12,5text{ }K/{{мин }^{2}}), ( displaystyle b=125text{ }K/мин).

Известно, что при температуре нагревательного элемента свыше ( displaystyle 1750 K) прибор может испортиться, поэтому его нужно отключить. Найдите, через какое наибольшее время после начала работы нужно отключить прибор. Ответ выразите в минутах.

Решение:

Действуем по отлаженной схеме, все, что дано, сперва выписываем:

Теперь берем формулу и приравниваем ее к значению температуры, до которой максимально можно нагреть прибор пока он не сгорит, то есть ( displaystyle {{T}_{max}}):

Как видишь, температура при работе прибора описывается квадратным уравнением, а значит, распределяется по параболе, т.е. прибор нагревается до какой-то температуры, а потом остывает.

Мы получили ответы ( displaystyle 4) и ( displaystyle 6), следовательно, при ( displaystyle 4) и при ( displaystyle 6) минутах нагревания температура равна критической, но между ( displaystyle 4) и ( displaystyle 6) минутами – она еще выше предельной!

А значит, отключить прибор нужно через ( displaystyle 4) минуты.

Самые бюджетные курсы по подготовке к ЕГЭ на 90+

• Курс

Ответственность за разрешение любых спорных моментов, касающихся самих материалов и их содержания,
берут на себя пользователи, разместившие материал на сайте. Однако администрация сайта
готова оказать всяческую поддержку в решении любых вопросов, связанных с работой и содержанием
сайта. Если Вы заметили, что на данном сайте незаконно используются материалы, сообщите об этом
администрации сайта через форму обратной связи.

Все материалы, размещенные на сайте, созданы авторами сайта либо размещены пользователями сайта
и представлены на сайте исключительно для ознакомления. Авторские права на материалы
принадлежат их законным авторам. Частичное или полное копирование материалов сайта без
письменного разрешения администрации сайта запрещено! Мнение администрации может не совпадать с точкой
зрения авторов.

Текстовые задачи — это одни из самых нелюбимых заданий, особенно у учеников старших классов, потому что чем дальше, тем запутаннее становится условие, тем сложнее становится составить уравнение и верно решить задачу. Но, как и в любой теме в математике, чтобы уверенно решать сложные задачи, необходимо разобраться с самыми основными приемами.

Разберем эти задачи с самого начала. Текстовая задача состоит из условия, в котором описана некоторая ситуация, и вопроса, на который нужно дать ответ.

Пример:

Решение любой текстовой задачи можно разделить на несколько основных этапов:

• Работа с условием
• Составление математической модели
• Проверка ответа

Работа с условием

Для облегчения работы с условием полезно использовать иллюстрацию или моделирование. Это может быть краткая запись условия математически или словесно. Также это может быть дополнительный рисунок или таблица.

Пример: Петя выше Коли, Сережа ниже Коли. Кто выше?

Иллюстрация:

Из рисунка сразу понятен ответ: Петя выше всех.

Пример.

Два поезда идут навстречу друг другу. Скорость одного из них 45 км/ч, скорость другого — 55 км/ч. Сейчас между ними 200 км. Через сколько часов они встретятся?

Иллюстрация:

Пусть х часов — время движения обоих поездов, тогда по рисунку видно, что первый проедет 45х км, а второй — 55х км.

Составим математическую модель:

45х + 55х = 200

100х = 200

х = 2 ч

Ответ: 2 ч.

Для составления уравнения по условию задачи используются различные приемы, в зависимости от данной в условии зависимости величин.

Математическая модель

Математика, в частности, занимается тем, что описывает различные реальные ситуации на математическом языке. В таблице приведены различные ситуации и их математические модели.

x — число девочек

y — число мальчиков

Реальная ситуация	Математическая модель
В классе поровну мальчиков и девочек	$ { x=y} $
Девочек на 5 больше, чем мальчиков	$ { x=y+5, ; или; x-y=5,; или; x-5=y} $
Мальчиков в 2 раза больше, чем девочек	$ { y=2x, ; или; frac{y}{2}=x,; или; frac{y}{x}=2} $
Если в класс перейдут 3 мальчика, то девочек станет в два раза больше	$ { y=2(y+3)} $

Алгебраическая зависимость

Такая зависимость выражается в словах: выше/ниже, больше/меньше, дороже/дешевле, длиннее/короче и т. д.

При составлении уравнения особое значение играют используемые предлоги: «в» и «на».

Пример: Петя выше Коли на 20 см, Сережа ниже Коли на 10 см. На сколько см Петя выше Сережи?

Решение: Пусть П — рост Пети, К — рост Коли, С — рост Сережи.

Кстати, обратите внимание на этот приём — выбирать «говорящие» переменные, а не безликие иксы и игреки, чтобы не запутаться при работе с уравнением.

Выразим рост мальчиков.

Петя выше Коли на 20 см: П – 20 = К

Сережа ниже Коли на 10 см: К = С + 10

Подставим в первое уравнение рост Коли: П – 20 = С + 10

Нам нужно найти, на сколько см Петя выше Сережи: П – С

П – 20 = С + 10

П – С = 20 + 10

П – С = 30

Получаем, что Петя выше Сережи на 30 см.

Пример: На уроке труда ученики делали снежинки. Всего было сделано 12 снежинок. Маша сделала в два раза больше снежинок, чем Коля. Коля сделал на 4 снежинки меньше, чем Рома. Сколько снежинок сделала Маша?

Решение:

Пусть М — количество снежинок, которое сделала Маша, К — снежинки Коли, Р — снежинки Ромы.

Маша сделала в два раза больше снежинок, чем Коля: К = М/2

Коля сделал на 4 снежинки меньше, чем Рома: Р = К + 4 = М/2 + 4

Вместе ребята сделали 12 снежинок: М + К + Р = 12

Подставим все выраженные через М значения: М + М/2 + М/2 + 4 = 12

М = 4.

Маша сделала 4 снежинки.

Процентная зависимость

С процентами нам постоянно приходиться сталкиваться в повседневной жизни. “Скидка 30%”, “Кредит без процентов за 5 минут”, “Арендная плата выросла на 12%” — со всех сторон на нас сыпятся рекламные слоганы и призывы. Но что же значит это таинственное слово “проценты”? И как ими оперировать?

Сегодня мы с вами дадим определение процентов, поймём, как находится процент от некоторого числа, как можно найти одно количество процентов, уже зная другое. И, конечно, рассмотрим каждый из этих случаев на конкретном примере.

Как кирка у каменщика, камертон у настройщика или световой меч у Джедая, в математике тоже существуют свои инструменты, нужные для выполнения тех или иных операций. И проценты как раз и являются таким удобным инструментом. Нужны они для нахождения части от чего-то. Вообще говоря, звучит похоже на определение дроби. И действительно, проценты очень тесно связаны с дробями, по сути, основываясь на них.

Так что же такое один процент?

Процент — это всегда доля какого-то числа.

100% — все число

50% — половина

25% — четверть

Чтобы найти 1%, необходимо поделить всё число на 100.

Пример:

Есть 100 яблок.

$ 1% ;от ;всех ;яблок; –frac{100}{100} = 1 ;яблоко. $

Есть 200 груш

$ 1% ;от ;всех ;груш; –frac{200}{100} = 2 ;груши. $

Для работы с процентами используется пропорция, в которой в одном столбце записываются реальные значения, в другом — соответствующие проценты.

Пример:

200 груш — 100 %

2 груши — 1 %

Пропорция отражает зависимость величин. По-другому это можно записать в виде двух дробей.

$ frac{200}{2}=frac{100}{1} $

Исходя из правил работы с дробями, получаем правила работы с пропорцией.

1. Внутри одной дроби можно сокращать значения.

2. Произведение накрест лежащих значений равно: 200 · 1 = 2 · 100

Эту тему мы еще подробно пройдем на курсе.

Рассмотрим несколько примеров работы с процентами в текстовых задачах.

Ситуация при работе с процентами усложняется, когда изначально нам известен не 1%, а несколько — например, 20. А требуют найти какое-нибудь неудобное число процентов

Пример: 38% населения деревни — это 76 человек. Сколько человек составляет 15% от общего населения?

Так как мы не можем сразу найти 15%, то нам вначале понадобится сделать промежуточный шаг — найти 1%. Если 38% — это 76 человек, то, разделив на 38, мы получим так нужный нам 1%. 38% = 76 человек ⇒1% = 2 человека. Тогда 15% = 30 человек

Но неугомонные математики не остановились и на этом. Что будет, если мы возьмём процент от какого-то числа, вычтем или прибавим к начальному числу, а затем снова возьмём то же количество процентов?

Пример: В 2010 дом стоял 2 тысячи рублей. В 2011 его цена увеличилась на 20%, а в 2012 — ещё на 20%. Сколько дом стоил к концу 2012 года?

На примере этой задаче мы посмотрим не только на то, как нужно брать проценты от разных величин, но и как переводить проценты в дроби. Решим её двумя способами:

Способ 1 Для начала давайте выясним, сколько стоил дом в 2011. Его стоимость увеличилась на 20%, т.е. на 400 рублей (1% = 2000:100 = 20, 20% = 400) и стала, соответственно, равна 2400. Теперь нам нужно узнать, сколько он стал стоить в 2012. Важно! Сейчас мы будем брать 20% от новой цены, т.е. той, которая была на дом в 2011 году. Если 1% = 2400:100 = 24, то 20% = 480, то есть новая цена в 2012 году — 2400 + 480 = 2880

Способ 2 Если 1% — это 0,01 от чего-то, то 20% — это 0,2. Тогда 20% от первоначальной цены это 2000⋅0,2 = 400, и цена на дом в 2011 году стала 2400. Теперь находим 20% от новой стоимости 2400⋅0,2 = 480 и итоговую стоимость в 2012 году: 2400 + 480 = 2880

Отлично! Итак, мы не только узнали, что такое проценты, как можно с ними обращаться, но и выяснили, как можно брать проценты от разных величин и как сопоставлять проценты с дробями. Больше интересных фактов и приёмов работы с процентами вы узнаете в процессе курса.

Также текстовые задачи могут быть посвящены прогрессиям, производительности, темпу — обо всем этом мы поговорим на нашем курсе. А сейчас приступайте к задачам для тренировки.