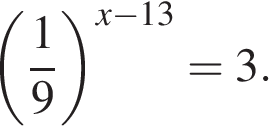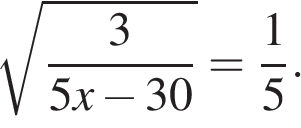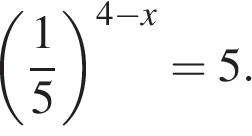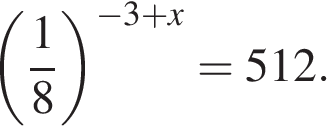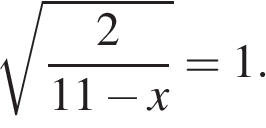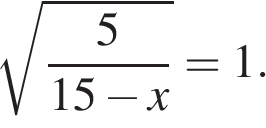Простейшие уравнения егэ профиль 2022

Новые задания №1 ЕГЭ 2022 по математике профильного уровня — простейшие уравнения.

Для успешного результата необходимо уметь решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы.

Задание №1 ЕГЭ 2022 математика профильный уровень Прототипы

Источник: math100.ru → Рациональные уравнения

→ Иррациональные уравнения

→ Показательные уравнения

→ Логарифмические уравнения

→ Тригонометрические уравнения
time4math.ru → скачать задания
vk.com/ekaterina_chekmareva → задания

При отработке данного задания будут полезны книги:

решение уравнений и неравенств

Купить ЕГЭ 2022 Математика. 100 баллов. Профильный уровень. Решение уравнений и неравенств

Задание 1 ЕГЭ по математике

Купить Математика: уравнения и неравенства. Подготовка к ЕГЭ: профильный уровень

Решение уравнений и неравенств задание 1 ЕГЭ профильная математика

Купить Показательные и логарифмические уравнения. ЕГЭ. Математика

Методы решения тригонометрических уравнений

Купить Методы решения тригонометрических уравнений. ЕГЭ. Математика

Связанные страницы:

Тренировочные варианты ЕГЭ 2022 по математике профильного уровня

Решение 17 задания ЕГЭ по профильной математике

Тренировочные варианты ЕГЭ 2022 по математике базового уровня

Купить сборники типовых вариантов ЕГЭ по математике

Задание 9 профильного ЕГЭ по математике. Практика

Источник

Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.

Линейные уравнения

Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$

Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.

$5 (5 + 3х) — 10х = 8$

Раскроем скобки.

$25 + 15х — 10х = 8$

Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.

$15х — 10х = 8 — 25$

Приведем подобные слагаемые.

$5х = -17$ — это конечный результат преобразований.

После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$

$х=-{17}/{5}$

$х = — 3,4$

Ответ: $- 3,4$

Квадратные уравнения

Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.

Числа $a, b, c$ называются коэффициентами квадратного уравнения.

  • $a$ — старший коэффициент;
  • $b$ — средний коэффициент;
  • $c$ — свободный член.

Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.

Решение неполных квадратных уравнений

Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.

1. Вынесем общий множитель $x$ за скобки.

Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:

$x = 0; ax + b = 0$

2. Решаем получившиеся уравнения каждое отдельно.

Мы получим $x = 0$ и $x={-b}/{a}$. Следовательно, данное квадратное уравнение имеет два корня $x = 0$ и $x={-b}/{a}$

$4х^2 — 5х = 0$

Вынесем х как общий множитель за скобки:

$х (4х — 5) = 0$

Приравняем каждый множитель к нулю и найдем корни уравнения.

$x = 0$ или $4х — 5 = 0$

$х_1 = 0   х_2 = 1,25$

Ответ: $х_1 = 0; х_2 = 1,25$

Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$

Для решения данного неполного квадратного уравнения выразим $x^2$.

$ax^2 + c = 0$

$ax^2 = — c$

$x_2 = {-c}/{a}$

При решении последнего уравнения возможны два случая:

если ${-c}/{a}>0$, то получаем два корня: $x = ±v{{-c}/{a}}$

если ${-c}/{a}<0$, то уравнение во множестве действительных числе не имеет решений.

$x^2 — 16 = 0$

$x^2 = 16$

$x = ±4$

Ответ: $х_1 = 4, х_2 = — 4$

Решение полного квадратного уравнения

Решение с помощью дискриминанта

Дискриминантом квадратного уравнения D называется выражение

$b^2 — 4ac$.

При решении уравнения с помощью дискриминанта возможны три случая:

1. $D > 0$. Тогда корни уравнения равны:

$x_{1,2}={-b±√D}/{2a}$

2. $D = 0$. В данном случае решение даёт два двукратных корня:

$x_{1}=x_{2}={-b}/{2a}$

3. $D < 0$. В этом случае уравнение не имеет корней.

$3х^2 — 11 = -8х$

Соберем все слагаемые в левую часть уравнения и расставим в порядке убывания степеней

$3х^2 + 8х — 11 = 0$

$a = 3 ,b = 8, c = — 11$

$D = b^2- 4ac = 82- 4 · 3 · (-11) = 196 = 142$

$x_{1}={-b+√D}/{2a}={-8+14}/{6}=1$

$x_{2}={-b-√D}/{2a}={-8-14}/{6}=-3{2}/{3}$

Ответ: $x_1=1, x_2=-3{2}/{3}$

Устные способы

Если сумма коэффициентов равна нулю $(а + b + c = 0)$, то $х_1= 1, х_2={с}/{а}$

$4х^2+ 3х — 7 = 0$

$4 + 3 — 7 = 0$, следовательно $х_1= 1, х_2=-{7}/{4}$

Ответ: $х_1= 1, х_2 = -{7}/{4}$

Если старший коэффициент в сумме со свободным равен среднему коэффициенту $(a + c = b)$, то $х_1= — 1, х_2=-{с}/{а}$

$5х^2+ 7х + 2 = 0$

$5 + 2 = 7$, следовательно, $х_1= -1, х_2 =-{2}/{5}$

Ответ: $х_1= -1, х_2 = -{2}/{5}$

Кубические уравнения

Для решения простых кубических уравнений необходимо обе части представить в виде основания в третьей степени. Далее извлечь кубический корень и получить простое линейное уравнение.

$(x — 3)^3 = 27$

Представим обе части как основания в третьей степени

$(x — 3)^3 = $33

Извлечем кубический корень из обеих частей

$х — 3 = 3$

Соберем известные слагаемые в правой части

$x = 6$

Ответ: $х = 6$

Дробно рациональные уравнения

Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.

Чтобы решить дробное уравнение, необходимо:

  1. найти общий знаменатель дробей, входящих в уравнение;
  2. умножить обе части уравнения на общий знаменатель;
  3. решить получившееся целое уравнение;
  4. исключить из его корней те, которые обращают в ноль общий знаменатель.

$4x + 1 — {3}/{x} = 0$

1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

2. находим общий знаменатель дробей и умножаем на него обе части уравнения

$4x + 1 — {3}/{x}= 0¦· x$

$4x · x + 1 · x — {3·x}/{x} = 0$

3. решаем полученное уравнение

$4x^2 + x — 3 = 0$

Решим вторым устным способом, т.к. $а + с = b$

Тогда $х_1 = — 1, х_2 = {3}/{4}$

4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $х_1 = — 1, х_2 = {3}/{4}$

При решении уравнения с двумя дробями можно использовать основное свойство пропорции.

Основное свойство пропорции: Если ${a}/{b} = {c}/{d}$, то $a · d = b · c$

${3х-5}/{-2}={1}/{х}$

Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

Воспользуемся основным свойством пропорции

$х (3х — 5) = -2$

Раскроем скобки и соберем все слагаемые в левой части уравнения

$3х^2- 5х + 2 = 0$

Решим данное квадратное уравнение первым устным способом, т.к.

$a + b + c = 0$

$x_1 = 1, x_2 = {2}/{3}$

В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $x_1 = 1, x_2 = {2}/{3}$

Рациональное уравнение – это уравнение вида $f(x)=g(x)$, где $f(x)$ и $g(x)$ — рациональные выражения.

Рациональные выражения — это целые и дробные выражения, соединённые между собой знаками арифметических действий: деления, умножения, сложения или вычитания, возведения в целую степень и знаками последовательности этих выражений.

Например,

${2}/{x}+5x=7$ – рациональное уравнение

$3x+√x=7$ — иррациональное уравнение (содержит корень)

Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно рациональным.

Чтобы решить дробно рациональное уравнение, необходимо:

  1. Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ);
  2. Найти общий знаменатель дробей, входящих в уравнение;
  3. Умножить обе части уравнения на общий знаменатель;
  4. Решить получившееся целое уравнение;
  5. Исключить из его корней те, которые обращают в ноль общий знаменатель.

Решить уравнение: $4x+1-{3}/{x}=0$

Решение:

1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x ≠ 0$

2. находим общий знаменатель дробей и умножаем на него обе части уравнения

$4x+1-{3}/{x}=0|·x$

$4x·x+1·x-{3·x}/{x}=0$

3. решаем полученное уравнение

$4x^2+x-3=0$

Решим вторым устным способом, т.к. $а+с=b$

Тогда, $x_1=-1, x_2=-{3}/{4}$

4. исключаем те корни, при которых общий знаменатель равен нулю

В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $x_1=-1, x_2=-{3}/{4}$

При решении уравнения с двумя дробями, можно использовать основное свойство пропорции.

Основное свойство пропорции: Если ${a}/{b}={c}/{d}$ — пропорция, то $a·d=b·c$

Решить уравнение ${3x-5}/{-2}={1}/{x}$

Решение:

Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

Воспользуемся основным свойством пропорции

$х(3х-5)=-2$

Раскроем скобки и соберем все слагаемые в левой стороне

$3х^2-5х+2=0$

Решим данное квадратное уравнение первым устным способом, т.к. $a+b+c=0$

$x_1=1, x_2={2}/{3}$

В первом пункте получилось, что при x = 0 уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $x_1=1, x_2={2}/{3}$

Уравнения, содержащие неизвестную под знаком корня, называются иррациональными.

Чтобы решить иррациональное уравнение, необходимо:

  1. Преобразовать заданное иррациональное уравнение к виду: $√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
  2. Обе части уравнение возвести в квадрат: $√{f(x)}^2=(g(x))^2$ или $√{f(x)}^2=√{g(x)}^2$
  3. Решить полученное рациональное уравнение.
  4. Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)

Решите уравнение $√{4х-3}=х$. Если уравнение имеет более одного корня, укажите наименьший из них.

Решение:

Обе части уравнение возведем в квадрат:

$√{4х-3}^2=х^2$

Получаем квадратное уравнение:

$4х-3=х^2$

Перенесем все слагаемые в левую часть уравнения:

${-х}^2+4х-3=0$

Решим данное квадратное уравнение устным способом, так как

$a+b+c=0$

$-1+4-3=0$, следовательно $х_1 = 1; х_2={с}/{а}={-3}/{-1}=3$

Проведем проверку корней, подставив их вместо икса в исходное уравнение

$√{4·1-3}=1$

$1=1$, получили в результате проверки верное равенство, следовательно $х_1=1$ подходит.

$√{4·(3)-3}=3$

$√9=3$

$3=3$, получили в результате проверки верное равенство, следовательно корень $х_2=3$ подходит

$х_1=1$ наименьший корень.

Ответ: $1$

Так как в иррациональных уравнениях иногда необходимо возводить в квадрат не только число, но и целое выражение, необходимо вспомнить формулы сокращенного умножения:

  1. Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе число плюс квадрат второго числа. $(a-b)^2=a^2-2ab+b^2$
  2. Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа. $(a+b)^2=a^2+2ab+b^2$

Решить уравнение: $х-6=√{8-х}$

Возведем обе части уравнения в квадрат

$(х-6)^2=8-х$

В левой части уравнения при возведении в квадрат получаем формулу сокращенного умножения квадрат разности. В правой части уравнения квадрат и корень компенсируют друг друга и в результате остается только подкоренное выражение

$х^2-2·6·х+6^2=8-х$

$х^2-12х+36=8-х$

Получили квадратное уравнение. Все слагаемые переносим в левую часть уравнения. При переносе слагаемых через знак равно их знаки меняются на противоположные.

$х^2-12х+36-8+х=0$

Приводим подобные слагаемые:

$х^2-11х+28=0$

Найдем корни уравнения через дискриминант:

$D=b^2-4ac=121-4·28=121-112=9=3^2$

$x_{1,2}={-b±√D}/{2a}={11±3}/{2}$

$x_1=7; x_2=4$

Проведем проверку корней, подставив их вместо икса в исходное уравнение

$x_1=7$

$7-6=√{8-7}$

$1=1$, получили верное равенство, следовательно, корень нам подходит.

$x_2=4$

$4-6=√{8-4}$

$-2=2$, получили неверное равенство, следовательно, данный корень посторонний.

Ответ: $7$

Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.

$a^x=b$

При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:

1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.

$a^n⋅a^m=a^{n+m}$

2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются

$a^n:a^m=a^{n-m}$

3. При возведении степени в степень основание остается прежним, а показатели перемножаются

$(a^n)^m=a^{n·m}$

4. При возведении в степень произведения в эту степень возводится каждый множитель

$(a·b)^n=a^n·b^n$

5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель

$({a}/{b})^n={a^n}/{b^n}$

6. При возведении любого основания в нулевой показатель степени результат равен единице

$a^0=1$

7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби

$a^{-n}={1}/{a^n}$

${a^{-n}}/{b^{-k}}={b^k}/{a^n}$

8. Радикал (корень) можно представить в виде степени с дробным показателем

$√^n{a^k}=a^{{k}/{n}}$

Показательные уравнения часто сводятся к решению уравнения $a^x=a^m$, где, $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели.

Решить уравнение $25·5^х=1$

Решение:

В левой части уравнения необходимо сделать одну степень с основанием $5$ и в правой части уравнения представить число $1$ в виде степени с основанием $5$

$5^2·5^х=5^0$

При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются

$5^{2+х}=5^0$

Далее проговариваем: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели

$2+х=0$

$х=-2$

Ответ: $-2$

Решить уравнение $2^{3х+2}-2^{3х-2}=30$

Решение:

Чтобы решить данное уравнение, вынесем степень с наименьшим показателем как общий множитель

$2^{3x+2}-2^{3x-2}=30$

$2^{3x-2}({2^{3x+2}}/{2^{3x-2}}-{2^{3x-2}}/{2^{3x-2}})=30$

$2^{3x-2}(2^{3x+2-(3x-2)}-1)=30$

$2^{3x-2}(2^4-1)=30$

$2^{3x-2}·15=30$

Разделим обе части уравнения на $15$

$2^{3х-2}=2$

$2^{3х-2}=2^1$

$3х-2=1$

$3х=3$

$х=1$

Ответ: $1$

Источник

В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Квадратные уравнения

Арифметический квадратный корень

Корни и степени

Показательная функция

Показательные уравнения

Логарифмическая функция

Логарифмические уравнения

Тригонометрический круг

Формулы приведения

Формулы тригонометрии

Простейшие тригонометрические уравнения 1

Уравнения, сводящиеся к квадратным

1. Решите уравнение frac{6}{13}x^2=19frac{1}{2}. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.

С левой частью уравнения все понятно. Дробь frac{6}{13} умножается на x^2. А в правой части — смешанное число 19frac{1}{2}. Его целая часть равна 19, а дробная часть равна frac{1}{2}. Запишем это число в виде неправильной дроби:

19frac{1}{2}= frac{19cdot 2+1}{2} = frac{39}{2}.

Получим:

frac{6}{13}x^2=frac{39}{2};

x^2=frac{39cdot 13}{2cdot 6}=frac{13cdot 3cdot 13}{2cdot 6}=frac{{13}^2}{4};

x=pm frac{13}{2};

x_1=-6,5 или x_2=6,5.

Выбираем меньший корень.

Ответ: -6,5.

2. Решите уравнение left ( x-6 right )^2=-24x.

Возведем в квадрат левую часть уравнения. Получим:

left ( x-6 right )^2=-24xLeftrightarrow x^2-12x+36=-24xLeftrightarrow

Leftrightarrow x^2+12x+36=0Leftrightarrow left ( x+6 right )^2=0Leftrightarrow x=-6.

Ответ: -6.

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как frac{4x-5}{4x-5} и приведем дроби к общему знаменателю:

frac{5x-3}{4x-5}-frac{4x-5}{4x-5}=0;

frac{x+2}{4x-5}=0;

x= - 2.

Ответ: -2.

Это довольно простой тип уравнений. Главное — внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.

4. Решите уравнение:

sqrt{frac{6}{4{x}-54} } =frac{1}{7}.

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, .

Возведём обе части уравнения в квадрат:

frac{6}{4{x}-{ 54}} =frac{1}{49}.

Решим пропорцию:

4{x}-{ 54}={ 6}cdot { 49};

4{x}=348;

{ x}={ 87}.

Условие  при этом выполняется.

Ответ: 87.

5. Решите уравнение sqrt{72-x}=x. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

left{begin{matrix} 72-x=x^2\72-xgeq 0 hfill \xgeq 0 hfill end{matrix}right..

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

sqrt{72-x}=x Leftrightarrow left{begin{matrix} 72-x=x^2\72-x geq 0 \x geq 0 end{matrix}right. Leftrightarrow

.

Мы получили, что x=8. Это единственный корень уравнения.

Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:

72-xge 0.

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: x^2+x-72=0. Находят его корни: x=8 или x=-9. Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

Ответ: 8.

6. Решите уравнение sqrt{45+4x}=x. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов:

.

Ответ: 9.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение 5^{x-7}=frac{1}{125}.

Вспомним, что 125 = 5{}^{3}. Уравнение приобретает вид: 5{}^{x}{}^{-}{}^{7 }= 5{}^{-}{}^{3}. Функция y = 5^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

x - 7 = -3, откуда x = 4.

Ответ: 4.

8. Решите уравнение {left(frac{1}{49}right)}^{x-8}=7.

Представим {left(frac{1}{49}right)}^{ } как 7^{-2};

{left(7^{-2}right)}^{x-8}=7;

7^{-2x+16}=7.

Функция y = 7^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

-2x+16=1;

-2x=-15;

x=7,5.

Ответ: 7,5.

9. Решите уравнение left(frac{1}{9} right)^{{ x}-13} =3.

Представим {textstylefrac{1}{9}} в виде степени с основанием 3 и воспользуемся тем, что left({ a}^{{ m}} right)^{{ n}} ={ a}^{{ mn}}.

left(3^{-2} right)^{{ x}-{ 13}} =3;
3^{-2{ x}+{ 26}} =3^{1} ;

-2{ x}+{ 26}={ 1};

{ x}={ 12,5}.

Ответ: 12,5.

Логарифмические уравнения

Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел.

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

{{log}_5 left(4+xright)=2 }.

Область допустимых значений: . Значит, 

Представим 2 в правой части уравнения как {{log}_5 25 }, чтобы слева и справа в уравнении были логарифмы по основанию 5.

{{log}_5 left(4+xright)={{log}_5 25 } }.

Функция y = {{log}_5 x } монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом 

4+x=25;
x=21.

Ответ: 21.

11. Решите уравнение: {{log}_8 left(x^2+xright)={{log}_8 left(x^2-4right) } }.

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

.

Ответ: -4.

12. Решите уравнение: 2^{{{log}_4 left(4x+5right) }}=9.

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

{{log}_4 b }=frac{{{log}_2 b }}{{{log}_2 4 }}=frac{{{log}_2 b }}{2}.

Записываем решение как цепочку равносильных переходов.

.

Ответ: 19.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

{{log}_{x-5} 49=2 }.

В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.

Получим систему:

small left{begin{matrix} left ( x-5 right )^2=49\x-50 \x-5 neq 1 end{matrix}right..

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: x=12 и x=-2.

Очевидно, корень x=-2 является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения: x=12.

Ответ: 12.

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.

14. Найдите корень уравнения: cos frac{pi (x+1)}{4}=frac{sqrt{2}}{2}. В ответе запишите наибольший отрицательный корень.

Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.

Сделаем замену frac{pi left(x+1right)}{4}=t. Получим: cos t=frac{sqrt{2}}{2}.

Получаем решения: t=pm frac{pi }{4}+2pi n, nin Z. Вернемся к переменной x.

frac{pi (x+1)}{4}=pm frac{pi }{4}+2pi n, nin Z. Поделим обе части уравнения на pi и умножим на 4.

x+1=pm 1+8n, nin Z;

left[ begin{array}{c}x=8n, nin Z \x=-2+8n end{array}right..

Первой серии принадлежат решения -8; 0; 8dots

Вторая серия включает решения -2; 6; 14dots

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это x = -2.

Ответ: -2.

15. Решите уравнение: tg frac{pi left( x+1right)}{4}= -1. В ответе напишите наименьший положительный корень.

Решение:

Сделаем замену frac{pi left(x+1right)}{4}=t. Получим:tgt=-1. Решения этого уравнения:

t=-frac{pi }{4}+pi n, nin Z. Вернемся к переменной х:

frac{pi left(x+1right)}{4}=-frac{pi }{4}+pi n, n in Z. Умножим обе части уравнения на 4 и разделим на pi.

x+1=-1+4n;

x=-2+4n.

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

x=-2 ;2; 6dots Наименьший положительный корень x = 2.

Ответ: 2.

Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

ЕГЭ-2022 (профиль)

Задание 1  Простейшие уравнения.

1.      Решите
уравнение   

2.   Найдите
наибольший корень уравнения 

3.   Решите
уравнение 

4.   Решите
уравнение 

5.   Найдите
сумму корней уравнения 

6.   Квадратный
трехчлен разложили на множители                                  . Найдите .

7.   Решите
уравнение

8.   Решите
уравнение

9.   Решите
уравнение 

10.  Решите
уравнение 

11.  Решите
уравнение 

12. Решите
уравнение 

13.  Решите
уравнение 

14.  Решите
уравнение 

15.  Найдите
наименьший корень уравнения 

16.  Найдите
сумму корней уравнения 

17. Найдите
наибольший корень уравнения                                                 

18. Решите
уравнение 

19. Найдите
наибольший корень уравнения 

20. Решите
уравнение 

21. Решите
уравнение 

22. Найдите
наименьший положительный корень уравнения            

23. Найдите
наибольший корень уравнения 

24. Найдите
наименьший корень уравнения 

25. Найдите
рациональный корень уравнения 

26. Найдите
наибольший корень уравнения 

27.  Найдите
наименьший корень уравнения                                               

28.  Решите
уравнение 

29.  Решите
уравнение 

30.  Найдите
наименьший корень уравнения  

31.  Решите
уравнение 

32.  Решите
уравнение 

33.  Решите
уравнение 

34. Найдите
наибольший отрицательный корень уравнения                           

35.  Найдите
наименьший положительный корень уравнения          

36. Найдите
наибольший отрицательный корень уравнения                

37.  Найдите
корни уравнения (в градусах)      из промежутка           

Ответы:  

1.  -4

11.  -4

21.  8

31. 
-0,5

2.  5

12.  16

22. 
0,75

32.  1

3.  -2

13.  -4

23.  2

33.  -2

4.  -3,3

14.  1,5

24.  2

34.

5.  0

15.  -2

25.  1

35.  4

6.  3

16.  0

26.  -8

36.  -7

7. 
-0,2; 0,2

17.  2

27.  -2

37.  330

8.  -4;
4

18.  1

28. 
-0,5

9.  1

19.  -2

29.  2

10.  -7

20.  2

30.  1,4
Источник

Вариант 1 5. Простейшие уравнения

1. Найдите корень уравнения 

2. Найдите корень уравнения:  Если уравнение имеет более одного корня, укажите меньший из них.

3. Найдите корень уравнения 

4. Найдите корень уравнения: 

5. Найдите корень уравнения: 

6. Найдите корень уравнения 

7. Решите уравнение  В ответе напишите наибольший отрицательный корень.

8. Найдите корень уравнения 

9. Найдите корень уравнения 

10. Решите уравнение 

Вариант 2 5. Простейшие уравнения

1. Найдите корень уравнения 

2. Найдите корень уравнения: 

3. Найдите корень уравнения:  В ответе запишите наибольший отрицательный корень.

4. Решите уравнение 

5. Найдите корень уравнения 

6. Решите уравнение 

7. Решите уравнение 

8. Найдите корень уравнения 

9. Найдите корень уравнения 

10. Решите уравнение 

Вариант 3 5. Простейшие уравнения

1. Найдите корень уравнения  Если уравнение имеет более одного корня, в ответе запишите больший из корней.

2. Найдите корень уравнения: 

3. Решите уравнение  В ответе напишите наибольший отрицательный корень.

4. Найдите корень уравнения 

5. Решите уравнение  Если уравнение имеет более одного корня, в ответе запишите больший из корней.

6. Найдите корень уравнения:  В ответе запишите наибольший отрицательный корень.

7. Найдите корень уравнения: 

8. Найдите корень уравнения 

9. Найдите корень уравнения 

10. Найдите корень уравнения: 

Вариант 4 5. Простейшие уравнения

1. Найдите корень уравнения: 

2. Найдите корень уравнения 

3. Найдите корень уравнения 

4. Найдите корень уравнения 

5. Решите уравнение 

6. Найдите корень уравнения 52 + x = 125x.

7. Решите уравнение  В ответе напишите наименьший положительный корень.

8. Найдите корень уравнения: 

9. Найдите корень уравнения 

10. Найдите корень уравнения 

Вариант 5 5. Простейшие уравнения

1. Найдите корень уравнения 

2. Найдите корень уравнения 

3. Найдите корень уравнения 

4. Найдите корень уравнения 

5. Найдите корни уравнения:  В ответ запишите наибольший отрицательный корень.

6. Решите уравнение  Если уравнение имеет более одного корня, в ответе запишите больший из корней.

7. Найдите корень уравнения 

8. Найдите корень уравнения 

9. Найдите корень уравнения 

10. Найдите корень уравнения 

Вариант 6 5. Простейшие уравнения

1. Решите уравнение  В ответе напишите наибольший отрицательный корень.

2. Решите уравнение 

3. Найдите корень уравнения: 

4. Решите уравнение  (Повторяется с №77369)

5. Найдите корень уравнения 

6. Найдите корень уравнения 

7. Найдите корень уравнения 

8. Найдите корень уравнения 

9. Найдите корень уравнения: 

10. Найдите корень уравнения: 

Вариант 7 5. Простейшие уравнения

1. Найдите корень уравнения 

2. Найдите корень уравнения 

3. Найдите корень уравнения: 

4. Найдите корень уравнения 

5. Решите уравнение  В ответе напишите наименьший положительный корень.

6. Найдите корень уравнения 

7. Найдите корень уравнения:  Если уравнение имеет более одного корня, в ответе укажите меньший из них.

8. Найдите корень уравнения 

9. Найдите корень уравнения 

10. Решите уравнение 

Вариант 8 5. Простейшие уравнения

1. Найдите корень уравнения:  Если уравнение имеет более одного корня, в ответе укажите меньший из них.

2. Найдите корень уравнения 

3. Найдите корень уравнения: 

4. Найдите корень уравнения 

5. Решите уравнение 

6. Решите уравнение  В ответе напишите наибольший отрицательный корень.

7. Найдите корень уравнения 

8. Найдите корень уравнения:  В ответе запишите наибольший отрицательный корень.

9. Найдите решение уравнения: 

10. Найдите корень уравнения:

Вариант 9 5. Простейшие уравнения

1. Найдите корень уравнения 

2. Найдите корень уравнения: 

3. Решите уравнение  В ответе напишите наибольший отрицательный корень.

4. Найдите корень уравнения 

5. Найдите корень уравнения 

6. Найдите корень уравнения 

7. Найдите корень уравнения 

8. Найдите корень уравнения 

9. Решите уравнение  Если уравнение имеет более одного корня, в ответе запишите больший из корней.

10. Найдите корень уравнения 

Вариант 10 5. Простейшие уравнения

1. Решите уравнение  В ответе напишите наибольший отрицательный корень.

2. Найдите корень уравнения 

3. Найдите корень уравнения: 

4. Найдите корень уравнения 

5. Найдите корень уравнения 

6. Решите уравнение 

7. Найдите корень уравнения 

8. Найдите корень уравнения  Если уравнение имеет более одного корня, в ответе запишите больший из корней.

9. Найдите корень уравнения 

10. Найдите корень уравнения 

5. Простейшие уравнения

Вариант 1

  1. 12,5

  2. -9

  3. 21

  4. -5

  5. 5

  6. 5

  7. -1

  8. -36

  9. -36

  10. 1,4

Вариант 2

  1. -0,2

  2. 0

  3. -4

  4. 9

  5. 93

  6. 12

  7. 0

  8. -12

  9. 3

  10. 10

Вариант 3

  1. 2

  2. 21

  3. -2

  4. -124

  5. 1

  6. -0,25

  7. -5

  8. 21

  9. -12

  10. 0

Вариант 4

  1. 5

  2. 3

  3. -4

  4. -94

  5. 3

  6. 1

  7. 1

  8. 0,3

  9. -4

  10. 5

Вариант 5

  1. 55

  2. -0,5

  3. 2

  4. 8,75

  5. -4

  6. 4,5

  7. -124

  8. -0,4

  9. 3

  10. 1

Вариант 6

  1. -2

  2. 2

  3. -1,25

  4. -6

  5. 4

  6. -4

  7. 122

  8. -4

  9. -5

  10. -5

Вариант 7

  1. 1

  2. 6

  3. 0

  4. 35

  5. 1

  6. -11

  7. -3

  8. 5

  9. 8,75

  10. 1,5

Вариант 8

  1. -3

  2. 8,75

  3. 13

  4. 5

  5. 10

  6. -3

  7. 226

  8. -0,5

  9. 0,5

  10. -6

Вариант 9

  1. 3

  2. 3

  3. -1

  4. -4

  5. 21

  6. -1

  7. -4

  8. -36

  9. 24

  10. 2

Вариант 10

  1. -1

  2. -0,4

  3. 14

  4. 6

  5. 3

  6. -1

  7. -4

  8. 2

  9. -11

  10. 10
Источник

За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 80.6%
Ответом к заданию 1 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=7$, $cos A={3} / {5}$
(см. рис.). Найдите $AB$.

Решение

$sin A = {BC}/{AB}$.

$sin^2A + cos^2A = 1$, то есть $sin A = √{1 — {9}/{25}} = {4}/{5}$.

${4}/{5} = {7}/{AB}, AB = {35}/{4}=8.75$.

Ответ: 8.75

Задача 2

Угол $ACO$ равен $32^°$. Его сторона $CA$ касается окружности с центром в точке $O$. Сторона $CO$ пересекает окружность в точках $B$ и $D$ (см. рис.). Найдите градусную меру дуги $AD$ окружности, заключённой внутри этого угла. Ответ дайте в градусах.

Решение

$∠ AOC=90°-∠ ACO$, так как $∠ OAC=90°$ (радиус, проведённый в точку касания, перпендикулярен касательной). $∠ AOC=90°-32°=58°$. $∠ AOC$ — центральный и измеряется дугой $AB$, то есть $⌣ AB=58°$. Отсюда: дуга $AD$ равна $180°-58°=122°$, так как дуга $DB=180°$.

Ответ: 122

Задача 3

Через концы $A$ и $B$ дуги окружности с центром $O$ проведены касательные $AC$ и $BC$ (см. рис.). Меньшая дуга $AB$ равна $48^°$. Найдите угол $ACB$. Ответ дайте в градусах.

Решение

$∠C AB = ∠C BA$, как углы между хордой и касательной, они измеряются половиной дуги $AB$, то есть $∠C AB = {1}/{2} ︶ AB$ и $∠C BA = {1}/{2} ︶ AB$.

Отсюда, $∠AC B = 180°- ︶AB = 180° — 48° = 132°$.

Ответ: 132

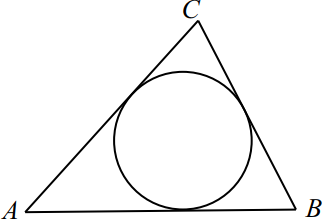
Задача 4

Периметр треугольника равен $73$, а радиус вписанной окружности равен $4$. Найдите площадь этого треугольника.

Решение

$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {73}/{2} · 4 = 146$.

Ответ: 146

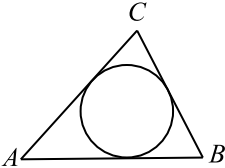
Задача 5

Периметр треугольника равен $40$, а радиус вписанной окружности равен $3$. Найдите площадь этого треугольника.

Решение

$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {40}/{2} · 3 = 60$.

Ответ: 60

Задача 6

Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $AOM$ равен $28^°$. Найдите вписанный угол $MNB$. Ответ дайте в градусах.

Решение

$∠AOM$ — центральный, он измеряется дугой $AM$, то есть $︶AM = 28°$. $AB$ — диаметр, значит $︶AB = 180°$, а $︶MB = 180° — 28° = 152°$. $∠MNB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠MNB = 76°$.

Ответ: 76

Задача 7

Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $MOB$ равен $116^°$. Найдите вписанный угол $MAB$. Ответ дайте в градусах.

Решение

$∠ MOB$ — центральный, он измеряется дугой $MB$. $∠ MAB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠ MAB={116°} / {2}=58°$.

Ответ: 58

Задача 8

В треугольнике $ABC$ равны боковые стороны $AC=BC$, $AH$ — высота, $AB=15$,
$sin ∠ BAC=0{,}6$ (см. рис.). Найдите $BH$.

Решение

В равнобедренном треугольнике углы при основании равны.

$∠BAC = ∠ABC, sin ∠ABC = {AH}/{AB}, AH = AB sin ∠ABC. AH = 15 · 0.6 = 9$.

Из $△AHB: HB = √{AB^2 — AH^2} = √{225 — 81} = √{144} = 12$.

Ответ: 12

Задача 9

В треугольнике $ABC$ $AC=BC$, $AH$ — высота, $AB=15$, $sin ∠ BAC={√ {5}} / {3}$ (см. рис.). Найдите $BH$.

Решение

В треугольнике напротив равных сторон лежат равные углы. $∠ BAC=∠ ABC$, $sin ∠ ABC={AH} / {AB}$, $AH=AB sin ∠ ABC$. $AH=15⋅ {√ {5}} / {3}=5√ {5}$. Из $▵ AHB:$ $HB=√ {AB^2-AH^2}=√ {225-125}=√ {100}=10$.

Ответ: 10

Задача 10

В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=9$, $sin A={4} / {11}$ (см. рис.). Найдите $AB$.

Решение

$sin A = {BC}/{AB}, AB = {BC}/{sin A} = {9}/{{4}/{11}} = {99}/{4} = 24.75$.

Ответ: 24.75

Задача 11

Найдите периметр прямоугольника, если его площадь равна $224$, а отношение соседних сторон равно ${2} / {7}$.

Решение

Рассмотрим прямоугольник $ABCD$

$AD : AB = 2 : 7, S_{ABCD} = AD · AB$

$S_{ABCD} = 224$, тогда $224 = AD · AB$

Пусть $x$ — некоторое положительное действительное число, тогда $AD = 2x, AB = 7x$

Отсюда, $224 = 2x · 7x$

$224 = 14x^2$

$x^2 = {224}/{14}$

$x^2 = 16$

$x = 4$

Следовательно, $P = 2(AD+AB) = 2(2·4+7·4) = 2·4(2+7) = 8·9 = 72$.

Ответ: 72

Задача 12

Найдите периметр прямоугольника, если его площадь равна $48$, а отношение соседних сторон равно $3:4$.

Решение

Рассмотрим прямоугольник $ABCD$ (см. рис.). $AD:AB=3:4$, $S_{ABCD}=AD⋅ AB$; $S_{ABCD}=48$, тогда
$48=AD⋅ AB$. Пусть $k$ — некоторое положительное действительное число и
$AD=3k$, $AB=4k$. Отсюда $48=3k⋅ 4k$; $48=12k^2$; $k^2=4$, $k=2$. Следовательно, $P=2(AD+AB)=2(3⋅ 2+4⋅ 2)=28$.

Ответ: 28

Задача 13

Площадь прямоугольника равна $22$. Найдите его большую сторону, если она на $9$ длиннее меньшей стороны.

Решение

$S_{ABCD} = AB·CB$.

Обозначим большую сторону через $x$, тогда меньшая сторона $x — 9$. Итак, $22 = x(x — 9)$

$ x^2 — 9x — 22 = 0$

$D = 81 + 88 = 169 = 13^2$

$ x = {9±13}/{2}$

$ x_1 = 11$

$ x_2 = -2$ (не подходит).

Ответ: 11

Задача 14

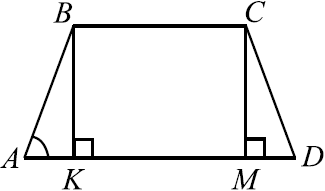
Основания равнобедренной трапеции равны $15$ и $9$. Высота трапеции равна $6$. Найдите тангенс острого угла.

Решение

Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ — высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.

$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {15 — 9}/{2} = 3, BK = 6$ (по условию). $tg ∠BAD = {6}/{3} = 2$.

Ответ: 2

Задача 15

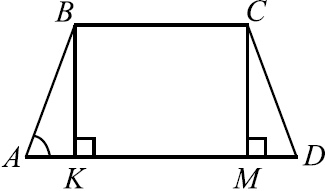
Основания равнобедренной трапеции равны $14$ и $6$. Высота трапеции равна $7$. Найдите тангенс острого угла.

Решение

Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.

$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {14 — 6}/{2} = 4, BK = 7$ (по условию). $tg ∠BAD = {7}/{4} = 1.75$.

Ответ: 1.75

Задача 16

В треугольнике $ABC$ угол $C$ равен $90^°$, $AC=6√ {3}$, $tg A={√ {3}} / {3}$ (см. рис.). Найдите $AB$.

Решение

$tgA = {BC}/{AC}, {√3}/{3} = {BC}/{6√3}, BC = {6√3·√3}/{3} = 6$.

Из $△ABC: AB^2 = AC^2 + BC^2$;

$AB^2 = (6√3)^2 + 6^2 = 36·3 + 36 = 36·4 = 144, AB = 12$.

Ответ: 12

Задача 17

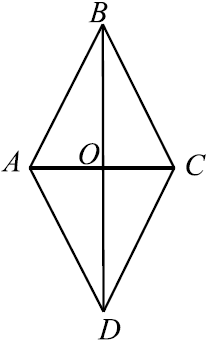
Найдите площадь ромба, если его диагонали равны $5$ и $16$.

Решение

Рассмотрим ромб $ABCD$.

$S_{ABCD} = {1}/{2}d_1d_2$, где $d_1$ и $d_2$ — диагонали ромба.

$S_{ABCD} = {1}/{2}·5·16 = 40$.

Ответ: 40

Задача 18

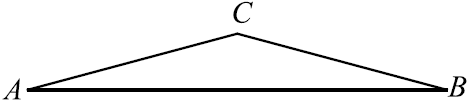
Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $150^°$. Боковая сторона треугольника равна $12$. Найдите площадь этого треугольника.

Решение

Пусть в $△ABC ∠C = 150°, AC = CB$.

$S_{ACB} = {1}/{2}AC·CB·sin∠ACB = {1}/{2}·12·12·sin150° = 72·sin 30° =72·{1}/{2} = 36$.

Ответ: 36

Задача 19

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $30^°$. Боковая сторона треугольника равна $7$. Найдите площадь этого треугольника.

Решение

Пусть в $▵ ABC$ $∠ C=30°$, $AC=BC=7$ (см. рис.). $S_{ACB}={1} / {2} AC⋅ CB⋅ sin ∠ ACB={1} / {2}⋅ 7⋅ 7⋅ sin 30°={1} / {2}⋅ 49⋅ {1} / {2}={49} / {4}=12{,}25$.

Ответ: 12.25

Задача 20

Периметр прямоугольника равен $28$, а площадь $48$. Найдите меньшую сторону прямоугольника.

Решение

Пусть $x$ и $y$ — две стороны прямоугольника. Из условия следует система уравнений:
${{table {2(x+y)=28{,}}; {xy=48{.}};}$

Из первого уравнения системы: $x+y=14$

$y=14-x$.

Подставляя выражение для переменной $y$ во второе уравнение системы, получим:

$x(14-x)=48$

$x^2-14x+48=0$

$x_1=8$

$x_2=6$

Тогда $y_1=14-8=6$

$y_2=14-6=8$

Следовательно, меньшая сторона прямоугольника равна $6$.

Ответ: 6

Рекомендуемые курсы подготовки

Источник

Прототипы задания №1 профильного ЕГЭ 2022 по математике

Новые задания №1 ЕГЭ 2022 по математике профильного уровня — простейшие уравнения.

Для успешного результата необходимо уметь решать рациональные, иррациональные, показательные, тригонометрические и логарифмические уравнения, их системы.

Задание №1 ЕГЭ 2022 математика профильный уровень Прототипы

Источник: math100.ru → Рациональные уравнения

→ Тригонометрические уравнения
time4math.ru → скачать задания
vk.com/ekaterina_chekmareva → задания

При отработке данного задания будут полезны книги:

Демоверсии ЕГЭ 2022 по математике

Утверждённые демоверсии ЕГЭ 2022 по математике от ФИПИ.

Обновлено 10 ноября.

→ Демоверсия профильного уровня: math-demo2022-pro-v2.pdf
→ Демоверсия базового уровня: math-demo2022-b-v2.pdf
→ Спецификация профильного уровня: math-s2022-pro-v2.pdf
→ Спецификация базового уровня: math-s2022-b-v2.pdf
→ Кодификатор: math-k2022-v2.pdf
→ Скачать одним архивом: math-demo2022-v2.zip

Изменения в КИМ ЕГЭ 2022 года профильного уровня в сравнении с КИМ 2021 года

1. Исключены задания 1 и 2, проверяющие умение использовать приобретённые знания и умения в практической и повседневной жизни, задание 3, проверяющее умение выполнять действия с геометрическими фигурами, координатами и векторами.

2. Добавлены задание 9, проверяющее умение выполнять действия с функциями, и задание 10, проверяющее умение моделировать реальные ситуации на языке теории вероятностей и статистики, вычислять в простейших случаях вероятности событий.

3. Внесено изменение в систему оценивания: максимальный балл за выполнение задания повышенного уровня 13, проверяющего умение выполнять действия с геометрическими фигурами, координатами и векторами, стал равен 3; максимальный балл за выполнение задания повышенного уровня 15, проверяющего умение использовать приобретённые знания и умения в практической деятельности и повседневной жизни, стал равен 2.

4. Количество заданий уменьшилось с 19 до 18, максимальный балл за выполнение всей работы стал равным 31.

Изменения в КИМ ЕГЭ 2022 года базового уровня в сравнении с КИМ 2021 года

1. Исключено задание 2, проверяющее умение выполнять вычисления и преобразования (данное требование внесено в позицию задачи 7 в новой нумерации).

2. Добавлены задание 5, проверяющее умение выполнять действия с геометрическими фигурами, и задание 20, проверяющее умение строить и исследовать простейшие математические модели.

3. Количество заданий увеличилось с 20 до 21, максимальный балл за выполнение всей работы стал равным 21.

Обобщенные планы вариантов КИМ ЕГЭ 2022 года по математике

ЕГЭ Математика. Профильный уровень. Проект 2022.

Перейти к заданию №

Ознакомьтесь с Проектом Демонстрационного варианта ЕГЭ 2022 по математике, который здесь представлен с решениями всех заданий первой части — заданий с кратким ответом.

Здесь вы можете ознакомиться с первой частью варианта и поработать над заданиями профильного уровня с кратким ответом. Вторая часть варианта – задания профильного уровня с развёрнутым ответом – представлена в разделе Профильный уровень. Задачи с развёрнутым ответом.

В демонстрационном варианте представлено по несколько примеров заданий на некоторые позиции экзаменационной работы. В реальных вариантах экзаменационной работы на каждую позицию будет предложено только одно задание.

Чтобы ознакомиться с содержанием экзамена базового уровня, перейдите на страницу с интерактивной Демоверсией базового уровня.

Сдадим ЕГЭ по математике? Легко!

Нужны такие материалы в сети? Узнайте, как поддержать сайт и помочь его развитию.

Задание 1

Найдите корень уравнения 3 x − 5 = 81 .

Найдите корень уравнения √3x + 49 ______ = 10.

Найдите корень уравнения log8(5x + 47) = 3 .

Решите уравнение √2x + 3 ______ = x.
Если корней окажется несколько, то в ответ запишите наименьший из них.

В ромбе ABCD угол DBA равен 13°. Найдите угол BCD. Ответ дайте в градусах.

Стороны параллелограмма равны 24 и 27. Высота, опущенная на меньшую из этих сторон, равна 18. Найдите высоту, опущенную на бóльшую сторону параллелограмма.

Задание 4

Найдите (sin<2alpha>) , если (cos <alpha>= 0,6) и π

Задание 5

В первом цилиндрическом сосуде уровень жидкости достигает 16 см. Эту жидкость перелили во второй цилиндрический сосуд, диаметр основания которого в 2 раза больше диаметра основания первого. На какой высоте будет находиться уровень жидкости во втором сосуде? Ответ дайте в сантиметрах.

Площадь боковой поверхности треугольной призмы равна 24. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.

Проведенная плоскость образует новую грань отсечённой призмы, которая также составляет половинку противолежащей грани исходной призмы (по свойствам средней линии треугольника). Таким образом, площадь боковой поверхности отсечённой треугольной призмы составляет половину заданной площади: 24:2 = 12.

Через точку, лежащую на высоте прямого кругового конуса и делящую её в отношении 1:2 , считая от вершины конуса, проведена плоскость, параллельная его основанию и делящая конус на две части. Каков объём той части конуса, которая примыкает к его основанию, если объём всего конуса равен 54?

Разделив высоту конуса в отношении 1:2, получим, что высота меньшего конуса (верхней части) составляет одну третью часть высоты большего (исходного) конуса.
Так как маленький конус полностью подобен большому, то можно воспользоваться правилами подобия: если линейные размеры подобных фигур относятся с коэффициентом (k), то их объёмы относятся с коэффициентом (k^3).

[k = frac<1><3>; ;; k^3 = frac<1><27>] Следовательно, объём маленького конуса равен (54:27=2,) а объём нижней части большого конуса (54-2 = 52.)

Задание 6

На рисунке изображён график дифференцируемой функции y = f(x) . На оси абсцисс отмечены девять точек: x1 , x2 , . x9.

На рисунке изображён график функции y = f(x) и касательная к нему в точке с абсциссой x0. Найдите значение производной функции f‘(x) в точке x0.

Для получения абсолютной величины числа нужно построить на клеточках прямоугольный треугольник так, чтобы его гипотенуза располагалась на касательной, а вершины строго в узлах клеток. Отношение длины катета, параллельного оси Oy к длине катета, параллельного оси Oх, даёт значение тангенса нужного угла.

Задание 7

Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковой сигнал частотой 749 МГц. Приёмник регистрирует частоту сигнала, отражённого от дна океана. Скорость погружения батискафа (в м/с) и частоты связаны соотношением

где c = 1500 м/с — скорость звука в воде; f0 — частота испускаемого сигнала (в МГц); f — частота отражённого сигнала (в МГц). Найдите частоту отражённого сигнала (в МГц), если батискаф погружается со скоростью 2 м/с.

Первым делом убеждаемся, что размерности всех величин в формуле, в условии задачи и в вопросе к заданию заданы в единой системе единиц. Если требуется, например, переход от километров к метрам или от секунд к часам, выполняем соответствующие вычисления.

Подставляем в формулу числовые значения [nu = ccdotfrac;\ 2 = 1500cdotfrac.] Решаем получившееся уравнение относительно неизвестной (f). [2(f+749) = 1500(f-749);\ 2f-1500f=-2cdot749-1500cdot749;\ 1498f = 1502cdot749; ;; 2f = 1502;;;f=751(МГц).]

Задание 8

Весной катер идёт против течения реки в 1 2 _ 3 раза медленнее, чем по течению. Летом течение становится на 1 км/ч медленнее. Поэтому летом катер идёт против течения в 1 1 _ 2 раза медленнее, чем по течению. Найдите скорость течения весной (в км/ч).

Обозначим символом v собственную скорость катера (км/ч), символом x — скорость течения реки весной (км/ч). Тогда скорость течения реки летом составляет (x — 1) км/ч. Имеем
весной: катер идёт против течения со скоростью (v — x), по течению со скоростью (v + x). По условию первая скорость в 1 2 /3 раза меньше, т.е.
(v + x)/(v — x) = 1 2 /3 ;
летом: катер идёт против течения со скоростью (v — (x — 1)), по течению со скоростью (v + (x — 1)). По условию первая скорость в 1 1 /2 раза меньше, т.е.
(v + (x — 1))/(v — (x — 1)) = 1 1 /2 .
Объединяем уравнения в систему и решаем её:

Ответ: 5

Смешав 45%-ный и 97%-ный растворы кислоты и добавив 10 кг чистой воды, получили 62%-ный раствор кислоты. Если бы вместо 10 кг воды добавили 10 кг 50%-ного раствора той же кислоты, то получили бы 72%-ный раствор кислоты. Сколько килограммов 45%-ного раствора использовали для получения смеси?

Автомобиль, движущийся с постоянной скоростью 70 км/ч по прямому шоссе, обгоняет другой автомобиль, движущийся в ту же сторону с постоянной скоростью 40 км/ч . Каким будет расстояние (в километрах) между этими автомобилями через 15 минут после обгона?

Задание 9

На рисунке изображён график функции вида (f(x)= ax^2 + bx + c,) где числа (a, b; и ;c) — целые. Найдите значение (f(-12)).

Формула функции – квадратный трёхчлен, график функции – парабола. Требуется определить значение функции в точке, которая не видна на графике, поэтому нужно воспользоваться формулой. Для этого сначала нужно уточнить формулу, т.е. определить неизвестные коэффициенты квадратного трёхчлена.

Три неизвестных коэффициента можно найти путём решения системы трёх линейных уравнений. Чтобы составить такую систему уравнений, берём на графике три «удобные» точки и подставляем их координаты в формулу функции.
Точки «удобны», если их координаты хорошо считываются, например, находятся в узлах сетки, или мы о них что-то знаем из теории. Для параболы очень хорошими точками являются вершина и точка пересечения с осью ординат. К сожалению, последняя на заданном участке графика также не видна.
На рисунке показаны выбранные мною точки, которые задают следующие соотношения [x_в=-4;Rightarrow;-frac <2a>= -4;\ f(-3)=-2; Rightarrow;a(-3)^2 + b(-3) + c = -2;\ f(-2)=1;Rightarrow;a(-2)^2 + b(-2) + c = 1.] Получили ситему уравнений [ begin -dfrac <2a>= -4,\ 9a -3b + c = -2,\ 4a -2b + c = 1. end] Решаем её [begin b = 8a,\9a -24a + c = -2,\4a -16a + c = 1; end; begin b = 8a,\c = 15a-2,\c = 12a+1; end; begin b = 8a,\0 = 3a-3,\c = 12a+1; end; begin b = 8,\a = 1,\c = 13.\ end] Таким образом, уравнение функции имеет вид (f(x)= x^2 + 8x + 13), чтобы найти её значение в заданной точке, подставляем −12 в формулу [f(-12)= (-12)^2 + 8cdot(-12) +13 = 144-96+13 = 61.]

Так как по графику хорошо считывается вершина параболы – точка с координатами (−4;−3), то имеет смысл вспомнить, что вершина параболы связана с коэффициентами квадратного трёхчлена формулами [x_в = -dfrac<2a>;;y_в = -dfrac<4a>.] И формулу функции (квадратный трёхчлен) представить в преобразованном виде [ax^2 + bx + c = aleft(x+frac<2a>right)^2-frac <4a>= a(x-x_в)^2 + y_в = a(x+4)^2 -3.] В формуле остался один неизвестный коэффициент. Чтобы найти его значение, считаем с графика координаты еще одной точки, например (−3;−2) и подставим их в уравнение. [f(x) = aleft(x+4right)^2 -3\ -2 = a(-3+4)^2 -3;; Rightarrow ;; a = 1.] Таким образом, формула приобрела вид (f(x) = (x+4)^2 -3). Подстановкой находим искомое значение (f(-12) = (-12+4)^2 -3 = 64-3=61.)

Ответ: 61

Задание 10

Симметричную игральную кость бросили три раза. Известно, что в сумме выпало 6 очков. Какова вероятность события «хотя бы раз выпало три очка»?

Используем классическое определение вероятности (P =dfrac,) где (n -) общее число исходов, (m -) число исходов, благоприятствующих запрашиваемому событию.
Чтобы найти количество исходов, рассмотрим из каких трёх слагаемых может состоять число 6.

1) 6 = 1+2+3;
2) 6 = 2+2+2;
3) 6 = 4+1+1.

При трёхкратном бросании игральной кости вариант 1 может реализоваться 6-ю способами, т.к. очки могут выпадать в любом порядке: перестановки из 3-ёх элементов 3! = 6.
Вариант 2 может реализоваться только одним способом.
Вариант 3 реализуется 3-мя способами: 4 очка могут выпасть при первом, или при втором, или при третьем бросании.
Итого (n = 6+1+3 = 10.)

В первом варианте тройка присутствует по одному разу в каждом из 6-ти способов. Во втором и третьем вариантах тройки вообще нет.
Итого (m = 6.) [P =frac = frac<6> <10>= 0,6.]

В городе 48% взрослого населения мужчины. Пенсионеры составляют 12,6% взрослого населения, причем доля пенсионеров среди женщин равна 15%. Для социологического опроса выбран случайным образом мужчина, проживающий в этом городе. Найдите вероятность события «выбранный мужчина является пенсионером».

Используем И/ИЛИ-правила (правила умножения/сложения вероятностей).

От долей населения в процентах перейдём к соответствующим вероятностям в десятичных дробях. (Это можно сделать, опираясь на такое доказательство: если в городе живёт N взрослых человек и 48% из них мужчины, то мужчин в городе живёт (dfrac<100>,) тогда вероятность встретить взрослого мужчину составляет (dfrac <100cdot N>= dfrac<48> <100>= 0,48.))

Неизвестную вероятность события «выбранный мужчина является пенсионером» обозначим x. А находить будем вероятность другого, более общего события «выбранный взрослый житель города является пенсионером». Это событие можно записать так:

«Житель города является пенсионером, если он мужчина И при этом пенсионер ИЛИ она женщина И при этом пенсионер».

Учитывая независимость и несовместимость событий (один человек не может быть одновременно женщиной и мужчиной, быть и не быть персионером), к «И» применяем правило умножения вероятностей, к «ИЛИ» — правило сложения вероятностей. Получим формулу для вероятностей

В этой формуле введены такие обозначения

  • Событие П — «Житель города является пенсионером». Вероятность этого события P(П) = 0,126 находим в условии задачи (пенсионеры составляют 12,6% взрослого населения).
  • Событие М — «Этот житель города является мужчиной». Вероятность этого события P(М) = 0,48 находим в условии задачи.
  • Событие МП — «Выбранный мужчина является пенсионером». Вероятность этого события мы приняли за x.
  • Событие Ж — «Этот житель города является женщиной». Вероятность этого события P(Ж) = 1 − 0,48 = 0,52, так как оно противоположно событию «житель города мужчина».
  • Событие ЖП — «Выбранная женщина является пенсионеркой». Вероятность этого события P(ЖП) = 0,15 находим в условии задачи (доля пенсионеров среди женщин равна 15%).

Получаем уравнение 0,126 = 0,48·x + 0,52·0,15,
из которого находим 0,48x = 0,126 − 0,52·0,15 = 0,048;
x = 0,048/0,48 = 0,1.

Задание 11

Найдите наименьшее значение функции [y = 9x — 9ln <(x + 11)>+ 7] на отрезке [−10,5; 0].

Ищем точку (точки, если их несколько), в которых производная равна нулю или не существует – точки возможных экстремумов.

[y’ = (9x — 9ln <(x + 11)>+ 7)’ = 9 — frac<9> = frac<9(x+10)>;\ frac = 0; Leftrightarrow ; x_1 = -10, ; x_2 = -11.] Так как «подозрительных» точек внутри отрезка мало, точнее, всего одна (x_1=-10) ((x_2 0 \ y'(-12) = dfrac<9(-12+10)> <-12+11>= dfrac<-18> <-1>= 18 >0.)

4) Делаем выводы: на заданном отрезке находится только точка минимума функции (x = -10), следовательно в ней и достигается наименьшее значение (y(-10) = -83.)

Замечание: Если всё-таки требуется оценить значения ln2 и ln11, нужно составить неравенства.
Вспомним, что натуральный логарифм — это логарифм по основанию (e = 2,718. ) и функция lnx является монотонно возрастающей, поэтому
(sqrt -87,5+9cdot0,5 > -83;\ e^2 7-9cdot3 > -83.)

Найдите точку максимума функции [y = (x + 8)^2cdot e^<3-x>.]

1) (y’=left((x + 8)^2cdot e^<3-x>right)’=left((x + 8)^2right)’cdot e^<3-x>+(x + 8)^2cdotleft( e^<3-x>right)’ = \ = 2(x+8)cdot e^ <3-x>+(x + 8)^2cdot e^<3-x>cdot(3-x)’ = 2(x+8)cdot e^ <3-x>— (x + 8)^2cdot e^ <3-x>= \= e^<3-x>cdot(x+8)cdot(2-x-8)=-e^<3-x>cdot(x+8)cdot(x+6);)

2) (-e^<3-x>cdot(x+8)cdot(x+6) = 0 ;;Leftrightarrow ;;(x+8)(x+6)= 0 ;; Rightarrow;; x_1 = -8,;x_2 = -6; )

Найдите точку минимума функции [y = -frac.]

2) (dfrac <(x^2+256)^2>= 0 ;;Leftrightarrow ;;x^2-256 = 0 ;; Rightarrow;; x_ <1,2>= pm16; )

Чтобы получить наиболее высокие баллы, нужно продолжить подготовку и перейти к решению задач ЕГЭ по математике с развёрнутым ответом.

источники:

http://4ege.ru/matematika/62607-demoversii-ege-2022-po-matematike.html

http://mathematichka.ru/ege/DEMO_part1_2022.html

Источник

Понравилась статья? Поделить с друзьями:
  • Простейшие тригонометрические уравнения примеры егэ
  • Простейшие тригонометрические уравнения егэ профиль 5 задание
  • Простейшие тригонометрические уравнения в егэ профильный уровень
  • Простейшие тригонометрические уравнения в егэ базовый уровень
  • Простейшие текстовые задачи егэ математика профиль