Простейшие уравнения егэ профиль 2023 - Помощь в подготовке к экзаменам и поступлению

Равенство, содержащее неизвестное число, обозначенное буквой, называется уравнением. Выражение, стоящее слева от знака равенства, называется левой частью уравнения, а выражение, стоящее справа, — правой частью уравнения.

Линейные уравнения

Линейным называется такое уравнение, в котором неизвестное $x$ находится в числителе уравнения и без показателей. Например: $2х – 5 = 3$

Линейные уравнения сводятся к виду $ax = b$, которое получается при помощи раскрытия скобок, приведения подобных слагаемых, переноса слагаемых из одной части уравнения в другую, а также умножения или деления обеих частей уравнения на число, отличное от нуля.

$5 (5 + 3х) — 10х = 8$

Раскроем скобки.

$25 + 15х — 10х = 8$

Перенесем неизвестные слагаемые в левую часть уравнения, а известные в правую. При переносе из одной части в другую, у слагаемого меняется знак на противоположный.

$15х — 10х = 8 — 25$

Приведем подобные слагаемые.

$5х = -17$ — это конечный результат преобразований.

После преобразований к виду $ax = b$, где, a=0, корень уравнения находим по формуле $х = {b}/{a}$

$х=-{17}/{5}$

$х = — 3,4$

Ответ: $- 3,4$

Квадратные уравнения

Квадратное уравнение — уравнение вида $ax^2 + bx + c = 0$, где $a, b, c$ — некоторые числа a$≠0$, $x$ — неизвестное. Перед тем как решать уравнение, необходимо раскрыть скобки и собрать все слагаемые в левой части уравнения.

Числа $a, b, c$ называются коэффициентами квадратного уравнения.

$a$ — старший коэффициент;
$b$ — средний коэффициент;
$c$ — свободный член.

Если в квадратном уравнении коэффициенты $b$ и $c$ не равны нулю, то уравнение называется полным квадратным уравнением. Например, уравнение $2x^2 – 8x + 3 = 0$. Если один из коэффициентов $b$ или $c$ равен нулю или оба коэффициента равны нулю, то квадратное уравнение называется неполным. Например, $5x^2 – 2x = 0$.

Решение неполных квадратных уравнений

Неполное квадратное уравнение имеет вид $ax^2 + bx = 0$, если $a$≠0$; $c$=0$. В левой части этого уравнения есть общий множитель $x$.

1. Вынесем общий множитель $x$ за скобки.

Мы получим $x (ax + b) = 0$. Произведение равно нулю, если хотя бы один из множителей равен нулю. Поэтому получаем $x = 0$ или $ax + b =0$. Таким образом, данное уравнение эквивалентно двум уравнениям:

$x = 0; ax + b = 0$

2. Решаем получившиеся уравнения каждое отдельно.

Мы получим $x = 0$ и $x={-b}/{a}$. Следовательно, данное квадратное уравнение имеет два корня $x = 0$ и $x={-b}/{a}$

$4х^2 — 5х = 0$

Вынесем х как общий множитель за скобки:

$х (4х — 5) = 0$

Приравняем каждый множитель к нулю и найдем корни уравнения.

$x = 0$ или $4х — 5 = 0$

$х_1 = 0 х_2 = 1,25$

Ответ: $х_1 = 0; х_2 = 1,25$

Неполное квадратное уравнение вида $ax^2 + c = 0, a≠0, b=0$

Для решения данного неполного квадратного уравнения выразим $x^2$.

$ax^2 + c = 0$

$ax^2 = — c$

$x_2 = {-c}/{a}$

При решении последнего уравнения возможны два случая:

если ${-c}/{a}>0$, то получаем два корня: $x = ±v{{-c}/{a}}$

если ${-c}/{a}<0$, то уравнение во множестве действительных числе не имеет решений.

$x^2 — 16 = 0$

$x^2 = 16$

$x = ±4$

Ответ: $х_1 = 4, х_2 = — 4$

Решение полного квадратного уравнения

Решение с помощью дискриминанта

Дискриминантом квадратного уравнения D называется выражение

$b^2 — 4ac$.

При решении уравнения с помощью дискриминанта возможны три случая:

1. $D > 0$. Тогда корни уравнения равны:

$x_{1,2}={-b±√D}/{2a}$

2. $D = 0$. В данном случае решение даёт два двукратных корня:

$x_{1}=x_{2}={-b}/{2a}$

3. $D < 0$. В этом случае уравнение не имеет корней.

$3х^2 — 11 = -8х$

Соберем все слагаемые в левую часть уравнения и расставим в порядке убывания степеней

$3х^2 + 8х — 11 = 0$

$a = 3 ,b = 8, c = — 11$

$D = b^2- 4ac = 82- 4 · 3 · (-11) = 196 = 142$

$x_{1}={-b+√D}/{2a}={-8+14}/{6}=1$

$x_{2}={-b-√D}/{2a}={-8-14}/{6}=-3{2}/{3}$

Ответ: $x_1=1, x_2=-3{2}/{3}$

Устные способы

Если сумма коэффициентов равна нулю $(а + b + c = 0)$, то $х_1= 1, х_2={с}/{а}$

$4х^2+ 3х — 7 = 0$

$4 + 3 — 7 = 0$, следовательно $х_1= 1, х_2=-{7}/{4}$

Ответ: $х_1= 1, х_2 = -{7}/{4}$

Если старший коэффициент в сумме со свободным равен среднему коэффициенту $(a + c = b)$, то $х_1= — 1, х_2=-{с}/{а}$

$5х^2+ 7х + 2 = 0$

$5 + 2 = 7$, следовательно, $х_1= -1, х_2 =-{2}/{5}$

Ответ: $х_1= -1, х_2 = -{2}/{5}$

Кубические уравнения

Для решения простых кубических уравнений необходимо обе части представить в виде основания в третьей степени. Далее извлечь кубический корень и получить простое линейное уравнение.

$(x — 3)^3 = 27$

Представим обе части как основания в третьей степени

$(x — 3)^3 = $3³

Извлечем кубический корень из обеих частей

$х — 3 = 3$

Соберем известные слагаемые в правой части

$x = 6$

Ответ: $х = 6$

Дробно рациональные уравнения

Рациональное уравнение, в котором левая или правая части являются дробными выражениями, называется дробным.

Чтобы решить дробное уравнение, необходимо:

найти общий знаменатель дробей, входящих в уравнение;
умножить обе части уравнения на общий знаменатель;
решить получившееся целое уравнение;
исключить из его корней те, которые обращают в ноль общий знаменатель.

$4x + 1 — {3}/{x} = 0$

1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

2. находим общий знаменатель дробей и умножаем на него обе части уравнения

$4x + 1 — {3}/{x}= 0¦· x$

$4x · x + 1 · x — {3·x}/{x} = 0$

3. решаем полученное уравнение

$4x^2 + x — 3 = 0$

Решим вторым устным способом, т.к. $а + с = b$

Тогда $х_1 = — 1, х_2 = {3}/{4}$

4. исключаем те корни, при которых общий знаменатель равен нулю В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $х_1 = — 1, х_2 = {3}/{4}$

При решении уравнения с двумя дробями можно использовать основное свойство пропорции.

Основное свойство пропорции: Если ${a}/{b} = {c}/{d}$, то $a · d = b · c$

${3х-5}/{-2}={1}/{х}$

Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

Воспользуемся основным свойством пропорции

$х (3х — 5) = -2$

Раскроем скобки и соберем все слагаемые в левой части уравнения

$3х^2- 5х + 2 = 0$

Решим данное квадратное уравнение первым устным способом, т.к.

$a + b + c = 0$

$x_1 = 1, x_2 = {2}/{3}$

В первом пункте получилось, что при $x = 0$ уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $x_1 = 1, x_2 = {2}/{3}$

Рациональное уравнение – это уравнение вида $f(x)=g(x)$, где $f(x)$ и $g(x)$ — рациональные выражения.

Рациональные выражения — это целые и дробные выражения, соединённые между собой знаками арифметических действий: деления, умножения, сложения или вычитания, возведения в целую степень и знаками последовательности этих выражений.

Например,

${2}/{x}+5x=7$ – рациональное уравнение

$3x+√x=7$ — иррациональное уравнение (содержит корень)

Если хотя бы в одной части рационального уравнения содержится дробь, то уравнение называется дробно рациональным.

Чтобы решить дробно рациональное уравнение, необходимо:

Найти значения переменной, при которых уравнение не имеет смысл (ОДЗ);
Найти общий знаменатель дробей, входящих в уравнение;
Умножить обе части уравнения на общий знаменатель;
Решить получившееся целое уравнение;
Исключить из его корней те, которые обращают в ноль общий знаменатель.

Решить уравнение: $4x+1-{3}/{x}=0$

Решение:

1. находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x ≠ 0$

2. находим общий знаменатель дробей и умножаем на него обе части уравнения

$4x+1-{3}/{x}=0|·x$

$4x·x+1·x-{3·x}/{x}=0$

3. решаем полученное уравнение

$4x^2+x-3=0$

Решим вторым устным способом, т.к. $а+с=b$

Тогда, $x_1=-1, x_2=-{3}/{4}$

4. исключаем те корни, при которых общий знаменатель равен нулю

Ответ: $x_1=-1, x_2=-{3}/{4}$

При решении уравнения с двумя дробями, можно использовать основное свойство пропорции.

Основное свойство пропорции: Если ${a}/{b}={c}/{d}$ — пропорция, то $a·d=b·c$

Решить уравнение ${3x-5}/{-2}={1}/{x}$

Решение:

Находим значения переменной, при которых уравнение не имеет смысл (ОДЗ)

$x≠0$

Воспользуемся основным свойством пропорции

$х(3х-5)=-2$

Раскроем скобки и соберем все слагаемые в левой стороне

$3х^2-5х+2=0$

Решим данное квадратное уравнение первым устным способом, т.к. $a+b+c=0$

$x_1=1, x_2={2}/{3}$

В первом пункте получилось, что при x = 0 уравнение не имеет смысл, среди корней уравнения нуля нет, значит, оба корня нам подходят.

Ответ: $x_1=1, x_2={2}/{3}$

Уравнения, содержащие неизвестную под знаком корня, называются иррациональными.

Чтобы решить иррациональное уравнение, необходимо:

Преобразовать заданное иррациональное уравнение к виду: $√{f(x)}=g(x)$ или $√{f(x)}=√{g(x)}$
Обе части уравнение возвести в квадрат: $√{f(x)}^2=(g(x))^2$ или $√{f(x)}^2=√{g(x)}^2$
Решить полученное рациональное уравнение.
Сделать проверку корней, так как возведение в четную степень может привести к появлению посторонних корней. (Проверку можно сделать при помощи подстановки найденных корней в исходное уравнение.)

Решите уравнение $√{4х-3}=х$. Если уравнение имеет более одного корня, укажите наименьший из них.

Решение:

Обе части уравнение возведем в квадрат:

$√{4х-3}^2=х^2$

Получаем квадратное уравнение:

$4х-3=х^2$

Перенесем все слагаемые в левую часть уравнения:

${-х}^2+4х-3=0$

Решим данное квадратное уравнение устным способом, так как

$a+b+c=0$

$-1+4-3=0$, следовательно $х_1 = 1; х_2={с}/{а}={-3}/{-1}=3$

Проведем проверку корней, подставив их вместо икса в исходное уравнение

$√{4·1-3}=1$

$1=1$, получили в результате проверки верное равенство, следовательно $х_1=1$ подходит.

$√{4·(3)-3}=3$

$√9=3$

$3=3$, получили в результате проверки верное равенство, следовательно корень $х_2=3$ подходит

$х_1=1$ наименьший корень.

Ответ: $1$

Так как в иррациональных уравнениях иногда необходимо возводить в квадрат не только число, но и целое выражение, необходимо вспомнить формулы сокращенного умножения:

Квадрат разности двух чисел равен квадрату первого числа минус удвоенное произведение первого на второе число плюс квадрат второго числа. $(a-b)^2=a^2-2ab+b^2$
Квадрат суммы двух чисел равен квадрату первого числа плюс удвоенное произведение первого числа на второе плюс квадрат второго числа. $(a+b)^2=a^2+2ab+b^2$

Решить уравнение: $х-6=√{8-х}$

Возведем обе части уравнения в квадрат

$(х-6)^2=8-х$

В левой части уравнения при возведении в квадрат получаем формулу сокращенного умножения квадрат разности. В правой части уравнения квадрат и корень компенсируют друг друга и в результате остается только подкоренное выражение

$х^2-2·6·х+6^2=8-х$

$х^2-12х+36=8-х$

Получили квадратное уравнение. Все слагаемые переносим в левую часть уравнения. При переносе слагаемых через знак равно их знаки меняются на противоположные.

$х^2-12х+36-8+х=0$

Приводим подобные слагаемые:

$х^2-11х+28=0$

Найдем корни уравнения через дискриминант:

$D=b^2-4ac=121-4·28=121-112=9=3^2$

$x_{1,2}={-b±√D}/{2a}={11±3}/{2}$

$x_1=7; x_2=4$

Проведем проверку корней, подставив их вместо икса в исходное уравнение

$x_1=7$

$7-6=√{8-7}$

$1=1$, получили верное равенство, следовательно, корень нам подходит.

$x_2=4$

$4-6=√{8-4}$

$-2=2$, получили неверное равенство, следовательно, данный корень посторонний.

Ответ: $7$

Показательными называют такие уравнения, в которых неизвестное содержится в показателе степени.

$a^x=b$

При решении показательных уравнений используются свойства степеней, вспомним некоторые из них:

1. При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются.

$a^n⋅a^m=a^{n+m}$

2. При делении степеней с одинаковыми основаниями основание остается прежним, а показатели вычитаются

$a^n:a^m=a^{n-m}$

3. При возведении степени в степень основание остается прежним, а показатели перемножаются

$(a^n)^m=a^{n·m}$

4. При возведении в степень произведения в эту степень возводится каждый множитель

$(a·b)^n=a^n·b^n$

5. При возведении в степень дроби в эту степень возводиться числитель и знаменатель

$({a}/{b})^n={a^n}/{b^n}$

6. При возведении любого основания в нулевой показатель степени результат равен единице

$a^0=1$

7. Основание в любом отрицательном показателе степени можно представить в виде основания в таком же положительном показателе степени, изменив положение основания относительно черты дроби

$a^{-n}={1}/{a^n}$

${a^{-n}}/{b^{-k}}={b^k}/{a^n}$

8. Радикал (корень) можно представить в виде степени с дробным показателем

$√^n{a^k}=a^{{k}/{n}}$

Показательные уравнения часто сводятся к решению уравнения $a^x=a^m$, где, $а >0, a≠1, x$ — неизвестное. Для решения таких уравнений воспользуемся свойством степеней: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели.

Решить уравнение $25·5^х=1$

Решение:

В левой части уравнения необходимо сделать одну степень с основанием $5$ и в правой части уравнения представить число $1$ в виде степени с основанием $5$

$5^2·5^х=5^0$

При умножении степеней с одинаковыми основаниями основание остается прежним, а показатели складываются

$5^{2+х}=5^0$

Далее проговариваем: степени с одинаковым основанием $(а >0, a≠1)$ равны только тогда, когда равны их показатели

$2+х=0$

$х=-2$

Ответ: $-2$

Решить уравнение $2^{3х+2}-2^{3х-2}=30$

Решение:

Чтобы решить данное уравнение, вынесем степень с наименьшим показателем как общий множитель

$2^{3x+2}-2^{3x-2}=30$

$2^{3x-2}({2^{3x+2}}/{2^{3x-2}}-{2^{3x-2}}/{2^{3x-2}})=30$

$2^{3x-2}(2^{3x+2-(3x-2)}-1)=30$

$2^{3x-2}(2^4-1)=30$

$2^{3x-2}·15=30$

Разделим обе части уравнения на $15$

$2^{3х-2}=2$

$2^{3х-2}=2^1$

$3х-2=1$

$3х=3$

$х=1$

Ответ: $1$

Источник

В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Квадратные уравнения

Арифметический квадратный корень

Корни и степени

Показательная функция

Показательные уравнения

Логарифмическая функция

Логарифмические уравнения

Тригонометрический круг

Формулы приведения

Формулы тригонометрии

Простейшие тригонометрические уравнения 1

Уравнения, сводящиеся к квадратным

1. Решите уравнение $frac{6}{13}x^2=19frac{1}{2}$ . Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.

С левой частью уравнения все понятно. Дробь $frac{6}{13}$ умножается на x^2. А в правой части — смешанное число $19frac{1}{2}.$ Его целая часть равна 19, а дробная часть равна $frac{1}{2}.$ Запишем это число в виде неправильной дроби:

$19frac{1}{2}= frac{19cdot 2+1}{2} = frac{39}{2}.$

Получим:

$frac{6}{13}x^2=frac{39}{2};$

$x^2=frac{39cdot 13}{2cdot 6}=frac{13cdot 3cdot 13}{2cdot 6}=frac{{13}^2}{4};$

$x=pm frac{13}{2};$

или

Выбираем меньший корень.

Ответ: -6,5.

2. Решите уравнение

Возведем в квадрат левую часть уравнения. Получим:

Ответ: -6.

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как $frac{4x-5}{4x-5}$ и приведем дроби к общему знаменателю:

$frac{5x-3}{4x-5}-frac{4x-5}{4x-5}=0;$

$frac{x+2}{4x-5}=0;$

x= - 2.

Ответ: -2.

Это довольно простой тип уравнений. Главное — внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.

4. Решите уравнение:

$sqrt{frac{6}{4{x}-54} } =frac{1}{7}.$

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, .

Возведём обе части уравнения в квадрат:

$frac{6}{4{x}-{ 54}} =frac{1}{49}.$

Решим пропорцию:

Условие при этом выполняется.

Ответ: 87.

5. Решите уравнение Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

$left{begin{matrix} 72-x=x^2\72-xgeq 0 hfill \xgeq 0 hfill end{matrix}right.$ .

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

$sqrt{72-x}=x Leftrightarrow left{begin{matrix} 72-x=x^2\72-x geq 0 \x geq 0 end{matrix}right. Leftrightarrow$

Мы получили, что x=8 . Это единственный корень уравнения.

Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: Находят его корни: x=8 или x=-9. Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

Ответ: 8.

6. Решите уравнение . Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов:

Ответ: 9.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение $5^{x-7}=frac{1}{125}.$

Вспомним, что $125 = 5{}^{3}.$ Уравнение приобретает вид: $5{}^{x}{}^{-}{}^{7 }= 5{}^{-}{}^{3}.$ Функция y = 5^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

откуда x = 4.

Ответ: 4.

8. Решите уравнение ${left(frac{1}{49}right)}^{x-8}=7.$

Представим ${left(frac{1}{49}right)}^{ }$ как $7^{-2};$

${left(7^{-2}right)}^{x-8}=7;$

$7^{-2x+16}=7.$

Функция y = 7^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

x=7,5.

Ответ: 7,5.

9. Решите уравнение $left(frac{1}{9} right)^{{ x}-13} =3.$

Представим ${textstylefrac{1}{9}}$ в виде степени с основанием 3 и воспользуемся тем, что $left({ a}^{{ m}} right)^{{ n}} ={ a}^{{ mn}}.$

$left(3^{-2} right)^{{ x}-{ 13}} =3;$
$3^{-2{ x}+{ 26}} =3^{1} ;$

Ответ: 12,5.

Логарифмические уравнения

Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел.

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

${{log}_5 left(4+xright)=2 }.$

Область допустимых значений: . Значит,

Представим 2 в правой части уравнения как ${{log}_5 25 }$ , чтобы слева и справа в уравнении были логарифмы по основанию 5.

${{log}_5 left(4+xright)={{log}_5 25 } }.$

Функция $y = {{log}_5 x }$ монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом

4+x=25;
x=21.

Ответ: 21.

11. Решите уравнение: ${{log}_8 left(x^2+xright)={{log}_8 left(x^2-4right) } }.$

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

Ответ: -4.

12. Решите уравнение: $2^{{{log}_4 left(4x+5right) }}=9.$

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

${{log}_4 b }=frac{{{log}_2 b }}{{{log}_2 4 }}=frac{{{log}_2 b }}{2}.$

Записываем решение как цепочку равносильных переходов.

Ответ: 19.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

${{log}_{x-5} 49=2 }.$

В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.

Получим систему:

$small left{begin{matrix} left ( x-5 right )^2=49\x-50 \x-5 neq 1 end{matrix}right..$

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: x=12 и x=-2.

Очевидно, корень x=-2 является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения: x=12.

Ответ: 12.

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.

14. Найдите корень уравнения: $cos frac{pi (x+1)}{4}=frac{sqrt{2}}{2}.$ В ответе запишите наибольший отрицательный корень.

Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.

Сделаем замену $frac{pi left(x+1right)}{4}=t.$ Получим: $cos t=frac{sqrt{2}}{2}.$

Получаем решения: $t=pm frac{pi }{4}+2pi n, nin Z.$ Вернемся к переменной x.

$frac{pi (x+1)}{4}=pm frac{pi }{4}+2pi n, nin Z.$ Поделим обе части уравнения на и умножим на 4.

$left[ begin{array}{c}x=8n, nin Z \x=-2+8n end{array}right..$

Первой серии принадлежат решения

Вторая серия включает решения

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это x = -2.

Ответ: -2.

15. Решите уравнение: $tg frac{pi left( x+1right)}{4}= -1.$ В ответе напишите наименьший положительный корень.

Решение:

Сделаем замену $frac{pi left(x+1right)}{4}=t.$ Получим: tgt=-1. Решения этого уравнения:

$t=-frac{pi }{4}+pi n, nin Z.$ Вернемся к переменной х:

$frac{pi left(x+1right)}{4}=-frac{pi }{4}+pi n, n in Z.$ Умножим обе части уравнения на 4 и разделим на .

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

Наименьший положительный корень x = 2.

Ответ: 2.

Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Каталог заданий.
Линейные, квадратные, кубические уравнения

Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

Тип 5 № 26662

Найдите корень уравнения:

Аналоги к заданию № 26662: 10149 9653 9659 9667 9669 9673 9677 9679 9691 9693 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 5 № 26663

Найдите корень уравнения:

Аналоги к заданию № 26663: 9655 10135 9657 9661 9663 9665 9671 9675 9681 9683 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 5 № 77368

Решите уравнение

Аналоги к заданию № 77368: 100259 100757 509597 509988 510118 513336 513357 100261 100263 100265 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 1.4.2 Преобразования выражений, включающих операцию возведения в степень, 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

Сообщить об ошибке · Помощь

Тип 5 № 77369

Решите уравнение

Аналоги к заданию № 77369: 100759 100787 100761 100763 100765 100767 100769 100771 100773 100775 … Все

Решение

Курс Д. Д. Гущина

2 комментария · Сообщить об ошибке · Помощь

Тип 5 № 77371

Найдите корень уравнения Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Аналоги к заданию № 77371: 100881 101379 524042 624069 624103 100883 100885 100887 100889 100891 … Все

Кодификатор ФИПИ/Решу ЕГЭ: 2.1.1 Квадратные уравнения, 2.1.2 Рациональные уравнения

Решение

Курс Д. Д. Гущина

3 комментария · Сообщить об ошибке · Помощь

Пройти тестирование по этим заданиям

Источник

Показательные уравнения

Рассмотрим уравнение 2^x = 8. В какую степень надо возвести 2, чтобы получить 8? Ясно, что в степень 3.

Более того, x = 3 — единственное решение данного уравнения. Почему? Это легко понять, посмотрев на график показательной функции y = 2^x: данная функция монотонно возрастает и потому каждое своё значение принимает ровно один раз. Иными словами, не существует других значений x, кроме 3, таких, что 2^x = 8.

Простейшее показательное уравнение — это уравнение вида

где a > 1 или 0 < a < 1.

Если b > 0, то уравнение (1) имеет решение, и притом единственное. Действительно, при a > 1 показательная функция монотонно возрастает, а при 0 < a < 1 — монотонно убывает; в любом случае она принимает каждое своё значение ровно один раз.

А вот если b ⩽ 0, то уравнение (1) не имеет решений: ведь показательная функция может принимать только положительные значения.

Любое показательное уравнение после соответствующих преобразований сводится к решению одного или нескольких простейших.

В задачах достаточно представить левую и правую части в виде степеней с одинаковым основанием.

Вспоминаем, что 125 = 5³. Уравнение приобретает вид: 5^x−7 = 5⁻³.

В силу монотонности показательной функции показатели степени равны: x − 7 = −3, откуда x = 4.

2.
Поскольку , уравнение можно записать в виде:
Дальнейшее ясно:
Теперь рассмотрим более сложные уравнения.

Здесь лучше всего вынести за скобку двойку в наименьшей степени:

4.

Делаем замену

Тогда и относительно t мы получаем квадратное уравнение: Его корни: и

В первом случае имеем: откуда

Во втором случае: решений нет.

Ответ: 3.

Замечаем, что а :

Делим обе части на положительную величину :

Делаем замену:
Полученное квадратное уравнение имеет корни −1 и .

В случае
решений нет.

В случае

имеем единственный корень

Ответ:

Вообще, показательные уравнения вида

называются однородными. Для них существует стандартный приём решения — деление обеих частей на (эта величина не равна нулю, так как показательная функция может принимать только положительные значения). Именно этим приёмом мы в данной задаче и воспользовались.

С однородными уравнениями, кстати, мы уже встречались — в тригонометрии. Это были уравнения вида
Их мы решали похожим приёмом — делением на

Спасибо за то, что пользуйтесь нашими публикациями.
Информация на странице «Показательные уравнения» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из данного раздела.

Публикация обновлена:
08.03.2023

Содержание

Определение
Свойства показательной функции
Методы решения показательных уравнений
Приведение к одинаковому основанию
- Пример 1.
- Пример 2.
Замена переменной
- Пример 1
- Пример 2
Выделение устойчивого выражения
- Пример 1
- Пример 2
Приведение к одинаковой степени
- Пример 1
- Пример 2
Графический метод
- Пример 1.
- Пример 2.
Примеры для самостоятельной работы
Заключение
- Методика самостоятельной работы

Определение

Показательным уравнением называется уравнение, содержащие неизвестную величину в показателе степени.

Пример
такого
уравнения: 2**x= 16.

В какую степень надо возвести 2, чтобы
получить 16? Понятно, что в степень 4.

При
том, x = 4 — единственное решение данного уравнения. Как вы

думаете почему? Это легко понять, посмотрев на график показательной функции y
= 2**x:

Рис. 1 График показательной функции

данная
функция монотонно возрастает (это когда x2 ˃ x1, y2 ˃ y1) и потому каждое своё значение
принимает ровно один раз. Не существует других

значений
x, кроме 4, таких, что 2**x = 16.

Простейшее показательное уравнение —
это уравнение вида

a**x= b, (1)

где a > 1 или 0 < a < 1.

Если
b > 0, то уравнение (1) имеет решение, и притом единственное. Действительно,
при a > 1 показательная функция монотонно возрастает, а при 0 < a < 1
— монотонно убывает; в любом случае она принимает каждое своё значение
ровно один раз.

А вот если b ⩽ 0, то уравнение (1) не имеет решений: ведь
показательная функция может принимать только положительные значения.

Свойства показательной функции

1. a**m х a**n = a**(m+n)

2. a**m : a**n = a **(m-n)

3. (a x b)*n = a**n x b**n

4. (a : b)**n = a**n : b**n

5. (a**n)**m = a**n x m

6. a**(-n) = 1/a**n

7. (a/b)**(-n) = (b/a)**n

8. n√a =a**(1/n)

Методы решения показательных уравнений

Любое
показательное уравнение после соответствующих преобразований сводится к решению
одного или нескольких простейших. На примерах будет показано, как использовать способы решения.

Вот эти методы:

Приведение к одинаковому основанию;
Замена переменной;
Выделение устойчивого выражения;
Приведение к одинаковой степени;
Графический метод

Приведение к одинаковому основанию

Левую и правую часть показательного уравнения представляем в виде

степеней с одинаковым основанием

Пример 1.

Вспоминаем,
что 125 = 5**3. Уравнение приобретает вид: 5**x-7 = 5**3

В
силу монотонности показательной функции показатели степени равны:

x − 7 = −3,
откуда x = 4.

Ответ: 4

Пример 2.

Поскольку

то уравнение можно записать в следующем виде:

Степени в левой части перемножаются по свойствам показательной функции и ясно что
:

Основания одинаковые, значит согласно свойств показательной функции, степень левой части уравнения равна правой

9+3x=9, 3x =0. откуда

x=0

Ответ: 0

Замена переменной

Такой способ решения показательных уравнений понадобится тем, кто не боится по-настоящему трудных задач. Ведь с помощью ввода новой переменной можно упростить даже самое сложное выражение. Его суть проста: мы заменяем «сложную » переменную на более простую и решаем уравнение, а затем производим обратную замену. Главное — определить, какую именно переменную заменить.

Пример 1

4**x- 2**(x+1)- 8 = 0

Очевидно, что в этом уравнении показательные функции легко привести к общему основанию: 4**х = 2**2х, а 2**(х+1) = 2 × 2**х.

2**(2х)- 2 × 2**х — 8 = 0

Что-то уже напоминает.

Если бы из этого выражения можно было волшебным образом убрать 2**х, получилось бы обычное квадратное уравнение.

Поэтому мы обозначим 2**х новой переменной — допустим, y.

Если 2**х = y, получается: у**2- 2*у — 8 = 0.

У такого уравнения есть два корня: у1 = 4, у2 = -2.

Проведем обратную замену: 2**х = 4, 2**х = -2.

Но показательная функция не может быть отрицательным числом, значит, 2**х = -2 корней не имеет. Отсюда следует, что 2**х = 4.

х = 2.

Ответ: 2

Пример 2

25**х — 6 × 5**х + 5 = 0

Присмотримся к этому равенству, ясно, что у него много общего с квадратным уравнением. Введем новую переменную:

5**х = у.

Получили квадратное уравнение

у**2 — 6*у + 5 = 0

Корни такого уравнения : 1 и 5.

Выполним обратную замену:

5**х = 1, значит х = 0, так как

5**х = 5**0;

5**х = 5, 5**х = 5**1,

значит х = 1.

Ответ: 0; 1

Выделение устойчивого выражения

В предыдущих примерах мы преобразовывали разные виды показательных уравнений путем разложения многочленов на множители, потому что хотели найти способ решения — получить одинаковые основания или выделить переменную, которую можно заменить. Так вот, когда мы выносим некий множитель за скобку или заменяем переменную, пытаясь упростить уравнение — это действие по сути и является выделением устойчивого выражения.

Устойчивое выражение — это некий многочлен, содержащий переменную, который в скрытом виде присутствует во всех показательных функциях уравнения. Его можно вынести за скобки или обозначить новой переменной, чтобы упростить уравнение.

То или иное устойчивое выражение можно найти почти в любом сложном уравнении. Проблема только в том, чтобы научиться верно определять такое выражение, а этот навык появляется лишь с опытом.

Пример 1

3**(х+1) + 3**х — 3**(х-2) = 35

В данном случае в качестве устойчивого выражения удобно взять 3**(х-2), как степень с наименьшим показателем и как у=3**(х-2) показательная функция и её значение положительное число по определению. В итоге мы получим: 3**(х+1)/(3**(х-2)) +3**х/ (3**(х-2) — 3**(х-2)/ (3**(х-2) =35, отсюда

3**(х-2)(3**3 + 3**2 — 1) = 35,

3**(х-2) × 35 = 35, делим левую и правую часть уравнения на 35, получаем

3**(х-2) = 1

Поскольку 1 равняется любое число в нулевой степени, мы можем записать:

3**(х-2) = 3**0

х — 2 = 0

х = 2

Ответ: 2

Пример 2

5 × 3**(-3х+1) + 3**(-3х+2) = 24

Для начала мы попробуем в левой части уравнения получить одинаковую степень: 3**(-3х+2) = 3**(-3х+1)+1 = 3 × 3**(-3х+1).

Теперь у нас есть устойчивое выражение 3**(-3х+1), которое можно вынести за скобки, чтобы получить более простое уравнение:

3**(-3х+1)(5+3) = 24

8 × 3-3х+1 = 24

3**(-3)**х+1 = 31

(-3)**х + 1 = 1

х = 0

Ответ: 0

Приведение к одинаковой степени

Не все показательные уравнения с разными основаниями можно решить предыдущим способом. Иногда проще преобразовать не основания, а показатели степени. Правда, пользоваться этим методом есть смысл только в том случае, когда мы имеем дело с умножением или делением.

При умножении чисел с разными основаниями, но одинаковыми степенными показателями можно перемножить только основания (степень останется прежней): a**x*b**x = (a*b)**x.

Пример 1

5**(2х-4) = 49**(2-х)

Общих множителей у левой и правой части уравнения нет и привести их к одинаковому основанию достаточно трудно. Поэтому стоит поработать с показателями степеней:

5**(2х-4) = 49**(2-х)

5**(2х-4) = 7**(4-2х)

5**(2х-4) = (1/7)**(2х-4), используем свойства показательной функции и получаем

5**(2х-4)/(1/7)**(2х-4) =(1/7)**(2х-4)

35**(2х-4) = 1,

это 35**(2х-4) = 35**0

2х — 4 = 0

х = 2

Пример 2

2**(х-2) = 5**(2-х)

Нам нужно привести обе части уравнения к одинаковым степенным показателям, и для этого вначале попробуем преобразовать правую часть, используя свойство степенных функций.

2**(х-2) = 1/5**(х-2)

Теперь умножим обе части на 5**(2-х) и придем к уравнению:

2**(х-2) × 5**(2-х) = 1

10**(х-2) = 1

10**(х-2) = 10**0

х — 2 = 0

x=2

Графический метод

Пример 1.

4**х = 16

Смотрим на рис.1 и находим значение х =2

Пример 2.

1.5**х =2.25

Находим по графику функции у =1.5**х значение 2.25 на оси у, проводим через эту точку прямую параллельную оси х. Из точки пересечения этой прямой с параболой у=1.5**х опускаем перпендикуляр на ось х и находим значение х = 2, что удовлетворяет нашему уравнению.

Примеры для самостоятельной работы

Заключение

В
данной статье рассмотрели методы решения простейших показательных
уравнений, подобные которым могут быть в в первом задании ЕГЭ, ЦТ, на школьном экзамене.

Повторим
эти основные методы:

1. Графический,
то есть по графику находим решение.

2. Решение
на основе свойства степеней: если две степени одного и того же положительного
числа, отличного от 1, равны, то равны и их показатели.

3. Путем
введения новой неизвестной показательное
уравнение сводится к алгебраическому уравнению и решается алгебраическими
методами.

Методика самостоятельной работы

Решаете
на основе разобранных примеров.

Ответы пишите в комментариях.

Если кому-то
будет непонятно, поясню в следующей статье.

Будем подробно разбирать примеры на все темы
ЕГЭ, начиная с простых и закончим олимпиадными.

Успехов!

До новых встреч!

Источник

За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 80.6%
Ответом к заданию 1 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=7$, $cos A={3} / {5}$
(см. рис.). Найдите $AB$.

Решение

$sin A = {BC}/{AB}$.

$sin^2A + cos^2A = 1$, то есть $sin A = √{1 — {9}/{25}} = {4}/{5}$.

${4}/{5} = {7}/{AB}, AB = {35}/{4}=8.75$.

Ответ: 8.75

Задача 2

Угол $ACO$ равен $32^°$. Его сторона $CA$ касается окружности с центром в точке $O$. Сторона $CO$ пересекает окружность в точках $B$ и $D$ (см. рис.). Найдите градусную меру дуги $AD$ окружности, заключённой внутри этого угла. Ответ дайте в градусах.

Решение

$∠ AOC=90°-∠ ACO$, так как $∠ OAC=90°$ (радиус, проведённый в точку касания, перпендикулярен касательной). $∠ AOC=90°-32°=58°$. $∠ AOC$ — центральный и измеряется дугой $AB$, то есть $⌣ AB=58°$. Отсюда: дуга $AD$ равна $180°-58°=122°$, так как дуга $DB=180°$.

Ответ: 122

Задача 3

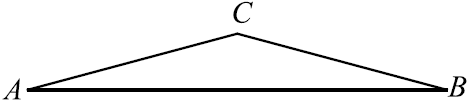
Через концы $A$ и $B$ дуги окружности с центром $O$ проведены касательные $AC$ и $BC$ (см. рис.). Меньшая дуга $AB$ равна $48^°$. Найдите угол $ACB$. Ответ дайте в градусах.

Решение

$∠C AB = ∠C BA$, как углы между хордой и касательной, они измеряются половиной дуги $AB$, то есть $∠C AB = {1}/{2} ︶ AB$ и $∠C BA = {1}/{2} ︶ AB$.

Отсюда, $∠AC B = 180°- ︶AB = 180° — 48° = 132°$.

Ответ: 132

Задача 4

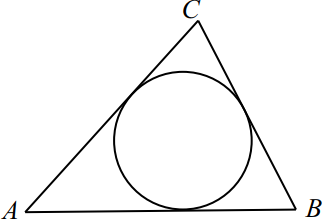
Периметр треугольника равен $73$, а радиус вписанной окружности равен $4$. Найдите площадь этого треугольника.

Решение

$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {73}/{2} · 4 = 146$.

Ответ: 146

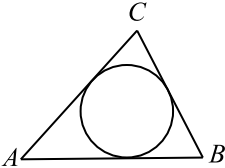
Задача 5

Периметр треугольника равен $40$, а радиус вписанной окружности равен $3$. Найдите площадь этого треугольника.

Решение

$S_{ABC} = p · r$, где $p$ — полупериметр треугольника, а $r$ — радиус вписанной окружности, тогда $S_{ABC} = {40}/{2} · 3 = 60$.

Ответ: 60

Задача 6

Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $AOM$ равен $28^°$. Найдите вписанный угол $MNB$. Ответ дайте в градусах.

Решение

$∠AOM$ — центральный, он измеряется дугой $AM$, то есть $︶AM = 28°$. $AB$ — диаметр, значит $︶AB = 180°$, а $︶MB = 180° — 28° = 152°$. $∠MNB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠MNB = 76°$.

Ответ: 76

Задача 7

Отрезки $MN$ и $AB$ — диаметры окружности с центром $O$ (см. рис.). Угол $MOB$ равен $116^°$. Найдите вписанный угол $MAB$. Ответ дайте в градусах.

Решение

$∠ MOB$ — центральный, он измеряется дугой $MB$. $∠ MAB$ — вписанный и он измеряется половиной дуги $MB$, то есть $∠ MAB={116°} / {2}=58°$.

Ответ: 58

Задача 8

В треугольнике $ABC$ равны боковые стороны $AC=BC$, $AH$ — высота, $AB=15$,
$sin ∠ BAC=0{,}6$ (см. рис.). Найдите $BH$.

Решение

В равнобедренном треугольнике углы при основании равны.

$∠BAC = ∠ABC, sin ∠ABC = {AH}/{AB}, AH = AB sin ∠ABC. AH = 15 · 0.6 = 9$.

Из $△AHB: HB = √{AB^2 — AH^2} = √{225 — 81} = √{144} = 12$.

Ответ: 12

Задача 9

В треугольнике $ABC$ $AC=BC$, $AH$ — высота, $AB=15$, $sin ∠ BAC={√ {5}} / {3}$ (см. рис.). Найдите $BH$.

Решение

В треугольнике напротив равных сторон лежат равные углы. $∠ BAC=∠ ABC$, $sin ∠ ABC={AH} / {AB}$, $AH=AB sin ∠ ABC$. $AH=15⋅ {√ {5}} / {3}=5√ {5}$. Из $▵ AHB:$ $HB=√ {AB^2-AH^2}=√ {225-125}=√ {100}=10$.

Ответ: 10

Задача 10

В треугольнике $ABC$ угол $C$ равен $90^°$, $BC=9$, $sin A={4} / {11}$ (см. рис.). Найдите $AB$.

Решение

$sin A = {BC}/{AB}, AB = {BC}/{sin A} = {9}/{{4}/{11}} = {99}/{4} = 24.75$.

Ответ: 24.75

Задача 11

Найдите периметр прямоугольника, если его площадь равна $224$, а отношение соседних сторон равно ${2} / {7}$.

Решение

Рассмотрим прямоугольник $ABCD$

$AD : AB = 2 : 7, S_{ABCD} = AD · AB$

$S_{ABCD} = 224$, тогда $224 = AD · AB$

Пусть $x$ — некоторое положительное действительное число, тогда $AD = 2x, AB = 7x$

Отсюда, $224 = 2x · 7x$

$224 = 14x^2$

$x^2 = {224}/{14}$

$x^2 = 16$

$x = 4$

Следовательно, $P = 2(AD+AB) = 2(2·4+7·4) = 2·4(2+7) = 8·9 = 72$.

Ответ: 72

Задача 12

Найдите периметр прямоугольника, если его площадь равна $48$, а отношение соседних сторон равно $3:4$.

Решение

Рассмотрим прямоугольник $ABCD$ (см. рис.). $AD:AB=3:4$, $S_{ABCD}=AD⋅ AB$; $S_{ABCD}=48$, тогда
$48=AD⋅ AB$. Пусть $k$ — некоторое положительное действительное число и
$AD=3k$, $AB=4k$. Отсюда $48=3k⋅ 4k$; $48=12k^2$; $k^2=4$, $k=2$. Следовательно, $P=2(AD+AB)=2(3⋅ 2+4⋅ 2)=28$.

Ответ: 28

Задача 13

Площадь прямоугольника равна $22$. Найдите его большую сторону, если она на $9$ длиннее меньшей стороны.

Решение

$S_{ABCD} = AB·CB$.

Обозначим большую сторону через $x$, тогда меньшая сторона $x — 9$. Итак, $22 = x(x — 9)$

$ x^2 — 9x — 22 = 0$

$D = 81 + 88 = 169 = 13^2$

$ x = {9±13}/{2}$

$ x_1 = 11$

$ x_2 = -2$ (не подходит).

Ответ: 11

Задача 14

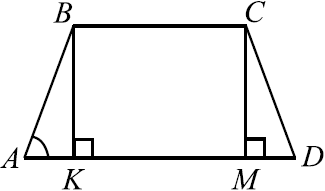
Основания равнобедренной трапеции равны $15$ и $9$. Высота трапеции равна $6$. Найдите тангенс острого угла.

Решение

Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ — высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.

$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {15 — 9}/{2} = 3, BK = 6$ (по условию). $tg ∠BAD = {6}/{3} = 2$.

Ответ: 2

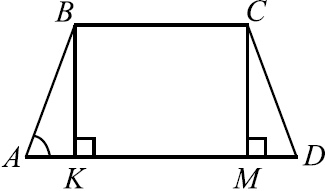
Задача 15

Основания равнобедренной трапеции равны $14$ и $6$. Высота трапеции равна $7$. Найдите тангенс острого угла.

Решение

Рассмотрим трапецию $ABCD$. Пусть $AB = CD, BK$ и $CM$ высоты. Тогда $AK = MD$ и $AD = BC + 2AK$.

$tg ∠BAD = {BK}/{AK}, AK = {AD — BC}/{2} = {14 — 6}/{2} = 4, BK = 7$ (по условию). $tg ∠BAD = {7}/{4} = 1.75$.

Ответ: 1.75

Задача 16

В треугольнике $ABC$ угол $C$ равен $90^°$, $AC=6√ {3}$, $tg A={√ {3}} / {3}$ (см. рис.). Найдите $AB$.

Решение

$tgA = {BC}/{AC}, {√3}/{3} = {BC}/{6√3}, BC = {6√3·√3}/{3} = 6$.

Из $△ABC: AB^2 = AC^2 + BC^2$;

$AB^2 = (6√3)^2 + 6^2 = 36·3 + 36 = 36·4 = 144, AB = 12$.

Ответ: 12

Задача 17

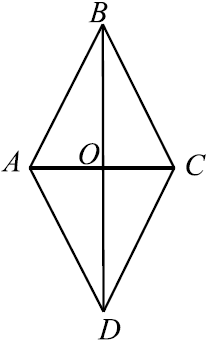
Найдите площадь ромба, если его диагонали равны $5$ и $16$.

Решение

Рассмотрим ромб $ABCD$.

$S_{ABCD} = {1}/{2}d_1d_2$, где $d_1$ и $d_2$ — диагонали ромба.

$S_{ABCD} = {1}/{2}·5·16 = 40$.

Ответ: 40

Задача 18

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $150^°$. Боковая сторона треугольника равна $12$. Найдите площадь этого треугольника.

Решение

Пусть в $△ABC ∠C = 150°, AC = CB$.

$S_{ACB} = {1}/{2}AC·CB·sin∠ACB = {1}/{2}·12·12·sin150° = 72·sin 30° =72·{1}/{2} = 36$.

Ответ: 36

Задача 19

Угол при вершине, противолежащей основанию равнобедренного треугольника, равен $30^°$. Боковая сторона треугольника равна $7$. Найдите площадь этого треугольника.

Решение

Пусть в $▵ ABC$ $∠ C=30°$, $AC=BC=7$ (см. рис.). $S_{ACB}={1} / {2} AC⋅ CB⋅ sin ∠ ACB={1} / {2}⋅ 7⋅ 7⋅ sin 30°={1} / {2}⋅ 49⋅ {1} / {2}={49} / {4}=12{,}25$.