ЗАДАНИЕ № 17. ( С 5 )
|
Содержание критерия |
Баллы. |
|
Обоснованно получен верный ответ. |
3 |
|
Верно построена математическая модель, решение сведено к исследованию этой модели, получен неверный ответ из-за вычислительной ошибки ИЛИ получен верный ответ, но решение недостаточно обосновано. |
2 |
|
Верно построена математическая модель и решение сведено к исследованию этой модели, при этом решение не завершено. |
1 |
|
Решение не соответствует ни одному из критериев, перечисленных выше. |
0 |
Задачи на сложные проценты:
I тип задач: на какой минимальный срок взят кредит.
II тип задач: под какой процент был взят кредит.
III тип задач: какую сумму взяли в кредит или сумма выплат по кредиту.
I тип задач: на какой минимальный срок взят кредит.
- Максим хочет взять кредит 1,5 млн. рублей. Погашение кредита происходит раз в год равными суммами (кроме, может быть последней), после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Максим взять кредит, чтобы ежегодные выплаты были бы не более 350 тыс. рублей?
Решение:
1) — остаток после первого погашения.
2) — остаток после второго погашения.
3) — остаток после третьего погашения.
4) — остаток после четвёртого погашения.
5) — остаток после пятого погашения.
6) — шестое погашение.
Ответ: 6 лет.
- 1 января 2015 года Андрей Владимирович взял в банке 1,1 млн. рублей в кредит. Схема выплат кредита следующая: 1 числа каждого следующего месяца банк начисляет 3% на оставшуюся сумму долга (то есть увеличивает долг на 3 %), затем Андрей Владимирович переводит в банк платёж. На какое минимальное количество месяцев Андрей Владимирович может взять кредит, чтобы ежемесячные выплаты были не более 220 тыс. рублей?
Решение:
1) остаток после первого погашения.
2) — остаток после второго погашения.
3) — остаток после третьего погашения.
4) — остаток после четвёртого погашения.
5) — остаток после пятого погашения.
6) шестое погашение кредита.
Ответ: 6 месяцев.
- Оля хочет взять в кредит 1 200 000 рублей. Погашение кредита происходит раз в год равными суммами ( кроме, может быть последней ) после начисления процентов. Ставка процентов 10 % годовых. На какое минимальное количество лет может Оля взять кредит, чтобы ежегодные выплаты были не более 320 000 рублей?
Решение:
|
Год |
Долг банку |
Остаток долга после выплат |
|
0 |
1 200 000 |
— |
|
1 |
1 200 000 |
1 320 000 — 320 000 = 1 000 000 |
|
2 |
1 000 000 |
1 000 000 — 320 000 = 780 000 |
|
3 |
780 000 |
858 000 — 320 000 = 538 000 |
|
4 |
538 000 |
591 800 — 320 000 = 271 800 |
|
5 |
271 800 |
0 |
Ответ: 5 лет
июнь 2015
4. В июле планируется взять кредит в банке на сумму 6 млн. рублей на некоторый срок. Условия его возврата таковы:
— каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. На какой минимальный срок следует брать кредит, чтобы наибольший годовой платёж по кредиту не превысил 1,8 млн. рублей?
Решение:
Пусть n срок, на который планируем взять кредит, тогда ежегодная сумма погашения составляет
( без начисления процентов). После первого погашения (т. е. в январе следующего года ) остаток по кредиту составит , после второго года
и т. д.
После начисления процентов на момент оформления кредита, долг банку составит , тогда по окончании первого года кредитования остаток увеличивается на 20% т. е.
.
Ежегодные выплаты банку находятся как разность между долгом банку и остатком по кредиту на данный момент. Составим таблицу по данным задачи:
|
Срок |
Кредит |
Долг |
Выплаты |
|
1 |
6 |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
… |
… |
… |
… |
По условию задачи, выплаты составляют арифметическую прогрессию, где и т.д. Наибольший годовой платёж по кредиту не превышает 1,8 млн. рублей или
Ответ: 10.
июнь 2015
5. В июле планируется взять кредит на сумму 20 млн. рублей на некоторый срок ( целое число лет). Условия его возврата таковы:
— каждый январь долг возрастает на 30 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась 47 млн. рублей?
Решение:
I способ:
|
Срок |
Кредит |
Долг |
Выплаты |
|
1 |
20 |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
…. |
… |
… |
|
|
Итого: |
47 |
Выплаты составляют арифметическую прогрессию, где
Ответ: 8 лет.
II способ:
Укажем общие формулы для решения задач этого типа. Пусть на n платежных периодов (дней, месяцев, лет) в кредит взята сумма S, причём каждый платежный период долг сначала возрастёт на r% по сравнению с концом предыдущего платежного периода, а затем вносится оплата так, что долг становится на одну и ту же сумму меньше долга на конец предыдущего платежного периода. Тогда величина переплаты П и полная величина выплат В за всё время выплаты кредита даются формулами
Ответ: 8 лет.
6. Гражданин Петров по случаю рождения сына открыл 1 сентября 2008 года в банке счёт, на который он ежегодно кладет 1000 рублей. По условиям вклада банк ежегодно начисляет 20% на сумму, находящуюся на счёте. Через 6 лет у гражданина Петрова родилась дочь, и 1 сентября 2014 года он открыл в другом банке счёт, на который ежегодно кладёт по 2200 рублей, а банк начисляет 44% в год. В каком году после очередного пополнения суммы вкладов сравняются, если деньги со счетов не снимают?
Решение:
Через n лет 1 сентября на первом счёте будет сумма
т.к. — сумма n — первых членов геометрической прогрессии, где
.
В это же время на втором счёте будет сумма
По условию задачи, суммы вкладов сравняются, тогда составляем уравнение:
Таким образом, суммы на счетах сравняются через 11 лет после открытия первого вклада то есть в 2019 году.
Ответ: 2019 году
7. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере
5 %, затем 12 %, потом и, наконец, 12,5 % в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на
. Определите срок хранения вклада.
Решение:
Пусть х рублей был первоначальный вклад (100 %), по истечении срока хранения первоначальная сумма вклада увеличилась на , то есть стала
от х или
.
По условию задачи,за время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5 %, затем 12 %, потом и, наконец, 12,5 % в месяц. Обозначим
целое число месяцев, соответствующей процентной ставки.
Из первого уравнения системы получаем, что . Из последнего уравнения системы получаем
, тогда
Ответ: 7 месяцев.
II тип задач: под какой процент был взят кредит.
8. 31 декабря 2014 года Борис взял в банке 1 млн. рублей в кредит. Схема выплаты следующая: 31 декабря каждого следующего года банк начисляет процент на оставшуюся сумму долга ( то есть увеличивает долг на определенное количество процентов), затем Борис переводит очередной транш. Борис выплатил кредит за два транша, переведя в первый раз 560 тыс. рублей, а во второй 644, 1 тыс. рублей. Под какой процент банк выдал кредит Борису?
Решение:
Пусть банк выдал кредит Борису под х% = 0,01х, тогда после начисления процентов Борис будет должен банку . После перевода первого транша сумма его долга станет
После перевода второго транша сумма долга будет равна нулю, тогда составляем уравнение:
— не удовлетворяет условию задачи.
Ответ: 13 %
июнь 2015
9. В июле планируется взять кредит в банке на сумму 100 000 рублей. Условия его возврата таковы:
— каждый январь долг возрастает на a% по сравнения с концом предыдущего года; — февраля по июнь каждого года необходимо выплатить часть долга. Найдите число a, если известно, что кредит был полностью погашен за два года, причём в первый год было переведено 55 000 рублей, а во второй год 69 000 рублей?
Решение:
Пусть банк выдал кредит под a% = 0,01a, тогда после начисления процентов долг банку будет. После перевода первого транша сумма его долга станет
После перевода второго транша сумма долга будет равна нулю, тогда составляем уравнение:
— не удовлетворяет условию задачи.
Ответ: 15 %
июнь 2015
10. В июле планируется взять кредит в банке на сумму 6 млн. рублей на срок 15 лет. Условия его возврата таковы:
— каждый январь долг возрастает на x% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же величину меньше долга за июль предыдущего года. Найти х, если известно, что наибольший годовой платёж по кредиту составит не более 1,9 млн. рублей, а наименьший — не менее 0,5 млн. рублей?
Решение:
|
Срок |
Кредит |
Долг |
Выплаты |
|
1 |
6 |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
… |
… |
||
|
15 |
|
|
|
По условию задачи: наибольший годовой платёж по кредиту составит не более 1,9 млн. рублей, а наименьший — не менее 0,5 млн. рублей.
Ответ: 25 %
июнь 2015
11. 15 — го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы: — 1 — го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число месяца необходимо выплатить часть долга; — 15 — го числа каждого месяца долг должен на одну и ту же сумму меньше долга на 15 — е число предыдущего месяца. Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит. Найти r.
Решение:
Iспособ:
Пусть первоначальная сумма кредита S.
|
Срок |
Кредит |
Долг |
Выплаты |
|
1 |
S |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
…. |
… |
… |
…. |
|
38 |
|
|
|
|
39 |
|
|
|
|
40 |
0 |
0 |
0 |
Сумма всех выплат составит:
Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит, тогда
или ( по формулам арифметической прогрессии )
тогда найдем разность прогрессии
Найдём сумму выплат по формуле суммы n — первых членов арифметической прогрессии
Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит, тогда
Ответ: 1%
II способ: Пусть — сумма долга в конце n — го месяца,
— первоначальная сумма долга.
, где
По условию задачи: сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц, тогда составляет арифметическую прогрессию, где
-формула n— го члена прогрессии.
Суммы выплат составляют арифметическую прогрессию.
Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит, тогда
Ответ: 1%
III способ:Укажем общие формулы для решения задач этого типа. Пусть на n платежных периодов (дней, месяцев, лет) в кредит взята сумма S, причём каждый платежный период долг сначала возрастёт на r% по сравнению с концом предыдущего платежного периода, а затем вносится оплата так, что долг становится на одну и ту же сумму меньше долга на конец предыдущего платежного периода. Тогда величина переплаты П и полная величина выплат В за всё время выплаты кредита даются формулами
По условию задачи
Ответ: 1 %
аналогичные задания:
— 15-го января планируется взять кредит в банке на 19 месяцев. Условия его возврата таковы:
— 1-го числа каждого месяца долг возрастёт на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число каждого месяца необходимо выплатить часть долга;
— 15-го числа каждого месяца долг должен быть на одну и ту же сумму меньше долга на 15-е число предыдущего месяца. Известно, что общая сумма выплат после полного погашения кредита на 30% больше суммы, взятой в кредит. Найдите r.
Ответ: 3 %
— Алексей взял кредит в банке на срок 12 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 13 % больше, чем сумма, взятая им в кредит. Найдите r.
Ответ: 2 %.
— Алексей взял кредит в банке на срок 17 месяцев. По договору Алексей должен вернуть кредит ежемесячными платежами. В конце каждого месяца к оставшейся сумме долга добавляется r % этой суммы и своим ежемесячным платежом Алексей погашает эти добавленные проценты и уменьшает сумму долга. Ежемесячные платежи подбираются так, чтобы долг уменьшался на одну и ту же величину каждый месяц (на практике такая схема называется «схемой с дифференцированными платежами»). Известно, что общая сумма, выплаченная Алексеем банку за весь срок кредитования, оказалась на 27 % больше, чем сумма, взятая им в кредит. Найдите r.
Ответ: 3 %.
12. 15 — го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг ( в % от кредита) |
100 % |
90 % |
80 % |
70 % |
60 % |
50 % |
40 % |
В конце каждого месяца, начиная с января, текущий долг увеличивается на 5 %, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
Решение:
Пусть 15 — го числа текущего месяца долг равен х рублей, а 15 го числа предыдущего месяца у рублей. Тогда в конце предыдущего месяца долг равен и выплата в первой половине текущего месяца равна
. В процентах отсуммы кредита выплаты в феврале составили
; в марте
в июне
Общая сумма выплат составила 15 + 14,5 + 14 + 13,5 + 13 + 52,5 = 122,5 %.
Ответ: 22,5 %
III тип задач: какую сумму взяли в кредит или сумма выплат по кредиту.
июнь 2015
13. В июле планируется взять кредит в банке на сумму 10 млн. рублей на 5 лет. Условия его возврата таковы:
— каждый январь долг возрастает на 10 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. Сколько млн. рублей составила общая сумма выплат после погашения кредита?
Решение:
|
год |
кредит |
долг |
Выплаты |
|
1 |
10 |
|
|
|
2 |
8 |
|
|
|
3 |
6 |
|
|
|
4 |
4 |
|
|
|
5 |
2 |
|
|
Найдем сумму всех выплат:.
Ответ: 13 млн. рублей.
июнь 2015
14. В июле планируется взять кредит на некоторую сумму. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга равную 2,16 млн. рублей. Сколько млн. рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за 3 года)?
Решение:
Пусть х рублей планируется взять в банке. Составим уравнение по условию задачи: долг был погашен тремя равными платежами по 2, 16 млн. рублей после начисления 20 % на оставшуюся сумму долга.
Ответ: 4,55 млн. рублей
15. 31 декабря 2014 года Сергей взял в банке некоторую сумму в кредит под 12 % годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг на 12 %), затем Сергей переводит в банк 3 512 320 рублей. Какую сумму взял Сергей в банке, если он выплатил долг тремя равными платежами ( то есть за три года)?
Решение:
Пусть х рублей взял Сергей в банке. Составим уравнение по условию задачи: долг был погашен тремя равными платежами по 3 512 320 рублей после начисления 12% на оставшуюся сумму долга.
Ответ: 8 436 000.
16. Жанна взяла в банке кредит 1,8 млн. рублей на срок 24 месяца. По договору Жанна должна возвращать в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?
Решение:
I способ:
|
Срок |
Кредит |
Долг |
Выплаты |
|
1 |
1,8 |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
…. |
… |
… |
Выплаты составляют арифметическую прогрессию, где
Ответ: 1,0665 млн. рублей.
IIспособ : Пусть — сумма долга в конце n — го месяца,
— первоначальная сумма долга.
, где
По условию задачи, надо найти сумму выплат Жанны за первый год кредитования, то есть
.
По условию задачи: сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц, тогда составляет арифметическую прогрессию, где
— формула n— го члена прогрессии.
Суммы выплат составляют арифметическую прогрессию.
.
Ответ: 1 066 500.
июнь 2015
17. В июле планируется взять кредит на сумму 8 052 000 рублей. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года; — с февраля по июнь каждого следующего года необходимо выплатить некоторую часть долга. Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами ( то есть за 4 года)?
Решение:
Пусть х рублей выплата по кредиту. Составим уравнение по условию задачи:погашение кредита за четыре года равными платежами по хруб. после начисления 20 % на оставшийся долг.
Ответ: 3 110 400
18. 31 декабря 2014 года Алексей взял в банке 9 282 000 рублей под 10 % годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет процент на оставшуюся сумму долга ( то есть увеличивает долг на 10 % ), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами ( за четыре года)?
Решение:
Пусть Х рублей выплата Алексея по кредиту. Составим уравнение по условию задачи:погашение кредита за четыре года равными платежами по х руб. после начисления 10 % на оставшийся долг.
Ответ: 2 928 200.
19. Фермер взял в банке кредит на сумму 3 640 000 рублей под 20% годовых. Схема погашения кредита: раз в год клиент выплачивает банку одну и ту же сумму, которая состоит из двух частей. Первая часть составляет 20 % от оставшейся суммы долга, а вторая часть направлена на погашение оставшейся суммы долга. Каждый следующий год проценты начисляются только на оставшуюся часть долга. Какой должна быть ежегодная сумма выплат ( в рублях ), чтобы фермер полностью погасил кредит тремя равными платежами?
Решение:
Пусть х рублей должна быть ежегодная сумма выплат. Составим уравнение по условию задачи:фермер взял в банке кредит на сумму 3 640 000 рублей под 20% годовых и погасил кредит тремя равными платежами.
Ответ: 1 728 000.
июнь 2015
20. В июле планируется взять кредит на сумму 4 026 000 рублей. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом прошлого года; — с февраля по июнь каждого года необходимо выплатить некоторую часть долга. На сколько рублей больше придётся отдать в случае, если кредит будет полностью погашен четырьмя равными платежами (то есть за 4 года ) по сравнению со случаем, если он будет полностью погашен двумя равными платежами ( то есть за 2 года )?
Решение:
I случай. Пусть по х рублей выплачивают , чтобы погасить кредит четырьмя равными платежами. Составим первое уравнение по условию задачи: кредит в размере 4 026 000 рублей под 20% годовых погасили четырьмя равными платежами.
II случай. Пусть по yрублей выплачивают, что бы погасить кредит двумя платежами. Составим второе уравнение по условию задачи: кредит в размере 4 026 000 рублей под 20% годовых погасили двумя равными платежами.
Вопрос задачи: на сколько рублей больше отдали бы банку, если бы выплатили долг за четыре равных платежа или найти разность
Ответ: 950 400.
21. 31 декабря 2014 года Фёдор взял в банке 6 951 000 рублей в кредит под 10 % годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляют проценты на оставшуюся сумму долга ( то есть увеличивает долг на 10 % ), затем Фёдор переводит в банк платёж. Весь долг Фёдор выплатил за три равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за два равных платежа?
Решение:
I случай. Пусть по х рублей выплачивал Фёдор, что бы погасить кредит тремя платежами. Составим первое уравнение по условию задачи: кредит в размере 6 951 000 рублей под 10% годовых он погасил тремя равными платежами.
II случай. Пусть по yрублей выплачивал Фёдор, чтобы погасить кредит двумя платежами. Составим второе уравнение по условию задачи: кредит в размере 6 951 000 рублей под 10% годовых он погасил двумя равными платежами.
Вопрос задачи: на сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за два равных платежа или найти разность
Ответ: 375 100.
Задачи на нахождение наибольшего или наименьшего значения.
досрочный 2015
1. Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно часов в неделю, то за эту неделю они производят 2t единиц товара, если рабочие на заводе, расположенном во втором городе, трудятся суммарно
часов в неделю, то за эту неделю они производят 5t единиц товара. За каждый час работы ( на каждом из заводов ) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 580 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?
Решение:
Пусть количество единиц товара, произведённого на первом заводе 2х, а на втором заводе 5у. (Тогда за неделю нужно произвести 580 единиц товара или
За каждый час работы Владимир платит рабочему 500 рублей, тогда составим функцию
и исследуем её на наименьшее значение.
Выразим из первого уравнения у через х:
— точка минимума.
Ответ: 5 800 000.
досрочный 2015
2. Антон является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, платит 200 рублей. Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Решение:
Пусть количество единиц товара, произведённого на первом заводе х и суммарные затраты времени будут .Тогда количество единиц товара, произведённого на втором заводе y и суммарные затраты времени будут
. Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, платит 200 рублей и готов выделять 900 000 рублей в неделю на оплату труда рабочих, тогда получаем уравнение
.
Составим функцию количества единиц товара за неделю на двух заводах: .
Выразим из первого уравнения у через х: (
— точка максимума.
Ответ: 90.
досрочный 2015
3. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно часов в неделю, то за эту неделю они производят 3t единиц товара, если рабочие на заводе, расположенном во втором городе, трудятся суммарно
часов в неделю, то за эту неделю они производят 4t единиц товара. За каждый час работы ( на каждом из заводов ) Григорий платит рабочему 500 рублей. Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
Решение:
Пусть количество единиц товара, произведённого на первом заводе 3х и суммарные затраты времени будут . Тогда количество единиц товара, произведённого на втором заводе 4y и суммарные затраты времени будут
. Григорий платит рабочему 500 рублей и готов выделять 5 000 000 рублей в неделю на оплату труда рабочих, тогда получаем уравнение
. или
Составим функцию количества единиц товара за неделю на двух заводах: .
Выразим из первого уравнения у через х: (
— точка максимума.
Ответ: 400.
4. Первичная информация разделяется по серверам № 1 и № 2 и обрабатывается на них. С сервера № 1 при объёме гб. входящей в него информации выходит 20t , с сервера № 2 при объёме
гб. входящей в него информации выходит 21tгб обработанной информации;
Каков наибольший общий объём выходящей информации при общем объёме входящей информации в 3364 гб?
Решение:
Пусть на севере № 1 обрабатывается , а на сервере № 2 обрабатывается
гб. из всей первичной информации. Тогда общий объём входящей информации 3364 гб., тогда
. Всего обработано будет
гб. информации. Исследуем эту функцию на наибольшее значение.
— точка максимума.
Ответ: 1 682.
июнь 2015
5. Зависимость объёма Q ( в шт.) купленного у фирмы товара по цене Р ( в рублях за штуку) выражается формулой Доход от продажи товара составляет
рублей. Затраты на производство Qединиц товара составляют
рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство. Стремясь привлечь внимание покупателей, фирма уменьшила цену на продукцию на 20 %, однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?
Решение:
|
Цена товара. |
P |
|
Объём товара. |
Q |
|
Доход от продажи |
|
|
Затраты на производство. |
|
|
Прибыль. |
|
Рассмотрим функцию: прибыль в зависимости от цены товара.
— это квадратичная функция, графиком, которой является парабола, принимающая наибольшее значение в вершине. Ось симметрии параболы: прямая, параллельная оси ординат и проходящая через вершину параболы. Вершина параболы соответствует 90% цены, так как прибыль не изменилась, когда цену уменьшили на 20 %, тогда составляем пропорцию:
Ответ: 12,5 %
6. В первые классы поступают 43 человека: 23 мальчика и 20 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом — 21. После распределения посчитали процент мальчиков в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?
Решение:
Пусть в меньший класс ( 21 человек) распределено х мальчиков ( . Тогда в больший класс попало ( 23 — х ) мальчиков.
Суммарная доля мальчиков в двух классах
— линейная функция с положительным угловым коэффициентом. Значит, эта функция достигает своего наибольшего значения на правом конце промежутка [ 1; 21 ] , то есть при х = 21. Таким образом, меньший класс полностью должен состоять из мальчиков, а в большем классе должно быть 20 девочек и 2 мальчика.
Ответ: В одном классе — 21 мальчик, в другом — 20 девочек и 2 мальчика.
7. Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера » люкс » площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2 000 рублей в сутки, а номер » люкс » — 4 000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель?
Решение:
|
Номера |
Площадь номера |
Количество номеров |
Общая площадь |
Стоимость в сутки |
Доход номера |
|
Обычный |
27 |
x |
27x |
2 000 |
2000x |
|
Люкс |
45 |
y |
45y |
4 000 |
4000y |
Составим уравнения по условию задачи: Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр.
Найдём общую прибыль номеров в сутки: Выразим из первого уравнения y:
( 1
линейная функция с отрицательным угловым коэффициентом. Значит, эта функция достигает своего наибольшего значения на левом конце промежутка ( при минимальном количестве обычных номеров ), то есть при х = 3, тогда y = 20. (
Ответ: 86 000 рублей.
аналогичная задача:
Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера » люкс » площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 855 квадратных метров. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2 000 рублей в сутки, а номер » люкс » — 3 000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель?
Ответ: 63 000 рублей.
8. В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 3 кг никеля. Во второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 1 кг никеля. Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог производить наибольшее количество сплава. Сколько сплава при таких условиях сможет произвести завод?
Решение:
Пусть за х часов на I шахте добывают алюминий, а за у часов на II шахте добывают алюминий.
|
Количество рабочих |
Суммарное время работы |
Добыча алюминия |
Добыча никеля |
|
|
I шахта |
100 |
500 |
|
|
|
II шахта |
300 |
1500 |
|
|
|
Итого: |
|
|
Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. Тогда составляем уравнение:
При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог производить наибольшее количество сплава. Рассмотрим функцию сплава:
Функция является убывающей, тогда наибольшее значение она достигает при наименьшем значении х,
при х = 0 S = 5 400.
Ответ: 5 400.
9. На каждом из двух комбинатов изготавливают детали А и В. На первом комбинате работает 40 человек, и один рабочий изготавливает за смену 5 деталей А или 15 деталей В. На втором комбинате работает 100 человек, и один рабочий изготавливает за смену 15 деталей А или 5 деталей В. Оба эти комбината поставляют детали на комбинат, из которых собирают изделие, для изготовления которого нужна 2 детали А и 1 деталь В. При этом комбинаты договариваются между собой изготавливать деталь так, чтобы можно было собрать наибольшее количество изделий. Сколько изделий при таких условиях может собрать комбинат за смену?
Решение:
|
Количество рабочих |
Деталь |
Количество деталей за смену ( 1 рабочий ) |
Количество рабочих |
Количество всех деталей за смену |
|
|
I комбинат |
40 |
А |
5 |
х |
5х |
|
В |
15 |
40 — х |
15(40 — х) |
||
|
II комбинат |
100 |
А |
15 |
у |
15у |
|
В |
5 |
100 — у |
5( 100 — у) |
||
|
Итого: |
А |
5х + 15у |
|||
|
В |
15(40 — х ) + 5(100 — у ) = 1 100 — 15х — 5у |
Оба эти комбината поставляют детали на комбинат, из которых собирают изделие, для изготовления которого нужна 2 детали А и 1 деталь В.
Рассмотрим функцию количества изделий из этих деталей:
Линейная функция с отрицательным угловым коэффициентом, будет достигать наибольшего значения при минимальном х .
Ответ: 1980
10. У фермера есть два поля, каждое площадью по 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц /га, а на втором 200 ц / га. Урожайность свёклы на первом поле составляет 200 ц / га, на втором 300 ц / га. Ферме может продавать картофель по цене 4 000 рублей за центнер, а свёклу по цене 5 000 рублей за центнер. Какой наибольший доход может получить фермер?
Решение:
|
Урожайность |
Площадь |
Цена |
||
|
I поле |
картофель |
300 |
x |
4 000 |
|
свёкла |
200 |
10- x |
5 000 |
|
|
II поле |
картофель |
200 |
y |
4 000 |
|
свёкла |
300 |
10 — y |
5 000 |
Составим функцию по условию задачи:
Наибольшего значение будет достигаться при у = 0, х = 10.
S =
Ответ: 27 000 000 рублей.
1 1. Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10 %. Втечение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
Решение:
Первоначальная стоимость ценной бумаги 7 тыс. рублей, цена бумаги возрастает каждый год на 2 тыс. рублей. Тогда рассматриваем арифметическую прогрессию, где
Нам надо найти номер максимального члена последовательности , где n — целое число,
;
Ответ: в течение восьмого года.
аналогичная задача:
Алексей приобрёл ценную бумагу за 8 тыс. рублей. Цена бумаги каждый год возрастает на 1 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 8 %. Втечение какого года после покупки Алексей должен продать ценную бумагу, чтобы через двадцать пять лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
Ответ: в течение шестого года.
июнь 2015
1 2. Строительство нового завода стоит 78 млн. рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны млн. рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы ( в млн. рублей) за один год составит
. Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более , чем за 3 года ?
Решение:
По условию задачи строительство завода должно окупиться не более, чем за три года. Так как годовая прибыль вычисляется по формуле тогда
;
Выразим p через х: . Исследуем эту функцию на наименьшее значение.
— точка минимума
Ответ: 10.
13. Производство х тыс. единиц продукции обходится в млн. рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции ( в млн. рублей ) составляет
При каком наименьшем значении p через три года суммарная прибыль составит не менее 75 млн. рублей?
Решение:
По условию задачи через три года суммарная прибыль должна быть не менее 75 млн. рублей. Так как годовая прибыль вычисляется по формуле тогда
;
Выразим p через х: . Исследуем эту функцию на наименьшее значение.
— точка минимума
Ответ: 9.
аналогичная задача:
— Производство х тыс. единиц продукции обходится в млн. рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции ( в млн. рублей ) составляет
При каком наименьшем значении p через четыре года суммарная прибыль составит не менее 52 млн. рублей?
Ответ: 6
Раздаточный материал:
ЗАДАНИЕ № 17.
|
Содержание критерия |
Баллы. |
|
Обоснованно получен верный ответ. |
3 |
|
Верно построена математическая модель, решение сведено к исследованию этой модели, получен неверный ответ из-за вычислительной ошибки ИЛИ получен верный ответ, но решение недостаточно обосновано. |
2 |
|
Верно построена математическая модель и решение сведено к исследованию этой модели, при этом решение не завершено. |
1 |
|
Решение не соответствует ни одному из критериев, перечисленных выше. |
0 |
I тип задач: на какой минимальный срок взят кредит.
1. Максим хочет взять кредит 1,5 млн. рублей. Погашение кредита происходит раз в год равными суммами ( кроме, может быть последней), после начисления процентов. Ставка процента 10% годовых. На какое минимальное количество лет может Максим взять кредит, чтобы ежегодные выплаты были бы не более 350 тыс. рублей?
2. 1 января 2015 года Андрей Владимирович взял в банке 1,1 млн. рублей в кредит. Схема выплат кредита следующая: 1 числа каждого следующего месяца банк начисляет 3% на оставшуюся сумму долга ( то есть увеличивает долг на 3 %), затем Андрей Владимирович переводит в банк платёж. На какое минимальное количество месяцев Андрей Владимирович может взять кредит.чтобы ежемесячные выплаты были не более 220 тыс. рублей?
3. Оля хочет взять в кредит 1 200 000 рублей. Погашение кредита происходит раз в год равными суммами ( кроме , может быть последней ) после начисления процентов. Ставка процентов 10 % годовых. На какое минимальное количество лет может Оля взять кредит, чтобы ежегодные выплаты были не более 320 000 рублей?
4. В июле планируется взять кредит в банке на сумму 6 млн. рублей на некоторый срок. Условия его возврата таковы: — каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. На какой минимальный срок следует брать кредит, чтобы наибольший годовой платёж по кредиту не превысил 1,8 млн. рублей?
5. В июле планируется взять кредит на сумму 20 млн. рублей на некоторый срок ( целое число лет). Условия его возврата таковы: — каждый январь долг возрастает на 30 % по сравнению с концом предыдущего года; — с февраля по июнь каждого года необходимо выплатить часть долга; — в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. На сколько лет был взят кредит, если известно, что общая сумма выплат после его погашения равнялась 47 млн. рублей?
6. Гражданин Петров по случаю рождения сына открыл 1 сентября 2008 года в банке счёт, на который он ежегодно кладет 1000 рублей. По условиям вклада банк ежегодно начисляет 20% на сумму, находящуюся на счёте. Через 6 лет у гражданина Петрова родилась дочь, и 1 сентября 2014 года он открыл в другом банке счёт, на который ежегодно кладёт по 2200 рублей, а банк начисляет 44% в год. В каком году после очередного пополнения суммы вкладов сравняются, если деньги со счетов не снимают?
7. За время хранения вклада в банке проценты по нему начислялись ежемесячно сначала в размере 5 %, затем 12 %, потом и, наконец, 12,5 % в месяц. Известно, что под действием каждой новой процентной ставки вклад находился целое число месяцев, а по истечении срока хранения первоначальная сумма вклада увеличилась на
. Определите срок хранения вклада.
II тип задач: под какой процент был взят кредит.
8. 31 декабря 2014 года Борис взял в банке 1 млн. рублей в кредит. Схема выплаты следующая: 31 декабря каждого следующего года банк начисляет процент на оставшуюся сумму долга ( то есть увеличивает долг на определенное количество процентов), затем Борис переводит очередной транш. Борис выплатил кредит за два транша, переведя в первый раз 560 тыс. рублей, а во второй 644, 1 тыс. рублей. Под какой процент банк выдал кредит Борису?
9. В июле планируется взять кредит в банке на сумму 100 000 рублей. Условия его возврата такова:
— каждый январь долг возрастает на a% по сравнения с концом предыдущего года;
— февраля по июнь каждого года необходимо выплатить часть долга. Найдите число a, если известно, что кредит был полностью погашен за два года, причём в первый год было переведено 55 000 рублей, а во второй год 69 000 рублей?
10. В июле планируется взять кредит в банке на сумму 6 млн. рублей на срок 15 лет. Условия его возврата таковы: — каждый январь долг возрастает на x% по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга за июль предыдущего года. Найти х, если известно, что наибольший годовой платёж по кредиту составит не более 1,9 млн. рублей.а наименьший — не менее 0,5 млн. рублей?
11. 15 — го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы:
— 1 — го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число месяца необходимо выплатить часть долга;
— 15 — го числа каждого месяца долг должен на одну и ту же сумму меньше долга на 15 — е число предыдущего месяца. Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит. Найти r.
12. 15 — го января был выдан полугодовой кредит на развитие бизнеса. В таблице представлен график его погашения.
|
Дата |
15.01 |
15.02 |
15.03 |
15.04 |
15.05 |
15.06 |
15.07 |
|
Долг ( в % от кредита) |
100 % |
90 % |
80 % |
70 % |
60 % |
50 % |
40 % |
В конце каждого месяца, начиная с января, текущий долг увеличивается на 5 %, а выплаты по погашению кредита происходили в первой половине каждого месяца, начиная с февраля. На сколько процентов общая сумма выплат при таких условиях больше суммы самого кредита?
III тип задач: какую сумму взяли в кредит или сумма выплат по кредиту.
13. В июле планируется взять кредит в банке на сумму 10 млн. рублей на 5 лет. Условия его возврата таковы: — каждый январь долг возрастает на 10 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга;
— в июле каждого года долг должен быть на одну и ту же величину меньше долга на июль предыдущего года. Сколько млн. рублей составила общая сумма выплат после погашения кредита?
14. В июле планируется взять кредит на некоторую сумму. Условия его возврата таковы:
— каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого года необходимо выплатить часть долга равную 2,16 млн. рублей. Сколько млн. рублей было взято в банке, если известно, что он был полностью погашен тремя равными платежами ( то есть за 3 года)?
15. 31 декабря 2014 года Сергей взял в банке некоторую сумму в кредит под 12 % годовых. Схема выплаты кредита следующая: 31 декабря каждого следующего года банк начисляет проценты на оставшуюся сумму долга ( то есть увеличивает долг на 12 %), затем Сергей переводит в банк 3 512 320 рублей. Какую сумму взял Сергей в банке, если он выплатил долг тремя равными платежами ( то есть за три года)?
16. Жанна взяла в банке кредит 1,8 млн. рублей на срок 24 месяца. По договору Жанна должна возвращать в банк часть денег в конце каждого месяца. Каждый месяц общая сумма долга возрастает на 1 %, а затем уменьшается на сумму, уплаченную Жанной банку в конце месяца. Суммы, выплачиваемые Жанной, подбираются так, чтобы сумма долга уменьшалась равномерно, то есть на одну и ту же величину каждый месяц. Какую сумму Жанна вернёт банку в течение первого года кредитования?
17. В июле планируется взять кредит на сумму 8 052 000 рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 20 % по сравнению с концом предыдущего года;
— с февраля по июнь каждого следующего года необходимо выплатить некоторую часть долга. Сколько рублей нужно платить ежегодно, чтобы кредит был полностью погашен четырьмя равными платежами ( то есть за 4 года)?
18. 31 декабря 2014 года Алексей взял в банке 9 282 000 рублей под 10 % годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляет процент на оставшуюся сумму долга ( то есть увеличивает долг на 10 % ), затем Алексей переводит в банк Х рублей. Какой должна быть сумма Х, чтобы Алексей выплатил долг четырьмя равными платежами ( за четыре года)?
19. Фермер взял в банке кредит на сумму 3 640 000 рублей под 20% годовых. Схема погашения кредита: раз в год клиент выплачивает банку одну и ту же сумму, которая состоит из двух частей. Первая часть составляет 20 % от оставшейся суммы долга, а вторая часть направлена на погашение оставшейся суммы долга. Каждый следующий год проценты начисляются только на оставшуюся часть долга. Какой должна быть ежегодная сумма выплат ( в рублях ), чтобы фермер полностью погасил кредит тремя равными платежами?
20. В июле планируется взять кредит на сумму 4 026 000 рублей. Условия его возврата таковы:
— каждый январь долг возрастает на 20 % по сравнению с концом прошлого года;
— с февраля по июнь каждого года необходимо выплатить некоторую часть долга. На сколько рублей больше придётся отдать в случае, если кредит будет полностью погашен четырьмя равными платежами ( то есть за 4 года ) по сравнению со случаем, если он будет полностью погашен двумя равными платежами ( то есть за 2 года )?
21. 31 декабря 2014 года Фёдор взял в банке 6 951 000 рублей в кредит под 10 % годовых. Схема выплат кредита следующая: 31 декабря каждого следующего года банк начисляют проценты на оставшуюся сумму долга ( то есть увеличивает долг на 10 % ), затем Фёдор переводит в банк платёж. Весь долг Фёдор выплатил за три равных платежа. На сколько рублей меньше он бы отдал банку, если бы смог выплатить долг за два равных платежа?
Задачи на нахождение наибольшего или наименьшего значения.
1. Владимир является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно часов в неделю, то за эту неделю они производят 2t единиц товара, если рабочие на заводе, расположенном во втором городе, трудятся суммарно
часов в неделю, то за эту неделю они производят 5t единиц товара. За каждый час работы ( на каждом из заводов ) Владимир платит рабочему 500 рублей. Владимиру нужно каждую неделю производить 580 единиц товара. Какую наименьшую сумму придётся тратить еженедельно на оплату труда рабочих?
2. Антон является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары при использовании одинаковых технологий. Если рабочие на одном из заводов трудятся суммарно часов в неделю, то за эту неделю они производят t единиц товара. За каждый час работы на заводе, расположенном в первом городе, Антон платит рабочему 250 рублей, а на заводе, расположенном во втором городе, платит 200 рублей. Антон готов выделять 900 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
3. Григорий является владельцем двух заводов в разных городах. На заводах производятся абсолютно одинаковые товары, но на заводе, расположенном во втором городе, используется более совершенное оборудование. В результате, если рабочие на заводе, расположенном в первом городе, трудятся суммарно часов в неделю, то за эту неделю они производят 3t единиц товара, если рабочие на заводе, расположенном во втором городе, трудятся суммарно
часов в неделю, то за эту неделю они производят 4t единиц товара. За каждый час работы ( на каждом из заводов ) Григорий платит рабочему 500 рублей. Григорий готов выделять 5 000 000 рублей в неделю на оплату труда рабочих. Какое наибольшее количество единиц товара можно произвести за неделю на этих двух заводах?
4. Первичная информация разделяется по серверам № 1 и № 2 и обрабатывается на них. С сервера № 1 при объёме гб. входящей в него информации выходит 20t , с сервера № 2 при объёме
гб. входящей в него информации выходит 21tгб. обработанной информации;
Каков наибольший общий объём выходящей информации при общем объёме входящей информации в 3364 гб.?
5. Зависимость объёма Q ( в шт.) купленного у фирмы товара по цене Р ( в рублях за штуку) выражается формулой Доход от продажи товара составляет
рублей. Затраты на производство Q единиц товара составляют
рублей. Прибыль равна разности дохода от продажи товара и затрат на его производство.стремясь привлечь внимание покупателей, фирма уменьшила цену на продукцию на 20 %, однако её прибыль не изменилась. На сколько процентов следует увеличить сниженную цену, чтобы добиться наибольшей прибыли?
6. В первые классы поступают 43 человека: 23 мальчика и 20 девочек. Их распределили по двум классам: в одном должно получиться 22 человека, а в другом — 21. После распределения посчитали процент мальчиков в каждом классе и полученные числа сложили. Каким должно быть распределение по классам, чтобы полученная сумма была наибольшей?
7. Предприниматель купил здание и собирается открыть в нём отель. В отеле могут быть стандартные номера площадью 27 квадратных метров и номера » люкс » площадью 45 квадратных метров. Общая площадь, которую можно отвести под номера, составляет 981 квадратный метр. Предприниматель может поделить эту площадь между номерами различных типов, как хочет. Обычный номер будет приносить отелю 2 000 рублей в сутки, а номер » люкс » — 4 000 рублей в сутки. Какую наибольшую сумму денег сможет заработать в сутки на своём отеле предприниматель?
8. В двух шахтах добывают алюминий и никель. В первой шахте имеется 100 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 1 кг алюминия или 3 кг никеля. В второй шахте имеется 300 рабочих, каждый из которых готов трудиться 5 часов в день. При этом один рабочий за час добывает 3 кг алюминия или 1 кг никеля. Обе шахты поставляют добытый металл на завод, где для нужд промышленности производится сплав алюминия и никеля, в котором на 2 кг алюминия приходится 1 кг никеля. При этом шахты договариваются между собой вести добычу металлов так, чтобы завод мог производить наибольшее количество сплава. Сколько сплава при таких условиях сможет произвести завод?
9. На каждом из двух комбинатов изготавливают детали А и В. На первом комбинате работает 40 человек, и один рабочий изготавливает за смену 5 деталей А или 15 деталей В. На втором комбинате работает 100 человек, и один рабочий изготавливает за смену 15 деталей А или 5 деталей В. Оба эти комбината поставляют детали на комбинат, из которых собирают изделие, для изготовления которого нужна 2 детали А и 1 деталь В. При этом комбинаты договариваются между собой изготавливать деталь так, чтобы можно было собрать наибольшее количество изделий. Сколько изделий при таких условиях может собрать комбинат за смену?
10. У фермера есть два поля, каждое площадью по 10 гектаров. На каждом поле можно выращивать картофель и свёклу, поля можно делить между этими культурами в любой пропорции. Урожайность картофеля на первом поле составляет 300 ц /га, а на втором 200 ц / га. Урожайность свёклы на первом поле составляет 200 ц / га, на втором 300 ц / га. Ферме может продавать картофель по цене 4 000 рублей за центнер, а свёклу по цене 5 000 рублей за центнер. Какой наибольший доход может получить фермер?
11. Алексей приобрёл ценную бумагу за 7 тыс. рублей. Цена бумаги каждый год возрастает на 2 тыс. рублей. В любой момент Алексей может продать бумагу и положить вырученные деньги на банковский счёт. Каждый год сумма на счёте будет увеличиваться на 10 %. В течение какого года после покупки Алексей должен продать ценную бумагу, чтобы через тридцать лет после покупки этой бумаги сумма на банковском счёте была наибольшей?
12. Строительство нового завода стоит 78 млн. рублей. Затраты на производство х тыс. ед. продукции на таком заводе равны млн. рублей в год. Если продукцию завода продать по цене р тыс. рублей за единицу, то прибыль фирмы ( в млн. рублей) за один год составит
. Когда завод будет построен, фирма будет выпускать продукцию в таком количестве, чтобы прибыль была наибольшей. При каком наименьшем значении р строительство завода окупится не более , чем за 3 года ?
13. Производство х тыс. единиц продукции обходится в млн. рублей в год. При цене p тыс. рублей за единицу годовая прибыль от продажи этой продукции ( в млн. рублей ) составляет
При каком наименьшем значении p через три года суммарная прибыль составит не менее 75 млн. рублей?
июнь 2015
11. 15 — го января планируется взять кредит в банке на 39 месяцев. Условия его возврата таковы: — 1 — го числа каждого месяца долг возрастает на r% по сравнению с концом предыдущего месяца;
— со 2-го по 14-е число месяца необходимо выплатить часть долга; — 15 — го числа каждого месяца долг должен на одну и ту же сумму меньше долга на 15 — е число предыдущего месяца. Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит. Найти r.
Решение:
I способ:
Пусть первоначальная сумма кредита S.
|
Срок |
Кредит |
Долг |
Выплаты |
|
1 |
S |
|
|
|
2 |
|
|
|
|
3 |
|
|
|
|
4 |
|
|
|
|
…. |
… |
… |
…. |
|
38 |
|
|
|
|
39 |
|
|
|
|
40 |
0 |
0 |
0 |
Сумма всех выплат составит:
Известно, что общая сумма после полного погашения кредита на 20 % больше суммы, взятой в кредит, тогда
Ответ: 1%
ЕГЭ Профиль №8. Рациональные уравнения и неравенства
Скачать файл в формате pdf.
ЕГЭ Профиль №8. Рациональные уравнения и неравенства
| Задача 1. При температуре ({0^ circ }{text{C}}) рельс имеет длину ({l_0} = 10) м. При возрастании температуры происходит тепловое расширение рельса, и его длина, выраженная в метрах, меняется по закону (lleft( {{t^ circ }} right) = {l_0}left( {1 + alpha cdot {t^ circ }} right)), где (alpha = 1,2 cdot {10^{ — 5}}{left( {{}^ circ {text{C}}} right)^{ — 1}}) — коэффициент теплового расширения, ({t^ circ }) — температура (в градусах Цельсия). При какой температуре рельс удлинится на 3 мм? Ответ выразите в градусах Цельсия.
Ответ
ОТВЕТ: 25. Решение
l – длина рельса. Так как рельс должен удлиниться на 3 мм, то его длина будет равна: l = 10 м + 3 мм = 10 м + 0,003 м = 10,003 м. (10,003 = 10left( {1 + 1,2 cdot {{10}^{ — 5}} cdot {t^ circ }} right)) (10,003 = 10 + 12 cdot {10^{ — 5}} cdot {t^ circ }) (12 cdot {10^{ — 5}} cdot {t^ circ } = 0,003) ({t^ circ } = frac{{0,003}}{{12 cdot {{10}^{ — 5}}}} = frac{{0,003 cdot {{10}^5}}}{{12}} = frac{{300}}{{12}} = 25) Ответ: 25. |
| Задача 2. Некоторая компания продает свою продукцию по цене (p = 500) руб. за единицу, переменные затраты на производство одной единицы продукции составляют (v = 300) руб., постоянные расходы предприятия (f = 700,,000) руб. в месяц. Месячная операционная прибыль предприятия (в рублях) вычисляется по формуле ( pileft( q right) = qleft( {p — v} right) — f. ) Определите наименьший месячный объeм производства q (единиц продукции), при котором месячная операционная прибыль предприятия будет не меньше 300 000 руб.
Ответ
ОТВЕТ: 5 000. Решение
(pi left( q right)) – операционная прибыль предприятия должна быть не меньше 300 000 руб. Следовательно, (pi left( q right) geqslant 300,,000) (qleft( {500 — 300} right) — 700,,000 geqslant 300,,000) (200,q geqslant 1,,000,,000) (q geqslant 5,,000) Наименьший месячный объём производства: (q = 5,,000.) Ответ: 5 000. |
| Задача 3. После дождя уровень воды в колодце может повыситься. Мальчик измеряет время t падения небольших камешков в колодец и рассчитывает расстояние до воды по формуле (h = 5,{t^2}), где h — расстояние в метрах, t — время падения в секундах. До дождя время падения камешков составляло 0,6 с. На сколько должен подняться уровень воды после дождя, чтобы измеряемое время изменилось на 0,2 с? Ответ выразите в метрах.
Ответ
ОТВЕТ: 1. Решение
До дождя время падения камешков: ({t_1} = 0,6,,c.) Тогда до дождя расстояние до воды: ({h_1} = 5 cdot {0,6^2} = 1,8,) м. Так как уровень воды после дождя поднялся, то время падения камешков уменьшится на 0,2 с; то есть: ({t_2} = 0,6 — 0,2 = 0,4,,c.) Тогда после дождя расстояние до воды: ({h_2} = 5 cdot {0,4^2} = 0,8,) м. Следовательно, уровень воды должен подняться на: (vartriangle h = {h_1} — {h_2} = 1,8 — 0,8 = 1,) м. Ответ: 1. |
| Задача 4. Зависимость объeма спроса q (единиц в месяц) на продукцию предприятия-монополиста от цены p (тыс. руб.) задаeтся формулой (q = 100 — 10p). Выручка предприятия за месяц r (в тыс. руб.) вычисляется по формуле (rleft( p right) = q cdot p). Определите наибольшую цену p, при которой месячная выручка (rleft( p right)) составит не менее 240 тыс. руб. Ответ приведите в тыс. руб.
Ответ
ОТВЕТ: 6. Решение
Задача сводится к решению неравенства: (rleft( p right) geqslant 240;,,,,,,q cdot p geqslant 240;,,,,pleft( {100 — 10p} right) geqslant 240) ( — 10{p^2} + 100p — 240 geqslant 0,,|,,:,left( { — 10} right)) ({p^2} — 10p + 24 leqslant 0) ({p^2} — 10p + 24 = 0;,,,,{p_1} = 4,,,,,,{p_2} = 6) Ответ: 6. |
| Задача 5. Высота над землeй подброшенного вверх мяча меняется по закону (hleft( t right) = 1,6 + 8t — 5{t^2}), где h — высота в метрах, t — время в секундах, прошедшее с момента броска. Сколько секунд мяч будет находиться на высоте не менее трeх метров?
Ответ
ОТВЕТ: 1,2. Решение
Так как мяч должен находиться на высоте не менее трёх метров, то задача сводится к решению неравенства: (hleft( t right) geqslant 3). (1,6 + 8t — 5{t^2} geqslant 3) (5{t^2} — 8t + 1,4 leqslant 0) (5{t^2} — 8t + 1,4 = 0;,,,,,,{t_1} = 0,2,,,,,,,{t_2} = 1,4) Ответ: 1,2. |
| Задача 6. Если достаточно быстро вращать ведeрко с водой на верeвке в вертикальной плоскости, то вода не будет выливаться. При вращении ведeрка сила давления воды на дно не остаeтся постоянной: она максимальна в нижней точке и минимальна в верхней. Вода не будет выливаться, если сила еe давления на дно будет положительной во всех точках траектории кроме верхней, где она может быть равной нулю. В верхней точке сила давления, выраженная в ньютонах, равна (P = mleft( {frac{{{v^2}}}{L} — g} right)), где m — масса воды в килограммах, v — скорость движения ведёрка в м/с, L — длина верёвки в метрах, g — ускорение свободного падения (считайте (g = 10) м/с2). С какой наименьшей скоростью надо вращать ведeрко, чтобы вода не выливалась, если длина верeвки равна 40 см? Ответ выразите в м/с.
Ответ
ОТВЕТ: 2. Решение
Вода не будет выливаться, если (Pleft( v right) geqslant 0.) Следовательно, задача сводится к решению неравенства: (mleft( {frac{{{v^2}}}{L} — g} right) geqslant 0). Так как m > 0, то (frac{{{v^2}}}{L} — g geqslant 0), где g = 10 м/c2 и L = 40 см = 0,4 м. (frac{{{v^2}}}{{0,4}} — 10 geqslant 0;,,,,,,,,{v^2} geqslant 4) Следовательно, (v in left( { — infty ;, — 2} right] cup left[ {2;,infty } right)), но так как v > 0, то (v in left[ {2;,infty } right)). Наименьшая скорость v = 2 м/с. Ответ: 2. |
| Задача 7. В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону (Hleft( t right) = {H_0} — sqrt {2g{H_0}} ,k,t + frac{g}{2}{k^2}{t^2}), где t — время в секундах, прошедшее с момента открытия крана, ({H_0} = 20) м — начальная высота столба воды, (k = frac{1}{{50}}) — отношение площадей поперечных сечений крана и бака, а g — ускорение свободного падения (считайте (g = 10) м/с2). Через сколько секунд после открытия крана в баке останется четверть первоначального объeма воды?
Ответ
ОТВЕТ: 50. Решение
Так как в баке должна остаться четверть первоначального объёма воды, то (H = frac{1}{4}{H_0} = frac{1}{4} cdot 20 = 5). (frac{g}{2}{k^2}{t^2} — sqrt {2g{H_0}} ,k,t + {H_0} = H) Пусть k t = x. Тогда: (frac{{10}}{2}{x^2} — sqrt {2 cdot 10 cdot 20} ,x + 20 = 5) (5{x^2} — 20,x + 15 = 0,,|,,:,,,5,,,,,,,,, Leftrightarrow ,,,,,,,,,{x^2} — 4,x + 3 = 0,) ({x_1} = 1;,,,,,,,,,,,,,,,,,,,,,,{x_2} = 3) (k,t = 1;,,,,,,,,,,,,,,,,,,,,k,t = 3) (frac{1}{{50}},t = 1;,,,,,,,,,,,,,,,,,,,,frac{1}{{50}},t = 3) (,{t_1} = 50;,,,,,,,,,,,,,,,,,,,,,{t_2} = 150) Следовательно, через t1 = 50 с в баке останется четверть первоначального объёма. Ответ: 50 Замечание: Почему не подходит t2 = 150 с? Если в исходную формулу вместо H подставить 0, то есть определить за какое время вода полностью вытечет из бака, то получим t = 100. Следовательно, через 100 секунд в баке не останется воды. Поэтому t2 = 150 с не подходит. |
| Задача 8. В боковой стенке высокого цилиндрического бака у самого дна закреплeн кран. После его открытия вода начинает вытекать из бака, при этом высота столба воды в нeм, выраженная в метрах, меняется по закону (Hleft( t right) = a,{t^2} + b,t + {H_0}), где ({H_0} = 4) м — начальный уровень воды, (a = frac{1}{{100}}) м/мин2, и (b = — frac{2}{5}) м/мин — постоянные, t — время в минутах, прошедшее с момента открытия крана. В течение какого времени вода будет вытекать из бака? Ответ приведите в минутах.
Ответ
ОТВЕТ: 20. Решение
Так как спрашивают в течение какого времени вода будет вытекать из бака, то H = 0. Следовательно, задача сводится к решению квадратного уравнения: (frac{1}{{100}}{t^2} — frac{2}{5}t + 4 = 0,,|, cdot ,100,,,,, Leftrightarrow ,,,,{t^2} — 40t + 400 = 0,,,, Leftrightarrow ,,,,t = 20.) Следовательно, за 20 минут вся вода вытечет из бака. Ответ: 20. |
| Задача 9. Камнеметательная машина выстреливает камни под некоторым острым углом к горизонту. Траектория полeта камня описывается формулой (y = a,{x^2} + b,x), где (a = — frac{1}{{100}}) м-1, (b = 1) — постоянные параметры, x (м) — смещение камня по горизонтали, y (м) — высота камня над землeй. На каком наибольшем расстоянии (в метрах) от крепостной стены высотой 8 м нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра?
Ответ
ОТВЕТ: 90. Решение
Высота стены равна 8 м. Так как камни должны пролетать над стеной на высоте не менее 1 метра, то задача сводится к решению неравенства: (y geqslant 8 + 1 = 9) ( — frac{1}{{100}}{x^2} + x geqslant 9,,|, cdot ,left( { — 100} right),,,,,,, Leftrightarrow ,,,,,,{x^2} — 100x + 900 leqslant 0,) ({x^2} — 100x + 900 = 0,,,,,,,, Leftrightarrow ,,,,,,{x_1} = 10;,,,,,,{x_2} = 90) Следовательно, (x in left[ {10;,90} right]) и наибольшее расстояние на котором нужно расположить машину, чтобы камни пролетали над стеной на высоте не менее 1 метра равно 90 метров. |
| Задача 10. Зависимость температуры (в градусах Кельвина) от времени для нагревательного элемента некоторого прибора была получена экспериментально и на исследуемом интервале температур определяется выражением (Tleft( t right) = {T_0} + b,t + a,{t^2}), где t — время в минутах, ({T_0} = 1400) К, (a, = — 10) К/мин2, (b = 200,) К/мин. Известно, что при температуре нагревателя свыше 1760 К прибор может испортиться, поэтому его нужно отключать. Определите, через какое наибольшее время после начала работы нужно отключать прибор. Ответ выразите в минутах
Ответ
ОТВЕТ: 2. Решение
Определим когда температура нагревателя будем не более 1 760 К. Для этого необходимо решить неравенство: (Tleft( t right) leqslant 1760.) (1400 + 200t — 10{t^2} leqslant 1760,,,,, Leftrightarrow ,,,,, — 10{t^2} + 200t — 360 leqslant 0,,|,:,left( { — 10} right)) ({t^2} — 20t + 36 geqslant 0,,,,, Leftrightarrow ,,,,,t in left( { — infty ;,2} right] cup left[ {18;,infty } right).) Через 2 минуты после включения прибор нагреется до 1760 К, и при дальнейшем нагревании может испортиться. Таким образом, наибольшее время после начала работы когда прибор нужно отключить это 2 минуты. Ответ: 2. |
| Задача 11. Для сматывания кабеля на заводе используют лебедку, которая равноускоренно наматывает кабель на катушку. Угол, на который поворачивается катушка, изменяется со временем по закону (varphi = omega ,t + frac{{beta ,{t^2}}}{2}), где t — время в минутах, — начальная угловая скорость вращения катушки, а — угловое ускорение, с которым наматывается кабель. Рабочий должен проверить ход его намотки не позже того момента, когда угол намотки (varphi ) достигнет ({1200^ circ }). Определите время после начала работы лебедки, не позже которого рабочий должен проверить еe работу. Ответ выразите в минутах.
Ответ
ОТВЕТ: 20. Решение
Задача сводится к решению следующего неравенства: (varphi leqslant 1200.) (20t + frac{{4{t^2}}}{2} leqslant 1200,,,,, Leftrightarrow ,,,,,{t^2} + 10t — 600 leqslant 0,,,,, Leftrightarrow ,,,,,t in left[ { — 30;,20} right].) Следовательно, не позже чем через 20 минут рабочий должен проверить работу лебёдки. Ответ: 20. |
| Задача 12. Мотоциклист, движущийся по городу со скоростью ({v_0} = 57) км/ч, выезжает из него и сразу после выезда начинает разгоняться с постоянным ускорением (a = 12) км/ч2. Расстояние от мотоциклиста до города, измеряемое в километрах, определяется выражением (S = {v_0}t + frac{{a,{t^2}}}{2}). Определите наибольшее время, в течение которого мотоциклист будет находиться в зоне функционирования сотовой связи, если оператор гарантирует покрытие на расстоянии не далее чем в 30 км от города. Ответ выразите в минутах.
Ответ
ОТВЕТ: 30. Решение
Мотоциклист будет находиться в зоне функционирования сотовой связи, если (S leqslant 30.) Следовательно, задача сводится к решению следующего неравенства: (57t + frac{{12{t^2}}}{2} leqslant 30,,,,, Leftrightarrow ,,,,,2{t^2} + 19t — 10 leqslant 0,,,,, Leftrightarrow ,,,,,t in left[ { — 10;,0,5} right].) Так как (t geqslant 0,) то (t in left[ {0;,0,5} right].) Следовательно, наибольшее время t = 0,5 ч = 30 минут. Ответ: 30. |
| Задача 13. Автомобиль, движущийся в начальный момент времени со скоростью ({v_0} = 20) м/с, начал торможение с постоянным ускорением (a = 5) м/с2. За t секунд после начала торможения он прошёл путь (S = {v_0}t — frac{{a,{t^2}}}{2})(м). Определите время, прошедшее от момента начала торможения, если известно, что за это время автомобиль проехал 30 метров. Ответ выразите в секундах.
Ответ
ОТВЕТ: 2. Решение
Задача сводится к решению следующего квадратного уравнения: (30 = 20t — frac{{5{t^2}}}{2},,,,, Leftrightarrow ,,,,,{t^2} — 8t + 12 = 0,,,,, Leftrightarrow ,,,,,{t_1} = 2,,,,,{t_2} = 6.) Следовательно, через 2 секунды автомобиль проедет 30 метров. Ответ: 2. Замечание: Почему не подходит t2 = 6 с? Автомобиль остановится в тот момент, когда будет пройден наибольший путь: (S = 20t — frac{{5{t^2}}}{2}.) Парабола, направленная ветвями вверх, достигнет наибольшего значения в вершине: ({t_0} = — frac{b}{{2a}} = — frac{{20}}{{2 cdot left( { — 2,5} right)}} = 4.) Следовательно, через 4 секунды автомобиль остановится, поэтому t2 = 6 с не подходит. |
Задача 14. Деталью некоторого прибора является вращающаяся катушка. Она состоит из трех однородных соосных цилиндров: центрального массой (m =  кг и радиуса (R = 10) см, и двух боковых с массами (M = 1) кг и с радиусами (R + h). При этом момент инерции катушки относительно оси вращения, выражаемый в , задается формулой (I = frac{{left( {m + 2M} right){R^2}}}{2} + Mleft( {2Rh + {h^2}} right)). При каком максимальном значении h момент инерции катушки не превышает предельного значения ? Ответ выразите в сантиметрах кг и радиуса (R = 10) см, и двух боковых с массами (M = 1) кг и с радиусами (R + h). При этом момент инерции катушки относительно оси вращения, выражаемый в , задается формулой (I = frac{{left( {m + 2M} right){R^2}}}{2} + Mleft( {2Rh + {h^2}} right)). При каком максимальном значении h момент инерции катушки не превышает предельного значения ? Ответ выразите в сантиметрах
Ответ
ОТВЕТ: 5. Решение
Задача сводится к нахождению наибольшего решения следующего неравенства: (I leqslant 625.) (frac{{left( {8 + 2 cdot 1} right) cdot {{10}^2}}}{2} + 1 cdot left( {2 cdot 10 cdot h + {h^2}} right) leqslant 625,,,,,, Leftrightarrow ,,,,,{h^2} + 20h — 125 leqslant 0,,,,, Leftrightarrow ,,,,,h in left[ { — 25;,5} right].) Следовательно, наибольшее значение h = 5 см. Ответ: 5. |
| Задача 15. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет кубическую форму, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: ({F_A} = rho ,g,{l^3}), где l — длина ребра куба в метрах, — плотность воды, а g — ускорение свободного падения (считайте (g = 9,8) Н/кг). Какой может быть максимальная длина ребра куба, чтобы обеспечить его эксплуатацию в условиях, когда выталкивающая сила при погружении будет не больше, чем 78 400 Н? Ответ выразите в метрах.
Ответ
ОТВЕТ: 2. Решение
Задача сводится к нахождению наибольшего решения следующего неравенства: ({F_A} leqslant 78,400.) (1000 cdot 9,8 cdot {l^3} leqslant 78400,,,,,, Leftrightarrow ,,,,,{l^3} leqslant 8,,,,, Leftrightarrow ,,,,,l leqslant 2.) Следовательно, наибольшее значение l = 2 м. Ответ: 2. |
| Задача 16. На верфи инженеры проектируют новый аппарат для погружения на небольшие глубины. Конструкция имеет форму сферы, а значит, действующая на аппарат выталкивающая (архимедова) сила, выражаемая в ньютонах, будет определяться по формуле: ({F_A} = alpha ,rho ,g,{r^3}), где (alpha = 4,2) — постоянная, r — радиус аппарата в метрах, — плотность воды, а g — ускорение свободного падения (считайте (g = 10) Н/кг). Каков может быть максимальный радиус аппарата, чтобы выталкивающая сила при погружении была не больше, чем 336 000 Н? Ответ выразите в метрах
Ответ
ОТВЕТ: 2. Решение
Задача сводится к нахождению наибольшего решения следующего неравенства: ({F_A} leqslant 336,000.) (4,2 cdot 1000 cdot 10 cdot {r^3} leqslant 336000,,,,,, Leftrightarrow ,,,,,{r^3} leqslant 8,,,,, Leftrightarrow ,,,,,r leqslant 2.) Следовательно, наибольшее значение r = 2 м. Ответ: 2. |
| Задача 17. Для определения эффективной температуры звезд используют закон Стефана–Больцмана, согласно которому мощность излучения нагретого тела P, измеряемая в ваттах, прямо пропорциональна площади его поверхности и четвёртой степени температуры: (P = sigma ,S,{T^4}), где (sigma = 5,7 cdot {10^{ — 8}}) — постоянная, площадь S измеряется в квадратных метрах, а температура T — в градусах Кельвина. Известно, что некоторая звезда имеет площадь (S = frac{1}{{16}} cdot {10^{20}})м2, а излучаемая ею мощность P не менее (9,12 cdot {10^{25}}) Вт. Определите наименьшую возможную температуру этой звезды. Приведите ответ в градусах Кельвина.
Ответ
ОТВЕТ: 4 000. Решение
Задача сводится к решению следующего уравнения: (9,12 cdot {10^{25}} = 5,7 cdot {10^{ — 8}} cdot frac{1}{{16}} cdot {10^{20}} cdot {T^4},,,,, Leftrightarrow ,,,,,{T^4} = frac{{16 cdot 9,12 cdot {{10}^{25}}}}{{5,7 cdot {{10}^{12}}}}) (T = sqrt[4]{{frac{{16 cdot 912 cdot {{10}^{12}}}}{{57}}}} = sqrt[4]{{16 cdot 16 cdot {{10}^{12}}}} = 2 cdot 2 cdot {10^3} = 4,000,,{text{K}}{text{.}}) Ответ: 4 000. |
| Задача 18. Для получения на экране увеличенного изображения лампочки в лаборатории используется собирающая линза с главным фокусным расстоянием (f = 30) см. Расстояние d1 от линзы до лампочки может изменяться в пределах от 30 до 50 см, а расстояние d2 от линзы до экрана — в пределах от 150 до 180 см. Изображение на экране будет четким, если выполнено соотношение (frac{1}{{{d_1}}} + frac{1}{{{d_2}}} = frac{1}{f}). Укажите, на каком наименьшем расстоянии от линзы можно поместить лампочку, чтобы ее изображение на экране было четким. Ответ выразите в сантиметрах.
Ответ
ОТВЕТ: 36. Решение
Так как f = 30 см, то (frac{1}{{{d_1}}} + frac{1}{{{d_2}}} = frac{1}{{30}}.) Расстояние от линзы до лампочки d1 должно быть наименьшим, тогда слагаемое (frac{1}{{{d_1}}}) должно принимать наибольшее значение, а слагаемое (frac{1}{{{d_2}}}) соответственно наоборот наименьшее, которое будет получено при наибольшем значении d2. Следовательно, d2 = 180. (frac{1}{{{d_1}}} + frac{1}{{180}} = frac{1}{{30}},,,,, Leftrightarrow ,,,,,frac{1}{{{d_1}}} = frac{1}{{30}}, — frac{1}{{180}},,,,, Leftrightarrow ,,,,,frac{1}{{{d_1}}} = frac{1}{{36}},,,,, Leftrightarrow ,,,,,{d_1} = 36) см. По условию задачи расстояние d1 от линзы до лампочки меняется в пределах от 30 до 50. Следовательно, найденное значение удовлетворяет условию задачи. Ответ: 36. |
| Задача 19. Перед отправкой тепловоз издал гудок с частотой ({f_0} = 440) Гц. Чуть позже издал гудок подъезжающий к платформе тепловоз. Из-за эффекта Доплера частота второго гудка f больше первого: она зависит от скорости тепловоза по закону (fleft( v right) = frac{{{f_0}}}{{1 — frac{v}{c}}}) (Гц), где c — скорость звука в (в м/с). Человек, стоящий на платформе, различает сигналы по тону, если они отличаются не менее чем на 10 Гц. Определите, с какой минимальной скоростью приближался к платформе тепловоз, если человек смог различить сигналы, а (c = 315) м/с. Ответ выразите в м/с.
Ответ
ОТВЕТ: 7. Решение
Так как частота второго гудка f больше первого и человек, стоящий на платформе, различает сигналы по тону, то задача сводится к решению рационального неравенства: (fleft( v right) geqslant 440 + 10 = 450.) (frac{{440}}{{1 — frac{v}{{315}}}} geqslant 450,,,,, Leftrightarrow ,,,,frac{{440}}{{450}} geqslant 1 — frac{v}{{315}},,,, Leftrightarrow ,,,,,frac{v}{{315}} geqslant 1 — frac{{44}}{{45}},,,, Leftrightarrow ,,,,frac{v}{{315}} geqslant frac{1}{{45}},,,, Leftrightarrow ,,,v geqslant 7) м/с. Следовательно, наименьшая скорость тепловоза v = 7 м/с. Ответ: 7. |
| Задача 20. По закону Ома для полной цепи сила тока, измеряемая в амперах, равна (I = frac{varepsilon }{{R + r}}), где (varepsilon ) — ЭДС источника (в вольтах), (r = 1) Ом — его внутреннее сопротивление, R — сопротивление цепи (в Омах). При каком наименьшем сопротивлении цепи сила тока будет составлять не более (20% ) от силы тока короткого замыкания? (Ответ выразите в Омах.)
Ответ
ОТВЕТ: 4. Решение
По условию задачи сила тока должна составлять не более 20% от силы тока короткого замыкания, то есть (I leqslant {I_{k3}} cdot frac{{20}}{{100}}.) (fracvarepsilon{{R{text{ + 1}}}} leqslant fracvarepsilon{1} cdot frac{1}{5},,|,:,varepsilon > 0,,,, Leftrightarrow ,,,,,frac{1}{{R + 1}} leqslant frac{1}{5},,|, cdot 5left( {R + 1} right) > 0,,,,,, Leftrightarrow ,,,,,R + 1 geqslant 5,,,,,, Leftrightarrow ,,,,,,R geqslant 4) Ом. Следовательно, наименьшее сопротивление цепи R = 4 Ом. Ответ: 4. |
| Задача 21. Сила тока в цепи I (в амперах) определяется напряжением в цепи и сопротивлением электроприбора по закону Ома: (I = frac{U}{R}), где U — напряжение в вольтах, R — сопротивление электроприбора в Омах. В электросеть включен предохранитель, который плавится, если сила тока превышает 4 А. Определите, какое минимальное сопротивление должно быть у электроприбора, подключаемого к розетке в 220 вольт, чтобы сеть продолжала работать. Ответ выразите в Омах.
Ответ
ОТВЕТ: 55. Решение
Задача сводится к решению неравенства: (I leqslant 4,{text{A}}{text{.}}) (frac{{220}}{R} leqslant 4,,|, cdot ,R > 0,,,,,,,, Leftrightarrow ,,,,220 leqslant 4R,,,,,, Leftrightarrow ,,,,,,R geqslant 55) Ом. Следовательно, наименьшее сопротивление R = 55 Ом. Ответ: 55. |
| Задача 22. Амплитуда колебаний маятника зависит от частоты вынуждающей силы, определяемой по формуле (Aleft( omega right) = frac{{{A_0},omega _p^2}}{{left| {,omega _p^2 — {omega ^2},} right|}}), где (omega ) — частота вынуждающей силы (в ({{text{c}}^{ — 1}})), ({A_0}) — постоянный параметр, (omega _p^{} = 360,{{text{c}}^{ — 1}}) — резонансная частота. Найдите максимальную частоту (omega ), меньшую резонансной, для которой амплитуда колебаний превосходит величину ({A_0}) не более чем на 12,5%. Ответ выразите в ({{text{c}}^{ — 1}})
Ответ
ОТВЕТ: 120. Решение
Так как амплитуда колебаний A(ω) должна превосходить величину А0 не более чем на 12,5%, то должно выполняться неравенство: (Aleft( omega right) leqslant {A_0} cdot frac{{112,5}}{{100}},,,,,, Leftrightarrow ,,,,,,frac{{A{_0}omega _p^2}}{{left| {,omega _p^2 — omega _{}^2} right|}} leqslant {A_0} cdot 1,125,,|,,:,,{A_0} > 0,,,,, Leftrightarrow ,,,,,,frac{{omega _p^2}}{{left| {,omega _p^2 — omega _{}^2} right|}} leqslant 1frac{1}{8}.) По условию задачи (omega < {omega _p},,,, Leftrightarrow ,,,,{omega _p} > omega ,,,,, Leftrightarrow ,,,,omega _p^2 > {omega ^2},,,,, Leftrightarrow ,,,,,,omega _p^2 — {omega ^2}, > 0). Поэтому: (left| {omega _p^2 — {omega ^2}} right|, > omega _p^2 — {omega ^2}.) (,frac{{omega _p^2}}{{omega _p^2 — omega _{}^2}} leqslant frac{9}{8},,|,, cdot ,8left( {omega _p^2 — omega _{}^2} right) > 0,,,,, Leftrightarrow ,,,,,8omega _p^2 leqslant 9 cdot omega _p^2 — 9omega _{}^2,,,,, Leftrightarrow ,,,,,,9omega _{}^2 leqslant omega _p^2,,,, Leftrightarrow ) (omega _{}^2 leqslant frac{{omega _p^2}}{9},,,,,, Leftrightarrow ,,,,,,omega leqslant frac{{{omega _p}}}{3},,,,,,, Leftrightarrow ,,,,,,omega leqslant frac{{360}}{3},,,,,,, Leftrightarrow ,,,,,,omega leqslant 120,{c^{ — 1}}.) Следовательно, максимальная частота ω = 120 с-1. Ответ: 120. |
| Задача 23. В розетку электросети подключены приборы, общее сопротивление которых составляет ({R_1} = 90) Ом. Параллельно с ними в розетку предполагается подключить электрообогреватель. Определите наименьшее возможное сопротивление ({R_2}) этого электрообогревателя, если известно, что при параллельном соединении двух проводников с сопротивлениями ({R_1}) Ом и ({R_2}) Ом их общее сопротивление дается формулой (Ом), а для нормального функционирования электросети общее сопротивление в ней должно быть не меньше 9 Ом. Ответ выразите в Омах.
Ответ
ОТВЕТ: 10. Решение
Задача сводится к решению следующего неравенства: Rобщ ≥ 9 Ом и нахождению наименьшего значения R2 при заданном R1 = 90 Ом. (frac{{90{R_2}}}{{90 + {R_2}}} geqslant 9,,|,, cdot left( {90 + {R_2}} right) > 0,,,, Leftrightarrow ,,,,90{R_2} geqslant 810 + 9{R_2},,,, Leftrightarrow ,,,,81{R_2} geqslant 810,,, Leftrightarrow ,,,{R_2} geqslant 10) Ом. Следовательно, наименьшее значение R2 = 10 Ом. Ответ: 10. |
| Задача 24. Коэффициент полезного действия (КПД) некоторого двигателя определяется формулой (eta = frac{{{T_1} — {T_2}}}{{{T_1}}} cdot 100% ), где ({T_1}) — температура нагревателя (в градусах Кельвина), ({T_2}) — температура холодильника (в градусах Кельвина). При какой минимальной температуре нагревателя ({T_1}) КПД этого двигателя будет не меньше 15%, если температура холодильника ({T_2} = 340) К? Ответ выразите в градусах Кельвина.
Ответ
ОТВЕТ: 400. Решение
Задача сводится к решению следующего неравенства: (eta geqslant 15% ) и нахождению наименьшего значения T1 при заданном T2 = 340 K. (frac{{{T_1} — 340}}{{{T_1}}} cdot 100 geqslant 15,,|, cdot {T_1} > 0,,, Leftrightarrow ,,,100{T_1} — 34000 geqslant 15{T_1},, Leftrightarrow ,,85{T_1} geqslant 34000,, Leftrightarrow ,,{T_1} geqslant 400)K. Следовательно, наименьшее значение T1 = 400 K. Ответ: 400. |
| Задача 25. Коэффициент полезного действия (КПД) кормозапарника равен отношению количества теплоты, затраченного на нагревание воды массой (в килограммах) от температуры ({t_1}) до температуры ({t_2}) (в градусах Цельсия) к количеству теплоты, полученному от сжигания дров массы кг. Он определяется формулой (eta = frac{{{c_в} cdot {m_в}left( {{t_2} — {t_1}} right)}}{{{q_{др}},{m_{др}}}} cdot 100% ), где ({c_в} = 4,2 cdot {10^3}) Дж/(кгК) — теплоёмкость воды, ({q_{др}} = 8,3 cdot {10^6}) Дж/кг — удельная теплота сгорания дров. Определите наименьшее количество дров, которое понадобится сжечь в кормозапарнике, чтобы нагреть (m = 83) кг воды от ({10^ circ }{text{C}}) до кипения, если известно, что КПД кормозапарника не больше 21%. Ответ выразите в килограммах
Ответ
ОТВЕТ: 18.
Решение
Задача сводится к решению следующего неравенства: (eta leqslant 21% ) и нахождению наименьшего значения mдр. (frac{{4,2 cdot {{10}^3} cdot 83 cdot left( {100 — 10} right)}}{{8,3 cdot {{10}^6} cdot m}} cdot 100 leqslant 21,,|, cdot m > 0,,,, Leftrightarrow ,,,,frac{{42 cdot {{10}^3} cdot 83 cdot 9 cdot {{10}^2}}}{{83 cdot {{10}^5}}} leqslant 21m,,,, Leftrightarrow ,) ( Leftrightarrow ,,,,42 cdot 9 leqslant 21m,,, Leftrightarrow ,,,m geqslant 18) кг. Следовательно, наименьшее значение m = 18 кг. Ответ: 18. |
| Задача 26. Опорные башмаки шагающего экскаватора, имеющего массу (m = 1260) тонн представляют собой две пустотелые балки длиной (l = 18) метров и шириной s метров каждая. Давление экскаватора на почву, выражаемое в килопаскалях, определяется формулой (p = frac{{m,g}}{{2,l,s}}), где m — масса экскаватора (в тоннах), l — длина балок в метрах, s — ширина балок в метрах, g — ускорение свободного падения (считайте (g = 10) м/с). Определите наименьшую возможную ширину опорных балок, если известно, что давление p не должно превышать 140 кПа. Ответ выразите в метрах.
Ответ
ОТВЕТ: 2,5. Решение
Задача сводится к решению следующего неравенства: (p leqslant 140)кПа и нахождению наименьшего значения s. (frac{{1260 cdot 10}}{{2 cdot 18 cdot s}} leqslant 140,,|, cdot s > 0,,,, Leftrightarrow ,,,,350 leqslant 140;s,,,, Leftrightarrow ,,,,,s geqslant 2,5)м. Следовательно, наименьшее значение s = 2,5 м. Ответ: 2,5. |
| Задача 27. К источнику с ЭДС (varepsilon = 55) В и внутренним сопротивлением (r = 0,5) Ом, хотят подключить нагрузку с сопротивлением R Ом. Напряжение на этой нагрузке, выражаемое в вольтах, дается формулой (U = frac{{varepsilon ,R}}{{R + r}}). При каком наименьшем значении сопротивления нагрузки напряжение на ней будет не менее 50 В? Ответ выразите в Омах.
Ответ
ОТВЕТ: 5. Решение
Задача сводится к решению следующего неравенства: (U geqslant 50) В и нахождению наименьшего значения R. (frac{{55 cdot R}}{{R + 0,5}} geqslant 50,,|, cdot left( {R + 0,5} right) > 0,,,, Leftrightarrow ,,,,55R geqslant 50R + 25,,,, Leftrightarrow ,,,,,R geqslant 5) Ом. Следовательно, наименьшее значение R = 5 Ом. Ответ: 5. |
| Задача 28. При сближении источника и приёмника звуковых сигналов движущихся в некоторой среде по прямой навстречу друг другу частота звукового сигнала, регистрируемого приемником, не совпадает с частотой исходного сигнала ({f_0} = 150) Гц и определяется следующим выражением: (f = {f_0}frac{{c + u}}{{c — v}}) (Гц), где c — скорость распространения сигнала в среде (в м/с), а (u = 10) м/с и (v = 15) м/с — скорости приемника и источника относительно среды соответственно. При какой максимальной скорости c (в м/с) распространения сигнала в среде частота сигнала в приемнике f будет не менее 160 Гц?
Ответ
ОТВЕТ: 390. Решение
Задача сводится к решению следующего неравенства: (f geqslant 160) Гц и нахождению наибольшего значения с. (150 cdot frac{{c + 10}}{{c — 15}} geqslant 160,,|, cdot left( {c — 15} right) > 0,,,, Leftrightarrow ,,,,150c + 1500 geqslant 160c — 2400,,,, Leftrightarrow ,,,,,,c leqslant 390) м/с. Следовательно, наибольшее значение с = 390 м/с. Ответ: 390. |
| Задача 29. Локатор батискафа, равномерно погружающегося вертикально вниз, испускает ультразвуковые импульсы частотой 749 МГц. Скорость спуска батискафа, выражаемая в м/с, определяется по формуле (v = cfrac{{f — {f_0}}}{{f + {f_0}}}), где (c = 1500) м/с — скорость звука в воде, ({f_0}) — частота испускаемых импульсов (в МГц), f — частота отраженного от дна сигнала, регистрируемая приемником (в МГц). Определите наибольшую возможную частоту отраженного сигнала f, если скорость погружения батискафа не должна превышать 2 м/с.
Ответ
ОТВЕТ: 751. Решение
Задача сводится к решению следующего неравенства: (v leqslant 2) м/c и нахождению наибольшего значения f. (1500 cdot frac{{f — 749}}{{f + 749}} leqslant 2,,|, cdot frac{{f + 749}}{2} > 0,,,, Leftrightarrow ,,,,750f — 750 cdot 749 leqslant f + 749,,,, Leftrightarrow ,) ( Leftrightarrow ,,,,749f leqslant 750 cdot 749 + 749,,,, Leftrightarrow ,,,,,749f leqslant 751 cdot 749,,,,, Leftrightarrow ,,,,,f leqslant 751) МГц. Следовательно, наибольшее значение f = 751 МГц. Ответ: 751. |
| Задача 30. Скорость автомобиля, разгоняющегося с места старта по прямолинейному отрезку пути длиной l км с постоянным ускорением a км/ч, вычисляется по формуле ({v^2} = 2,l,a). Определите, с какой наименьшей скоростью будет двигаться автомобиль на расстоянии 1 километра от старта, если по конструктивным особенностям автомобиля приобретаемое им ускорение не меньше 5000 км/ч2. Ответ выразите в км/ч.
Ответ
ОТВЕТ: 100. Решение
Так как (a = frac{{{v^2}}}{{2,,l}}), то задача сводится к решению неравенства: (a geqslant 5000) км/ч2 и нахождению наименьшего значения v. (frac{{{v^2}}}{{2 cdot 1}} geqslant 5000,,,,,, Leftrightarrow ,,,,{v^2} geqslant 10000,,,, Leftrightarrow ,,,,,,v geqslant 100) км/ч. Следовательно, наименьшее значение v = 100 км/ч. Ответ: 100. |
| Задача 31. Для поддержания навеса планируется использовать цилиндрическую колонну. Давление P (в паскалях), оказываемое навесом и колонной на опору, определяется по формуле (P = frac{{4,m,g}}{{pi ,{D^2}}}), где (m = 1200) кг — общая масса навеса и колонны, D — диаметр колонны (в метрах). Считая ускорение свободного падения (g = 10) м/с2, а (pi = 3), определите наименьший возможный диаметр колонны, если давление, оказываемое на опору, не должно быть больше 400000 Па. Ответ выразите в метрах.
Ответ
ОТВЕТ: 0,2. Решение
Задача сводится к решению неравенства: (P leqslant 400000) Па и нахождению наименьшего значения D. (frac{{4 cdot 1200 cdot 10}}{{3 cdot {D^2}}} leqslant 400000,|, cdot ,{D^2} > 0,,,,, Leftrightarrow ,,,,4 cdot 4 leqslant 400{D^2},,,, Leftrightarrow ,,,,,,{D^2} geqslant frac{1}{{25}},,,,, Leftrightarrow ,,,,,D geqslant 0,2) м. Следовательно, наименьшее значение D = 0,2 м. Ответ: 0,2. |
| Задача 32. Автомобиль, масса которого равна (m = 2160) кг, начинает двигаться с ускорением, которое в течение t секунд остается неизменным, и проходит за это время путь (S = 500) метров. Значение силы (в ньютонах), приложенной в это время к автомобилю, равно (F = frac{{2,m,S}}{{{t^2}}}). Определите наибольшее время после начала движения автомобиля, за которое он пройдет указанный путь, если известно, что сила F, приложенная к автомобилю, не меньше 2400 Н. Ответ выразите в секундах
Ответ
ОТВЕТ: 30. Решение
Задача сводится к решению неравенства: (F geqslant 2400) Н и нахождению наибольшего значения t. (frac{{2 cdot 2160 cdot 500}}{{{t^2}}} geqslant 2400,,|, cdot ,{t^2} > 0,,,,, Leftrightarrow ,,,,21600 geqslant 24{t^2},,,, Leftrightarrow ,,,,,,{t^2} leqslant 900,,,, Leftrightarrow ,,,,,t leqslant 30) c. Следовательно, наибольшее значение t = 30 c. Ответ: 30. |
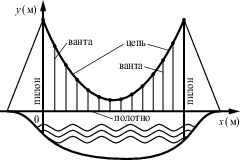 Задача 33. На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами. Введём систему координат: ось Oy направим вертикально вдоль одного из пилонов, а ось Ox направим вдоль полотна моста, как показано на рисунке. В этой системе координат линия, по которой провисает цепь моста, задаётся формулой (y = 0,005{x^2} — 0,74x + 25), где x и y измеряются в метрах. Найдите длину ванты, расположенной в 30 метрах от пилона. Ответ дайте в метрах. Задача 33. На рисунке изображена схема вантового моста. Вертикальные пилоны связаны провисающей цепью. Тросы, которые свисают с цепи и поддерживают полотно моста, называются вантами. Введём систему координат: ось Oy направим вертикально вдоль одного из пилонов, а ось Ox направим вдоль полотна моста, как показано на рисунке. В этой системе координат линия, по которой провисает цепь моста, задаётся формулой (y = 0,005{x^2} — 0,74x + 25), где x и y измеряются в метрах. Найдите длину ванты, расположенной в 30 метрах от пилона. Ответ дайте в метрах.
Ответ
ОТВЕТ: 7,3. Решение
Вычислим длину ванты на расстоянии 30 метров от пилона, то есть найдём y (30). (yleft( {30} right) = 0,005 cdot {30^2} — 0,74 cdot 30 + 25 = 4,5 — 22,2 + 25 = 7,3) м. Ответ: 7,3. |
Прототипы задания №8 ЕГЭ по математике профильного уровня — текстовые задачи. Практический материал для подготовки к экзамену в 11 классе.
Для успешного выполнения задания №8 необходимо уметь строить и исследовать простейшие математические модели.
Практика
Коды проверяемых элементов содержания (по кодификатору) — 2.1, 2.2
Уровень сложности задания — повышенный.
Максимальный балл за выполнение задания — 1
Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне (в мин.) — 7
Примеры заданий:
Из пункта A в пункт B одновременно выехали два автомобиля. Первый проехал с постоянной скоростью весь путь. Второй проехал первую половину пути со скоростью, меньшей скорости первого на 13 км/ч, а вторую половину пути — со скоростью 78 км/ч, в результате чего прибыл в пункт В одновременно с первым автомобилем. Найдите скорость первого автомобиля, если известно, что она больше 48 км/ч. Ответ дайте в км/ч.
Из одной точки круговой трассы, длина которой равна 14 км, одновременно в одном направлении стартовали два автомобиля. Скорость первого автомобиля равна 80 км/ч, и через 40 минут после старта он опережал второй автомобиль на один круг. Найдите скорость второго автомобиля. Ответ дайте в км/ч.
Теплоход проходит по течению реки до пункта назначения 200 км и после стоянки возвращается в пункт отправления. Найдите скорость течения, если скорость теплохода в неподвижной воде равна 15 км/ч, стоянка длится 10 часов, а в пункт отправления теплоход возвращается через 40 часов после отплытия из него. Ответ дайте в км/ч.
Двое рабочих, работая вместе, могут выполнить работу за 12 дней. За сколько дней, работая отдельно, выполнит эту работу первый рабочий, если он за два дня выполняет такую же часть работы, какую второй — за три дня?
Семья состоит из мужа, жены и их дочери студентки. Если бы зарплата мужа увеличилась вдвое, общий доход семьи вырос бы на 67%. Если бы стипендия дочери уменьшилась втрое, общий доход семьи сократился бы на 4%. Сколько процентов от общего дохода семьи составляет зарплата жены?
Турист идет из одного города в другой, каждый день проходя больше, чем в предыдущий день, на одно и то же расстояние. Известно, что за первый день турист прошел 10 километров. Определите, сколько километров прошел турист за третий день, если весь путь он прошел за 6 дней, а расстояние между городами составляет 120 километров.
Связанные страницы:


Сайт репетитора по математике Фельдман Инны Владимировны. Профессиональные услуги репетитора по математике в Москве. Подготовка к ГИА и ЕГЭ, помощь отстающим.
2015-11-07
07
Ноя 2015
НОВОСТИ
Публикую подборку прототипов заданий 1-14 (по нумерации прошлого года), составленную учителем МБОУ СОШ №5 — «Школа здоровья и развития» г. Радужный ХМАО — Югра Семеновой Еленой Юрьевной. Сайт http://semenova-klass.moy.su/
Соответствие номеров заданий с нумерацией этого года:
Прототипы заданий 1-14 ЕГЭ по математике с ответами

Инна |
Отзывов нет
Задания 1-14 из открытого банка заданий. Источник: http://alexlarin.net
Задания 1-14 профильного уровня из открытого банка заданий
Читать далее: http://4ege.ru/matematika/6384-prototipy-zadaniy-ege-po-matematike-profilnogo-urovnya.html
Автор: Кривилев Александр Викторович
Среда, 20.04.2022, 20:26
Приветствую Вас
Гость | RSS
Главная Регистрация Вход
|
Категории раздела
ЕГЭ и ОГЭ онлайн ГЕНЕРАТОР ЕГЭ ПРОФИЛЬНЫЙ 2021 (alexlarin.net) ГЕНЕРАТОР ЕГЭ БАЗОВЫЙ 2021 (alexlarin.net) ГЕНЕРАТОР ВАРИАНТОВ ОГЭ 2021 (alexlarin.net) ПРОТОТИПЫ ЗАДАЧ 1-12 ЕГЭ (alexlarin.net) =»http:> ПРОТОТИПЫ ЗАДАЧ 20-25 ОГЭ (alexlarin.net) =»http:> ГЕНЕРАТОР ЕГЭ БАЗОВЫЙ 2018 (егэ-легко.рф) =»http:> ГЕНЕРАТОР ВАРИАНТОВ ОГЭ 2018 (егэ-легко.рф) Онлайн всего: 1 Гостей: 1 Пользователей: 0 |
Прототипы заданий открытого банка ЕГЭ 2016. Базовый уровень (с ответами).
|
Поиск Погода Погода в Заозерном
Подробнее Сайт в каталогах
|
||||||||||||||||||
Copyright MyCorp © 2022
Бесплатный конструктор сайтов — uCoz
Тест «Витамины»
Проверочная работа по биологии в 8 классе.
Консультация по физике
Онлайн-трансляция по вопросам подготовки к ЕГЭ по физике.
|
Все прототипы задания №1 открытого банка заданий ЕГЭ по математике 2016 года профильного уровня
Добавлять комментарии могут только зарегистрированные пользователи. [ Регистрация | Вход ] |
|
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
1
На диаграмме показана среднемесячная температура в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру в 1994 году. Ответ дайте в градусах Цельсия.
2
На диаграмме показана среднемесячная температура воздуха в Минске за каждый месяц 2003 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру в 2003 году. Ответ дайте в градусах Цельсия.
3
На диаграмме показана среднемесячная температура воздуха в Санкт-Петербурге за каждый месяц 1999 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наименьшую среднемесячную температуру во второй половине 1999 года. Ответ дайте в градусах Цельсия.
4
На диаграмме показана среднемесячная температура воздуха в Екатеринбурге (Свердловске) за каждый месяц 1973 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме наибольшую среднемесячную температуру во второй половине 1973 года. Ответ дайте в градусах Цельсия.
Источник: ЕГЭ по математике 29.06.2021. Резервная волна. Центр. Вариант 401
5
На диаграмме показана среднемесячная температура воздуха в Нижнем Новгороде (Горьком) за каждый месяц 1994 года. По горизонтали указываются месяцы, по вертикали — температура в градусах Цельсия. Определите по диаграмме, сколько было месяцев с положительной среднемесячной температурой.
Пройти тестирование по этим заданиям
Профиль – 8 (2019)
1). Найдите объём многогранника, изображённого на рисунке (все двугранные углы – прямые).
2). Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы – прямые).
3). Найдите объём многогранника, изображённого на рисунке (все двугранные углы — прямые).
4). Найдите площадь поверхности многогранника, изображённого на рисунке (все двугранные углы — прямые).
5). В правильной четырёхугольной пирамиде высота равна 3, боковое ребро равно 5. Найдите её объём.
6). В правильной четырёхугольной пирамиде SABCD с вершиной S точка O – центр основания, SO=35, SD=37.Найдите длину отрезка BD.
7). В правильной четырёхугольной пирамиде боковое ребро равно 7,5, а сторона основания равна 10. Найдите высоту пирамиды.
8). В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SO=48, SC=73. Найдите длину отрезка AC.
9). В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SD=26, AC=20. Найдите длину отрезка SO.
10). В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SO=21, AC=40. Найдите длину отрезка SB.
11). В правильной четырёхугольной пирамиде SABCD
с вершиной S точка O — центр основания, SO=35, BD=24. Найдите длину отрезка SD.
12). В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SB=29, AC=40. Найдите длину отрезка SO.
13). В правильной четырёхугольной пирамиде SABCD с вершиной S точка O — центр основания, SO=15, AC=40. Найдите длину отрезка SA.
14). В правильной четырёхугольной пирамиде SABCD точка O — центр основания, S — вершина, SO=6, SA=10. Найдите длину отрезка BD.
15). В правильной четырёхугольной пирамиде SABCD точка O — центр основания, S — вершина, SO=30, SA=34. Найдите длину отрезка AC.
16). В правильной четырёхугольной пирамиде SABCD с основанием ABCD боковое ребро SC равно 37, сторона основания равна 35√2. Найдите объём пирамиды.
17). В правильной четырёхугольной пирамиде SABCD с основанием ABCD боковое ребро SC равно 17, сторона основания равна 15√2. Найдите объём пирамиды.
18). В правильной шестиугольной пирамиде боковое ребро равно 6,5, а сторона основания равна 2,5. Найдите высоту пирамиды.
19). В правильной треугольной пирамиде боковое ребро равно 7, а сторона основания равна 10,5. Найдите высоту пирамиды.
20). Объём треугольной пирамиды равен 78. Через вершину пирамиды и среднюю линию её основания проведена плоскость (см. рисунок). Найдите объём отсечённой треугольной пирамиды.
21). Объём правильной четырёхугольной пирамиды SABCD равен 116. Точка E — середина ребра SB. Найдите объём треугольной пирамиды EABC.
22). Площадь боковой поверхности треугольной призмы равна 75. Через среднюю линию основания призмы проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсечённой треугольной призмы.
23). Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсечённой треугольной призмы равна 37. Найдите площадь боковой поверхности исходной призмы.
24). Основанием прямой треугольной призмы является прямоугольный треугольник с катетами 2 и 7, боковое ребро призмы равно 6. Найдите объём призмы.
25). Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 4 и 7, объём призмы равен 56. Найдите боковое ребро призмы.
26). Найдите объём многогранника, вершинами которого являются точки A, D, A1, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB=3, AD=4, AA1=5.
27). В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1=16, A1B1=2, A1D1=8. Найдите длину диагонали AC1.
28). В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1=8, CD=8, AD=14. Найдите длину диагонали BD1.
29). В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что CC1=6, CD=17, AD=6. Найдите длину диагонали CA1.
30). В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=6, AD=8, AA1=9. Найдите синус угла между прямыми CD и A1C1.
31). В кубе ABCDA1B1C1D1 найдите угол между прямыми BA1 и D1C1. Ответ дайте в градусах.
32). В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=6, BC=5, AA1=4. Найдите объём многогранника, вершинами которого являются точки A, B, C, D, A1, B1.
33). В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AB=9, BC=6, AA1=5. Найдите объём многогранника, вершинами которого являются точки A, B, C, B1.
34). Дана правильная треугольная призма ABCA1B1C1, площадь основания которой равна 9, а боковое ребро равно 4. Найдите объём многогранника, вершинами которого являются точки A, A1, B1, C1.
35). Найдите объём многогранника, вершинами которого являются точки C, A1, B1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 4, а боковое ребро равно 9.
36). Найдите объём многогранника, вершинами которого являются точки A, B, C, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 7, а боковое ребро равно 6.
37). Найдите объём многогранника, вершинами которого являются точки A, A1, B1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 3, а боковое ребро равно 9.
38). Найдите объём многогранника, вершинами которого являются точки A, B, C, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 6, а боковое ребро равно 9.
39). Найдите объём многогранника, вершинами которого являются вершины A, C, A1, B1, C1 правильной треугольной призмы ABCA1B1C1. Площадь основания призмы равна 7, а боковое ребро равно 9.
40). Найдите объём многогранника, вершинами которого являются точки D, A1, B1, C1, D1, E1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 2.
41). Найдите объём многогранника, вершинами которого являются вершины A, C, D, F, A1, C1, D1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 9, а боковое ребро равно 11.
42). Найдите объём многогранника, вершинами которого являются точки D, E, F, D1, E1, F1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 8, а боковое ребро равно 9.
43). Найдите объём многогранника, вершинами которого являются вершины A1, B1, F1, A правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 12, а боковое ребро равно 15.
44). В цилиндрическом сосуде уровень жидкости достигает 48 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 2 раза больше диаметра первого? Ответ выразите в см.
45). В цилиндрическом сосуде уровень жидкости достигает 98 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 7 раз больше диаметра первого? Ответ выразите в сантиметрах.
46). В цилиндрический сосуд налили 500 куб. см воды. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде увеличился в 1,2 раза. Найдите объём детали. Ответ выразите в куб. см.
47). В цилиндрическом сосуде уровень жидкости достигает 2 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 6 раз меньше диаметра первого? Ответ выразите в сантиметрах.
48). В цилиндрический сосуд, в котором находится 8 дм3 воды, опустили деталь. При этом уровень жидкости в сосуде поднялся в 1,5 раза. Чему равен объём детали? Ответ выразите в дм3.
49). В цилиндрическом сосуде уровень жидкости достигает 2 см. На какой высоте будет находиться уровень жидкости, если её перелить во второй цилиндрический сосуд, диаметр которого в 3 раза меньше диаметра первого? Ответ выразите в сантиметрах.
50). В цилиндрический сосуд налили 2800 см3 воды. Уровень жидкости оказался равным 16 см. В воду полностью погрузили деталь. При этом уровень жидкости в сосуде поднялся на 13 см. Найдите объём детали. Ответ выразите в куб. см.
51). Во сколько раз увеличится объём конуса, если радиус его основания увеличить в 6 раз, а высоту оставить прежней?
52). Во сколько раз увеличится объём конуса, если радиус его основания увеличить в 5 раз, а высоту оставить прежней?
53). Цилиндр и конус имеют общие основание и высоту. Объём конуса равен 9. Найдите объём цилиндра.
54). Цилиндр и конус имеют общие основание и высоту. Объём цилиндра равен 18. Найдите объём конуса.
55). Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём конуса, если объём цилиндра равен 252.
56). Конус и цилиндр имеют общее основание и общую высоту (конус вписан в цилиндр). Вычислите объём цилиндра, если объём конуса равен 63.
57). Высота конуса равна 12, а диаметр основания равен 70. Найдите длину образующей конуса.
58). Высота конуса равна 32, а диаметр основания равен 48. Найдите длину образующей конуса.
59). Высота конуса равна 24, а длина образующей равна 25. Найдите диаметр основания конуса.
60). Диаметр основания конуса равен 18, а длина образующей равна 41. Найдите высоту конуса.
61). Высота конуса равна 21, а длина образующей равна 29. Найдите диаметр основания конуса.
62). Диаметр основания конуса равен 40, а длина образующей – 25. Найдите высоту конуса.
63). Площадь полной поверхности конуса равна 35. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 3:2, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
64). Площадь полной поверхности конуса равна 15. Параллельно основанию конуса проведено сечение, делящее высоту в отношении 2:3, считая от вершины конуса. Найдите площадь полной поверхности отсечённого конуса.
65). Площадь боковой поверхности цилиндра равна 12 π, а диаметр основания равен 6. Найдите высоту цилиндра.
66). Площадь боковой поверхности цилиндра равна 24 π, а диаметр основания равен 8. Найдите высоту цилиндра.
67). Площадь боковой поверхности цилиндра равна 20 π, а высота равна 4. Найдите диаметр основания.
68). В основании прямой призмы лежит прямоугольный треугольник с катетами 10 и 9. Боковые рёбра призмы равны 2/π. Найдите объём цилиндра, описанного около этой призмы.
69). Прямоугольный параллелепипед описан около цилиндра, радиус основания которого равен 3. Объём параллелепипеда равен 36. Найдите высоту цилиндра.
70). Прямоугольный параллелепипед описан около цилиндра, радиус основания и высота которого равны 2. Найдите объём параллелепипеда.
71). Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности цилиндра равна 5√2. Найдите площадь боковой поверхности конуса.
72). Цилиндр и конус имеют общие основание и высоту. Высота цилиндра равна радиусу основания. Площадь боковой поверхности конуса равна 3√2. Найдите площадь боковой поверхности цилиндра.
73). В сосуде, имеющем форму конуса, уровень жидкости достигает 1/2 высоты. Объём жидкости равен 25 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
74). В сосуде, имеющем форму конуса, уровень жидкости достигает 2/3 высоты. Объём жидкости равен 144 мл. Сколько миллилитров жидкости нужно долить, чтобы полностью наполнить сосуд?
75). Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 10√2. Найдите образующую конуса.
76). Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Образующая конуса равна 50√2. Найдите радиус сферы.
77). Конус вписан в шар (см. рисунок). Радиус основания конуса равен радиусу шара. Объём конуса равен 39. Найдите объём шара.
78). Конус вписан в шар (см. рисунок). Радиус основания конуса равен радиусу шара. Объём конуса равен 47. Найдите объём шара.
79). Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Радиус сферы равен 26√2. Найдите образующую конуса.
80). Около конуса описана сфера (сфера содержит окружность основания конуса и его вершину). Центр сферы совпадает с центром основания конуса. Образующая конуса равна 36√2. Найдите радиус сферы.
81). Прямоугольный параллелепипед описан около сферы радиуса 16. Найдите его объём.
82). Шар, объём которого равен 18, вписан в цилиндр. Найдите объём цилиндра.
83). Цилиндр, объём которого равен 18, описан около шара. Найдите объём шара.
84). Шар вписан в цилиндр. Площадь поверхности шара равна 120. Найдите площадь полной поверхности цилиндра.
85). Шар вписан в цилиндр. Площадь поверхности шара равна 29. Найдите площадь полной поверхности цилиндра.
86). Цилиндр описан около шара. Объём шара равен 50. Найдите объём цилиндра.
87). Прямоугольный параллелепипед описан около сферы радиуса 8,5. Найдите его объём.
88). Прямоугольный параллелепипед описан около сферы радиуса 17. Найдите его объём.
89). Радиусы двух шаров равны 9 и 12. Найдите радиус шара, площадь поверхности которого равна сумме площадей поверхностей двух данных шаров.
90). Первая цилиндрическая кружка вдвое выше второй, зато вторая в три раза шире. Найдите отношение объёма второй кружки к объёму первой.
91). В кубе ABCDA1B1C1D1 найдите угол между прямыми BA1 и D1C1. Ответ дайте в градусах.
92). В кубе ABCDA1B1C1D1 найдите угол между прямыми CD1 и AD. Ответ дайте в градусах.
93). В кубе ABCDA1B1C1D1 найдите угол между прямыми AC и BB1. Ответ дайте в градусах.
94). В кубе ABCDA1B1C1D1 найдите угол между прямыми AB1 и CD. Ответ дайте в градусах.
94). В кубе ABCDA1B1C1D1 найдите угол между прямыми A1D и B1D1. Ответ дайте в градусах.
95). В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=9, AD=12, AA1=18. Найдите синус угла между прямыми A1D1 и AC.
96). В кубе ABCDA1B1C1D1 найдите угол между прямыми AC и BC1. Ответ дайте в градусах.
97). В кубе ABCDA1B1C1D1 найдите угол между прямыми BC1 и A1B1. Ответ дайте в градусах.
98). В кубе ABCDA1B1C1D1 найдите угол между прямыми CB1 и AD. Ответ дайте в градусах.
99). В кубе ABCDA1B1C1D1 найдите угол между прямыми BA1 и AD1. Ответ дайте в градусах.
100). В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=8, AD=6, AA1=21. Найдите синус угла между прямыми A1D1 и AC.
101). В кубе ABCDA1B1C1D1 найдите угол между прямыми CB1 и C1D1. Ответ дайте в градусах.
102). В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=8, AD=22, AA1=6. Найдите синус угла между прямыми C1D и AB.
103). В прямоугольном параллелепипеде ABCDA1B1C1D1 известны длины рёбер: AB=6, AD=8, AA1=9. Найдите синус угла между прямыми CD и A1C1.
104). В кубе ABCDA1B1C1D1 найдите угол между прямыми BD и A1D1. Ответ дайте в градусах.
105). В кубе ABCDA1B1C1D1 найдите угол между прямыми CD1 и BC1. Ответ дайте в градусах.
|
106). Дана правильная четырёхугольная призма ABCDA1B1C1D1, площадь основания которой равна 6, а боковое ребро равно 7. Найдите объём многогранника, вершинами которого являются точки A, B, C, A1, B1. |
107).Впрямоугольномпараллелепипеде ABCDA1B1C1D1 известно,что AB=9, BC=6,
AA1=5. Найдите объём многогранника, вершинами которого являются точки A, B, C, B1.

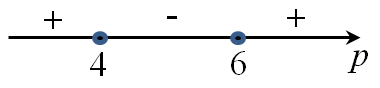 Следовательно,
Следовательно,