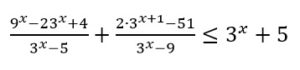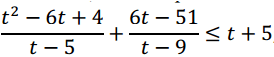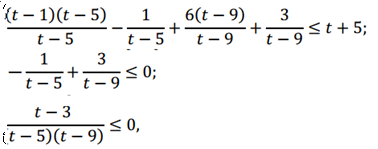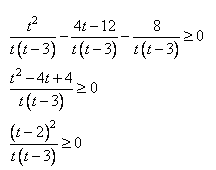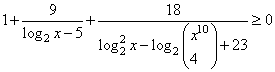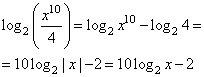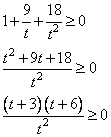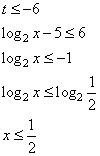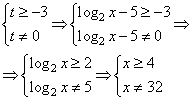Путеводитель по неравенствам задачи 15 егэ по математике

Решите неравенство

!!! Смотрите также подборку задач С3 (с ответами) для подготовки к ЕГЭ !!!

Список всех неравенств (С3), разобранных на сайте:   

-11. (Реальный ЕГЭ, 2021) Решите неравенство:

(9^x-3^{x+1})^2+8cdot 3^{x+1}<8cdot 9^x+20.

Ответ: (-infty;0)cup (log_32;log_35). Решение

-10. (Реальный ЕГЭ, 2021) Решите неравенство: 16^{frac{1}{x}-1}-4^{frac{1}{x}-1}-2geq 0.

Ответ: (0;frac{2}{3}]. Решение

-9. (Демо ЕГЭ, 2020) Решите неравенство

log_{11}(8x^2+7)-log_{11}(x^2+x+1)geq log_{11}(frac{x}{x+5}+7).

Ответ: (-infty;-12]cup (-frac{35}{8};0].  Видеорешение New*

-8. (Реальный ЕГЭ, 2019) Решите неравенство

log_{frac{1}{3}}(18-9x)<log_{frac{1}{3}}(x^2-6x+5)+ log_{frac{1}{3}}(x+2).

Ответ: (-2;1). Решение Видеорешение New*

-7. (Реальный ЕГЭ, 2019) Решите неравенство log_4(6-6x)<log_4(x^2-5x+4)+ log_4(x+3).

Ответ: (-2;1). Решение

-6. (Реальный ЕГЭ, 2018) Решите неравенство

log_7(2x^2+12)-log_7(x^2-x+12)geq log_7(2-frac{1}{x}).

Ответ: (frac{1}{2};frac{4}{3}]cup [3;+infty). Решение  Видеорешение New*

-5. (Досрочный резервный ЕГЭ, 2018) Решите неравенство  frac{6^x-4cdot 3^x}{xcdot 2^x-5cdot 2^x-4x+20}leq frac{1}{x-5}.

Ответ: [0;2)cup (2;5). Решение Видеорешение New*

-4. (Досрочный ЕГЭ, 2018) Решите неравенство 3^{x^2}cdot 5^{x-1}geq 3.

Ответ: (-infty;-1-log_35]cup [1;+infty). Решение Видеорешение New*

-3. (Резервный ЕГЭ, 2017) Решите неравенство frac{1}{3^x-1}+frac{9^{x+frac{1}{2}}-3^{x+3}+3}{3^x-9}geq 3^{x+1}.

Ответ: (0;1]cup (2;+infty). Решение

-2. (Резервный ЕГЭ, 2017) Решить неравенство 9^{4x-x^2-1}-36cdot 3^{4x-x^2-1}+243geq 0.

Ответ: (-infty;1]cup {2}cup[3;+infty). Решение Видеорешение New*

-1. (Реальный ЕГЭ, 2017) Решить неравенство frac{log_2(4x^2)+35}{log_2^2x-36}geq -1.

Ответ: (0;frac{1}{64})cup{frac{1}{2}}cup (64;+infty). Решение

0. (Реальный ЕГЭ, 2017) Решить неравенство frac{log_4(64x)}{log_4x-3}+frac{log_4x-3}{log_4(64x)}geq frac{log_4x^4+16}{log_4^2x-9}.

Ответ: (0;frac{1}{64})cup{4}cup (64;+infty). Решение

1. (Досрочн. ЕГЭ, 2017) Решите неравенство log_2^2(25-x^2)-7log_2(25-x^2)+12geq 0.

 Ответ: (-5;-sqrt{17}]cup [-3;3]cup [sqrt{17};5). Решение  Видеорешение New*

2. (Резервн. ЕГЭ, 2016) Решите неравенство

frac{9^x-3^{x+1}-19}{3^x-6}+frac{9^{x+1}-3^{x+4}+2}{3^x-9}leq 10cdot 3^x+3.

Ответ: (-infty;1]cup (log_36;2).  Решение Видеорешение New*

 3. (ЕГЭ, 2016) Решите неравенство

frac{25^x-5^{x+2}+26}{5^x-1}+frac{25^x-7cdot 5^{x}+1}{5^x-7}leq 2cdot 5^x-24.

Ответ: (-infty;0)cup [1;log_57).  Решение

 4. (Т/Р, 2016) Решите неравенство

2^{frac{x}{x+1}}-2^{frac{5x+3}{x+1}}+8leq 2^{frac{2x}{x+1}}.

Ответ: (-infty;-1)cup [0;+infty). Решение

 5. (Досрочн. ЕГЭ, 2016) Решите неравенство

(5x-13)log_{2x-5}(x^2-6x+10)geq 0.

Ответ: (2,5;2,6]cup (3;+infty). Решение Видеорешение New*

 6. (ЕГЭ, 2015) Решите неравенство

frac{3}{(2^{2-x^2}-1)^2}-frac{4}{2^{2-x^2}-1}+1geq 0.

Ответ: (-infty;-sqrt2)cup (-sqrt2;-1]cup{0}cup [1;sqrt2)cup(sqrt2;+infty). Решение

7. (Т/Р 2013) Решите систему неравенств

begin{cases} 9^x-5cdot 3^x+4geq 0,;(1)& &log_{frac{3x^2+4x+1}{4x+1}}|frac{x}{2}|leq 0;;(2) end{cases}

Ответ: (-frac{1}{3};0)cup[log_53;1]. Решение

8. (Т/Р 2013) Решите систему неравенств

begin{cases} 1-frac{2}{|x|}leq frac{23}{x^2},;(1)& & frac{2-(x-5)^{-1}}{2(x-5)^{-1}-1}leq -0,5;;(2) end{cases}

Ответ: [2-2sqrt6;0 )cup (0;6). Решение

9. (Т/Р 2013) Решите систему неравенств

 begin{cases} log_{6x^2-x-1}(2x^2-5x+3)geq 0,& & frac{12x^2-31x+14}{4x^2+3x-1}leq 0; end{cases}

Ответ: (-2;-1)cup [frac{1}{10};frac{1}{6})cup{frac{3}{2}}. Решение

10. (ДЕМО 2014) Решите систему неравенств

begin{cases} 4^xle9cdot 2^x+22,& & log_3(x^2-x-2)le1+log_3frac{x+1}{x-2}; end{cases}

Ответ: (2;log_211]. Решение

11. (ЕГЭ 2013) Решите систему неравенств

begin{cases}log_{6-x}frac{x+5}{(x-6)^{12}}ge - 12,& & x^3+7x^2+frac{30x^2+7x-42}{x-6}le 7;& end{cases}

Ответ: {-4;0}cup [3;5). Решение

12. (Т/Р А. Ларина) Решите неравенство

log_4(x^2-4)^2+log_2(frac{x-1}{x^2-4})>0.

Ответ: (-2;0)cup (2;+infty). Решение

13. (Т/Р А. Ларина) Решите неравенство

log_5(2+x)(x-5)>log_{25}(x-5)^2.

Ответ: (-infty;-3)cup (5;+infty). Решение

14. (Т/Р А. Ларина) Решите неравенство

 sqrt{7-log_2x^2}+log_2x^4>4.

Ответ: [-8sqrt2;-sqrt[8]{8})cup (sqrt[8]{8};8sqrt2]. Решение

15. (Т/Р А. Ларина) Решите неравенство

frac{1}{2}log_{x-1}(x^2-8x+16)+log_{4-x}(-x^2+5x-4)>3.

Ответ: (2;2,5)cup (2,5;3). Решение Видеорешение  

16. (Т/Р А. Ларина) Решите неравенство

log_2(5-x)log_2(x+1)leq log_2frac{(x^2-4x-5)^2}{16}.

Ответ: (-1;1]cup [3;5). Решение

17. (Т/Р А. Ларина) Решите неравенство

frac{x^4-2x^2+1}{2x^2-x-6}geq frac{1-2x^2+x^4}{2x^2-7x+6}.

Ответ: (-infty;-1,5)cup{-1;1}cup(1,5;2). Решение

18. (Т/Р А. Ларина) Решите неравенство

frac{(3^x-3)^3}{2cdot 3^x-4}leq frac{27^x-2cdot 3^{2x+1}+3^{x+2}}{3^x-9^x+2}.

Ответ: [frac{1}{2};log_32)cup{1}. Решение

19. (Т/Р А. Ларина) Решите неравенство

log_x(log_2(4^x-6))leq 1.

Ответ: (log_47;log_23]. Решение

20. (Т/Р А. Ларина) Решите неравенство

frac{4^{x^2-2x}-16cdot 2^{(x-1)^2}+35}{1-2^{(x-1)^2}}leq 4^xcdot 2^{(x-2)^2}.

Ответ: (-infty;1)cup (1;+infty). Решение

21. (Т/Р А. Ларина) Решите неравенство

frac{log_{x+0,5}(4^x-3cdot 2^{x+1}+8)}{log_{sqrt{x+0,5}}2}leq x.

Ответ: [2-log_23;0,5)cup (0,5;1)cup (2;+infty). Решение

22. (Т/Р А. Ларина) Решите неравенство

sqrt{1+x^2}-xleq frac{5}{2sqrt{1+x^2}}.

Ответ: [-frac{3}{4};+infty). Решение

23. (Т/Р А. Ларина) Решите неравенство

frac{1}{2}log_{134+tg^2(frac{x}{2})}(21x+16)<log_{134+tg^2(frac{x}{2})}(20+sqrt{x-4}).

Ответ: [4;3pi)cup (3pi;5pi)cup (5pi;7pi)cup (7pi;9pi)cup (9pi;29). Решение

24. (Т/Р А. Ларина) Решите неравенство

log_2(log_3(log_4(log_5^2(133-2x)+7)+25)-1)leq 1.

Ответ: [4;66,496]. Решение

25. (Т/Р А. Ларина) Решите неравенство

frac{x^3-18x^2+89x-132}{(sqrt x-2)(5^x-25)(|x|-1)}leq 0.

Ответ: (1;2)cup [3;4)cup(4;11]. Решение

26. (Т/Р А. Ларина) Решите неравенство

2sqrt{x+131}-frac{5}{sqrt{x+131}-3}leq 15.

Ответ: [-131;-124,75]cup (-122;-67]. Решение

27. (Т/Р А. Ларина) Решите неравенство

x^2+xsqrt{3-3x^2}geq 0,5+x.

Ответ: [-1;-sinfrac{5pi}{18}]cup [frac{1}{2};sinfrac{7pi}{18}]. Решение

28. (Т/Р А. Ларина) Решите неравенство

log_{x+1}2leq log_{3-x}2.

Ответ: (-1;0)cup [1;2). Решение

29. (Т/Р А. Ларина) Решите неравенство

 frac{2x^2}{x+3}+frac{x+3}{x^2}leq 3.

Ответ: (-infty;-3)cup [frac{1-sqrt{13}}{2};-1]cup [frac{3}{2};frac{1+sqrt{13}}{2}]. Решение

30. (Т/Р А. Ларина) Решите неравенство

log_{2x}(x+4)cdot log_x(2-x)leq 0.

Ответ: (0,5;1)cup (1;2). Решение

31. (Т/Р А. Ларина) Решите неравенство

 log_{(x-2)^2}frac{5-x}{4-x}leq 1+log_{(2-x)^2}frac{1}{x^2-9x+20}.

Ответ: (1;2)cup (2;3)cup [3,5;4)cup (5;+infty). Решение

33. (Т/Р А. Ларина) Решите неравенство

frac{2sqrt{x+3}}{x+1}leq frac{3sqrt{x+3}}{x+2}.

Ответ: {-3}cup (-2;-1)cup [1;+infty). Решение

34. (Т/Р А. Ларина) Решите неравенство

log_{9x}27leq frac{1}{log_3x}.

Ответ: (0;frac{1}{9})cup(1;3]. Решение

35. (Т/Р А. Ларина) Решите неравенство

frac{7-71cdot 3^{-x}}{3^x+10cdot 3^{-x}-11}leq 1.

Ответ: (-infty;0)cup{2}cup (log_310;+infty). Решение

36. (Т/Р А. Ларина) Решите неравенство

log_x512leq log_2frac{64}{x}.

Ответ: (0;1)cup{8}. Решение

37. (Т/Р А. Ларина) Решите неравенство

xsqrt x+2sqrt x+3leq frac{6}{2-sqrt x}.

Ответ: {0}cup [1;4). Решение

38. (Т/Р А. Ларина) Решите неравенство

log_x(11x-2x^2)+log_{11-2x}x^4leq 5.

Ответ: (0;1)cup{-1+2sqrt3}(5;5,5).  Решение

39. (Т/Р А. Ларина) Решите неравенство

frac{log_{(-36x)}6^{x+2}}{log_{36}6^{x+2}}leq log_{x^2}36.

Ответ: [-36;-2)cup (-2;-1)cup (-frac{1}{36};0). Решение

40. (Т/Р А. Ларина) Решите неравенство

log^2_2frac{x-5}{x+2}-log_2(x-5)^2cdot log_{(x-5)^2}frac{x-5}{x+2}geq 0.

Ответ: [-9;-2)cup (5;6)cup (6;+infty). Решение

41. (Т/Р А. Ларина) Решите неравенство

log_x(1-2x)leq 3-log_{(frac{1}{x}-2)}x.

Ответ: (0;frac{1}{3})cup{sqrt2-1}. Решение

42. (Т/Р А. Ларина) Решите неравенство

log_3(x+1,5)-log_{sqrt2}(3,5-x)+log_{x+1,5}3cdot log_2^2(3,5-x)leq 0.

Ответ: (-1,5;-0,5)cup {1,5}. Решение

43. (Т/Р А. Ларина) Решите неравенство

frac{log_{3-x}sqrt x}{1-log_{x^2}(3-x)}leq 1.

Ответ: (0;1)cup (1;frac{sqrt{13}-1}{2})cup{1,5}cup(2;3). Решение

44. (Т/Р А. Ларина) Решите неравенство

|6-7^x|leq (7^x-6)cdot log_6(x+1).

Ответ: (-1;-frac{5}{6}]cup{log_76}[5;+infty). Решение

45. (Т/Р А. Ларина) Решите неравенство

(x+3)(x+1)+3(x+3)sqrt{frac{x+1}{x+3}}+2leq 0.

Ответ: [-2-sqrt5;-2-sqrt2]. Решение

46. (Т/Р А. Ларина) Решите неравенство

log_{5-x}(5+9x-2x^2)+log_{1+2x}(x^2-10x+25)^2leq 5.

Ответ: (-0,5;0)cup{6-2sqrt3}cup (4;5). Решение

47. (Т/Р А. Ларина) Решите неравенство

log_2(x^2-8x+6)geq 2+frac{1}{2}log_2(2x-1).

Ответ: (frac{1}{2};2-sqrt2]cup [6+sqrt{10};+infty). Решение

48. (Т/Р А. Ларина) Решите неравенство

frac{sqrt{2x-1}+sqrt{x-3}-3x+10}{sqrt{2x^2-7x+3}}>2.

Ответ: (3;25-6sqrt{13}). Решение

49. (Т/Р А. Ларина) Решите неравенство

frac{6-3x+sqrt{2x^2-5x+2}}{3x-sqrt{2x^2-5x+2}}geq frac{1-x}{x}.

Ответ: [-1;0)cup (frac{2}{7};frac{1}{2}]cup [2;+infty). Решение

50. (Т/Р А. Ларина) Решите неравенство

log_{4x}2x-log_{2x^2}4x^2geq -frac{3}{2}.

Ответ: (0;frac{1}{4})cup [frac{1}{sqrt8};frac{1}{sqrt2})cup [1;+infty). Решение

51. (Т/Р А. Ларина) Решите неравенство

frac{log_2(2cdot 4^x-11cdot 2^x+9)}{x+3}leq 1.

Ответ: (-infty;-3)cup [-1;0)cup (2log_23-1;2log_23]. Решение

52. (Т/Р А. Ларина) Решите неравенство

log_x(3-x)log_x(4-x)-log_x(x^2-7x+12)+1geq 0.

Ответ: (0;1)cup (1;1,5]cup [2;3). Решение

53. (Т/Р А. Ларина) Решите неравенство

frac{sqrt{6+x-x^2}}{log_2(5-2x)}leq frac{sqrt{6+x-x^2}}{log_2(x+4)}.

Ответ: [-2;frac{1}{3}]cup (2;2,5). Решение

54. (Т/Р А. Ларина) Решите неравенство

log_3(x^2-4x+5)leq frac{2x}{log_{x^2-4x+5}(9^x+3^x-12)}.

Ответ: (log_3frac{-1+sqrt{53}}{2};2)cup (2;log_312]. Решение

55. (Т/Р А. Ларина) Решите неравенство

log_x(frac{100}{x})leq sqrt{log_x(100x^5)}.

Ответ: (0;frac{1}{sqrt[5]100}]cup [sqrt{10};+infty). Решение

56. (Т/Р А. Ларина) Решите неравенство

log_{2x^2-x}(3x-1)cdot log_{2x-x^2}(3-2x)geq 0.

Ответ: [frac{2}{3};1)cup (1;1,5). Решение

57. (Т/Р А. Ларина) Решите неравенство

log_{2x}(x-4)log_{x-1}(6-x)<0.

Ответ: (4;5)cup (5;6). Решение

58. (Т/Р А. Ларина) Решите неравенство

 log_3(x+6)leq (1-log_{9x}(6-x))cdot log_3(9x).

Ответ: [3;6). Решение

59. (Т/Р А. Ларина) Решите неравенство

sqrt{1-log_5(x^2-2x+2)}<frac{1}{2}log_{sqrt5}(5x^2-10x+10).

Ответ: [-1;1)cup (1;3]. Решение

60. (Т/Р А. Ларина) Решите неравенство

log_xlog_2(3-4^{x-1})leq 1.

Ответ: (0;1)cup (1;1,5). Решение

61. (Т/Р А. Ларина) Решите неравенство

frac{log_5(x^2-4x-11)^2-log_{11}(x^2-4x-11)^3}{2-5x-3x^2}geq 0.

Ответ: (-infty;-2)cup (-2;2-sqrt{15})cup [6;+infty). Решение

62. (Т/Р А. Ларина) Решите неравенство

frac{log_{2^{x+3}}4}{log_{2^{x+3}}(-4x)}leq frac{1}{log_2(log_{frac{1}{2}}2^x)}.

Ответ: [-4;-3)cup (-3;-1)cup (-frac{1}{4};0). Решение

63. (Т/Р А. Ларина) Решите неравенство

log_x(1-2x)leq 3-log _{frac{1}{x}-2}x.

Ответ:  (0;frac{1}{3})cup{-1+sqrt2}. Решение

64. (Т/Р А. Ларина) Решите неравенство

log_2(5-x)cdot log_{x+1}frac{1}{8}geq -6.

Ответ: (-1;0)cup [1;5). Решение

65. (Т/Р А. Ларина) Решите неравенство

frac{log_712}{log_7(x^2-9)}geq frac{log_5(x^2+8x+12)}{log_5(x^2-9)}.

Ответ: [-8;-6)cup (3;sqrt{10}). Решение

66. (Т/Р А. Ларина) Решите неравенство

4log_2x+log_2frac{x^2}{8(x-1)}leq 4-log_2(x-1)-log^2_2x.

Ответ: (1;2]. Решение

67. (Т/Р А. Ларина) Решите неравенство

sqrt{1-log_5(x^2-2x+2)}<log_5(5x^2-10x+10).

Ответ: [-1;1)cup(1;3]. Решение 

68. (Т/Р А. Ларина) Решите неравенство

log_{frac{x^2-18x+91}{90}}(5x-frac{3}{10})leq0.

Ответ: [frac{13}{50};9+4sqrt5). Решение

69. (Т/Р А. Ларина) Решите неравенство

log_{cosx^2}(frac{3}{x}-2x)<log_{cosx^2}(2x-1).

Ответ: (frac{1}{2};1). Решение

70. (Т/Р А. Ларина) Решите систему неравенств

begin{cases} log_2(5-x)(2-x)>log_4(x-2)^2,& &frac{2^x-2^{2-x}-3}{2^x-2}geq 0; end{cases}

Ответ: (-infty;1)cup(6;+infty). Решение

71. (Т/Р А. Ларина) Решите систему неравенств

begin{cases} 4^{x+1}-33cdot 2^x+8leq 0,& & 2log_2frac{x-1}{x+1,3}+log_2(x+1,3)^2geq 2. end{cases}

Ответ:

Показать скрытое содержание
{-4}cup (3,7;4] Решение

72. (Т/Р А. Ларина) Решите систему неравенств

begin{cases} frac{|x-5|-1}{2|x-6|-4}leq 1,& & frac{1}{4}log_2(x-2)-frac{1}{2}leq log_{frac{1}{4}}sqrt{x-5}. end{cases}

Ответ: (5;6]. Решение

73. (Т/Р А. Ларина)  Решите неравенство

frac{x^2-x+1}{x-1}+frac{x^2-3x-1}{x-3}leq 2x+2.

Ответ: (-infty;1)cup{2}cup (3;+infty). Решение

 74. (Т/Р А. Ларина)  Решите неравенство

frac{2^{cosx}-1}{3cdot 2^{cosx}-1}leq 2^{1+cosx}-2.

Ответ: [-frac{pi}{2}+2pi n;frac{pi}{2}+2pi n]cup{pi+2pi n}, nin Z. Решение

75. (Т/Р А. Ларина)  Решите неравенство

frac{5(x-6sqrt x+8)}{x-16}leq sqrt x-2.

Ответ: [0;1]cup [4;16)cup (16;+infty). Решение

76. (Т/Р А. Ларина)  Решите неравенство

frac{2^{x+1}sqrt{2^{x+1}-1}}{2^x-15}leq frac{sqrt{2^{x+1}-1}}{2^x-8}.

Ответ: {-1}cup [0;log_215-1]cup (3;log_215). Решение

77. (Т/Р А. Ларина) Решите неравенство

frac{4^{x}-3cdot 2^x+3}{2^x-2}+frac{4^{x}-5cdot 2^x+3}{2^x-4}leq 2^{x+1}.

Ответ: (-infty;1)cup{log_23}cup (2;+infty). Решение

78. (Т/Р А. Ларина)  Решите неравенство

log_{6x-x^2-8}(5-x)geq log_{6x-x^2-8}(4x^2-17x+20).

Ответ: [2,5;3)cup (3;4). Решение

79. (Т/Р А. Ларина) Найдите область определения функции y=sqrt{1-frac{2^{x+1}-14}{4^x-2^{x+2}-5}}.

Ответ: {log_23}cup (log_25;+infty). Решение

80. (Т/Р А. Ларина)  Решите неравенство |3^{x+1}-9^x|+|9^x-5cdot 3^x+6|leq 6-2cdot 3^x.

Ответ: (-infty;log_32)cup{1}. Решение

81. (Т/Р А. Ларина)   Решите неравенство frac{9}{3+log_3xcdot log_3frac{9}{x}}leq log_3^2x-log_3frac{x^2}{27}.

Ответ: (0;frac{1}{3})cup{1;9}cup (27;+infty). Решение

82. (Т/Р А. Ларина)  Решите неравенство frac{8^x-3cdot 2^{2x+1}+2^{x+3}+1}{4^x-3cdot 2^{x+1}+8}geq 2^x-1.

Ответ: (-infty;1)cup{log_23}cup (2;+infty). Решение

83. (Т/Р А. Ларина) Решите неравенство frac{(2^x-2)^3}{2^{x+2}-12}geq frac{8^x-4^{x+1}+2^{x+2}}{9-4^x}.

Ответ: (-infty;0]cup{1}cup (log_23;+infty). Решение

84. (Т/Р А. Ларина)  Решите неравенство sqrt{4sqrt3 sinfrac{pi x}{3}-4sin^2frac{pi x}{3}-3}cdot (log_{frac{2}{3}}frac{3x+22}{14-x})leq 0.

Ответ:  {-5;-4;1;2;7;8;13}. Решение

85. (Т/Р, 2017)  Решите неравенство 3^{|x|}-8-frac{3^{|x|}+9}{9^{|x|}-4cdot 3^{|x|}+3}leq frac{5}{3^{|x|}-1}.

Ответ: [-2;-1)cup [-log_32;0)cup (0;log_32]cup (1;2]. Решение

86. (Т/Р А. Ларина)  Решите неравенство

frac{sqrt{(x-1)(x-2)log_{x^2}frac{2}{x^2}}}{|x+2|}>frac{x^2-3x+1+log_{|x|}sqrt2}{x+2}.

Ответ: [sqrt2;2]. Решение

87. (Т/Р А. Ларина) Решите неравенство

3sqrt{x^2+6x+9}-(sqrt{3x+7})^2-2|x-1|leq 0.

Ответ: [-frac{7}{3};0]cup[2;+infty). Решение

88. (Т/Р А. Ларина)  Решите неравенство

2^{1+2x-x^2}-3geq frac{3}{2^{2x-x^2}-2}.

Ответ: [1-sqrt2;1)cup (1;1+sqrt2]. Решение

89. (Т/Р А. Ларина)  Решите неравенство

frac{log_2(|x|-1)log_2(frac{|x|-1}{16})+3}{sqrt{log_2(7-|x+4|)}}geq 0.

Ответ: (-10;-9]cup[-3;-1)cup (1;2). Решение

90. (Т/Р А. Ларина)  Решите неравенство

frac{4^{sqrt{x-1}}-5cdot 2^{sqrt{x-1}}+4}{log^2_2(7-x)}}geq 0.

Ответ: {1}cup [5;6)cup (6;7). Решение

91. (Т/Р А. Ларина) Решите неравенство

frac{2^{x+1}-7}{4^x-2^{x+1}-3}leq 1.

Ответ: {1}cup (log_23;+infty). Решение

92. (Т/Р А. Ларина) Решите неравенство

frac{5-7log_x3}{log_3x-log_x3}geq 1.

Ответ: (frac{1}{3};1)cup(1;3)cup [9;27]. Решение

93. (Т/Р А. Ларина) Решите неравенство

frac{x+6sqrt x+28}{120}leq frac{2-sqrt x}{x-6sqrt x+8}.

Ответ: [0;4)cup (4;16). Решение

94. (Т/Р А. Ларина) Решите неравенство

frac{9}{log_2(4x)}leq 4-log_2x.

Ответ: (0;0,25)cup left { 2 right }. Решение

 95. (Т/Р А. Ларина) Решите неравенство

frac{1}{log_3(2x-1)cdot log_{x-1}9}< frac{log_3sqrt{2x-1}}{log_3(x-1)}.

Ответ: (1;1,5)cup (2;+infty). Решение

96. (Т/Р А. Ларина) Решите неравенство

log_{frac{5-x}{4}}(x-2)cdot log_{x-2}(6x-x^2)geq log_{frac{5-x}{4}}(3x^2-10x+15).

Ответ: [2,5;3)cup (3;5). Решение

97. (Т/Р А. Ларина) Решите неравенство

log_3(2^x+1)+log_{2^x+1}3geq 2,5.

Ответ: (-infty;log_2(sqrt3-1)]cup [3;+infty). Решение

98. (Т/Р А. Ларина) Решите неравенство

frac{83-17cdot 2^{x+1}}{4^x-2^{x+2}+3}leq 4^x+3cdot 2^{x+1}+17.

Ответ: [0;1,5)cup(log_23;+infty). Решение

99. (Т/Р А. Ларина) Решите неравенство

xlog_2frac{x}{2}+log_x4leq 2.

Ответ: (0;1)cup {2}. Решение

100. (Т/Р А. Ларина) Решите неравенство

(3^x-2^x)(6^{x+1}+1)+6^xgeq 3^{2x+1}-2^{2x+1}.

Ответ: {-1}cup [0;+infty). Решение

 101. (Т/Р А. Ларина) Решите неравенство

2sqrt{sin^2x-sinx-1}geq cos^2x+sinx+3.

Ответ: -frac{pi}{2}+2pi n,nin Z. Решение

102. (Т/Р А. Ларина)  Решите неравенство

frac{log_8x}{log_2(1+2x)}leq frac{log_2sqrt[3]{1+2x}}{log_2x}.

Ответ: (0;0,5]cup (1;+infty).  Решение

103. (Т/Р А. Ларина) Решите неравенство

-3log_{(x-1)}frac{1}{3}+log_{frac{1}{3}}(x-1)>2|log_{frac{1}{3}}(x-1)|.

Ответ: (2;4). Решение

104. (Т/Р 283 А. Ларина) Решите неравенство

log_{sqrt3-1}(9^{|x|}-2cdot 3^{|x|})leq log_{sqrt3-1}(2cdot 3^{|x|-3).

Ответ: (-infty;-1]cup [1;+infty) Видеорешение

Источник

Задание 14 Профильного ЕГЭ по математике можно считать границей между «неплохо сдал ЕГЭ» и «поступил в вуз с профильной математикой». Здесь не обойтись без отличного знания алгебры. Потому что встретиться вам может любое неравенство: показательное, логарифмическое, комбинированное (например, логарифмы и тригонометрия). И еще бывают неравенства с модулем и иррациональные неравенства. Некоторые из них мы разберем в этой статье.

Хотите получить на Профильном ЕГЭ не менее 70 баллов? Учитесь решать неравенства!

Темы для повторения:

New 

Решаем задачи из сборника И. В. Ященко, 2021

Квадратичные неравенства

Метод интервалов 

Уравнения и неравенства с модулем 

Иррациональные неравенства

Показательные неравенства

Логарифмические неравенства

Метод замены множителя (рационализации)

Решение неравенств: основные ошибки и полезные лайфхаки

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 8, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 32, задача 15

Решаем задачи из сборника И. В. Ященко, 2020. Вариант 36, задача 15

Логарифмические неравенства повышенной сложности

Разберем неравенства разных типов из вариантов ЕГЭ по математике.

Дробно-рациональные неравенства 

1. Решите неравенство:

frac{{ 2}}{{ 0,5x}sqrt{{ 5}}{ -}{ 1}}{ +}frac{{ 0,5x}sqrt{{ 5}}{ -}{ 2}}{{ 0,5x}sqrt{{ 5}}{ -}{ 3}} geq { 2.}

Сделаем замену { 0,5x}sqrt{{ 5}}{ -}{ 2=t}.

Тогда { 0,5x}sqrt{{ 5}}{ -}{ 1=t+1}, а { 0,5x}sqrt{{ 5}}{ -}{ 3=t-1}.

Получим:

frac{{ 2}}{{ t+1}}{ +}frac{{ t}}{{ t-1}} geq { 2};

frac{{ 2}{ t}{ -}{ 2+}{{ t}}^{{ 2}}{ +}{ t}}{{{ t}}^{{ 2}}{ -}{ 1}}{ -}{ 2} geq{ 0};

frac{{{ t}}^{{ 2}}{ +3}{ t}{ -}{ 2-2}{{ t}}^{{ 2}}{ +2}}{{{ t}}^{{ 2}}{ -}{ 1}} geq { 0};

frac{{ 3}{ t}{ -}{{ t}}^{{ 2}}}{{{ t}}^{{ 2}}{ -}{ 1}} geq { 0};

frac{{ t}left({ t}{ -}{ 3}right)}{left({ t}{ -}{ 1}right)left({ t}{ +1}right)}le { 0}.

Решим неравенство относительно t методом интервалов:

Получим:

left[ begin{array}{c}{ -}{ 1 textless t}le { 0} \{ 1 textless t}le { 3} end{array}right..

Вернемся к переменной x: left[ begin{array}{c} -1 textless 0,5xsqrt{5}-2leq0 \ 1 textless 0,5xsqrt{5}-2leq 3 end{array} right. .

left[ begin{array}{c} {{2}over{sqrt{5}}} textless xleq {{4}over{sqrt{5}}}\ {{6}over{sqrt{5}}} textless xleq {{10}over{sqrt{5}}} end{array} right. .

Ответ: xin left(frac{{ 2}}{sqrt{{ 5}}};frac{{ 4}}{sqrt{{ 5}}}right]cup left(frac{{ 6}}{sqrt{{ 5}}};{ 2}sqrt{{ 5}}right].

Показательные неравенства

2. Решите неравенство 2^x+17cdot 2^{3-x}le 25.

2^x+17cdot frac{8}{2^x}le 25.

Сделаем замену 2^x=t,t textgreater 0. Получим:

t+17cdot frac{8}{t}-25le 0. Умножим неравенство на t textgreater 0.

t^2-25t+136le 0.

Дискриминант квадратного уравнения t^2-25t+136=0.

D={left(-25right)}^2-4cdot 136=625-544=81. Значит, корни этого уравнения: left[ begin{array}{c}t_1=17 \t_2=8 end{array}.right.

Разложим квадратный трехчлен t^2-25t+136 на множители.

t^2-25t+136le 0 Longleftrightarrow left(t-17right)left(t-8right)le 0.

8le tle 17. Вернемся к переменной x.

8le 2^xle 17.

Внимание. Сначала решаем неравенство относительно переменной t. Только после этого возвращаемся к переменной x. Запомнили?

2^3le 2^xle 2^{{{log }_2 17}};

3le xle {{log }_2 17};

Ответ: xin left[3;{{log }_2 17}right].

Следующая задача — с секретом. Да, такие тоже встречаются в вариантах ЕГЭ.

3. Решите неравенство 2^{2x-x^2-1}+frac{1}{2^{2x-x^2}-1}le 2.

Сделаем замену 2^{2x-x^2}=t,t textgreater 0. Получим:

frac{t}{2}+frac{1}{t-1}-2le 0;

frac{t^2-t+2-4t+4}{2left(t-1right)}le 0;

frac{t^2-5t+6}{t-1}le 0;

frac{left(t-2right)left(t-3right)}{t-1}le 0.

left[ begin{array}{c}t textless 1 \2le tle 3 end{array} .right.

Вернемся к переменной x:left[ begin{array}{c}2^{2x-x^2} textless 1 \{2le 2}^{2x-x^2}le 3 end{array}.right.

Первое неравенство решим легко: 2x-x^2 textless 0. С неравенством {2le 2}^{2x-x^2} тоже все просто. Но что делать с неравенством 2^{2x-x^2}le 3? Ведь 3 = 2^{{{log }_2 3}}. Представляете, как трудно будет выразить х?

Оценим t=2^{2x-x^2}. Для этого рассмотрим функцию tleft(xright)=2^{2x-x^2}.

Сначала оценим показатель степени. Пусть zleft(xright)=2x-x^2. Это парабола с ветвями вниз, и наибольшее значение этой функции достигается в вершине параболы, при х = 1. При этом y(1) = 1.

Мы получили, что zleft(xright)le 1.

Тогда 2^{zleft(xright)}le 2, и это значит, что tleft(xright)le 2. Значение tleft(xright)=3 не достигается ни при каких х.

Но если {2le 2}^{2x-x^2} и 2^{2x-x^2}le 2, то 2^{2x-x^2}=2.

Мы получили:

left[ begin{array}{c} 2x-x^2 textless 0\ 2x-x^2=1end{array} right. Leftrightarrow left[ begin{array}{c} x(x-2) textgreater 0\ x^2-2x+1=0end{array} right. Leftrightarrow left[ begin{array}{c} x textless 0\ x textgreater 2\(x-1)^2=0end{array} right. Leftrightarrow

Leftrightarrow left[ begin{array}{c} x textless 0\ x textgreater 2\ x=1end{array}. right.

Ответ: xin left(-infty ;0right)cup left{1right}cup left(2;+infty right){ }.

Логарифмические неравенства

4. Решите неравенство 2{{log}_{frac{1}{2}} left(1-xright) textless {{log}_{frac{1}{2}} left(3x+1right)}}.

Запишем решение как цепочку равносильных переходов. Лучше всего оформлять решение неравенства именно так.

2log_{{1}over{2}}(1-x) textless log_{{1}over{2}}(3x+1)Leftrightarrow left{begin{matrix} 1-x textgreater 0\3x+1 textgreater 0 \(1-x)^2 textgreater 3x+1 end{matrix}right.Leftrightarrow left{begin{matrix} x textless 1\x textgreater -{{1}over{3}} \ 1+x^2-2x textgreater 3x+1 end{matrix}right.Leftrightarrow

Leftrightarrow left{begin{matrix} x textless 1\x textgreater {-{{1}over{3}}} \ x^2-5x textgreater 0 end{matrix}right.Leftrightarrow left{begin{matrix} x textless 1\ x textgreater {-{{1}over{3}}} \ x(x-5) textgreater 0 end{matrix} .right.

Ответ: xin left(-frac{1}{3};0right).

Следующее неравенство — комбинированное. И логарифмы, и тригонометрия!

5. Решите неравенство 2{{{log}_2}^2 {{cos}^2 x+7{{log}_2 {cos x} geq 1}}}.

2{{{log }_2}^2 {{cos }^{{ 2}} x+7{{log }_2 {cos x} geq 1}}}.

ОДЗ: {cos x} textgreater 0.

Замена {{log }_2 {cos x}=t} Rightarrow {{log }_2 {{cos }^{{ 2}} x}}=2{{log }_2 {cos x=2t}}.

2cdot {left(2tright)}^2+7t-1 geq 0;

8t^2+7t-1 geq 0;

D=7^2-4cdot 8cdot left(-1right)=49+32=81;

t_1=frac{-7-9}{16}=-1;

t_2=frac{-7+9}{16}=frac{1}{8}.

(t+1)(t-{{1}over{8}})geq 0Leftrightarrow left[ begin{array}{c} t leq -1 \ t geq {{1}over{8}} end{array} right. Leftrightarrow left[ begin{array}{c} log_2,cosx leq-1 \ log_2,cosx geq {{1}over{8}} end{array} right.
Leftrightarrow left{begin{matrix} left[ begin{array}{c} cosxleq{{1}over{2}} \ cosxgeqsqrt[8]{2} end{array} right. \ cosx textgreater 0 end{matrix}right.Leftrightarrow 0 textless cosxleq{{1}over{2}}.

Ответ: xin left(-frac{pi }{2}+2pi k;left.-frac{pi }{3}+2pi kright]right.cup left[frac{pi }{3}+2pi k;left.frac{pi }{2}+2pi kright), kright.in Z.

А вот и метод замены множителя (рационализации). Смотрите, как он применяется. А на ЕГЭ не забудьте доказать формулы, по которым мы заменяем логарифмический множитель на алгебраический.

6. Решите неравенство: {{log }_{{ 3-x}} frac{{ x+4}}{{left({ x-3}right)}^{{ 2}}}} geq { -2}.

log_{3-x}frac{x+4}{(x-3)^2}geq-2Leftrightarrow left{begin{matrix} 3-x textgreater 0\3-xneq1 \ {x+4over (x-3)^2} textgreater 0 \ log_{3-x} {{x+4}over(x-3)^2}+2geq 0 end{matrix} .right.

Мы объединили в систему и область допустимых значений, и само неравенство. Применим формулу логарифма частного, учитывая, что {left({ a-b}right)}^{{ 2}}{ =}{left({ b-a}right)}^{{ 2}}{ }. Используем также условия { 3-x textgreater 0}; , { x+4 textgreater 0.}

left{begin{matrix} x textless 3\xneq2 \ x+4 textgreater 0 \ log_{3-x}(x+4)-log_{3-x}(3-x)^2+2geq0 end{matrix}right. Leftrightarrow

Leftrightarrow left{begin{matrix} x textless 3\xneq2 \ x textgreater -4 \ log_{3-x}(x+4)geq0 end{matrix}.right.

Обратите внимание, как мы применили формулу для логарифма степени. Строго говоря, {{log }_{{ a}} {left({ b}left({ x}right)right)}^{{ 2}}{ =2}{{log }_{{ a}} left|{ b}left({ x}right)right|}}.

Поскольку { 3-}{ x}{ textgreater 0,}{{ log}}_{{ 3-x}}{left({ 3-x}right)}^{{ 2}}{ =2}{{log }_{{ 3-x}} left|{ 3-x}right|{ =}}{ 2}{{log }_{{ 3-x}} left({ 3-x}right){ =2.}}

Согласно методу замены множителя, выражение {{ log}}_{{ 3-x}}left({ x+4}right) заменим на left({ 3-x-1}right)left({ x+4-1}right).

Получим систему:

left{ begin{array}{c}{ x}ne { 2} \{ -}{ 4}{ textless x textless 3} \left({ 2-x}right)left({ x+3}right) geq { 0} end{array}.right.

Решить ее легко.

Ответ: { x}in left[{ -}{ 3};{ 2}right).

Разберем какое-нибудь нестандартное неравенство. Такое, что не решается обычными способами.

7. Решите неравенство:

{{log }_2 left(x-5right)+{{log }_3 xleq 4}}.

ОДЗ: left{ begin{array}{c}x-5 textgreater 0 \x textgreater 0 end{array}Longleftrightarrow x textgreater 5.right.

Привести обе части к одному основанию не получается. Ищем другой способ.

Заметим, что при x = 9 оба слагаемых равны 2 и их сумма равна 4.

{{log }_2 left(9-5right)={{log }_2 4=2}};

{{log }_3 9=2};

{{log }_2 left(9-5right)+{{log }_3 9=4}}.

Функции y_1=log_2 left(x-5right) и y_2 =log _3 x — монотонно возрастающие, следовательно, их сумма также является монотонно возрастающей функцией и каждое свое значение принимает только один раз.

Поскольку при x=9 значение монотонно возрастающей функции {{{ y=}log }_2 left(x-5right)+{{log }_3 x}} равно 4, при x textless 9 значения этой функции меньше 4. Конечно, при этом x textgreater 5, то есть x принадлежит ОДЗ.

Ответ: (5; 9].

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 14. Неравенства u0026#8212; профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать необходимые и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Неравенства

В задании №15 профильного уровня ЕГЭ по математике необходимо решить неравенство. Чаще всего неравенство связано с логарифмами или степенными выражениями. Для успешного выполнения необходимо хорошо оперировать данными выражениями.

Разбор типовых вариантов заданий №15 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

Решите неравенство:

[/su_note]

Алгоритм решения:
  1. Вводим подстановку.
  2. Записываем выражение неравенства в ином виде.
  3. Решаем неравенство.
  4. Возвращаемся к подстановке.
  5. Записываем ответ.
Решение:

1. Вводим замену  t = 3x . Тогда исходное неравенство примет вид:

2. Преобразуем его:

3. Отсюда получаем решение t ≤ 3; 5 < t < 9.

4. Возвратимся к переменной х.

При t ≤ 3 получим: 3x ≤ 3 , следовательно x ≤ 1

При 5 < t < 9 получим: 5 < 3x < 9, следовательно log35 < x < 2.

5. Решение исходного неравенства:  x ≤ 1 и log35 < x < 2.

Ответ: (-∞;1] (log35;2)

Второй вариант задания (из Ященко, №1)

[su_note note_color=”#defae6″]

Решите неравенство 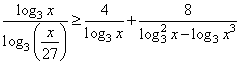http://self-edu.ru/htm/2018/ege2018_36/files/1_15.files/image001.gif .

[/su_note]

Алгоритм решения задания:
  1. Вводим замену.
  2. Записываем неравенство в новом виде.
  3. Решаем неравенство.
  4. Возвращаемся к переменной х.
  5. Записываем ответ.
Решение:

1. Вводим замену t = 3x.

2. Тогда неравенство примет вид:

3. Решаем его:

Отсюда t < 0; t = 2; t> 3.

4. Возвращаемся к переменной х.

При t < 0 получаем:

,

откуда 0 < x < 1.

При t = 2 получаем:

,

откуда x = 9.

При t > 3 получаем:

,

откуда x > 27.

5. Решения исходного неравенства:

.

Ответ: .

Третий вариант (Ященко, № 5)

[su_note note_color=”#defae6″]

Решите неравенство http://self-edu.ru/htm/2018/ege2018_36/files/5_15.files/image001.gif

[/su_note]

Алгоритм решения:
  1. Находим ОДЗ выражения в неравенстве.
  2. Преобразуем неравенство к иному виду.
  3. Вводим замену и решаем новое неравенство.
  4. Возвращаемся к переменной х.
  5. Записываем ответ.
Решение:

1. Запишем ОДЗ: .

log2х-5≠0, log2х≠5, х≠32

2. Преобразуем неравенство:

или

Получаем новое неравенство:

.

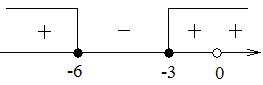
Вводим замену , тогда неравенство принимает новый вид. И его легко решить:

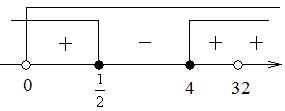
Размещаем полученные решения на числовую ось:

http://self-edu.ru/htm/2018/ege2018_36/files/5_15.files/image009.jpg

Возвращаемся к переменной х. Рассмотрим два случая:



http://self-edu.ru/htm/2018/ege2018_36/files/5_15.files/image012.jpg

Ответ:

Даниил Романович | Просмотров: 8.5k

Источник

Как подготовиться к решению задач ЕГЭ по неравенствам | 1С:Репетитор

Задание № 15 варианта КИМ ЕГЭ по математике профильного уровня

Обычно это показательное или логарифмическое неравенство. Оно может быть непростым для школьника, который не учился в профильном классе или специализированной математической школе. Чтобы его решить, необходимо не только уметь применять свойства показательной и логарифмической функций, но и знать основные методы решения алгебраических неравенств вообще. Тем не менее, именно это задание — одно из тех, которое можно выполнить на экзамене без ошибок, если заранее потренироваться в решении подобных задач.

С чего начать подготовку к решению задачи 15

Прежде всего, усвойте два понятия:
 равносильные неравенства — неравенства, множества решений которых совпадают;
 равносильные преобразования — такие действия с неравенством, при совершении которых мы заменяем данное неравенство равносильным ему, но более простым.

Необходимо следить за равносильностью преобразований на каждом шаге решения: если преобразование оказалось не равносильным, то велика вероятность получения лишних решений или их потери. В большинстве случаев эта ошибка приведет к неправильному ответу, а уж само решение точно будет неверным.
После того, как вы разобрались с равносильностью, следует изучить основные методы решения неравенств, связанных практически со всеми функциями, изучаемыми в школьном курсе математики (за исключением, может быть, тригонометрических; хотя простейшие тригонометрические неравенства могут встретиться в задаче № 13).

Основные методы решения неравенств

1. Метод интервалов для рациональных и дробно-рациональных функций.

В качестве примера рассмотрим неравенство, которое предлагалось на экзамене в 2016 году:

4x-2x+4+302x-2+4x-7⋅2x+32x-7 ≤ 2x+1-14

После ведения новой переменной t = 2x это неравенство приводится к дробно-рациональному, для решения которого как раз и нужен метод интервалов.

2. Метод равносильных переходов

Необходимо запомнить готовые схемы решения для некоторых типов неравенств с модулем, а хорошо бы  — и для иррациональных неравенств (с корнями), это может пригодиться и при решении задачи с параметром.

3. Основные методы решения показательных и логарифмических неравенств:

  • Приведение к простейшему неравенству
  • Решение неравенств с переменным основанием степени или логарифма (с помощью равносильных переходов или так называемого метода рационализации)
  • Введение новых неизвестных
  • Логарифмирование
  • Обобщенный метод интервалов

Неравенства, в которых основание степени или логарифма зависит от переменной, встречаются на экзамене достаточно часто, например, такого вида (ЕГЭ 2017 года):

2logx2-6x+102⁡5×2+3≤logx2-6x+10⁡4×2+7x+3

Здесь для решения нужно использовать равносильный переход или рационализировать неравенство.

4. Использование свойств функций при решении неравенств

Иногда область определения или область значений входящих в неравенство выражений, их четность, симметричность либо еще какие-то свойства являются ключом к решению задачи. Такие задачи в вариантах КИМ ЕГЭ встречаются нечасто, тем не менее, ознакомиться с методами их решения полезно.
Для успеха на экзамене нужно не просто знать о существовании перечисленных выше методов. Нужно уметь их применять, не допускать досадных Для успеха на экзамене нужно не просто знать о существовании перечисленных выше методов. Нужно уметь их применять, не допускать досадных ошибок в преобразованиях и вычислениях, комбинировать методы для решения конкретной задачи, выбирать оптимальный путь решения. Время на экзамене ограничено, а задач (в том числе и весьма непростых) много. К тому же большинство методов имеет свои «подводные камни», обнаружить которые самостоятельно сложно. Гораздо эффективнее в этой ситуации воспользоваться помощью опытного преподавателя.
Регулярные и систематизированные занятия при подготовке к ЕГЭ по математике профильного уровня могут значительно повлиять на финальную экзаменационную оценку. Наша статистика показывает, что учащиеся, уделившие достаточное внимание такой подготовке, на ЕГЭ получили баллы существенно выше средних (вплоть до 100 баллов) и успешно поступили в выбранные технические вузы.

Регулярно тренируйтесь в решении задач

Чтобы начать заниматься на портале «1С:Репетитор», достаточно Зарегистрироваться.
Вы можете:

  • Начать заниматься бесплатно.
  • Получить доступ ко всей теории и тренажерам задачи №15. Это стоит всего 990 рублей.
  • Купить доступ к этой задаче в составе экспресс-курса «Алгебра» и научиться решать задачи №13, №15, №17, №18 и №19 на максимальный балл.

Все курсы состоят из методически правильной последовательности теории и практики, необходимой для успешного решения задач. Включают теорию в форме текстов, слайдов и видео, задачи с решениями, интерактивные тренажеры, модели, и тесты.

Остались вопросы? Позвоните нам по телефону 8 800 551-50-78 или напишите в онлайн-чат.

Здесь ключевые фразы, чтобы поисковые роботы лучше находили наши советы:
Как решать задание 15 в экзамене ЕГЭ на неравенства, показательные неравенства ЕГЭ, задания с параметром ЕГЭ, решение параметров ЕГЭ, решение уравнений неравенств ЕГЭ по математике профильного уровня выпускникам 11 класса в 2018 году, поступающим в технический вуз.

Источник
Skip to content

Результат поиска:

ЕГЭ Профиль №15. Рациональные неравенства

ЕГЭ Профиль №15. Рациональные неравенстваadmin2020-02-05T19:22:31+03:00

Скачать ЕГЭ Профиль №15.Рациональные неравенства в формате pdf.

Нашли ошибку в заданиях? Оставьте, пожалуйста, отзыв.

15 заданием профильного ЕГЭ по математике является неравенство. Одним из видов неравенств которое может оказаться в 15 задание является рациональное неравенство. Прежде чем решать рациональные неравенства, следует научиться решать рациональные уравнения. Как правило, рациональное неравенство решается методом интервалов, который не требует каких-то специальных навыков, но при этом решение оказывается достаточно объемным и требует внимательности. Также не следует забывать про метод замен. Без умения решать рациональные неравенства невозможно будет научиться решать все остальные неравенства (показательные, логарифмические и т.д.). Поэтому изучение темы «Неравенства и системы неравенств» необходимо начинать именно с рациональных неравенств. В данном разделе представлены рациональные неравенства (всего 113) разбитые на два уровня сложности. Уровень А — это простейшие рациональные неравенства, которые являются подготовительными для решения реальных рациональных неравенств предлагаемых на экзамене. Уровень В — состоит из неравенств, которые предлагали на реальных ЕГЭ и в диагностических работах прошлых лет.

Вставить формулу как
Блок
Строка

Дополнительные настройки
Цвет формулы
Цвет текста
#333333

ID формулы

Классы формулы

Используйте LaTeX для набора формулы
Предпросмотр
({})
Формула не набрана

Вставить
Источник

Понравилась статья? Поделить с друзьями:
  • Путеводитель егэ математика
  • Путевка в жизнь сочинение по фильму
  • Пусть это сделает кто то а я приду на готовое сочинение
  • Пункты для сочинения егэ по русскому языку
  • Пункты брачного договора примеры егэ