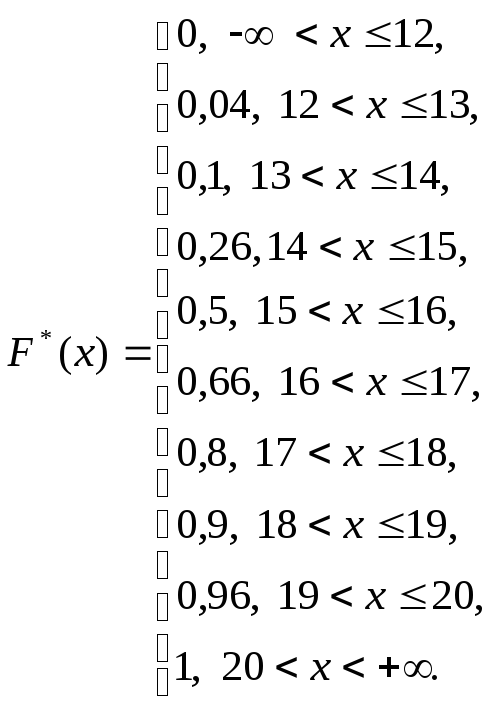Пятьдесят абитуриентов получили на вступительных экзаменах следующие баллы

Тема:
Генеральная
совокупность и выборка. Вариационные
ряды. Полигон и гистограмма. Числовые
характеристики выборки.

Пример.
Пятьдесят абитуриентов получили на
вступительных экзаменах следующие
баллы:

12, 14, 19, 15, 14, 18, 13, 16, 17, 12,

20, 17, 15, 13, 17, 16, 20, 14, 14, 13,

17, 16, 15, 19, 16, 15, 18, 17, 15, 14,

16, 15, 15, 18, 15, 15, 19, 14, 16, 18,

18, 15, 15, 17, 15, 16, 16, 14, 14, 17

Требуется:

1. составить
   вариационный ряд.

2. записать таблицу
   частот и относительных частот.

3. построить полигон
   частот и полигон относительных частот.

4. найти
   эмпирическую функцию распределения
   F^*(x).
   Построить ее график.

5. Найти
   числовые характеристики данной выборки:
   ,
   D_в,
   σ_в,
   D_испр.в.,
   моменты второго порядка ν^*_в,
   μ^*_в,
   коэффициент вариации V.
   Для нахождения воспользуйтесь
   определениями и известными теоремами,
   а полученные результаты проверьте с
   помощью статистических функций Excel.

Решение.

1)
Объем данной выборки n
= 50. Вариационный ряд (варианты,
расположенные в порядке возрастания):
12, 13, 14, 15, 16, 17, 18, 19, 20.¹

2)
Составим таблицу частот и относительных
частот. Частота
n_k
варианты –
это количество повторов варианты в
выборке. Относительная
частота (частость) варианты –
это отношение её частоты к объёму выборки

. (1)

Скопируем
данную выборку в таблицу Excel
и построим для нее таблицу частот и
относительных частот. Для этого выполним
следующие действия:

1. Заголовки
   строк (значения первого столбца) этой
   таблицы создадим в редакторе
   Microsoft Equation 3.0,
   для вызова которого выполним команды
   Вставка /
   Объект … / Microsoft Equation 3.0.

2. Подсчет
   частот вариант осуществим статистической
   функцией СЧЕТЕСЛИ.
   Для этого выполним команды Вставка /
   Функция / Статистические / СЧЕТЕСЛИ.
   В появившемся диалоговом окне в качестве
   диапазона введем диапазон ячеек, в
   котором располагаются значения вариант
   данной выборки, а в качестве условия
   введем =x_i,
   где x_i
   – это фиксированное значение варианты.
   Если выборка располагается в диапазоне
   A1:J5,
   то в ячейку B10
   со значением частоты варианты x₁ = 12
   следует ввести формулу СЧЕТЕСЛИ($A1:$J5; “=12”)
   (см. рис. 1, строка формул отображает
   формулу в выделенной ячейке).

3. Относительные
   частоты определяются формулой (1),
   которая для ячейки B11
   примет вид = B10/50.

4. Итоговая
   таблица находится в диапазоне А9
   : J11(см.
   рис. 1).

Замечание. При заполнении таблицы используйте операцию копирования и не забывайте об относительных и абсолютных ссылках!

Рис.1.

3)
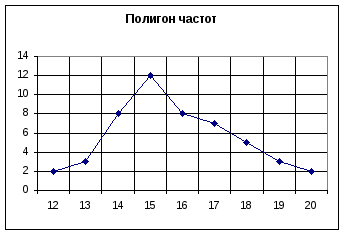
По полученной в п. 2) таблице построим
полигон частот и полигон относительных
частот. Полигоном
частот
(относительных
частот)
называется
ломаная линия, соединяющая точки с
координатами (x_i; n_i)
(соответственно ( x_i , μ_i)).
Для построения
этих ломанных воспользуемся графическими
средствами Excel.

1. Выполним
   команды Вставка /
   Диаграмма.
   В появившемся диалоговом окне выберем
   тип диаграммы – график с маркерами,
   помечающими точки данных. Нажмем кнопку
   Далее.

2. В
   следующем окне Мастера
   диаграмм
   укажем диапазон – диапазон частот
   B10:J10,
   расположив ряды в строках. На вкладке
   Ряд
   выберем в качестве подписей по оси Х
   диапазон значений вариант B9:J9.
   Нажмем кнопку Далее.

3. На
   третьем шаге Мастера
   на вкладке Линии
   сетки добавим
   по оси Х основные линии. Нажмем кнопку
   Далее.

4. На
   последнем шаге разместим диаграмму на
   имеющемся листе и нажмем кнопку Готово.

Полученная
диаграмма представляет собой полигон
частот (см. рис.2). Аналогично тому, как
это делалось выше, построим полигон
относительных частот (см. рис. 3).

Рис.2

Рис.3

4)
Если закон
распределения выборки задан таблицей
относительных частот

x	x	x	x	…	x
				…

то эмпирическая
функция распределения имеет вид

(2)

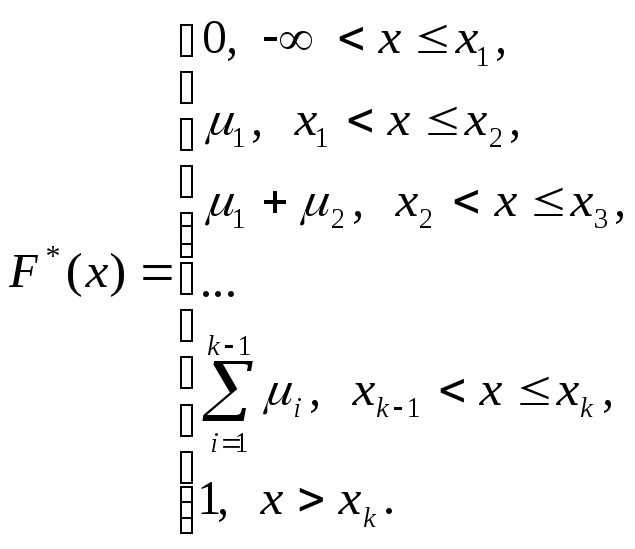
Для
вычисления значений этой функции и
построения ее графика в Excel
создадим таблицу (см. рис. 4, диапазон
ячеек A32 : K33).
В первую строку введем значения правых
концов промежутков |x_i
, x_i+1|
задания функции F^*(x).
Поскольку далее требуется построить
график этой функции, то в ячейку K32
вместо значения «»
поместим любое значение, большее x_k = 20,
например, «21». Во второй строке таблицы
вычислим значения функции F^*(x)
на соответствующем промежутке. Для
этого в ячейку B32
введем значение «0», в ячейку С32
поместим формулу «=B33+B11»
(в ячейке B11
находится значение относительной
частоты
)
и распространим ее путем копирования
на последующие ячейки этой строки. По
полученной таблице, воспользовавшись
редактором формул Microsoft Equation 3.0,
запишем функцию F^*(x)
в виде (2). Например, значение «0,04»
находится в ячейке С33,
соответствующей ячейке С32,
содержимое которой есть число «13» –
правый конец промежутка
.
Следовательно, при

функция F^*(x)
принимает значение «0,04». В результате
получим

Соседние файлы в предмете [НЕСОРТИРОВАННОЕ]

• #
• #
• #
• #
• #
• #
• #
• #
• #
• #
• #

Решение

Отсортируем полученные количество баллов по величине и расположим их в порядке возрастания, то есть составим ранжированный дискретный ряд вариантов
13 14 14 15 15 16 17 17 18 19
13 14 15 15 16 16 17 17 18 19
13 14 15 15 16 16 17 17 18 19
14 14 15 15 16 16 17 17 18 20
14 14 15 15 16 16 17 18 19 20
Объем выборки равен n=50
Составим вариационный ряд, записав в первую строку таблицы наблюдаемые значения (варианты) xi, а во вторую соответствующие им частоты ni:
xi
13 14 15 16 17 18 19 20
ni
3 8 10 9 9 5 4 2
Контроль: n=ni=3+8+10+9+9+5+4+2=50
Вычислим относительные частоты по формуле:
wi=nin
Тогда
xi
13 14 15 16 17 18 19 20
wi
0,06 0,16 0,2 0,18 0,18 0,1 0,08 0,04
Контроль:
wi=0,06+0,16+0,2+0,18+0,18+0,1+0,08+0,04=1
в) Вычислим выборочное среднее по формуле
xв=1ni=18xini
Тогда
xв=150∙(13∙3+14∙8+15∙10+16∙9+17∙9+18∙5+19∙4+20∙2)
=150∙39+112+150+144+153+90+76+40=
=80450=16,08
г) Запишем выборочную функцию распределения и построим ее график
Если х≤13, то F*(х)=0
Если 13<х≤14, то F*x=0,06
Если 14<х≤15, то F*x=0,06+0,16=0,22
Если 15<х≤16, то F*x=0,22+0,2=0,42
Если 16<х≤17, то F*x=0,42+0,18=0,6
Если 17<х≤18, то F*x=0,6+0,18=0,78
Если 18<х≤19, то F*x=0,78+0,1=0,88
Если 19<х≤20, то F*x=0,88+0,08=0,96
Если х>20, то F*x=0,96+0,04=1
Тогда функция F*(х) имеет вид:
F*х=0 при х≤130,06 при13<х≤14 0,22 при 14<х≤150,42 при 15<х≤160,6 при 16<х≤170,78 при 17<х≤180,88 при 18<х≤190,96 при 19<х≤201 при х>20
График функции распределения имеет вид:
д) Построим полигон частот

2019-05-08 09:35:10

Общий ряд — просто переписать все оценки в порядке возрастания.
Сгруппировать — объединить в скобки каждую оценку.
(2, 2, 2, 2, 2, 2, 2, 2, 2, 2), (3, 3, 3, 3), (4, 4, 4, 4, 4, 4), (5, 5, 5, 5),
(6, 6, 6, 6, 6, 6, 6), (7, 7, 7, 7, 7, 7, 7, 7), (8, 8), (9, 9, 9, 9), (10,10,10,10,10)
Таблица рассредотачивания данных и частот (всего 50 оценок):
Оценки _ 2 _ _3_ _4_ _5_ _6_ _7_ _8 _ _9 __10 _
Кол-во_ _10_ _4_ _6_ _4 _ _7 _ _8_ _2_ _4 _ _5 _
Частота10/504/506/504/507/508/502/504/505/50
Графики сам строй, это совершенно просто.
Размах — это разность меж наибольшим и минимальным значением,
это 10 — 2 = 8
Мода — это значение, которое встречается почаще всего. Это 2, их 10.
Среднее — это сумма всех значений, деленная на их количество.
Это (2*10+3*4+4*6+5*4+6*7+7*8+8*2+9*4+10*5)/50 = 276/50 = 5,52