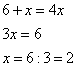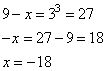Пятое задание решу егэ математика профиль


Пройти тестирование по этим заданиям
Вернуться к каталогу заданий

Версия для печати и копирования в MS Word

1

Флакон шампуня стоит 160 рублей. Какое наибольшее число флаконов можно купить на 1000 рублей во время распродажи, когда скидка составляет 25% ?

2

Шариковая ручка стоит 40 рублей. Какое наибольшее число таких ручек можно будет купить на 900 рублей после повышения цены на 10%?

3

Тетрадь стоит 40 рублей. Какое наибольшее число таких тетрадей можно будет купить на 750 рублей после понижения цены на 10%?

Источник: Пробный экзамен по математике Санкт-Петербург 2015. Вариант 2.

4

Магазин закупает цветочные горшки по оптовой цене 120 рублей за штуку и продает с наценкой 20%. Какое наибольшее число таких горшков можно купить в этом магазине на 1000 рублей?

5

Оптовая цена учебника 170 рублей. Розничная цена на 20% выше оптовой. Какое наибольшее число таких учебников можно купить по розничной цене на 7000 рублей?

Пройти тестирование по этим заданиям

Источник

Решу ЕГЭ задание №5 по математике 11 класс профильный уровень с ответами и решением для практики и подготовки, задание 5 профильного ЕГЭ по математике – это основы стереометрии.

  • Скачать задания куб, прямоугольный параллелепипед
  • Скачать задания составные многогранники
  • Скачать задания площадь поверхности многогранника
  • Скачать задания призма
  • Скачать задания пирамида
  • Скачать задания цилиндр, конус шар
  • Скачать задания комбинация тел

Куб, прямоугольный параллелепипед решу задания и ответы:

Составные многогранники решу задания и ответы:

Площадь поверхности многогранника решу задания и ответы:

Призма решу задания и ответы:

Пирамида задания и ответы:

Цилиндр и конус шар задания и ответы:

Комбинация тел задания и ответы:

Задания и ответы:

1)Площадь поверхности куба равна 18. Найдите его диагональ.

Правильный ответ: 3

2)Объем куба равен 8. Найдите площадь его поверхности.

Правильный ответ: 24

3)Если каждое ребро куба увеличить на 1, то его площадь поверхности увеличится на 54. Найдите ребро куба.

Правильный ответ: 4

4)Во сколько раз увеличится объем куба, если его ребра увеличить в три раза?

Правильный ответ: 27

5)Диагональ куба равна 12 . Найдите его объем.

Правильный ответ: 8

6)Объем куба равен 24 3 . Найдите его диагональ.

Правильный ответ: 6

7)Если каждое ребро куба увеличить на 1, то его объем увеличится на 19. Найдите ребро куба.

Правильный ответ: 2

8)Диагональ куба равна 1. Найдите площадь его поверхности.

Правильный ответ: 2

9)Площадь поверхности куба равна 24. Найдите его объем.

Правильный ответ: 8

10)Объем одного куба в 8 раз больше объема другого куба. Во сколько раз площадь поверхности первого куба больше площади поверхности второго куба?

Правильный ответ: 4

11)В кубе ABCDA1B1C1D1 точка K — середина ребра AA1, точка L — середина ребра A1B1, точка M — середина ребра A1D1. Найдите угол MLK. Ответ дайте в градусах.

Правильный ответ: 60

12)В кубе ABCDA1B1C1D1 найдите угол между прямыми AD1 и B1D1. Ответ дайте в градусах.

Правильный ответ: 60

13)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 3 и 4. Площадь поверхности этого параллелепипеда равна 94. Найдите третье ребро, выходящее из той же вершины.

Правильный ответ: 5

14)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Площадь поверхности параллелепипеда равна 16. Найдите его диагональ.

Правильный ответ: 3

15)Прямоугольный параллелепипед описан около единичной сферы. Найдите его площадь поверхности.

Правильный ответ: 24

16)Площадь грани прямоугольного параллелепипеда равна 12. Ребро, перпендикулярное этой грани, равно 4. Найдите объем параллелепипеда.

Правильный ответ: 48

17)Объем прямоугольного параллелепипеда равен 24. Одно из его ребер равно 3. Найдите площадь грани параллелепипеда, перпендикулярной этому ребру.

Правильный ответ: 8

18)Объем прямоугольного параллелепипеда равен 60. Площадь одной его грани равна 12. Найдите ребро параллелепипеда, перпендикулярное этой грани.

Правильный ответ: 5

19)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2 и 6. Объем параллелепипеда равен 48. Найдите третье ребро параллелепипеда, выходящее из той же вершины.

Правильный ответ: 4

20)Три ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 4, 6, 9. Найдите ребро равновеликого ему куба.

Правильный ответ: 6

21)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите объем параллелепипеда.

Правильный ответ: 32

22)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 3. Объем параллелепипеда равен 36. Найдите его диагональ.

Правильный ответ: 7

23)Одна из граней прямоугольного параллелепипеда – квадрат. Диагональ параллелепипеда равна 8 и образует с плоскостью этой грани угол 45o . Найдите объем параллелепипеда.

Правильный ответ: 4

24)Диагональ прямоугольного параллелепипеда равна 8 и образует углы 30o , 30o и 45o с плоскостями граней параллелепипеда. Найдите объем параллелепипеда.

Правильный ответ: 4

25)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 2, 4. Диагональ параллелепипеда равна 6. Найдите площадь поверхности параллелепипеда.

Правильный ответ: 64

26)Два ребра прямоугольного параллелепипеда, выходящие из одной вершины, равны 1, 2. Объем параллелепипеда равен 6. Найдите площадь его поверхности.

Правильный ответ: 22

27)Объем параллелепипеда ABCDA1B1C1D1 равен 4,5. Найдите объем треугольной пирамиды AD1CB1.

Правильный ответ: 1,5

28)Найдите объем многогранника, вершинами которого являются точки A, D, A1, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 3, AD = 4, AA1 = 5.

Правильный ответ: 30

29)Найдите объем многогранника, вершинами которого являются точки A, B, C, D1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 4, AD = 3, AA1 = 4.

Правильный ответ: 8

30)Найдите объем многогранника, вершинами которого являются точки A1, B, C, C1, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 4, AD = 3, AA1 = 4.

Правильный ответ: 16

31)Найдите объем многогранника, вершинами которого являются точки A, B, C, B1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 3, AD = 3, AA1 = 4.

Правильный ответ: 3

32)Найдите объем многогранника, вершинами которого являются точки A, B, B1, C1 прямоугольного параллелепипеда ABCDA1B1C1D1, у которого AB = 5, AD = 3, AA1 = 4.

Правильный ответ: 10

33)Найдите угол ABD1 прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 3. Ответ дайте в градусах.

Правильный ответ: 45

34)Найдите угол C1BC прямоугольного параллелепипеда, для которого AB = 5, AD = 4, AA1 = 4. Ответ дайте в градусах.

Правильный ответ: 45

35)Найдите угол DBD1 прямоугольного параллелепипеда, для которого AB = 4, AD = 3, AA1 = 5. Ответ дайте в градусах.

Правильный ответ: 45

36)В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что AC1 = 13, C1D1 = 3, B1C1 = 12. Найдите длину ребра AA1.

Правильный ответ: 4

37)В прямоугольном параллелепипеде ABCDA1B1C1D1 известно, что BB1 = 11, C1D1 = 16, B1C1 = 8. Найдите длину диагонали DB1.

Правильный ответ: 21

38)В прямоугольном параллелепипеде ABCDA1B1C1D1 ребро AB 2 , ребро AD 5 , ребро 1 AA 2 . Точка K — середина ребра BB1. Найдите площадь сечения, проходящего через точки A1, D1 и K.

Правильный ответ: 5

39)В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра AB = 24, AD = 10, AA1 =22. Найдите площадь сечения, проходящего через точки A, A1 и С.

Правильный ответ: 572

40)В прямоугольном параллелепипеде ABCDA1B1C1D1 известны ребра AB = 8, AD = 6, AA1 =21. Найдите синус угла между прямыми CD и A1C1.

Правильный ответ: 0,6

41)Найдите расстояние между вершинами A и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Правильный ответ: 3

42)Найдите квадрат расстояния между вершинами D и C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Правильный ответ: 5

43)Найдите расстояние между вершинами B1 и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Правильный ответ: 3

44)Найдите угол CAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

Правильный ответ: 60

45)Найдите угол ABD многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

Правильный ответ: 45

46)Найдите тангенс угла B2A2C2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Правильный ответ: 2

47)Найдите квадрат расстояния между вершинами B2 и D3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Правильный ответ: 11

48)Найдите квадрат расстояния между вершинами B и D2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Правильный ответ: 14

49)Найдите квадрат расстояния между вершинами A и C3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Правильный ответ: 17

50)Найдите тангенс угла C2C3B2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Правильный ответ: 3

51)Найдите тангенс угла ABB3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Правильный ответ: 2

52)Найдите тангенс угла C3D3B3 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Правильный ответ: 3

53)Найдите квадрат расстояния между вершинами E и B2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые.

Правильный ответ: 53

54)Найдите угол D2EF многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

Правильный ответ: 45

55)Найдите угол EAD2 многогранника, изображенного на рисунке. Все двугранные углы многогранника прямые. Ответ дайте в градусах.

Правильный ответ: 60

56)Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Правильный ответ: 18

57)Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Правильный ответ: 76

58)Найдите площадь поверхности многогранника, изображенного на рисунке (все двугранные углы прямые).

Правильный ответ: 92

59)В сосуд, имеющий форму правильной треугольной призмы, налили 2300 см3 воды и полностью в нее погрузили деталь. При этом уровень жидкости в сосуде поднялся с отметки 25 см до отметки 27 см. Чему равен объем детали? Ответ выразите в cм3 .

Правильный ответ: 184

60)В сосуд, имеющий форму правильной треугольной призмы, налили воду. Уровень воды достигает 80 см. На какой высоте будет находиться уровень воды, если ее перелить в другой такой же сосуд, у которого сторона основания в 4 раза больше, чем у первого? Ответ выразите в см.

Правильный ответ: 5

61)Найдите площадь боковой поверхности правильной шестиугольной призмы, сторона основания которой равна 5, а высота — 10.

Правильный ответ: 300

62)Найдите площадь поверхности прямой призмы, в основании которой лежит ромб с диагоналями, равными 6 и 8, и боковым ребром, равным 10.

Правильный ответ: 248

63)Найдите боковое ребро правильной четырехугольной призмы, если сторона ее основания равна 5, а площадь поверхности равна 190.

Правильный ответ: 7

64)Через среднюю линию основания треугольной призмы, площадь боковой поверхности которой равна 24, проведена плоскость, параллельная боковому ребру. Найдите площадь боковой поверхности отсеченной треугольной призмы.

Правильный ответ: 12

65)Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 3 и 5. Объем призмы равен 30. Найдите ее боковое ребро.

Правильный ответ: 4

66)Найдите объем правильной шестиугольной призмы, стороны основания которой равны 1, а боковые ребра равны 3 .

Правильный ответ: 4,5

67)Через среднюю линию основания треугольной призмы, объем которой равен 32, проведена плоскость, параллельная боковому ребру. Найдите объем отсеченной треугольной призмы.

Правильный ответ: 8

68)Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Объем отсеченной треугольной призмы равен 5. Найдите объем исходной призмы.

Правильный ответ: 20

69)Найдите объем призмы, в основаниях которой лежат правильные шестиугольники со сторонами 2, а боковые ребра равны 2 3 и наклонены к плоскости основания под углом 30o .

Правильный ответ: 18

70)От треугольной призмы, объем которой равен 6, отсечена треугольная пирамида плоскостью, проходящей через сторону одного основания и противоположную вершину другого основания. Найдите объем оставшейся части.

Правильный ответ: 4

71)Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8, высота призмы равна 10. Найдите площадь ее поверхности.

Правильный ответ: 288

72)В основании прямой призмы лежит ромб с диагоналями, равными 6 и 8. Площадь ее поверхности равна 248. Найдите боковое ребро этой призмы.

Правильный ответ: 10

73)В треугольной призме две боковые грани перпендикулярны. Их общее ребро равно 10 и отстоит от других боковых ребер на 6 и 8. Найдите площадь боковой поверхности этой призмы.

Правильный ответ: 240

74)Основанием прямой треугольной призмы служит прямоугольный треугольник с катетами 6 и 8. Площадь ее поверхности равна 288. Найдите высоту призмы.

Правильный ответ: 10

75)Через среднюю линию основания треугольной призмы проведена плоскость, параллельная боковому ребру. Площадь боковой поверхности отсеченной треугольной призмы равна 8. Найдите площадь боковой поверхности исходной призмы.

Правильный ответ: 16

76)Объем куба равен 12. Найдите объем треугольной призмы, отсекаемой от него плоскостью, проходящей через середины двух ребер, выходящих из одной вершины и параллельной третьему ребру, выходящему из этой же вершины.

Правильный ответ: 1,5

77)Найдите объем многогранника, вершинами которого являются точки A, B, C, A1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 2, а боковое ребро равно 3.

Правильный ответ: 2

78)Найдите объем многогранника, вершинами которого являются точки A, B, C, A1, C1 правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 3, а боковое ребро равно 2.

Правильный ответ: 4

79)Найдите объем многогранника, вершинами которого являются точки A1, B1, B, C правильной треугольной призмы ABCA1B1C1, площадь основания которой равна 4, а боковое ребро равно 3.

Правильный ответ: 4

80)Найдите объем многогранника, вершинами которого являются точки A, B, C, D, E, F, A1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 4, а боковое ребро равно 3.

Правильный ответ: 4

81)Найдите объем многогранника, вершинами которого являются точки A, B, C, A1, B1, C1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 3.

Правильный ответ: 3

82)Найдите объем многогранника, вершинами которого являются точки A, B, D, E, A1, B1, D1, E1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.

Правильный ответ: 8

83)Найдите объем многогранника, вершинами которого являются точки A, B, C, D, A1, B1, C1, D1 правильной шестиугольной призмы ABCDEFA1B1C1D1E1F1, площадь основания которой равна 6, а боковое ребро равно 2.

Правильный ответ: 6

84)Стороны основания правильной четырехугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь поверхности этой пирамиды.

Правильный ответ: 340

85)Стороны основания правильной шестиугольной пирамиды равны 10, боковые ребра равны 13. Найдите площадь боковой поверхности этой пирамиды.

Правильный ответ: 360

86)Объем параллелепипеда ABCDA1B1C1D1 равен 9. Найдите объем треугольной пирамиды ABCA1.

Правильный ответ: 1,5

87)Во сколько раз увеличится объем правильного тетраэдра, если все его ребра увеличить в два раза?

Правильный ответ: 8

88)Основанием пирамиды является прямоугольник со сторонами 3 и 4. Ее объем равен 16. Найдите высоту этой пирамиды.

Правильный ответ: 4

89)Найдите объем правильной треугольной пирамиды, стороны основания которой равны 1, а высота равна 3 .

Правильный ответ: 0,25

90)Найдите высоту правильной треугольной пирамиды, стороны основания которой равны 2, а объем равен 3 .

Правильный ответ: 3

91)Во сколько раз увеличится объем пирамиды, если ее высоту увеличить в четыре раза?

Правильный ответ: 4

92)В правильной четырехугольной пирамиде высота равна 6, боковое ребро равно 10. Найдите ее объем.

Правильный ответ: 256

93)Основанием пирамиды служит прямоугольник, одна боковая грань перпендикулярна плоскости основания, а три другие боковые грани наклонены к плоскости основания под углом 60o . Высота пирамиды равна 6. Найдите объем пирамиды.

Правильный ответ: 48

94)Боковые ребра треугольной пирамиды взаимно перпендикулярны, каждое из них равно 3. Найдите объем пирамиды.

Правильный ответ: 4,5

95)Объем треугольной пирамиды SABC, являющейся частью правильной шестиугольной пирамиды SABCDEF, равен 1. Найдите объем шестиугольной пирамиды.

Правильный ответ: 6

96)Объем правильной четырехугольной пирамиды SABCD равен 12. Точка E — середина ребра SB. Найдите объем треугольной пирамиды EABC.

Правильный ответ: 3

97)От треугольной пирамиды, объем которой равен 12, отсечена треугольная пирамида плоскостью, проходящей через вершину пирамиды и среднюю линию основания. Найдите объем отсеченной треугольной пирамиды.

Правильный ответ: 3

98)Объем треугольной пирамиды равен 15. Плоскость проходит через сторону основания этой пирамиды и пересекает противоположное боковое ребро в точке, делящей его в отношении 1:2, считая от вершины пирамиды. Найдите больший из объемов пирамид, на которые плоскость разбивает исходную пирамиду.

Правильный ответ: 10

99)Во сколько раз увеличится площадь поверхности правильного тетраэдра, если все его ребра увеличить в два раза?

Правильный ответ: 4

100)Найдите площадь поверхности правильной четырехугольной пирамиды, стороны основания которой равны 6 и высота равна 4.

Правильный ответ: 96

101)Во сколько раз увеличится площадь поверхности октаэдра, если все его ребра увеличить в 3 раза?

Правильный ответ: 9

102)Найдите площадь боковой поверхности правильной четырехугольной пирамиды, сторона основания которой равна 6 и высота равна 4.

Правильный ответ: 60

103)Во сколько раз увеличится площадь поверхности пирамиды, если все ее ребра увеличить в 2 раза?

Правильный ответ: 4

104)Ребра правильного тетраэдра равны 1. Найдите площадь сечения, проходящего через середины четырех его ребер.

Правильный ответ: 0,25

105)Найдите объем пирамиды, высота которой равна 6, а основание — прямоугольник со сторонами 3 и 4.

Правильный ответ: 24

106)В правильной четырехугольной пирамиде высота равна 12, объем равен 200. Найдите боковое ребро этой пирамиды.

Правильный ответ: 13

107)Сторона основания правильной шестиугольной пирамиды равна 2, боковое ребро равно 4. Найдите объем пирамиды.

Правильный ответ: 12

108)Объем правильной шестиугольной пирамиды 6. Сторона основания равна 1. Найдите боковое ребро.

Правильный ответ: 7

109)Сторона основания правильной шестиугольной пирамиды равна 4, а угол между боковой гранью и основанием равен 45o . Найдите объем пирамиды.

Правильный ответ: 48

110)Объем параллелепипеда ABCDA1B1C1D1 равен 12. Найдите объем треугольной пирамиды B1ABC.

Правильный ответ: 2

Тренировочные варианты ЕГЭ 2022 по математике профиль

ПОДЕЛИТЬСЯ МАТЕРИАЛОМ

Источник

Прототипы задания №5 ЕГЭ по математике профильного уровня — стереометрия. Практический материал для подготовки к ЕГЭ.

Для успешного выполнения задания №5 необходимо уметь выполнять действия с геометрическими фигурами, координатами и векторами

Практика

time4math.ru Скачать задания
math100.ru Куб, прямоугольный параллелепипед

Элементы составных многогранников

Площадь поверхности и объем составного многогранника

Призма

Пирамида

Цилиндр, конус, шар

Комбинация тел
vk.com/ekaterina_chekmareva Скачать задания

Примерное время выполнения задания выпускником, изучавшим математику на профильном уровне — 3 минуты.

Связанные страницы:

Прототипы задания №2 профильного ЕГЭ 2022 по математике

Решение 17 задания ЕГЭ по профильной математике

Задания первой части ЕГЭ по математике

Задание 4 ЕГЭ по математике (профиль) — вычисления и преобразования

Задание 11 ЕГЭ 2022 по математике: «Наибольшее и наименьшее значения функции»

Источник

За это задание ты можешь получить 1 балл. На решение дается около 3 минут. Уровень сложности: базовый.
Средний процент выполнения: 93.6%
Ответом к заданию 5 по математике (профильной) может быть целое число или конечная десятичная дробь.

Разбор сложных заданий в тг-канале

Задачи для практики

Задача 1

Найдите корень уравнения $log_{x+5}{64} = 2$.

Решение

Найдем ОДЗ: ${tablex + 5 > 0; x + 5 ≠ 1;$ ${tablex > -5; x ≠ -4;$ $x ∈ (-5; -4) ∪ (-4; +∞)$.

По определению логарифма если $log_b a=c$, то $b^c=a$

$(x + 5)^2 = 64$,

$x + 5 = 8$ или $x + 5 = -8$,

$x = 3 $ или $x = -13 $

$x = -13$ — не входит в ОДЗ.

Ответ: 3

Задача 2

Найдите корень уравнения $log_{5}{(x^2+26x + 169)}-2 =log_{√5}{(5x-7)}$.

Решение

$log_{5}{(x^2+26x + 169)}-2 =log_{√5}{(5x-7)}$,

$log_{5}{(x+13)^2}-log_{5}{25} =log_{5^{1/2}}{(5x-7)}$,

$log_{5}{(x+13)^2/{25}} =2log_{5}{(5x-7)}$,

$log_{5}{(x+13)^2/{25}} =log_{5}{(5x-7)^2}$,

$(x+13)^2/{25} =(5x-7)^2$,

$(x+13)/{5} =(5x-7)$ или $(x+13)/{5} =-(5x-7)$,

Откуда: $x=2$ или $x=11/13 — $ второй корень не удовлетворяет ОДЗ,

Ответ: 2

Задача 3

Найдите корень уравнения $log_{3}{(4x-15)} =log_{3}{(x+3)}$.

Решение

$log_3 (4x — 15) = log_3 (x + 3)$,

$4x — 15 = x + 3$,

$3x = 18, x = 6$.

Проверка. При $x = 6$ получаем $log_3 (6 · 4 — 15) = log_3 (6 + 3)$ — верное равенство.

$x = 6$ — корень уравнения.

Ответ: 6

Задача 4

Найдите корень уравнения $625^{x+1}={1} / {5}$.

Решение

$(5^4)^{x+1} = 5^{-1}$, применим свойство $(a^b)^c=a^{bc}$

$5^{4x+4} = 5^{-1}$,

$4x + 4 = -1$,

$4x = -5$,

$x = -1.25$.

Ответ: -1.25

Задача 5

Найдите корень уравнения $9^{x-12}={1} / {3}$.

Решение

$(3^2)^{x-12}=3^{-1} $, применим свойство $(a^b)^c=a^{bc}$

$ 3^{2x-24} = 3^{-1} $,

$2x-24=-1 $,

$ 2x=23 $,

$ x=11{,}5$.

Ответ: 11.5

Задача 6

Найдите корень уравнения $(x-12)^3=-27$.

Решение

$(x-12)^3=-27$

$ (x-12)^3=(-3)^3 $,
$ x-12=-3 $,
$x=9$.

Ответ: 9

Задача 7

Найдите корень уравнения $log_{2}{(12+x)} =-2$.

Решение

По определению логарифма $12+x = 2^{-2}, 12+x = 0.25, x = 0.25-12, x = -11.75$.

Ответ: -11.75

Задача 8

Найдите корень уравнения $log_{3}{(4-x)} =5$.

Решение

По определению логарифма если $log_b a=c$, то $b^c=a$

$4-x = 3^5 $,

$ 4-x=243 $,

$x=-239$.

Ответ: -239

Задача 9

Решите уравнение $(x+7)^2 = x^2+7$. Если уравнение имеет более одного корня, в ответе запишите меньший из них.

Решение

Воспользуемся формулой квадрата суммы: $(a+b)^2=a^2+2ab+b^2$
$x^2 + 14x + 49 = x^2 + 7$,
$14x = -42$,
$x = -3$.

Ответ: -3

Задача 10

Решите уравнение $(5x+11)^2 = (5x-2)^2$. Если уравнение имеет более одного корня, в ответе запишите меньший из них.

Решение

Воспользуемся формулами сокращенного умножения:

$(a+b)^2=a^2+2ab+b^2$

$(a-b)^2=a^2-2ab+b^2$
Таким образом:

$25x^2+110x+121=25x^2-20x+4$,

$ 110x+20x=-117$,
$130x=-117$
$x=-117/130$
$x=-0.9$.

Ответ: -0.9

Задача 11

Найдите корень уравнения $√ {14-5x}=-x$. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Решение

Так как левая часть уравнения неотрицательна, то и правая тоже неотрицательна:

$-x ⩾ 0$, — домножим обе части на -1, в таком случае знак неравенства меняется

$ x ⩽ 0$.

Возведя обе части в квадрат, получим уравнение $14-5x=x^2$,

$x^2+5x-14=0$,

$ x_1=-7$,

$ x_2=2$ — не удовлетворяет условию $x⩽ 0$.

Пояснение: $(-x)^2=(-x)(-x)=x^2$

Ответ: -7

Задача 12

Найдите корень уравнения ${x+3} / {2x-11}={x+3} / {3x-7}$. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Решение

Найдем ОДЗ: ${table2x-11 ≠ 0; 3x-7≠ 0;$ ${tablex ≠ 5.5; x ≠7/3;$

Удобно домножить обе стороны равенства на знаменатели, проще говоря «крест накрест»

$(x+3)(3x-7)=(2x-11)(x+3)$

${3x}^2-7x+9x-21={2x}^2+6x-11x-33$

$x^2+7x+12=0$

$x_1=-3, x_2=-4$ — оба корня удовлетворяют ОДЗ

Наибольший корень: $x=-3$

Ответ: -3

Задача 13

Найдите корень уравнения ${9-5x} / {x+3}=x$. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Решение

При $x ≠ -3$ получим

$x(x + 3) = 9 — 5x$,

$x^2 + 3x + 5x — 9 = 0$,

$x^2 + 8x — 9 = 0$

По теореме Виета $х_1=1$, $х_2=-9$.

Больший корень $x_1=1$

Ответ: 1

Задача 14

Найдите корень уравнения $√ {{4x-21} / {117}}={1} / {3}$.

Решение

ОДЗ: ${4x — 21}/{117}⩾0, 4x-21⩾0, x⩾21/4, x⩾5.25$

$(√{{4x — 21}/{117}})^2 = ({1}/{3})^2$,

${4x — 21}/{117} = {1}/{9}$,

$9(4x — 21) = 117$,

$36x — 189 = 117$,

$36x = 306$,

$x = 8.5$ — удовлетворяет ОДЗ.

Ответ: 8.5

Задача 15

Решите уравнение $log_{{1} / {3}}(13 + x) = — 2$.

Решение

ОДЗ: $13+x>0, x>-13$

По определению логарифма если $log_b a=c$, то $b^c=a$

$(1/3)^(-2)=13+x$
$ 13+x=9$
$ x=-4$ — удовлетворяет ОДЗ

Ответ: -4

Задача 16

Решите уравнение $√^3{5+x}=2$.

Решение

Возведем обе части уравнения в третью степень:
$5+х=2^3$,
$5+х=8$,
$х=3$.

Ответ: 3

Задача 17

Решите уравнение ${x-9} / {3x-1}={x-9} / {x+33}$. Если уравнение имеет несколько корней, в ответ запишите меньший из них

Решение

Допустимые значения переменной: $3х-1≠0$, $х≠1/3$;

$х+33≠0$, $х≠-33$;

Домножим обе части уравнения на $(3х-1)(х+33)≠0 — $ говорят умножим «крест -накрест»

$(х-9)(х+33)=(х-9)(3х-1) — $ вынесем общий множитель

$(х-9)(х+33)-(х-9)(3х-1)=0$

$(х-9)(х+33-(3х-1))=0$

$(х-9)(х+33-3х+1)=0$

$(х-9)(-2х+34)=0$

$ х-9=0$, $х=9$ или

$-2х+34=0$, $х=17$;

$9<17$ — значит наименьший корень $x=9$

Ответ: 9

Рекомендуемые курсы подготовки

Источник

В задании №5 варианта ЕГЭ вам встретятся всевозможные уравнения: квадратные и сводящиеся к квадратным, дробно-рациональные, иррациональные, степенные, показательные и логарифмические и даже тригонометрические. Видите, как много нужно знать, чтобы справиться с заданием! И еще ловушки и «подводные камни», которые ждут вас в самом неожиданном месте.

Вот список тем, которые стоит повторить:

Квадратные уравнения

Арифметический квадратный корень

Корни и степени

Показательная функция

Показательные уравнения

Логарифмическая функция

Логарифмические уравнения

Тригонометрический круг

Формулы приведения

Формулы тригонометрии

Простейшие тригонометрические уравнения 1

Уравнения, сводящиеся к квадратным

1. Решите уравнение frac{6}{13}x^2=19frac{1}{2}. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

Кажется, что уравнение очень простое. Но иногда здесь ошибаются даже отличники. А вот шестиклассник бы не ошибся.

С левой частью уравнения все понятно. Дробь frac{6}{13} умножается на x^2. А в правой части — смешанное число 19frac{1}{2}. Его целая часть равна 19, а дробная часть равна frac{1}{2}. Запишем это число в виде неправильной дроби:

19frac{1}{2}= frac{19cdot 2+1}{2} = frac{39}{2}.

Получим:

frac{6}{13}x^2=frac{39}{2};

x^2=frac{39cdot 13}{2cdot 6}=frac{13cdot 3cdot 13}{2cdot 6}=frac{{13}^2}{4};

x=pm frac{13}{2};

x_1=-6,5 или x_2=6,5.

Выбираем меньший корень.

Ответ: -6,5.

2. Решите уравнение left ( x-6 right )^2=-24x.

Возведем в квадрат левую часть уравнения. Получим:

left ( x-6 right )^2=-24xLeftrightarrow x^2-12x+36=-24xLeftrightarrow

Leftrightarrow x^2+12x+36=0Leftrightarrow left ( x+6 right )^2=0Leftrightarrow x=-6.

Ответ: -6.

Дробно-рациональные уравнения

3. Найдите корень уравнения

Перенесем единицу в левую часть уравнения. Представим 1 как frac{4x-5}{4x-5} и приведем дроби к общему знаменателю:

frac{5x-3}{4x-5}-frac{4x-5}{4x-5}=0;

frac{x+2}{4x-5}=0;

x= - 2.

Ответ: -2.

Это довольно простой тип уравнений. Главное — внимательность.

Иррациональные уравнения

Так называются уравнения, содержащие знак корня — квадратного, кубического или n-ной степени.

4. Решите уравнение:

sqrt{frac{6}{4{x}-54} } =frac{1}{7}.

Выражение под корнем должно быть неотрицательно, а знаменатель дроби не равен нулю.

Значит, .

Возведём обе части уравнения в квадрат:

frac{6}{4{x}-{ 54}} =frac{1}{49}.

Решим пропорцию:

4{x}-{ 54}={ 6}cdot { 49};

4{x}=348;

{ x}={ 87}.

Условие  при этом выполняется.

Ответ: 87.

5. Решите уравнение sqrt{72-x}=x. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

А в этом уравнении есть ловушка. Решите его самостоятельно и после этого читайте дальше.

Выражение под корнем должно быть неотрицательно. И сам корень — величина неотрицательная. Значит, и правая часть должна быть больше или равна нуля. Следовательно, уравнение равносильно системе:

left{begin{matrix} 72-x=x^2\72-xgeq 0 hfill \xgeq 0 hfill end{matrix}right..

Решение таких уравнений лучше всего записывать в виде цепочки равносильных переходов:

sqrt{72-x}=x Leftrightarrow left{begin{matrix} 72-x=x^2\72-x geq 0 \x geq 0 end{matrix}right. Leftrightarrow

.

Мы получили, что x=8. Это единственный корень уравнения.

Типичная ошибка в решении этого уравнения такая. Учащиеся честно пишут ОДЗ, помня, что выражение под корнем должно быть неотрицательно:

72-xge 0.

Возводят обе части уравнения в квадрат. Получают квадратное уравнение: x^2+x-72=0. Находят его корни: x=8 или x=-9. Пишут в ответ: -9 (как меньший из корней). В итоге ноль баллов.

Теперь вы знаете, в чем дело. Конечно же, число -9 корнем этого уравнения быть не может.

Ответ: 8.

6. Решите уравнение sqrt{45+4x}=x. Если уравнение имеет более одного корня, в ответе запишите больший из корней.

Запишем решение как цепочку равносильных переходов:

.

Ответ: 9.

Показательные уравнения

При решении показательных уравнений мы пользуемся свойством монотонности показательной функции.

7. Решите уравнение 5^{x-7}=frac{1}{125}.

Вспомним, что 125 = 5{}^{3}. Уравнение приобретает вид: 5{}^{x}{}^{-}{}^{7 }= 5{}^{-}{}^{3}. Функция y = 5^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

x - 7 = -3, откуда x = 4.

Ответ: 4.

8. Решите уравнение {left(frac{1}{49}right)}^{x-8}=7.

Представим {left(frac{1}{49}right)}^{ } как 7^{-2};

{left(7^{-2}right)}^{x-8}=7;

7^{-2x+16}=7.

Функция y = 7^x монотонно возрастает и каждое свое значение принимает только один раз. Степени равны, их основания, значит, и показатели равны.

-2x+16=1;

-2x=-15;

x=7,5.

Ответ: 7,5.

9. Решите уравнение left(frac{1}{9} right)^{{ x}-13} =3.

Представим {textstylefrac{1}{9}} в виде степени с основанием 3 и воспользуемся тем, что left({ a}^{{ m}} right)^{{ n}} ={ a}^{{ mn}}.

left(3^{-2} right)^{{ x}-{ 13}} =3;
3^{-2{ x}+{ 26}} =3^{1} ;

-2{ x}+{ 26}={ 1};

{ x}={ 12,5}.

Ответ: 12,5.

Логарифмические уравнения

Решая логарифмические уравнения, мы также пользуемся монотонностью логарифмической функции: каждое свое значение она принимает только один раз. Это значит, что если логарифмы двух чисел по какому-либо основанию равны, значит, равны и сами числа.

И конечно, помним про область допустимых значений логарифма:

Логарифмы определены только для положительных чисел.

Основание логарифма должно быть положительно и не равно единице.

10. Решите уравнение:

{{log}_5 left(4+xright)=2 }.

Область допустимых значений: . Значит, 

Представим 2 в правой части уравнения как {{log}_5 25 }, чтобы слева и справа в уравнении были логарифмы по основанию 5.

{{log}_5 left(4+xright)={{log}_5 25 } }.

Функция y = {{log}_5 x } монотонно возрастает и каждое свое значение принимает ровно один раз. Логарифмы равны, их основания равны. «Отбросим» логарифмы! Конечно, при этом 

4+x=25;
x=21.

Ответ: 21.

11. Решите уравнение: {{log}_8 left(x^2+xright)={{log}_8 left(x^2-4right) } }.

Запишем решение как цепочку равносильных переходов. Записываем ОДЗ и «убираем» логарифмы:

.

Ответ: -4.

12. Решите уравнение: 2^{{{log}_4 left(4x+5right) }}=9.

Перейдем от логарифма по основанию 4 (в показателе) к логарифму по основанию 2. Мы делаем это по формуле перехода к другому основанию:

{{log}_4 b }=frac{{{log}_2 b }}{{{log}_2 4 }}=frac{{{log}_2 b }}{2}.

Записываем решение как цепочку равносильных переходов.

.

Ответ: 19.

13. Решите уравнение. Если уравнение имеет более одного корня, в ответе запишите меньший из корней.

{{log}_{x-5} 49=2 }.

В этом уравнении тоже есть ловушка. Мы помним, что основание логарифма должно быть положительно и не равно единице.

Получим систему:

small left{begin{matrix} left ( x-5 right )^2=49\x-50 \x-5 neq 1 end{matrix}right..

Первое уравнение мы получили просто из определения логарифма.

Квадратное уравнение имеет два корня: x=12 и x=-2.

Очевидно, корень x=-2 является посторонним, поскольку основание логарифма должно быть положительным. Значит, единственный корень уравнения: x=12.

Ответ: 12.

Тригонометрические уравнения (Часть 1 ЕГЭ по математике)

Тригонометрические уравнения? В первой части вариантов ЕГЭ? — Да. Причем это задание не проще, чем задача 13 из второй части варианта Профильного ЕГЭ.

14. Найдите корень уравнения: cos frac{pi (x+1)}{4}=frac{sqrt{2}}{2}. В ответе запишите наибольший отрицательный корень.

Типичная ошибка — решать это уравнение в уме. Мы не будем так делать! Несмотря на то, что это задание включено в первую части варианта ЕГЭ, оно является полноценным тригонометрическим уравнением, причем с отбором решений.

Сделаем замену frac{pi left(x+1right)}{4}=t. Получим: cos t=frac{sqrt{2}}{2}.

Получаем решения: t=pm frac{pi }{4}+2pi n, nin Z. Вернемся к переменной x.

frac{pi (x+1)}{4}=pm frac{pi }{4}+2pi n, nin Z. Поделим обе части уравнения на pi и умножим на 4.

x+1=pm 1+8n, nin Z;

left[ begin{array}{c}x=8n, nin Z \x=-2+8n end{array}right..

Первой серии принадлежат решения -8; 0; 8dots

Вторая серия включает решения -2; 6; 14dots

Наибольший отрицательный корень — тот из отрицательных, который ближе всех к нулю. Это x = -2.

Ответ: -2.

15. Решите уравнение: tg frac{pi left( x+1right)}{4}= -1. В ответе напишите наименьший положительный корень.

Решение:

Сделаем замену frac{pi left(x+1right)}{4}=t. Получим:tgt=-1. Решения этого уравнения:

t=-frac{pi }{4}+pi n, nin Z. Вернемся к переменной х:

frac{pi left(x+1right)}{4}=-frac{pi }{4}+pi n, n in Z. Умножим обе части уравнения на 4 и разделим на pi.

x+1=-1+4n;

x=-2+4n.

Выпишем несколько решений уравнения и выберем наименьший положительный корень:

x=-2 ;2; 6dots Наименьший положительный корень x = 2.

Ответ: 2.

Мы разобрали основные типы уравнений, встречающихся в задании №5 Профильного ЕГЭ по математике. Конечно, это не все, и видов уравнений в этой задаче существует намного больше. Именно поэтому мы рекомендуем начинать подготовку к ЕГЭ по математике не с задания 1, а с текстовых задач на проценты, движение и работу и основ теории вероятностей.
Успеха вам в подготовке к ЕГЭ!

Благодарим за то, что пользуйтесь нашими статьями.
Информация на странице «Задание №5. Простейшие уравнения. Профильный ЕГЭ по математике» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к ЕГЭ и ОГЭ.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.

Публикация обновлена:
09.03.2023

Источник

Простейшие уравнения

Задание №5 профильного уровня ЕГЭ по математике – решение простейшего уравнения, чаще всего степенного. Обычно, требуется сделать несколько операций и приравнять степени – после этого уравнение становится линейным и решается легко – как и любое линейное уравнение.

Разбор типовых вариантов заданий №5 ЕГЭ по математике профильного уровня

Первый вариант задания (демонстрационный вариант 2018)

[su_note note_color=”#defae6″]

Найдите корень уравнения 3х-5=81

[/su_note]

Алгоритм решения задания:
  1. Определяем вид уравнения.
  2. Представляем правую часть в виде степени.
  3. Отбрасываем основание и решаем уравнение.
  4. Записываем ответ.
Решение:

1. Данное уравнение относится к показательным. Поэтому решаем его, приведя к виду: аf(x)=ag(x).

2. Представляем правую часть уравнения 81 в виде степени с основанием 3: 81=34. Тогда уравнение примет вид: 3х-5=34.

3. Так как основания одинаковы, можно отбросить их. Получаем: х – 5=4.

Решаем полученное уравнение: х=4+5,

х=9.

Ответ: 9.

Второй вариант задания (из Ященко, №1)

[su_note note_color=”#defae6″]

Найдите корень уравнения http://self-edu.ru/htm/2018/ege2018_36/files/1_5.files/image001.gif

[/su_note]

Алгоритм решения задания:
  1. Определяем вид уравнения.
  2. Представляем правую часть в виде степени с основанием 9.
  3. Отбрасываем основание и решаем уравнение.
  4. Записываем ответ.
Решение:

1. Данное уравнение является показательным. Решаем его, приводя к виду: аf(x)=ag(x).

2. Число 81 справа представить в виде http://self-edu.ru/htm/2018/ege2018_36/files/1_5.files/image002.gif , откуда получаем в правой части http://self-edu.ru/htm/2018/ege2018_36/files/1_5.files/image003.gif .

Исходное уравнение принимает вид:

http://self-edu.ru/htm/2018/ege2018_36/files/1_5.files/image004.gif

Так как у степеней в обеих частях уравнения равны, можно перейти к равенству степеней и решить уравнение:

http://self-edu.ru/htm/2018/ege2018_36/files/1_5.files/image005.gif

Ответ: 2.

Третий вариант задания (из Ященко, №4)

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм решения задания:
  1. Определяем вид уравнения.
  2. Представляем правую часть в виде степени с основанием 9.
  3. Отбрасываем основание и решаем уравнение.
  4. Записываем ответ.
Решение:

1. Уравнение показательного вида, значит можно решить его приведя к виду: f(x)a=g(x)a

2. Число представляем в виде степени с основанием 8: , тогда исходное уравнение можем записать таким образом:

Поскольку степени равны, должны быть равны и их основания. Имеем:

Ответ: 5.

Четвертый вариант задания (из Ященко, №8)

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм решения задания:
  1. Определяем вид уравнения.
  2. Представляем правую часть в виде логарифма с основанием 7.
  3. Отбрасываем логарифм и решаем уравнение.
  4. Проверяем корни.
  5. Записываем ответ.
Решение:

1. Уравнение логарифмическое, приводимое к виду: logag(x)=logag(x).

2. Преобразуем правую часть уравнения так, чтобы там стоял логарифм с основанием 7:

Отбрасываем знак логарифма, получим:

Проверяем полученный корень на принадлежность ОДЗ: 9 – (-18)=27>0, значит, корень принадлежит ОДЗ.

Ответ: -18.

Пятый вариант задания (из Ященко, №18)

[su_note note_color=”#defae6″]

Найдите корень уравнения

[/su_note]

Алгоритм решения задания:
  1. Определяем вид уравнения.
  2. Представляем правую часть в виде логарифма с основанием 7.
  3. Отбрасываем логарифм и решаем уравнение.
  4. Проверяем корни.
  5. Записываем ответ.
Решение:

1. Уравнение логарифмическое, приводимое к виду: logag(x)=logag(x).

2. Преобразуем правую часть уравнения, чтобы там стоял логарифм с основанием 4. Для этого используем свойства логарифмов:

log1625=log4225=1/2∙log425

Получаем уравнение:

2log4(2 – x)=log425

Решаем полученное уравнение:

http://self-edu.ru/htm/ege2016_36/files/12_5.files/image003.gif

Или 2 – x = – 5

x=2+5=7

Проверим на принадлежность ОДЗ: 2 – (-3)=5>0, корень принадлежит ОДЗ.

2 – 7 = -5 < 0, корень не принадлежит ОДЗ.

Ответ: -3.

Даниил Романович | Просмотров: 9.4k

Источник

Понравилась статья? Поделить с друзьями:
  • Пятое задание егэ химия теория
  • Работа в microsoft excel 2010 экзамен ответы
  • Работа с текстом при написании сочинения подготовка к егэ
  • Пятое задание егэ по русскому языку
  • Работа с текстом обществознание 11 класс егэ 2022