Продолжаем наш видеокурс по подготовке к ЕГЭ по информатике 2022. Сегодня разоблачим второе задание!
Кто незнаком с основными логическими операциями, можете посмотреть прошлогоднюю статью по заданию 2 из ЕГЭ по информатике.
В этой статье будут раскрыты методики решения 2 задания через язык программирования Питон.
Будем перебирать для каждой логической переменной все возможные варианты в программе. А логическая переменная всего два значения может принимать: 1 или 0 (истину или ложь). Таким образом, если к примеру у нас 4 переменные, мы получим 24=16 различных комбинаций.
Кто знаком с мощнейшим методом для 2 задания из ЕГЭ по информатике, о котором я рассказывал в прошлогодней статье, тот поймёт, что мы будем применять тот же самый мощнейший метод, но автоматизированный с помощью питона.
Нам нужно будет запрограммировать логическую функцию на языке Питон. Вот таблица, которая поможет это сделать.
| Логическая операция | Представление в Питоне |
| Отрицание ¬ | not() |
| Логическое умножение ∧ | and |
| Логическое сложение ∨ | or |
| Следование A ⟶ B | not(A) or B |
| Равносильность ≡ | == |
Перейдём к практике решения задач задания 2 с помощью языка программирования Python.
Задача (Классическая)
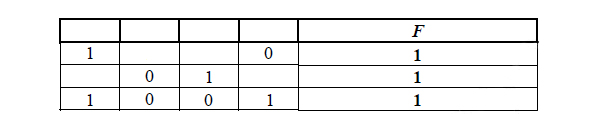
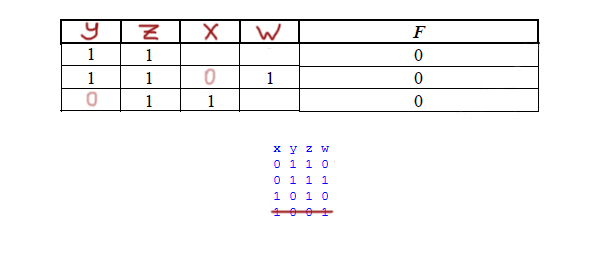
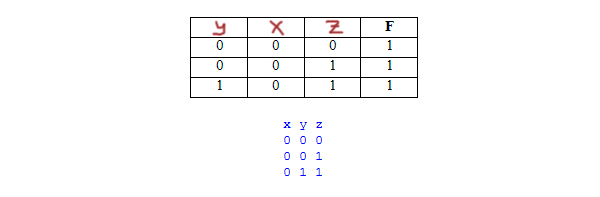
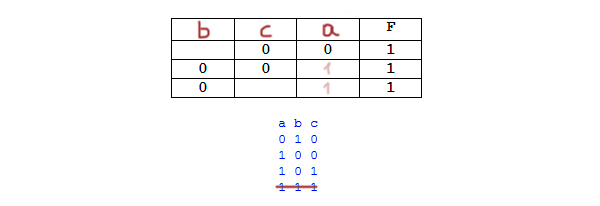
Миша заполнял таблицу истинности логической функции F
(w → z) ∧ ((y → x) ≡ (z → y)),
но успел заполнить лишь фрагмент из трёх различных её строк, даже
не указав, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
Определите, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут
соответствующие им столбцы (сначала буква, соответствующая первому
столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы
в ответе пишите подряд, никаких разделителей между буквами ставить
не нужно.
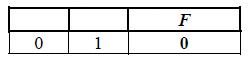
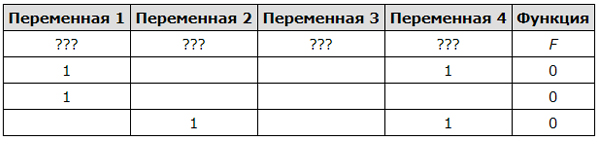
Пример. Функция F задана выражением ¬x / y, зависящим от двух
переменных, а фрагмент таблицы имеет следующий вид.
В этом случае первому столбцу соответствует переменная y, а второму
столбцу – переменная x. В ответе следует написать: yx.
Решение:
Решать задачу будем с помощью шаблона на языке Python (Питон).
print('x y z w') for x in range(0, 2): for y in range(0, 2): for w in range(0, 2): for z in range(0, 2): if (not(w) or z) and ((not(y) or x) == (not(z) or y)): print(x, y, z, w)
В задаче у нас 4 переменные, значит, формируем 4 вложенных цикла. В каждом цикле перебираем все возможные значения для конкретной переменной. Мы перебираем значения 0 и 1.
Функция должна выдавать всегда 1 (единицу, истину). Внутри всех циклов прописываем условие, которое срабатывает как раз на истину. В этом условии прописываем нашу функцию. Если наша функция будет выдавать истину, то мы распечатаем значения переменных, при которых это произошло. Если функция будет выдавать ложь, значит, ничего распечатано не будет.
Четыре вложенных цикла проверяют все возможные варианты (24 = 16 вариантов), и мы получим таблицу истинности, почти такую же, как нам и дали в условии задачи.
Так же вверху печатаем названия переменных, чтобы знать, какие значения каким переменным принадлежат.
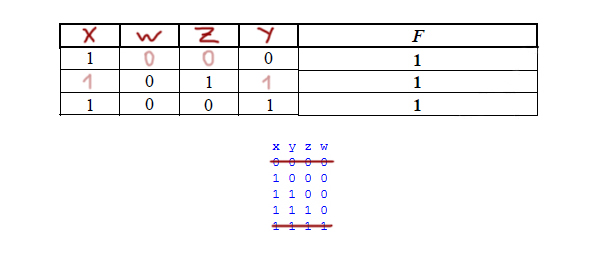
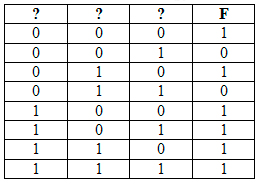
Запустим программу, и на экране распечатается табличка:
В получившийся табличке может быть больше строчек, чем в условии. Так же при поиске переменных нельзя опираться на порядок, в котором идут нули и единицы в нашей табличке. А можно опираться лишь на количество нулей и единиц в строчках или столбцах.
Можно вычеркнуть первую строчку и последнюю, потому что в таблице, которую дали в условии, в каждой строчке есть хотя бы один ноль и хотя бы одна единица.
Сразу видно, что первый столбец принадлежит переменной x, только там могут быть все единицы.
Второй столбец принадлежит переменной w, только там могут быть все нули.
У нас остались две пустые клеточки в самой таблице. Нам нужно где-то поставить единицу, а где-то ноль, потому что у нас остались столбцы с двумя единицами и одним нулём, а так же с двумя нулями и одной единицей. Если мы в третий столбец поставим единицу, а в четвёртый ноль, то первая строчка и вторая будут совпадать.
А в условии сказано, что строки не должны повторяться. Поэтому нужно ноль и единицу расставить наоборот.
Получается, что в третий столбец идёт z, а в четвёртый y
Ответ: xwzy
Посмотрим, как решать задачи второго задания из ЕГЭ по информатике, когда функция выдаёт нули в таблице истинности.
Задача (Классическая, закрепление)
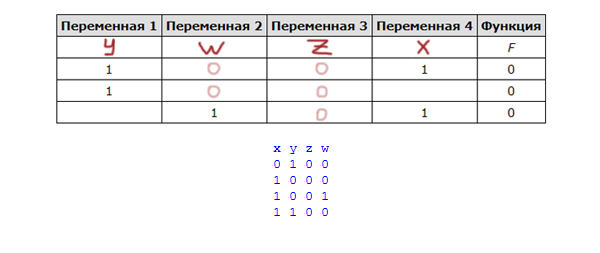
Миша заполнял таблицу истинности функции (x ≡ ¬y) → ((x ∧ w) ≡ z), но успел заполнить лишь фрагмент из трёх различных её строк, даже не указав, какому столбцу таблицы соответствует каждая из переменных w, x, y, z.
Определите, какому столбцу таблицы соответствует каждая из переменных
w, x, y, z.
В ответе напишите буквы w, x, y, z в том порядке, в котором идут
соответствующие им столбцы (сначала буква, соответствующая первому
столбцу; затем буква, соответствующая второму столбцу, и т.д.). Буквы
в ответе пишите подряд, никаких разделителей между буквами ставить
не нужно.
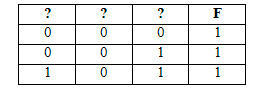
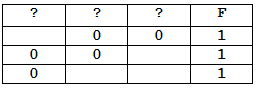
Пример. Функция F задана выражением ¬x / y, зависящим от двух
переменных, а фрагмент таблицы имеет следующий вид.
В этом случае первому столбцу соответствует переменная y, а второму
столбцу – переменная x. В ответе следует написать: yx.
Решение:
Воспользуемся программой на языке Python.
print('x y z w') for x in range(0, 2): for y in range(0, 2): for w in range(0, 2): for z in range(0, 2): if not( not(( x == (not(y)) )) or ((x and w) == z) ): print(x, y, z, w)
От прошлой программы эта программа отличается только функцией!
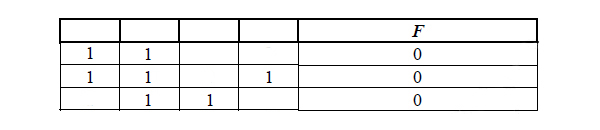
В таблице видим, что функция должна выдавать ноль. Поэтому в условии мы функцию «оборачиваем» в not().
После == операцию not() мы заключили в скобки, чтобы не было синтаксической ошибки.
Получаем следующую таблицу истинности:
Разгадаем, где какая переменная находится.
Последнюю строку из нашей таблицы можно вычеркнуть, потому что, если мы вычеркнем другую строку, то не получится столбца, где все три единицы, а он должен быть.
Получается, что второй столбец достаётся переменной z.
В первом столбце должно быть две единицы. На эту роль подходит переменная y.
В нашей таблице нет строчки, где все единицы, значит, во второй строчке в пустом окошке выставляем ноль. И в этой строчке нулём обладает переменная x. Следовательно, в третьем столбце будет находится x.
А в последний столбец идёт переменная w по остаточному принципу.
Ответ: yzxw
А как Питон справится с более сложной функцией из примерного варианта ЕГЭ по информатике?
Задача (Сложная функция)
Логическая функция F задаётся выражением ((x → y ) ∧ (y → w)) ∨ (z ≡ ( x ∨ y)).
Дан частично заполненный фрагмент, содержащий неповторяющиеся строки таблицы истинности функции F.
Определите, какому столбцу таблицы истинности соответствует каждая из переменных x, y, z, w.
В ответе напишите буквы x, y, z, w в том порядке, в котором идут соответствующие им столбцы (сначала — буква, соответствующая первому столбцу; затем — буква, соответствующая второму столбцу, и т. д.). Буквы в ответе пишите подряд, никаких разделителей между буквами ставить не нужно.
Пример. Пусть задано выражение x → y, зависящее от двух переменных x и y, и фрагмент таблицы истинности:
Тогда первому столбцу соответствует переменная y, а второму столбцу соответствует переменная x. В ответе нужно написать: yx.
Источник задачи сайт решу ЕГЭ: https://inf-ege.sdamgia.ru/
Решение:
Запрограммируем функцию на языке Python.
print('x y z w') for x in range(0, 2): for y in range(0, 2): for w in range(0, 2): for z in range(0, 2): if not( ((not(x) or y) and (not(y) or w)) or (z == (x or y)) ): print(x, y, z, w)
Запустим программу и расставим переменные по своим местам.
Переменная z может быть только в третьем столбце.
Во второй столбец идёт переменная w, только этот столбец может иметь одну единицу.
Посмотрим на строчку, где у w стоит единица. В этой же строчке и у x единица. Значит, x идёт в последний столбец, а y в первый столбец.
Ответ: ywzx
Тот же шаблон работает, когда у нас во втором задании три переменные.
Задача (Три переменные)
(№ 1608) Логическая функция F задаётся выражением (¬x ∧ z) ∨ (¬x ∧ ¬y ∧ ¬z)
На рисунке приведён фрагмент таблицы истинности функции F, содержащий все наборы аргументов, при которых функция F истинна. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных x, y, z.
Источник задачи сайт К. Ю. Полякова: https://kpolyakov.spb.ru/
Решение:
Для трёх переменных шаблон на Питоне отлично работает.
print('x y z') for x in range(0, 2): for y in range(0, 2): for z in range(0, 2): if (not(x) and z) or (not(x) and not(y) and not(z)): print(x, y, z)
Здесь и так понятно, куда какая переменная идёт.
Ответ: yxz
Посмотрим, как решать задачи из второго задания ЕГЭ по информатике, когда в таблице истинности разные значения у функции F.
Задача (Разные значения функции)
Логическая функция F задаётся выражением (¬a ∨ b ∨ ¬c) ∧ (b ∨ ¬c). Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
В ответе напишите буквы a, b, c в том порядке, в котором идут соответствующие им столбцы (без разделителей).
Источник задачи сайт К. Ю. Полякова: https://kpolyakov.spb.ru/
Решение:
Когда такая ситуация, что функция имеет различные значения в таблице, мы можем проверить, какие значения переменных дают единицу у всей функции. А потом проверить, какие значения выдают ноль у всей функции, если это потребуется.
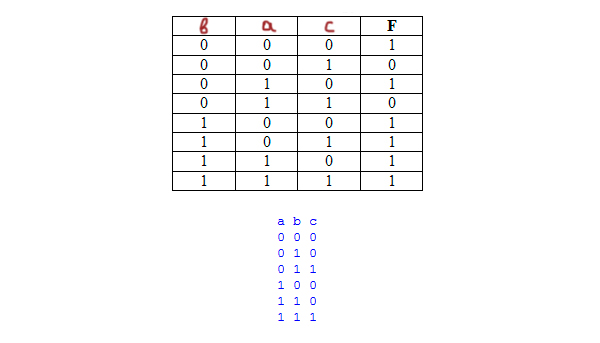
print('a b c') for a in range(0, 2): for b in range(0, 2): for c in range(0, 2): if (not(a) or b or not(c)) and (b or not(c)): print(a, b, c)
В таблице 6 строчек, в которых главная функция превращается в единицу. Далее эти строчки и будем рассматривать. У нас тоже получилось 6 строчек.
Переменная a имеет три единицы. Это второй столбец, потому что там три единицы.
Переменная b имеет четыре единицы, значит, она расположена в первом столбце.
Переменной c достаётся последний столбец.
Ответ: bac
Ещё одна интересная задача для подготовки к ЕГЭ по информатике 2022.
Задача(С подвохом)
Логическая функция F задаётся выражением a ≡ b ∨ b → c.
На рисунке приведён частично заполненный фрагмент таблицы истинности функции F, содержащий неповторяющиеся строки. Определите, какому столбцу таблицы истинности функции F соответствует каждая из переменных a, b, c.
Источник задачи группа Евгения Джобса: https://vk.com/inform_web
Решение:
Подвох заключается в том, что если мы переведём бездумно функцию на язык Питон, то получится a==b or not(b) or c. Но у нас существуют приоритеты для логических операций, которые описаны в прошлогодней статье по подготовке к ЕГЭ по информатике.
В начале должно обрабатываться или, которое было изначально. Затем должно обработаться следование, а потом равносильность. А если мы переведём формулу бездумно, порядок будет не правильный.
Операцию b ∨ b можно представить, как просто b. Ведь, если b принимает значение 0, тогда будет 0 ∨ 0 = 0. Если значение будет 1, то 1 ∨ 1 = 1. Поэтому формулу можно переписать следующим образом:
a ≡ b → c
a == (not(b) or c)
В предыдущих задачах нам не приходилось думать над приоритетами, потому что везде были расставлены скобки. И в основном они уже расставлены в задачах второго задания из ЕГЭ по информатике.
Дальше решаем как обычно.
print('a b c') for a in range(0, 2): for b in range(0, 2): for c in range(0, 2): if a == (not(b) or c): print(a, b, c)
Последнюю строчку можно вычеркнуть из нашей таблицы, т.к. у нас в каждой строчке есть хотя бы один ноль.
Последний столбец занимает переменная a, т.к. только в последний столбец может влезть две единицы.
В строчке, где у a ноль, так же ноль и у переменной c. Значит, во второй столбец идёт переменная c. Если мы ноль поставим в первой строчке в первом столбце, то получится первый столбец из всех нулей. А такого у нас в таблице истинности нет.
Тогда переменная b в первом столбце.
Ответ: bca
слишком много лишних скобок ни к чему. Код очень грязный
А есть какой-нибудь простой код, который смог бы помочь с таким заданием: «Сколькими способами можно поставить в соответствие переменные w, x, y, z столбцам таблицы истинности функции F, опираясь на информацию из данного фрагмента?», или же в данном случае нужно самому подбирать комбинации?
Доброго времени суток, есть вопрос про операции в последней задаче. Вот там написано что b ∨ b можно представить как b. А если будет b ∧ b, то это можно будет представить как b? И можете объяснить почему?
Как в циклах идут переменные, это не важно. Это просто перебор всех возможных вариантов.
Володя, b ∧ b = b, эти формулы приведены в материале, на который я даю ссылку в начале статьи.
В данном курсе рассмотрен язык Python, но только в рамках ЕГЭ по информатике. Если хотите изучить необходимый минимум для ЕГЭ, то добро пожаловать на курс!
About this course
В курсе рассмотрены темы необходимые для сдачи ЕГЭ по информатике. Курс подходит для начинающего уровня, если вы хотите изучить язык Python, то можете начать этот курс для базового ознакомления с языком.
Meet the Instructors
Course content
Share this course
https://stepik.org/course/67400/promo
Документация
Библиотека работает в Python 3.6+
Немного терминологии
Модуль — это файл с расширением .py, находящийся в библиотеке.
Например, модуль constants — это файл constants.py.
Модуль decorators
1. Декоратор cache
Для чего: мемоизация работы функции.
Пример использования:
from infEGE import cache @cache def fib(n): if n in {0,1}: return 1 return fib(n - 1) + fib(n - 2) fib(50)
Если убрать @cache, то вычисляться будет очень долго.
Модуль constants
Для чего: константы для использования в алгоритмах.
Содержимое:
E = 2.718281828459045 PI = 3.141592653589793 maxValue = float('inf') minValue = float('-inf')
Модуль algebra_logic
1. Функция print_true_table
Синтаксис: print_true_table(variables: str, expretion: str, value: Union[int, bool, ‘all’] = ‘all’) -> None
Для чего:
Вывод таблицы истинности лог.функции expretion от переменных variables.
Если value='all', выводятся все строки таблицы;
Если value=1 или True, выводятся строки таблицы, где функция истинна;
Если value=0 или False, выводятся строки таблицы, где функция ложна.
В качестве лог.операций можно использовать обычные операции Python
или такие эквиваленты:
{"&": " and ", "|": " or ", "~": " not ", "->": "<="}.
Пример использования #1:
from infEGE import print_true_table print_true_table("xy", "x->y", 1)
Вывод:
xy F
00 1
01 1
11 1
Внимание: в Python приоритет <= выше, чем and, or, not! Ставьте скобки!
Пример использования #2:
from infEGE import print_true_table print_true_table("xy", "x&(y|x)|y", 0)
Вывод:
xy F
00 0
Пример использования #3:
from infEGE import print_true_table print_true_table("xzy", "x or z and (y or not x)")
Вывод:
xzy F
000 0
001 0
010 1
011 1
100 1
101 1
110 1
111 1
Модуль combinatorics
1. Функция permutation_with_repeat
Синтаксис: permutation_with_repeat(seq: Union[list, tuple, str], repeat: int = 1)
Для чего:
Возвращает перестановки элкементов итерируемого
обьекта seq с repeat повторениями.
Пример использования:
from infEGE import permutation_with_repeat for el in permutation_with_repeat('123', 2): print(el)
Вывод:
('1', '1')
('1', '2')
('1', '3')
('2', '1')
('2', '2')
('2', '3')
('3', '1')
('3', '2')
('3', '3')
2. Функция permutations
Синтаксис: permutations(seq: Union[list, tuple, str]):
Для чего:
Возвращает перестановки элкементов итерируемого объекта seq.
Пример использования:
from infEGE import permutations for el in permutations('abc'): print(el)
Вывод:
abc
acb
bac
bca
cab
cba
Модуль lists_and_other
1. Функция prod
Синтаксис: prod(seq: Union[list, tuple, set]) -> Union[int, float]
Для чего:
Возввращает произведение элементов итерируемого объекта seq.
Пример использования:
from infEGE import prod print(prod([5, 8, 6, 100, 54]))
Вывод:
1296000
Модуль string
1. Функция replacing
Синтаксис: replacing(string: str, substring: str, new_string: str, mode: str = ‘обычно’, cnt: Union[int, str] = ‘all’) -> str
Для чего:
Возвращает строку string с заменённой подстрокой
substring на подстроку new_string в количестве cnt.
Режим "обычно":
замена стандартным replace
Режим "целиком":
замена подстроки substring если она не
является частью большей подстроки.
Пример использования #1:
from infEGE import replacing print(replacing("Питон плохой тон", "тон", "нот"))
Вывод:
Пинот плохой нот
Пример использования #2:
from infEGE import replacing print(replacing("Питон плохой тон", "тон", "нот", cnt=1))
Вывод:
Пинот плохой тон
Пример использования #3:
from infEGE import replacing print(replacing("Питон плохой тон", "тон", "нот", "целиком"))
Вывод:
Питон плохой нот
2. Функция index_n
Синтаксис: index_n(string: str, substring: str, n: int = 1) -> int
Для чего:
Возвращает индекс n-го вхождения СЛЕВА подстроки
substring в строку string. Если такого вхождения
нет, возвращается -1000.
Пример использования #1:
from infEGE import index_n print(index_n("01230123", "1"))
Вывод:
1
Пример использования #2:
from infEGE import index_n print(index_n("01230123", "1", 2))
Вывод:
5
Пример использования #3:
from infEGE import index_n print(index_n("01230123", "1", 3))
Вывод:
-1000
3. Функция is_number
Синтаксис: is_number(n: str) -> bool
Для чего:
Проверяет является ли строка n числом.
Если да возвращается True, иначе - False.
Пример использования #1:
from infEGE import is_number print(is_number("23"))
Вывод:
True
Пример использования #2:
from infEGE import is_number print(is_number("2n3"))
Вывод:
False
Модуль system_count
1. Функция to_base
Синтаксис: to_base(number: Union[int, str], old_base: int = 10, new_base: int = 10) -> Union[int, str]
Для чего:
Переводит число number с основанием old_base в число
с основанием new_base.
Пример использования #1:
from infEGE import to_base print(to_base(5, new_base=2))
Вывод:
101
Пример использования #2:
from infEGE import to_base print(to_base(15, new_base=16))
Вывод:
F
Пример использования #3:
from infEGE import to_base print(to_base("FA32", old_base=17, new_base=10))
Вывод:
76638
Пример использования #4:
from infEGE import to_base print(to_base("FA32", old_base=17, new_base=6))
Вывод:
1350450
Модуль mathematics
1. Функция is_prime
Синтаксис: is_prime(n: int) -> bool
Для чего:
Если n - простое, то возващается True, иначе - False.
Пример использования #1:
from infEGE import is_prime print(is_prime(5))
Вывод:
True
Пример использования #2:
from infEGE import is_prime print(is_prime(25))
Вывод:
False
Пример использования #3:
from infEGE import is_prime print(is_prime(1))
Вывод:
False
2. Функция is_even
Синтаксис: is_even(n: int) -> bool
Для чего:
Если n - чётно, то возващается True, иначе - False.
Пример использования #1:
from infEGE import is_even print(is_even(12))
Вывод:
True
Пример использования #2:
from infEGE import is_even print(is_even(25))
Вывод:
False
3. Функция is_odd
Синтаксис: is_odd(n: int) -> bool
Для чего:
Если n - нечётно, то возващается True, иначе - False.
Пример использования #1:
from infEGE import is_odd print(is_odd(12))
Вывод:
False
Пример использования #2:
from infEGE import is_odd print(is_odd(25))
Вывод:
True
4. Функция divided
Синтаксис: divided(n: int, d: int) -> bool
Для чего:
Если n нацело делится на d, то возвращается True, иначе - False.
Пример использования #1:
from infEGE import divided print(divided(12, 5))
Вывод:
False
Пример использования #2:
from infEGE import divided print(divided(121, 11))
Вывод:
True
5. Функция not_divisible
Синтаксис: not_divisible(n: int, d: int) -> bool
Для чего:
Если n не делится нацело на d, то возвращается True, иначе - False.
Пример использования #1:
from infEGE import not_divisible print(not_divisible(12, 5))
Вывод:
True
Пример использования #2:
from infEGE import not_divisible print(not_divisible(121, 11))
Вывод:
False
6. Функция factorial
Синтаксис: factorial(n: int) -> int
Для чего:
Возвращает n! (0! = 1)
Пример использования:
from infEGE import factorial print(factorial(6))
Вывод:
720
7. Функция factorize
Синтаксис: factorize(number: int) -> list
Для чего:
Возвращает разложение числа number на простые множители в list.
Пример использования #1:
from infEGE import factorize print(factorize(1))
Вывод:
[]
Пример использования #2:
from infEGE import factorize print(factorize(11))
Вывод:
[11]
Пример использования #3:
from infEGE import factorize print(factorize(55))
Вывод:
[5, 11]
8. Функция divisors
Синтаксис: divisors(n: int) -> list
Для чего:
Возвращает все натуральные делители числа n на интервале (1; n).
Пример использования #1:
from infEGE import divisors print(divisors(1))
Вывод:
[]
Пример использования #2:
from infEGE import divisors print(divisors(720))
Вывод:
[2, 3, 4, 5, 6, 8, 9, 10, 12, 15, 16, 18, 20, 24, 30, 36, 40, 45, 48, 60, 72, 80, 90, 120, 144, 180, 240, 360]
9. Функция fib
Синтаксис: fib(n: int) -> int
Для чего:
Возвращает n-ый член последовательности Фибоначчи. Нумерация с 0.
Пример использования #1:
from infEGE import fib print(fib(0))
Вывод:
0
Пример использования #2:
from infEGE import fib print(fib(1))
Вывод:
1
Пример использования #3:
from infEGE import fib print(fib(2))
Вывод:
1
Пример использования #4:
from infEGE import fib print(fib(3))
Вывод:
2
Пример использования #5:
from infEGE import fib print(fib(2001))
Вывод:
6835702259575806647045396549170580107055408029365524565407553367798082454408054014954534318953113802726603726769523447478238192192714526677939943338306101405105414819705664090901813637296453767095528104868264704914433529355579148731044685634135487735897954629842516947101494253575869699893400976539545740214819819151952085089538422954565146720383752121972115725761141759114990448978941370030912401573418221496592822626
Примечание: Данный алгоритм работает быстрее рекурсивного! Асимптоматика: O(N)