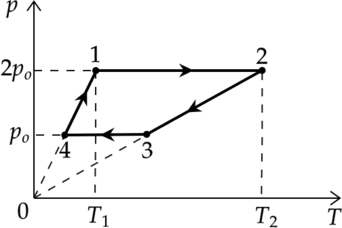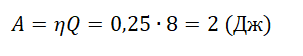СДАМ ГИА:
РЕШУ ЕГЭ
Образовательный портал для подготовки к экзаменам
Физика
Физика
≡ Математика
Базовый уровень
Профильный уровень
Информатика
Русский язык
Английский язык
Немецкий язык
Французский язык
Испанский язык
Физика
Химия
Биология
География
Обществознание
Литература
История
Сайты, меню, вход, новости
СДАМ ГИАРЕШУ ЕГЭРЕШУ ОГЭРЕШУ ВПРРЕШУ ЦТ
Об экзамене
Каталог заданий
Варианты
Ученику
Учителю
Школа
Карточки
Справочник
Сказать спасибо
Вопрос — ответ
Чужой компьютер
Зарегистрироваться
Восстановить пароль
Войти через ВКонтакте
Играть в ЕГЭ-игрушку
Новости
10 марта
Как подготовиться к ЕГЭ и ОГЭ за 45 дней
6 марта
Изменения ВПР 2023
3 марта
Разместили утвержденное расписание ЕГЭ
27 января
Вариант экзамена блокадного Ленинграда
23 января
ДДОС-атака на Решу ЕГЭ. Шантаж.
6 января
Открываем новый сервис: «папки в избранном»
22 декабря
Открыли новый портал Решу Олимп. Для подготовки к перечневым олимпиадам!
4 ноября
Материалы для подготовки к итоговому сочинению 2022–2023
31 октября
Сертификаты для учителей о работе на Решу ЕГЭ, ОГЭ, ВПР
21 марта
Новый сервис: рисование
31 января
Внедрили тёмную тему!
НАШИ БОТЫ
Все новости
ЧУЖОЕ НЕ БРАТЬ!
Экзамер из Таганрога
10 апреля
Предприниматель Щеголихин скопировал сайт Решу ЕГЭ
Наша группа
Каталог заданий.
Работа идеального газа
Пройти тестирование по этим заданиям
Вернуться к каталогу заданий
Версия для печати и копирования в MS Word
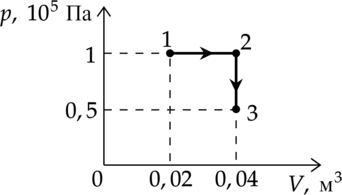
1
Тип 9 № 1021
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в килоджоулях.)
Раздел кодификатора ФИПИ/Решу ЕГЭ: 2.2.6 Элементарная работа в термодинамике
Решение
·
·
Сообщить об ошибке · Помощь
2
Тип 9 № 1022
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в килоджоулях.)
Раздел кодификатора ФИПИ/Решу ЕГЭ: 2.2.6 Элементарная работа в термодинамике
Решение
·
·
3 комментария · Сообщить об ошибке · Помощь
3
Тип 9 № 1023
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в килоджоулях.)
Раздел кодификатора ФИПИ/Решу ЕГЭ: 2.2.6 Элементарная работа в термодинамике
Решение
·
·
Сообщить об ошибке · Помощь
4
Тип 9 № 1024
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в килоджоулях.)
Раздел кодификатора ФИПИ/Решу ЕГЭ: 2.2.6 Элементарная работа в термодинамике
Решение
·
·
1 комментарий · Сообщить об ошибке · Помощь
5
Тип 9 № 1025
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в килоджоулях.)
Раздел кодификатора ФИПИ/Решу ЕГЭ: 2.2.6 Элементарная работа в термодинамике
Решение
·
·
Сообщить об ошибке · Помощь
Пройти тестирование по этим заданиям
О проекте · Редакция · Правовая информация · О рекламе
© Гущин Д. Д., 2011—2023
1. Вспоминай формулы по каждой теме
2. Решай новые задачи каждый день
3. Вдумчиво разбирай решения
Работа идеального газа
Какую работу совершает газ при переходе из состояния 1 в состояние 3? (Ответ дайте в кДж.)
Работа газа – площадь под графиком: [A=p_1cdot(V_2-V_1)=10^5text{ Па}cdot(0,04text{ м$^3$}-0,02text{ м$^3$})=2000text{ Дж}=2text{ кДж}]
Ответ: 2
Идеальный газ получил количество теплоты 300 Дж и при этом внутренняя энергия газа увеличилась на 100 Дж. Какова работа, совершенная газом? (Ответ дать в джоулях.)
Первое начало термодинамики: [Q=Delta U+A] [A=Q-Delta U=300text{ Дж}-100text{ Дж}=200 text{ Дж}]
Ответ: 200
Идеальный газ получил количество теплоты 100 Дж и при этом внутренняя энергия газа уменьшилась на 100 Дж. Какова работа, совершенная газом? (Ответ дать в джоулях.)
Первое начало термодинамики: [Q=Delta U+A] [A=Q-Delta U=100text{ Дж}-(-100text{ Дж})=200 text{ Дж}]
Ответ: 200
На pV-диаграмме изображены циклические процессы, совершаемые идеальным газом в количестве 1 моль. Определите отношение работы газа в циклическом процессе ВСDВ к работе газа в циклическом процессе АВDFА.
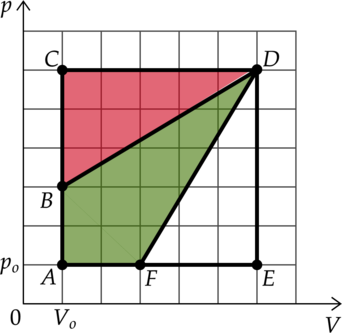
Ответ: 0,75
В некотором процессе газ отдал окружающей среде количество теплоты, равное 10 кДж. При этом внутренняя энергия газа увеличилась на 30 кДж. Определите работу, которую совершили внешние силы, сжав газ. Ответ выразите в кДж.
Первое начало термодинамики: [Q=Delta U+A_{text{г}}] [A_{text{г}}=Q-Delta U]
Подставим исходные значения: [A_{text{г}}=Q-Delta U=-10text{ кДж}-30text{ кДж}=-40 text{ кДж}] [A_{text{вн.с.}}=-A_{text{г}}=40 text{ кДж}]
Ответ: 40
В цилиндр с подвижным поршнем накачали (nu = 2) моля идеального одноатомного газа при температуре (t_1 = 50) (^{circ}C). Накачивание вели так, что давление газа было постоянным. Затем накачку прекратили и дали газу в цилиндре расшириться без теплообмена с окружающей средой до давления p = 1 атм. При этом газ остыл до температуры (t_2 = 20) (^{circ}C). Какую суммарную работу совершил газ в этих двух процессах? В исходном состоянии цилиндр был пуст и поршень касался дна. Универсальная газовая постоянная (R = 8,3) Дж/(моль·К). Ответ дайте в кДж округлите до целых.
В первом процессе газ расширяется при постоянном давлении. От объема 0 до (V_1) [A_{1-2}=p(V_1-0)=pV_1=nu RT_1]
Без теплообмена с окружающей средой означает, что процесс – адиабатический [Q=Delta U+A_{2-3}=0] [A_{2-3}=-Delta U_{2-3}]
Подставим исходные значения: [A=A_{1-2}+A_{2-3}=nu RT_1+frac{3}{2}nu R(T_1-T_2)=] [=2text{ моль}cdot8,3text{ Дж/моль·К}cdot323text{ K}+frac{3}{2}cdot2text{ моль}cdot8,3text{ Дж/моль·К}cdot30{ K}approx 6000text{ Дж}approx 6 text{ кДж}]
Ответ: 6
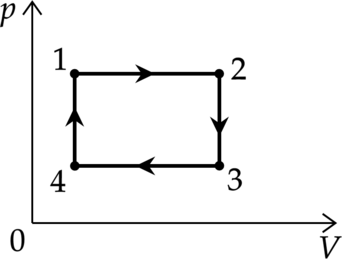
С массой (m = 80) г идеального газа, молярная масса которого (M = 28) г/моль, совершается циклический процесс, изображенный на рисунке. Какую работу (A) совершает такой двигатель за один цикл, если (T_1 = 300) К, (T_2 = 1000) К, а при нагревании на участке 4 – 1 давление газа увеличивается в 2 раза? Универсальная газовая постоянная (R = 8,3) Дж/(моль·К). Ответ округлите до целых.
1-2 и 3-4 – изобарные процессы
2-3 и 4-1 – изохорные процессы
Перерисуем график в координатах (pV)
Так как 2-3 и 4-1 – изохорные процессы, то (Tsim p). Давление увеличивается в 2 раза, то температура увеличивается в 2 раза. Следовательно: [T_4=frac{T_1}{2}=150 text{ К}] [T_3=frac{T_2}{2}=500 text{ К}]
Работа газа цикл – площадь внутри графика в координатах (pV) [A=(p_1-p_4)cdot(V_2-V_1)=(2p_4-p_4)cdot(V_2-V_1)=p_4cdot(V_2-V_1)=p_4V_2-p_4V_1]
Подставим исходные значения,переведя все единицы в систему СИ: [A=p_4V_2-p_4V_1=nu RT_3-nu RT_4=nu R(T_3-T_4)=frac{m}{M}R(T_3-T_4)=] [=frac{0,08text{ кг}}{0,028text{ кг/моль}}cdot8,31text{ Дж/(моль$cdot$ К)}cdot(500 text{ К} — 150 text{ К})= 8310 text{ Дж}]
Ответ: 8310

Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Курс Глицин. Любовь, друзья, спорт и подготовка к ЕГЭ
Первый закон термодинамики
-
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
-
Работа газа в изобарном процессе
-
Работа газа в произвольном процессе
-
Работа, совершаемая над газом
-
Применение первого закона термодинамики к изопроцессам
-
Адиабатный процесс
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: работа в термодинамике, первый закон термодинамики, адиабатный процесс.
Начнём с обсуждения работы газа.
Газ, находящийся в сосуде под поршнем, действует на поршень с силой , где
— давление газа,
— площадь поршня. Если при этом поршень перемещается, то газ совершает работу.
При расширении газа эта работа будет положительной (сила давления газа и перемещение поршня направлены в одну сторону). При сжатии работа газа отрицательна (сила давления газа и перемещение поршня направлены в противоположные стороны).
к оглавлению ▴
Работа газа в изобарном процессе
Предположим, что газ расширяется при постоянном давлении . Тогда сила
, с которой газ действует на поршень, также постоянна. Пусть поршень переместился на расстояние
(рис. 1).
Рис. 1.
Работа газа равна:
Но — изменение объёма газа. Поэтому для работы газа при изобарном расширении мы получаем формулу:
(1)
Если и
— начальный и конечный объём газа, то для работы газа имеем:
. Изобразив данный процесс на
-диаграмме, мы видим, что работа газа равна площади прямоугольника под графиком нашего процесса (рис. 2).
Рис. 2. Работа газа как площадь
Пусть теперь газ изобарно сжимается от объёма до объёма
. С помощью аналогичных рассуждений приходим к формуле:
Но , и снова получается формула (1).
Работа газа опять-таки будет равна площади под графиком процесса на -диаграмме, но теперь со знаком минус.
Итак, формула выражает работу газа при постоянном давлении — как в процессе расширения газа, так и в процессе сжатия.
к оглавлению ▴
Работа газа в произвольном процессе
Геометрическая интерпретация работы газа (как площади под графиком процесса на -диаграмме) сохраняется и в общем случае неизобарного процесса.
Действительно, рассмотрим малое изменение объёма газа — настолько малое, что давление
будет оставаться приблизительно постоянным. Газ совершит малую работу
. Тогда работа
газа во всём процессе найдётся суммированием этих малых работ:
Но данный интеграл как раз и является площадью криволинейной трапеции (рис. 3):
Рис. 3. Работа газа как площадь
к оглавлению ▴
Работа, совершаемая над газом
Наряду с работой , которую совершает газ по передвижению поршня, рассматривают также работу
, которую поршень совершает над газом.
Если газ действует на поршень с силой , то по третьему закону Ньютона поршень действует на газ с силой
, равной силе
по модулю и противоположной по направлению:
(рис. 4).
Рис. 4. Внешняя сила , действующая на газ
Следовательно, работа поршня равна по модулю и противоположна по знаку работе газа:
Так, в процессе расширения газ совершает положительную работу ; при этом работа, совершаемая над газом, отрицательна
. Наоборот, при сжатии работа газа отрицательна
, а работа, совершаемая поршнем над газом, положительна
0 right )’ class=’tex’ alt=’left ( {A}’ > 0 right )’ />.
Будьте внимательны: если в задаче просят найти работу, совершённую над газом, то имеется в виду работа .
Как мы знаем, существует лишь два способа изменения внутренней энергии тела: теплопередача и совершение работы.
Опыт показывает, что эти способы независимы — в том смысле, что их результаты складываются. Если телу в процессе теплообмена передано количество теплоты , и если в то же время над телом совершена работа
, то изменение внутренней энергии тела будет равно:
(2)
Нас больше всего интересует случай, когда тело является газом. Тогда (где
, как всегда, есть работа самого газа). Формула (2) принимает вид:
, или
(3)
Соотношение (3) называется первым законом термодинамики. Смысл его прост: количество теплоты, переданное газу, идёт на изменение внутренней энергии газа и на совершение газом работы.
Напомним, что величина может быть и отрицательной: в таком случае тепло отводится от газа. Но первый закон термодинамики остаётся справедливым в любом случае. Он является одним из фундаментальных физических законов и находит подтверждение в многочисленных явлениях и экспериментах.
к оглавлению ▴
Применение первого закона термодинамики к изопроцессам
Напомним, что в изопроцессе остаётся неизменным значение некоторой величины, характеризующей состояние газа — температуры, объёма или давления. Для каждого вида изопроцессов запись первого закона термодинамики упрощается.
1. Изотермический процесс, .
Внутренняя энергия идеального газа зависит только от его температуры. Если температура газа не меняется, то не меняется и внутренняя энергия: . Тогда формула (3) даёт:
Всё подведённое к газу тепло идёт на совершение газом работы.
2. Изохорный процесс, .
Если объём газа остаётся постоянным, то поршень не перемещается, и потому работа газа равна нулю: . Тогда первый закон термодинамики даёт:
Всё тепло, переданное газу, идёт на изменение его внутренней энергии.
3. Изобарный процесс, .
Подведённое к газу тепло идёт как на изменение внутренней энергии, так и на совершение работы (для которой справедлива формула (1)). Имеем:
к оглавлению ▴
Адиабатный процесс
Процесс называется адиабатным, если он идёт без теплообмена с окружающими телами.
Адиабатный процесс совершается газом, находящимся в теплоизолированном сосуде. Такой сосуд препятствует всем видам теплопередачи: теплопроводности, конвекции, излучению. Пример теплоизолированного сосуда — термос.
Приблизительно адиабатным будет всякий процесс, протекающий достаточно быстро: в течение процесса теплообмен просто не успевает произойти.
При адиабатном процессе . Из первого закона термодинамики получаем:
, или
.
В процессе адиабатного расширения газ совершает положительную работу, поэтому (работа совершается за счёт убыли внутренней энергии). Следовательно, газ охлаждается. Если заставить газ совершить достаточно большую работу, охладить его можно весьма сильно. Именно на этом основаны методы сжижения газов.
Наоборот, в процессе адиабатного сжатия будет , поэтому
: газ нагревается. Адиабатное нагревание воздуха используется в дизельных двигателях для воспламенения топлива.
Кривая, изображающая ход адиабатного процесса, называется адиабатой. Интересно сравнить ход адиабаты и изотермы на -диаграмме (рис. 5).
Рис. 5. Сравнительный ход изотермы и адиабаты
В обоих процессах давление убывает с увеличением объёма, но в адиабатном процессе убывание идёт быстрее. Почему?
При изотермическом расширении давление падает потому, что уменьшается концентрация частиц газа, в результате чего удары частиц по стенкам сосуда становятся реже. Однако интенсивность этих ударов остаётся прежней: ведь температура газа не меняется — значит, не меняется и средняя кинетическая энергия его частиц.
А при адиабатном расширении, наряду с уменьшением концентрации частиц, падает также и температура газа. Удары частиц становятся не только более редкими, но и более слабыми. Вот почему адиабата убывает быстрее изотермы.
Благодарим за то, что пользуйтесь нашими материалами.
Информация на странице «Первый закон термодинамики» подготовлена нашими авторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в высшее учебное заведение или техникум нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими статьями из данного раздела.
Публикация обновлена:
09.03.2023
В задании №9 ЕГЭ по физике необходимо продемонстрировать знания в области такого раздела физики, как термодинамика. Работа идеального газа, КПД тепловых машин, циклы — вот, что ждет нас в девятом задании.
Задание EF17966
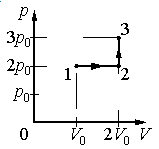
Ответ:
а) р0V0
б) 2р0V0
в) 4р0V0
г) 6р0V0
Алгоритм решения
1.Определить, на каком участке графика совершается работа.
2.Записать геометрический смысл работы.
3.Извлекая данные из графика, вычислить работу, совершенную газом.
Решение
Работа совершается только тогда, когда газ меняет объем. Поэтому работа совершается только на участке 1–2.
Работа идеального газа равна площади фигуры, заключенной под графиком термодинамического процесса в координатах (p, V).
Давление газа при этом равно 2p0, а объем равен разности 2V0 и V0. Следовательно, работа, совершенная газом, будет равна произведению:
A=2p0(2V0−V0)=2p0V0
Ответ: б
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17562
Газу передали изохорно количество теплоты 300 Дж. Как изменилась его внутренняя энергия в этом процессе?
Ответ:
а) увеличилась на 300 Дж
б) уменьшилась на 300 Дж
в) увеличилась на 600 Дж
г) уменьшилась на 600 Дж
Алгоритм решения
1.Записать исходные данные.
2.Записать первое начало термодинамики.
3.Установить, как меняется внутренняя энергия идеального газа.
Решение
Запишем исходные данные:
• Количество теплоты, переданное газу: Q = 300 Дж.
Первое начало термодинамики:
ΔU=Q+A
Так как по условию задачи это изохорный процесс, то работа равна 0. Следовательно, изменение внутренней энергии газа равно количеству теплоты:
ΔU=Q=300 (Дж)
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF17597
Находясь в цилиндре двигателя, газ получил от нагревателя количество теплоты, равное 10 кДж. Затем он расширился, совершив работу 15 кДж. В результате всех этих процессов внутренняя энергия газа уменьшилась на
Ответ:
а) 5 кДж
б) 10 кДж
в) 15 кДж
г) 25 кДж
Алгоритм решения
1.Записать исходные данные.
2.Записать первое начало термодинамики.
3.Установить, как меняется внутренняя энергия идеального газа.
Решение
Запишем исходные данные:
• Количество теплоты, переданное газу: Q = 10 кДж.
• Работа, совершенная газом: A = 15 кДж.
Первое начало термодинамики:
ΔU=Q+A
В этой формуле за работу принимается та работа, что совершается над газом. Но в данном случае газ сам совершает работу. Поэтому первое начало термодинамики примет вид:
ΔU=Q−A=10−15=−5 (кДж)
Знак «–» указывает на то, что внутренняя энергия газа уменьшилась на 5 кДж.
Ответ: а
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задание EF18994
Рабочее тело идеальной тепловой машины с КПД, равным 0,25, за цикл своей работы получает от нагревателя количество теплоты, равное 8 Дж. Какова работа, совершаемая за цикл этой машиной?
Алгоритм решения
1.Записать исходные данные.
2.Записать формулу КПД тепловой машины.
3.Записать решение в общем виде.
4.Выполнить вычисление искомой величины.
Решение
Запишем исходные данные:
• КПД тепловой машины: η = 0,25.
• Количество теплоты, полученное газом от нагревателя за цикл: Q = 8 Дж.
Формула КПД тепловой машины:
η=AQ
Отсюда:
Ответ: 2
pазбирался: Алиса Никитина | обсудить разбор | оценить
Задачи с графиками: работа газа и внутренняя энергия
Задачи средней сложности, для решения нужна только внимательность. Никаких «подвохов»- все математически четко и понятно.
Задача 1.
Температура идеального газа в состоянии 1 была . Чему равна температура в состоянии 3 после осуществления процесса 1-2-3, изображенного на диаграмме
?
К.
К задаче 1
Процесс 1-2 – изохорный. Запишем закон Шарля.
Процесс 2-3 – не изотермический, поэтому просто запишем уравнение состояния:
Откуда
Ответ: 1800 К.
Задача 2.
Идеальный одноатомный газ, находящийся при нормальных условиях, переводят из состояния 1 в состояние 2 двумя способами: 1-3-2 и 1-4-2. Найдите отношение количеств теплоты, которые необходимо сообщить 1 кмоль газа в этих двух процессах.
К задаче 2
Рассмотрим переход 1-3-2. Процесс 1-3 – изохора, работа не совершается. Но температура растет, определим, как.
Процесс 3-2 – изобара. Работа в процессе 3-2 равна
Изменение температуры составило . Следовательно, можем определить изменение внутренней энергии:
Теперь найдем общее количество теплоты, переданное газу при таком переходе:
Процесс перехода 1-4-2 отличается только совершенной работой. Определим ее:
Определим отношение количеств теплоты:
Ответ: .
Задача 3.
Идеальный одноатомный газ, взятый в количестве 1 моль, переводят из состояния 1 в состояние 4. Какое количество теплоты сообщили в этом процессе газу? Масса газа во время процесса не меняется.
К задаче 3
Определим сначала изменение внутренней энергии, для этого составим объединенный газовый закон для точек 1 и 4.
Изменение внутренней энергии равно
Теперь определим работу. Работу удобно определить как площадь под кривой процесса. Разобьем эту площадь на удобные «куски» — трапеции.
К задаче 3. Определяем работу
Теперь найдем общее количество теплоты, переданное газу:
Ответ: 1450 Дж.
Задача 4.
На рисунке представлена диаграмма цикла с одноатомным идеальным газом, взятым в количестве 0,3 моль. Участки и
— адиабаты. Определите работу, совершенную газом на участке
.
К задаче 4
Участок по условию – адиабата, то есть передачи тепла газу на этом участке не происходит, следовательно, работа будет совершена за счет «внутренних резервов» — то есть внутренней энергии. Нужно, следовательно, найти, как она изменилась.
Задачу можно решить двумя способами. Во-первых, просто определить температуры в точках и
, это легко сделать из данных графика с помощью уравнения Менделеева-Клапейрона, и затем посчитать
. Но, так как
, а
,то изменение внутренней энергии будет равно
Ответ: 1350 Дж.
Задача 5.
Один моль одноатомного идеального газа расширяется сначала изобарно, а затем по линейному закону, причем прямая линия проходит через начало координат .
. Найдите
, если количество тепла, сообщенное газу на участке 1-2, в 4 раза меньше работы, совершенной на участке 2-3.
К задаче 5
Определим количество тепла, сообщенное газу на участке 1-2, и работу, совершенную на участке 2-3.
Для изобарного процесса 1-2 запишем закон Гей-Люссака:
Откуда
Следовательно, изменение внутренней энергии газа равно
Работа на этом участке равна площади под графиком, под участком 1-2:
Тогда тепло, переданное газу, равно
Теперь рассмотрим процесс 2-3. Нам нужно определить лишь работу газа на этом участке. Площадь под этим участком – трапеция, поэтому
Из подобия треугольников и
запишем:
Тогда
Так как по условию , то
Так как , то
Сократим, что возможно:
Из первой записанной нами формулы (закона Гей-Люссака) следует, что
Тогда
Или
Введем замену :
Понятно, отрицательный корень нас не интересует.
Ответ: .
Работа в термодинамике
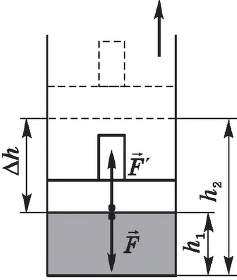
В термодинамике, в отличие от механики, рассматривается не движение тела как целого, а лишь относительное изменение частей термодинамической системы, в результате которого меняется ее объем.
Рассмотрим работу газа при изобарическом расширении.
Вычислим работу, совершаемую газом при его действии на поршень с силой ${F’}↖{→}$, равной по величине и противоположной по направлению силе ${F’}↖{→}$, действующей на газ со стороны поршня: ${F’}↖{→}=-{F’}↖{→}$ (согласно третьему закону Ньютона), $F’=pS$, где $p$ — давление газа, а $S$ — площадь поверхности поршня. Если перемещение поршня $∆h$ в результате расширения мало, то давление газа можно считать постоянным и работа газа равна:
$A’=F’∆h=pS∆h=p∆V$
Если газ расширяется, он совершает положительную работу, та к как перемещение поршня совпадает по направлению с силой ${F’}↖{→}$. Если газ сжимается, то работа газа отрицательна, поскольку перемещение поршня противоположно силе ${F’}↖{→}$. В формуле $A’=F’∆h=pS∆h=p∆V$ появится знак «минус»: $∆V < 0$, поскольку $∆h < 0$.
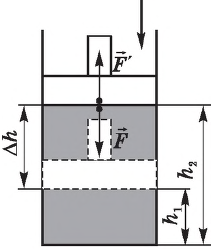
Работа внешних сил $А$, наоборот, положительна при сжатии газа и отрицательна при расширении:
$A=-A’=-p∆V$
Совершая над газом положительную работу, внешние тела передают ему часть своей энергии. При расширении газа внешние тела отбирают у газа часть его энергии — работа внешних сил отрицательна.
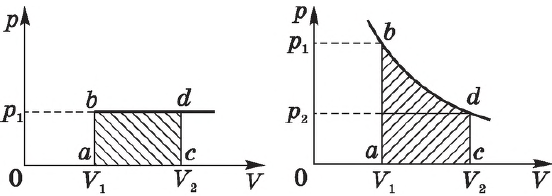
На графике зависимости давления от объема $р(V)$ работа определяется как площадь, ограниченная кривой $р(V)$, осью $V$ и отрезками $ab$ и $cd$, равными давлениям $р_1$ в начальном ($V_1$) и $р_2$ в конечном ($V_2$) состояниях, как для изобарного, так и для изотермического процессов.
Первый закон термодинамики
Первое начало (первый закон) термодинамики — это закон сохранения и превращения энергии для термодинамической системы.
Согласно первому началу термодинамики, работа может совершаться только за счет теплоты или какой-либо другой формы энергии. Следовательно, работу и количество теплоты измеряют в одних единицах — джоулях (как и энергию).
Первое начало термодинамики было сформулировано немецким ученым Ю. Л. Майером в 1842 г. и подтверждено экспериментально английским ученым Дж. Джоулем в 1843 г.
Первый закон термодинамики формулируется так:
Изменение внутренней энергии системы при переходе ее из одного состояния в другое равно сумме работы внешних сил и количества теплоты, переданного системе:
$∆U=A+Q$
где $∆U$ — изменение внутренней энергии, $А$ — работа внешних сил, $Q$ — количество теплоты, переданной системе.
Из $∆U=A+Q$ следует закон сохранения внутренней энергии. Если систему изолировать от внешних воздействий, $A=0$ и $Q=0$,а следовательно, $∆U=0$.
При любых процессах, происходящих в изолированной системе, ее внутренняя энергия остается постоянной.
Если работу совершает система, а не внешние силы, то уравнение ($∆U=A+Q$) записывается в виде:
$Q=∆U+A’$
где $А’$ — работа, совершаемая системой ($А’=-А$).
Количество теплоты, переданное системе, идет на изменение ее внутренней энергии и на совершение системой работы над внешними телами.
Первое начало термодинамики может быть сформулировано как невозможность существования вечного двигателя первого рода, который совершал бы работу, не черпая энергию из какого-либо источника, т. е. только за счет внутренней энергии.
Действительно, если к телу не поступает теплота ($Q=0$), то работа $А’$, согласно уравнению $Q=∆U+A’$, совершается только за счет убыли внутренней энергии $A’=-∆U$. После того, как запас энергии окажется исчерпанным, двигатель перестает работать.
Следует помнить, что как работа, так и количество теплоты являются характеристиками процесса изменения внутренней энергии, поэтому нельзя говорить, что в системе содержится определенное количество теплоты или работы. Система в любом состоянии обладает лишь определенной внутренней энергией.
Применение первого закона термодинамики к различным процессам
Рассмотрим применение первого закона термодинамики к различным термодинамическим процессам.
Изохорный процесс. Зависимость $р(Т)$ на термодинамической диаграмме изображается изохорой.
Изохорный (изохорический) процесс — термодинмический процесс, происходящий в системе при постоянном объеме.
Изохорный процесс можно осуществить в газах и жидкостях, заключенных в сосуд с постоянным объемом.
При изохорном процессе объем газа не меняется ($∆V=0$), и, согласно первому началу термодинамики $Q=∆U+A’$,
$∆U=Q$
т. е. изменение внутренней энергии равно количеству переданного тепла, т. к. работа ($A=p∆V=0$) газом не совершается.
Если газ нагревается, то $Q > 0$ и $∆U > 0$, его внутренняя энергия увеличивается. При охлаждении газа $Q < 0$ и $∆U < 0$, внутренняя энергия уменьшается.
Изотермический процесс графически изображается изотермой.
Изотермический процесс — это термодинамический процесс, происходящий в системе при постоянной температуре.
Поскольку при изотермическом процессе внутренняя энергия газа не меняется ($T=const$), то все переданное газу количество теплоты идет на совершение работы:
$Q=A’$
При получении газом теплоты ($Q > 0$) он совершает положительную работу ($А’ > 0$). Если газ отдает тепло окружающей среде, $Q < 0$ и $А’ < 0$. В этом случае над газом совершается работа внешними силами. Для внешних сил работа положительна. Геометрически работа при изотермическом процессе определяется площадью под кривой $р(V)$.
Изобарный процесс на термодинамической диаграмме изображается изобарой.
Изобарный (изобарический) процесс — термодинамический процесс, происходящий в системе с постоянным давлением $p$.
Примером изобарного процесса является расширение газа в цилиндре со свободно ходящим нагруженным поршнем.
При изобарном процессе согласно формуле $Q=∆U+A’$ передаваемое газу количество теплоты идет на изменение его внутренней энергии $∆U$ и на совершение им работы $A’$ при постоянном давлении:
$Q=∆U+A’$
Работа идеального газа определяется по графику зависимости $p(V)$ для изобарного процесса ($A’=p∆V$).
Для идеального газа при изобарном процессе объем пропорционален температуре, в реальных газах часть теплоты расходуется на изменение средней энергии взаимодействия частиц.
Адиабатический процесс
Адиабатический процесс (адиабатный процесс) — это термодинамический процесс, происходящий в системе без теплообмена с окружающей средой ($Q=0$).
Адиабатическая изоляция системы приближенно достигается в сосудах Дьюара, в так называемых адиабатных оболочках. На адиабатически изолированную систему не оказывает влияния изменение температуры окружающих тел. Ее внутренняя энергия и может меняться только за счет работы, совершаемой внешними телами над системой, или самой системой.
Согласно первому началу термодинамики ($∆U=A+Q$), в адиабатной системе
$∆U=A$
где $А$ — работа внешних сил.
При адиабатном расширении газа $А < 0$.
Следовательно,
$∆U={i}/{2}·{m}/{M}R∆T < 0,$
что означает уменьшение температуры при адиабатном расширении. Оно приводит к тому, что давление газа уменьшается более резко, чем при изотермическом процессе.
На рисунке адиабата $1—2$, проходящая между двумя изотермами, наглядно иллюстрирует сказанное. Площадь под адиабатой численно равна работе, совершаемой газом при его адиабатическом расширении от объема $V_1$ до $V_2$.
Адиабатное сжатие приводит к повышению температуры газа, т. к. в результате упругих соударений молекул газа с поршнем их средняя кинетическая энергия возрастает, в отличие от расширения, когда она уменьшается (в первом случае скорости молекул газа увеличиваются, во втором — уменьшаются).
Резкое нагревание воздуха при адиабатическом сжатии используется в двигателях Дизеля.
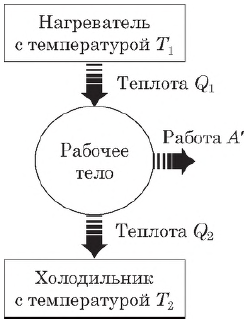
Принцип действия тепловых двигателей
Тепловой двигатель — это устройство, преобразующее внутреннюю энергию топлива в механическую энергию.
Согласно второму началу термодинамики, тепловой двигатель может непрерывно совершать периодически повторяющуюся механическую работу за счет охлаждения окружающих тел, если он не только получает теплоту от более горячего тела (нагревателя), но при этом отдает теплоту менее нагретому телу (холодильнику). Следовательно, на совершение работы идет не все количество теплоты, полученное от нагревателя, а только часть ее.
Таким образом, основными элементами любого теплового двигателя являются:
- рабочее тело (газ или пар), совершающее работу;
- нагреватель, сообщающий энергию рабочему телу;
- холодильник, поглощающий часть энергии от рабочего тела.
Коэффициент полезного действия теплового двигателя
Согласно закону сохранения энергии, работа, совершаемая двигателем, равна:
$A’=|Q_1|-|Q_2|$
где $Q_1$ — количество теплоты, полученное от нагревателя, $Q_2$ — количество теплоты, отданное холодильнику.
Коэффициентом полезного действия (КПД) теплового двигателя называется отношение работы $А’$, совершаемой двигателем, к количеству теплоты, полученному от нагревателя:
$η={A’}/{|Q_1|}={|Q_1|-|Q_2|}/{|Q_1|}=1-{|Q_2|}/{|Q_1|}$
Так как у всех двигателей некоторое количество теплоты передается холодильнику, то $η < 1$.
КПД теплового двигателя пропорционален разности температур нагревателя и холодильника. При $T_1 — T_2=0$ двигатель не может работать.
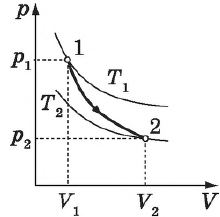
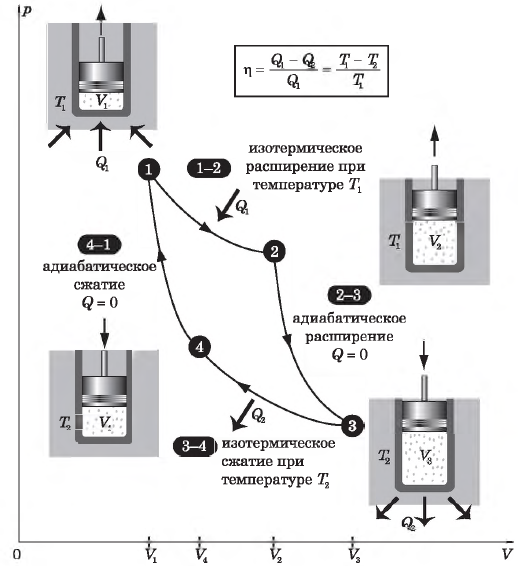
Цикл Карно
Цикл Карно — это круговой обратимый процесс, состоящий из двух изотермических и двух адиабатических процессов.
Впервые этот процесс был рассмотрен французским инженером и ученым Н. Л. С. Карно в 1824 г. в книге «Размышления о движущей силе огня и о машинах, способных развивать эту силу».
Целью исследований Карно было выяснение причин несовершенства тепловых машин того времени (они имели КПД $< 5%$)и поиски путей их усовершенствования.
Выбор двух изотермических и двух адиабатических процессов был обусловлен тем, что работа газа при изотермическом расширении совершается за счет внутренней энергии нагревателя, а при адиабатном процессе — за счет внутренней энергии расширяющегося газа. В этом цикле исключен контакт тел с разной температурой, следовательно, исключена теплопередача без совершения работы.
Цикл Карно — самый эффективный из всех возможных. Его КПД максимален.
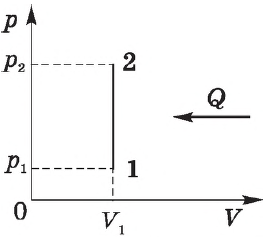
На рисунке изображены термодинамические процессы цикла. В процессе изотермического расширения ($1-2$) при температуре $Т_1$ работа совершается за счет изменения внутренней энергии нагревателя, т. е. за счет подведения к газу количества теплоты $Q_1$:
$A_{12}=Q_1.$ Охлаждение газа перед сжатием ($3-4$) происходит при адиабатном расширении ($2-3$). Изменение внутренней энергии $∆U_{23}$ при адиабатном процессе ($Q=0$) полностью преобразуется в механическую работу:
$A_{23}=-∆U_{23}$
Температура газа в результате адиабатического расширения ($2-3$) понижается до температуры холодильника $Т_2 < Т_1$. В процессе ($3-4$) газ изотермически сжимается, передавая холодильнику количество теплоты $Q_2$:
$A_{34}=Q_2,$
Цикл завершается процессом адиабатического сжатия ($4—1$), при котором газ нагревается до температуры $Т_1$.
Максимальное значение КПД тепловых двигателей, работающих на идеальном газе, по циклу Карно:
$η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$
Суть формулы $η={T_1-T_2}/{T_1}=1-{T_2}/{T_1}$ выражена в доказанной С. Карно теореме о том, что КПД любого теплового двигателя не может превышать КПД цикла Карно, осуществляемого при той же температуре нагревателя и холодильника.