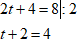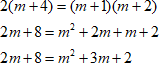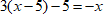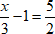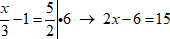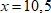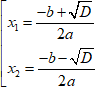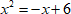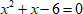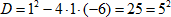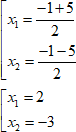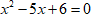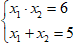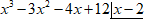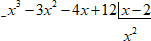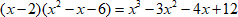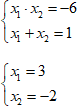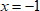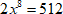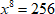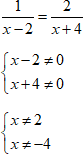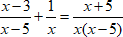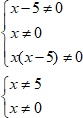Правила преобразования уравнений
Первым этапом решения уравнения является приведение его к нужному виду с помощью разрешенных преобразований.
1. Любое слагаемое в уравнении можно перенести из одной части уравнения в другую, изменив его знак на противоположный. Это относится как к числам:
$ 2x+1=2 \ 2x=2-1 \ 2x=1 $
Так и к выражениям, содержащим переменные:
$ 1-x=0 \ 1=x $
2. Можно умножать и делить левую и правую части уравнения на одно и то же ненулевое число или выражение (при умножении на ноль уравнение теряет смысл; а делить на ноль нельзя). Умножение помогает избавиться от знаменателей:
$ frac{x}{5}+2=frac{2}{3} big| cdot 15 \ 3x+30=10 $
А деление – уменьшить коэффициент в уравнении:
$ 2t+4=8|:2 \ t+2=4 $
3. Можно раскрывать скобки и упрощать выражения в обеих частях:
$ 2(m+4)=(m+1)(m+2) \ 2m+8=m^{2}+2m+m+2 \ 2m+8=m^{2}+3m+2 $
Рациональные уравнения
Уравнение называется рациональным, если содержит переменную в целой степени, например, 1, 2, -5. Чаще всего встречаются следующие типы рациональных уравнений:
1. Линейные
2. Квадратные
3. Кубические
4. Уравнения высших степеней
5. Дробно-рациональные
Линейные уравнения
Линейным называется уравнение, содержащее переменную в первой степени. С помощью преобразований его можно привести к виду
$ ax=b, $ где $ a neq 0, b $ ‒ некоторые числа.
Для решения достаточно поделить обе части равенства на $ a $:
$ x= frac{b}{a} $
Рассмотрим пример:
$ 3(x-5)-5=-x $
1. Приведем выражение к виду $ ax=b $. Для этого раскроем скобки и соберем слагаемые, содержащие переменные, с одной стороны равенства, а не содержащие – с другой.
$ 3x-15-5=-x rightarrow 3x-20=-x rightarrow 3x-20+x=0 rightarrow 4x-20=0 rightarrow 4x=20 $
2. Разделим обе части равенства на коэффициент при x.
$ 4x=20 rightarrow x=5 $
Ответ: 5
Уравнение будет линейным, даже если в нем присутствуют дроби. Главное, чтобы переменной не было в знаменателе. Рассмотрим еще один пример:
$ frac {x}{3}-1= frac{5}{2} $
1. Умножим обе части равенства на общий знаменатель дробей, входящих в уравнение, чтобы избавиться от дробей.
$ frac {x}{3}-1= frac{5}{2} big| cdot 6 rightarrow 2x-6=15 $
2. Приведем выражение к виду $ ax=b $.
$ 2x=21 $
3. Разделим обе части равенства на коэффициент при x.
$ x=10,5 $
Ответ:10,5
Квадратные уравнения
Квадратным называется уравнение, содержащее переменную во второй степени. В общем виде оно выглядит следующим образом:
$ ax^{2} + bx+с=0, $ где $ a neq 0, b, c $ – некоторые числа.
Корни уравнения можно определить с помощью дискриминанта $ D=b^{2}-4ac $ по
$ left [ begin{array}{c}x_{1}=frac {-b+sqrt{D}}{2a} \ x_{2}=frac {-b-sqrt{D}}{2a} end{array} right. $
Если дискриминант равен нулю, то уравнение имеет один корень. Если же дискриминант меньше нуля, то корней нет.
Рассмотрим пример:
$ x^{2}=-x+6 $
1. Преобразуем уравнение к стандартному виду, перенеся все слагаемые в левую часть:
$ x^{2} + x-6=0 $
2. Определим дискриминант полученного уравнения:
$ D=1^{2} -4 cdot 1 cdot (-6)=25=5^{2} $
3. С помощью дискриминанта найдем корни по формулам:
$ left [ begin{array}{c}x_{1}=frac {-1+5}{2} \ x_{2}=frac {-1-5}{2} end{array} right. \ left [ begin{array}{c}x_{1}= 2 ;;; \ x_{2}= -3 end{array} right. $
Ответ: 2; -3
В некоторых случаях (например, $ a=1 $ ) корни проще искать по теореме Виета, решая подбором систему уравнений:
$ begin{cases} x_{1} cdot x_{2} = frac {c}{a} \ x_{1} + x_{2} = — frac {b}{a} end{cases} $
Применим эту теорему для нахождения корней уравнения $ x^{2}-5x+6=0 $
1. Составим систему:
$ begin{cases} x_{1} cdot x_{2} = 6 \ x_{1} + x_{2} = 5 end{cases} $
2. Подберем $ x_{1}, x_{2} $ так, чтобы оба равенства выполнялись. В данном случае подходят числа $ x_{1}=2,x_{2}=3 $ .
Ответ: 2; 3
Кубические уравнения
Общий вид уравнения третьей степени представлен ниже:
$ ax^{3}+bx^{2}+cx+d=0 $, где $ a neq 0, b, c, d $ — некоторые числа.
Целые корни такого уравнения (в случае, если коэффициенты тоже целые) находятся среди делителей свободного члена $ d $.
У уравнения $ x^{3} -3x^{2}-4x+12=0 $ свободный член $ d=12 $. Его делителями являются числа $ pm 1, pm2, pm 3, pm 4 $. Для того, чтобы определить, какие из этих чисел являются решениями, подставим их по очереди в исходное уравнение. Если при этом получится верное равенство, то поздравляю, вы нашли корень.
Проверим: $ x=1:-1-3+4+12=12 neq 0 $. Не является корнем.
Проверим: $ x=2:8-12-8+12=0 $. Является корнем.
Возможна ситуация, когда ни один из делителей корнем не будет. В таком случае говорят, что исходное уравнение не имеет целых решений.
После того, как будет определено хотя бы одно решение, можно понизить степень уравнения, превратив его в квадратное. Для этого разделим столбиком исходное уравнение на выражение $ (x-a) $, где $ a $ – корень.
Алгоритм деления многочлена на многочлен столбиком.
1. Упрощаем выражение и переносим все слагаемые влево.
2. Записываем выражения как для деления в столбик:
$ x^{3}-3x^{2}-4x+12| underline{x-2} $
3. Определяем выражение, на которое нужно умножить старший коэффициент в делителе, чтобы получить старший коэффициент в делимом. В данном примере это $ x^{2}$.
$ _x^{3}-3x^{2}-4x+12| underline{x-2} \ qquadqquadqquadqquadquad x^{2} $
4. Умножаем на это выражение делитель и вычитаем его из делимого. «Сносим» следующее слагаемое.
$ _x^{3}-3x^{2}-4x+12| underline{x-2} \ underline{x^{3}-2x^{2}}qquadqquadquad x^{2} \ qquad -x^{2}-4x $
5. Повторяем процедуру до тех пор, пока не получим разность, равную 0.
$ _x^{3}-3x^{2}-4x+12| underline{x-2} \ underline{x^{3}-2x^{2}}qquadqquadquad x^{2}-x-6 \ qquad _-x^{2}-4x \ qquadquad -x^{2}+2x \ qquadqquadqquad _-6x+12 \ qquadqquadqquadquad underline{-6x+12} \ qquadqquadqquadqquadquadquad 0 $
6. -Проверяем ответ. Произведение частного и делителя должно совпасть с делимым.
$ (x-2)(x^{2}-x-6)=x^{3}-3x^{2}-4x+12 $
Корни квадратного уравнения $ x^{2}-x-6=0 $ можно определить с помощью дискриминанта или по теореме Виета.
$ begin{cases}x_{1} cdot x_{2} = -6 \ x_{1} + x_{2} = 1 end{cases} \ begin{cases}x_{1} = 3 \ x_{2} = 2 end{cases}$
Значит, уравнение $ x^{3}-3x^{2}-4x+12=0 $ имеет три решения: $ x=-2, x=2, x=3 $.
Как действовать в частном случае, когда $ b=c=0 $, рассмотрим в следующем разделе.
Уравнения высших степеней
$ ax^{n}=b, a neq 0 $
В таком уравнении переменная может содержаться в любой степени. Рассмотрим пример:
$ 6x^{3}+15=9 $
1. Соберем слагаемые, содержащие переменную с одной стороны, а не содержащие – с другой:
$ 6x^{3}=-15+9 rightarrow 6x^{3}=-6 $
2. Упростим уравнение с помощью разрешенных преобразований:
$ 6x^{3}=-6 rightarrow x^{3}=-1 $
3. Извлечем корень 3 степени из обеих частей равенства. Обратите внимание, что в данном случае не важно, какой знак имеет число, так как степень нечетная.
$ x=-1 $
Ответ: -1
Точно так же можно решить уравнение с любой, даже самой страшной, степенью.
$ 2x^{8}=512 $
4. Разделим обе части уравнения на 2. Чтобы уравнение имело решения, необходимо, чтобы справа стояло неотрицательное число, так как степень переменной четная.
$ x^{8}=256 $
5. Извлечем корень 8 степени из обеих частей равенства. В силу четности степени, уравнение будет иметь два решения:
$ left[ begin{array}{c} x=2 ;; \ x=-2 end{array} right. $
Ответ: -2, 2
Дробно-рациональные уравнения
Данный тип уравнений отличается тем, что содержит в знаменателе выражение с переменной. Поэтому может возникнуть опасная ситуация – переменная примет такое значение, что знаменатель обратиться в ноль. Чтобы этого не произошло, заранее исключим из рассмотрения нули знаменателя и определим область допустимых значений:
$ frac {1}{x-2} = frac {2}{x+4} \ begin{cases}x-2 neq 0\x+4 neq 0end{cases} \ begin{cases}x neq 2\x neq -4end{cases} $
То есть решением данного уравнения может быть любое число кроме 2 и -4.
Алгоритм решения дробно-рационального уравнения рассмотрим на примере:
$ frac {x-3}{x-5} + frac {1}{x} = frac {x+5}{x(x-5)} $
1. Определим область допустимых значений:
$ begin{cases}x-5 neq 0\x neq 0 \ x(x-5) neq 0end{cases} \ begin{cases}x neq 5\ x neq 0end{cases}$
2. Умножим обе части равенства на общий знаменатель всех дробей и сократим одинаковые выражения в числителе и знаменателе там, где это возможно:
$ frac {x-3}{x-5} + frac {1}{x} = frac {x+5}{x(x-5)} big| cdot x(x-5) $
$ frac {(x-3)x(x-5)}{x-5} + frac {x(x-5)}{x} = frac {(x+5)x(x-5)}{x(x-5)} $
$ (x-3)x+x=x+5 $
3. Упрощаем уравнение с помощью разрешенных преобразований:
$ x^{2}-3x+x-5=x+5 rightarrow x^{2}-2x-5-x-5=0 rightarrow x^{2}-3x-10=0 $
4. Определяем тип получившегося уравнения (линейное, квадратное или кубическое) и решаем подходящим методом. В данном случае получилось квадратное уравнение, причем коэффициент при $ x^{2} $ равен 1. Значит, удобно использовать теорему Виета:
$ begin{cases}x_{1} cdot x_{2}=-10 \ x_{1} + x_{2}=3 end{cases} $
Подходит пара чисел -2 и 5.
5. Исключаем те значения корней, которые обращают в ноль знаменатель, то есть не входят в область допустимых значений (ОДЗ).
Ответ: -2
При подстановке корней в уравнение должно получится верное равенство. Это свойство можно использовать для проверки полученных ответов.
Целые рациональные уравнения
Важно знать, что рациональные уравнения в свою очередь тоже разные бывают.
Если в дроби нет деления на переменную (то есть на ( displaystyle x), ( displaystyle y) и т.д.), тогда рациональное уравнение будет называться целым (или линейным) уравнением, вот примеры:
( displaystyle begin{array}{l}frac{2x}{3}=13-frac{3x}{2};\4(2y-3)=y-9.end{array})
Умеешь такие решать? – конечно, умеешь, упрощаешь и находишь неизвестное, тема-то 5-ого или 6-ого класса.
Ну, рассмотрим первый из примеров на всякий случай и по порядочку. Все неизвестные переносим влево, все известные вправо:
( displaystyle frac{2x}{3}+frac{3x}{2}=13);
Какой наименьший общий знаменатель будет?
Правильно ( displaystyle 6)!
Чтоб к нему привести домножаем и числитель и знаменатель первого слагаемое на ( displaystyle 2), а второго на ( displaystyle 3), этого делать не запрещено, если и числитель и знаменатель дроби умножить на одно и то же значение, то дробь от этого не изменится, т.к. ее можно будет сократить на то же число.
А ( displaystyle 13) не трогаем, оно нам не мешает, имеем:
( displaystyle frac{4x}{6}+frac{9x}{6}=13)
( displaystyle frac{13x}{6}=13),
А теперь делим обе части на ( displaystyle 13):
( displaystyle begin{array}{l}frac{x}{6}=1\x=6end{array})
Тут все просто?
Поскольку уравнение целое, что мы уже определили, то и ограничений никаких нет, ( displaystyle 6), так ( displaystyle 6), ну можно для верности подставить этот ответ в исходное уравнение, получим ( displaystyle 0=0), значит все верно и ответ подходит (ты можешь пересчитать, а вообще должно сойтись).
Дробно-рациональные уравнения
А вот еще одно уравнение ( displaystyle frac{5}{x+1}+frac{4{x}-6}{(x+1)cdot (x+3)}=3).
Это уравнение целое? НЕТ!!! Тут есть деление на переменную ( displaystyle x), а это говорит о том, что уравнение не целое. Тогда какое же оно? Это дробно рациональное уравнение.
Дробно-рациональное уравнение – рациональное (без знака корня) уравнение, в котором левая или правая части являются дробными выражениями.
На первый взгляд особой разницы не видно, ну давай попробуем решать его как мы решали целое (линейное) уравнение.
Для начала найдем наименьший общий знаменатель, это будет ( displaystyle (x+1)cdot (x+3)).
Важный момент!
В предыдущем примере, где было целое уравнение мы не стали свободный член ( displaystyle 13) приводить к знаменателю, т.к. умножали все на числа без переменных, но тут-то наименьший общий знаменатель ( displaystyle (x+1)cdot (x+3)).
А это тебе не шутки, переменная в знаменателе!
Решая дробно-рациональное уравнение, обе его части умножаем на наименьший общий знаменатель!
Это надеюсь, ты запомнишь, но давай посмотрим что вышло:
( displaystyle frac{5(x+1)cdot (x+3)}{x+1}+frac{(4{x}-6)cdot (x+1)cdot (x+3)}{(x+1)cdot (x+3)}=3cdot (x+1)cdot (x+3)).
Что-то оно огромное получилось, надо все посокращать:
( displaystyle 5(x+3)+(4{x}-6)=3cdot (x+1)cdot (x+3)).
Раскроем скобки и приведем подобные члены:
( displaystyle begin{array}{l}9x+9=3{{x}^{2}}+12x+9\3{{x}^{2}}+3x=0.end{array})
Ну как, это уже попроще выглядит, чем в начале было?
Выносим за скобку общий множитель: ( displaystyle 3xcdot (x+1)=0)
У этого уравнения два решения, его левая сторона принимает нулевое значение при ( displaystyle x=0) и ( displaystyle x=-1).
Вроде бы все, ну ладно давайте напоследок подставим корни ( displaystyle x=0) и ( displaystyle x=-1) в исходное уравнение, чтобы проверить, нет ли ошибок. Сначала подставим ( displaystyle 0), получается ( displaystyle 3=3) –нет претензий?
С ним все нормально. А теперь ( displaystyle -1), и тут же видим в знаменателе первого члена ( displaystyle -1+1)!
Но ведь это же будет ноль!
На ноль делить нельзя, это все знают, в чем же дело???
Дело в ОДЗ – Области Допустимых Значений!
(если забыл что это, повтори тему «ОДЗ – область допустимых значений»!)
Всякий раз когда ты видишь уравнение, где есть переменные (( displaystyle x,y) и т.д.) в знаменателе, прежде всего, нужно найти ОДЗ, найти какие значения может принимать икс.
Хотя удобнее в ОДЗ написать, чему икс НЕ может быть равен, ведь таких значений не так много, как правило.
Просто запомни, что на ноль делить нельзя! И перед тем как решать наше уравнение нам следовало сделать так:
ОДЗ: ( displaystyle x+1ne 0) и ( displaystyle x+3ne 0) ( displaystyle Rightarrow xne -1) и ( displaystyle xne -3).
Если бы мы сразу так написали, то заранее бы знали, что эти ответы стоит исключить и так, из полученных нами ( displaystyle x=0) и ( displaystyle x=-1) мы смело исключаем ( displaystyle x=-1), т.к. он противоречит ОДЗ.
Значит, какой ответ будет у решенного уравнения?
В ответ стоит написать только один корень, ( displaystyle x=0).
Стоит заметить, что ОДЗ не всегда сказывается на ответе, возможны случаи, когда корни, которые мы получили, не попадают под ограничения ОДЗ.
Но писать ОДЗ в дробно рациональных уравнениях стоит всегда – так просто спокойнее, что ты ничего не упустил и да,
ВСЕГДА по окончании решения сверяй свои корни и область допустимых значений!
Рациональные выражения, уравнения и дробно-рациональные уравнения
Повторим еще раз то, что прошил в предыдущих разделах, больше используя язык математики.
Рациональное выражение – это алгебраическое выражение, составленное из чисел и переменной ( displaystyle x) с помощью операций сложения, вычитания, умножения, деления и возведения в степень с натуральным показателем.
Ну а рациональное уравнение – это равенство двух рациональных выражений.
Дробно-рациональные уравнения – рациональные (без знака корня) уравнения, в которых левая или правая части являются дробными выражениями.
Например:
( displaystyle frac{{{x}^{2}}-2{x}-3}{{x}-1}-frac{x+1}{{x}-3}={{x}^{2}}-1) (чаще всего мы встречаем именно дробно рациональные уравнения).
В общем случае при решении рациональных уравнений мы стремимся преобразовать его к виду: Произведение = “( displaystyle 0)” или Дробь = “( displaystyle 0)“, например:
( displaystyle frac{left( {x}-2 right)left( x+3 right)left( {{x}^{2}}+1 right)}{xcdot left( {x}-3 right)}=0).
Тогда мы сможем сказать, что любой из множителей числителя может быть равен нулю, но знаменатель при этом нулю не равен.
Для этого нам нужно сначала всё перенести в левую часть уравнения (не забываем при этом поменять знаки между слагаемыми: “( displaystyle +)” на “( displaystyle –)” и наоборот).
Затем мы обычно приводим все к общему знаменателю, и пишем систему:
( displaystyle left{ begin{array}{l}Числитель=0,\Знаменательne 0.end{array} right.)
Например:
( displaystyle begin{array}{l}frac{{x}-2}{{{x}^{2}}+2{x}-3}-frac{x+1}{{{x}^{2}}+5x+6}=frac{3}{x+3}Leftrightarrow \Leftrightarrow frac{{x}-2}{left( {x}-1 right)left( x+3 right)}-frac{x+1}{left( x+2 right)left( x+3 right)}-frac{3}{x+3}=0Leftrightarrow end{array})
( displaystyle Leftrightarrow frac{{{x}^{2}}-4-left( {{x}^{2}}-1 right)-3left( {{x}^{2}}+{x}-2 right)}{left( {x}-1 right)left( x+2 right)left( x+3 right)}=0Leftrightarrow frac{-3{{x}^{2}}-3x+3}{left( {x}-1 right)left( x+2 right)left( x+3 right)}=0Leftrightarrow )
( displaystyle Leftrightarrow left{ begin{array}{l}{{x}^{2}}+{x}-1=0\left( {x}-1 right)left( x+2 right)left( x+3 right)ne 0end{array} right.Leftrightarrow left{ begin{array}{l}left[ begin{array}{l}x=frac{-1+sqrt{5}}{2}\x=frac{-1-sqrt{5}}{2}end{array} right.\xne 1\xne -2\xne -3end{array} right.Leftrightarrow left[ begin{array}{l}x=frac{-1+sqrt{5}}{2}\x=frac{-1-sqrt{5}}{2}.end{array} right.)
Если знаменателя нет, или он является числом, – тем лучше, не придется решать неравенство.
Как бы то ни было, в ЕГЭ все рациональные выражения степени больше ( displaystyle 2) легко преобразуются в произведение более простых выражений при помощи либо перегруппировки, либо замены переменных (см. раздел «Разложение многочлена на множители»).
Темы
ЕГЭ Профиль
←
Уравнения
Рациональные уравнения
→
Задание 15927
А) Решите уравнение
$$x^2-12+frac{36}{x^2}+2(frac{x}{2}-frac{3}{x})=0$$
Б) Найдите все корни уравнения, принадлежащие отрезку $$[-2,5;2]$$
Ответ: А)$$pmsqrt{6};2;-3$$ Б)$$2;-sqrt{6}$$
Решение 1
Предложить свое решение / сообщить об ошибке
Скрыть
Правила преобразования уравнений
Первым этапом решения уравнения является приведение его к нужному виду с помощью разрешенных преобразований.
1. Любое слагаемое в уравнении можно перенести из одной части уравнения в другую, изменив его знак на противоположный. Это относится как к числам:
Так и к выражениям, содержащим переменные:
2. Можно умножать и делить левую и правую части уравнения на одно и то же ненулевое число или выражение (при умножении на ноль уравнение теряет смысл; а делить на ноль нельзя). Умножение помогает избавиться от знаменателей:
А деление – уменьшить коэффициент в уравнении:
3. Можно раскрывать скобки и упрощать выражения в обеих частях:
Рациональные уравнения
Уравнение называется рациональным, если содержит переменную в целой степени, например, 1, 2, -5. Чаще всего встречаются следующие типы рациональных уравнений:
1. Линейные
2. Квадратные
3. Кубические
4. Уравнения высших степеней
5. Дробно-рациональные
Линейные уравнения
Линейным называется уравнение, содержащее переменную в первой степени. С помощью преобразований его можно привести к виду

Для решения достаточно поделить обе части равенства на 
Рассмотрим пример:
1. Приведем выражение к виду 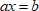
2. Разделим обе части равенства на коэффициент при x.
Ответ: 5
Уравнение будет линейным, даже если в нем присутствуют дроби. Главное, чтобы переменной не было в знаменателе. Рассмотрим еще один пример:
1. Умножим обе части равенства на общий знаменатель дробей, входящих в уравнение, чтобы избавиться от дробей.
2. Приведем выражение к виду 
3. Разделим обе части равенства на коэффициент при x.
Ответ:10,5
Квадратные уравнения
Квадратным называется уравнение, содержащее переменную во второй степени. В общем виде оно выглядит следующим образом:


Корни уравнения можно определить с помощью дискриминанта 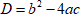
Если дискриминант равен нулю, то уравнение имеет один корень. Если же дискриминант меньше нуля, то корней нет.
Рассмотрим пример:
1. Преобразуем уравнение к стандартному виду, перенеся все слагаемые в левую часть:
2. Определим дискриминант полученного уравнения:
3. С помощью дискриминанта найдем корни по формулам:
Ответ: 2; -3
В некоторых случаях (например, 
Применим эту теорему для нахождения корней уравнения
1. Составим систему:
2. Подберем 
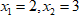
Ответ: 2; 3
Кубические уравнения
Общий вид уравнения третьей степени представлен ниже:
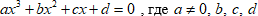
Целые корни такого уравнения (в случае, если коэффициенты тоже целые) находятся среди делителей свободного члена 
У уравнения 
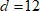

Проверим: 
Проверим: 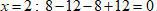
Возможна ситуация, когда ни один из делителей корнем не будет. В таком случае говорят, что исходное уравнение не имеет целых решений.
После того, как будет определено хотя бы одно решение, можно понизить степень уравнения, превратив его в квадратное. Для этого разделим столбиком исходное уравнение на выражение 

Алгоритм деления многочлена на многочлен столбиком.
1. Упрощаем выражение и переносим все слагаемые влево.
2. Записываем выражения как для деления в столбик:
3. Определяем выражение, на которое нужно умножить старший коэффициент в делителе, чтобы получить старший коэффициент в делимом. В данном примере это 
4. Умножаем на это выражение делитель и вычитаем его из делимого. «Сносим» следующее слагаемое.
5. Повторяем процедуру до тех пор, пока не получим разность, равную 0.
6. -Проверяем ответ. Произведение частного и делителя должно совпасть с делимым.
Корни квадратного уравнения 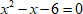
Значит, уравнение 
Как действовать в частном случае, когда 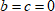
Уравнения высших степеней
В таком уравнении переменная может содержаться в любой степени. Рассмотрим пример:
1. Соберем слагаемые, содержащие переменную с одной стороны, а не содержащие – с другой:
2. Упростим уравнение с помощью разрешенных преобразований:
3. Извлечем корень 3 степени из обеих частей равенства. Обратите внимание, что в данном случае не важно, какой знак имеет число, так как степень нечетная.
Ответ: -1
Точно так же можно решить уравнение с любой, даже самой страшной, степенью.
4. Разделим обе части уравнения на 2. Чтобы уравнение имело решения, необходимо, чтобы справа стояло неотрицательное число, так как степень переменной четная.
5. Извлечем корень 8 степени из обеих частей равенства. В силу четности степени, уравнение будет иметь два решения:
Ответ: -2, 2
Дробно-рациональные уравнения
Данный тип уравнений отличается тем, что содержит в знаменателе выражение с переменной. Поэтому может возникнуть опасная ситуация – переменная примет такое значение, что знаменатель обратиться в ноль. Чтобы этого не произошло, заранее исключим из рассмотрения нули знаменателя и определим область допустимых значений:
То есть решением данного уравнения может быть любое число кроме 2 и -4.
Алгоритм решения дробно-рационального уравнения рассмотрим на примере:
1. Определим область допустимых значений:
2. Умножим обе части равенства на общий знаменатель всех дробей и сократим одинаковые выражения в числителе и знаменателе там, где это возможно:
3. Упрощаем уравнение с помощью разрешенных преобразований:
4. Определяем тип получившегося уравнения (линейное, квадратное или кубическое) и решаем подходящим методом. В данном случае получилось квадратное уравнение, причем коэффициент при равен 1. Значит, удобно использовать теорему Виета:
Подходит пара чисел -2 и 5.
5. Исключаем те значения корней, которые обращают в ноль знаменатель, то есть не входят в область допустимых значений (ОДЗ).
Ответ: -2
При подстановке корней в уравнение должно получится верное равенство. Это свойство можно использовать для проверки полученных ответов.
-
Решение
-
Видеорешение
Извлечем корень девятой степени из обеих частей уравнения, чтобы избавиться от степени:
(displaystyle sqrt[9]{(x-8)^9}=sqrt[9]{-1}{ small ,})
и воспользуемся правилом.
Правило
Корень из степени
(displaystyle sqrt[n]{f(x)^{n}}=left{begin{aligned}&f(x), , если , n, нечетное,\&|f(x)|, , если , n, четное.end{aligned}right.)
Так как (displaystyle 9) нечетное число, то
(displaystyle sqrt[9]{(x-8)^9}=x-8{small ;})
(displaystyle sqrt[9]{-1}=sqrt[9]{(-1)^9}=-1{small .})
Получаем линейное уравнение
(displaystyle x-8=-1{ small ,})
(displaystyle x=-1+8{ small ,})
(displaystyle x=7{small .})
Ответ: (displaystyle 7{small .})
Рациональные уравнения на ЕГЭ
- 08.11.2013
Материал для подготовки к ЕГЭ по математике на тему: «Рациональные уравнения».
Содержание темы:
6. РАЦИОНАЛЬНЫЕ УРАВНЕНИЯ
6.1. Основные понятия и определения
6.2. Преобразование уравнений в равносильные им уравнения
Тест для проверки теоретических знаний
Примеры
Задачи для самостоятельного решения
Контрольный тест
Рекомендуем использовать этот материал при тщательной подготовке к сдаче ЕГЭ на высокий балл.
В теме содержатся теория и практические задания различного уровня сложности.
Смотреть в PDF:
Или прямо сейчас: Скачайте в pdf файле.
(bullet) Рациональное уравнение — это уравнение, представимое в виде [dfrac{P(x)}{Q(x)}=0] где (P(x), Q(x)) — многочлены (сумма “иксов” в различных степенях, умноженных на различные числа).
Выражение в левой части уравнения называется рациональным выражением.
ОДЗ (область допустимых значений) рационального уравнения – это все значения (x), при которых знаменатель НЕ обращается в нуль, то есть (Q(x)ne 0).
(bullet) Например, уравнения [dfrac{x+2}{x-3}=0,qquad dfrac 2{x^2-1}=3, qquad x^5-3x=2] являются рациональными уравнениями.
В первом уравнении ОДЗ – это все (x), такие что (xne 3) (пишут (xin (-infty;3)cup(3;+infty))); во втором уравнении – это все (x), такие что (xne -1; xne 1) (пишут (xin
(-infty;-1)cup(-1;1)cup(1;+infty))); а в третьем уравнении никаких ограничений на ОДЗ нет, то есть ОДЗ – это все (x) (пишут (xinmathbb{R})).
(bullet) Теоремы:
1) Произведение двух множителей равно нулю тогда и только тогда, когда один из них равен нулю, а другой при этом не теряет смысла, следовательно, уравнение (f(x)cdot g(x)=0) равносильно системе [begin{cases} left[ begin{gathered}begin{aligned}
&f(x)=0\
&g(x)=0 end{aligned} end{gathered} right.\ text{ОДЗ уравнения}
end{cases}] 2) Дробь равна нулю тогда и только тогда, когда числитель равен нулю, а знаменатель не равен нулю, следовательно, уравнение (dfrac{f(x)}{g(x)}=0) равносильно системе уравнений [begin{cases}
f(x)=0\
g(x)ne 0 end{cases}] (bullet) Рассмотрим несколько примеров.
1) Решите уравнение (x+1=dfrac 2x).
Найдем ОДЗ данного уравнения – это (xne 0) (так как (x) находится в знаменателе).
Значит, ОДЗ можно записать так: (xin (-infty;0)cup(0;+infty)).
Перенесем все слагаемые в одну часть и приведем к общему знаменателю: [dfrac{(x+1)cdot x}x-dfrac 2x=0quadLeftrightarrowquad
dfrac{x^2+x-2}x=0quadLeftrightarrowquad begin{cases}
x^2+x-2=0\xne 0end{cases}] Решением первого уравнения системы будут (x=-2, x=1). Видим, что оба корня ненулевые. Следовательно, ответ: (xin {-2;1}).
2) Решите уравнение (left(dfrac4x — 2right)cdot
(x^2-x)=0).
Найдем ОДЗ данного уравнения. Видим, что единственное значение (x), при котором левая часть не имеет смысла – это (x=0). Значит, ОДЗ можно записать так: (xin (-infty;0)cup(0;+infty)).
Таким образом, данное уравнение равносильно системе:
[begin{cases} left[ begin{gathered}begin{aligned}
&dfrac 4x-2=0\
&x^2-x=0 end{aligned} end{gathered} right.\ xne 0
end{cases} quad Leftrightarrow quad
begin{cases} left[ begin{gathered}begin{aligned}
&dfrac 4x=2\
&x(x-1)=0 end{aligned} end{gathered} right.\ xne 0
end{cases} quad Leftrightarrow quad
begin{cases} left[ begin{gathered}begin{aligned}
&x=2\
&x=1\
&x=0 end{aligned} end{gathered} right.\ xne 0
end{cases} quad Leftrightarrow quad
left[ begin{gathered}begin{aligned}
&x=2\
&x=1 end{aligned} end{gathered} right.] Действительно, несмотря на то, что (x=0) — корень второго множителя, если подставить (x=0) в изначальное уравнение, то оно не будет иметь смысла, т.к. не определено выражение (dfrac 40).
Таким образом, решением данного уравнения являются (xin
{1;2}).
3) Решите уравнение [dfrac{x^2+4x}{4x^2-1}=dfrac{3-x-x^2}{4x^2-1}] В нашем уравнении (4x^2-1ne 0), откуда ((2x-1)(2x+1)ne 0), то есть (xne -frac12; frac12).
Перенесем все слагаемые в левую часть и приведем к общему знаменателю:
(dfrac{x^2+4x}{4x^2-1}=dfrac{3-x-x^2}{4x^2-1} quad
Leftrightarrow quad dfrac{x^2+4x-3+x+x^2}{4x^2-1}=0quad
Leftrightarrow quad
dfrac{2x^2+5x-3}{4x^2-1}=0 quad Leftrightarrow)
(Leftrightarrow quad
begin{cases} 2x^2+5x-3=0\ 4x^2-1ne 0
end{cases} quad Leftrightarrow quad
begin{cases} (2x-1)(x+3)=0\
(2x-1)(2x+1)ne 0 end{cases} quad Leftrightarrow quad
begin{cases} left[
begin{gathered}
begin{aligned} &x=dfrac12\[2ex] &x=-3 end{aligned}end{gathered}
right.\[2ex] xne dfrac 12\[2ex] xne -dfrac 12 end{cases}
quad Leftrightarrow quad x=-3)
Ответ: (xin {-3}).
Замечание. Если ответ состоит из конечного набора чисел, то их можно записывать через точку с запятой в фигурных скобках, как показано в предыдущих примерах.