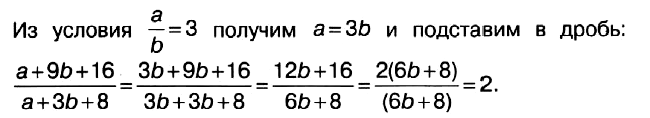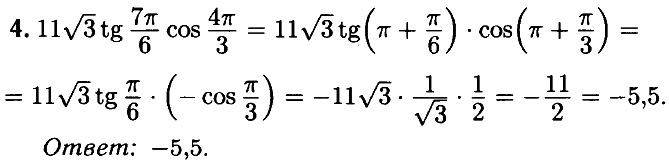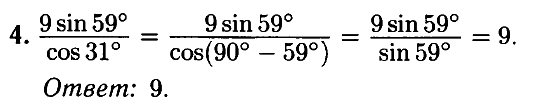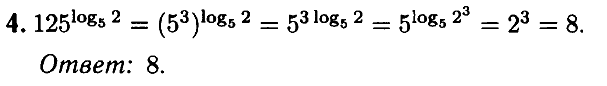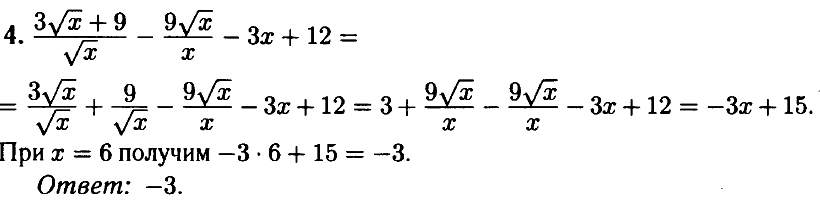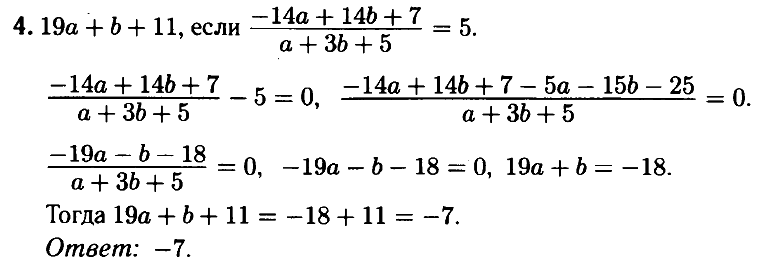Рациональные выражения егэ профиль

Skip to content

ЕГЭ Профиль №6. Вычисление значений рациональных выражений

ЕГЭ Профиль №6. Вычисление значений рациональных выраженийadmin2022-11-28T09:55:43+03:00

Скачать файл в формате pdf.

ЕГЭ Профиль №6. Вычисление значений рациональных выражений

Задача 1. Найдите значение выражения   (frac{{{{left( {11alpha } right)}^2} — 11alpha }}{{11{alpha ^2} — alpha }})

Ответ

ОТВЕТ: 11.

Решение

(frac{{{{left( {11alpha } right)}^2} — 11alpha }}{{11{alpha ^2} — alpha }} = frac{{11alpha left( {11alpha  — 1} right)}}{{alpha left( {11alpha  — 1} right)}} = 11.)

Ответ: 11.
Задача 2. Найдите значение выражения   (frac{{9{x^2} — 4}}{{3x + 2}} — 3x)

Ответ

ОТВЕТ: — 2.

Решение

(frac{{9{x^2} — 4}}{{3x + 2}} — 3x = frac{{left( {3x — 2} right)left( {3x + 2} right)}}{{3x + 2}} — 3x = 3x — 2 — 3x =  — 2.)

Ответ: — 2.
Задача 3. Найдите значение выражения   (left( {4{a^2} — 9} right) cdot left( {frac{1}{{2a — 3}} — frac{1}{{2a + 3}}} right))

Ответ

ОТВЕТ: 6.

Решение

(left( {4{a^2} — 9} right) cdot left( {frac{1}{{2a — 3}} — frac{1}{{2a + 3}}} right) = left( {2a — 3} right)left( {2a + 3} right) cdot frac{{2a + 3 — left( {2a — 3} right)}}{{left( {2a — 3} right) cdot left( {2a + 3} right)}} = 2a + 3 — 2a + 3 = 6.)

Ответ: 6.
Задача 4. Найдите   (frac{a}{b}),    если    (frac{{2a + 5b}}{{5a + 2b}} = 1).

Ответ

ОТВЕТ: 1.

Решение

(frac{{2a + 5b}}{{5a + 2b}} = 1,,,,, Leftrightarrow ,,,,,2a + 5b = 5a + 2b,,,,, Leftrightarrow ,,,,,3b = 3a,left| {,:,} right.3,,,,, Leftrightarrow ,,,,,a = b,,,,,, Leftrightarrow ,,,,frac{a}{b} = 1.)

Ответ: 1.
Задача 5. Найдите   (61a — 11b + 50),   если   (frac{{2a — 7b + 5}}{{7a — 2b + 5}} = 9).

Ответ

ОТВЕТ: 10.

Решение

(frac{{2a — 7b + 5}}{{7a — 2b + 5}} = 9,,,,, Leftrightarrow ,,,,,9left( {7a — 2b + 5} right) = 2a — 7b + 5,,,,, Leftrightarrow )

( Leftrightarrow ,,,,,63a — 18b + 45 = 2a — 7b + 5,,,,, Leftrightarrow ,,,,,61a — 11b =  — 40.)

Следовательно: (61a — 11b + 50 =  — 40 + 50 = 10.)

Ответ: 10.
Задача 6. Найдите   (frac{{a + 9b + 16}}{{a + 3b + 8}}),   если   (frac{a}{b} = 3).

Ответ

ОТВЕТ: 2.

Решение

Так как (frac{a}{b} = 3), то (a = 3b.) Следовательно:  (frac{{a + 9b + 16}}{{a + 3b + 8}} = frac{{3b + 9b + 16}}{{3b + 3b + 8}} = frac{{12b + 16}}{{6b + 8}} = frac{{2left( {6b + 8} right)}}{{6b + 8}} = 2.)

Ответ: 2.
Задача 7. Найдите значение выражения   (left( {4{x^2} + {y^2} — {{left( {2x — y} right)}^2}} right):2xy)

Ответ

ОТВЕТ: 2.

Решение

(left( {4{x^2} + {y^2} — {{left( {2x — y} right)}^2}} right):2xy = frac{{4{x^2} + {y^2} — left( {4{x^2} — 4xy + {y^2}} right)}}{{2xy}} = frac{{4{x^2} + {y^2} — 4{x^2} + 4xy — {y^2}}}{{2xy}} = frac{{4xy}}{{2xy}} = 2.)

Ответ: 2.
Задача 8. Найдите значение выражения    (left( {{{left( {3x — 5y} right)}^2} — 9{x^2} — 25{y^2}} right):6xy)

Ответ

ОТВЕТ: — 5.

Решение

(left( {{{left( {3x — 5y} right)}^2} — 9{x^2} — 25{y^2}} right):6xy = frac{{9{x^2} — 30xy + 25{y^2} — 9{x^2} — 25{y^2}}}{{6xy}} =  — frac{{30xy}}{{6xy}} =  — 5.)

Ответ: — 5.
Задача 9. Найдите значение выражения    (left( {{{left( {4x — 3y} right)}^2} — {{left( {4x + 3y} right)}^2}} right):4xy)

Ответ

ОТВЕТ: — 12.

Решение

(left( {{{left( {4x — 3y} right)}^2} — {{left( {4x + 3y} right)}^2}} right):4xy = frac{{16{x^2} — 24xy + 9{y^2} — left( {16{x^2} + 24xy + 9{y^2}} right)}}{{4xy}} = )

( = frac{{16{x^2} — 24xy + 9{y^2} — 16{x^2} — 24xy — 9{y^2}}}{{4xy}} = frac{{ — 48xy}}{{4xy}} =  — 12.)

Ответ: — 12.
Задача 10. Найдите значение выражения   (left( {2x — 5} right)left( {2x + 5} right) — 4{x^2})

Ответ

ОТВЕТ: — 25.

Решение

(left( {2x — 5} right)left( {2x + 5} right) — 4{x^2} = 4{x^2} — 25 — 4{x^2} =  — 25.)

Ответ: — 25.
Задача 11. Найдите значение выражения   (left( {9axy — left( { — 7xya} right)} right):4yax)

Ответ

ОТВЕТ: 4.

Решение

(left( {9axy — left( { — 7xya} right)} right):4yax = frac{{9axy + 7axy}}{{4axy}} = frac{{16axy}}{{4axy}} = 4.)

Ответ: 4.
Задача 12. Найдите значение выражения (2x + y + 6z), если (4x + y = 5), (12z + y = 7)

Ответ

ОТВЕТ: 6.

Решение

(left{ {begin{array}{*{20}{c}}{4x + y = 5}\{12z + y = 7}end{array}} right.)

Прибавим к первому уравнению второе:

(4x + 2y + 12z = 12,left| {,:2,,,,, Leftrightarrow ,,,,,2x + y + 6z = 6.} right.)

Ответ: 6.
Задача 13. Найдите значение выражения (left( {7x — 13} right)left( {7x + 13} right) — 49{x^2} + 6x + 22)     при   (x = 80)

Ответ

ОТВЕТ: 333.

Решение

(left( {7x — 13} right)left( {7x + 13} right) — 49{x^2} + 6x + 22 = 49{x^2} — 169 — 49{x^2} + 6x + 22 = )

( = 6x — 147 = 6 cdot 80 — 147 = 480 — 147 = 333.)

Ответ: 333.
Задача 14. Найдите значение выражения     (left( {frac{3}{4} + 2frac{3}{8}} right) cdot 25,8)

Ответ

ОТВЕТ: 80,625.

Решение

(left( {frac{3}{4} + 2frac{3}{8}} right) cdot 25,8 = left( {frac{6}{8} + frac{{19}}{8}} right) cdot 25,8 = frac{{25}}{8} cdot 25,8 = 3,125 cdot 25,8 = 80,625.)

Ответ: 80,625.
Задача 15. Найдите значение выражения   (aleft( {36{a^2} — 25} right)left( {frac{1}{{6a + 5}} — frac{1}{{6a — 5}}} right))      при   (a = 36,7)

Ответ

ОТВЕТ: — 367.

Решение

(aleft( {36{a^2} — 25} right) cdot left( {frac{1}{{6a + 5}} — frac{1}{{6a — 5}}} right) = a cdot left( {6a — 5} right)left( {6a + 5} right) cdot frac{{6a — 5 — left( {6a + 5} right)}}{{left( {6a + 5} right)left( {6a — 5} right)}} = )

( = a cdot left( {6a — 5 — 6a — 5} right) =  — 10 cdot 36,7 =  — 367.)

Ответ: — 367.
Задача 16. Найдите значение выражения  (left( {9{b^2} — 49} right)left( {frac{1}{{3b — 7}} — frac{1}{{3b + 7}}} right) + b — 13)    при   (b = 345)

Ответ

ОТВЕТ: 346.

Решение

(left( {9{b^2} — 49} right) cdot left( {frac{1}{{3b — 7}} — frac{1}{{3b + 7}}} right) + b — 13 = left( {3b — 7} right)left( {3b + 7} right) cdot frac{{3b + 7 — left( {3b — 7} right)}}{{left( {3b — 7} right)left( {3b + 7} right)}} + b — 13 = )

( = 3b + 7 — 3b + 7 + b — 13 = b + 1 = 345 + 1 = 346.)

Ответ: 346.
Задача 17. Найдите значение выражения    (left( {2frac{4}{7} — 1,2} right) cdot 5frac{5}{6})

Ответ

ОТВЕТ: 8.

Решение

(left( {2frac{4}{7} — 1,2} right) cdot 5frac{5}{6} = left( {frac{{18}}{7} — frac{6}{5}} right) cdot frac{{35}}{6} = frac{{90 — 42}}{{35}} cdot frac{{35}}{6} = frac{{48}}{6} = 8.)

Ответ: 8.
Задача 18. Найдите значение выражения   (left( {2frac{4}{7} — 2,5} right):frac{1}{{70}})

Ответ

ОТВЕТ: 5.

Решение

(left( {2frac{4}{7} — 2,5} right):frac{1}{{70}} = left( {frac{{18}}{7} — frac{5}{2}} right) cdot 70 = frac{{36 — 35}}{{14}} cdot 70 = frac{{70}}{{14}} = 5.)

Ответ: 5.
Задача 19. Найдите значение выражения    (left( {{{432}^2} — {{568}^2}} right):1000)

Ответ

ОТВЕТ: — 136.

Решение

(left( {{{432}^2} — {{568}^2}} right):1000 = frac{{left( {432 — 568} right)left( {432 + 568} right)}}{{1000}} = frac{{ — 136 cdot 1000}}{{1000}} =  — 136.)

Ответ: — 136.
Задача 20. Найдите значение выражения    (4frac{4}{9}:frac{4}{9})

Ответ

ОТВЕТ: 10.

Решение

(4frac{4}{9}:frac{4}{9} = frac{{40}}{9} cdot frac{9}{4} = frac{{40}}{4} = 10.)

Ответ: 10.
Задача 21. Найдите значение выражения    (frac{{1,23 cdot 45,7}}{{12,3 cdot 0,457}})

Ответ

ОТВЕТ: 10.

Решение

(frac{{1,23 cdot 45,7}}{{12,3 cdot 0,457}} = frac{{123 cdot 457 cdot 10}}{{123 cdot 457}} = 10.)

Ответ: 10.
Задача 22. Найдите значение выражения   (3pleft( a right) — 6a + 7), если (pleft( a right) = 2a — 3)

Ответ

ОТВЕТ: — 2.

Решение

(3pleft( a right) — 6a + 7 = 3left( {2a — 3} right) — 6a + 7 = 6a — 9 — 6a + 7 =  — 2.)

Ответ: — 2.
Задача 23. Найдите значение выражения    (qleft( {b — 2} right) — qleft( {b + 2} right)),  если (qleft( b right) = 3b)

Ответ

ОТВЕТ: — 12.

Решение

(qleft( {b — 2} right) = 3left( {b — 2} right) = 3b — 6;,,,,,,,,,,,qleft( {b + 2} right) = 3left( {b + 2} right) = 3b + 6.)

(qleft( {b — 2} right) — qleft( {b + 2} right) = 3b — 6 — left( {3b + 6} right) = 3b — 6 — 3b — 6 =  — 12.)

Ответ: — 12.
Задача 24. Найдите значение выражения  (5left( {pleft( {2x} right) — 2pleft( {x + 5} right)} right)),  если (pleft( x right) = x — 10)

Ответ

ОТВЕТ: 0.

Решение

(pleft( {2x} right) = 2x — 10;,,,,,,,,,,,pleft( {x + 5} right) = x + 5 — 10 = x — 5.)

(5left( {pleft( {2x} right) — 2pleft( {x + 5} right)} right) = 5left( {2x — 10 — 2 cdot left( {x — 5} right)} right) = 5left( {2x — 10 — 2x + 10} right) = 5 cdot 0 = 0.)

Ответ: 0.
Задача 25. Найдите значение выражения   (pleft( {x — 7} right) + pleft( {13 — x} right)),  если  (pleft( x right) = 2x + 1)

Ответ

ОТВЕТ: 14.

Решение

(pleft( {x — 7} right) = 2left( {x — 7} right) + 1 = 2x — 14 + 1 = 2x — 13)

(pleft( {13 — x} right) = 2left( {13 — x} right) + 1 = 26 — 2x + 1 = 27 — 2x)

(pleft( {x — 7} right) + pleft( {13 — x} right) = 2x — 13 + 27 — 2x = 14.)

Ответ: 14.
Задача 26. Найдите значение выражения   (2pleft( {x — 7} right) — pleft( {2x} right)),  если  (pleft( x right) = x — 3)

Ответ

ОТВЕТ: — 17.

Решение

(pleft( {x — 7} right) = x — 7 — 3 = x — 10;,,,,,,,,,,,pleft( {2x} right) = 2x — 3.)

(2pleft( {x — 7} right) — pleft( {2x} right) = 2left( {x — 10} right) — left( {2x — 3} right) = 2x — 20 — 2x + 3 =  — 17.)

Ответ: — 17.
Задача 27. Найдите   (frac{{gleft( {2 — x} right)}}{{gleft( {2 + x} right)}}),   если   (gleft( x right) = sqrt[3]{{xleft( {4 — x} right)}})   при   (left| x right| ne 2)

Ответ

ОТВЕТ: 1.

Решение

(gleft( {2 — x} right) = sqrt[3]{{left( {2 — x} right)left( {4 — left( {2 — x} right)} right)}} = sqrt[3]{{left( {2 — x} right)left( {4 — 2 + x} right)}} = sqrt[3]{{left( {2 — x} right)left( {2 + x} right)}})

(gleft( {2 + x} right) = sqrt[3]{{left( {2 + x} right)left( {4 — left( {2 + x} right)} right)}} = sqrt[3]{{left( {2 + x} right)left( {4 — 2 — x} right)}} = sqrt[3]{{left( {2 + x} right)left( {2 — x} right)}})

(frac{{gleft( {2 — x} right)}}{{gleft( {2 + x} right)}} = frac{{sqrt[3]{{left( {2 — x} right)left( {2 + x} right)}}}}{{sqrt[3]{{left( {2 + x} right)left( {2 — x} right)}}}} = 1.)

Ответ: 1.
Задача 28. Найдите   (hleft( {5 + x} right) + hleft( {5 — x} right)),   если   (hleft( x right) = sqrt[3]{x} + sqrt[3]{{x — 10}})

Ответ

ОТВЕТ: 0.

Решение

(hleft( {5 + x} right) = sqrt[3]{{5 + x}} + sqrt[3]{{5 + x — 10}} = sqrt[3]{{5 + x}} + sqrt[3]{{x — 5}})

(hleft( {5 — x} right) = sqrt[3]{{5 — x}} + sqrt[3]{{5 — x — 10}} = sqrt[3]{{5 — x}} + sqrt[3]{{ — x — 5}})

(hleft( {5 + x} right) + hleft( {5 — x} right) = sqrt[3]{{5 + x}} + sqrt[3]{{x — 5}} + sqrt[3]{{ — left( {x — 5} right)}} + sqrt[3]{{ — left( {x + 5} right)}} = )

( = sqrt[3]{{5 + x}} + sqrt[3]{{x — 5}} — sqrt[3]{{x — 5}} — sqrt[3]{{x + 5}} = 0.)

Ответ: 0.
Задача 29. Найдите значение выражения    (frac{{gleft( {x — 9} right)}}{{gleft( {x — 11} right)}})    при  (gleft( x right) = {8^x})

Ответ

ОТВЕТ: 64.

Решение

(gleft( {x — 9} right) = {8^{x — 9}};,,,,,,,,,,,,gleft( {x — 11} right) = {8^{x — 11}})

(frac{{gleft( {x — 9} right)}}{{gleft( {x — 11} right)}} = frac{{{8^{x — 9}}}}{{{8^{x — 11}}}} = {8^{x — 9 — left( {x — 11} right)}} = {8^{x — 9 — x + 11}} = {8^2} = 64.)

Ответ: 64.
Задача 30. Найдите   (frac{{pleft( b right)}}{{pleft( {frac{1}{b}} right)}}),   если   (pleft( b right) = left( {b + frac{3}{b}} right)left( {3b + frac{1}{b}} right))   при  (b ne 0).

Ответ

ОТВЕТ: 1.

Решение

(pleft( {frac{1}{b}} right) = left( {frac{1}{b} + frac{3}{{frac{1}{b}}}} right)left( {3 cdot frac{1}{b} + frac{1}{{frac{1}{b}}}} right) = left( {frac{1}{b} + 3b} right)left( {frac{3}{b} + b} right))

(frac{{pleft( b right)}}{{pleft( {frac{1}{b}} right)}} = frac{{left( {b + frac{3}{b}} right)left( {3b + frac{1}{b}} right)}}{{left( {frac{1}{b} + 3b} right)left( {frac{3}{b} + b} right)}} = 1.)

Ответ: 1.
Задача 31. Найдите   (pleft( x right) + pleft( {6 — x} right)),   если (pleft( x right) = frac{{xleft( {6 — x} right)}}{{x — 3}})   при (x ne 3).

Ответ

ОТВЕТ: 0.

Решение

(pleft( {6 — x} right) = frac{{left( {6 — x} right)left( {6 — left( {6 — x} right)} right)}}{{6 — x — 3}} = frac{{left( {6 — x} right)left( {6 — 6 + x} right)}}{{3 — x}} = frac{{left( {6 — x} right) cdot x}}{{3 — x}}.)

(pleft( x right) + pleft( {6 — x} right) = frac{{xleft( {6 — x} right)}}{{x — 3}} + frac{{left( {6 — x} right) cdot x}}{{3 — x}} = frac{{xleft( {6 — x} right)}}{{x — 3}} — frac{{left( {6 — x} right)x}}{{x — 3}} = 0.)

Ответ: 0.

Источник

Задание 1015

Найдите значение выражения $$frac{(0.1)^{-1}-(0.1)^{0}}{(frac{3^{2}}{2^{3}})^{-1}*(frac{3}{2})^{3}-(frac{1}{3})^{-2}}$$

Ответ: -1.5

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$frac{(0.1)^{-1}-(0.1)^{0}}{(frac{3^{2}}{2^{3}})^{-1}*(frac{3}{2})^{3}-(frac{1}{3})^{-2}}=$$ $$=frac{10-1}{frac{2^{3}}{3^{2}}*frac{27}{8}-9}=frac{9}{frac{8}{9}*frac{27}{8}-9}=$$ $$frac{9}{3-9}=frac{9}{-6}=-1.5$$

Задание 1082

Най­ди­те зна­че­ние вы­ра­же­ния $$(frac{3}{4}+2frac{3}{8})*25,8$$

Ответ: 80,625

Задание 1083

Най­ди­те зна­че­ние вы­ра­же­ния $$(2frac{4}{7}-2,5):frac{1}{10}$$

Ответ: 5

Задание 1084

Най­ди­те зна­че­ние вы­ра­же­ния  $$(432^{2}-568^{2}):1000$$

Ответ: -136

Задание 1085

Най­ди­те зна­че­ние вы­ра­же­ния $$4frac{4}{9}:frac{4}{9}$$

Ответ: 10

Задание 1086

Най­ди­те зна­че­ние вы­ра­же­ния  $$frac{1,23*45,7}{12,3*0,457}$$

Ответ: 10

Задание 2366

Найдите $$f(x)$$, если $$f(x)=(x-frac{9}{x})cdot (frac{1}{x}-9x)$$, где $$xneq 0$$.

Ответ: 0

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Задание 3200

Коэффициент полезного действия некоторого двигателя определяется формулой $$eta=frac{T_{1}-T_{2}}{T_{1}}cdot 100$$%. При каком наименьшем значении температуры нагревателя Т1 КПД этого двигателя будет не меньше 70%, если температура холодильника Т2=90?

Ответ: 300

Скрыть

Больше разборов вы найдете на моем ютуб-канале! Не забудьте подписаться!


Скрыть

$$70=frac{T_{1}-90}{T_{1}}cdot100$$ $$frac{7}{10}=frac{T_{1}-90}{T_{1}}$$ $$Leftrightarrow$$ $$7T_{1}=10T_{1}-900$$ $$Leftrightarrow$$ $$900=3T_{1}$$ $$Leftrightarrow$$ $$T_{1}=300$$

Задание 3953

Най­ди­те зна­че­ние вы­ра­же­ния: $$frac{(11a)^{2}-11a}{11a^{2}-a}$$

Ответ: 11

Задание 3954

Най­ди­те зна­че­ние вы­ра­же­ния: $$frac{9x^{2}-4}{3x+2}-3x$$

Ответ: -2

Задание 3955

Най­ди­те зна­че­ние вы­ра­же­ния: $$(4a^{2}-9)cdot(frac{1}{2a-3}-frac{1}{2a+3})$$

Ответ: 6

Задание 3956

Най­ди­те $$frac{p(b)}{p(frac{1}{b})}$$, если $$p(b)=(b+frac{3}{b})(3b+frac{1}{b})$$ при $$bneq0$$

Ответ: 1

Задание 3957

Най­ди­те $$p(x)+p(6-x)$$, если $$p(x)=frac{x(6-x)}{x-3}$$ при $$xneq3$$

Ответ: 0

Задание 3958

Най­ди­те $$frac{a}{b}$$, если $$frac{2a+5b}{5a+2b}=1$$

Ответ: 1

Задание 3959

Най­ди­те $$61a-11b+50$$, если $$frac{2a-7b+5}{7a-2b+5}=9$$

Ответ: 10

Источник

06
Авг 2013

Категория: 06 ВычисленияРациональные выражения, уравнения и неравенства

06. Преобразование рациональных выражений

2013-08-06
2022-09-11

Преобразование числовых рациональных выражений

Задача 1. Найдите значение выражения 3frac{3}{5}:frac{1}{5}.

Решение: + показать


Задача 2. Найдите значение выражения  frac{30,9cdot 0,356}{3,09cdot 35,6}.

Решение: + показать


Задача 3. Найдите значение выражения (252^2-23^2):275.

Решение: + показать


Задача 4. Найдите значение выражения: (-2frac{1}{7}-2frac{1}{5})cdot 5,6.

Решение: + показать


Преобразование буквенных рациональных выражений

Задача 5. Найдите значение выражения (x^2+16y^2-(x+4y)^2):4xy.

Решение: + показать


Задача 6. Найдите значение выражения (x+2)(x-2)-x^2.

Решение: + показать


Задача 7. Найдите значение выражения (7axy-(-4xya)):11yax.

 Решение: + показать


Задача 8. Найдите значение выражения frac{(3x+y)^2-(3x-y)^2}{3xy}.

 Решение: + показать


Задача 9. Найдите значение выражения frac{9x^2-4}{3x+2}-3x.

 Решение: + показать


Задача 10. Найдите значение выражения frac{(17a)^2-17a}{17a^2-a}.

Решение: + показать


Задача 11. Найдите значение выражения frac{(7a^2)^3cdot (3b)^2}{(21a^3b)^2}.

Решение: + показать


Задача 12.Найдите значение выражения (25a^2-16)cdot (frac{1}{5a+4}-frac{1}{5a-4}).

Решение: + показать


Задача 13. Найдите frac{p(b)}{p(frac{1}{b})}, если p(b)=(b+frac{3}{b})(3b+frac{1}{b}) при bneq 0.

Решение: + показать


Задача 14. Найдите p(x)+p(8-x), если p(x)=frac{x(8-x)}{x-4}  при xneq 4.

Решение: + показать


Задача 15. Найдите frac{a}{b}, если frac{3a+6b}{3b+6a}=3.

Решение: + показать


Задача 16. Найдите frac{a+5b+18}{a+b+9}, если frac{a}{b}=3.

Решение: + показать


Задача 17. Найдите значение выражения  2x+y+6z, если 4x+y=5, 12z+y=7.

Решение: + показать


Задача 18. Найдите значение выражения  38a-26b-2, если frac{7a-9b+2}{9a-7b+2}=5.

Решение: + показать


тестВы можете пройти «Преобразования рациональных выражений».

Автор: egeMax |

комментариев 14

Источник

Система подготовки к ЕГЭ

Задание №9 профиль

Задание
№9 предполагает проверку умений вычислять и преобразовывать различные
математические выражения. Оно входит в первые 12 заданий с кратким вариантом
ответа, каждое из которых оценивается в 1 балл. Время выполнения задания 5 мин.
Проверяются знания и умения по следующим темам:

1.     
Преобразование
числовых рациональных выражений.

2.     
Преобразование
алгебраических выражений и дробей.

3.     
Преобразование
числовых иррациональных выражений .

4.     
Преобразование
буквенных иррациональных выражений.

5.     
Вычисление
значений степенных выражений.

6.     
Преобразование
тригонометрических выражений.

7.     
Преобразование
логарифмических выражений

Каждый
учащийся в свободном режиме до определенного дня прорешивает данные задания по
изученным темам из Открытого банка. В определенный день я даю диагностическую
работу, составленную из этих заданий по всем темам. Выявляю ошибки. Провожу
коррекцию индивидуально с каждым учащимся. Затем – контрольная работа и
выставление оценок в журнал.

Преобразование числовых рациональных
выражений

Образцы выполнения заданий:

1.

2.

3.

Задания для самостоятельного решения:

http://prof.mathege.ru/tasks/58023/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/56020/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/59025/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/59526/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/60027/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/60528/problem.png?cache=1546416440.6277893

Преобразование алгебраических выражений
и дробей

Образцы выполнения заданий:

1.

2.

3.

4.

5.

Задания для самостоятельного решения:

http://prof.mathege.ru/tasks/48922/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/49060/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/49117/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/49195/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/49174/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/49219/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/49389/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/49426/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/49483/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/49574/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/49665/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/49756/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/49847/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/50348/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/50399/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/50456/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/50505/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/50556/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/50607/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/57021/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/55019/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/57522/problem.png?cache=1546416208.1774557

Преобразование числовых
иррациональных выражений

Образцы выполнения заданий:

1.

2.

3.

Задания для самостоятельного решения:

http://prof.mathege.ru/tasks/43686/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/44187/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/44249/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/72716/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/44916/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/44957/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/45346/problem.png?cache=1546414440.8073316

Преобразование буквенных
иррациональных выражений

Основные формулы

Образцы выполнения заданий:

1.

2.

3.

4.

5.

Задания для самостоятельного решения:

http://prof.mathege.ru/tasks/50658/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/50997/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/51047/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/58524/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/45007/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/45069/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/51243/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/66611/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/51164/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/50709/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/51368/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/51435/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/51484/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/55520/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/68931/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/51699/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/69432/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/68430/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/51533/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/51584/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/65108/problem.png?cache=1546416440.6277893

Вычисление значений степенных
выражений

Основные формулы

Образцы выполнения заданий:

1.

2.

3.

http://prof.mathege.ru/tasks/66776/problem.png?cache=1546416440.6277893

4.

5.

Задания для самостоятельного решения:

http://prof.mathege.ru/tasks/67943/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/67442/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/66941/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/51332/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/51296/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/44431/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/44500/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/44589/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/44807/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/44863/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/45144/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/45195/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/61530/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/45265/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/54571/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/45416/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/63534/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/45543/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/48960/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/50183/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/50235/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/50760/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/51635/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/50839/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/51103/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/66110/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/50918/problem.png?cache=1546415764.916614

http://prof.mathege.ru/tasks/61029/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/64607/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/65609/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/50012/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/50067/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/50125/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/56520/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/62532/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/64035/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/62031/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/63033/problem.png?cache=1546416440.6277893

http://prof.mathege.ru/tasks/50290/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/49961/problem.png?cache=1546415495.938436

http://prof.mathege.ru/tasks/48981/problem.png?cache=1546415182.2370977

Преобразование тригонометрических
выражений

Образцы выполнения заданий:

1.

2.

3.

4.

5.

6.

Задания для самостоятельного решения:

http://prof.mathege.ru/tasks/45825/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/46225/problem.png?cache=1546414440.8073316

http://prof.mathege.ru/tasks/46412/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/46502/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/46551/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/46599/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/46735/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/46800/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/46865/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/46930/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/46987/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/47044/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/70434/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/47102/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/158632/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/47215/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/47272/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/47329/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/47386/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/47443/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/69933/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/70935/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/72817/problem.png?cache=1546416645.2025752http://prof.mathege.ru/tasks/72538/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/72898/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/73080/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/47499/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/47564/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/47637/problem.png?cache=1546414914.4701722

http://prof.mathege.ru/tasks/47683/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/47720/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/72979/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/48870/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/47763/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/47858/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/47929/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/48000/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/48075/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/48333/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/48204/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/48470/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/48533/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/48582/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/48631/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/48678/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/48740/problem.png?cache=1546415182.2370977

http://prof.mathege.ru/tasks/48805/problem.png?cache=1546415182.2370977

Преобразование логарифмических
выражений

Основные формулы

  ;  

;; 

Образцы выполнения заданий:

1.

2.

3.

4.

5.

6.

7.

Задания для самостоятельного решения:

http://prof.mathege.ru/tasks/51758/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/150083/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/52688/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/52808/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/52852/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/52896/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/52993/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/53037/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/53105/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/53181/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/53283/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/53303/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/53384/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/53441/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/53509/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/53600/problem.png?cache=1546415993.2683833

http://prof.mathege.ru/tasks/53652/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/53704/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/53761/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/53781/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/53854/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/53916/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/54012/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/54080/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/54157/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/54239/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/54292/problem.png?cache=1546416208.1774557

http://prof.mathege.ru/tasks/54377/problem.png?cache=1546416208.1774557

Образцы выполнения заданий:

1.

2.

Задания для самостоятельного решения:

http://prof.mathege.ru/tasks/71035/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/71536/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/72037/problem.png?cache=1546416645.2025752

http://prof.mathege.ru/tasks/72619/problem.png?cache=1546416645.2025752

Источник

ЕГЭ по математике Профиль. Задание 4: Уметь выполнять вычисления и преобразования. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».

ЕГЭ Профиль. Задание № 4

АЛГОРИТМ ВЫПОЛНЕНИЯ

Задание № 4 проверяет умение производить вычисления и преобразования рациональных, иррациональных, степенных, логарифмических и тригонометрических выражений. Задание состоит из числового или алгебраического выражения, значение которого необходимо найти, применяя математические преобразования. Ответом является целое число или конечная десятичная дробь.

План выполнения:

  1. Внимательно прочитайте условие задачи.
  2. Выполните преобразования.
  3. Найдите числовое значение выражения.
  4. Запишите полученное число в поле ответа КИМ и бланк ответов № 1.

Вычисление значений рациональных выражений

Задачи этого типа заключаются в вычислении значений рациональных, то есть дробных выражений. При подготовке необходимо повторить правила действий с дробями, формулы сокращённого умножения.

ЕГЭ по математике Профиль. Задание 4

Задача № 4 (1). Найдите значение выражения
ЕГЭ по математике Профиль. Задание 4

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 1.

Задача № 4 (2). Найдите (a + 9b + 16)/(a + 3b + 8), если a/b = 3.

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 2.

Вычисление значений иррациональных выражений

Задачи этого типа заключаются в вычислении значений иррациональных (содержащих корни) выражений. При подготовке следует повторить правила вычисления корней, свойства корней.

ЕГЭ по математике Профиль. Задание 4

Задача № 4 (3). Найдите значение выражения (3√5 • 6√5) : √5.

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 1.

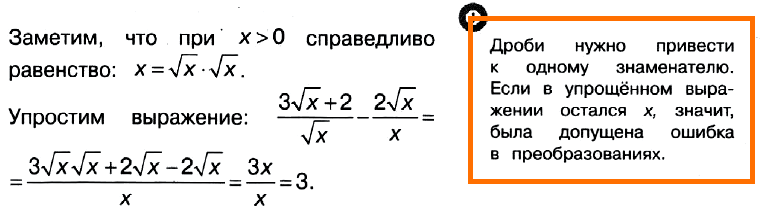
Задача № 4 (4). Найдите значение выражения (3√x + 2)/√x – 2√x/x при х > 0.

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 3.

Вычисление значений степенных выражений

Задачи этого типа заключаются в вычислении значений степенных выражений. При подготовке нужно повторить правила действий со степенями, правило возведения числа в степень.

ЕГЭ по математике Профиль. Задание 4

Задача № 4 (5). Найдите значение выражения 21,5 • 80,5.

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 8.

Задача № 4 (6). Найдите значение выражения (3 – 140,25)(3 + 140,25) : (9 + (70,5 – 21/2)2).

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 27.

Вычисление значений логарифмических выражений

Задачи этого типа заключаются в вычислении значений логарифмических выражений. При подготовке нужно повторить понятие логарифма, основные свойства логарифмов.

ЕГЭ по математике Профиль. Задание 4

Задача № 4 (7). Вычислите log1/2 4√2.

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: –0,25.

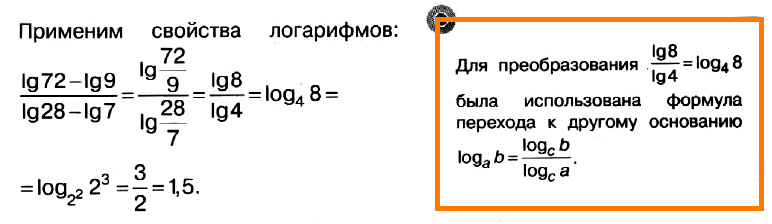
Задача № 4 (8). Найдите значение выражения (lg 72 – lg 9) : (lg 28 – lg 7).

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 1,5.

Вычисление значений тригонометрических выражений

Задачи этого типа заключаются в вычислении значений тригонометрических выражений. При подготовке необходимо повторить основное тригонометрическое тождество, знаки синуса, косинуса, тангенса, формулы приведения, формулы синуса и косинуса двойного аргумента, понятие периодичности тригонометрических функций и табличные значения тригонометрических функций основных углов.

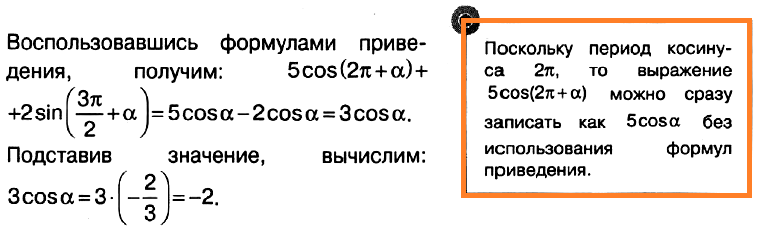
ЕГЭ по математике Профиль. Задание 4

Задача № 4 (9). Найдите значение выражения 5 cos (2π + α) + 2 sin (3π/2 + α), если cos α = –2/3.

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: –2.

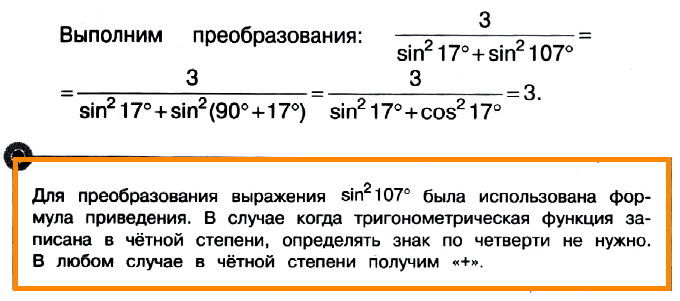
Задача № 4 (10). Найдите значение выражения 3/(sin2 17° + sin2 107°).

Решение:
ЕГЭ по математике Профиль. Задание 4

Ответ: 3.

Тренировочные задания с самопроверкой

№ 4.1. Найдите значение выражения 11√3 • tg (7π/6) • cos (4π/3).

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 4

№ 4.2. Найдите значение выражения (9 sin 59°) / (cos 31°).

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 4

№ 4.3. Найдите значение выражения ЕГЭ по математике Профиль. Задание 4

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 4

№ 4.4. Найдите значение выражения (3√x + 9)/√x – (9√x)/x – 3x + 12 при х = 6.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 4

№ 4.5. Найдите значение выражения 19а + b + 11, если (–14a + 14b + 7) : (a + 3b + 5) = 5.

Открыть ОТВЕТ

ЕГЭ по математике Профиль. Задание 4

Вы смотрели: ЕГЭ по математике Профиль. Задание 4: Уметь выполнять вычисления и преобразования. Материалы для подготовки к итоговой аттестации. Алгоритм выполнения задания. Примеры с объяснением выбора правильного ответа. Анализ типичных ошибок.

Вернуться к Оглавлению раздела «Анализ заданий ЕГЭ по математике».


Просмотров:
14 869

Источник

Лучшие репетиторы для сдачи ЕГЭ

Задания по теме «Числовые рациональные выражения»

Открытый банк заданий по теме числовые рациональные выражения. Задания B9 из ЕГЭ по математике (профильный уровень)

Геометрические фигуры в пространстве: нахождение длины, площади, объема

Задание №144

Тип задания: 9
Тема:
Числовые рациональные выражения

Условие

Найдите значение выражения 4frac27:frac37.

Показать решение

Решение

Выполним преобразования:

4frac27:frac37=frac{30}{7}cdotfrac73=10

Ответ

10

Задание №143

Тип задания: 9
Тема:
Числовые рациональные выражения

Условие

Найдите значение выражения frac{1,21cdot17,8}{12,1cdot1,78}.

Показать решение

Решение

Выполним преобразования, представив исходную дробь как произведение дробей.

frac{1,21cdot17,8}{12,1cdot1,78}= frac{1,21}{12,1}cdotfrac{17,8}{1,78}= frac{1,21}{1,21cdot10}cdotfrac{1,78cdot10}{1,78}= frac{1}{10}cdotfrac{10}{1}=1.

Ответ

1

Задание №142

Тип задания: 9
Тема:
Числовые рациональные выражения

Условие

Найдите значение выражения left ( 1frac56-1,2 right )cdot7frac12.

Показать решение

Решение

Выполним преобразования:

left ( 1frac56-1,2 right )cdot7frac12= left (frac{11}{6}-frac{12}{10} right )cdotfrac{15}{2}= frac{5cdot11-3cdot12}{30}cdotfrac{15}{2}= frac{55-36}{30}cdotfrac{15}{2}= frac{19}{30}cdotfrac{15}{2}= frac{19}{2}cdotfrac12= frac{19}{4}=4frac34=4,75.

Ответ

4,75

Задание №141

Тип задания: 9
Тема:
Числовые рациональные выражения

Условие

Найдите значение выражения frac{832^2-691^2}{1523}.

Показать решение

Решение

Используем формулу сокращенного умножения.

a^2-b^2=(a+b)(a-b)

Получим:

frac{832^2-691^2}{1523}= frac{(832-691)(832+691)}{1523}= frac{141cdot1523}{1523}=141

Ответ

141

Лучшие репетиторы для сдачи ЕГЭ

Сложно со сдачей ЕГЭ?

Звоните, и подберем для вас репетитора: 78007750928

Источник

Есть в Профильном ЕГЭ по математике, и даже в первой его части, такие задачи, для решения которых нужно знать ВСЁ. То есть всю школьную программу алгебры, с 5 класса до 11. Или почти всю.

Например, задание №6 Профильного ЕГЭ по математике – вычисления и преобразования. Вам могут встретиться и совсем простые задачи (на сложение дробей), и задания, которые не решить без подготовки. Например, вычисление и преобразование иррациональных выражений, тригонометрических, логарифмических. Задачи на определение модуля и понятие функции. В общем, типов задач здесь множество, по всему курсу алгебры.

И помните, что в ответе в заданиях первой части Профильного ЕГЭ по математике у вас должны получаться целые числа или конечные десятичные дроби.

Дробно-рациональные выражения. Формулы сокращенного умножения

Темы для повторения: Формулы сокращенного умножения, Приемы быстрого счета

Если вам встретится такое задание на ЕГЭ – значит, повезло!

1. Найдите значение выражения frac{2,88cdot 44,5}{0,288cdot 4,45}.

Не спешите перемножать десятичные дроби. Посмотрите на задачу внимательно.

frac{2,88cdot 44,5}{0,288cdot 4,45}=frac{2,88cdot 44,5}{2,88cdot 0,445}=frac{44,5}{0,445}=100.

Первый множитель в знаменателе умножили на 10, а второй поделили на 10, просто передвинув запятую.

Ответ: 100.

2. Найдите значение выражения 7frac{9}{13}:frac{5}{13}.

7frac{9}{13}:frac{5}{13}=frac{100}{13}cdot frac{13}{5}=20.

Ответ: 20.

Корни и степени. Иррациональные выражения

Темы для повторения: Арифметический квадратный корень.

Арифметический квадратный корень из числа a — это такое неотрицательное число, квадрат которого равен a.

left ( sqrt{a} right )^{2}=a;;sqrt{a}geq 0;;ageq 0 .

3. Вычислите sqrt{12+4sqrt{5}}cdot sqrt{12-4sqrt{5}} .

sqrt{12+4sqrt{5}}cdot sqrt{12-4sqrt{5}}=sqrt{left ( 12+4sqrt{5} right )left ( 12-4sqrt{5} right )}=

=sqrt{144-80}=sqrt{64}=8.

Применили одну из формул сокращенного умножения.

Ответ: 8.

4. Вычислите:
left ( sqrt{28}-sqrt{12} right )cdot sqrt{10+sqrt{84}}.

Упростим множители:

sqrt{28}-sqrt{12}=sqrt{4cdot 7}-sqrt{3cdot 4}=2left ( sqrt{7}-sqrt{3} right );

sqrt{84}=sqrt{3cdot 7cdot 4}=2sqrt{3cdot 7};

left ( sqrt{28}-sqrt{12} right )cdot sqrt{10+sqrt{84}}=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{10+2sqrt{3cdot 7}}=

=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7} right )^{2}+2sqrt{3}cdot sqrt{7}+left ( sqrt{3} right )^{2}}=

=2left ( sqrt{7}-sqrt{3} right )cdot sqrt{left ( sqrt{7}+sqrt{3}right )^{2}}=2left ( sqrt{7}-sqrt{3} right )left ( sqrt{7}+sqrt{3} right )=

=2cdot left ( 7-3 right )=8.

Ответ: 8.

Действия со степенями

Темы для повторения:
Вспомним правила действий со степенями.

a^{m}cdot a^{n}=a^{m+n}.

frac{a^{m}}{a^{n}}=a^{m-n}.

left ( a^{m} right )^{n}=left ( a^{n} right )^{m}=a^{mn}.

a^{n}b^{n}=left ( ab right )^{n}.

frac{a^{n}}{b^{n}}=left ( frac{a}{b} right )^{n}.

5. Найдите значение выражения: frac{a^{8,9}}{a^{4,9}} при a=4.

frac{a^{8,9}}{a^{4,9}}=a^{8,9-4,9}=a^{4}=4^{4}=256.

Применили формулу частного степеней frac{a^{m}}{a^{n}}=a^{m-n}.

Ответ: 256.

6. Вычислите left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}.

left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{sqrt[12]{2}} right )^{2}=left ( frac{2^{frac{1}{3}}cdot 2^{frac{1}{4}}}{2^{frac{1}{12}}} right )^{2}=left ( 2^{frac{1}{3}+frac{1}{4}-frac{1}{12}} right )^{2}=left ( 2^{frac{4}{12}+frac{3}{12}-frac{1}{12}} right )^{2}=

=left (2^{frac{1}{2}} right )^{2}=2.

Ответ: 2.

7. Вычислите frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}, если m=3,7.

Спокойно, не пугаемся. И конечно, не спешим подставлять значение m=3,7. Сначала упростим выражение.

frac{5left ( m^{6} right )^{5}+13left ( m^{10} right )^{3}}{left ( 2m^{15} right )^{2}}=frac{5m^{30}+13m^{30}}{4m^{30}}=frac{18m^{30}}{4m^{30}}=4,5.

Ответ: 4,5.

8. Вычислите 0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}.

0,75^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 12^{frac{7}{8}}=left ( frac{3}{4} right )^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot left ( 3cdot 4 right )^{frac{7}{8}}=frac{3^{frac{1}{8}}cdot 4^{frac{1}{4}}cdot 3^{frac{7}{8}}cdot 4^{frac{7}{8}}}{4^{frac{1}{8}}}=3cdot 4=12.

Применили формулу для произведения степеней: a^{m}cdot a^{n}=a^{m+n}.

Ответ: 12.

9. Вычислите frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}.

frac{sqrt[28]{3}cdot 3cdot sqrt[21]{3}}{sqrt[12]{3}}=frac{3^{frac{1}{28}}cdot 3cdot 3^{frac{1}{21}}}{3^{frac{1}{12}}}=3^{frac{1}{28}+1+frac{1}{21}-frac{1}{12}}=3^{frac{3}{84}+1+frac{4}{84}-frac{7}{84}}=3.

Записали корни в виде степеней (это удобно!) и применили формулу произведения степеней.

Ответ: 3.

Логарифмические выражения

Темы для повторения:
Логарифмы

Логарифм положительного числа b по основанию a — это показатель степени, в которую надо возвести a, чтобы получить b.

log _{a}b=cLeftrightarrow a^{c}=b.

При этом b> 0, a > 0, aneq 1.

Основные логарифмические формулы:

Основное логарифмическое тождество: boldsymbol{log _{a}a^{c}=c, ; a^{log _{a}b}=b}.

Логарифм произведения равен сумме логарифмов: boldsymbol{log _{a}left ( bc right )=log _{a}b+log _{a}c}.

Логарифм частного равен разности логарифмов: boldsymbol{log _{a}left ( frac{b}{c} right )=log _{a}b-log _{a}c}.

Формула для логарифма степени: boldsymbol{log _{a}b^{m}=mlog_{a}b}.

Формула перехода к новому основанию: boldsymbol{log _{a}b=frac{1}{log _{b}a},; log _{a}b=frac{log _{c}b}{log _{c}a}}.

10. Вычислите: log _{5}7cdot log _{7}25.

log _{5}7cdot log _{7}25=log _{5}7cdot log _{7}5^{2}=2log _{5}7cdot log _{7}5=2.

Снова формула перехода к другому основанию.

log _{a}b=frac{1}{log _{b}a}, поэтому
log _{a}bcdot log _{b};a=1.

11. Найдите log _{a}frac{a^{6}}{b^{4}}, если log _{a}b=-2.

log _{a}frac{a^{6}}{b^{4}}=log _{a}a^{6}-log _{a}b^{6}=6-4log _{a}b=6-4cdot left ( -2 right )=6+8=14.

12. Найдите значение выражения frac{log _{2}80}{3+log _{2}10}.

frac{log _{2}80}{3+log _{2}10}=frac{log _{2}left (8cdot 10 right )}{3+log _{2}10}=frac{log _{2}8+log _{2}10}{3+log _{2}10}=frac{3+log _{2}10}{3+log _{2}10}=1.

13. Найдите значение выражения frac{log _{9}sqrt[10]{8}}{log _{9}8}.

frac{log _{9}sqrt[10]{8}}{log _{9}8}=frac{log _{9}8^{frac{1}{10}}}{log _{9}8}=frac{1}{10}=0,1.

14. Найдите значение выражения left ( 1-log _{3}18 right )left ( log _{6}54 -1right ).

left ( 1-log _{3}18 right )left ( log _{6}54 -1right )=-left ( log _{3}18-log _{3}3 right )cdot left ( log _{6}54-log _{6}6 right )=-log _{3}6cdot log _{6}9=-2log _{3}6cdot log _{6}3=-2.

Тригонометрия. Формулы тригонометрии и формулы приведения

Темы для повторения:
Тригонометрический круг.
Формулы тригонометрии.
Формулы приведения.

15. Вычислите: 44sqrt{3}tgleft ( -480^{circ} right ).

44sqrt{3}tgleft ( -480^{circ} right )=44sqrt{3}cdot frac{sin left ( -480^{circ} right )}{cos left ( -480^{circ} right )}=-44sqrt{3}cdot frac{sin 480^{circ}}{cos 480^{circ}}=-44sqrt{3}cdot frac{sin 120^{circ}}{cos 120^{circ}}=-44sqrt{3}cdot frac{sqrt{3}}{2}:left ( -frac{1}{2} right )=132.

16. Найдите 3cos alpha, если sin alpha =-frac{2sqrt{2}}{3} и alpha in left ( frac{3pi }{2};;2pi right ).

cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{2sqrt{2}}{3} right )^{2}=1-frac{8}{9}=frac{1}{9}.

Т.к. alpha in left ( frac{3pi }{2};;2pi right ), то cos alpha =frac{1}{3}.
3cos alpha =3cdot frac{1}{3}=1.

17. Найдите tgalpha, если sin alpha =-frac{1}{sqrt{5}} и alpha in left ( 1,5pi ;;2pi right ).

cos ^{2}alpha =1-sin ^{2}alpha =1-left ( -frac{1}{sqrt{5}} right )^{2}=1-frac{1}{5}=frac{4}{5}.

Т.к. alpha in left ( 1,5pi ;;2pi right ), то
cos alpha =frac{2}{sqrt{5}}.

tgalpha =frac{sin alpha }{cos alpha }=-frac{1}{sqrt{5}}:frac{2}{sqrt{5}}=-2.

18. Найдите значение выражения: frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}.

frac{13sin 152^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{13cdot 2sin 76^{circ}cdot cos 76^{circ}}{cos 76^{circ}cdot cos 14^{circ}}=frac{26sin 76^{circ}}{cos 14^{circ}}=frac{26sin left ( 90^{circ}-14^{circ} right )}{cos 14^{circ}}=

=frac{26cos 14^{circ}}{cos 14^{circ}}=26.

Применили формулу приведения.

19. Упростите выражение: frac{3cos(pi - beta)+sin(frac{pi}{2}+beta)}{cos(beta+3pi)}.

frac{3cos left ( pi -beta right )+sin left ( frac{pi }{2}+beta right )}{cos left ( beta +3pi right )}=frac{-3cos beta +cos beta }{-cos beta }=frac{-2cos beta }{-cos beta }=2.

Применили формулу приведения.

20. Найдите 2cos 2alpha, если sin alpha =-0,7..

2cos 2alpha =2left ( 1-2sin ^{2}alpha right )=2-4sin ^{2}alpha =2-4cdot left ( -0,7 right )^{2}=0,04.

21. Вычислите frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }, если tgalpha =0,3.

frac{1-cos 2alpha +sin 2alpha }{1+cos 2alpha +sin 2alpha }=frac{1-cos ^{2}alpha +sin ^{2}alpha +2sin alpha cos alpha }{1+cos ^{2}alpha -sin ^{2}alpha +2sin alpha cos alpha }=

=frac{2sin ^{2}alpha +2sin alpha cos alpha }{2cos ^{2}alpha +2sin alpha cos alpha }=frac{sin alpha left ( sin alpha +cos alpha right )}{cos alpha left ( cos alpha +sin alpha right )}=frac{sin alpha }{cos alpha }=tgalpha =0,3.

Алгебраические выражения, корни, степени и логарифмы. И еще тригонометрия. Это всё, что может встретиться в задании 6 Профильного ЕГЭ по математике?

Оказывается, и это не всё! Еще нужно знать, что такое модуль. И как найти sqrt{a^{2}}.

Другие типы заданий

Темы для повторения:
Модуль числа.
Что такое функция.

22. Найдите значение выражения
sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}} при 2leq aleq 4.

Запомним: sqrt{a^{2}}=left | a right |.

sqrt{left ( a-2 right )^{2}}+sqrt{left ( a-4 right )^{2}}=left | a-2 right |+left | a-4 right |.

Если 2leq aleq 4, то a-2geq 0 и left | a-2 right |=a-2.

При этом a-4leq 0 и left | a-4 right |=4-a.

При 2leq aleq 4 получаем: left | a-2 right |+left | a-4 right |=a-2+4-a=2.

Ответ: 2.

23. Найдите значение выражения

x+sqrt{x^{2}-24x+144} при xleq 12.

При xleq 12 получим:

x+sqrt{x^{2}-24x+144}=x+sqrt{left ( x-12 right )^{2}}=x+left | x-12 right |=x+12-x=12.

Ответ: 12.

24. Найдите frac{gleft ( 5-x right )}{gleft ( 5+x right )}, если gleft ( x right )=sqrt[9]{xleft ( 10-x right )}, при left | x right |neq 5.

Что такое gleft ( x right )? Это функция, каждому числу ставящая в соответствие число sqrt[9]{xleft ( 10-x right )}. Например, gleft ( 0 right )=0;

gleft ( 1 right )=sqrt[9]{1cdot left ( 10-1 right )}=sqrt[9]{9}.

Тогда:

gleft ( 5-x right )=sqrt[9]{left ( 5-x right )left ( 10-5+x right )}=sqrt[9]{left ( 5-x right )left ( 5+x right )};

gleft ( 5+x right )=sqrt[9]{left ( 5+x right )left ( 10-5-x right )}=sqrt[9]{left ( 5+x right )left ( 5-x right )}.

Заметим, что gleft ( 5-x right )=gleft ( 5+x right ).

Значит, при left | x right |neq 5.
frac{gleft ( 5-x right )}{gleft ( 5+x right )}=1.

25. Найдите frac{pleft ( b right )}{pleft ( frac{1}{b} right )}, если pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right ), при bneq 0.

pleft ( b right )=left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right ) — функция, каждому числу b ставящая в соответствии число
left ( b-frac{9}{b} right )left ( -9b+frac{1}{b} right ).

Тогда при bneq 0.

pleft ( frac{1}{b} right )=left ( frac{1}{b}-9b right )left ( -frac{9}{b} +bright )=left ( b-frac{9}{b} right )left (-9b +frac{1}{b} right )=pleft ( b right ), и значение выражения frac{pleft ( b right )}{pleft ( frac{1}{b} right )} равно 1.

Благодарим за то, что пользуйтесь нашими публикациями.
Информация на странице «Задание 6 ЕГЭ по математике. Вычисления и преобразования» подготовлена нашими редакторами специально, чтобы помочь вам в освоении предмета и подготовке к экзаменам.
Чтобы успешно сдать нужные и поступить в ВУЗ или колледж нужно использовать все инструменты: учеба, контрольные, олимпиады, онлайн-лекции, видеоуроки, сборники заданий.
Также вы можете воспользоваться другими материалами из разделов нашего сайта.

Публикация обновлена:
09.03.2023

Источник

Понравилась статья? Поделить с друзьями:
  • Рациональное экономическое поведение производителя план егэ
  • Рациональное экономическое поведение егэ обществознание тест
  • Рациональное экономическое поведение егэ обществознание теория
  • Рациональное экономическое поведение егэ обществознание презентация
  • Рациональное природопользование экзамен